Definite Integrals Questions and Answers

Calculus
Definite IntegralsFind f'(x) and find the value(s) of x where the tangent line is horizontal.
f(x)=x6(x-13)7
f'(x) =
Select the correct choice below and, if necessary, fill in the answer box within your choice.
A. The tangent line is horizontal at x =
(Use a comma to separate answers as needed.)
B. The tangent line is never horizontal.

Calculus
Definite IntegralsFind the area of the region bounded by the x-axis and the graph of the function.
f(x)= = x/(6 + x²)^2

Calculus
Definite IntegralsFind the area of the region under the curve y = f(x) over the indicated interval.
f(x) = 4 (x + 5)^3 X 20

Calculus
Definite IntegralsFind the amount of a continuous money flow in which 1500 per year is being invested at 5.5%, compounded continuously for 40 years. Round the answer to the nearest cent.
A. $218,864.00
B. $246,136.73
C. $1,203,752.02
D. $273,409.46


Calculus
Definite IntegralsFind the accumulated future value of the continuous income stream at rate R(t), for the given time T, and interest rate k, compounded continuously.
R(t) = $500,000, T = 17 years, k=6%

Calculus
Definite IntegralsFind the accumulated present value of the following continuous income stream at rate R(t), for the given time T and interest rate k, compounded continuously.
R(t) = 0.04t+100, T=10, k= 4%

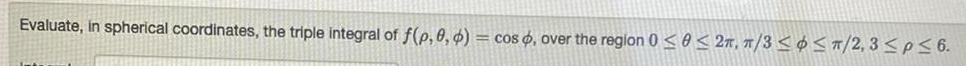
Calculus
Definite IntegralsEvaluate, in spherical coordinates, the triple integral of f(ρ, θ, Φ) = cos , over the region 0 ≤ θ ≤ 2π, π/3 ≤ Φ ≤ π/2,3 ≤ ρ,≤ 6.
![Factor the polynomial completely. [Hint: Do not use space in your answer.]
m³ - 125](https://media.kunduz.com/media/sug-question/raw/84422528-1657985213.2438097.jpeg?w=256)
Calculus
Definite IntegralsFactor the polynomial completely. [Hint: Do not use space in your answer.]
m³ - 125

Calculus
Definite IntegralsEvaluate the integral sinx from 0 to pi/2 by 1) using trapezoidal rule 2) Simpson rule Using 11 ordinates. Also estimate the errors by finding the value of the integral
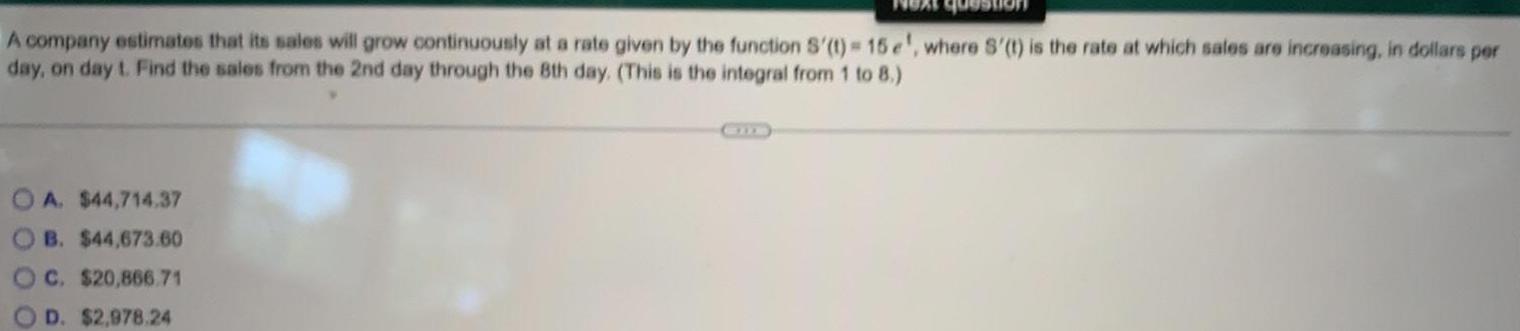
Calculus
Definite IntegralsA company estimates that its sales will grow continuously at a rate given by the function S'(t) = 15 e', where S'(t) is the rate at which sales are increasing, in dollars per day, on day t. Find the sales from the 2nd day through the 8th day. (This is the integral from 1 to 8.)
A. $44,714.37
B. $44,673.60
C. $20,866.71
D. $2,978.24

Calculus
Definite IntegralsFind the area bounded by the given curves. Round to two decimal places.
x=0, x= -2₁ y=e^x, y=0
A. 0.96
B. 0.86
C. 0.68
D. 0.78

![Approximate the area under the graph of f(x) = 0.05x^4 -3.61x² +95 over the interval [5,9] by dividing the interval into 4 subintervals.](https://media.kunduz.com/media/sug-question/raw/84344435-1657739072.1871128.jpeg?w=256)
Calculus
Definite IntegralsApproximate the area under the graph of f(x) = 0.05x^4 -3.61x² +95 over the interval [5,9] by dividing the interval into 4 subintervals.
![Find the area under the graph of f over the interval [1,9].
f(x)= 8x +9, for x ≤3
48 - 5/2x, for x>3](https://media.kunduz.com/media/sug-question/raw/84344310-1657738952.8400447.jpeg?w=256)
Calculus
Definite IntegralsFind the area under the graph of f over the interval [1,9].
f(x)= 8x +9, for x ≤3
48 - 5/2x, for x>3

Calculus
Definite IntegralsA company determined that the marginal cost, C'(x) of producing the xth unit of a product is given by C'(x)=x4-2x. Find the total cost function C, assuming that C(x) is in dollars and that fixed costs are $4000.
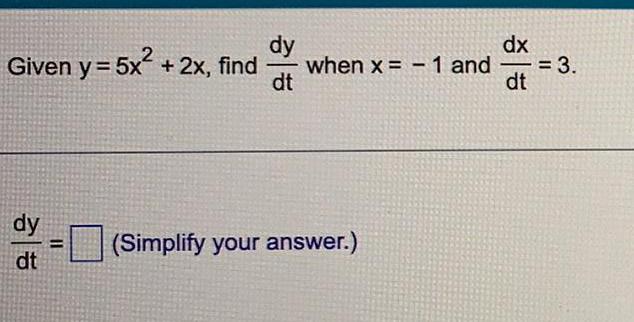

Calculus
Definite IntegralsSin t and cost are given. Use identities to find the indicated value. Where necessary, rationalize
denominators.
sin t =2/7, cos t = -3√5/7. Find tan t.

Calculus
Definite IntegralsLet C be the curve of intersection of the parabolic cylinder x² = 2y, and the surface 3z = xy. Find the exact length of C from the origin to the point (5, 25/2 125/6)
![Find the two x-intercepts of f(x)=√x and show that f'(x) = 0 at some point between the two x-intercepts. Determine whether Rolle's Theorem can be applied to f on the closed interval [0, 8]. If Rolle's Theorem can be applied, find all values of c in the open interval (0, 8) such that f'(c) = 0.](https://media.kunduz.com/media/sug-question/raw/84302515-1657650536.7093782.jpeg?w=256)
Calculus
Definite IntegralsFind the two x-intercepts of f(x)=√x and show that f'(x) = 0 at some point between the two x-intercepts. Determine whether Rolle's Theorem can be applied to f on the closed interval [0, 8]. If Rolle's Theorem can be applied, find all values of c in the open interval (0, 8) such that f'(c) = 0.
![d the area (in square units) of the region under the graph of the function f on the interval [-1, 2].
f(x) = -x² + 5
2
square units](https://media.kunduz.com/media/sug-question/raw/84266928-1657635256.3688507.jpeg?w=256)
Calculus
Definite Integralsd the area (in square units) of the region under the graph of the function f on the interval [-1, 2].
f(x) = -x² + 5
2
square units
![Find the area (in square units) of the region under the graph of the function f on the interval [1, 2], using the Fundamental
Theorem of Calculus. Then verify your result using geometry.
f(x)
-
1
-x+1
2
square units](https://media.kunduz.com/media/sug-question/raw/84266922-1657635240.7438684.jpeg?w=256)
Calculus
Definite IntegralsFind the area (in square units) of the region under the graph of the function f on the interval [1, 2], using the Fundamental
Theorem of Calculus. Then verify your result using geometry.
f(x)
-
1
-x+1
2
square units
![Find the area of the region under the graph of the function f on the interval [1¹, 5].
f(x) = 4x³
square units](https://media.kunduz.com/media/sug-question/raw/84266933-1657635160.3237689.jpeg?w=256)
Calculus
Definite IntegralsFind the area of the region under the graph of the function f on the interval [1¹, 5].
f(x) = 4x³
square units

Calculus
Definite IntegralsFind the area between the curves y = e^ -0.1x and y = 1.2x + 1 from x= 0 to x = 5.

Calculus
Definite IntegralsFind c > 0 such that the area of the region enclosed by the parabolas y = x² - c²and y=-c²-x² is 300.

Calculus
Definite IntegralsWhich statement is true?
There are many derivatives of a function g(x).
There is only one anti-derivative, f(x), for a function g(x).
There are many anti-derivatives, f(x), of a function g(x).
There are only two anti-derivative f(x), for a function g(x).

Calculus
Definite IntegralsAn object with an initial velocity of v(0) = 3 has an acceleration of a(t) = 5 + 6t.
What is its velocity at t = 5?
35
97
100
103
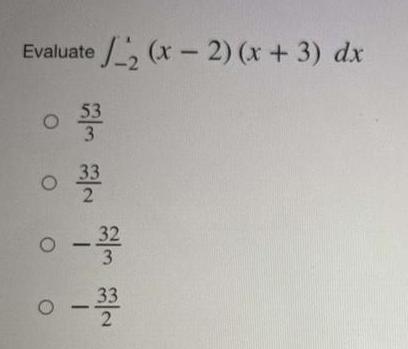
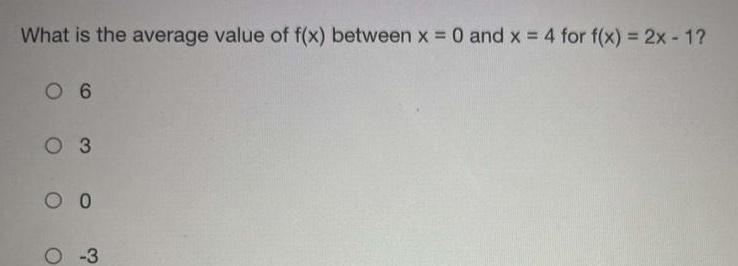
Calculus
Definite IntegralsWhat is the average value of f(x) between x = 0 and x = 4 for f(x) = 2x - 1?
A. 6
B. 3
C. 0
D. -3

Calculus
Definite IntegralsAn object is moving along a horizontal line such that it's velocity is v(t) = 3/(3t+4)
What is the object's displacement between t = 0 and t = 5?
A. 1.558
B. 1.944
C. 2.558
D. 2.944
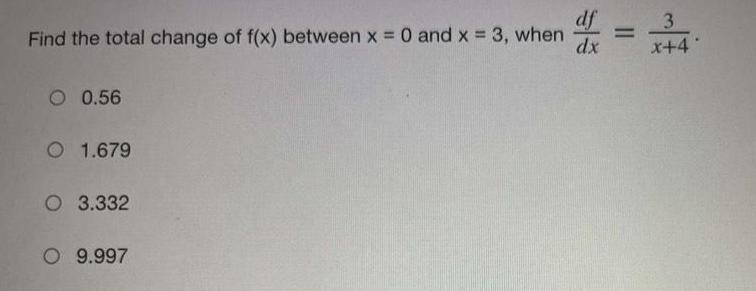
Calculus
Definite IntegralsFind the total change of f(x) between x = 0 and x = 3, when df/dx = 3/x+4
A. 0.56
B. 1.679
C. 3.332
D. 9.997
![What is the total change of f(x), if f'(x) = 3x + 1, over the interval [1, 5]?
A. -40
B. 40
C. 42.5
D. 45](https://media.kunduz.com/media/sug-question/raw/84170740-1657371268.9012835.jpeg?w=256)
Calculus
Definite IntegralsWhat is the total change of f(x), if f'(x) = 3x + 1, over the interval [1, 5]?
A. -40
B. 40
C. 42.5
D. 45
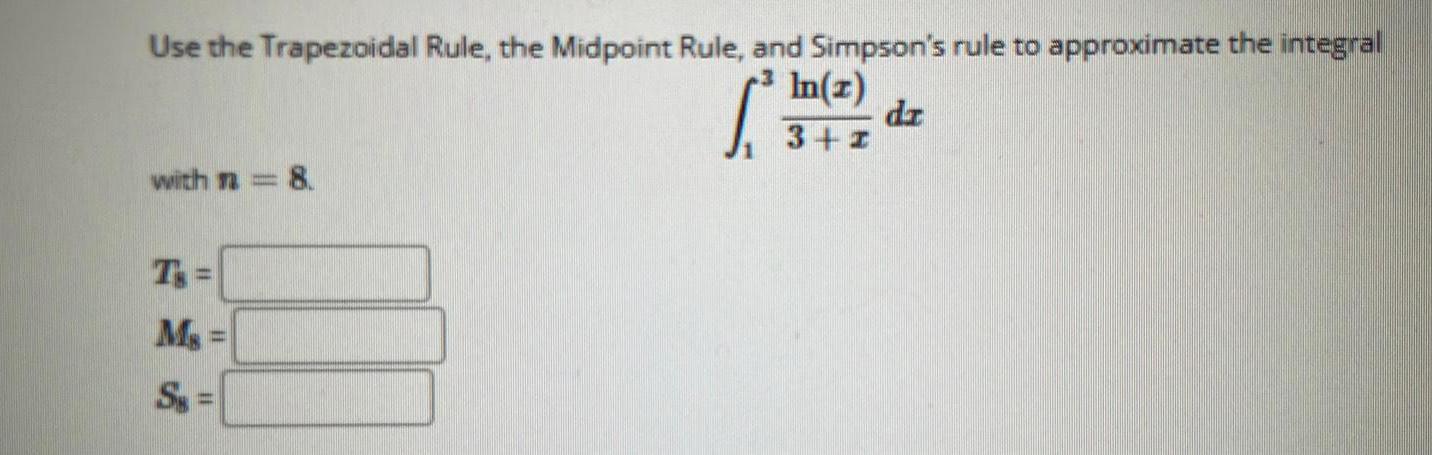
Calculus
Definite IntegralsUse the Trapezoidal Rule, the Midpoint Rule, and Simpson's rule to approximate the integral
₁∫³ ln(x)/3+x dx
with n = 8.

Calculus
Definite IntegralsIf 0<k<π/2 and the area under the curve y=cosx from x=k to x=π/2 is 0.1, then k=
(A) 1.471
(B) 1.414
(C) 1.277
(D) 1.120
(E) 0.436
Calculus
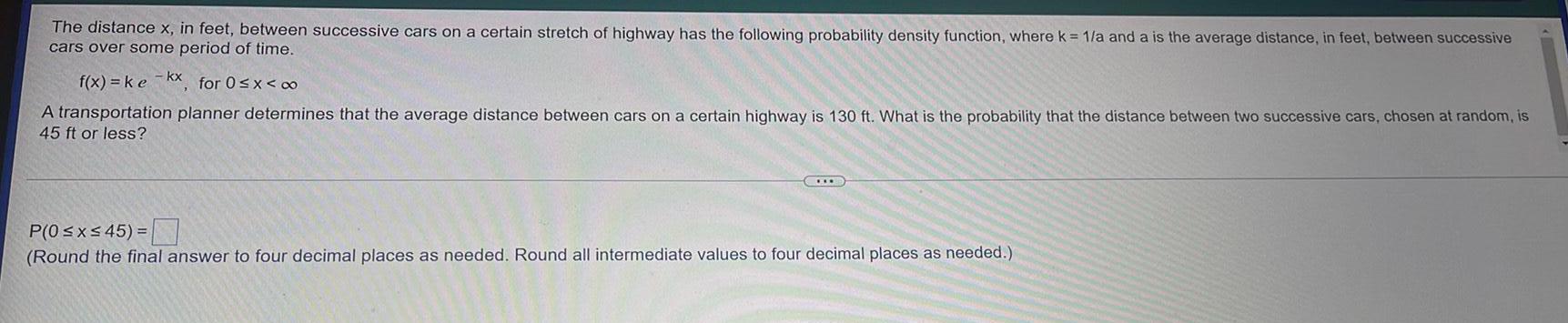
Definite IntegralsThe distance x, in feet, between successive cars on a certain stretch of highway has the following probability density function, where k = 1/a and a is the average distance, in feet, between successive
cars over some period of time.
f(x)=ke-kx, for 0 ≤ x <∞
A transportation planner determines that the average distance between cars on a certain highway is 130 ft. What is the probability that the distance between two successive cars, chosen at random, is
45 ft or less?
P(0≤x≤45)=
(Round the final answer to four decimal places as needed. Round all intermediate values to four decimal places as needed.)

Calculus
Definite Integrals*4. Use the comparison theorem for improper integrals to prove that
S
verges.
sin r
1³
Hint: Use your answer from question 3(a) combined with the fact that sin r ≤ 1.
de con-
![2. Using the disk method, find the volume of the solid of revolution formed by revolving
and the z-axis over the interval [1, 2] around the x-axis.
1
the region bounded y =
√x(3-x)
Use graphing software or a graphing calculator to help see the situation.](https://media.kunduz.com/media/sug-question/raw/84211669-1656959984.6697052.jpeg?w=256)
Calculus
Definite Integrals2. Using the disk method, find the volume of the solid of revolution formed by revolving
and the z-axis over the interval [1, 2] around the x-axis.
1
the region bounded y =
√x(3-x)
Use graphing software or a graphing calculator to help see the situation.