Definite Integrals Questions and Answers
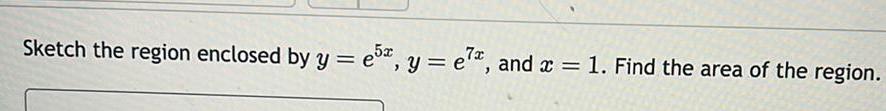
Calculus
Definite IntegralsSketch the region enclosed by y e5 y e7 and x 1 Find the area of the region

Calculus
Definite IntegralsFind the volume of the solid generated by rotating the region bounded by y sin x and y 0 2 between 0 and about the x axis
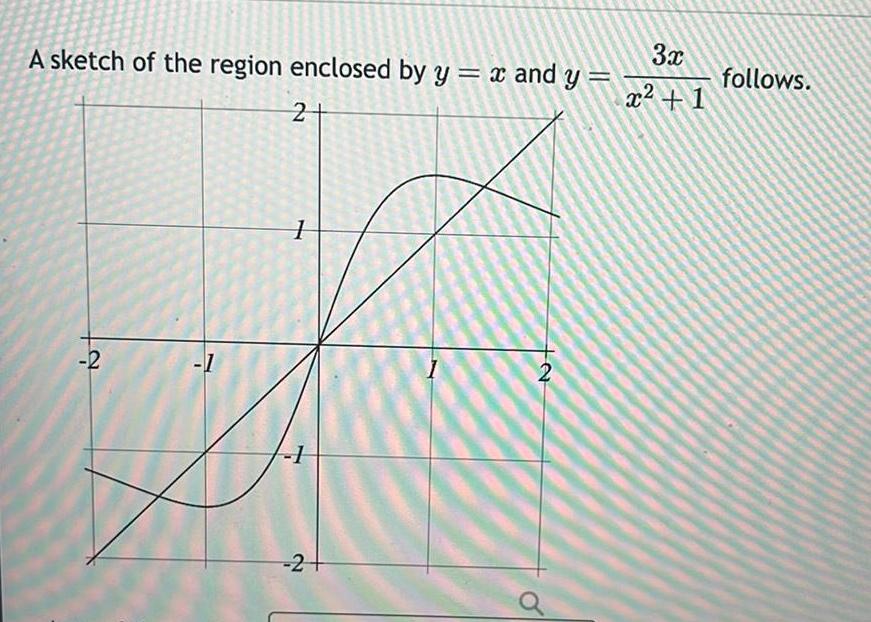
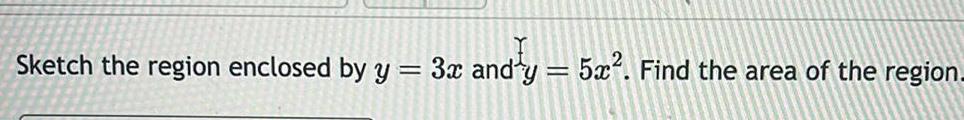
Calculus
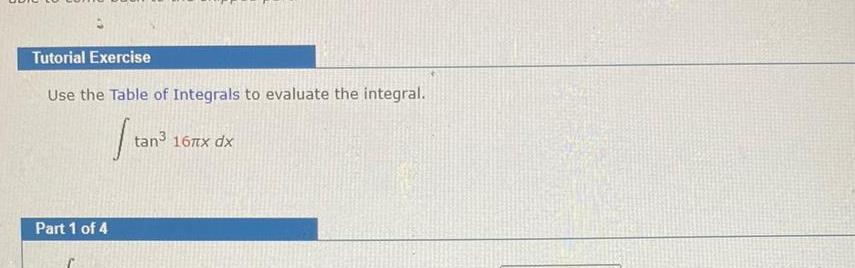
Definite IntegralsTutorial Exercise Use the Table of Integrals to evaluate the integral Stan Part 1 of 4 tan 16 x dx
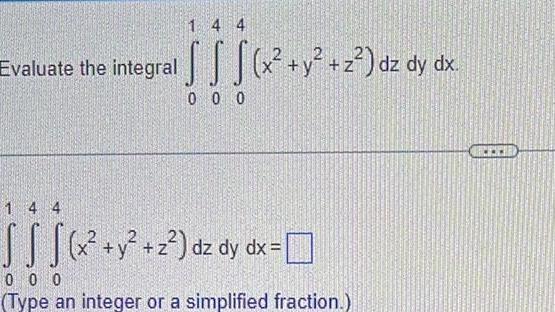
Calculus
Definite Integrals14 4 Evaluate the integral S x y z dz dy dx SS 0 0 0 SS S x y z dz dy dx 000 Type an integer or a simplified fraction
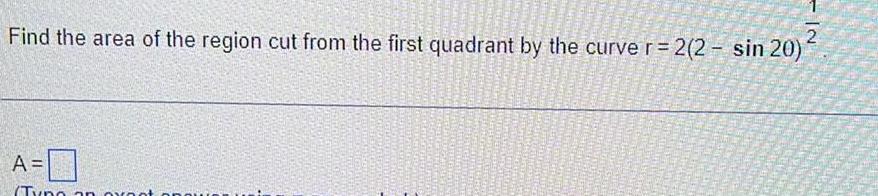
Calculus
Definite Integrals2 Find the area of the region cut from the first quadrant by the curve r 2 2 sin 20 A 0 Typo an oxnot
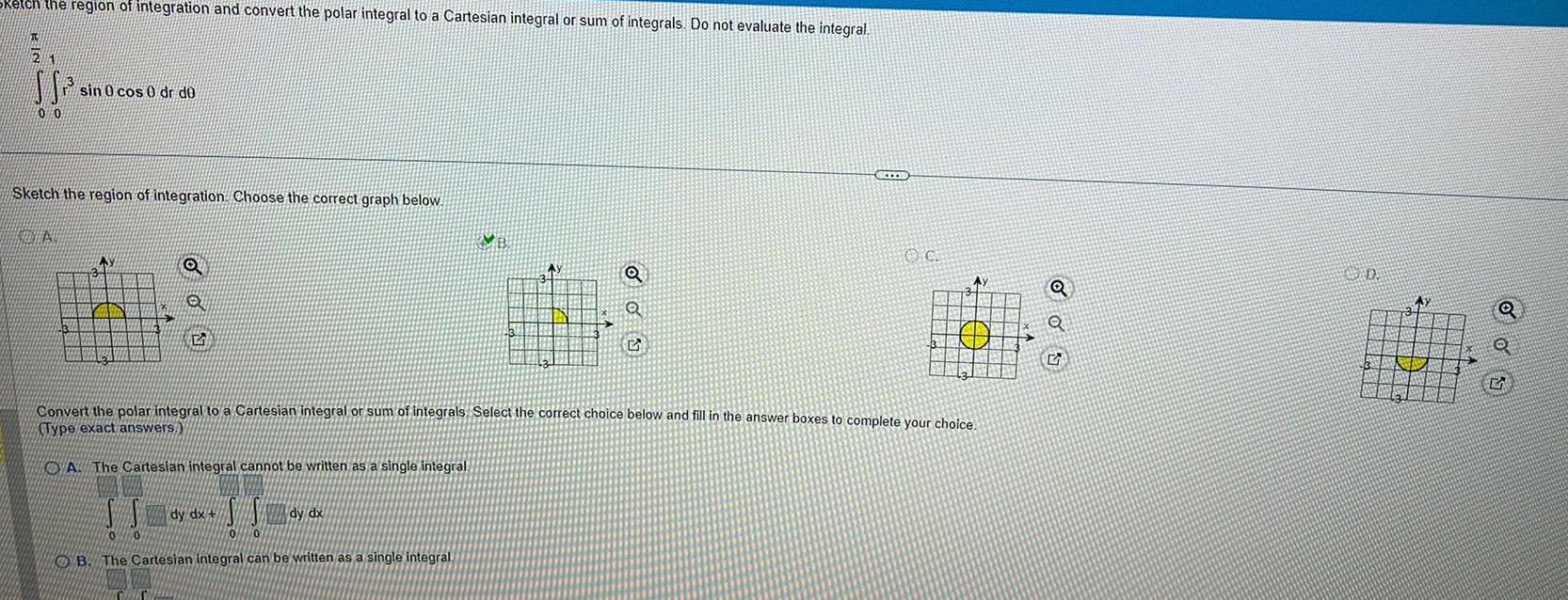
Calculus
Definite IntegralsJU 2 the region of integration and convert the polar integral to a Cartesian integral or sum of integrals Do not evaluate the integral 00 sin 0 cos 0 dr de Sketch the region of integration Choose the correct graph below VENTA AY 3 O SS 0 0 B The Cartesian integral can be written as a single integral dy dx SS 10 Convert the polar integral to a Cartesian integral or sum of integrals Select the correct choice below and fill in the answer boxes to complete your choice Type exact answers A The Cartesian integral cannot be written as a single integral Q Q 2 dy dx B Q Q OD Ay Q S

Calculus
Definite IntegralsCalculate the work in Joules to empty a tank full of water through the top knowing the shape and position of the tank cylinder of radius 5 m positioned horizontally along a stretch of 10 m
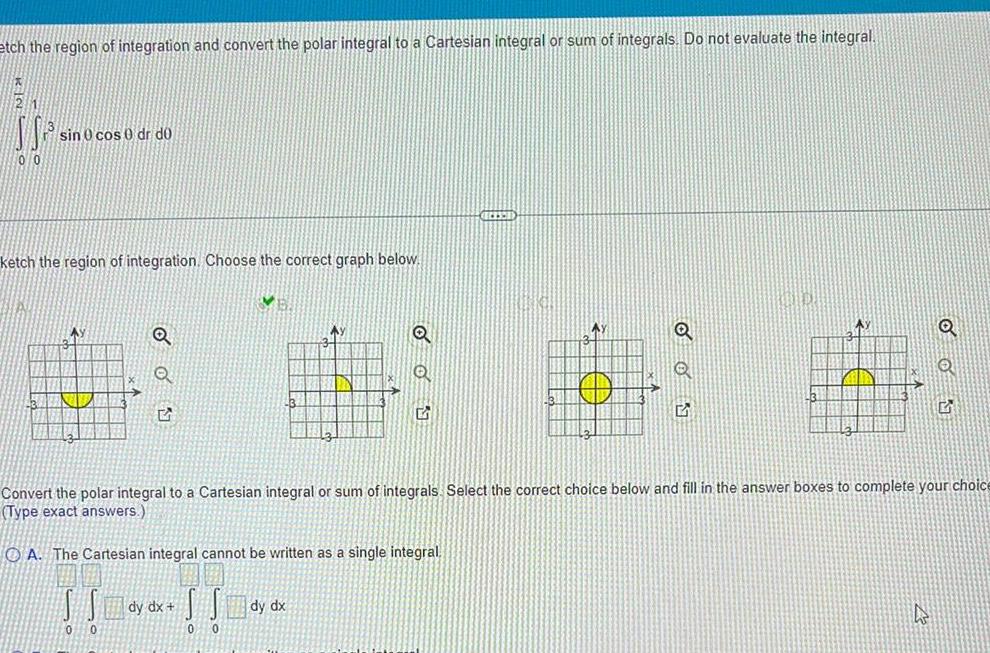
Calculus
Definite Integralsetch the region of integration and convert the polar integral to a Cartesian integral or sum of integrals Do not evaluate the integral K21 SS 00 sin 0 cos 0 dr do ketch the region of integration Choose the correct graph below Ay 0 5 0 dy dx V 0 0 3 Ay 12 Q Convert the polar integral to a Cartesian integral or sum of integrals Select the correct choice below and fill in the answer boxes to complete your choice Type exact answers OA The Cartesian integral cannot be written as a single integral Q Q 5 Q G
Calculus
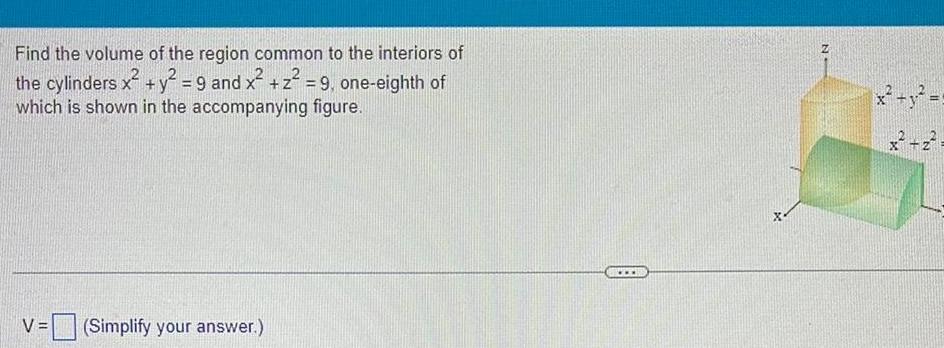
Definite IntegralsFind the volume of the region common to the interiors of the cylinders x y 9 and x z 9 one eighth of which is shown in the accompanying figure V Simplify your answer X N x y x
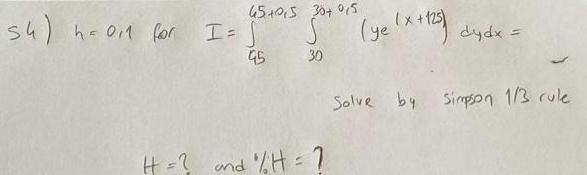
Calculus
Definite Integrals54 h 011 for 45 05 30 0 5 I 45 joto ye x 125 dy dx 30 H and H Solve by Simpson 1 3 rule
Calculus
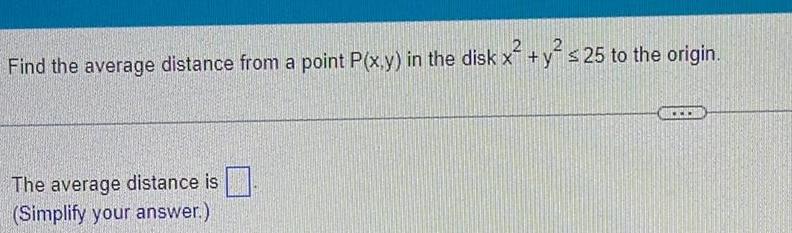
Definite IntegralsFind the average distance from a point P x y in the disk x y 25 to the origin The average distance is Simplify your answer

Calculus
Definite IntegralsEvaluate the integral 2t S S e dx dt dv In sec v 3 In sec v 2t ITI D Se ex dx dt dv 8 00 0 0 Type an exact answer using and radicals as needed
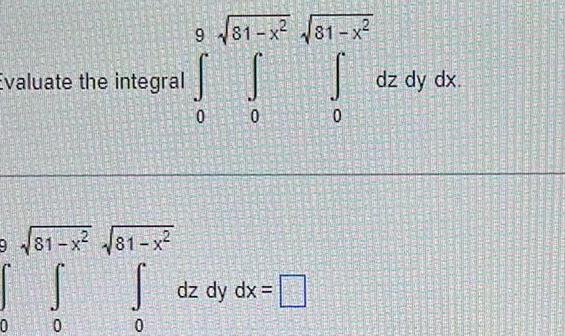
Calculus
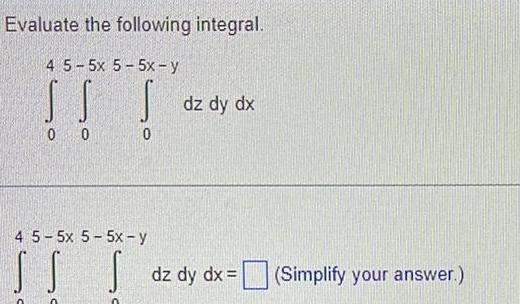
Definite IntegralsEvaluate the following integral 4 5 5x 5 5x y I T 0 0 0 4 5 5x 5 5x y SS C dz dy dx dz dy dx Simplify your answer
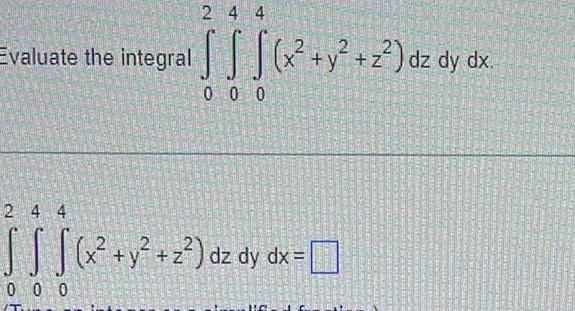
Calculus
Definite Integrals244 2 Evaluate the integral x y 2 dz dy dx S S S 000 2 4 4 S S S x y z dz dy dx 0 0 0
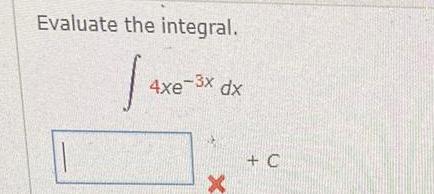
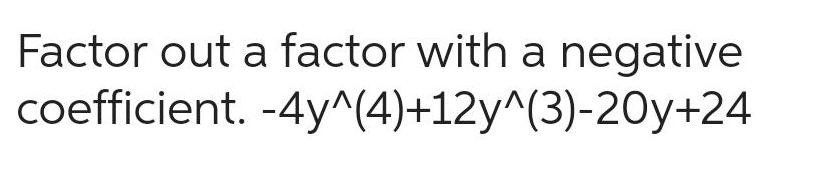
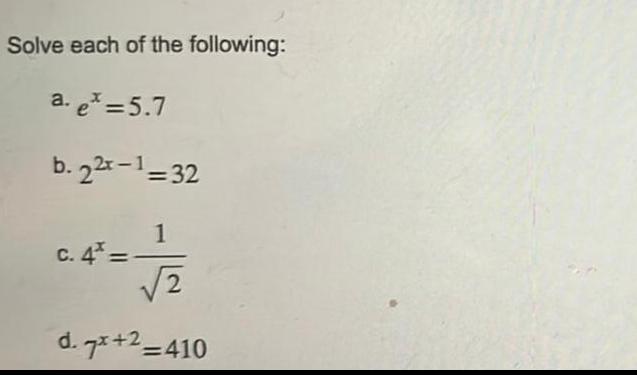
Calculus
Definite IntegralsWe can now use the substitution u sin 8 so du 8 sec ec 4 u Step 4 sec 4 cos 0 sin 0 15 4 JAS 4 We have determined that if we let u sin 8 then du cos 8 de on the interval V15 4 V1 1 329 4 de cos 0 cos 0 du de Once more we must also make a substitution for the limits of integration When 0 V3 v15 2 14 Applying the substitution gives us the following result 15

Calculus
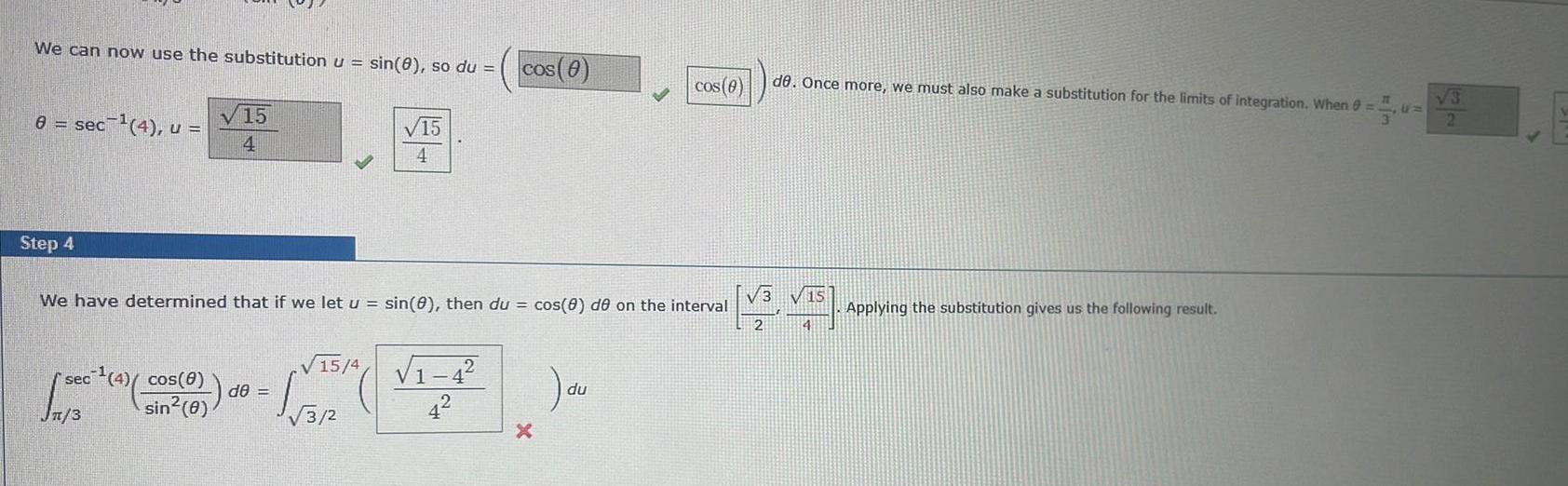
Definite IntegralsStep 3 So far we have the following 10metric integral we put everything in terms of sin 0 and cos 0 Doing so gives the following result cos 8 sec 4 sec 0 tan e de tan 8 3 Step 4 8 sec 4 u sec 4 3 3 We can now use the substitution u sin 0 so du cos 8 sin 8 sec 4 cos 8 sin 0 4 de 15 4 sec 2007 4 Jn 3 15 4 de 3 2 15 4 sin 0 cos 8 We have determined that if we let u sin 0 then du cos 8 de on the interval sin 0 du cos 6 de de Once more we must also make a substitution for the limits of integration When 15 Applying the substitution gives us the following result
Calculus
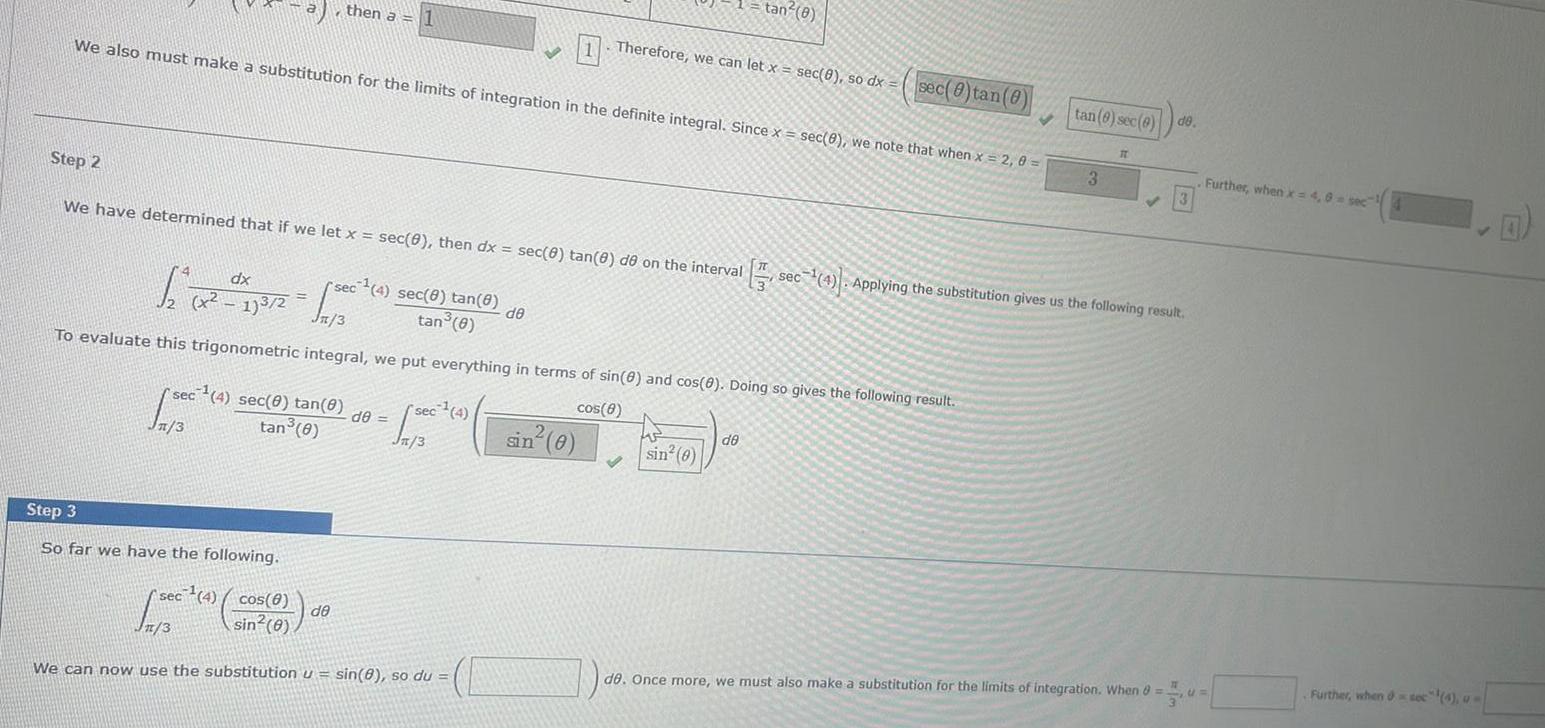
Definite IntegralsWe also must make a substitution for the limits of integration in the definite integral Since x sec 8 we note that when x 2 0 then a 1 Step 2 We have determined that if we let x sec 0 then dx sec 8 tan 8 de on the interval sec 4 sec 0 tan 0 1 3 tan 0 Step 3 So far we have the following rsec 4 sec 8 tan 8 tan 0 dx 1 x x 173 2 1500 Jn 3 To evaluate this trigonometric integral we put everything in terms of sin 8 and cos 0 Doing so gives the following result cos 8 de de sec 4 Jn 3 sec 4 cos 8 Jn 3 sin 0 We can now use the substitution u sin 8 so du de Therefore we can let x sec 0 so dx sin 0 tan 8 V sin 0 de sec 0 tan 0 tan 6 sec 0 de 3 IT 3 sec 4 Applying the substitution gives us the following result de Once more we must also make a substitution for the limits of integration When 8 CI Further when x 4 8 sec Further when soc 4 u

Calculus
Definite IntegralsWe note that x 1 3 2 x 1 Therefore the following entry from the Table of Trigonometric Substitutions is appropriate Expression x a If x 1 x a then a 1 Submit x a sec 8 0 0 Substitution dx 12 12 X17 2 100 0 S sec 4 sec 8 tan 8 tan 8 0 1 or or 8 2 We also must make a substitution for the limits of integration in the definite integral Since x sec 0 we note that when x 2 0 sec 4 sec 8 tan e de tan 0 Skip you cannot come back sec 4 Jn 3 2 1 Step 2 We have determined that if we let x sec 8 then dx sec 8 tan 8 de on the interval sec 4 Applying the substitution gives us the following result 3 2 de n 3 To evaluate this trigonometric integral we put everything in terms of sin 0 and cos 8 Doing so gives the following result cos 8 Identity sec 0 1 tan 0 Therefore we can let x sec 0 so dx sec 0 tan 0 de tan 8 sec 8 de 3 TL 3 Further when x 4 8 sec 4
Calculus
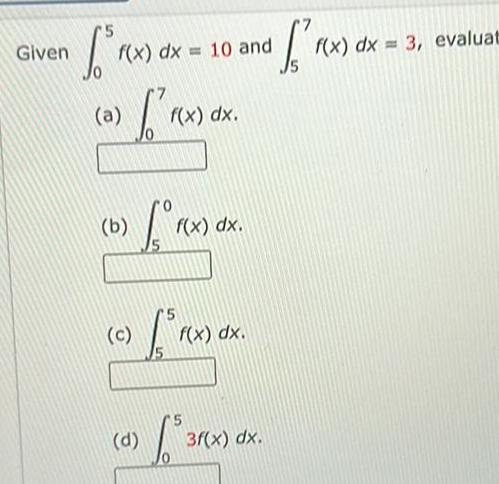
Definite IntegralsGiven r x a f x dx 10 and b f c f x dx d f x dx f x dx S af rex 3f x dx f x dx 3 evaluat
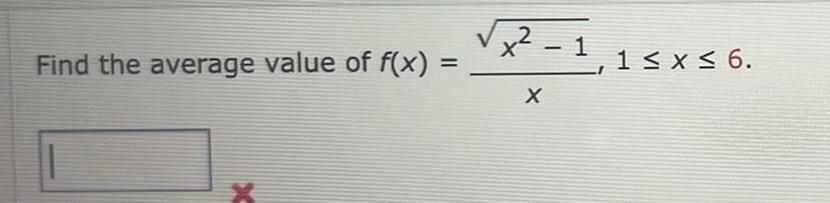
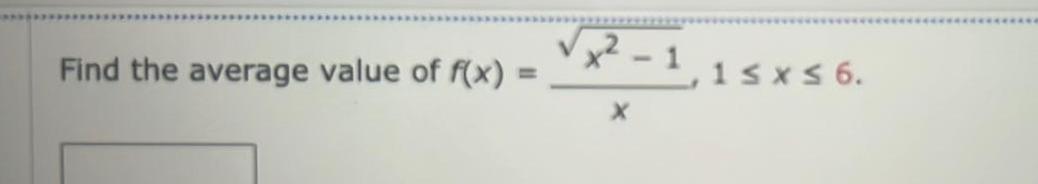

Calculus
Definite IntegralsThe linear density p in a rod 7 m long is 12 X 9 Pave kg m where x is measured in meters from one end of the rod Find the average density Pave in kg m of the rod kg m
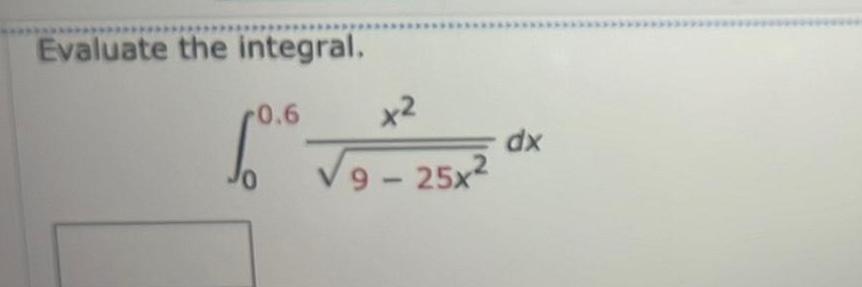
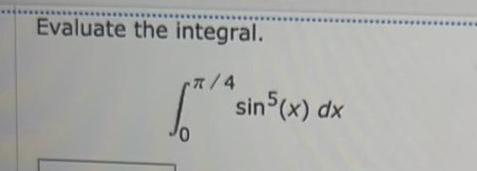
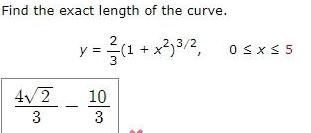

Calculus
Definite IntegralsProblem 66 Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of f x 3x5 5x Domain Range Increasing Decreasing interval s Concavity or concavities Inflection point s Max and or min Asymptotes

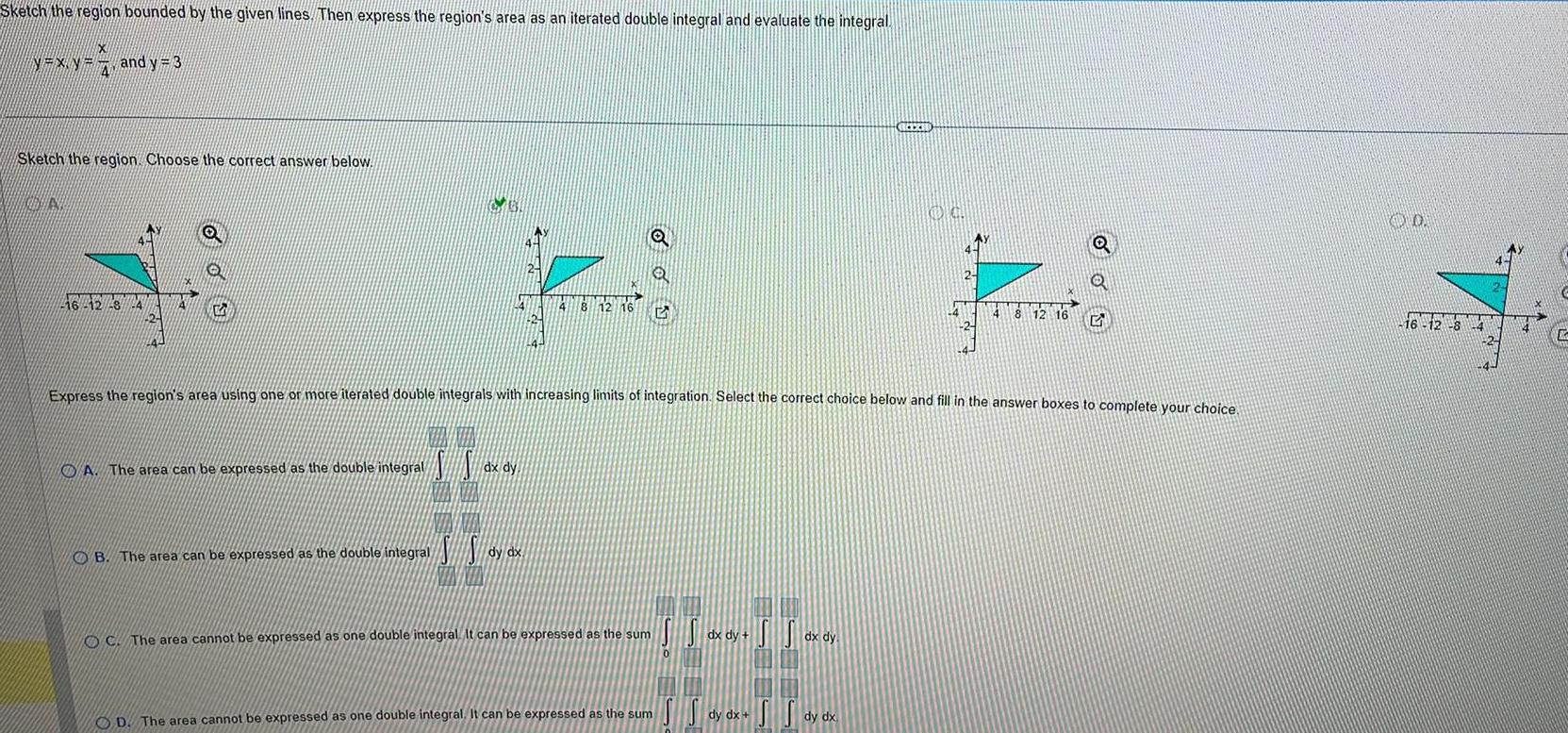
Calculus
Definite IntegralsSketch the region bounded by the given lines Then express the region s area as an iterated double integral and evaluate the integral N XN X NXX and y 3 4 Sketch the region Choose the correct answer below N 46 42 8 24 O Q G A The area can be expressed as the double integral I l dx dy 8 12 16 O B The area can be expressed as the double integral SS dy dx OC The area cannot be expressed as one double integral It can be expressed as the sum D The area cannot be expressed as one double integral It can be expressed as the sum dx dy Express the region s area using one or more iterated double integrals with increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice dx dy REEZID SS dy dx dy dx OG 4 2 Q 4 8 12 16 5 20 16 12 8 14 C
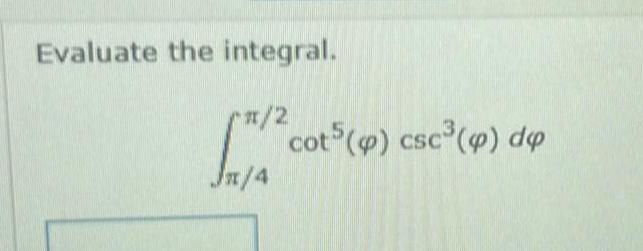
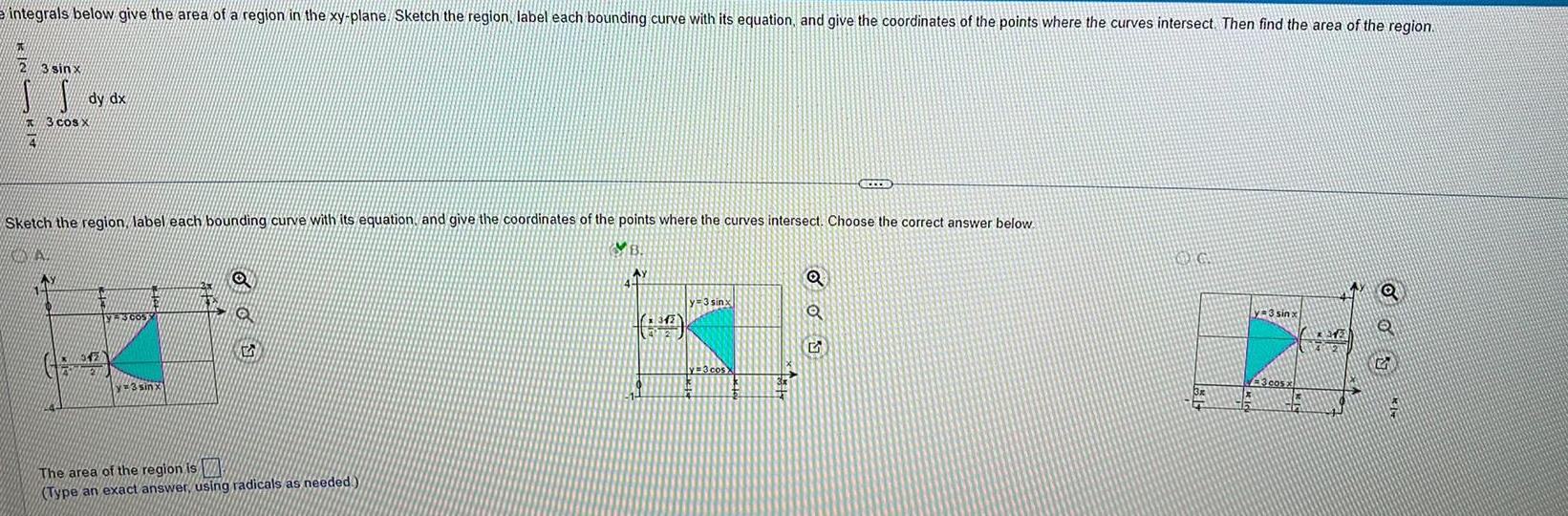
Calculus
Definite Integralsintegrals below give the area of a region in the xy plane Sketch the region label each bounding curve with its equation and give the coordinates of the points where the curves intersect Then find the area of the region 4 3 sinx dy dx 3 cos x Sketch the region label each bounding curve with its equation and give the coordinates of the points where the curves intersect Choose the correct answer below KINIS 342 VE3005 y 3 sinx 5 The area of the region is Type an exact answer using radicals as needed AY 6 y 3 sinx y 3 cos X SECES Q Q 5 OG 3x 1x 16 y 3 sinx 3 cos X thr Q Q G
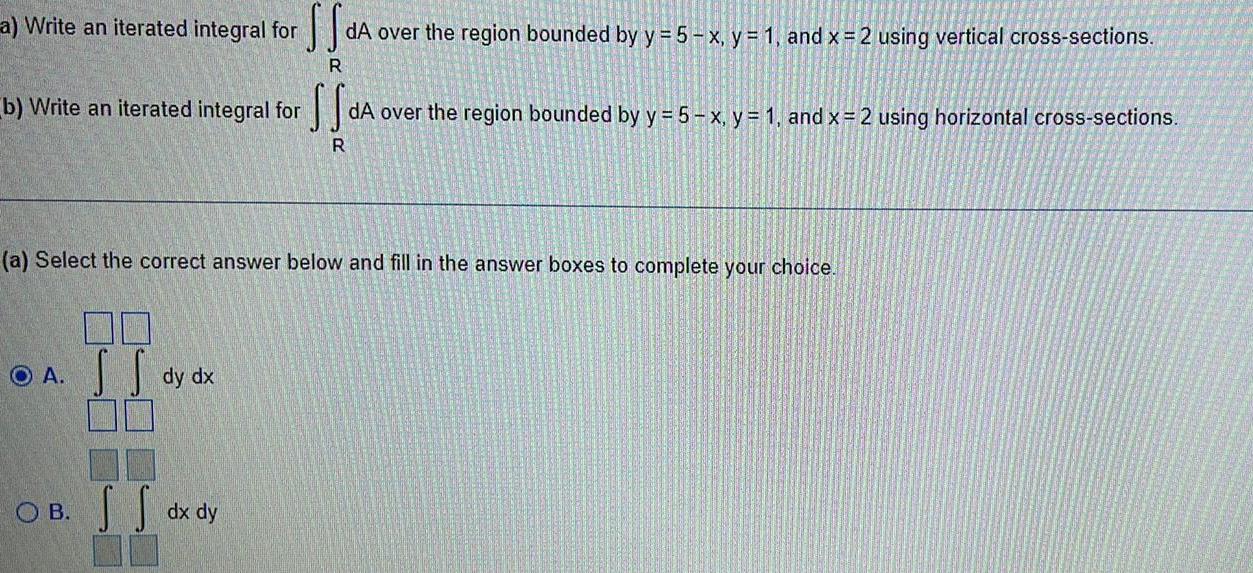
Calculus
Definite Integralsa Write an iterated integral for b Write an iterated integral for f R O A a Select the correct answer below and fill in the answer boxes to complete your choice S S SS dA over the region bounded by y 5 x y 1 and x 2 using vertical cross sections R dy dx OB dx dy dA over the region bounded by y 5 x y 1 and x 2 using horizontal cross sections
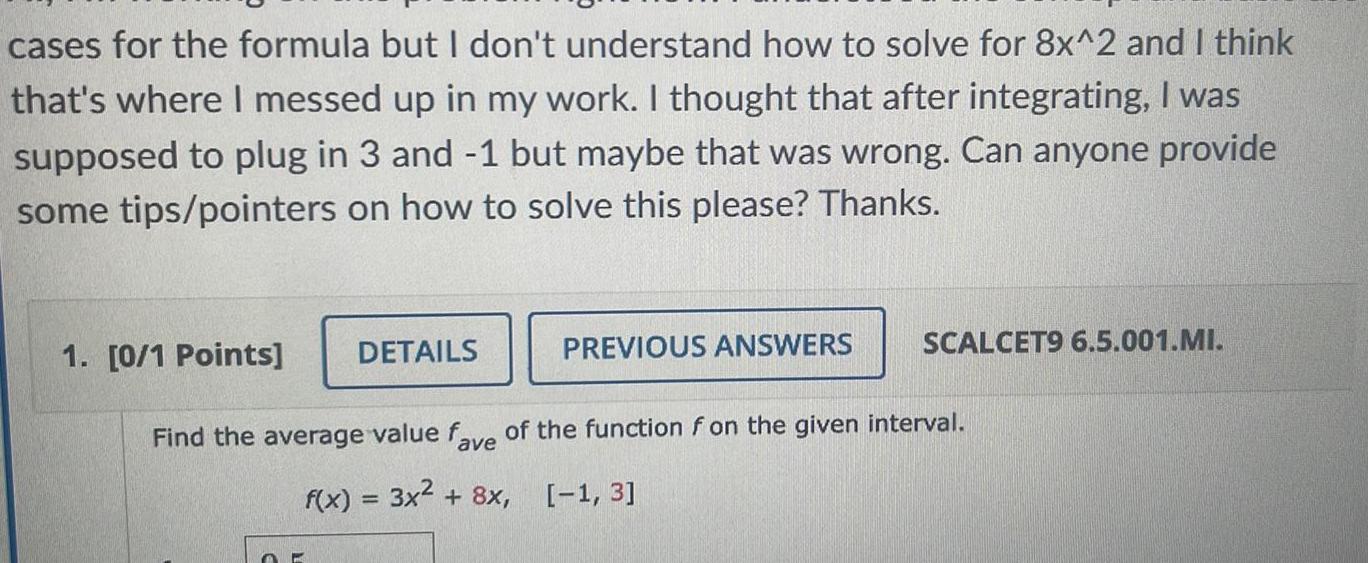
Calculus
Definite Integralscases for the formula but I don t understand how to solve for 8x 2 and I think that s where I messed up in my work I thought that after integrating I was supposed to plug in 3 and 1 but maybe that was wrong Can anyone provide some tips pointers on how to solve this please Thanks 1 0 1 Points DETAILS O PREVIOUS ANSWERS SCALCET9 6 5 001 MI Find the average value fave of the function f on the given interval f x 3x 8x 1 3

Calculus
Definite IntegralsTV 4 1 sin5 x dx 0 At first I divided sin5 x dx to sin4 x sin x dx And I changed sin x to 1 cos x in terms of the Cosine function After that I solved it by using integral rules But I couldn t solve it Can anyone give me a hint to solve it I attached my calculations below

Calculus
Definite IntegralsQuestion Find the average value fave of the function fon the given interval f x 3x 4x 1 5 At first I calculated using the two formulas The average value of function f over the interval a b and the Power Rule that I wrote in the picture but couldn t solve it I attached the picture below Can anyone give me a hint of what I missed B
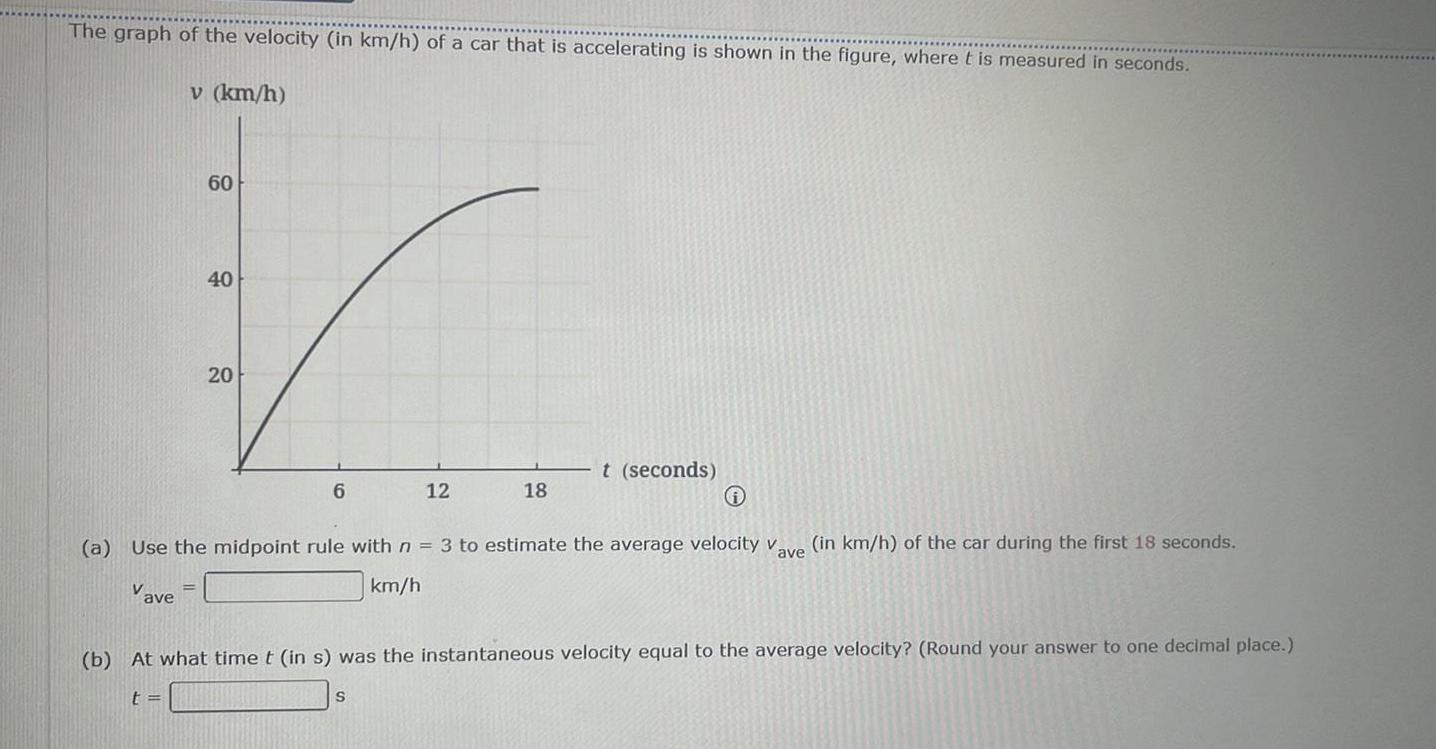
Calculus
Definite IntegralsThe graph of the velocity in km h of a car that is accelerating is shown in the figure where t is measured in seconds v km h Vave 60 40 20 6 12 i a Use the midpoint rule with n 3 to estimate the average velocity va in km h of the car during the first 18 seconds ave km h 18 S t seconds b At what time t in s was the instantaneous velocity equal to the average velocity Round your answer to one decimal place t
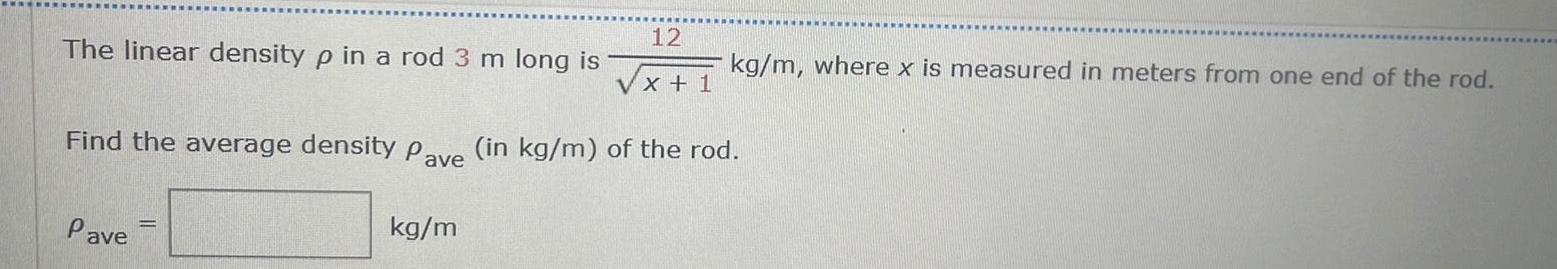
Calculus
Definite Integrals12 x 1 Find the average density Pave in kg m of the rod The linear density p in a rod Pave kg m m long is kg m where x is measured in meters from one end of the rod

Calculus
Definite IntegralsFind the average value h have ave 0 3238 of the function h on the given interval h u In u 1 5 U

Calculus
Definite Integralsketch the region bounded by the given line and curve Then express the region s area as an iterat and evaluate the integral 2 The parabola x y and the line y x 2 A The area can be expressed as the double integral dy dx B The area cannot be expressed as one double integral It can be expressed as the sum s so dy dx x S S dy dx C The area can be expressed as the double integral OD The value of the integral is dx dy 1 y The area cannot be expressed as one double integral It can be expressed as the sum S S dx dy SS S dx dy 2 y 2 Simplify your answer Type an integer or a fraction
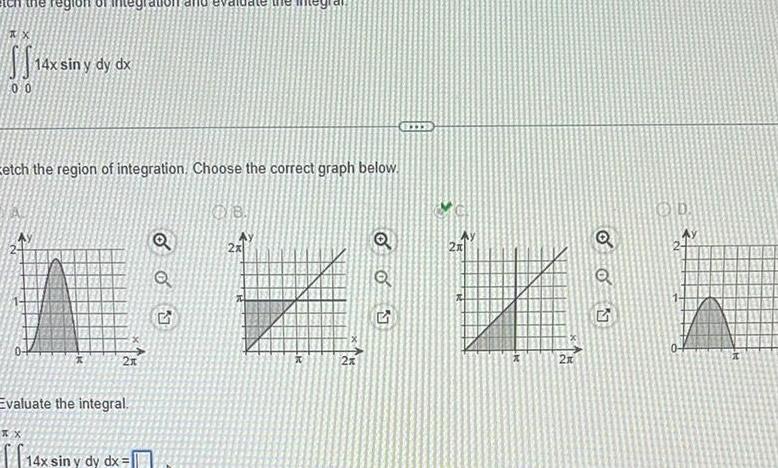
Calculus
Definite Integrals12x in 00 14x sin y dy dx Eetch the region of integration Choose the correct graph below xx X 2x Evaluate the integral 14x sin y dy dx Q Q 5 08 2x x 2x Q oo 9 2x W 2x Q OON Q O
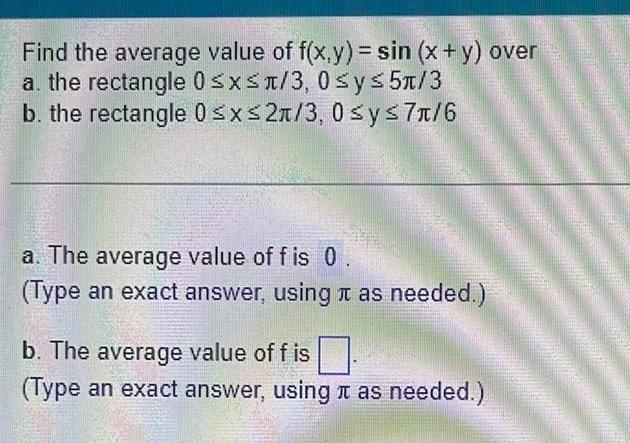
Calculus
Definite IntegralsFind the average value of f x y sin x y over a the rectangle 0 x 3 0 y 5 3 b the rectangle 0 x 2 3 0 y 7 6 a The average value of fis 0 Type an exact answer using as needed b The average value of f is Type an exact answer using it as needed
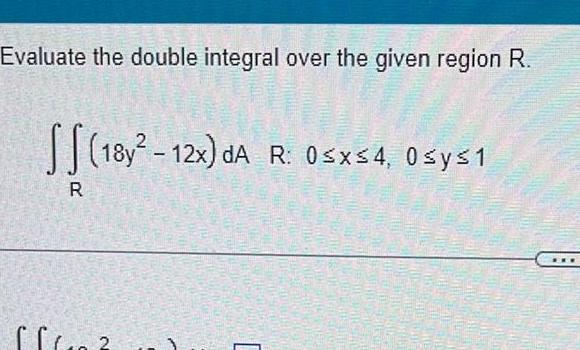
Calculus
Definite IntegralsEvaluate the double integral over the given region R R 18y 12x dA R 0 x 4 0sys1
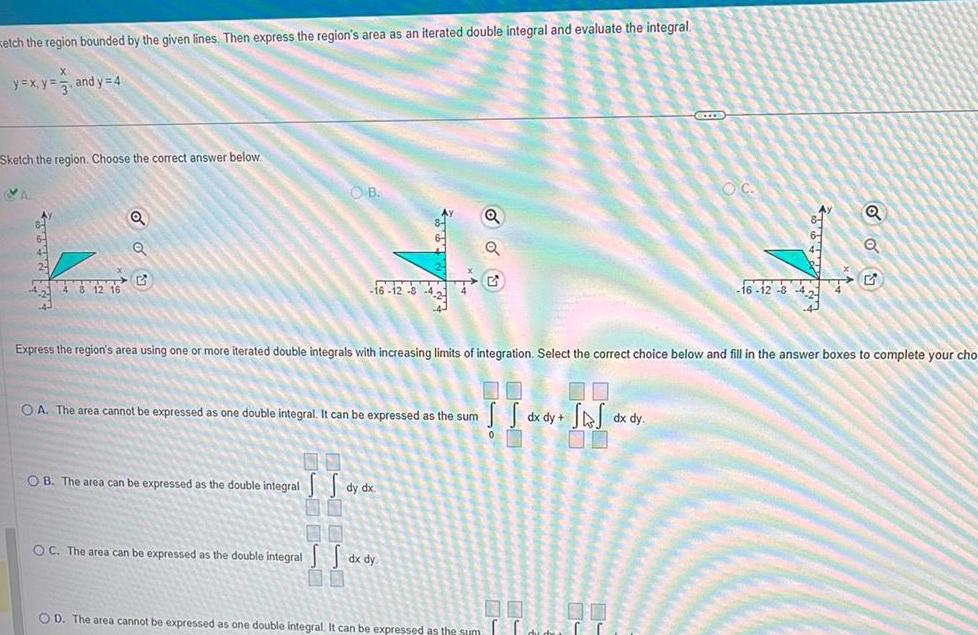
Calculus
Definite IntegralsKetch the region bounded by the given lines Then express the region s area as an iterated double integral and evaluate the integral X y x y and y 4 Sketch the region Choose the correct answer below VA ATTR 4 8 12 16 O O OB 16 12 8 43 4 OB The area can be expressed as the double integral OA The area cannot be expressed as one double integral It can be expressed as the sum Express the region s area using one or more iterated double integrals with increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your cho S S dy dx OC The area can be expressed as the double integral dx dy 00 OD The area cannot be expressed as one double integral It can be expressed as the sum S S dx dy SAJ dx dy GEEEE 00 00 OC Q Q 16 12 34 G
Calculus
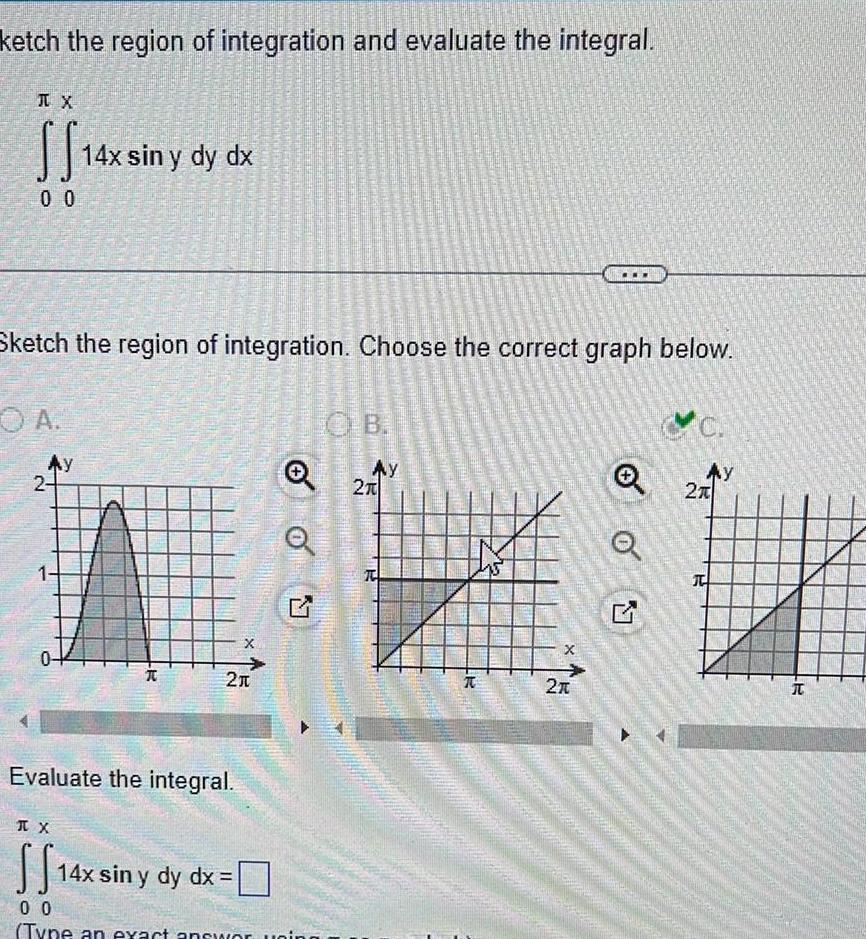
Definite Integralsketch the region of integration and evaluate the integral TX SS14x 14x sin y dy dx 0 0 A Sketch the region of integration Choose the correct graph below Ay 2 1 0 CAMATER TX SS14x FROM AU YETER R Evaluate the integral 21 X 14x sin y dy dx Q 00 Type an exact answor uning OB AY 2T T X 2 Q Ay 2T T R
Calculus
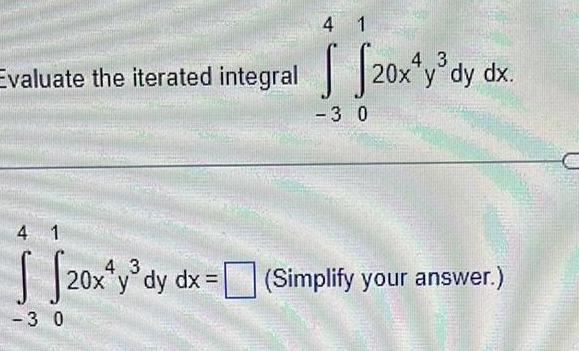
Definite Integrals4 1 3 0 4 3 Evaluate the iterated integral 20x y dy dx 4 1 4 3 20x y dy dx Simplify your answer 3 0