Differential equations Questions and Answers

Calculus
Differential equationsUse the intermediate value theorem to verify the given polynomial has at least one zero c in the intervals specified Do not find the zeroes H x 2x 3x 14x 9x 8 a 4 3 b 2 11
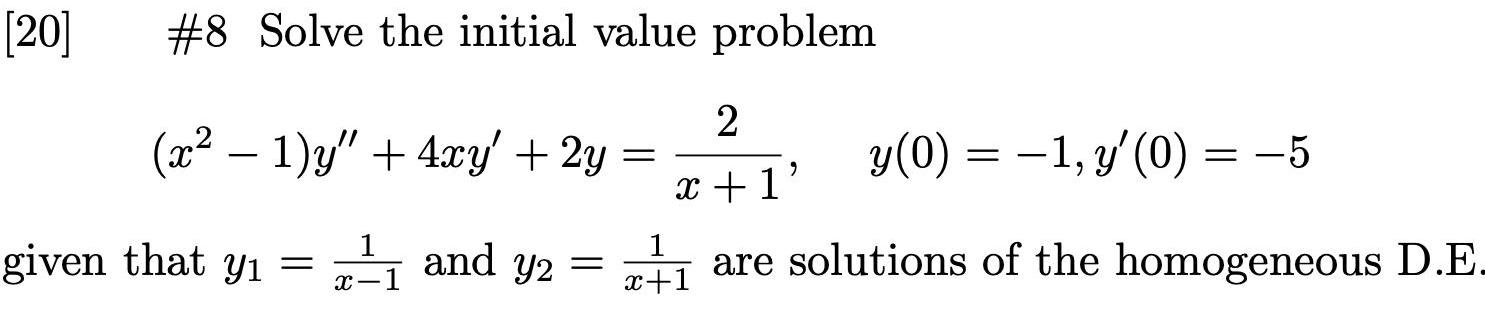
Calculus
Differential equations20 8 Solve the initial value problem x 1 y 4xy 2y 1 and y y2 given that y x 1 2 x 1 are solutions of the homogeneous D E 1 x 1 y 0 1 y 0 5
Calculus
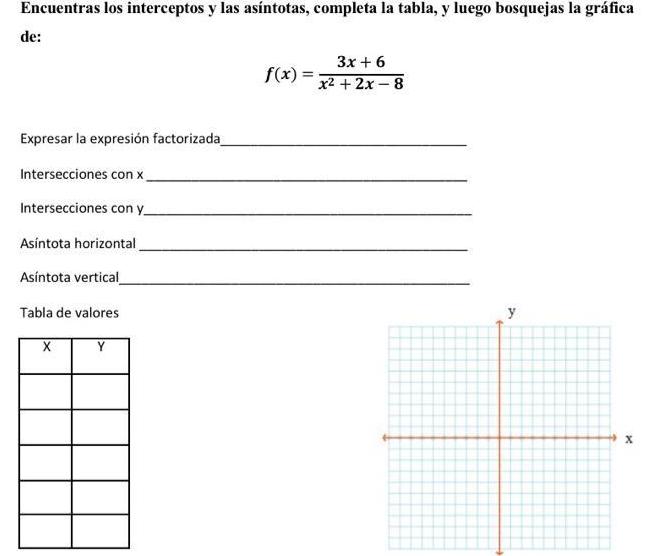
Differential equationsEncuentras los interceptos y las as ntotas completa la tabla y luego bosquejas la gr fica de Expresar la expresi n factorizada Intersecciones con x Intersecciones con y As ntota horizontal As ntota vertical Tabla de valores X Y f x 3x 6 x2 2x 8 y X
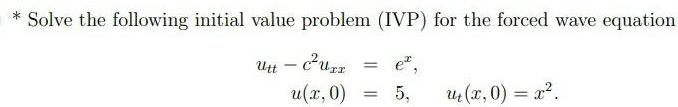
Calculus
Differential equationsSolve the following initial value problem IVP for the forced wave equation Utt c Uzz u x 0 5 u x 0 x
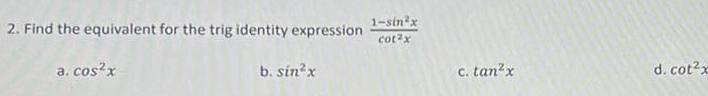
Calculus
Differential equations1 sin x 2 Find the equivalent for the trig identity expression cotx a cos x b sin x c tan x d cot2x

Calculus
Differential equations3 10 Pts Find the critical points of the function f x y x 8xy 2y 3 and use the discriminant D to classify each point as either a local minimum local maximum or a saddle point

Calculus
Differential equationsProblem An object of 5 kilogram mass is thrown from the top of a 100 story building about 305 meters above the earth s surface If it takes the object 10 seconds to reach the earth from the height of 100 meters determine the object s velocity while it is still at the height of 100 meters Start with the sketching of the free body diagram formulate the differential equation then do the manipulation


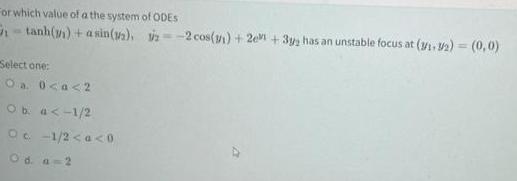
Calculus
Differential equationsFor which value of a the system of ODES 2 2 cos 11 2 3y has an unstable focus at 3 1 3 2 0 0 tanh asin 12 Select one O a 0 a 2 O b a 1 2 Oc 1 2 a 0 Od a 2

Calculus
Differential equationsFind the critical number s of the function f x x5 O There are no critical numbers 0 x 0 0 x 1 x 8
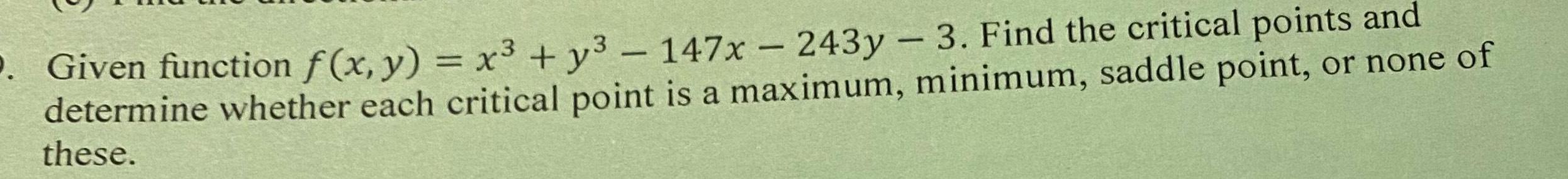
Calculus
Differential equationsP Given function f x y x y 147x 243y 3 Find the critical points and determine whether each critical point is a maximum minimum saddle point or none of these
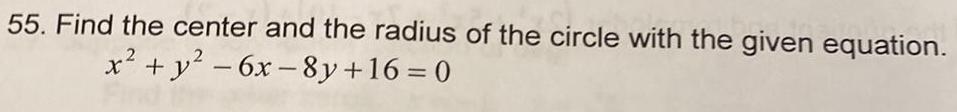
Calculus
Differential equations55 Find the center and the radius of the circle with the given equation x y 6x 8y 16 0

Calculus
Differential equationsf is a function of g f 6 3 f 6 2 You know that g is a function of t g 3 6 g 3 4 a Draw the relevant calcutus schematics with differentials for f and 9 b Find dy dl

Calculus
Differential equationsConsider the function 1 f x x x x x subject to 2x x 1 Find the range of values of constant y so that a f x has a unique global minimum b f x has a local minimum c f x has a local maximum

Calculus
Differential equationsDetermine if the DE is homogeneous or nonhomogeneous Explain your answer 2y 5y 12y 0 y 2y2ex 0 a b

Calculus
Differential equationsDescribe the surface with the parametric representation shown below r u v v cos u v sin u 4v for Osus2 0 vs5 Select the correct choice below and fill in the answer boxes within your choice OA The surface is a cylinder with a height of and a radius of B The surface is a sphere with its center at and a radius of C The surface is a cone with height of and radius of at the widest point

Calculus
Differential equationsConsider the following vector field the circle C and two points P and Q F x x y a Without computing the divergence does the graph suggest that the divergence is positive or negative at P and Q b Compute the divergence and confirm your conjecture in part a c On what part of C is the flux outward Inward d Is the net flux across C positive or negative FRED P 1 1 2011 F x x y
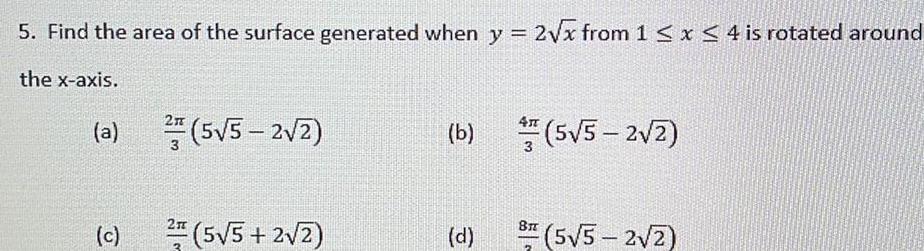
Calculus
Differential equations5 Find the area of the surface generated when y 2 x from 1 x 4 is rotated around the x axis a c 2A 3 2 5 5 2 2 5 5 2 2 b 5 5 2 2 d 8 5 5 2 2
Calculus
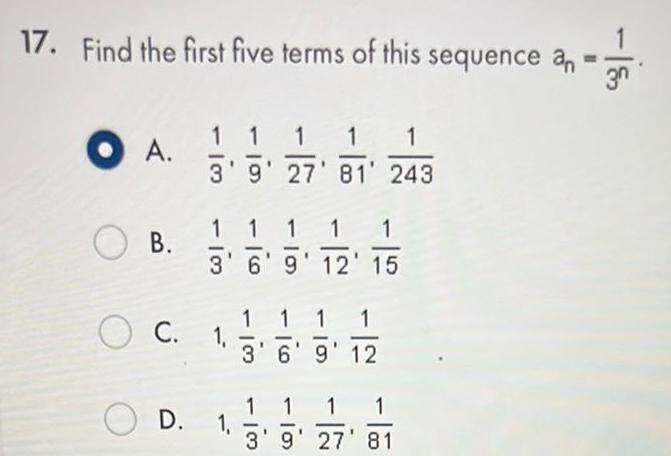
Differential equations17 Find the first five terms of this sequence an O A B O C D 1 1 1 1 3 9 27 81 243 1 1 100 Im 1 3 6 9 12 15 1 1 1 1 1 Im 1 1 1 3 6 9 12 ion IN 1 1 1 1 1 3 9 27 81 3n
Calculus
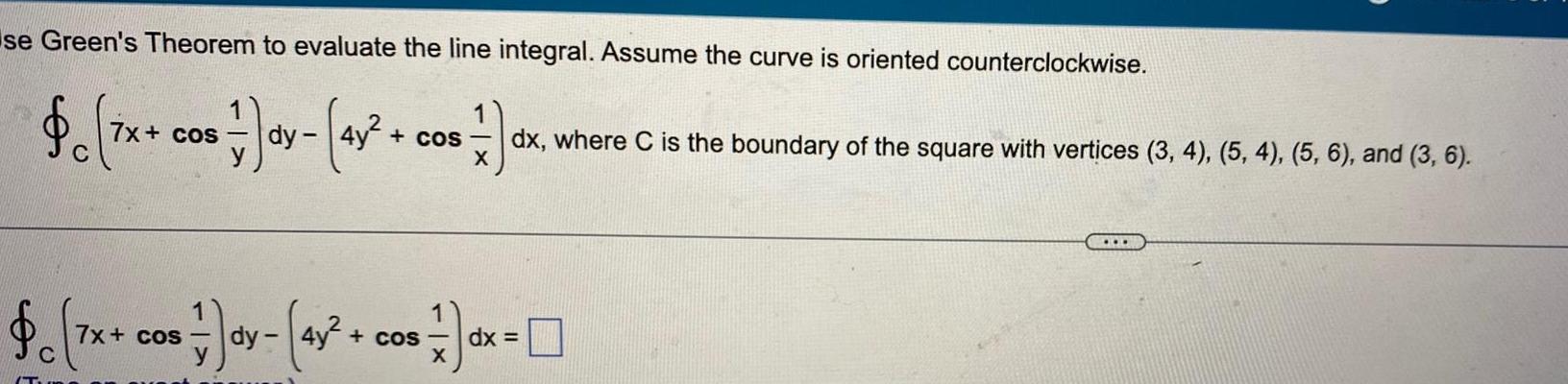
Differential equationsse Green s Theorem to evaluate the line integral Assume the curve is oriented counterclockwise 7x cos dy 4x cos ex dx where C is the boundary of the square with vertices 3 4 5 4 5 6 and 3 6 C X 7x cos 7x cos 4y cos 1 X dx

Calculus
Differential equationsConsider the following e 10x 9 a Find the exact solution of the exponential equation in terms of logarithms X b Use a calculator to find an approximation to the solution rounded to six decimal plac X

Calculus
Differential equationsUsing the Fourier transform solve the following ordinary differential equatio y y g t
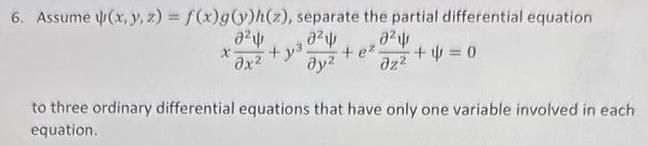
Calculus
Differential equations6 Assume x y z f x g y h z separate the partial differential equation 2 22 0 X y x y zz e 0 to three ordinary differential equations that have only one variable involved in each equation

Calculus
Differential equations5 A model for the population growth of China is P t 0 000788t 0 00431 7 24623t 1286 78 in year t where t is measured in years with t 0 corresponding to the year 2000 and P t is measured in millions a Show that the population of China is forecast to peak during 2057 b Find what the population of China will be when it peaks poleaga
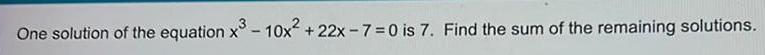
Calculus
Differential equationsOne solution of the equation x^3 - 10x² +22x-7=0 is 7. Find the sum of the remaining solutions.
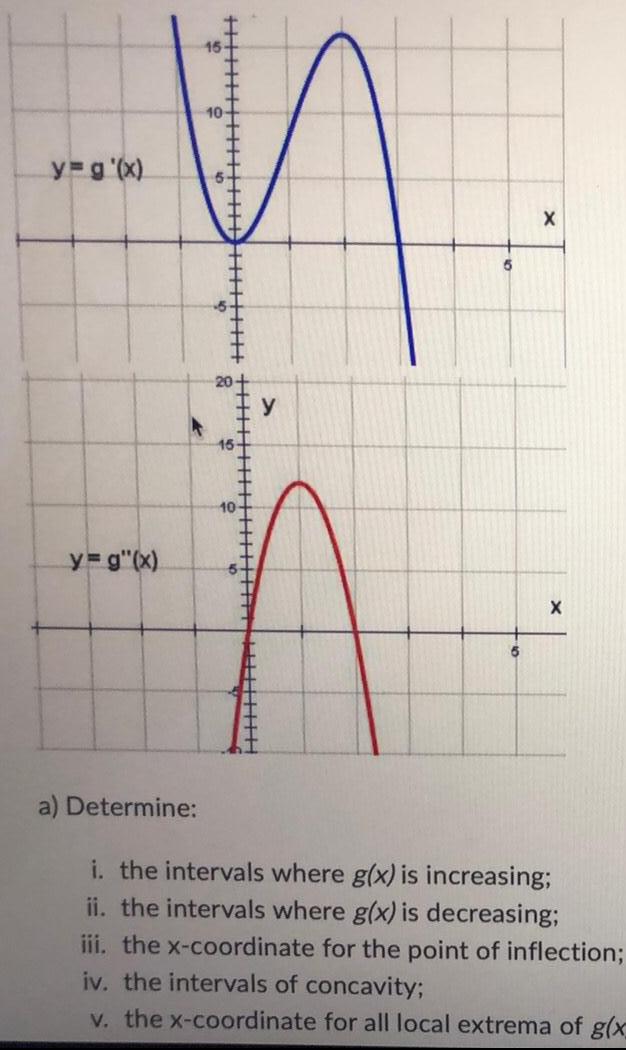
Calculus
Differential equationsi. the intervals where g(x) is increasing;
ii. the intervals where g(x) is decreasing;
iii. the x-coordinate for the point of inflection;
iv. the intervals of concavity;
v. the x-coordinate for all local extrema of g(x

Calculus
Differential equationsThe growth rate of the population of India is directly proportional to the current population. Write and solve a differential equation that expresses the rate of change of the population in terms of the current population under the following conditions: Initially in 2011, the population was 1.221 billion people, and at the same time in 2012 the population was 1.237 billion people. Round decimals to 3 places.

Calculus
Differential equationsIf investment A has an annual return of 4% with continuously compounded interest, and Jane has $500 after 4 years, how much money did she start out with?
A(t) is the amount of money at t years.
O 426.07
O 420
O 410
O 350

Calculus
Differential equationsNew-cars have a distinctive smell which is caused by the out-gassing of chemicals from the carpet, glues, and upholstery. Over time the chemicals in these items evaporate into the air at a rate proportional to N. You measured the "new car smell," N(t).as 100 when purchased and at t = 6 months and there was N(t) = 1. Write and solve the differential equation which describes the amount of new car smell between t = 0 and t = 6 months, where t is measured in months.
ON(t) = 100e(-0.767)t
O N(t) = .99e(-0.767)1
ON(t) = 100e(-0.99)
O N(t) = 100e(0.767)t
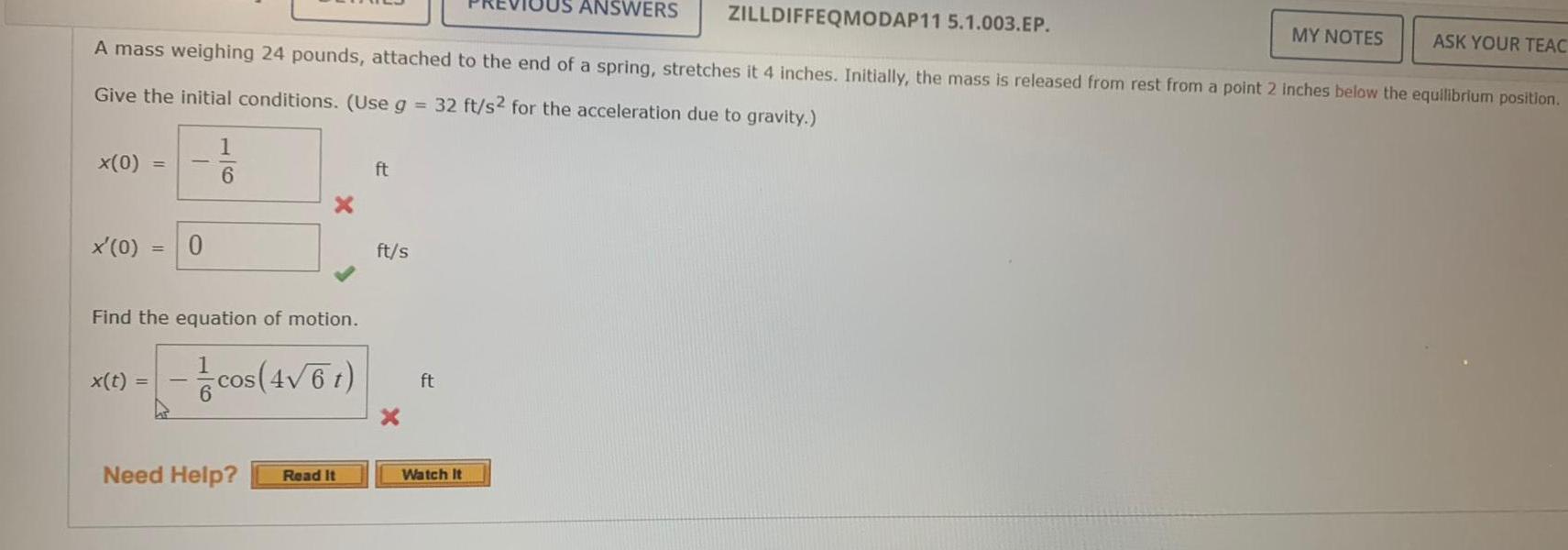
Calculus
Differential equationsA mass weighing 24 pounds, attached to the end of a spring, stretches it 4 inches. Initially, the mass is released from rest from a point 2 inches below the equilibrium position.
Give the initial conditions. (Use g = 32 ft/s2 for the acceleration due to gravity.)
x(0)=
x'(0)=
Find the equation of motion.
x(t)=

Calculus
Differential equationsIII. (20 pt) Find the complete dimensionless formulation for the following PDE.
(Do not solve the problem)
Ut
=
9 UII
0 < x < 5
u(0, t) = 0,
u(5, t) = 10,
u(x,0) = cos(2x), 0≤x≤ 5.
t> 0,

Calculus
Differential equationsIdentify the open interval on which the function is increasing or decreasing. (Enter your answers using interval notation.)
h(x) = cos(³), 0 < x < 2#
increasing
decreasing

Calculus
Differential equationsDoes the relation represent y as a function of x?
Yes, because y may be positive or negative
y=+√4-x4
No, because some values of a correspond to more than one value of y
No, because x may not be greater than 4
OYes, because each value of a corresponds to exactly one value of y

Calculus
Differential equations#8 Write an algebraic equation to represent the given information of a rectangle. Let w be the
width and / be the length of the rectangle.
a) The perimeter of the rectangle is 30 cm.
b) The area of the rectangle is 50 cm².
The length is 5 cm longer than the width.
d) The width is 80% of the length.
![1. Evaluate the following integrals using integration by parts. Clearly denote what is playing
the role of u, du, du, and v.
(a) [In rd.r
Hint: The integral is equivalent to
(b) In²
]nrdr
of
-0
Hint: Set u = ln² r as in the integration by parts formula. Use your answer from part (a)!
(e) | arctan(r)dr
Hint: Use the same hint from part (a).
(e) |_=
fimr.
*(d) [2²³ cos (1²)da
Hint: Rewrite the integrand as 1². r cos(2²). Now experiment as to what to set u and du
equal to. Do not use online resources!
r sin ædr
In z 1dx.](https://media.kunduz.com/media/sug-question/raw/84102450-1660406078.1246743.jpeg?w=256)
Calculus
Differential equations1. Evaluate the following integrals using integration by parts. Clearly denote what is playing
the role of u, du, du, and v.
(a) [In rd.r
Hint: The integral is equivalent to
(b) In²
]nrdr
of
-0
Hint: Set u = ln² r as in the integration by parts formula. Use your answer from part (a)!
(e) | arctan(r)dr
Hint: Use the same hint from part (a).
(e) |_=
fimr.
*(d) [2²³ cos (1²)da
Hint: Rewrite the integrand as 1². r cos(2²). Now experiment as to what to set u and du
equal to. Do not use online resources!
r sin ædr
In z 1dx.
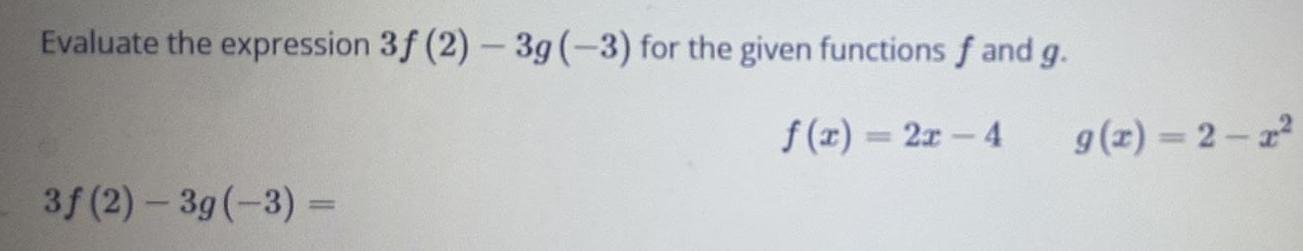
Calculus
Differential equationsEvaluate the expression 3f (2) - 3g (-3) for the given functions f and g.
3f (2)-3g (-3) =
f(x)=2x-4 g(x)=2-2²
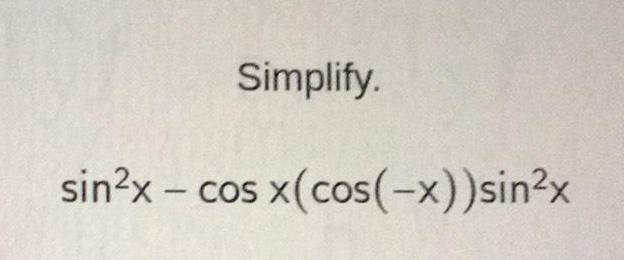

Calculus
Differential equationsRewrite the following equation with the variables separated.
y' = 6xy2 + 2xy + 6y² + 2y

Calculus
Differential equationsUsing the Midpoint Method, calculate y(0.4) for the following:
y' -5x¹y², y (0) = 1, h = 0.2
The solution for this ODE is given by: y = 1/(1+x)^5
Use 6 decimal places.
0.998400
0.991815.
0.985663
0.989156

Calculus
Differential equationsdy
The differential equation = xy + y is separable. Select the
da
most appropriate statement from among the following choices.
O
False. d
dy
= xy + y is not a separable differential equation.
O True. The differential equation can be more easily separated after
dy
we factor, like this: = y(x + 1).
dz
True. The differential equation can be easily separated, like this:
dy
dz
xy = y.
-
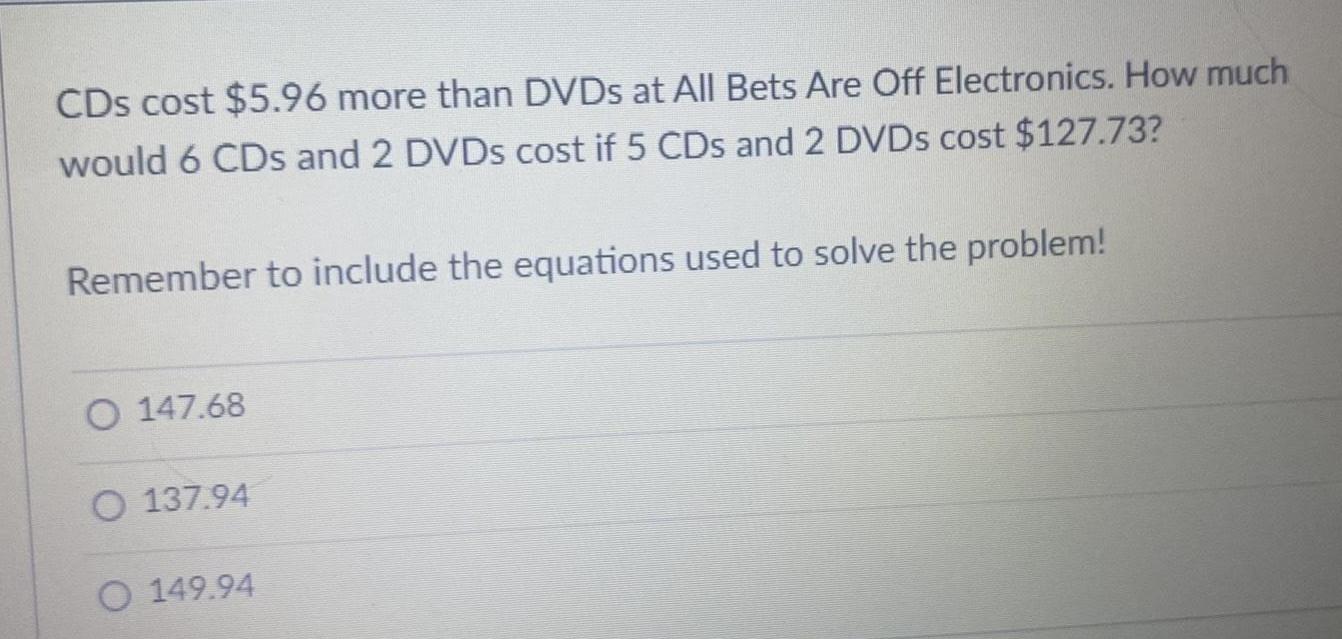
Calculus
Differential equationsCDs cost $5.96 more than DVDs at All Bets Are Off Electronics. How much
would 6 CDs and 2 DVDs cost if 5 CDs and 2 DVDs cost $127.73?
Remember to include the equations used to solve the problem!
O 147.68
O 137.94
O 149.94
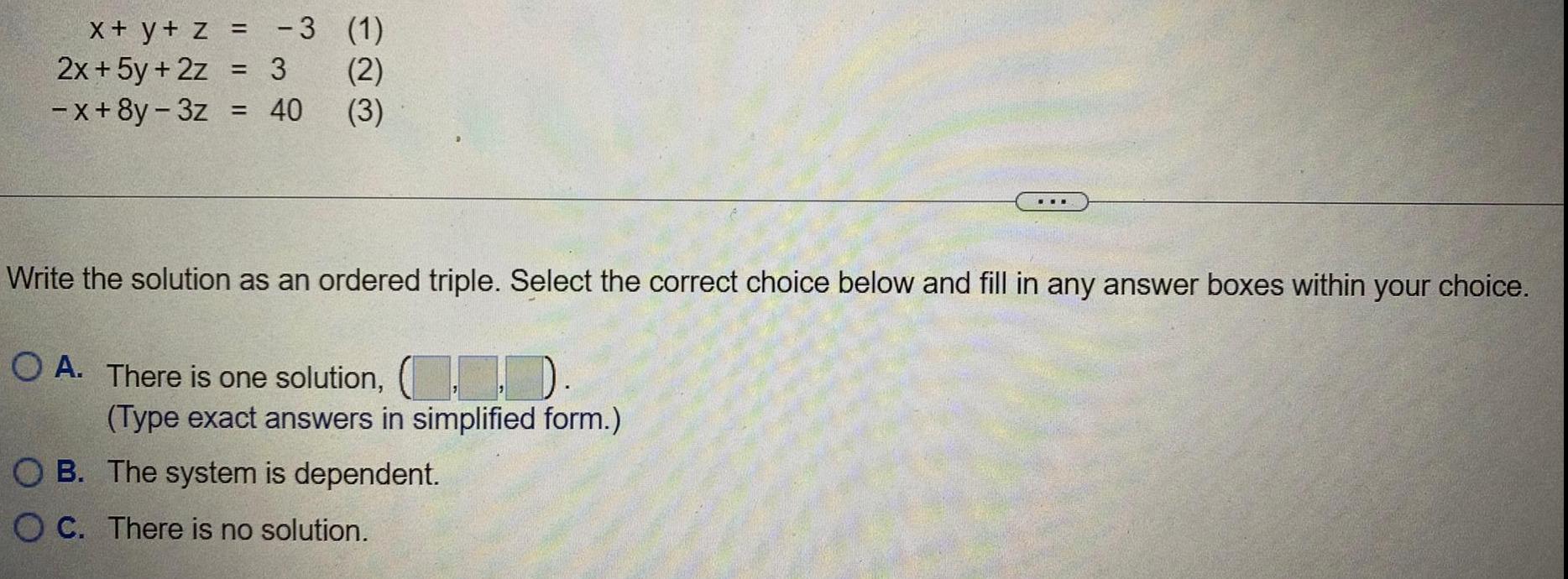
Calculus
Differential equationsx + y + z =
-3 (1)
2x + 5y + 2z = 3
(2)
-x+8y-3z = 40 (3)
...
Write the solution as an ordered triple. Select the correct choice below and fill in any answer boxes within your choice.
O A. There is one solution, (...
(Type exact answers in simplified form.)
OB. The system is dependent.
OC. There is no solution.

Calculus
Differential equationsLet y = sin(4x). If Ax = 0.2 at x = 0, use linear approximation to estimate Ay
Ay dy =
Find the percentage error
error =
%

Calculus
Differential equationsWhat value of C makes the trinomial a perfect square trinomial?
T²+18x+c

Calculus
Differential equationsGiven a solid bounded by the paraboloid z = 16-2² - y² in the first octant.
Draw the projection of diagram using mathematical application (GeoGebra etc.) from:
x-axis (2 m)
y-axis (2 m)
C. z-axis (2 m)
Hence, find the volume of the integral from each projection.
x-axis (8 m)
y-axis (8 m)
z-axis (8 m)
a.
b.
a.
b.
C.

Calculus
Differential equationsA police car is located 40 feet to the side of a straight road.
A red car is driving along the road in the direction of the police car and is 100 feet up the road from
the location of the police car. The police radar reads that the distance between the police car and
the red car is decreasing at a rate of 85 feet per second. How fast is the red car actually traveling
along the road?
The actual speed (along the road) of the red car is
feet per second

Calculus
Differential equationsPart I: Evaluate f(0)
A. Identify the function that will be used when x = 0. (1 point)
B. Find the value of this function when x = 0. (1 point)
Part II: Graph f(x).
-5
5
A. Graph the first function completely. (1 point)
B. On the same graph you used to answer part (A), graph the second
function completely. (1 point)
C. Identify the value of x at which the functions change. Remove the parts of
each line that are not included in domain of the corresponding function. (2
points)

Calculus
Differential equationsGiven: (x is number of items)
Demand function: d(z) =
Supply function: a(z) = 5√√z
Find the equilibrium quantity:
1805
Find the producer surplus at the equilibrium quantity: S
items

Calculus
Differential equationsFor the real-valued functions f(x) =
x + 2
and g(x) = 4x+5, find the composition fg and specify Its domain using interval notation.
x+3