Differentiation Questions and Answers

Calculus
DifferentiationSolve the following equation For an equation with real solutions support your answer graphically x 81 The solution set is Use a comma to separate answers Express complex numbers in terms of i
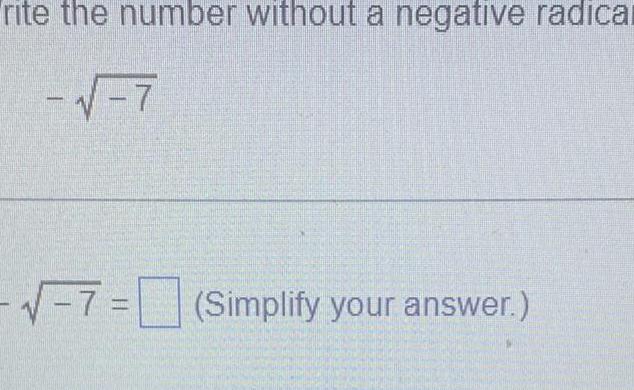

Calculus
DifferentiationDETAILS 07 A ladder that is 15 feet long leans against the side of a house The angle of elevation of the ladder is 80 Find the height from the top of the ladder one decimal place ft the ground Round your dis
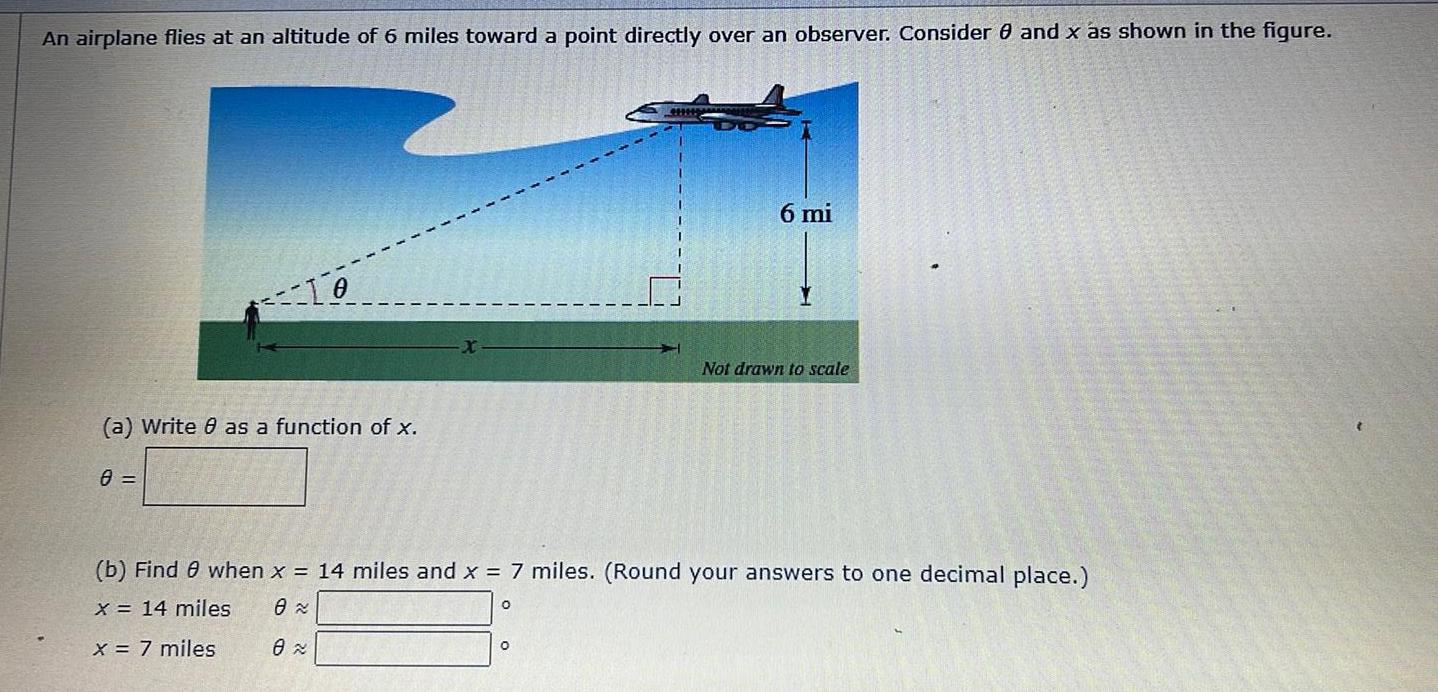
Calculus
DifferentiationAn airplane flies at an altitude of 6 miles toward a point directly over an observer Consider 0 and x as shown in the figure To a Write 8 as a function of x 8 0 6 mi b Find 8 when x 14 miles and x 7 miles Round your answers to one decimal place x 14 miles 8 x 7 miles 0 O Not drawn to scale
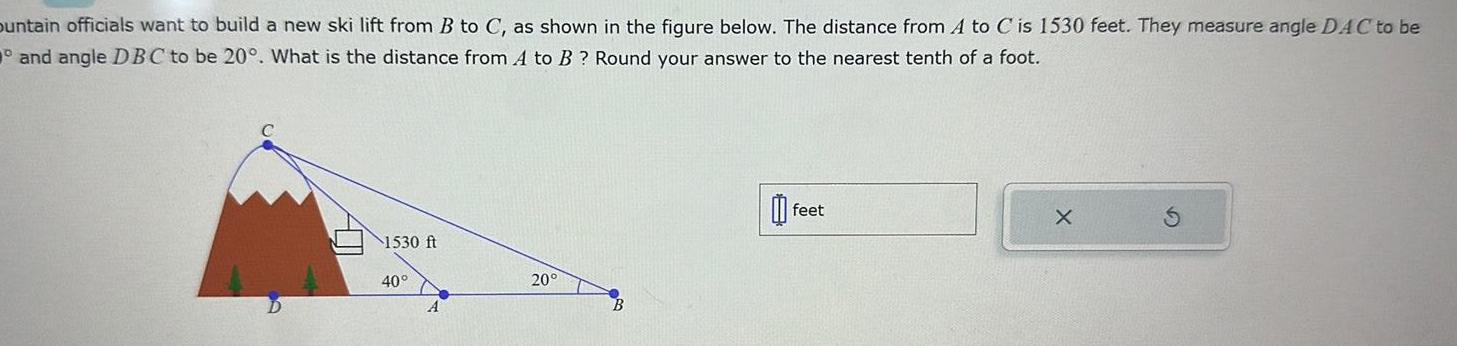
Calculus
Differentiationountain officials want to build a new ski lift from B to C as shown in the figure below The distance from A to C is 1530 feet They measure angle DAC to be and angle DBC to be 20 What is the distance from A to B Round your answer to the nearest tenth of a foot 1530 ft 40 A 20 feet

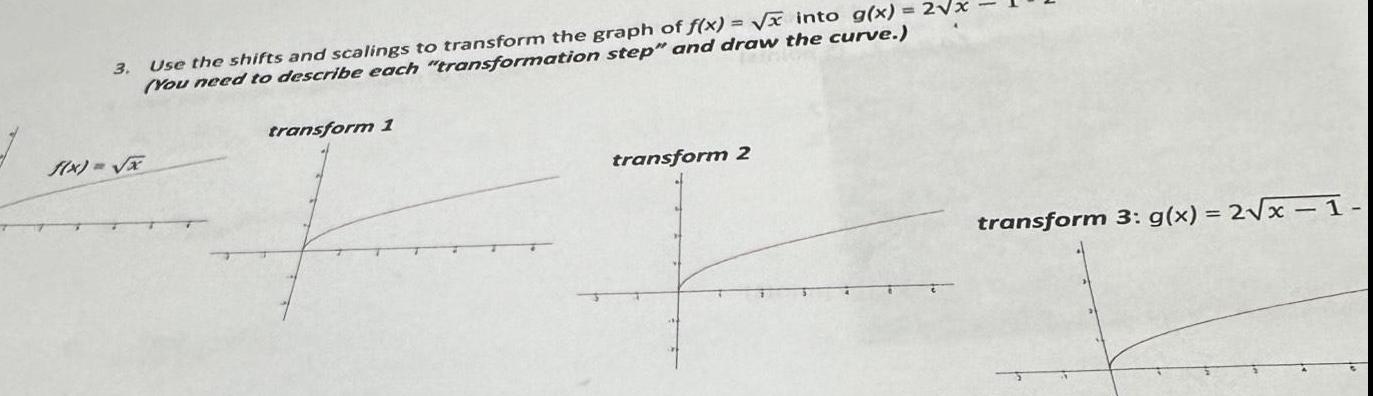
Calculus
Differentiation3 f x x Use the shifts and scalings to transform the graph of f x x into g x 2 x You need to describe each transformation step and draw the curve transform 1 transform 2 transform 3 g x 2 x 1
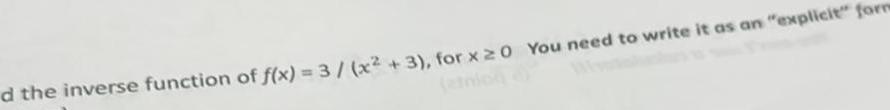
Calculus
Differentiationd the inverse function of f x 3 x 3 for x 20 You need to write it as an explicit form
Calculus
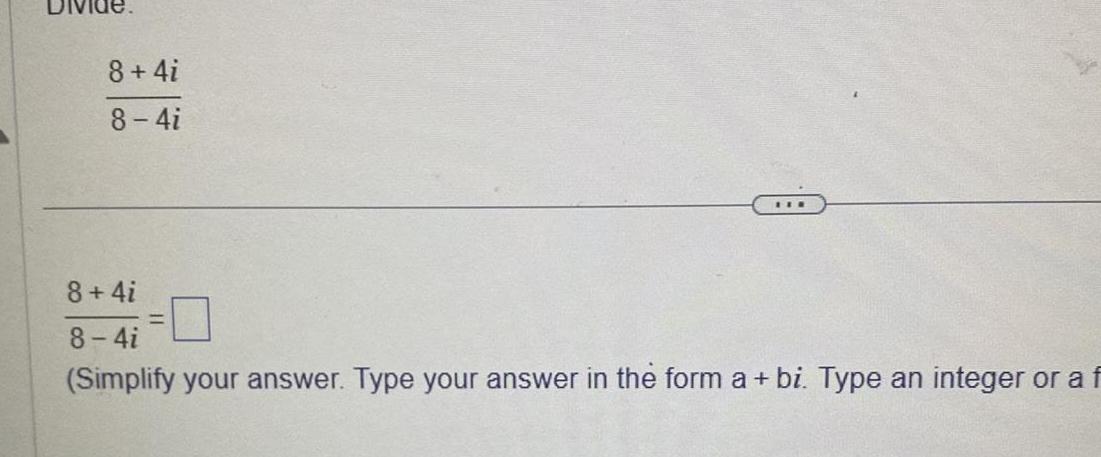
Differentiation8 4i 8 4i TIE 8 4i 8 4i Simplify your answer Type your answer in the form a bi Type an integer or a f
Calculus
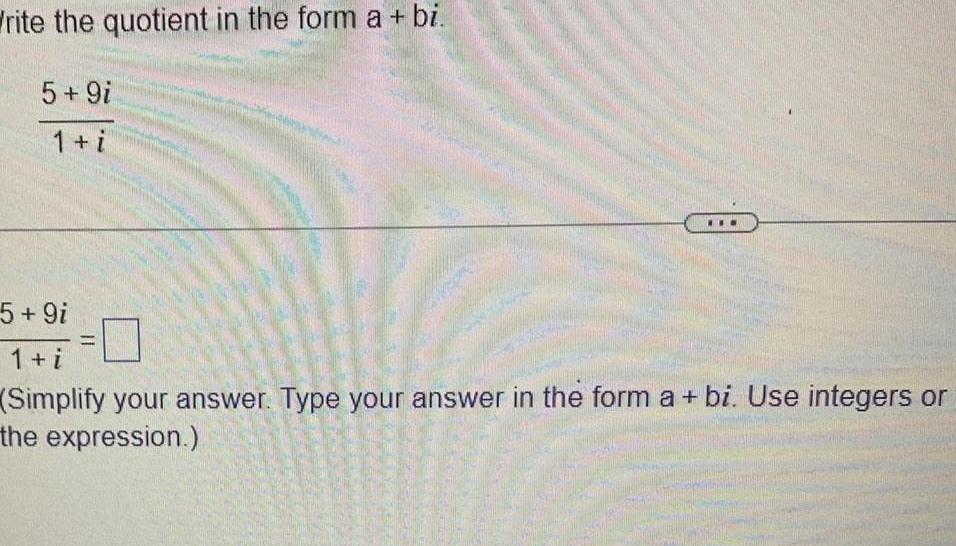
DifferentiationWrite the quotient in the form a bi 5 9i 1 i 5 9i 1 i Simplify your answer Type your answer in the form a bi Use integers or the expression

Calculus
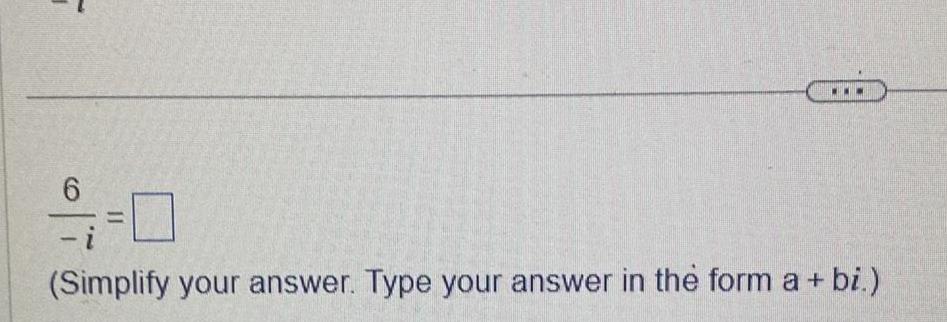
DifferentiationDivide as indicated 21 3 21 3 Simplify your answer Type an exact answer using radicals and i as needed Use integers or frac numbers in the expression

Calculus
DifferentiationSuppose f z is continuous on 4 7 and 4 f x 4 for all az in 4 7 Use the Mean Value Theorem to estimate f 7 f 4 Answer f 7 4

Calculus
DifferentiationUse a calculator to find an approximate value in radians of the expression rounded to five decimal places if it is defined If a answer is undefined enter UNDEFINED 8 cos 8 X

Calculus
Differentiation0 1 Points 8 DETAILS sin PREVIOUS ANSWERS MY NOTES Find all angles between 0 and 180 satisfying the given equation Round your answer to one decimal place Enter your answers as a comma separated list Enter degrees P
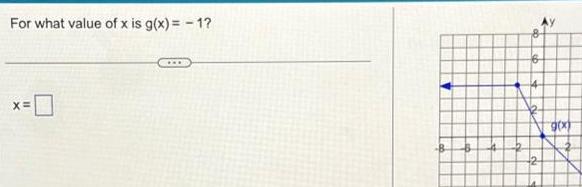
Calculus
DifferentiationK A sample of 12 grams of radioactive material is placed in a vault Let P t be the amount remaining after t years and let P t satisfy the differential equation P t 0 027P t Answer parts a through g d How much of the material will remain after 5 years 10 5 gram s Type an integer or decimal rounded to one decimal place as needed e How fast is the sample disintegrating when just 1 gram remains Use the differential equation Choose the correct process to find how fast the sample disintegrating when just 1 gram remains OA Solve P 1 0 027P t for P t B Evaluate P t 0 027P 1 C Solve 1 0 027P t for P t D Evaluate P t 0 027 1 The sample is disintegrating by about 0 027 gram s per year when just 1 gram remains f What amount of radioactive material remains when it is disintegrating at a rate of 0 111 gram per year Choose the correct process to find the amount of radioactive material that remains when it is disintegrating at a rate of 0 111 gram per year OA Solve P 0 111 0 027P t for P t OB Solve 0 111 0 027P t for P t C Evaluate P t 0 027 0 111

Calculus
DifferentiationA man is lying on the beach flying a kite He holds the end of the kite string at ground level and estimates the angle of elevation of the kite to be 50 If the string is 400 ft long how high is the kite above the ground Round your answer to the nearest foot Need Help MY NOTES PRACTICE ANOTH

Calculus
DifferentiationA 21 ft ladder leans against a building so that the angle between the ground and the ladder is 66 How high does the ladder reach on the building Round your answer to the nearest foot ft

Calculus
DifferentiationThe differential equation 1EJ The initial conditions Remarks Xlo X dX dt dX dt An da X dr 1 W a A dt f d X to dt 1 MATHEMATICS I Though the independent variable t of the function X t in the ODE 1 is stipulated to range in the interval I we expect the solution t X t of the initial value problems 4 to be defined only on a sub internal J of I with to EJ Indeed we come across concrete cases of the IVP in which a solution exists only on a sub inter J of I and therefore we grant this concession a solution need be defined only on a sub interval J of I II Often the initial conditions are expressed more explicitly in terms of dX the equations xt Xo to W dt da W 1 Let f RR be the function fx 1 x 0 1 x20 di dik 1 for all important special case of the ODE 3 is dX d X d X fx 6 di di di initial value problem f X x o 0 dt in which the function f is independent of the variable t f 0xR x xR R In this case we say that the ODE 6 is autonomous Returning to the initial value problem 5 there are two questions Does the initial value problem 5 admit a solution at all If it does is the solution unique Clearly because fis the main ingredient of the ODE the answer to both of there questions naturally depends on the properties of f especially on its behaviour around the initial condition t WW i e how if varies continuously differentially etc around too WW Following two examples illustrate that answers to both the questions are in general in the negative For this function we consider the first order autonomous case of the dX We contend that this initial value problem has no solution For if there was a solution X J R with OEJ then 0 f 0 1 0 implies that the solution tX t is strictly

Calculus
DifferentiationI Though the independent variable t of the function X t in the ODE 1 is stipulated to range in the interval I we expect the solution X t of the initial value problems 4 to be defined only on a sub internal J of I with to EJ Indeed we come across concrete cases of the IVP in which a solution exists only on a sub inter J of I and therefore we grant this concession a solution need be defined only on a sub interval J of I II Often the initial conditions are expressed more explicitly in terms of dX the equations X to Xo to W dt An important special fX dX dx d X d X di di di case MATHEMATICS di 1 in which the function f is independent of the variable t f 0xR x xR R In this case we say that the ODE 6 is autonomous Let f RR be the function f x 1 x 0 1 x 0 Returning to the initial value problem 5 there are two questions Does the initial value problem 5 admit a solution at all If it does is the solution unique Clearly because fis the main ingredient of the ODE the answer to both of there questions naturally depends on the properties of f especially on its behaviour around the initial condition to Ww i e how if varies continuously differentially etc around X WW Following two examples illustrate that answers to both the questions are in general in the negative Wk 1 of the ODE 3 is 6 For this function we consider the first order autonomous case of the dX initial value problem f X x o 0 dt dX di We contend that this initial value problem has no solution For if there was a solution X J R with OEJ then 0 f 0 1 0 implies that the solution X t is strictly dt monotonic increasing in a neighborhood 8 8 of O On the other hand 1 0 f t for all re 8 0 implies that t X t t is strictly monotonic decreasing in 8 0 Thus if the solution of the above IVP exists then it is strictly monotonic increasing as well as strictly monotonic decreasing This prevents a solution

Calculus
Differentiation0 as k MATHEMATICS This last observation is true because converging te Note that in the inequalities M K 1 10 j 1 MK Kj XI K MK n Kj X 1 x 1 the right hand sides are independent Kj lim x X lim of t and therefore 1 x 1 Ouniformly on to 1 1 as k p being arbitrary This completes the proof of our claim that the sequence x kEZ of functions is uniformly Cauchy on to to 1 X Using this last mentioned property of the sequence xk Z we define a function x 4 1 1x8 x 8 by putting x t lim x 1 t to to 1 The function x thus defined is the uniform limit of the sequence x kEN Therefore we have lim x 1 x 11 x1 x f s X 5 5 1 de ff s x s ds ff s lim x s ds ff s x s ds Kn lim f s x s ds is convergent Finally the identity All the above equations being valid because of the uniform convergence of of x fox on to 1 1 s x s ds t 1 1 1 1 derived above has the following two consequences 1 Differentiation of the identity implies

Calculus
DifferentiationAbout the sequence XKEZ we have the following x 1 EBx b for each 1 to b t b MKk a X 1 1 x 1 k 1 1E10 b t b k 20 c x k Z is uniformly Cauchy on t b t b verification of these properties is left for the reader We consider the uniform limit of the sequence x to 8 to 8 B x b C which is given by tet b t b b Thus x t lim xo kin x t lim x 1 4 00 1 2 x lim ff s x s ds 76 x A f s x s ds S s lim x s ds x ff s x s ds Thus the function rx 1 satisfying the integral equation x 1 x S f s x s ds for all te t b to b Finally the validity of this integral equation has the following two implications 4 x X t xo f s x s ds x 0 xo 50 4 S A dx d 0 af f s x s ds f t X 1 di dt Proposition 2 This now proves that the curve X 1 8 1 82 thus obtained is a solution of the initial value problem 20 2 3 UNIQUENESS OF A SOLUTION lim f s x s ds We prove an inequality which will lead us to the uniqueness of the solutions Gronwall s f a b 0x g a b 0 o be Chapter 2 Systmes of First Order ODE Let Inequality continuous functions and

Calculus
DifferentiationProposition 3 Let x J y J be two solutions of the initial value problem dx f t x x t x dt then x t y t for all 1 JOJ Proof Recall that both x and y being solutions of the initial value problem satisfy the integral equations on their domain intervals x 1 x f s x s ds y t x f s y s ds Therefore x 1 y 1 f s x s f s y s ds which implies x 1 y 1 0 s x s s y s 0 SK x s y s for all 12 Applying Gronwalls result with A 0 we get 0 x 1 y 1 0 for all t t This gives the desired equality x t y t for all 1JJ Towards the uniqueness of the solution of the initial value problem 3 we consider all the solutions of the initial value problem 3 Let the totality of them be denoted by J XEA the solutions x being thus indexed by a suitable indexing set A Above we have verified that any two solutions say x and xx are equal on the overlap JJ of their domains Therefore we patch together all the solutions to get a maximal solution is the solution defined on the largest open interval It is obtained as follows Let J UJ e clearly Jis an open sub internal of I with x J and all the solutions x patch up to get a solution x J of the initial value problem 3

Calculus
DifferentiationProof Let Ix be arbitrary Using openness of IxJ choose 8 0 such that t 8 1 8 x 8 x 8 IXJ Of Now the function is continuous on IxJ and therefore it is x bounded on the compact subset to 8 to 8 x 8 x 8 We consider any constant k 0 with the property 1 0 K K for all tto 8 1 8 and for all xx 8 x 8 x Finally let 1 t 8 1 8 x y in x 8 x 8 be arbitrary By the mean value theorem of differential calculus we have Of fty f t x y x 1 Z x for some z between x and y Therefore 1 350 3053 1 1 2 K yx If t y f t x z Ox Since 1 2 18 1 8 x x 8 x 8 and therefore of 1 Z K t Z K This proves the locally Lipschitz property of f dx Theorem 1 Emil Picard If f 1 J Ris locally Lipschitz then for any to EI x EJ the initial value problem df f t x x to dx has a solution x 8 to 8J for some 8 0 Proof Choose 8 0 such that to 8 1 8 1 8 x 8 J and there exists K 0 for which f 1 x f t y Kx y holds for all t 8 8 x 8 x 8 We choose M 0 such that f 1 x M for all te t 8 1 8 x x 8 x 8 Using the constants 8 0 K 0 M 0 chosen above we choose 18 one more constant 7 satisfying 0 n min KM We define a sequence of functions 1 1 R keZ recursively as follows

Calculus
DifferentiationThis shows that the solutions of the order k ODE 4 can be studied in terms of the solutions of the first order ODE 5 Note that if f of the ODE 4 is continuously differentiable on its domain namely the set IxQxR R then F is continuously differentiable on its own domain consequently the existence and uniqueness result for the first order ODE applies to the initial value problem The solution of which giving the solution of the above initial value problem dt to the system dx dt y X dx di has a unique solution 2 dx dt XoXo fo W di We summarize this observation in the following Theorem 3 If the function f 1xxR x R R is continuously differentiable on its domain of definition then the initial value problem dx dk 1x dx 1 x dr dr 1 condition 3 dx dx dt dt dt y To dy F t y dt 1 The second order ODE dx di dy di dz di Illustrative Examples These examples explain how we obtain a system of first order ODE from a given higher order ODE 10 W d x dr kx Moreover the initial condition xoxo yo gives the initial dx The initial value problem d x 4d x dx dr 10 W dr 1 y x 0 1 31 1 x 1 dt d x dt2 z y 0 2 for the reduced first order system dx x 0 1 0 2 0 3 dt to W 1 Chapter 2 Systmes of First Order ODE kx k being a given constant gives rise reduces to the following system of first order ODE along with the initial conditions 28 42 3ty 1 x 1 z 0 3 The third order system of ODE d x x y dt y x y is equivalent to the following system of first order ODE in 2 2 2 23 24 25 26 35
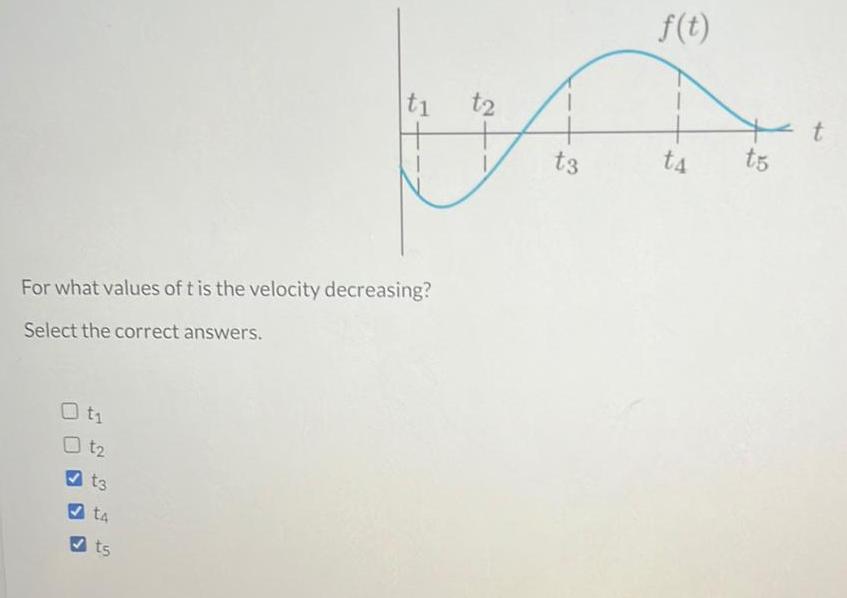
Calculus
DifferentiationFor what values of t is the velocity decreasing Select the correct answers t t2 t3 t4 s ts t t3 f t ta t5 t

Calculus
DifferentiationFind equations of the tangent lines to the curve X 1 X 1 that are parallel to the line x 2y 5 Enter your answers as a comma separated list of equations y Need Help Read It
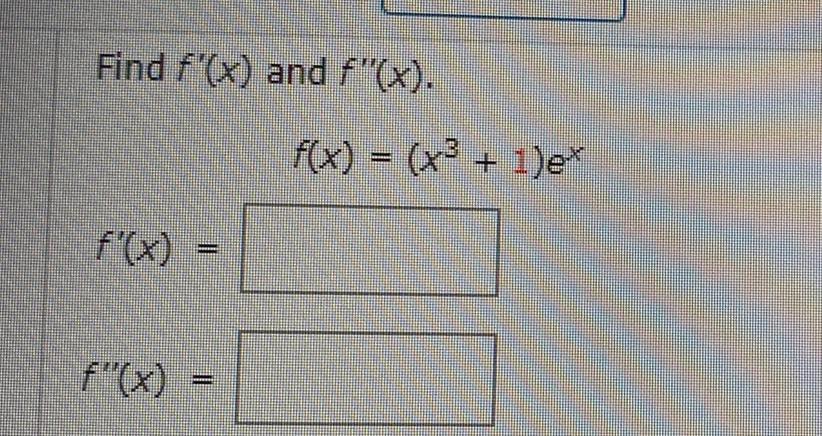
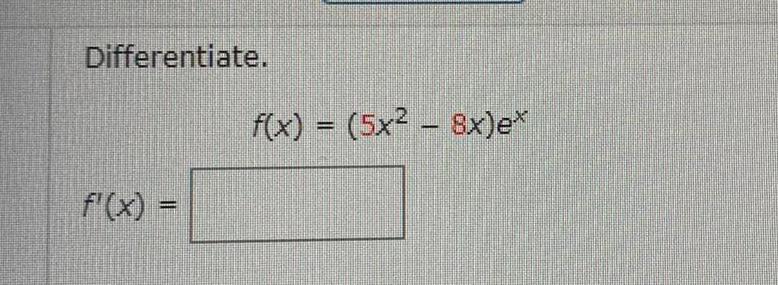
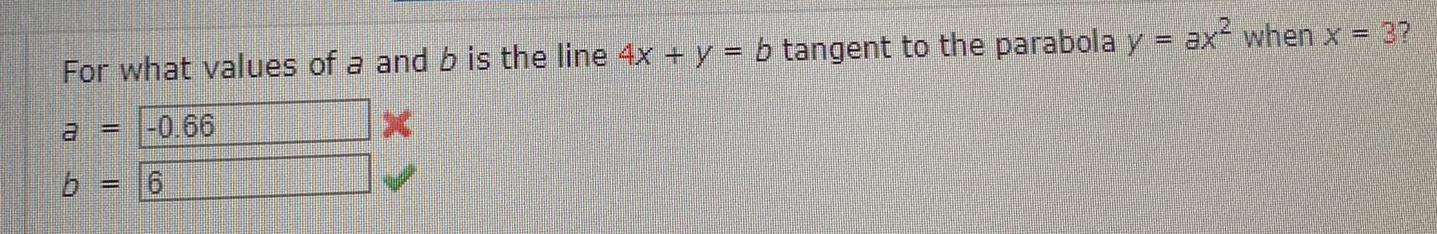
Calculus
DifferentiationFor what values of a and b is the line 4x y b tangent to the parabola y ax when x 3 a 0 66 6
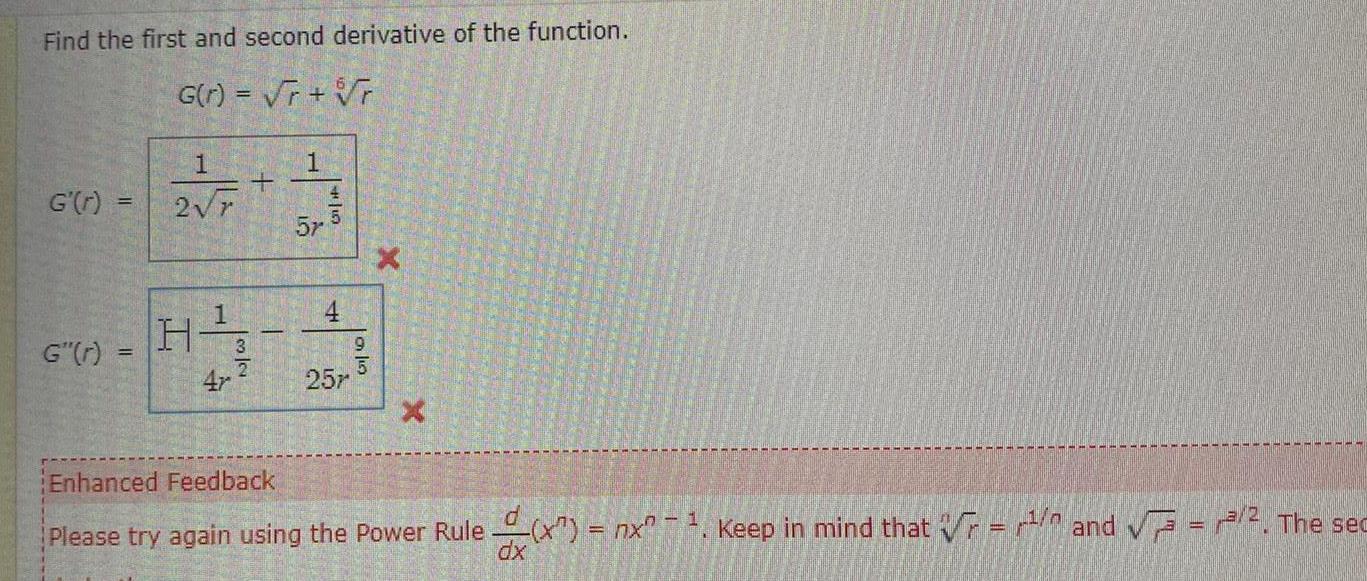
Calculus
DifferentiationFind the first and second derivative of the function G r r r G r G r 1 2 r H 1 4r 3 1 4 5 57 4 195 257 Enhanced Feedback Please try again using the Power Rule x nx Keep in mind that and The sec

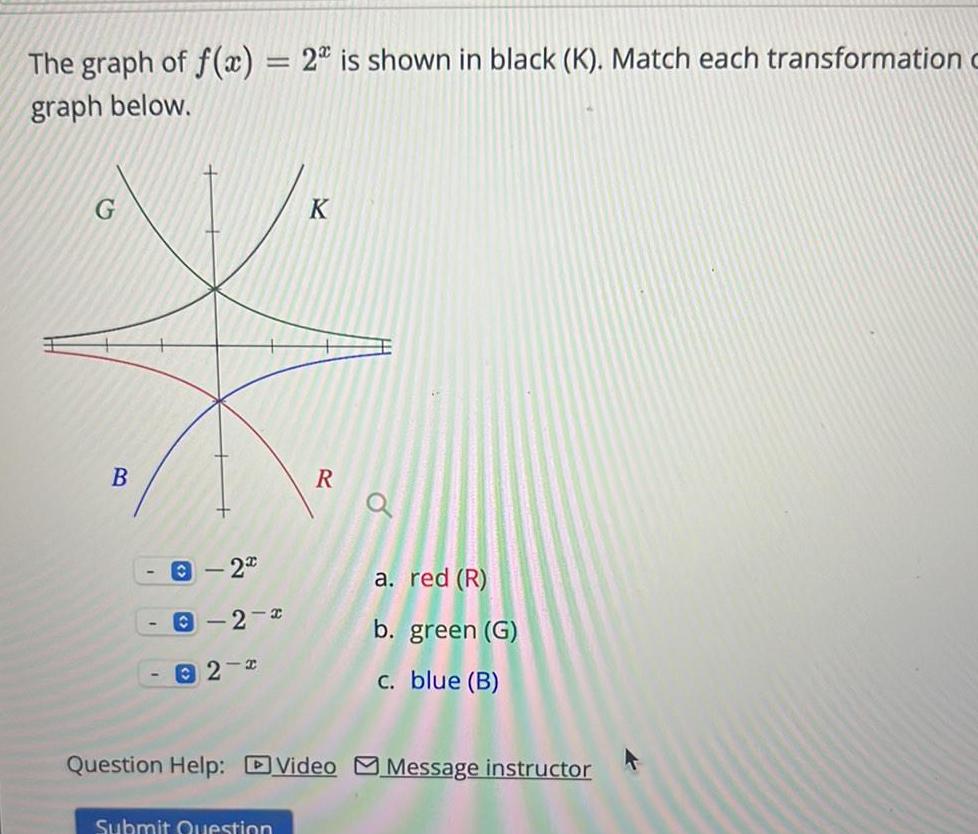
Calculus
DifferentiationThe graph of f x 2 is shown in black K Match each transformation c graph below B I 22 1 C 2 2 2 2 K Submit Question R a a red R b green G c blue B Question Help Video Message instructor

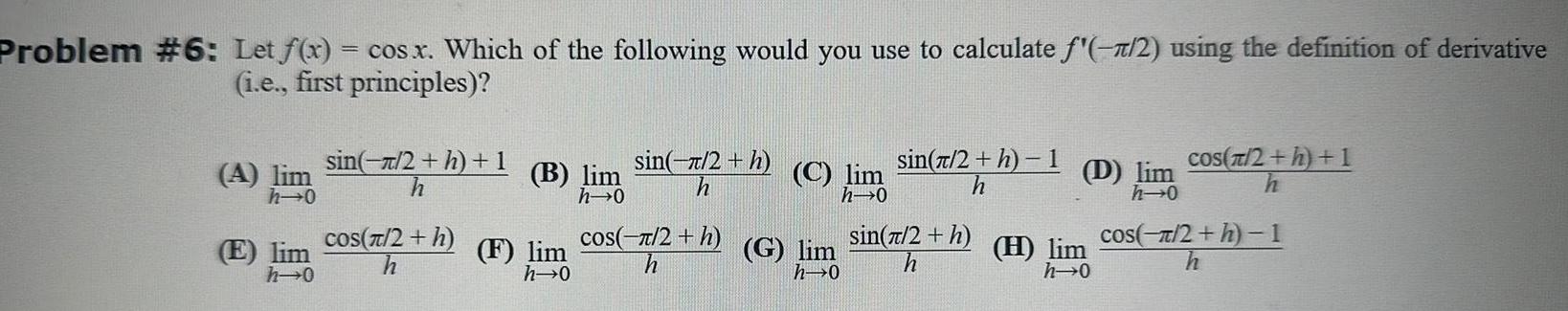
Calculus
DifferentiationProblem 6 Let f x cos x Which of the following would you use to calculate 2 using the definition of derivative i e first principles A E h 0 h 0 sin 2 h 1 h cos 2 h B lim F lim h 0 sin 2 h h os 2 h C lim h 0 G lim h 0 sin 2 h 1 h sin 2 h h D lim h 0 H lim h 0 cos 2 h 1 cos 2 h 1
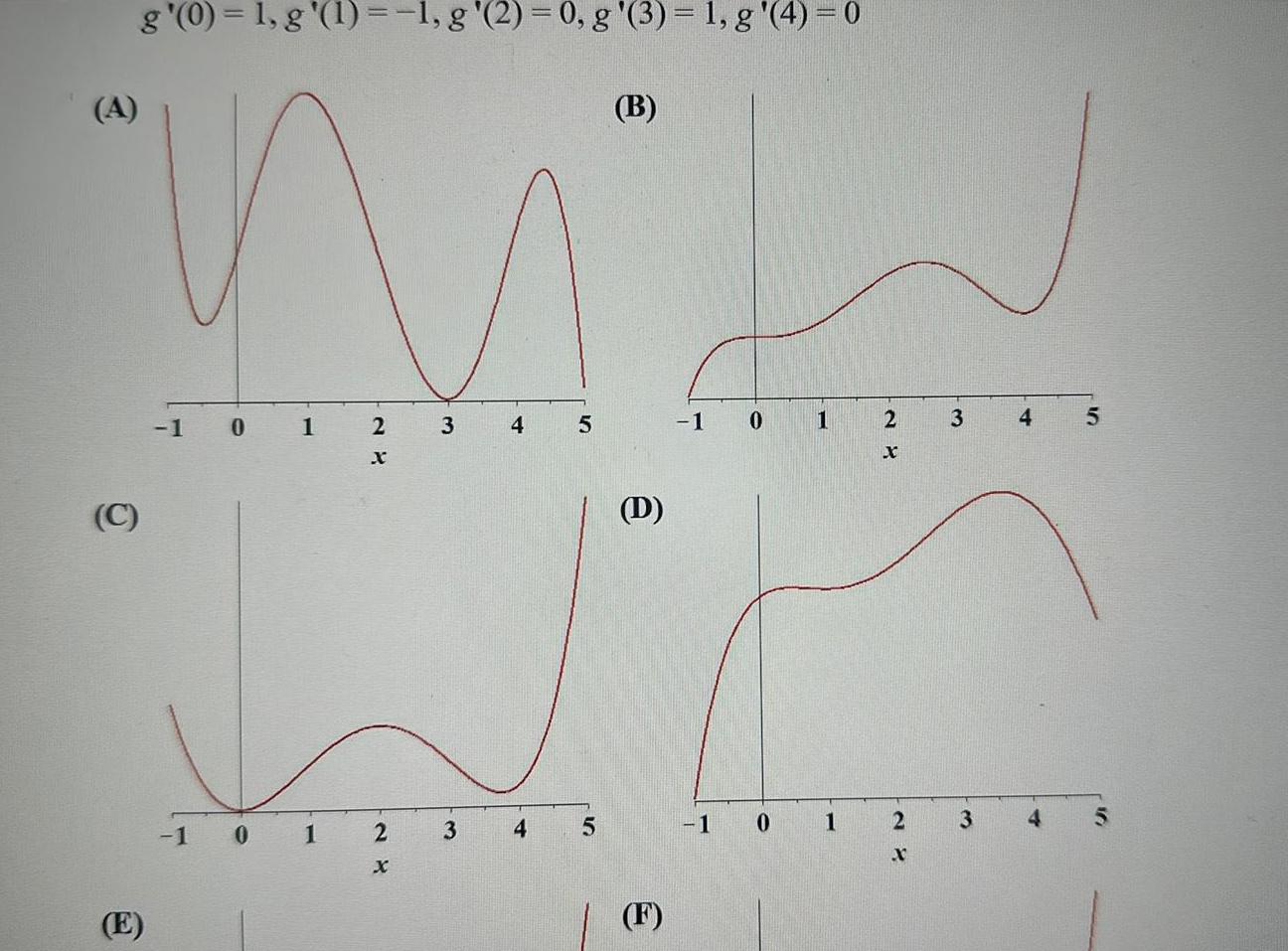
Calculus
Differentiationg 0 1 g 1 1 g 2 0 g 3 1 g 4 0 B Mit A C 1 0 1 1 0 1 2 X 2 3 3 4 4 5 5 D F 1 0 1 0 1 1 2 X 2 X 3 3 4 4 5
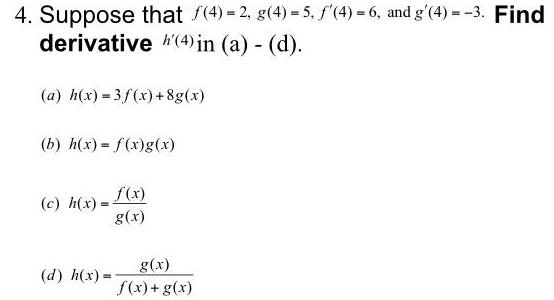
Calculus
Differentiation4 Suppose that 4 2 g 4 5 f 4 6 and g 4 3 Find derivative 4 in a d a h x 3f x 8g x b h x f x g x c h x d h x f x g x g x f x g x

Calculus
Differentiation8 12 17 20 1 2est log e C 22 tan 7 4x C 24 log 2sin x 3cos x C 1 21 C 9 x 1 C 10 2log x 1 C x 4 x 8 C 70x n x c log x 1 m 32 26 2sin x C 29 log sin x C C x 1 22 1 37 39 B C 34 2 tanx C x 1 15 log19 4x 1 C 16 18 C cos tan x C sin 2x C NCERT 35 1 log x C sin 4x 10 C 1 13 18 2 3x 30 log 1 cos x C 31 Rationalised 2023 24 19 log e EXERCISE 7 3 sin12r r sin8r si 25 ottone repurushed tan 2x 3 x C 33 1 1 tan x 28 2v1 sinx C 1 1 cos x sin x C C 22 38 D 14 C log cos x sin x C 36 x log x C ANSWERS cos 7x cos x C 441
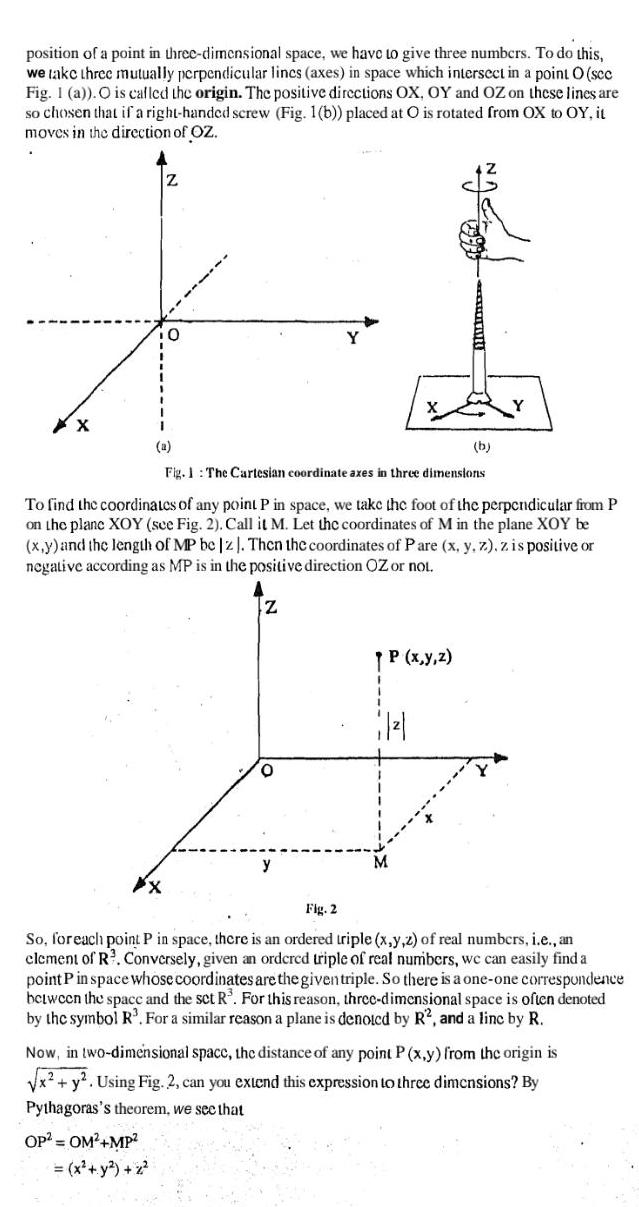
Calculus
Differentiationposition of a point in three dimensional space we have to give three numbers To do this we take three mutually perpendicular lincs axes in space which intersect in a point O sec Fig 1 a O is called the origin The positive directions OX OY and OZ on these lines are so chosen that if a right handed screw Fig 1 b placed at O is rotated from OX to OY it moves in the direction of OZ XX Z X 0 OP OM MP x y z a Fig 1 The Cartesian coordinate axes in three dimensions To find the coordinates of any point P in space we take the foot of the perpendicular from P on the plane XOY see Fig 2 Call it M Let the coordinates of M in the plane XOY be x y and the length of MP be z Then the coordinates of Pare x y z z is positive or negative according as MP is in the positive direction OZ or not Z O NACE P x y z 662 1 b Fig 2 So for each point P in space there is an ordered triple x y z of real numbers i e an element of R Conversely given an ordcrcd triple of real numbers we can easily find a point P in space whose coordinates are the given triple So there is a one one correspondence between the space and the set R For this reason three dimensional space is often denoted by the symbol R For a similar reason a plane is denoted by R2 and a linc by R Now in two dimensional space the distance of any point P x y from the origin is x y Using Fig 2 can you extend this expression to three dimensions By Pythagoras s theorem we see that

Calculus
DifferentiationFig 2 Look at the graph of f in Fig 2 You will see that when x is small x is also small As x comes closer and closer to er to 0 x also comes closer and closer to zero It is reasonable to expect that lim f x 0 as x 0 Let us prove that this is what happens Take any real number e 0 Then I f x 01 ix i x e Therefore if we choose 8 we get 1 f x Oke whenever 0 1x 01 This gives us lim f x 0 3 2 A useful general rule to prove lim f x Lis to write down f x L and then express it in terms of x a as much as possible Let us now see how to use this rule to calculate the limit in the following examples x 1 Example 2 Let us calculate lim lim 241 12 X is not We know that division by zero is not defined Thus the function f x defined at x 1 But as we have mentioned earlier when we calculate the limit as x approaches I we do not take the value of the function at x 1 Now to obtain x 1 we first note that x 1 x 1 x 1 so that x 1 for x 1 lim x 1 741 Therefore lim As x approaches 1 we can intuitively see that this limit approaches 2 To prove that the limit is 2 we first write f x L x 1 2 x 1 which is itself in the form x a since a 1 in this case Let us take any number e 0 Now 1 x 1 21 E lx 1 E Thus if we choose 8 E in our definition of limit we see that x 1 x 1 8 E if x L1 1x 11 e This shows that lim x 1 2 Hence X41 1 1 X 1 Example 3 Let us prove that lim x 4 13 13 That is we shall prove that e 0 38 0 such that 1 x 4 131 e whenever Ix 3 Here f x L x 4 13 x 9 and x a x 3
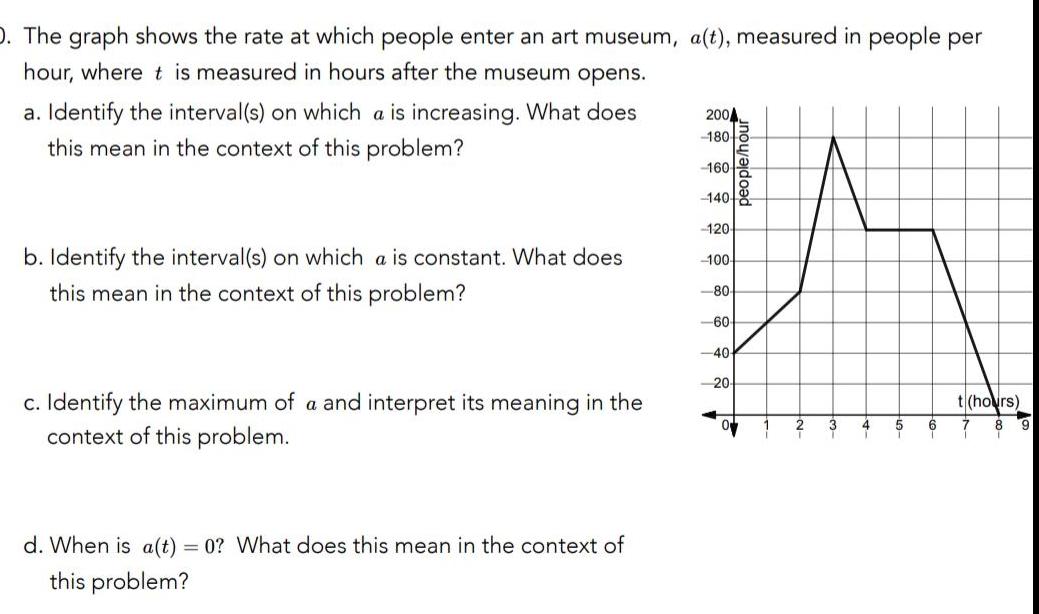
Calculus
DifferentiationD The graph shows the rate at which people enter an art museum a t measured in people per hour where t is measured in hours after the museum opens a Identify the interval s on which a is increasing What does this mean in the context of this problem b Identify the interval s on which a is constant What does this mean in the context of this problem c Identify the maximum of a and interpret its meaning in the context of this problem d When is a t 0 What does this mean in the context of this problem 2004 180 160 140 120 100 80 60 40 20 people hou 3 4 5 6 t hours 7 8
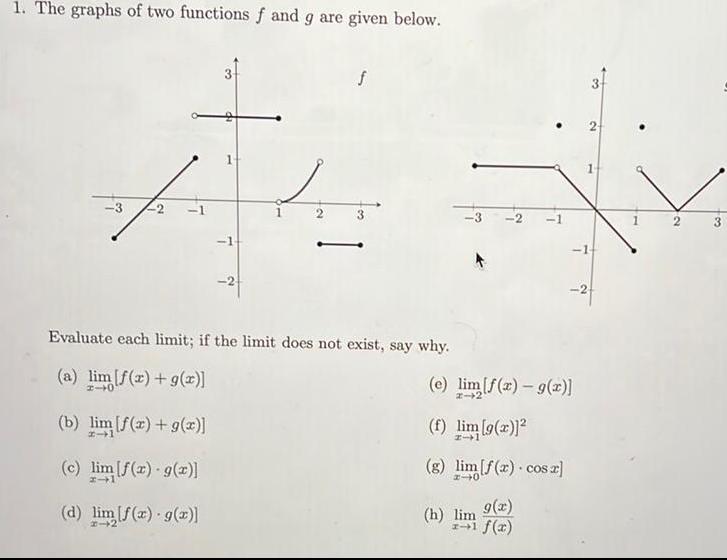
Calculus
Differentiation1 The graphs of two functions f and g are given below 11 Evaluate each limit if the limit does not exist say why a lim f x g x 40 b lim f x g x c lim f x g x d lim f x g x 14 e lim f x g x f lim 9 2 g lim f x cos z g x h lim f x 2 3
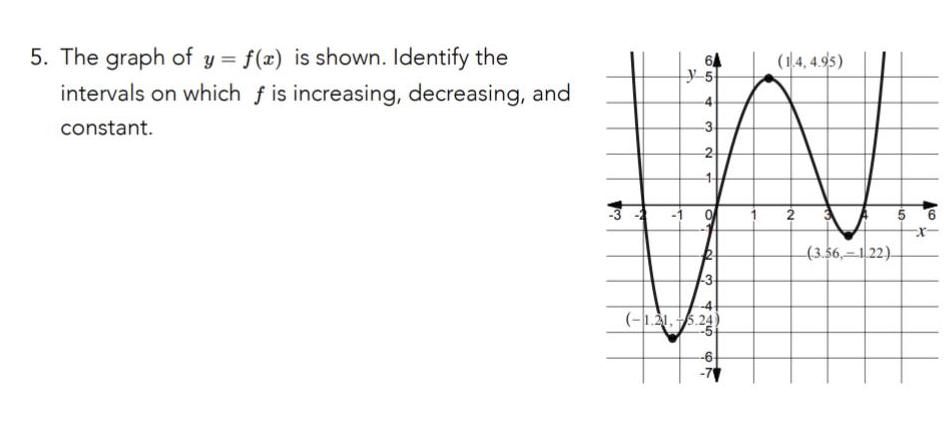
Calculus
Differentiation5 The graph of y f x is shown Identify the intervals on which f is increasing decreasing and constant 3 y 5 3 2 N 3 1 215 24 6 14 4 95 2 3 56 122 5 6

Calculus
Differentiation9 After doing some market research Crunchy Cookie Inc has found that their profit on cookies after spending amount on advertising can be modeled by P x 5000 1000x 5a Both x and P x are measured in thousands of dollars a What is the most profit that Crunchy Cookie Inc can make b How much would they have to spend on advertising to achieve this result c Is there ever a time when Crunchy Cookie Inc will make no profit Explain why or why not Profit in thousands 55000 50000 45000 E 40000 35000 50 30000 25000 20000 15000 10000 5000 PM 50 Advertising in thousands 100 150 200
Calculus
Differentiation5 Sketch the graph of a function that is increasing for a 5 constant for 5 x 0 increasing for 0 x 2 and decreasing for x 2 6 5 4 3 2 1 8 7 6 5 4 3 2 10 1 2 3 4 5 1 2 3 4 5 6 7 8 tr
Calculus
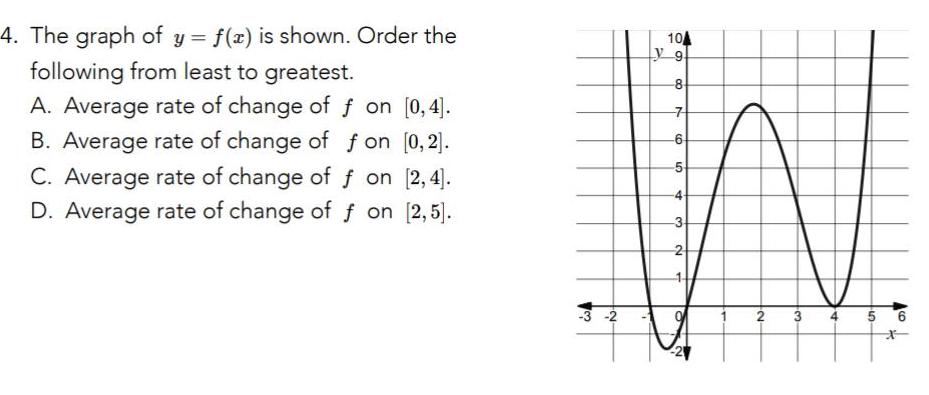
Differentiation4 The graph of y f x is shown Order the following from least to greatest A Average rate of change of f on 0 4 B Average rate of change of fon 0 2 C Average rate of change of f on 2 4 D Average rate of change of on 2 5 w 104 Ly9 8 N 7 6 5 4 3 2 O 2 3 A 5 6 x


Calculus
Differentiation2 The temperature of a mug of hot chocolate t minutes after it is prepared is given by the function H t where H is measured in degrees Fahrenheit Selected values of H t are given below t 0 2 5 10 13 20 H t 170 137 107 83 77 72 Find the average rate of change of the temperature of the hot chocolate between t 0 and t 2 Use proper units in your answer