Differentiation Questions and Answers

Calculus
DifferentiationLet g(w) = -arctan(17^w)
Determine the critical values of g. If multiple such values exist, enter the solutions using a comma-separated list.

Calculus
DifferentiationLet g(z)=5ze^3z
Determine the critical values of g. If multiple such values exist, enter the solutions using a comma-separated list.

Calculus
DifferentiationLet h(y) = 10y - 5
Determine the critical values of h. If multiple such values exist, enter the solutions using a comma-separated list.

Calculus
DifferentiationLet h(w) = -3.8ʷw⁸
Determine the critical values of h. If multiple such values exist, enter the solutions using a comma-separated list.

Calculus
DifferentiationLet g(v) = -6v² + 18v³ +7 - 16v
Determine the critical values of g. If multiple such values exist, enter the solutions using a comma-separated list.

Calculus
DifferentiationLet f(u) = -14u(u + 10)1/3
Determine the critical values of f. If multiple such values exist, enter the solutions using a comma-separated list.
u =
No critical values exist.

Calculus
DifferentiationLet g(x)=x√9+10x
Determine the critical values of g. If multiple such values exist, enter the solutions using a comma-separated list.
x =
No critical values exist.
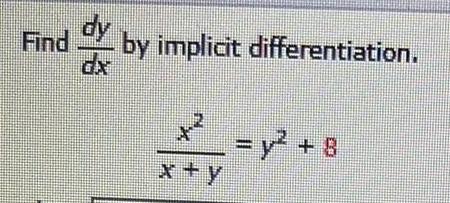
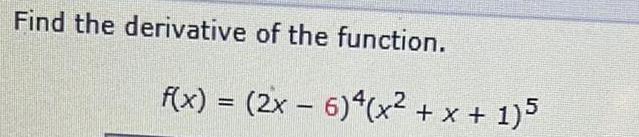
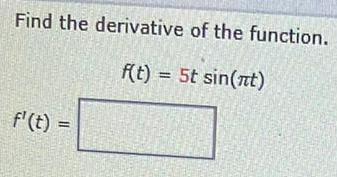
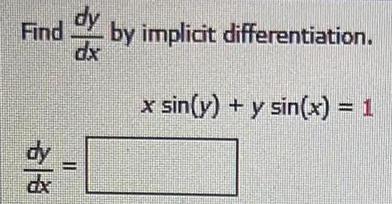
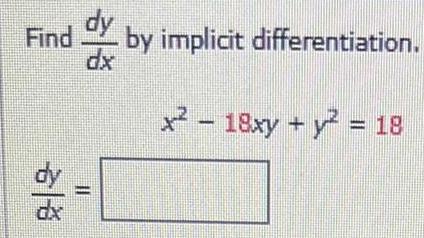
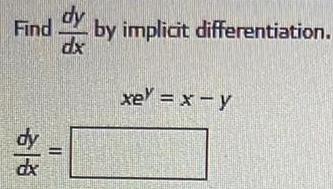
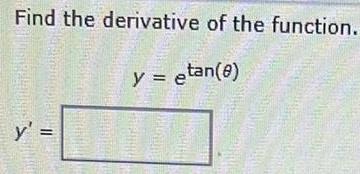
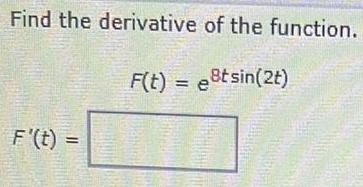
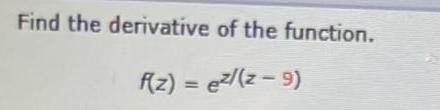
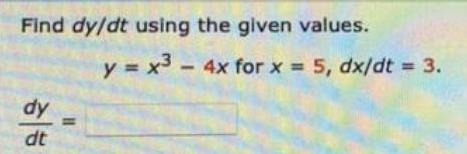
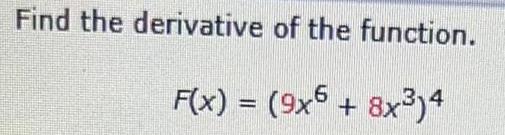
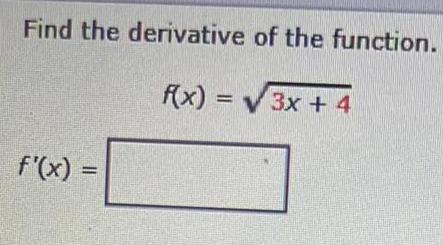
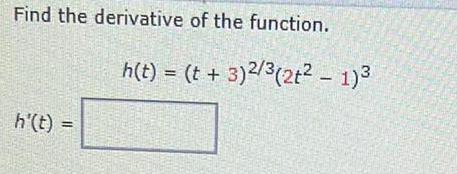

Calculus
DifferentiationUse the implicit differentiation to find the derivative dy/dx= y', given the implicit
equations:e^3xy = 3x + y²


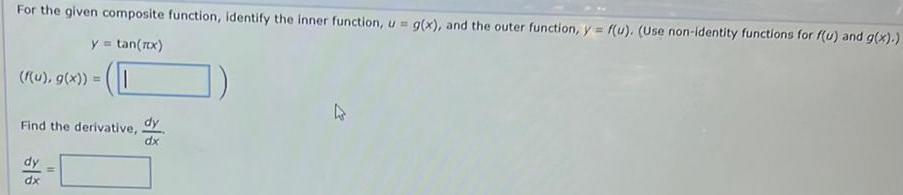
Calculus
DifferentiationFor the given composite function, identify the inner function, u = g(x), and the outer function, y = f(u). (Use non-identity functions for f(u) and g(x).)
y = tan(πx)
(f(u), g(x)) =
Find the derivative, dy/dx

Calculus
DifferentiationTwo trains leave from the same station, one going north at 30 miles/hr and one going west at 40 miles/hr. The one going west leaves 1 hour later than the one going north. When the northbound train is 120 miles from the station, how fast is the distance between the trains changing?



Calculus
DifferentiationThe function p(t) = 2000t/ 4t+75 gives the population p of deer in an area after t months.
a) Find p'(5), p'(25), and p'(50).
b) Find p''(5), p''(25), and p''(50).
c) Interpret the meaning of your answers to part (a) and (b). What is happening to the population of deer in the long term?

Calculus
DifferentiationThe equation of motion of a particle is s= t³ - 27t, where s is measured in meters and t is in seconds.
(a) Find the velocity and acceleration as functions of t.
v(t) =
a(t) =
(b) Find the acceleration, in m/s2, after 9 seconds.
m/s²
(c) Find the acceleration, in m/s2, when the velocity is 0.
m/s²
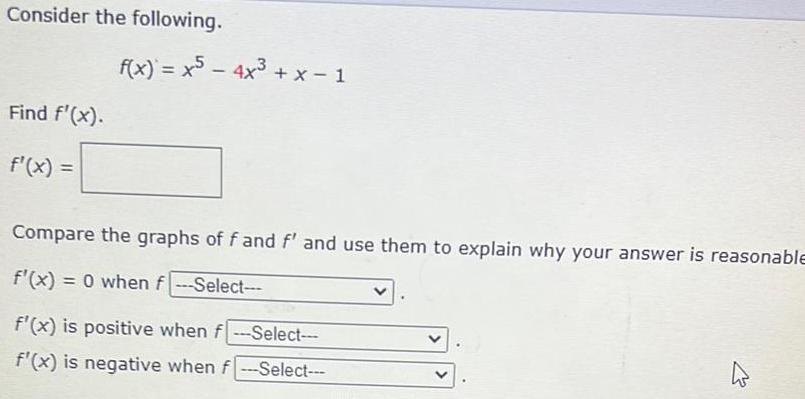
Calculus
DifferentiationConsider the following.
Find f'(x).
f'(x) =
f(x) = x5 - 4x³ + x-1
Compare the graphs of f and f' and use them to explain why your answer is reasonable
f'(x) = 0 when f_________
f'(x) is positive when f ____
f'(x) is negative when f ______

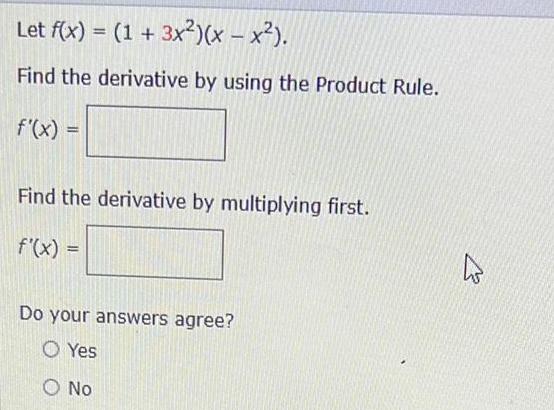
Calculus
DifferentiationLet f(x) = (1 + 3x²)(x - x²).
Find the derivative by using the Product Rule.
f'(x) =
Find the derivative by multiplying first.
f'(x) =
Do your answers agree?
Yes
No

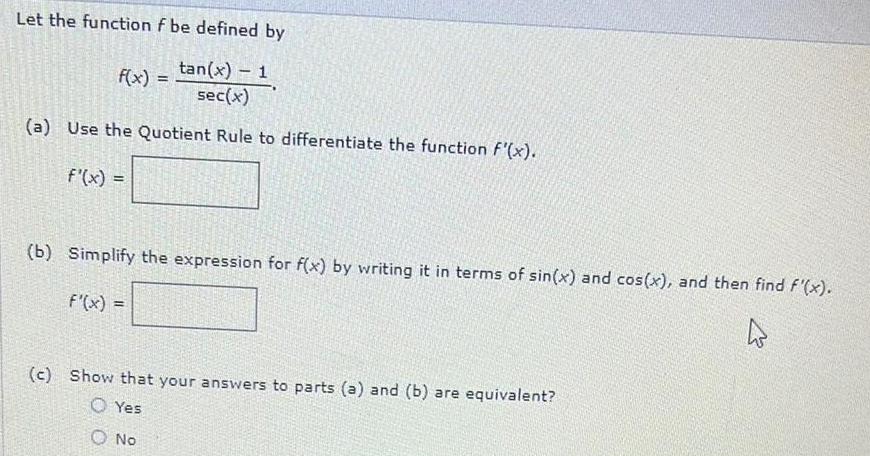
Calculus
DifferentiationLet the function f be defined by
f(x)=tan(x) -1/sec(x)
(a) Use the Quotient Rule to differentiate the function F'(x).
f'(x) =
(b) Simplify the expression for f(x) by writing it in terms of sin(x) and cos(x), and then find f'(x).
F'(x) =
(c) Show that your answers to parts (a) and (b) are equivalent?
Yes
No
![Write the composite function in the form f(g(x)). [Identify the inner function u = g(x) and the outer function y = f(u).] (Use non-identity functions for f(u) and g(x).)
y=e³√x
(f(u), g(x)) =
Find the derivative
dy/dx=](https://media.kunduz.com/media/sug-question/raw/84230383-1657012945.933773.jpeg?w=256)
Calculus
DifferentiationWrite the composite function in the form f(g(x)). [Identify the inner function u = g(x) and the outer function y = f(u).] (Use non-identity functions for f(u) and g(x).)
y=e³√x
(f(u), g(x)) =
Find the derivative
dy/dx=

Calculus
DifferentiationGraph the parabola.
y=-2x²-12x-14
Plot five points on the parabola: the vertex, two points to the left of the vertex, and two points to the right of the vertex. Then click on the graph-a-function
button.
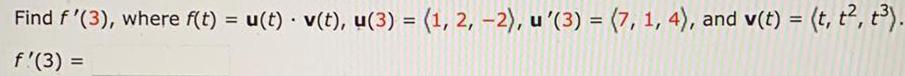
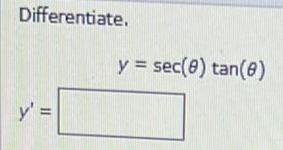
Calculus
DifferentiationFind f '(3), where f(t) = u(t) · v(t), u(3) = (1, 2, -2), u'(3) = (7, 1, 4), and v(t) = (t, t², t³).
f'(3) =
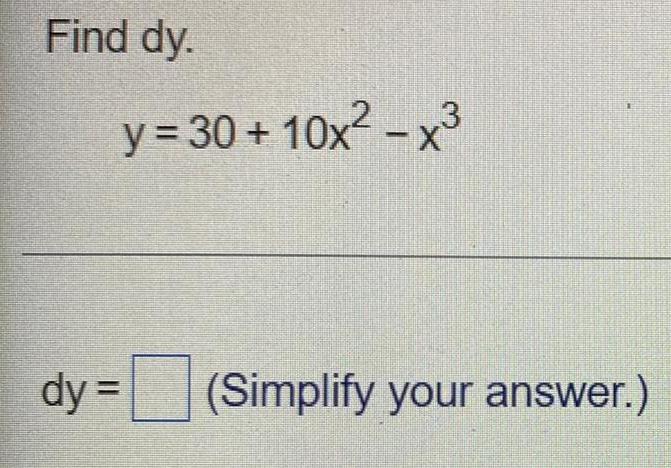

Calculus
DifferentiationConsider the following vector equation.
r(t) = 4 sin(t)i - 3 cos(t)j
(a) Find r'(t).
r' (t) =
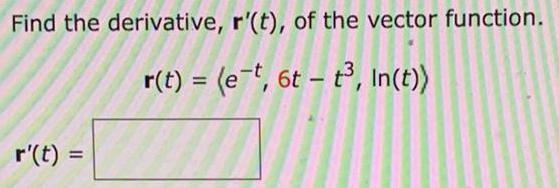
Calculus
DifferentiationFind the derivative, r'(t), of the vector function.
r(t) = (e^-t, 6t - t³, In(t))
r'(t) =
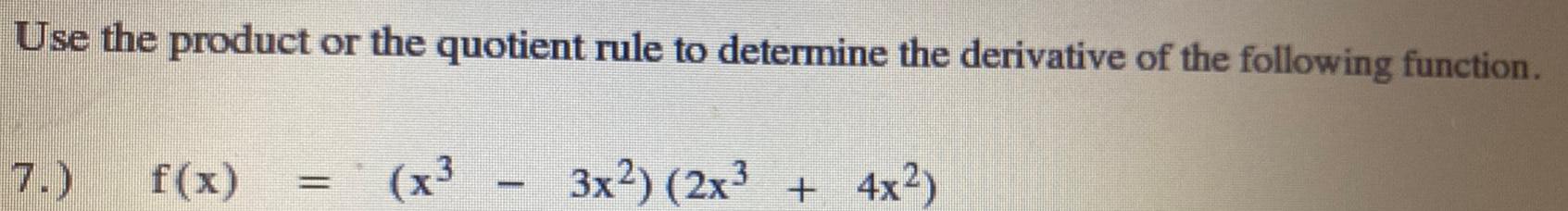
Calculus
DifferentiationUse the product or the quotient rule to determine the derivative of the following function.
f(x)=(x³-3x²) (2x³+4x²)

Calculus
DifferentiationFind the average cost function if cost and revenue are given by C(x) = 112+ 4.2x and R(x) = 9x-0.04x².
The average cost function is C(x) =______

Calculus
DifferentiationFind the slope and an equation of the line tangent to the graph of the given function at the indicated f(x)=(√x²)^1/3+5/3 x ,(8,4)

Calculus
DifferentiationA non-linear system is governed by the following differential equation
dx
+x²u; x(0) 0.1; u = 1
dt
a. (5) Solve the diff-eq numerically and plot the response
b. (5) Linearize the diff-eq about u=1. Write down the diff-eq
c. (5) Plot the numerical solution of linearized differential equation.
d. (5) Solve the diff-eq analytically (variable separable) for u=1.
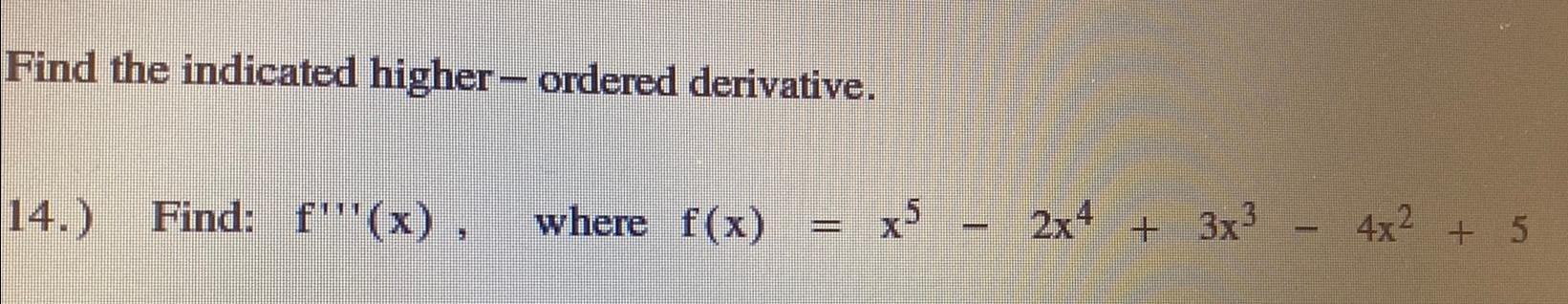
Calculus
DifferentiationFind the indicated higher - ordered derivative.
Find: f'''(x), where f(x) = x5 - 2x4+ 3x³ - 4x² + 5
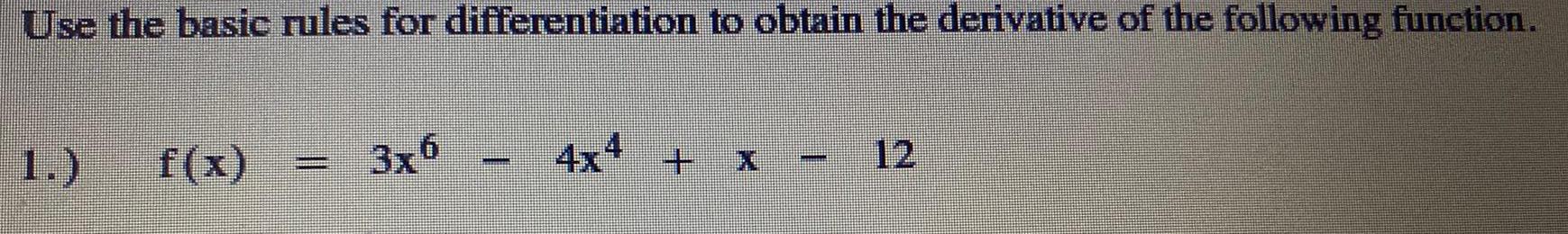
Calculus
DifferentiationUse the basic rules for differentiation to obtain the derivative of the following function.
f(x) =3x6 - 4x4+ x - 12
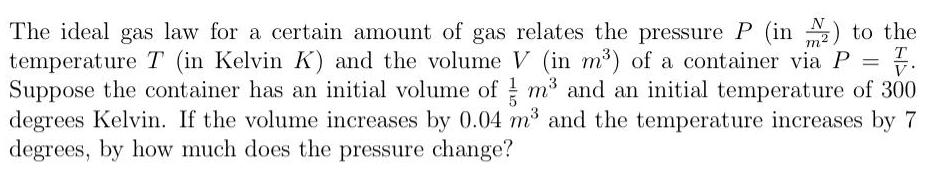
Calculus
DifferentiationThe ideal gas law for a certain amount of gas relates the pressure P (in N/m2) to the temperature T (in Kelvin K) and the volume V (in m³) of a container via P= T/V. Suppose the container has an initial volume of 1/5 m³ and an initial temperature of 300 degrees Kelvin. If the volume increases by 0.04 m³ and the temperature increases by 7 degrees, by how much does the pressure change?