Differentiation Questions and Answers

Calculus
DifferentiationUse transformations of the graph of f x 3 to graph the given function Be sure to graph and give the equation of the asymptote Use the graph to determine the function s domain and range If applicable use a graphing utility to confirm your hand drawn graphs 9 x 3 5 Graph g x 3 5 and its asymptote Use the graphing tool to graph the function as a solid curve and the asymptote as a dashed line Click to enlarge graph The equation of the asymptote for g x 3 5is Type an equation The domain of g x 3 Tune vranewer in interval notation 1 40 48 16

Calculus
DifferentiationShow that the curve x 7 cos t y 4 sin t cos t has two tangents at 0 0 and find their equations Enter your answers as a comma separated list Since x 7 cos t and y 4 sin t cos t we have the following dx dt dy dt m At the point 0 0 we know that cos t 0 y X At the smallest of these values Graph the curve dx which only occurs at odd and ddy so dx V At the largest of these values found to meet the condition in 0 2 dx ddy SO o dx dt dt dx Thus there are two tangents to the curve x 7 cos t y 4 sin t cos t and their equations are as follows Enter your answers as a comma separated list multiples of On the interval 0 27 this only occurs at the following values Enter your answers as a comma separated list and


Calculus
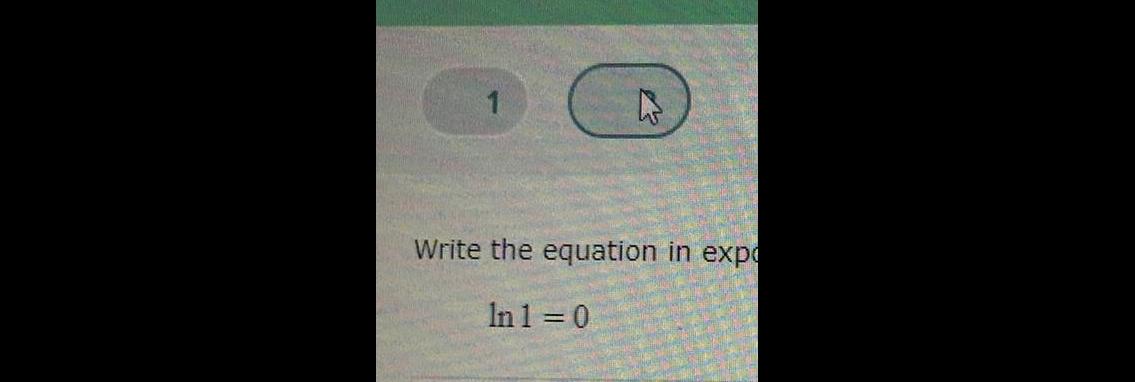
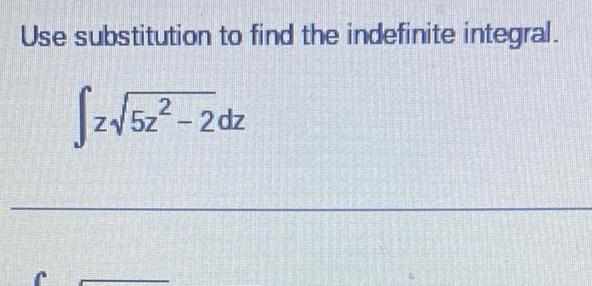
DifferentiationUse substitution to find the indefinite integra 3 x 3x 4 6x 7 2 X 3 x 3x 4 X x 6x 2 dx dx 0 7

Calculus
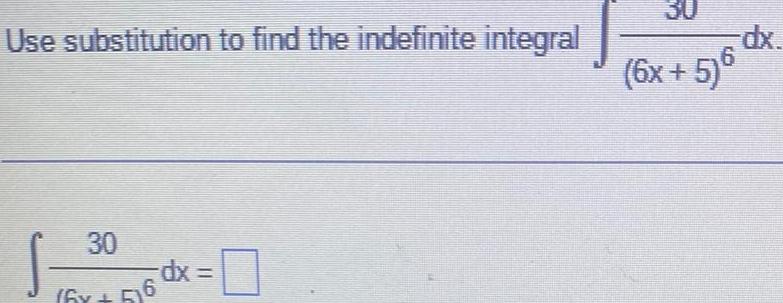
DifferentiationUse substitution to find the indefinite integral 4x 7 dx 2 4x 14x 4 x S 4x 7 4x 14x dx

Calculus
DifferentiationFind the cost function if the marginal cost function is C x 9x 4 and the fixed cost is 12 C x
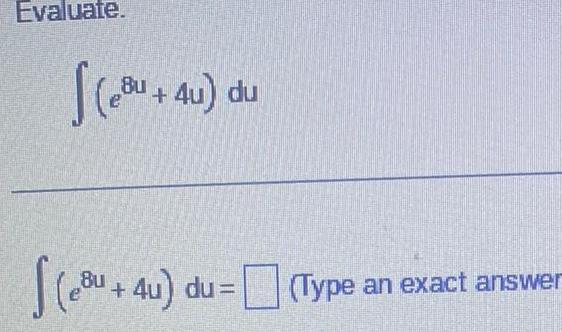
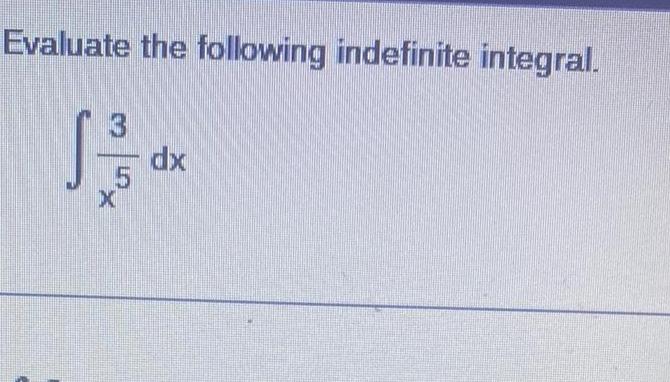
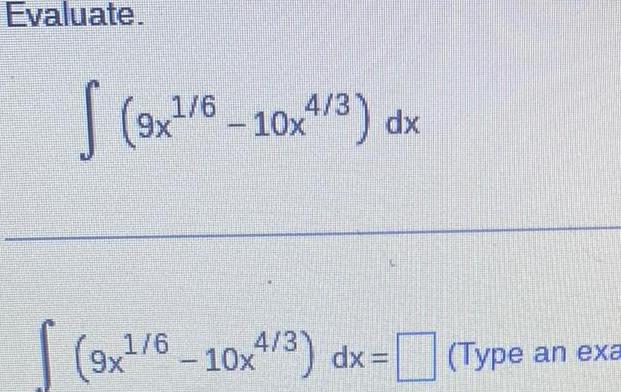


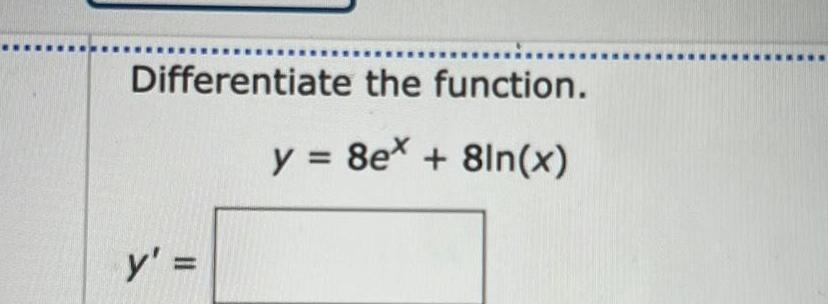


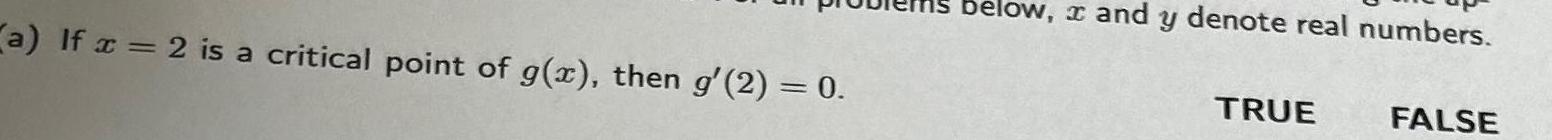
Calculus
Differentiationa If x 2 is a critical point of g x then g 2 0 below and y denote real numbers TRUE FALSE

Calculus
Differentiationb Functions always switch from increasing to decreasing or from decreasing to increasing at critical points TRUE FALSE


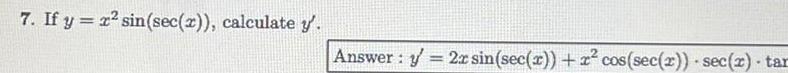
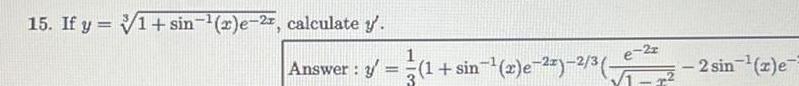
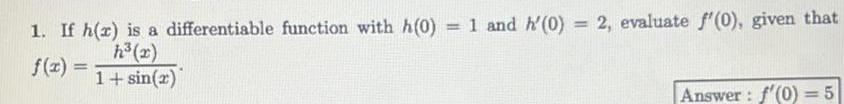
Calculus
Differentiation1 If h r is a differentiable function with h 0 1 and h 0 2 evaluate f 0 given that h x 1 sin 2 Answer f 0 5

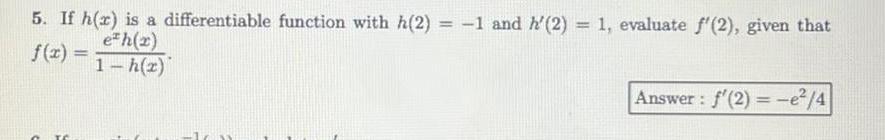
Calculus
Differentiation5 If h r is a differentiable function with h 2 1 and h 2 1 evaluate f 2 given that f x eth x 1 h z TC Answer f 2 e 4




Calculus
Differentiationrectangle is inscribed wit bossible area 1 6329 5 333 can earn partial credit on t


Calculus
Differentiationignment 11 Prob us Problem Problem List Next Pr Let f x x47x3 8x 7 Find is concave up on the intervals down on the intervals

Calculus
DifferentiationFind a unit vector u in the direction of the given vector 4 3 O A 20 15 5 5 4 3 O B O C D 4 3 5 5 1 3 5 5

Calculus
DifferentiationWrite the vector v in the form v i v j given v and the direction angle of v v 3 3 0 150 2 9 OA 21 3 3 4 4 O B O C 2 2 2 3 3 2 9 i 4 2 2 OD 2 2 2

Calculus
DifferentiationConsider the function f x 2x8 8x5 4x 7 An antiderivative of f x is F x Ax Bx Cx Dx where A is and n is and B is and m is and Cis and p is and Dis and q is 100

Calculus
Differentiationg tan O 1 O a function and inside O is an expression in terms of t Find f t and show 1 how you set up the problem 2 each step and 3 the name of differentiation rules that you used Type your answer in the space provided Suppose f t where g is

Calculus
DifferentiationComplete the table by finding the appropriate logarithmic or exponential form of the equation as in Example 1 Logarithmic form logg 9 1 logg 729 3 00 log 1 Exponential form 91 2 3 9 81 9 2 1 81
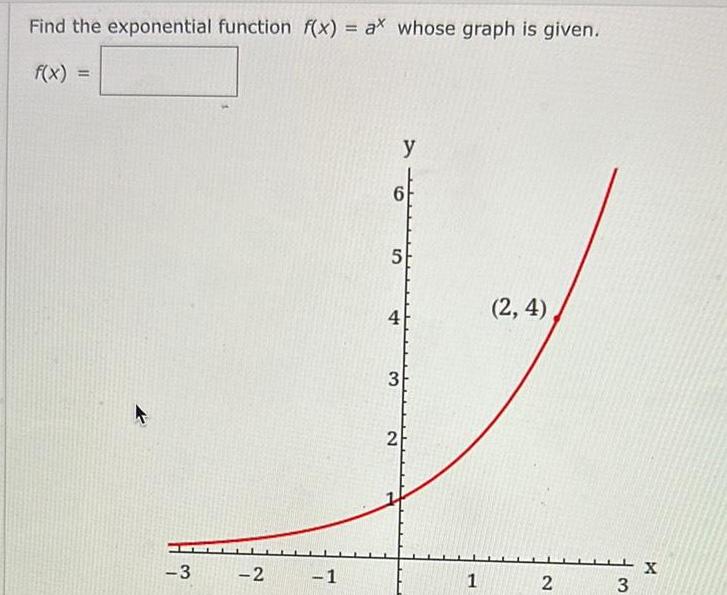
Calculus
DifferentiationFind the exponential function f x ax whose graph is given f x 3 2 1 6 y 5 4 3 2 1 2 4 2 3 X

Calculus
DifferentiationFind the derivative of the function given beld without using the Quotient or the Produc Rules Write your solution on paper and upl an image or PDF of your solution f x 3 x 1 x ex x2
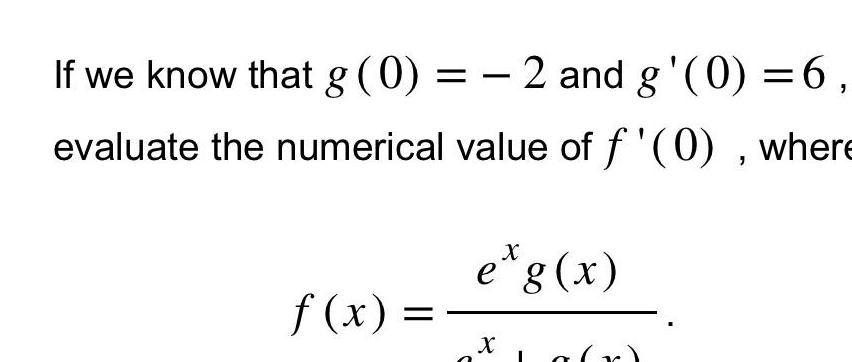
Calculus
DifferentiationIf we know that g 0 2 and g 0 6 evaluate the numerical value of f 0 where f x e g x X a r

Calculus
Differentiation1 Find dy dx given y f x 2 a Find dy dx using implicit differentiation given an the equation f x y 0 b Find the tangent line to the graph of f x y 0 at a given point 3 Given that x y and z are functions in t find dx dt in terms of x y z dy dt and dz dt 4 a Draw a curve y f x given the sign chart of its derivative y b Draw a curve y f x given the sign chart of its 2nd derivative of y 5 Use derivatives to find approximate changes in geometric measurements For all the formulas below be able to find the differential of one variable with respect to another variable and find the rate of changes at given specified values Perimeter and Area of Plane Figures Triangle P a b c Rectangle P 21 2 Amlw Parallelogram P 2a 2b Ambi Trapezoid P a b c d A a b Circle C 2xr A r A A 4 Volume and Surface Area of Solid Figures Rectangular Prism V Iwk 5 2 2 2 Right Circular Cylinder Vwar h S 2xr 2ark Sphere V Sm4r Right Circular Cone 1 V S a ars For the circle and sphere 1 a Find dC in term of dr What is dC if dr 1cm b Express the radius r in terms of the circumference C Find dr in terms of dC Find dr if dC 2 cm Ans a dC 2ndr dC 2 cm if dr 1 cm b r C 2a dr dC 2n dr 1 n cm 2 a Find dA in term of dr What is dA if when r 12 cm and dr 0 1 cm b Express the radius r in terms of the area A Find dr in terms of dA Find dr if A 167 cm and that dA 1 cm 3 a Find area A in terms of the circumference C Find dA in term of dC What is dA if when C 8 cm and dC 0 1 cm b Find the circumference C in terms of the area A Find dC in terms of dA Find dC if A 167 cm and that dA 1 cm Ans a A C 4n dA C 2n dC dA 0 4 cm b C 2n 2A 2 dC 2A 12dA dC 4 cm 1 a Find dV in term of dr What is dV if dr 0 1cm when r 10 cm b Express the radius r in terms of the volume V Find dr in terms of dV Find dr if dV 1 cm when V 36 cm Ans b r 2 V dr 2 vav dr 360 190 2 a Find dS in term of dr What is dS if dr 0 1cm when r 10 cm b Express the radius r in terms of the surface area S Find dr in terms of ds Find dS if dV 1 cm when V 36 cm Ans a dS 8 r dr ds 8 cm 3 a Find volume V in terms of the surface S Find dV in term of ds What is dV if when S 167 cm and that dS 1 cm b Find the surface S in terms of the volume V Find dS in terms of dV Find dS if V 367 cm and that dV cm x16022623 2 IC untout

Calculus
Differentiation2 of 2 Auth Trapezoid P a b c d Circle C 2ar A ar Right Circular Cylinder Vwr h S 2x 2xrk Sphere V S 4x Right Circular Come V ark Swar 312 For the circle and sphere 1 a Find dC in term of dr What is dC if dr 1cm b Express the radius r in terms of the circumference C Find dr in terms of dC Find dr if dC 2 cm Ans a dC 2ndr dC 2 cm if dr 1 cm b r C 2n dr dC 2 dr 1 cm 2 a Find dA in term of dr What is dA if when r 12 cm and dr 0 1 cm b Express the radius r in terms of the area A Find dr in terms of dA Find dr if A 167 cm and that dA 1 cm 3 a Find area A in terms of the circumference C Find dA in term of dC What is dA if when C 87 cm and dC 0 1 cm Ans b r b Find the circumference C in terms of the area A Find dC in terms of dA Find dC if A 167 cm and that dA 1 cm Ans a A C 4x dA C 2n dC dA 0 4 cm b C 2n 2A 2 dC 2A 1 2dA dC 4 cm 1 a Find dV in term of dr What is dV if dr 0 1cm when r 10 cm b Express the radius r in terms of the volume V Find dr in terms of dV Find dr if dV 1 cm when V 36 x cm dr V dV dr 0 190 2 a Find dS in term of dr What is dS if dr 0 1cm when r 10 cm b Express the radius r in terms of the surface area S Find dr in terms of ds Find dS if dV 1 cm when V 36 cm Ans a ds 8 r dr ds 8 cm 3 a Find volume V in terms of the surface S Find dV in term of ds What is dV if when S 167 cm and that dS 1 cm 1 36 b Find the surface S in terms of the volume V Find dS in terms of dV Find dS if V 367 cm and that dV cm Ans b S 4x 3 3 25V 2 3 ds 4m 3 v dv ds 4n 3 36n 1 3 Also be able to explain what each result means 6 Determine if a given function is continuous at a point x a Justify your answer clearly by showing all the algebra with limits 6 Continuous vs Differentiable Functions Vid Is the following function continuous at x 1 Justify your answer clearly 1 x f x x 1 1 x x 1 x 1

Calculus
DifferentiationFind the general solution to the system of differential equations using linear algebra techniques x 3x 5y y 2x 3y 2

Calculus
Differentiation5 Use derivatives to find approximate changes in geometric measurements For all the formulas below be able to find the differential of one variable with respect to another variable and find the rate of changes at given specified values Perimeter and Area of Plane Figures Triangle P a b c A Rectangle P 21 2 Parallelogram P 2a 26 A bk Trapezoid Pwa b c d Circle C 2tr A ar Volume and Surface Area of Solid Figures Rectangular Prism V Ink S 2w 2h 2wh Right Circular Cylinder Vwr h S 2x 2xrk Sphere Smlar Right Circular Cone Swar ars For the circle and sphere 1 a Find dC in term of dr What is dC if dr 1cm b Express the radius r in terms of the circumference C Find dr in terms of dC Find dr if dC 2 cm Ans a dC 2ndr dC 2 cm if dr 1 cm b r C 2n dr dC 2n dr 1 cm 2 a Find dA in term of dr What is dA if when r 12 cm and dr 0 1 cm b Express the radius r in terms of the area A Find dr in terms of dA Find dr if A 16 cm and that dA 1 cm 3 a Find area A in terms of the circumference C Find dA in term of dC What is dA if when C 87 cm and dC 0 1 cm b Find the circumference C in terms of the area A Find dC in terms of dA Find dC if A 167 cm and that dA 1 cm Ans a A C 4x dA C 2n dC dA 0 4 cm b C 2n A 2 dC 2A 2dA dC 4 cm 1 a Find dV in term of dr What is dV if dr 0 1 cm when r 10 cm b Express the radius r in terms of the volume V Find dr in terms of dV Find dr if dV 1 cm when V 36 cm Ans b r v dr 2 vdv dr 36 0 190 2 dV 2 a Find dS in term of dr What is dS if dr 0 1cm when r 10 cm b Express the radius r in terms of the surface area S Find dr in terms of dS
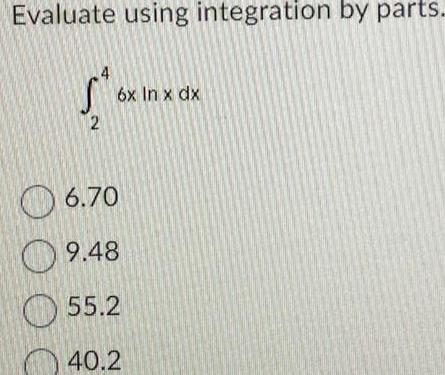
Calculus
DifferentiationEvaluate using integration by parts 5 2 O O O C 6x In x dx 6 70 9 48 55 2 40 2

Calculus
DifferentiationFind the area between the graph of f x e0 2x 2 and the x axis over the interval 2 x 5 Round answer to two decimal places if necessary 20 13 8 97 12 13 3 22

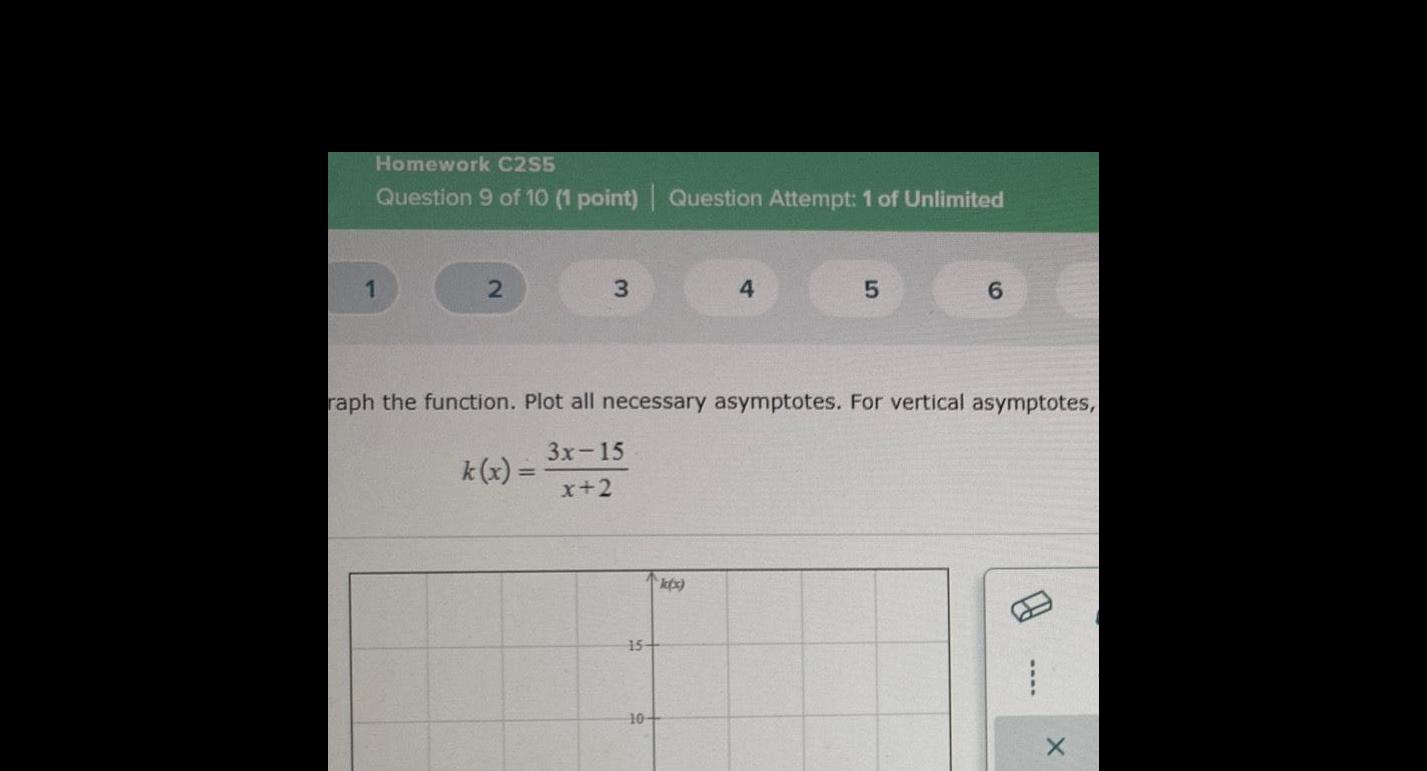
Calculus
DifferentiationHomework C2S5 Question 9 of 10 1 point Question Attempt 1 of Unlimited 1 2 3 k x 15 raph the function Plot all necessary asymptotes For vertical asymptotes 3x 15 x 2 10 4 k x 5 6 X
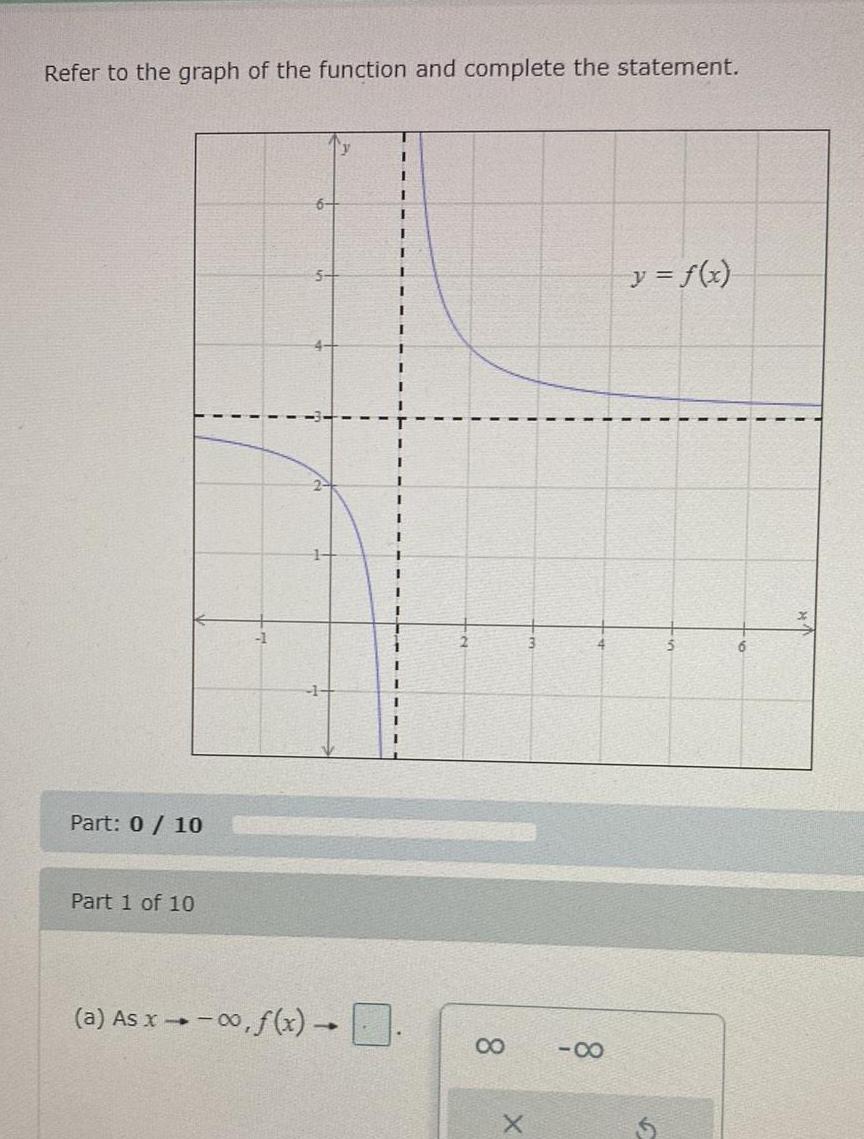
Calculus
DifferentiationRefer to the graph of the function and complete the statement Part 0 10 Part 1 of 10 a As x 00 f x I I 1 1 I I I I I I I I 1 I 1 I I 8 X 4 y f x