Indefinite Integration Questions and Answers
Calculus
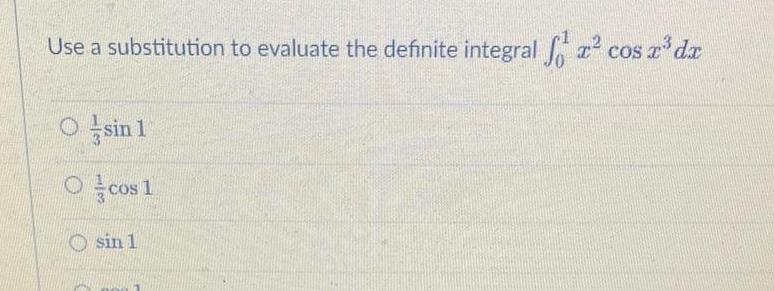
Indefinite IntegrationUse a substitution to evaluate the definite integral cos x da Osin 1 Ocos 1 sin 1

Calculus
Indefinite IntegrationGiven S is a surface for a part of the sphere x y z 4 that lies above the cone z x y Find a parametric representation for the surface S in term of o and 8 Then determine the domain of and 0 Based on the expression written previously show that rx rell 4 sin o Hence compute the surface integral of ffs ds where the surface S is given parametrically by r 0 0 Let C is the boundary curve along the bottom of the upper half of the sphere thus use Stokes theorem to compute the line integral of fo F dr where F x y z xzi yzj xyk and upwards orientation
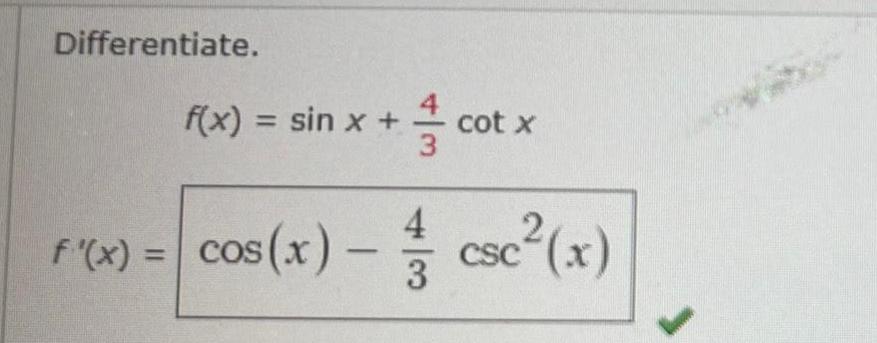

Calculus
Indefinite IntegrationUse integration by parts together with the techniques of this section to evaluate the integral Use C for the constant of integration x tan tan x dx
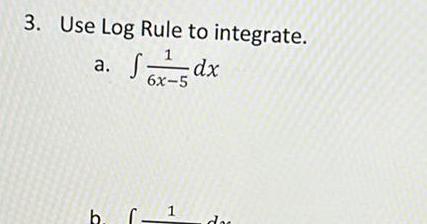
Calculus
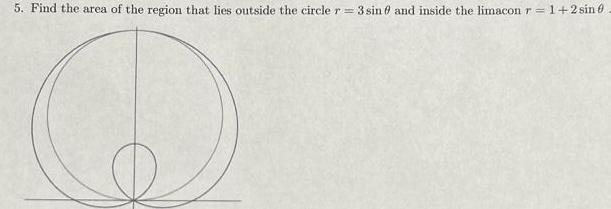
Indefinite Integration5 Find the area of the region that lies outside the circle r 3 sin 0 and inside the limacon r 1 2 sin

Calculus
Indefinite IntegrationIn a Use a substitution to find f Show your work and final answer in the provided area using HTML Editor s Insert Math Equation function an da

Calculus
Indefinite IntegrationUse a substitution to find f sin x cos xdx O cos zsin x C 6 sin z cos x C OCCO E C in 2 C
Calculus
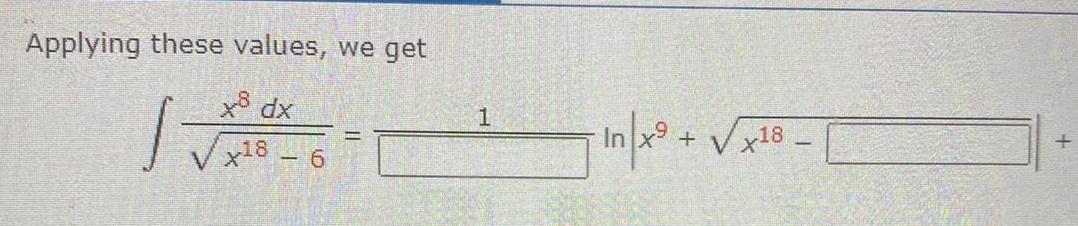
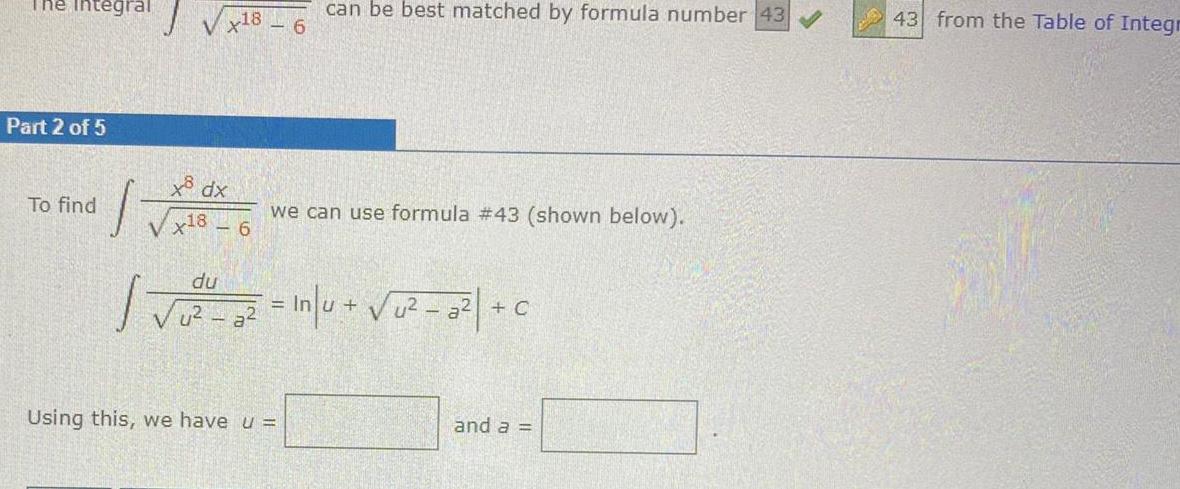
Indefinite IntegrationThe Integral Part 2 of 5 To find 1 X18 x dx Vx18 6 TV 6 can be best matched by formula number 43 we can use formula 43 shown below du u a2 In u u a C Using this we have u and a 43 from the Table of Integr
Calculus
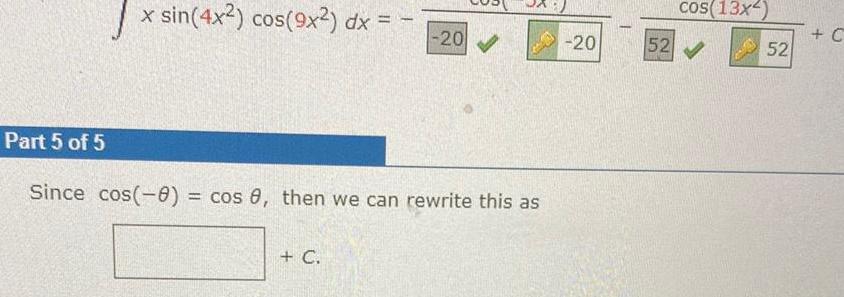
Indefinite IntegrationPart 5 of 5 x sin 4x2 cos 9x2 dx 20 Since cos 0 cos 8 then we can rewrite this as C 20 cos 13x 52 52 C
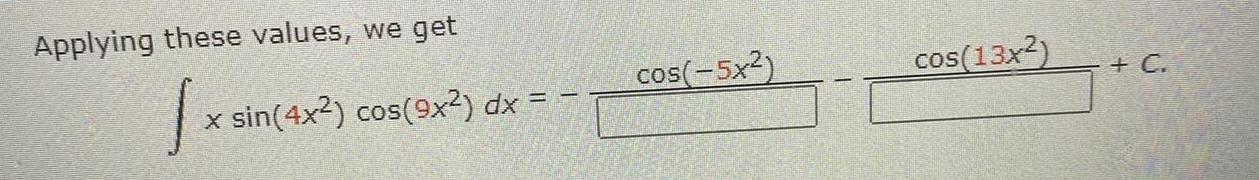

Calculus
Indefinite IntegrationUse the Table of Integrals to evaluate the integral sin 20 V 5 3 sin 8 C de
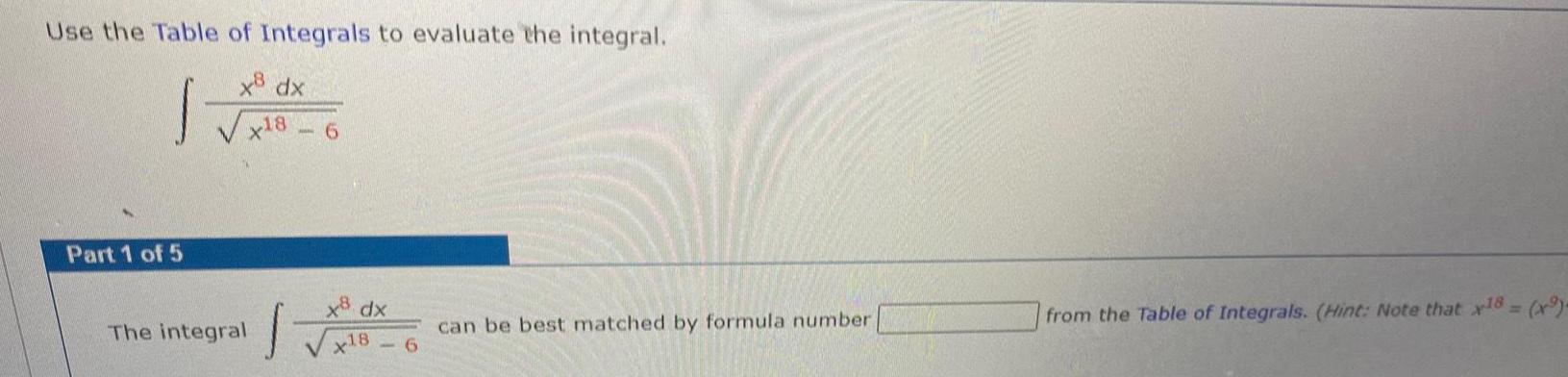
Calculus
Indefinite IntegrationUse the Table of Integrals to evaluate the integral 1 x dx x18 6 Part 1 of 5 The integral J dx x18 6 can be best matched by formula number from the Table of Integrals Hint Note that x18 9
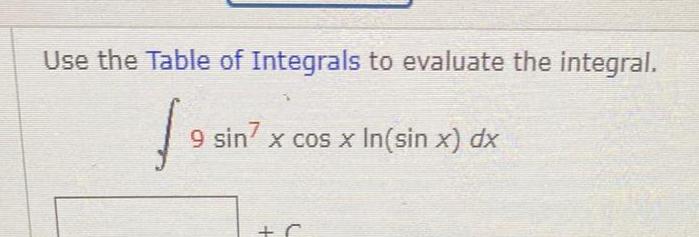
Calculus
Indefinite IntegrationUse the Table of Integrals to evaluate the integral 9 si 9 sin7 x cos x In sin x dx
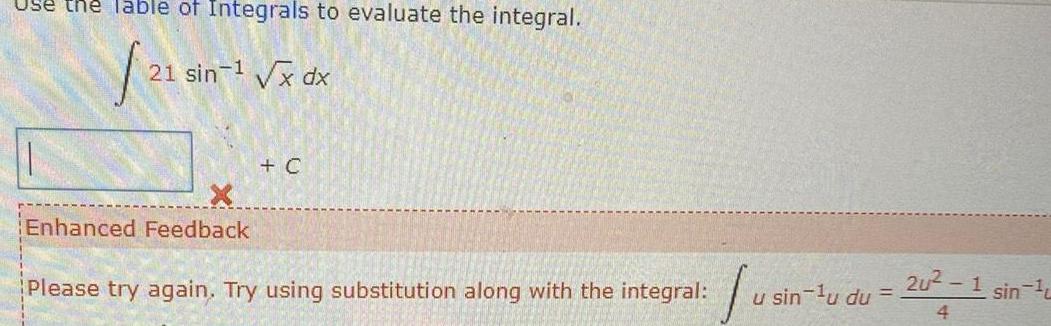
Calculus
Indefinite IntegrationUse the Table of Integrals to evaluate the integral 21 sin 21 sin x dx Enhanced Feedback C Please try again Try using substitution along with the integral Ju u sin u du 2u 1 sin 4
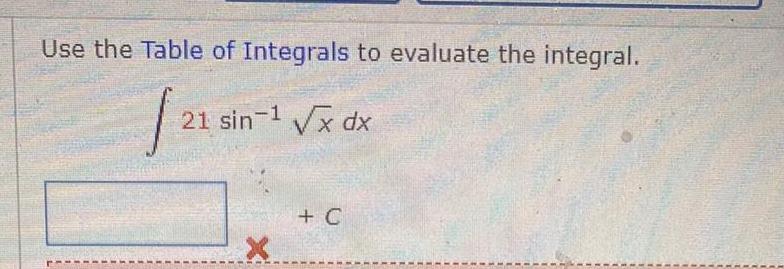
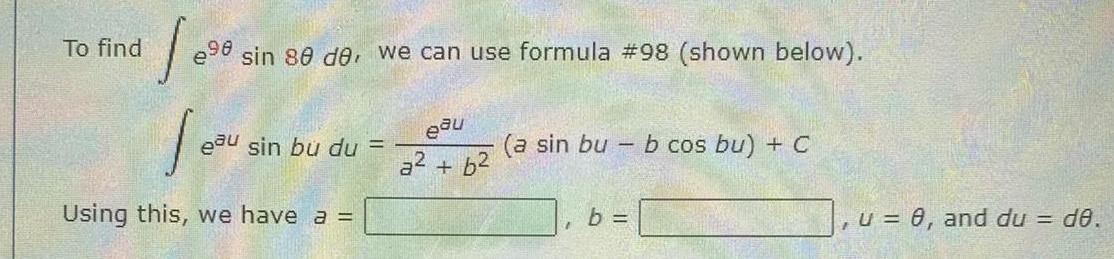
Calculus
Indefinite Integration298 sin 80 de we can use formula 98 shown below Je Using this we have a To find eau sin bu du eau a b a sin bu b cos bu C I b u 0 and du d0
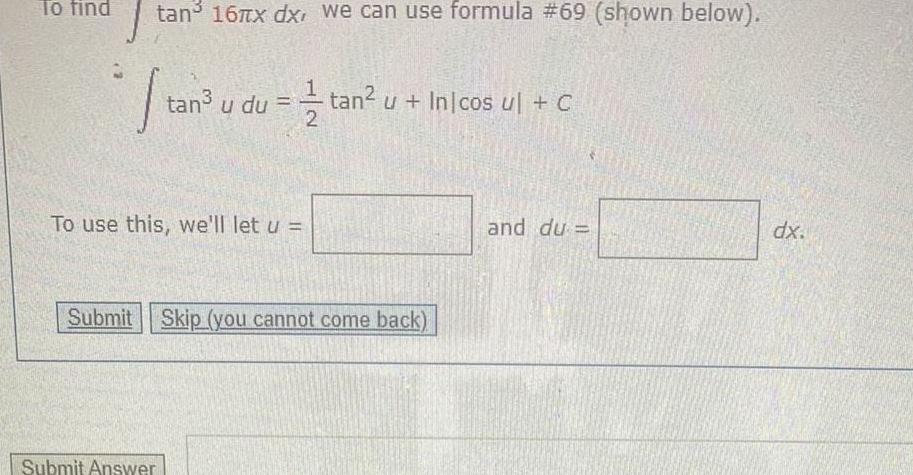
Calculus
Indefinite IntegrationTo find tan 16 x dx we can use formula 69 shown below tan u du tan u Inicos ul C To use this we ll let u Submit Skip you cannot come back Submit Answer and du dx
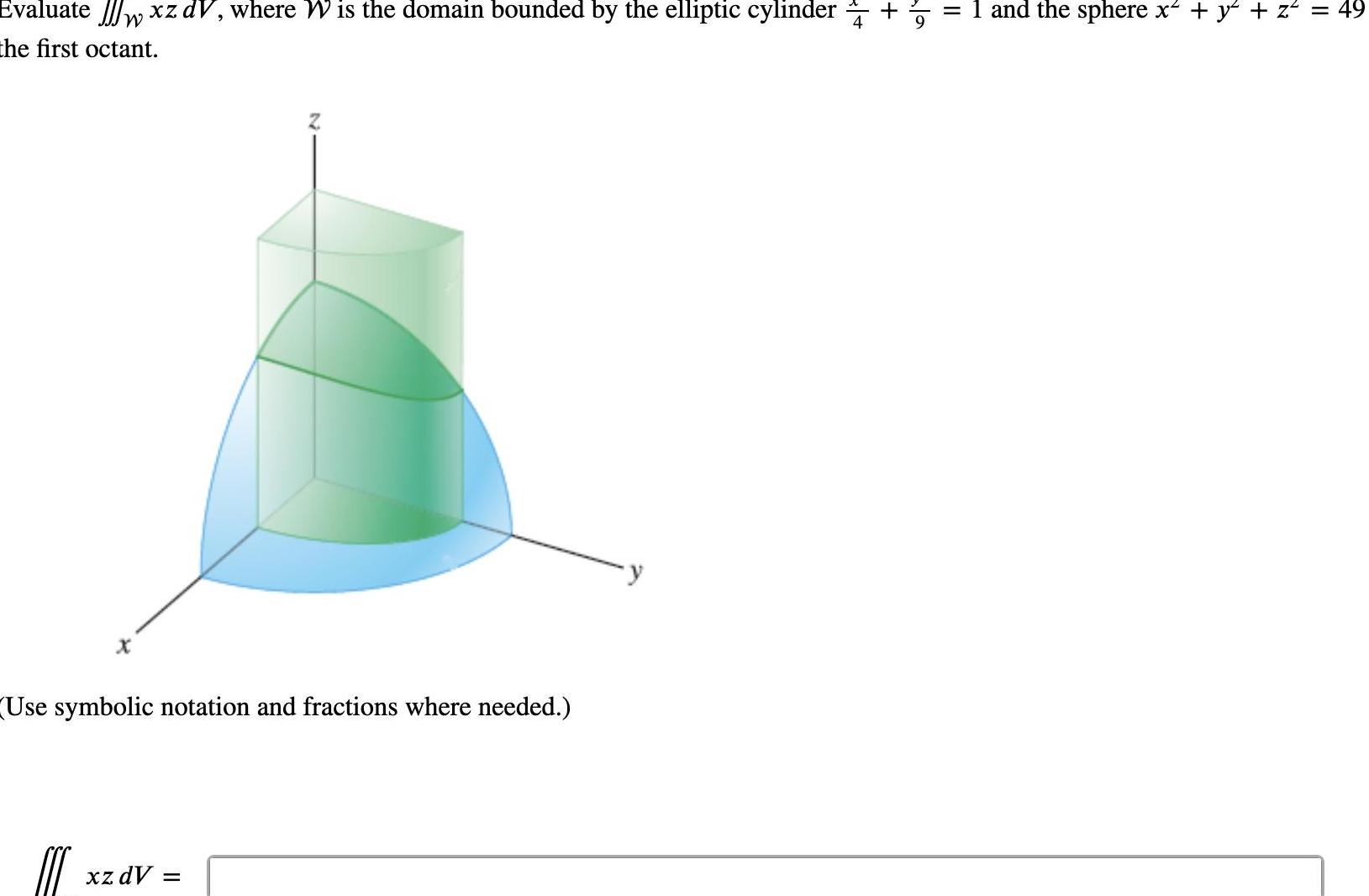
Calculus
Indefinite IntegrationEvaluate w xz dV where W is the domain bounded by the elliptic cylinder the first octant W Use symbolic notation and fractions where needed C xz dV II and the sphere x y z

Calculus
Indefinite IntegrationCalculate the following antiderivatives a 13 b 13t5t 2 dt S c 1 u9 4 1 504 4 u du C dx C C
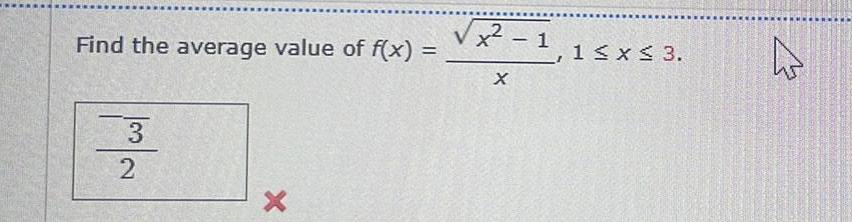
Calculus
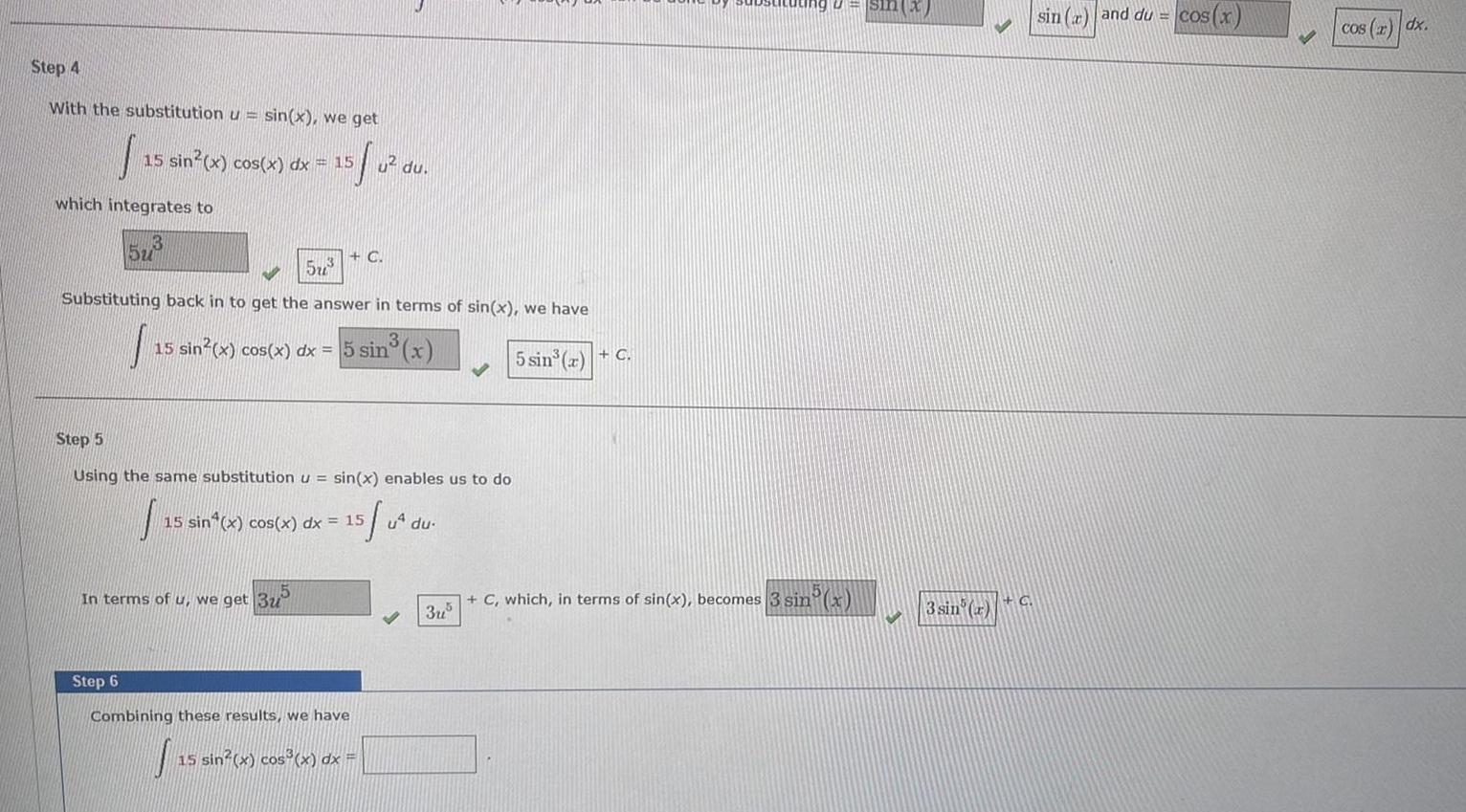
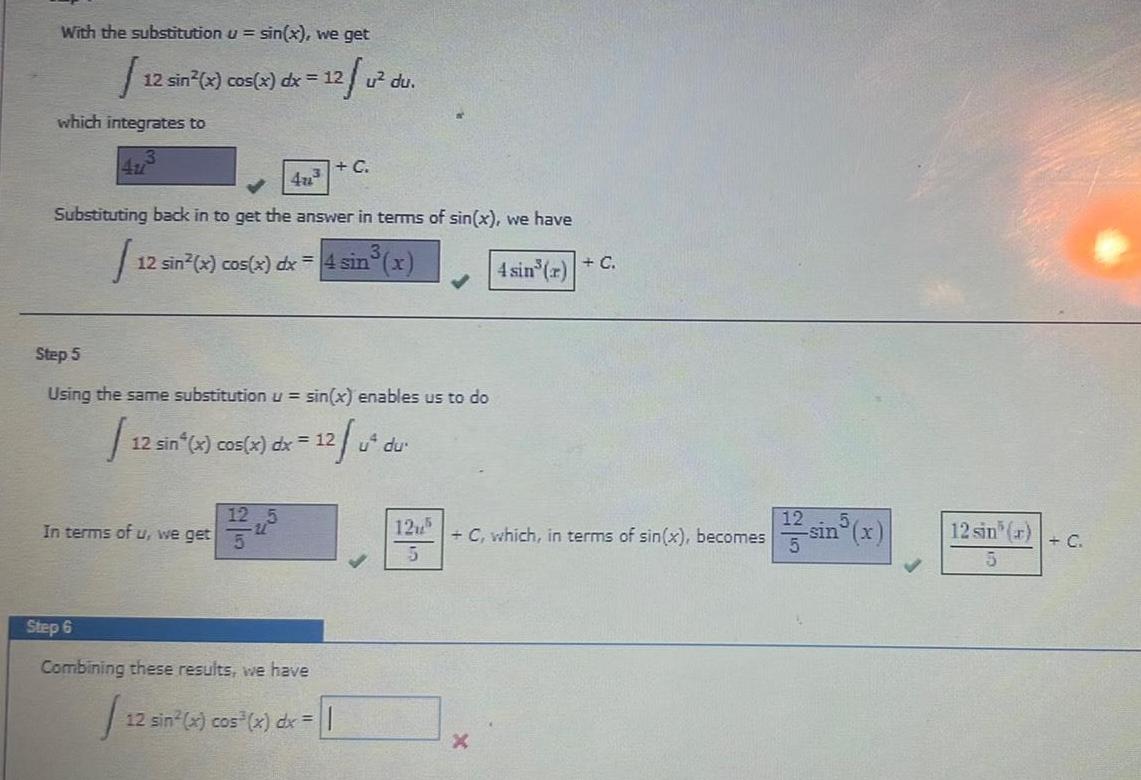
Indefinite IntegrationStep 4 With the substitution u sin x we get 15 sin x cos x dx 15 S which integrates to 13 5u 573 u du G Substituting back in to get the answer in terms of sin x we have sin x In terms of u we get 3u 15 sin x cos x dx 5 sin Step 5 Using the same substitution u sin x enables us to do 15 sin x cos x dx 15 Step 6 Combining these results we have J 15 sin x cos x dx 5 u du 3u 5 sin a C sin x C which in terms of sin x becomes 3 sin x 3 sin x C sin r and du cos x cos x dx
Calculus
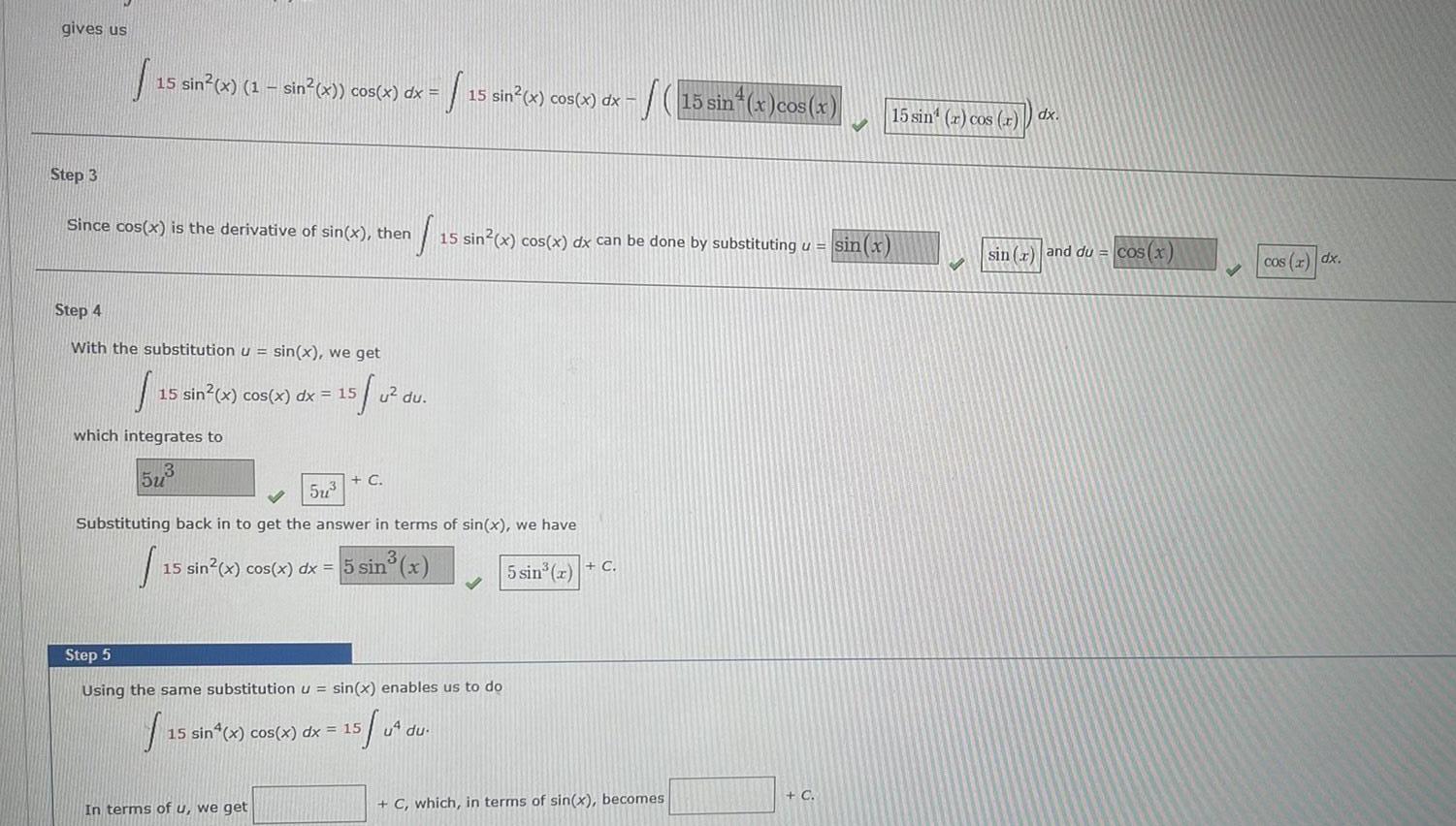
Indefinite Integrationgives us Step 3 15 sin x 1 sin x cos x dx 15 sin x cos x dx Since cos x is the derivative of sin x then S 15 sin x cos x dx can be done by substituting u sin x Step 4 With the substitution u sin x we get 15 0 15 which integrates to 15 sin x cos x dx 15 5u u du C 5u Substituting back in to get the answer in terms of sin x we have 15 sin x cos x dx 5 sin x 5 sin x C In terms of u we get Step 5 Using the same substitution u sin x enables us to do f 15 15 sin x cos x dx 15 5 04 S 15 sin x cos x u du C which in terms of sin x becomes C 15 sin r cos r dx sin x and du cos x cos x dx
Calculus
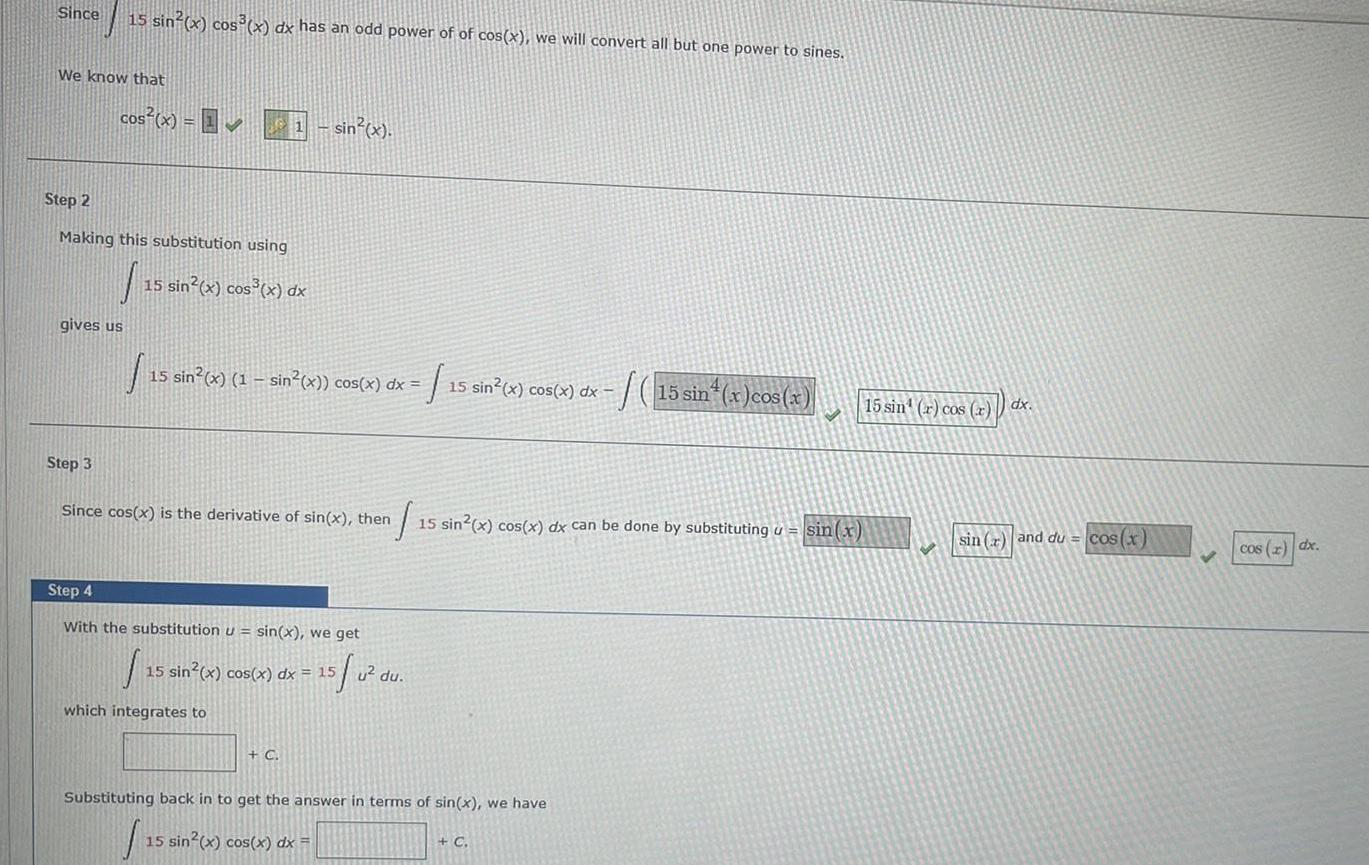
Indefinite IntegrationSince We know that 15 sin x cos x dx has an odd power of of cos x we will convert all but one power to sines cos x Step 2 Making this substitution using 15 sin x cos x dx gives us Step 3 15 sin x 1 sin x cos x dx 15 sin x cos x dx sin x Since cos x is the derivative of sin x then Step 4 With the substitution u sin x we get 15 0 which integrates to 15 sin x cos x dx 15 C 15 15 sin x cos x dx can be done by substituting u sin x u du Substituting back in to get the answer in terms of sin x we have 15 sin x cos x dx 15 sin x cos x C 15 sin r cos r dx sin r and du cos x cos x dx

Calculus
Indefinite IntegrationConsider the following function 3 JO R 64 dx a Determine an appropriate trigonometric substitution Use x 8 sin 0 where 1 0 1 since the integrand contains the expression 82 x 2 Use x 8 tan 8 where x3 64 x IT 2 0x dx S 0 O Use x 8 sec 0 where 0 0 0 or 0 31 TT 2 TT since the integrand contains the expression 8 x 2 b Apply the substitution to transform the integral into a trigonometric integral Do not evaluate the integral 8 sin 0 8 cos 0 X since the integrand contains the expression 8 x de
Calculus
Indefinite IntegrationWith the substitution u sin x we get J which integrates to 12 sin x cos x dx 12 u du Substituting back in to get the answer in terms of sin x we have I 12 sin x cos x dx 4 sin x 4 sin r C 12 sin 4u Step 5 Using the same substitution u sin x enables us to do 12 u dur 12 sin x cos x dx 12 In terms of u we get 12 C Step 6 Combining these results we have 12 sin x cos x dx 125 5 C which in terms of sin x becomes 12 sin r 5 C

Calculus
Indefinite IntegrationSince u 2 3x then converting back to an expression in x we get the following Remember to use absolute values where appropriate Inl Injul C

Calculus
Indefinite IntegrationSince u 8 x then converting back to an expression in x we get 1 c 28 C
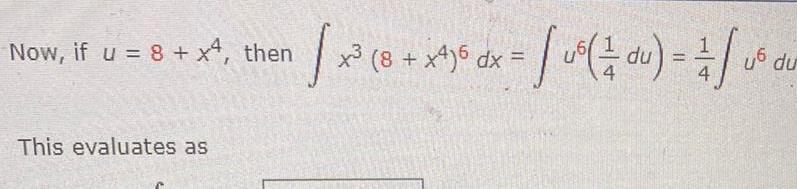

Calculus
Indefinite Integrationx 18 We must also convert x dx into an expression involving u If u 8 x is substituted into x 8 x4 6 dx then we have We know that du 4x dx and so x dx du x u dx x x3 U6 x dx
Calculus
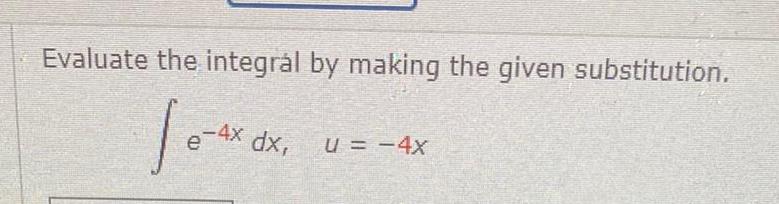
Indefinite IntegrationEvaluate the integr l by making the given substitution Je 4x 4x dx U 4x
Calculus
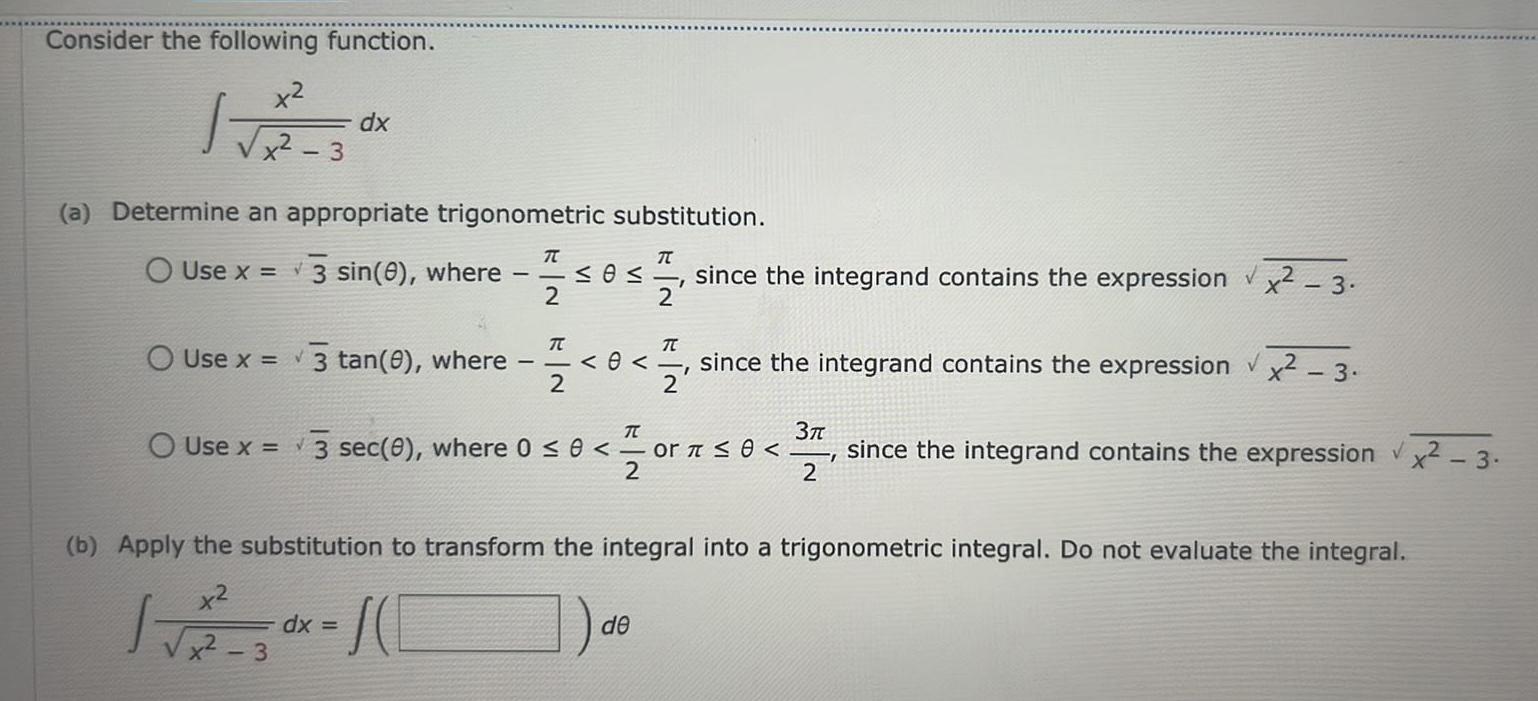
Indefinite IntegrationConsider the following function x x 3 a Determine an appropriate trigonometric substitution O Use x 3 sin 0 where 1505 12 24 0 since the integrand contains the expression x 3 I 2 dx O Use x 3 tan 0 where 3 T dx T O Use x 3 sec 0 where 0 0 or 0 2 TC 2 0 since the integrand contains the expression x2 3 V 2 b Apply the substitution to transform the integral into a trigonometric integral Do not evaluate the integral x x2 de 37 since the integrand contains the expression x2 3 2

Calculus
Indefinite IntegrationConsider the following function x6 dx 1 x a Determine an appropriate trigonometric substitution Use x Use x sin 8 where tan 8 where T T 0 since the integrand contains the expression 1 x 2 2 dx T T 0 since the integrand contains the expression 1 x 2 2 Use x sec 0 where 0 0 or 0 since the integrand contains the expression 1 x V 2 3 2 b Apply the substitution to transform the integral into a trigonometric integral Do not evaluate the integral de

Calculus
Indefinite Integrationsin x Since cos x is the derivative of sin x then 12 sin x cos x dx can be done by substituting u Step 4 With the substitution u sin x we get 12 12 sin x cos x dx 12 u du 12 which integrates to C X Substituting back in to get the answer in terms of sin x we have S 12 sin x cos x dx C

Calculus
Indefinite IntegrationTutorial Exercise Evaluate the integral 1 Step 1 12 sin x cos x dx Since S 12 sin x cos x dx has an odd power of of cos x we will convert all but one power to sines We know that cos x sin x

Calculus
Indefinite IntegrationTwo marbles are drawn without replacement from a box with 4 blue 3 white and 2 red marbles Find the probability of selecting a blue and a red marble in order 0 111 O 0 486 O 0 591 0 227 0347
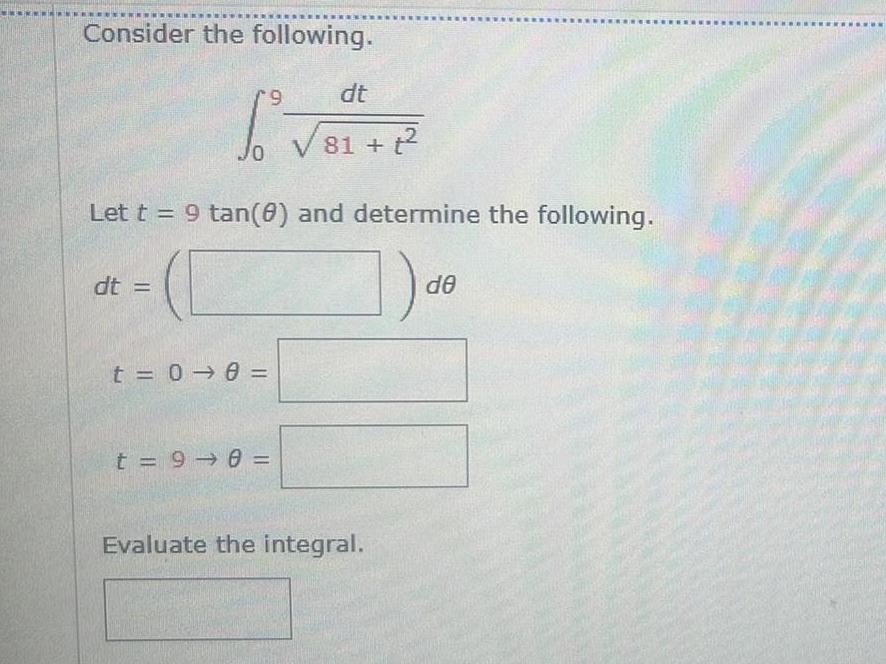
Calculus
Indefinite IntegrationConsider the following 9 6 3 Let t 9 tan 0 and determine the following a dt t 0 0 dt 81 2 t 9 0 Evaluate the integral de
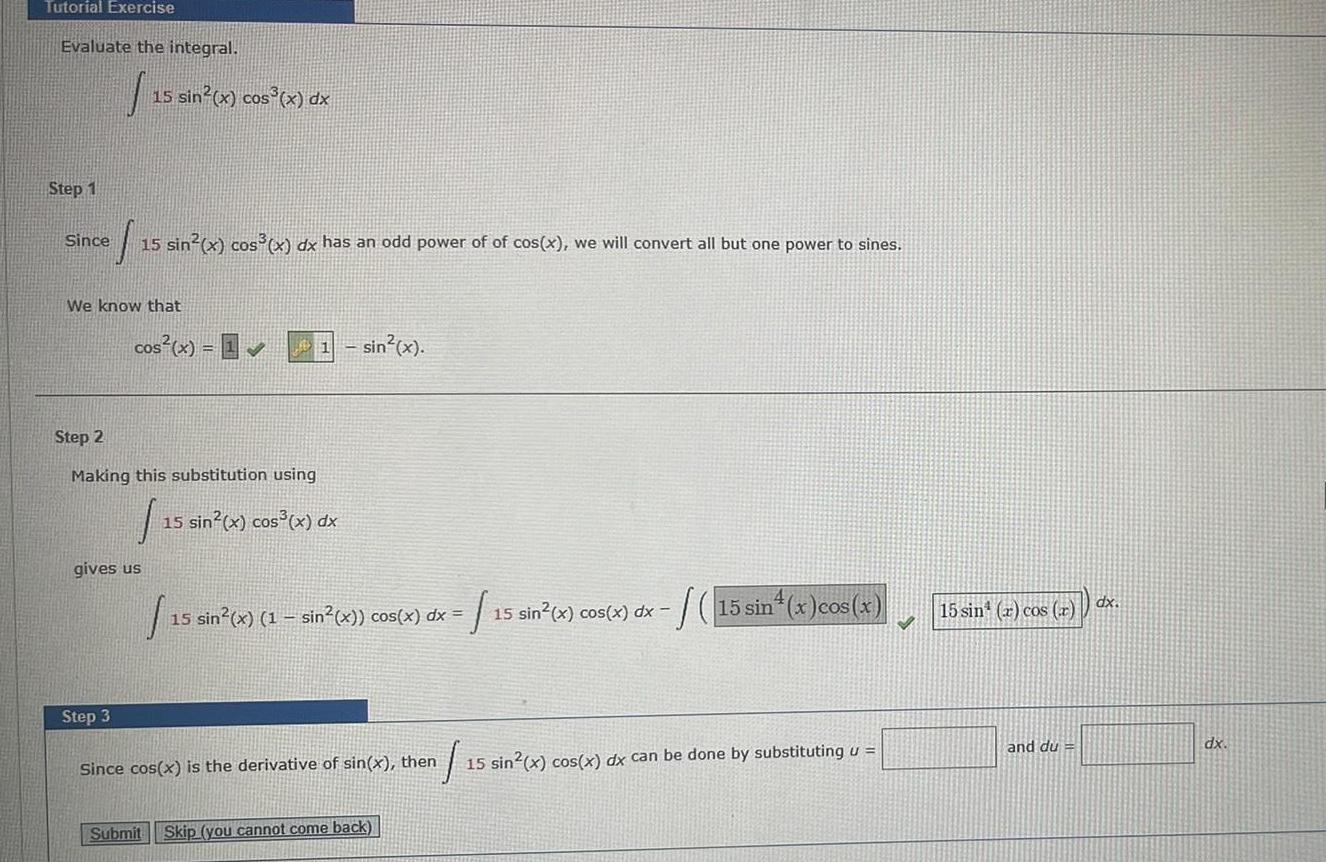
Calculus
Indefinite IntegrationTutorial Exercise Evaluate the integral Step 1 Since S 15 sin x cos x dx has an odd power of of cos x we will convert all but one power to sines We know that 15 sin x cos x dx cos x 1 11 sin x Step 2 Making this substitution using 1 15 sin x cos x dx gives us Step 3 Submit 15 15 sin x 1 sin x cos x dx 1 Skip you cannot come back 1 15 sin x cos x dx Since cos x is the derivative of sin x then 1 15 sin x cos x dx can be done by substituting u 15 sin x cos x 15 sin r cos r and du dx dx
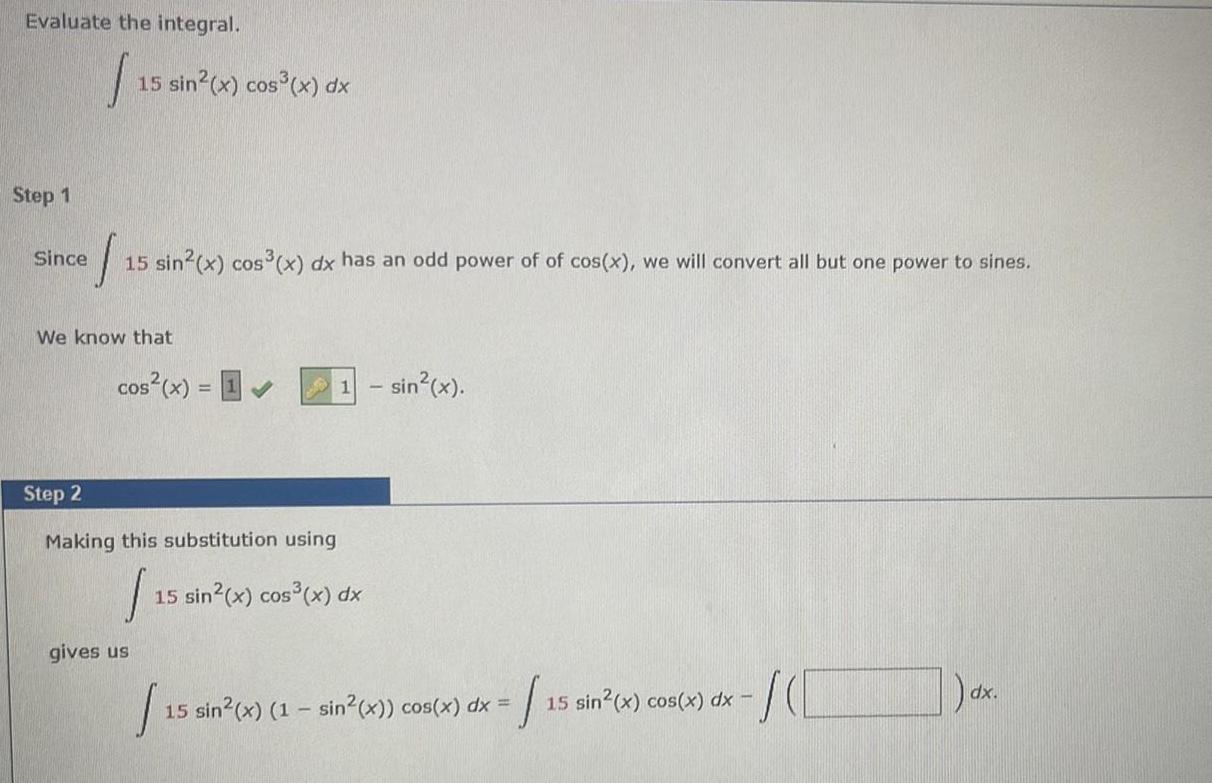
Calculus
Indefinite IntegrationEvaluate the integral I Step 1 15 sin x cos x dx Since 1 15 sin x cos x dx has an odd power of of cos x we will convert all but one power to sines We know that cos x 1 Step 2 Making this substitution using 1 gives us 1 sin x 15 sin x cos x dx 15 sin 15 sin x 1 sin x cos x dx 15 sin x cos x dx 155 SCC dx

Calculus
Indefinite IntegrationTutorial Exercise Evaluate the integral 15 Step 1 15 sin x cos x dx Since J 15 sin x cos x dx has an odd power of of cos x we will convert all but one power to sines We know that cos x sin x
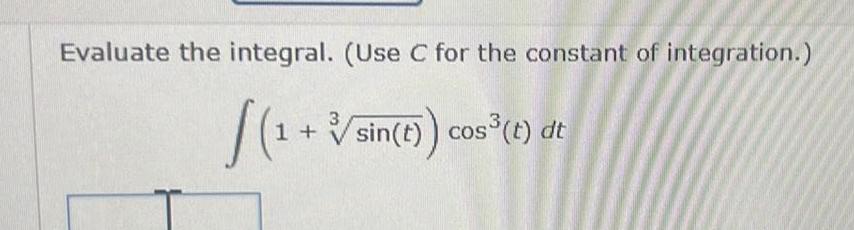
Calculus
Indefinite IntegrationEvaluate the integral Use C for the constant of integration 1 sin t cos t dt
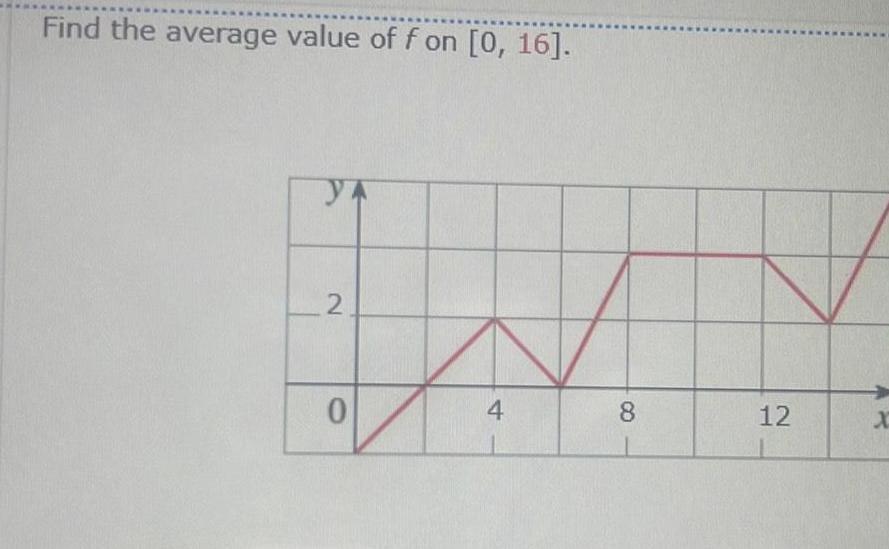
Calculus
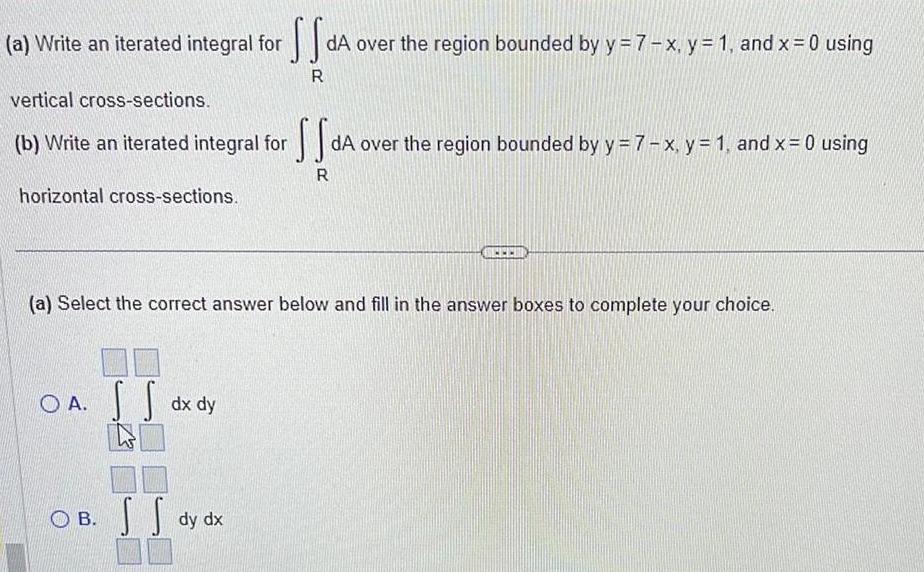
Indefinite Integrationa Write an iterated integral for SS dA over the region bounded by y 7 x y 1 and x 0 using R vertical cross sections b Write an iterated integral for horizontal cross sections OA dx dy SS a Select the correct answer below and fill in the answer boxes to complete your choice OB S dy dx S SS dA over the region bounded by y 7 x y 1 and x 0 using R

Calculus
Indefinite IntegrationUse Fubini s Theorem to evaluate Apply Fubini s Theorem 3xexy Gellan ng3 RECENTLY Honorer CROCHERISING SS3 00 exy dy dx Tyne exact opp 3xexy dx dy


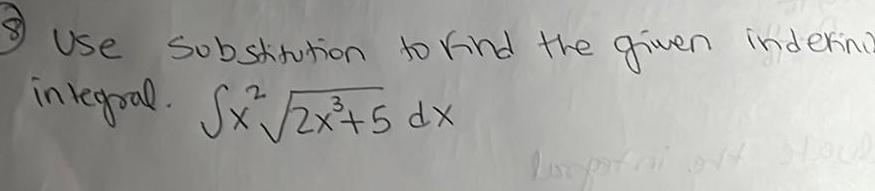

Calculus
Indefinite Integrationfind the given indefinite intergal state whether inte by Substitution or integrat integration by parts was used Please tell me if this parts or substitution dx use integration by L xex dx dx