Indefinite Integration Questions and Answers
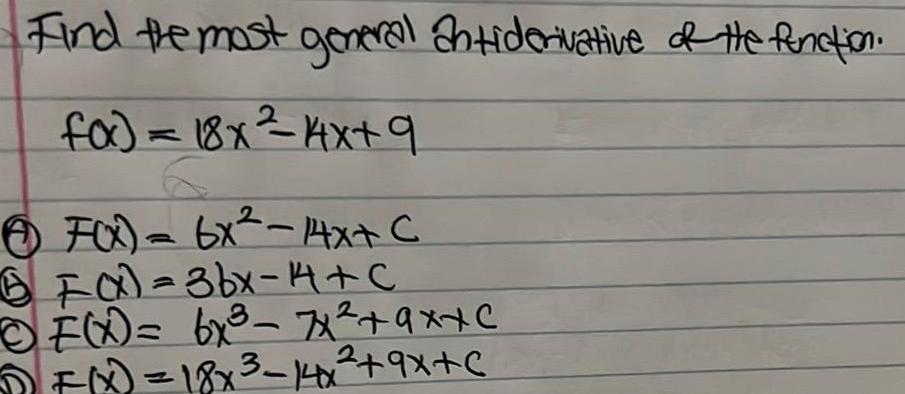
Calculus
Indefinite IntegrationFind the most general antiderivative of the function for 18x 4x 9 F x 6x 14x C BI x 3bx 14 C F x 6x 7 9x c F x 18x 14x 9X C
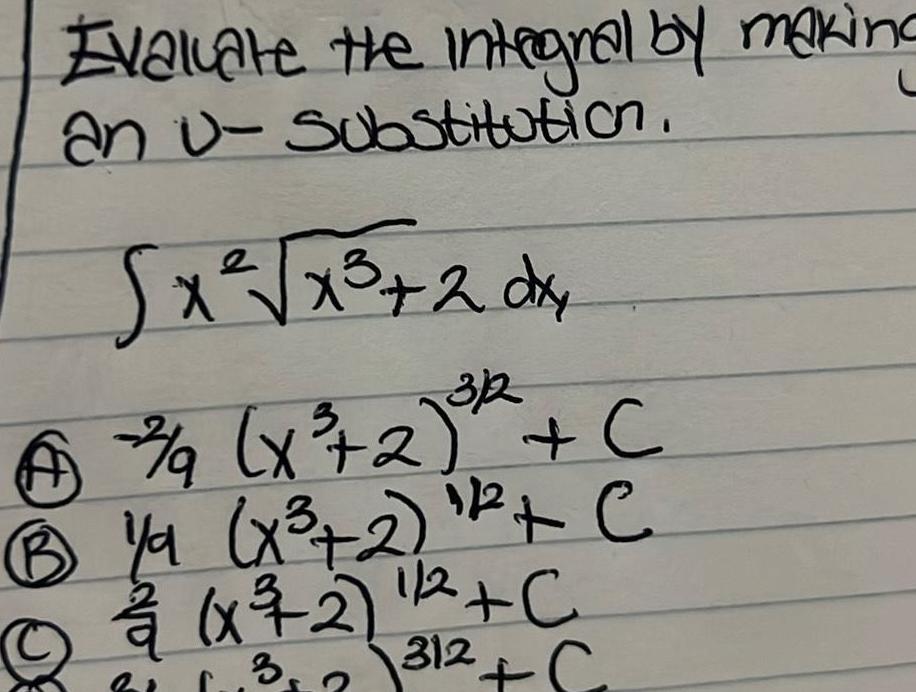
Calculus
Indefinite IntegrationEvaluate the integral by making an u Substitution x 2 dxy 312 13 x 2 C B Ya x 2 2 C xXx 7 2 1 2 C 11 11 1 C 312 3 X
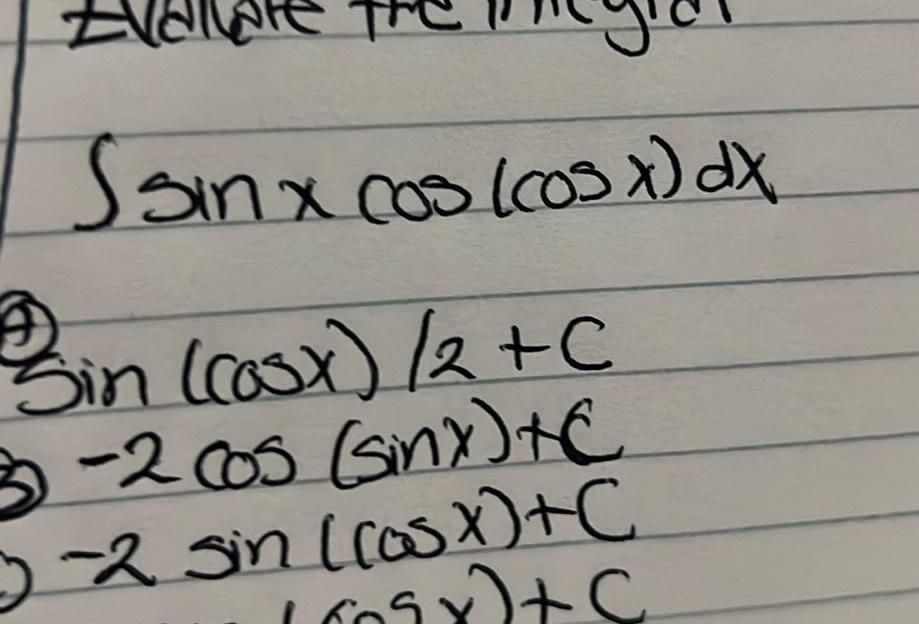
Calculus
Indefinite IntegrationEval Ssin x cos cos x dx Bin casx 2 C 3 2 cos sinx C 3 2 sin los x C wants

Calculus
Indefinite IntegrationEvaluate the indefinite intera S 4 10X 7 4x 5x 2 2 A 2 7 4x 5x C B 7 4x 5x C C 2 7 4X 5x C
Calculus
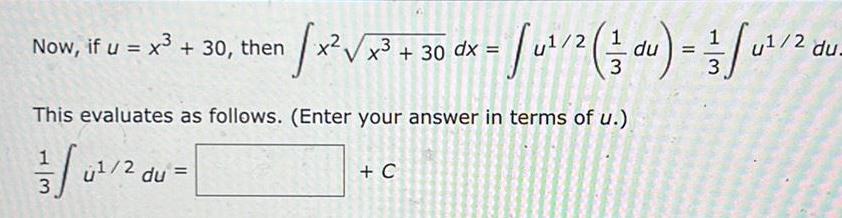
Indefinite IntegrationNow if u x 30 then 3 x x 30 dx u 2 1 1 du u 2 du x x 3 3 This evaluates as follows Enter your answer in terms of u 13 01 20 du C
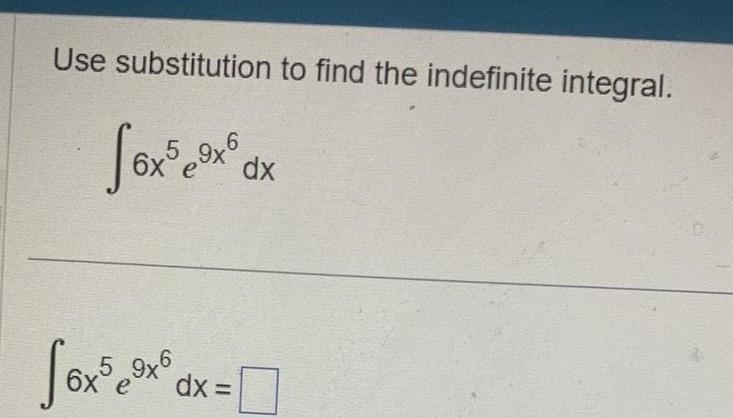
Calculus
Indefinite IntegrationUse substitution to find the indefinite integral 6 fox 5x x ax e dx Sox 6x59x6 dx

Calculus
Indefinite IntegrationEvaluate the cylindrical coordinate integral The value is 0 0 r r dz dr d

Calculus
Indefinite IntegrationMake a substitution to express the integrand as a rational function and then evaluate the integral Use C for the constant of integration 7e2x 11e 18 e2x dx 9 ln e 9 2 ln e 2 C X
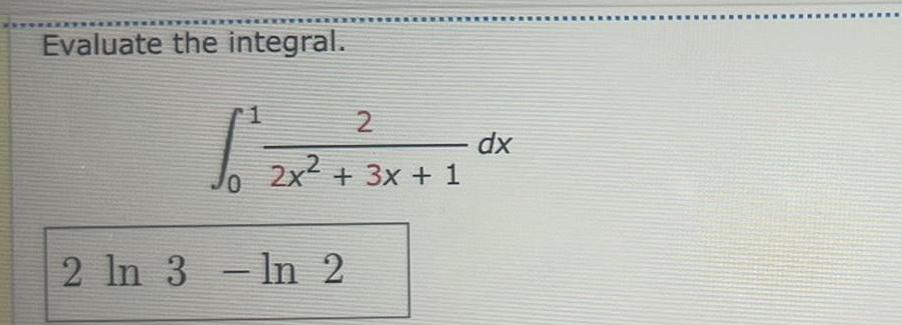

Calculus
Indefinite IntegrationEvaluate the integral Remember to use absolute values where appropriate Use C for the constant of integration y 2 5y 1 dy In y 2 In 5y 1 C 11 X
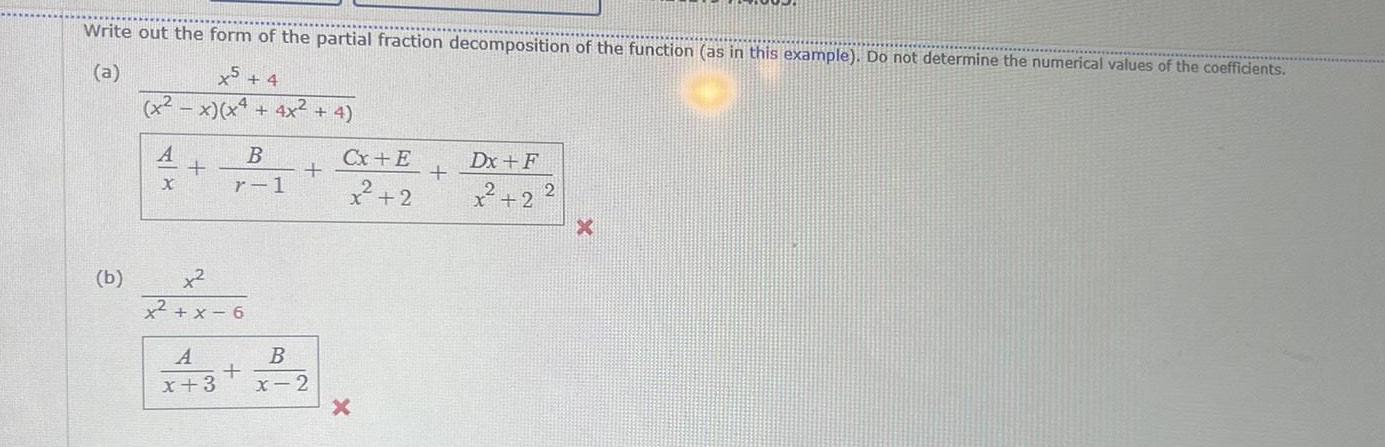
Calculus
Indefinite IntegrationWrite out the form of the partial fraction decomposition of the function as in this example Do not determine the numerical values of the coefficients a x5 4 x x x 4x 4 b A B r 1 x x x 6 B A x 3 x 2 Cx E x 2 X Dx F x 2 X

Calculus
Indefinite Integrationolution of the differential equation that satisfies the given initial condition dA Ab cos br A 0 b dr b sin br In 6 e No REVIOUS ANSWERS SCALCET9 9 3 015
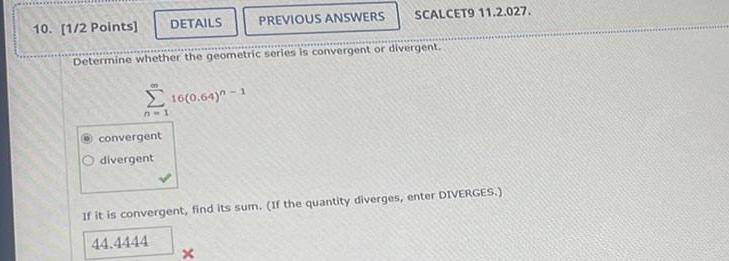
Calculus
Indefinite Integration10 1 2 Points DETAILS Determine whether the geometric series is convergent or divergent n 1 convergent divergent 16 0 64 1 PREVIOUS ANSWERS SCALCET9 11 2 027 x If it is convergent find its sum If the quantity diverges enter DIVERGES 44 4444
Calculus
Indefinite IntegrationConsider the following series 1 2 4 4 n 1 Does the function f x O Yes O No 1 x 4 satisfy the conditions of the Integral Test Evaluate the following integral If it is convergent evaluate it If the quantity diverges enter DIVERGES 1 x 2 40x dx 4 Orient finite the series is Select
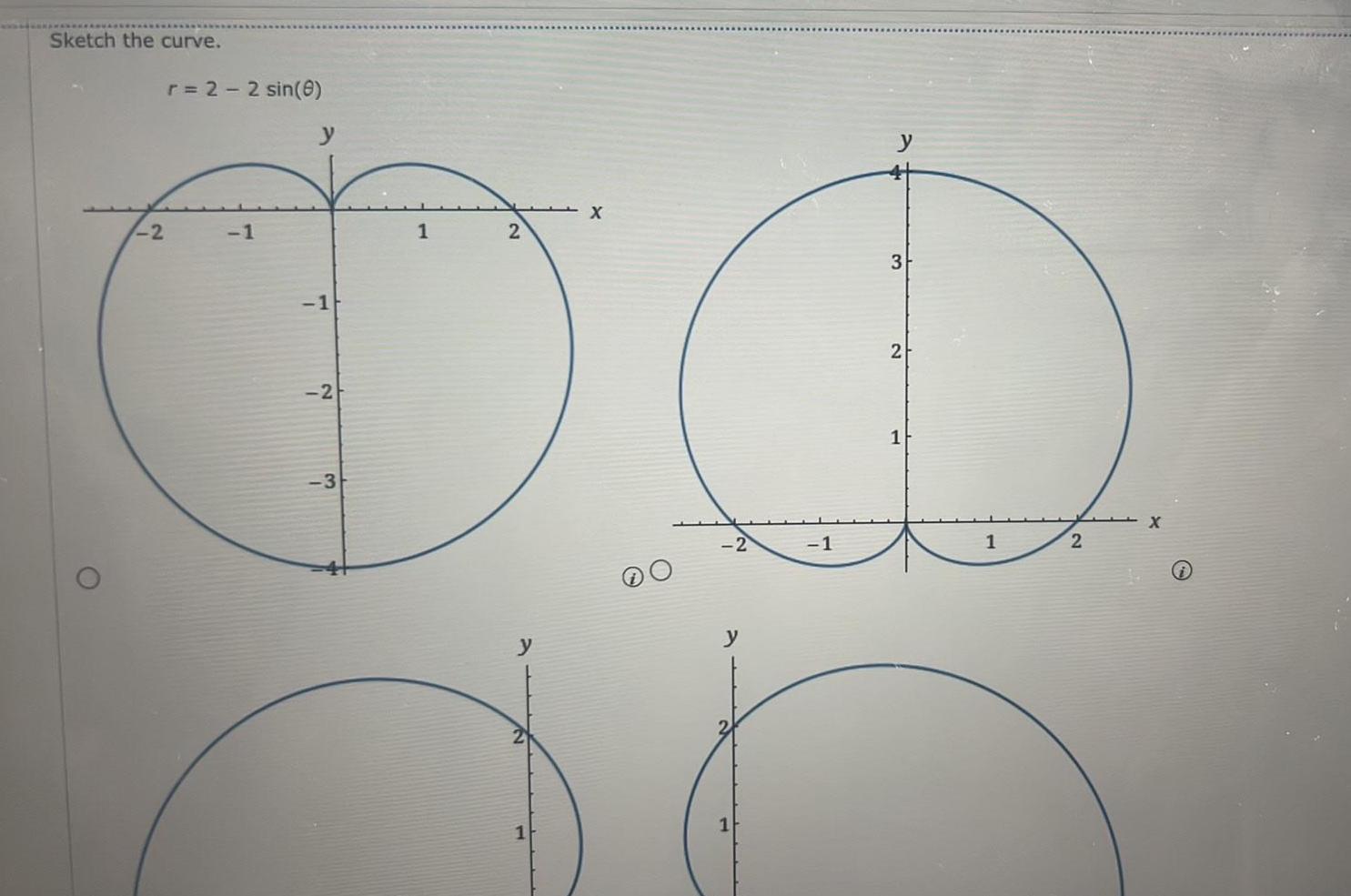

Calculus
Indefinite IntegrationWrite the given function as a power series cos x 1 X n 1 1 n 1 1 X Evaluate the indefinite integral as an infinite series cos X 1 1 x2n 2n 2n x2n 2n 2n dx C c

Calculus
Indefinite IntegrationWe can now solve 1 u Ke 2 2t for u 1 Notice that since u 1 is a solution This also means that K could be 0 and so we could simply write u

Calculus
Indefinite IntegrationPart 5 of 6 We now have In 1 ul 11 2 2 2t C 2 2t C This can be re written as 11 u e 2 2t C Letting K e e can be re written as K
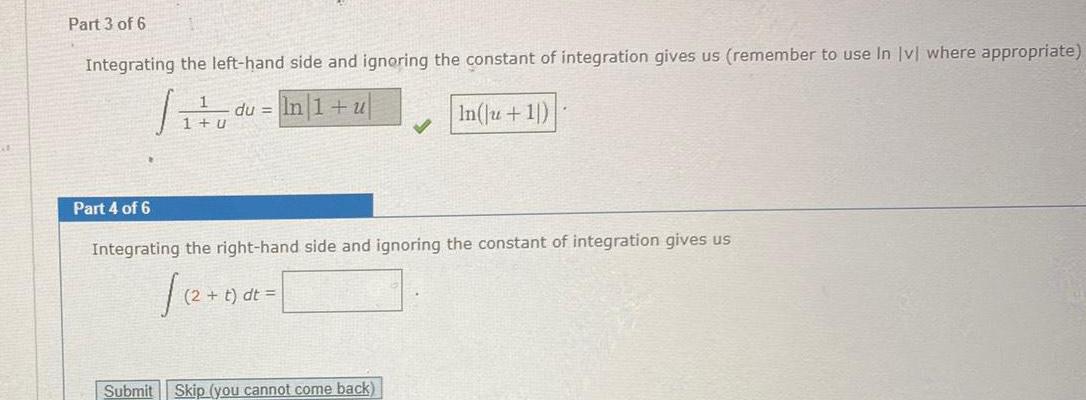
Calculus
Indefinite IntegrationPart 3 of 6 Integrating the left hand side and ignoring the constant of integration gives us remember to use In lvl where appropriate In 1 u In Ju 1 Part 4 of 6 1 u du Integrating the right hand side and ignoring the constant of integration gives us t dt Submit Skip you cannot come back
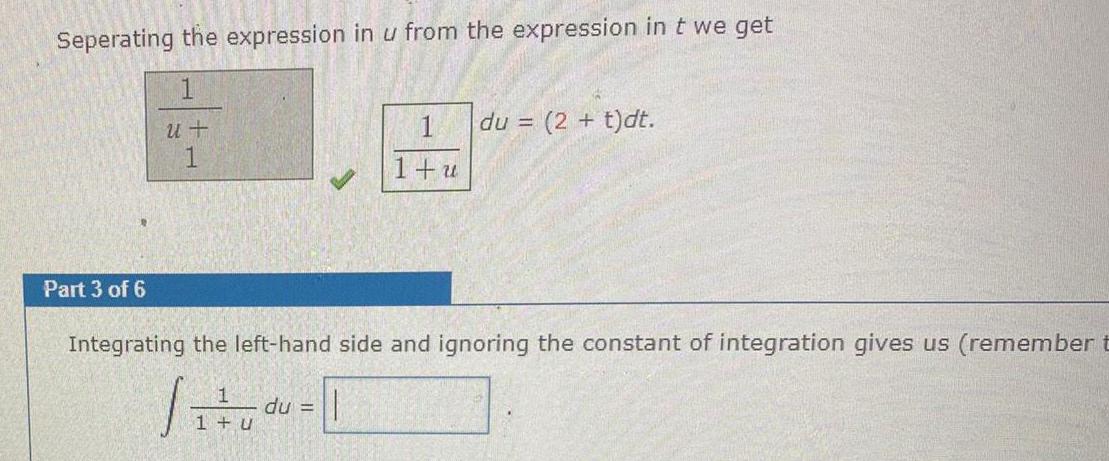
Calculus
Indefinite IntegrationSeperating the expression in u from the expression in t we get 1 u 1 Part 3 of 6 1 1 u du 2 t dt Integrating the left hand side and ignoring the constant of integration gives us remember t du 1 u
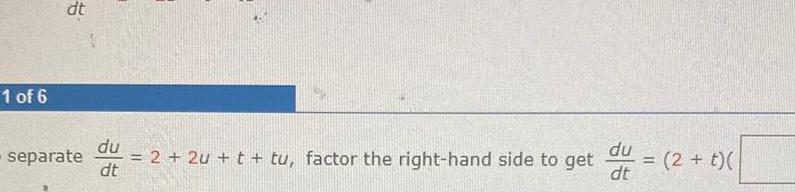
Calculus
Indefinite Integration1 of 6 dt separate du 2 2u t tu factor the right hand side to get dt du dt 2 t

Calculus
Indefinite IntegrationUsing the substitution u x2 88 and again ignoring the constant of integration gives us du
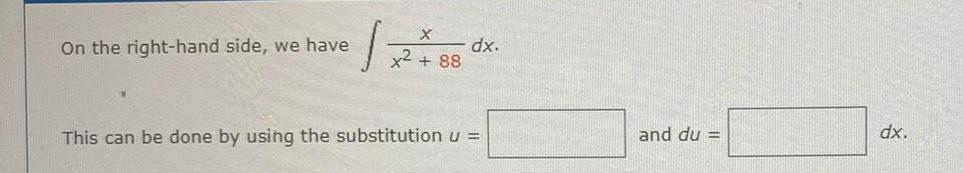
Calculus
Indefinite IntegrationOn the right hand side we have X 12 x2 88 dx This can be done by using the substitution u and du dx

Calculus
Indefinite IntegrationWrite the given function as a power series 2 C 1 7 Evaluate the indefinite integral as an infinite series cos x 1 dx cos x 1 1 c

Calculus
Indefinite Integration2 Use Stoke s Theorem to evaluate SF d C F x y x 3zsin x x e y cos z S z 1x y z 0 Z

Calculus
Indefinite Integrationstion 24 A hot air balloon is flying at a height of 152 feet and is directly above Marshall Space Flight Center in Huntsville Alabama THe pilot looks down at the airport which is known to be 5 miles from Marshall Space Flight Center What is the angle of depression in degrees for the baloon to the airport Round to the tenth

Calculus
Indefinite Integration1 Compute the value of f x 7 3xy 5 dr if C is the curve consisting of the circle centered at the origin of radius 3 and the line y x as depicted in the picture 3

Calculus
Indefinite IntegrationIf sin x in Quadrant 1 find 27 28 tan 2x Please enter answer accurate to 4 decimal places

Calculus
Indefinite IntegrationDirections Draw a diagram create an equation and then solve for the desired measurement Kami is standing 12 feet from a rock climbing wall When she looks up to see her friend ascend the wall the angle of elevation is 56 How high up the wall is her friend V HINT Round to the nearest thousandths if necessary
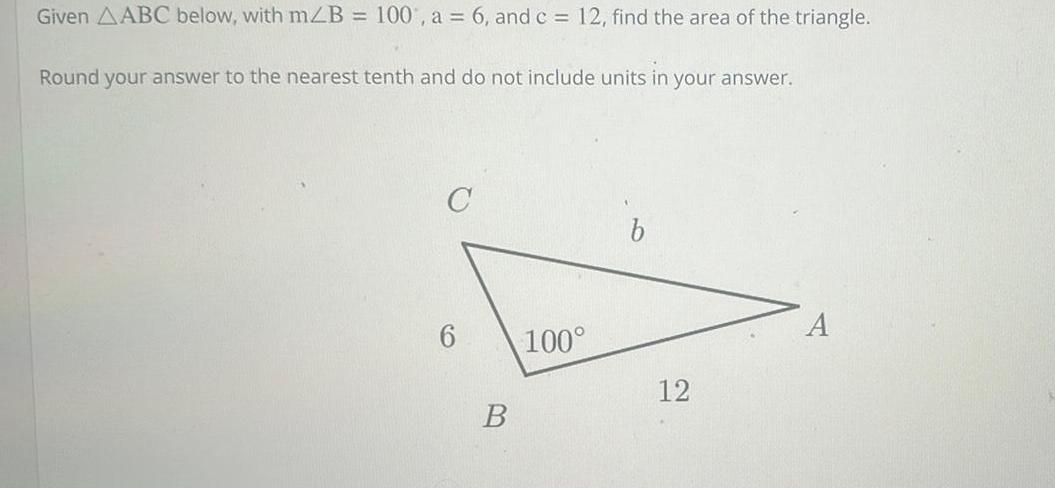
Calculus
Indefinite IntegrationGiven AABC below with m B 100 a 6 and c 12 find the area of the triangle Round your answer to the nearest tenth and do not include units in your answer C B 100 b 12 A

Calculus
Indefinite Integrationnd the most general antiderivative of the function Check your answer by differentiation Use C for the constant of the antiderivative f x x 9 2

Calculus
Indefinite IntegrationNow we must find f x which is given by the general antiderivative of f x 18x2 C We note that f x is the sum of two functions h x 18x and b x C such that f x h x b x This means that f x will be given by the following where H x is the general antiderivative of h x B x is the general antiderivative of b x and D is an arbitrary constant f x H x B x D Furthermore we note that h x 18x2 is the product of a constant and a function k x x such that h x 18k x Finally we note that b x C is a constant function and can be written in the form b x Cx Applying the formulas described in this step and those used in the previous step we can now state the following letting D represent the arbitrary constant Do not add any additional constants f x 18x C 18 f x 18 Cx D To conclude give an equation for f Use C for the constant of the first antiderivative and D for the constant of the second antiderivative f x

Calculus
Indefinite IntegrationThe values of y yo and t are given For an equation of the form y yoekt give the exact value of k in terms of natural logarithms Yo 120 t 3 y 40 k 0 se integers or fractions for any numbers in the expression www

Calculus
Indefinite IntegrationProblem 4 20pts Use the Divergence Theorem to evaluate the following Surface Integral fr where the vector field F is given by F dS F 2x 2 i x y j xz k and the closed surface S is given by the unit cube where the coordinates x y and z take values from 1to1 raspectively

Calculus
Indefinite IntegrationConsider the following function f x 36x Find f x Use C for the constant of the first antiderivative f x Find f Use D for the constant of the second antiderivative f x

Calculus
Indefinite IntegrationFind an antiderivative of the function Remember to use absolute values where appropriate 5 t a g t G t b r 0 sec 0 R 8

Calculus
Indefinite IntegrationWe have determined that w 22 Recalling from a previous step that 44 w allows us to determine the other dimension 1 44 w To conclude we state the dimensions of the rectangle in m with perimeter 88 m whose area is as large as possible Enter the dimensions as a comma separated list m

Calculus
Indefinite IntegrationIF bao lun 848 and Couluate 1 b lon 31 A The series will absolutly converge B Notenough informaler The series will Conditionally convere 5 The serves will

Calculus
Indefinite IntegrationUse a power reducing formula to simplify 32sinacos a Write your answer as an equivalent expression that does not contain any powers of sine or cosine greater than 1

Calculus
Indefinite IntegrationYou are given that tan A 4 and tan B 7 Find tan A B Give your answer as a fraction
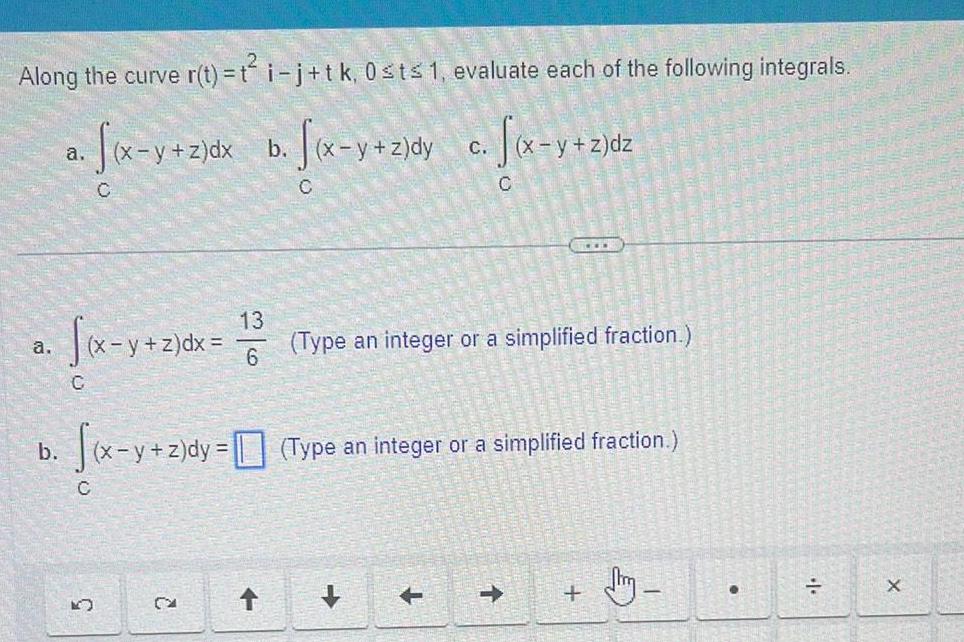
Calculus
Indefinite IntegrationAlong the curve r t t i j tk 0 st 1 evaluate each of the following integrals a x y z dx b x y z dy x y z dy c f x y z a b C C C K y z dx 13 6 CA C f x y z dy z dy Type an integer or a simplified fraction C Type an integer or a simplified fraction dm X
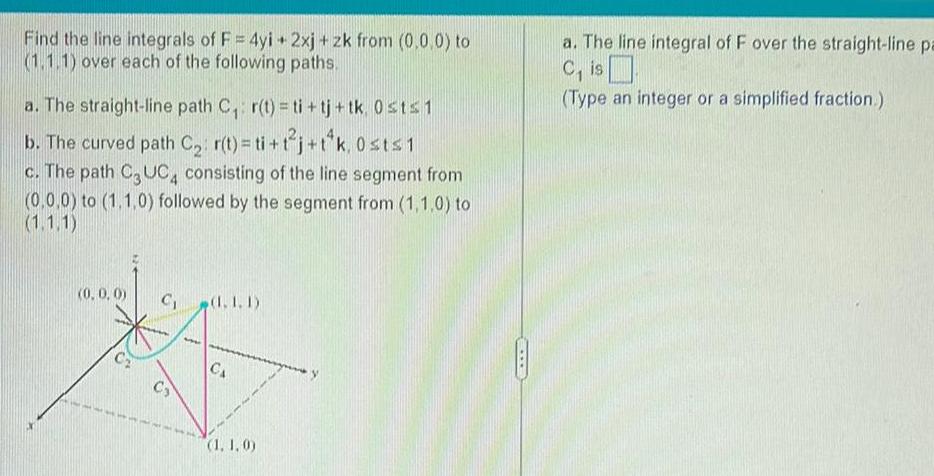
Calculus
Indefinite IntegrationFind the line integrals of F 4yi 2xj zk from 0 0 0 to 1 1 1 over each of the following paths a The straight line path C r t ti tj tk 0 st 1 b The curved path C r t ti t j t k 0st 1 c The path C3UC4 consisting of the line segment from 0 0 0 to 1 1 0 followed by the segment from 1 1 0 to 1 1 1 0 0 0 C 1 1 CS CA 1 1 0 a The line integral of F over the straight line pa C is Type an integer or a simplified fraction
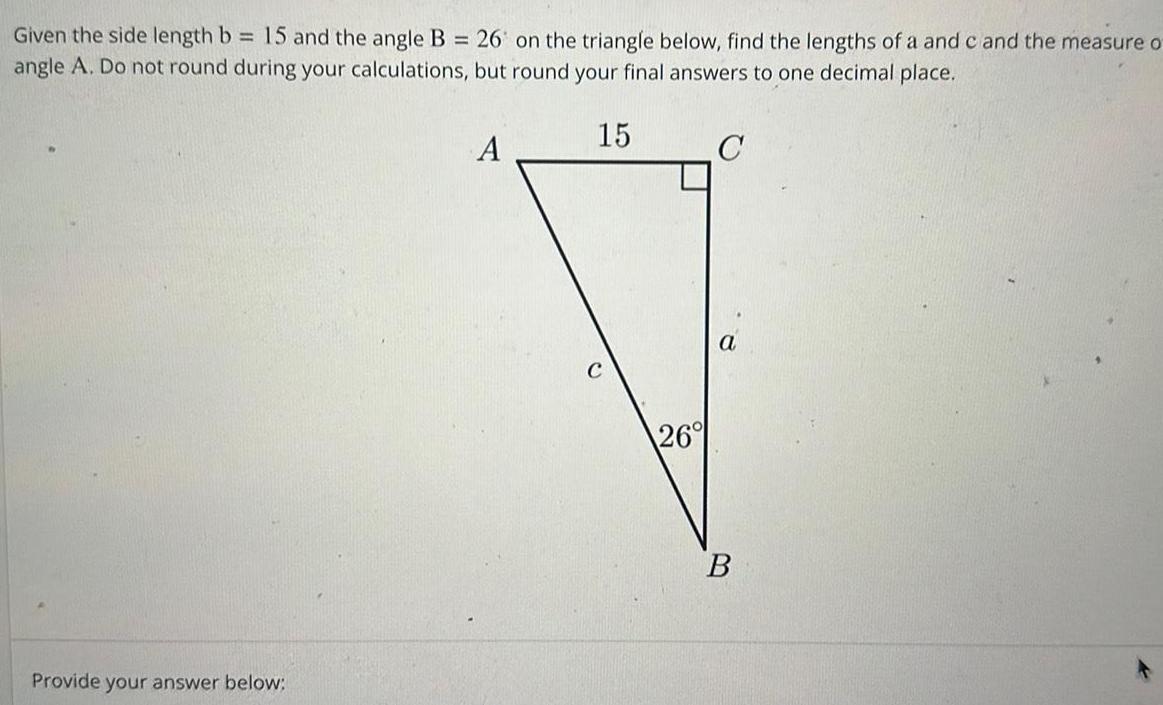
Calculus
Indefinite IntegrationGiven the side length b 15 and the angle B 26 on the triangle below find the lengths of a and c and the measure o angle A Do not round during your calculations but round your final answers to one decimal place 15 C Provide your answer below A 26 a B
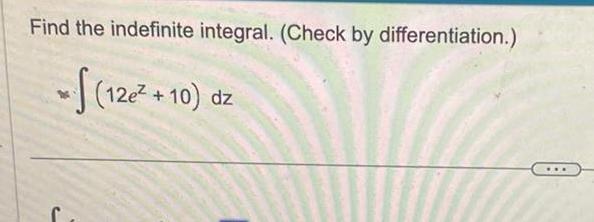

Calculus
Indefinite Integration6 Prove the following 1 cosx sinx cosx 1 a sinx cosx sinx cos x 1 cos x b sin x 2csc x 1 c cos x cotx cot x cos x 1 sinx secx tanx d 1 sinx e sec x tan x tan x sec x

Calculus
Indefinite IntegrationUse Half Angle or Double Angle Formula to find f sin 5xdx You must show your work to receive full credit

Calculus
Indefinite IntegrationUse partial fractions to evaluate d dx O 5 ln 2 1 6 C O In x 2 x 3 C O In C O In C 5 x x 6

Calculus
Indefinite IntegrationUse Integration by Parts Formula to find e dx Or e 2re e C O e 2re e C e 2xe 2e C

