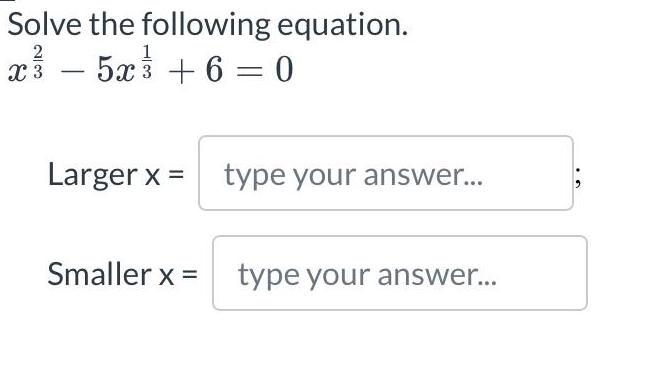
Indefinite Integration Questions and Answers
Calculus
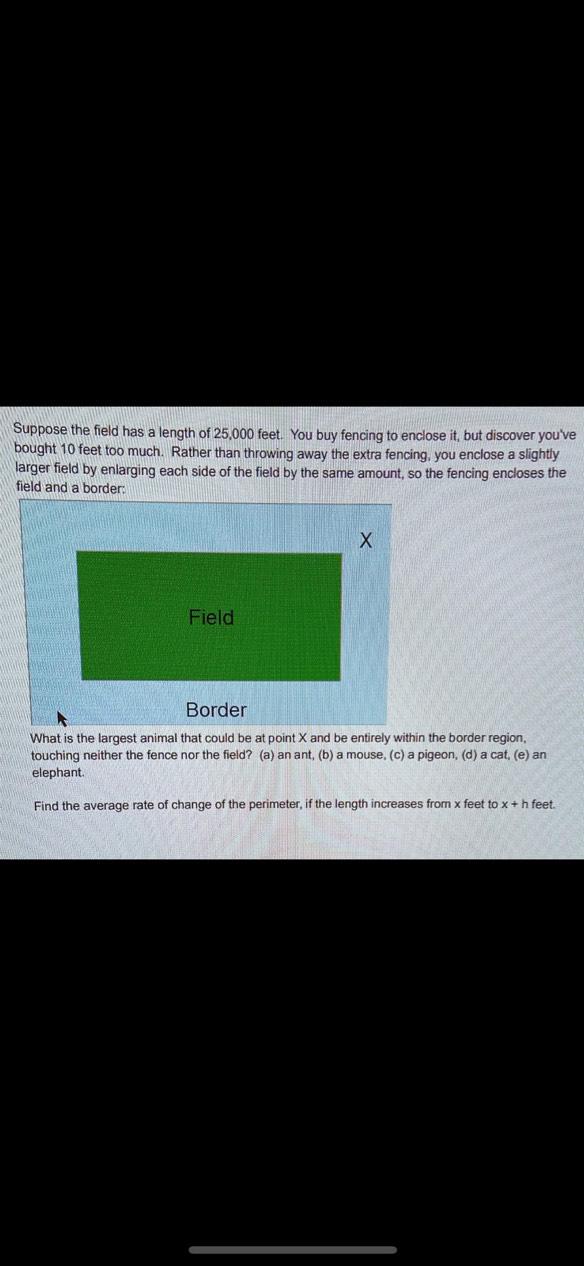
Indefinite IntegrationSuppose the field has a length of 25,000 feet. You buy fencing to enclose it, but discover you've bought 10 feet too much. Rather than throwing away the extra fencing, you enclose a slightly larger field by enlarging each side of the field by the same amount, so the fencing encloses the field and a border:
What is the largest animal that could be at point X and be entirely within the border region, touching neither the fence nor the field? (a) an ant, (b) a mouse, (c) a pigeon, (d) a cat, (e) an elephant.
Find the average rate of change of the perimeter, if the length increases from x feet to x+h feet.

Calculus
Indefinite IntegrationA maintenance worker fills a swimming pool with water at a rate of 10
m^3/minute.
Suppose at t = 0, the swimming pool is filled with 100 m³ of water.
How much water will be in the swimming pool at t = 17 minutes? ______m^3
A function giving the volume V of water in the swimming pool after t minutes is V(t) = ____________________.
When will the swimming pool contain 430 m³ of water? ___________minutes.

Calculus
Indefinite IntegrationKen flies a drone in a circular path around an object that is 210 feet west and 190 feet north of his position.The drone's path takes it over a point that is 170 feet east and 250 feet south of him. Find an equation for the drone's path. (Assume Ken is located at the origin, with the horizontal axis running east-west and the vertical axis running north-south) The drone's path follows the equation_________
When the drone passes due west of Ken's position, it will be______ feet west of him (round your answer to three decimal places).

Calculus
Indefinite IntegrationEvaluate the expression cos^-1(sin(4π/3))
________________
Give your answer as an exact value

Calculus
Indefinite IntegrationSuppose cos θ = 3/4
Find the following.
cos(- θ) =
cos (180° - θ) =
cos(180° + θ) =
Calculus
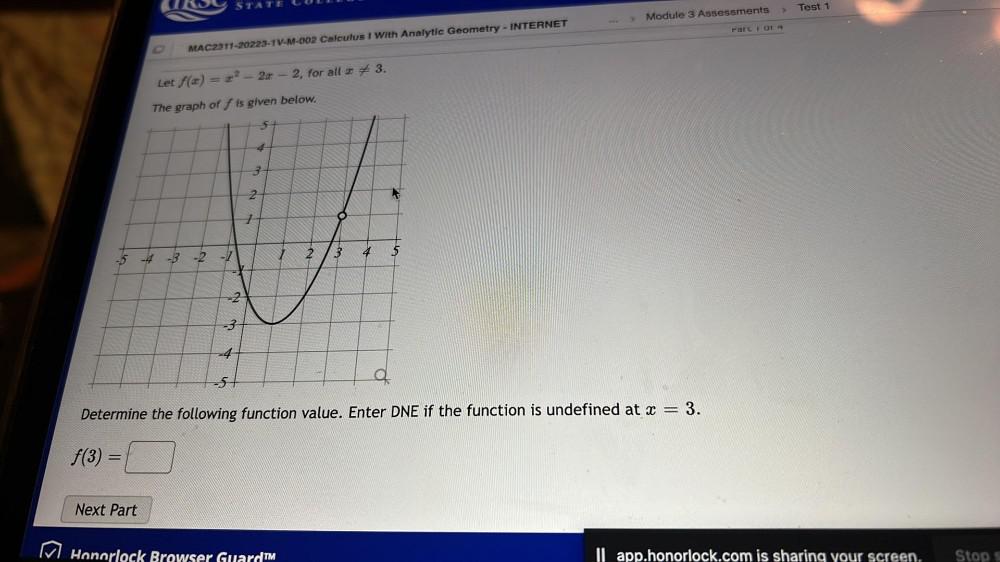
Indefinite IntegrationLet f(x) = x² - 2x - 2 for all x ≠ 3
The graph of f is given below
Determine the following function value . Enter DNE if the function is undefined at x = 3
f(3) = _______

Calculus
Indefinite IntegrationFind the length of an are of a circle of radius 18 feet intercepted by a central angle of 120°.

Calculus
Indefinite IntegrationRead and understand the problem, then solve.
Stating what is asked in the problem. During the Apollo 14 mission, Alan Shepard hit a golf ball on the Moon. The function h(t)=18t-0.8t² models the height of the golf ball's trajectory on the Moon, where h(t) is the height, in metres, of the ball above the surface of the Moon and t is the time in seconds. Determine the instantaneous rate of change in the height of the ball at 5 seconds.
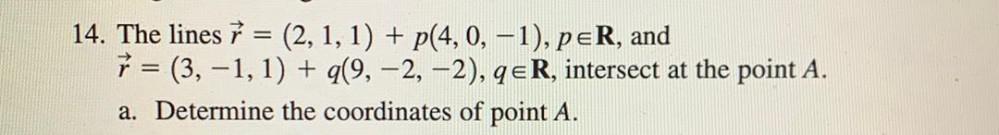
Calculus
Indefinite IntegrationThe lines r = (2, 1, 1) + p(4, 0, -1), p∈ R, and q = (3,−1, 1) + q(9, −2, −2), q∈ R, intersect at the point A.
Determine the coordinates of point A.
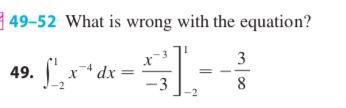
Calculus
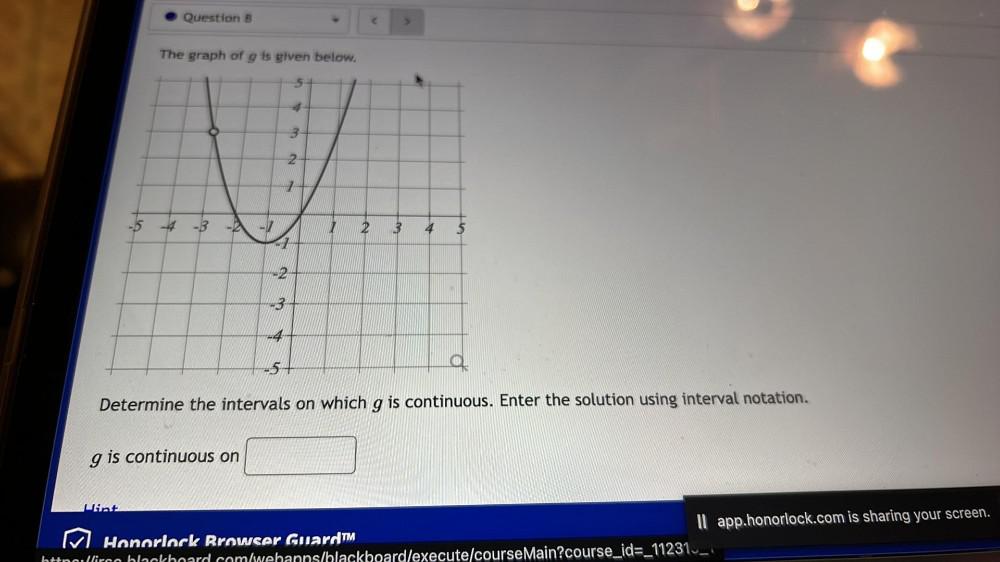
Indefinite IntegrationThe graph of g is given below.
Determine the intervals on which g is continuous. Enter the solution using interval notation.
g is continuous on _____

Calculus
Indefinite IntegrationU xx + U yy = 2x, 0 < x < 1, 0 < y < 1
u(x,0) = 0, u(1, y) = 0
u(x,0) = 0, u(x, 1) = 0
Solve your problem
Calculus
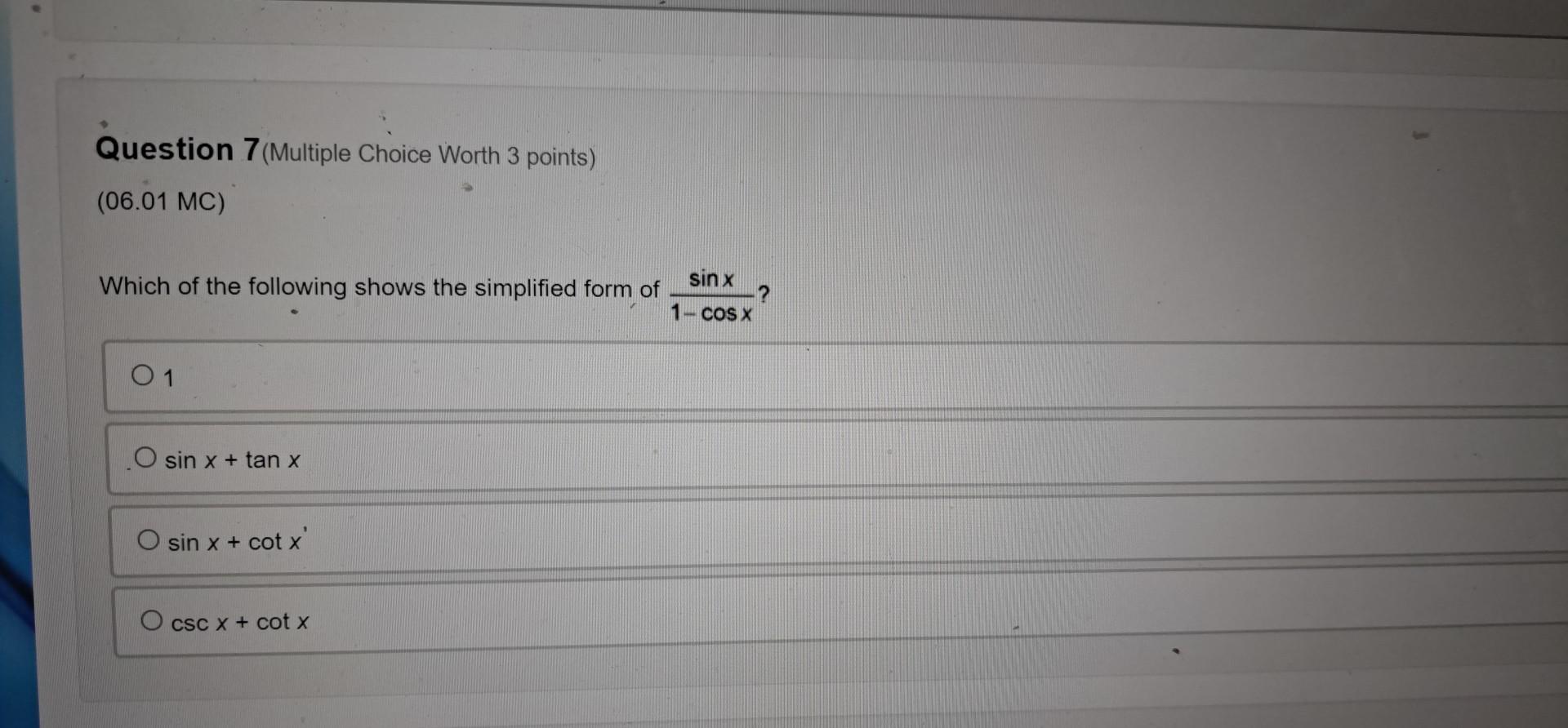
Indefinite IntegrationWhich of the following shows the simplified form of sinx/(1-cosx)?
a)1
b) sin x + tan x
c) sin x + cot x
d) csc x + cot x
Calculus
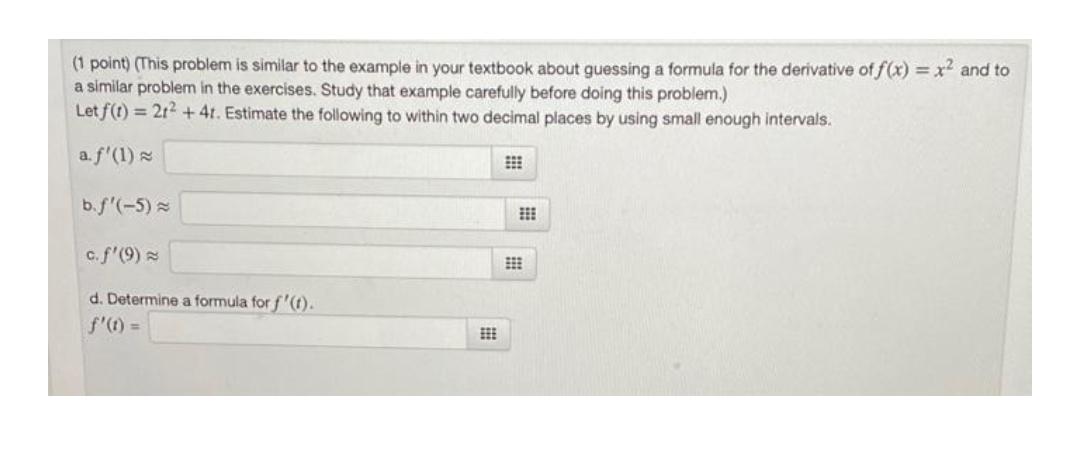
Indefinite Integration(This problem is similar to the example in your textbook about guessing a formula for the derivative of f(x) = x² and to a similar problem in the exercises. Study that example carefully before doing this problem.) Let f(t) = 2t² +4t. Estimate the following to within two decimal places by using small enough intervals.
(a.) f'(1) ≈
(b.) f'(-5) =
(c.) f'(9) ≈
(d.) Determine a formula for f'(t).
f'(t) =

Calculus
Indefinite IntegrationSolve the following system of equations.
3x+5y-5z-21
-4x=5z+17
2x-5y+6z=-16

Calculus
Indefinite IntegrationUsing the shift or stretch theorem find the Fourier transform of
{1 for 2 ≤ t ≤0
b(t)= { 0, otherwise
given the transform of unit square pulse function a(t)={1, for -1≤t≤1
{ 0, otherwise
is ā (k) =2sin(k)/k
b(k)=___
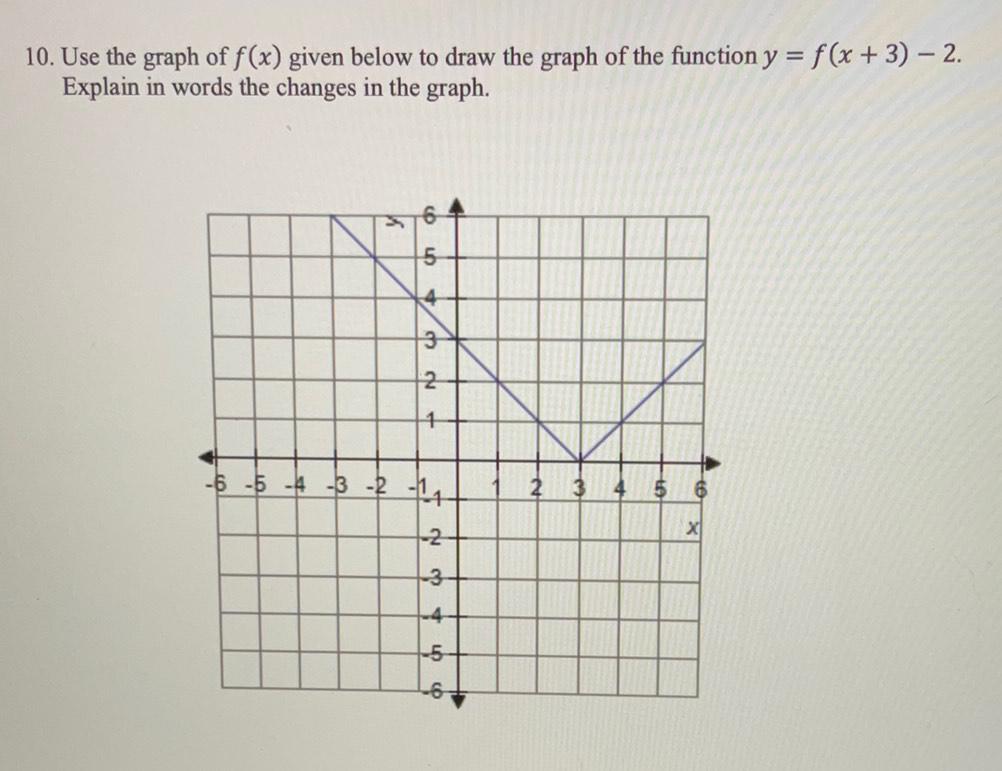
Calculus
Indefinite IntegrationUse the graph of f(x) given below to draw the graph of the function y = f(x + 3) - 2. Explain in words the changes in the graph.
![Find two solutions of the equation. Give exact answers in radians in the interval [0,2π].
sin(t)=-(3^1/2)/2](https://media.kunduz.com/media/sug-question/raw/80433287-1660159468.2701483.jpeg?w=256)
Calculus
Indefinite IntegrationFind two solutions of the equation. Give exact answers in radians in the interval [0,2π].
sin(t)=-(3^1/2)/2

Calculus
Indefinite IntegrationNow let's write down an iterated double integral that is equal to ∬ e√(x² + y²) dA in polar coordinates in the dA = r dr dθ order.
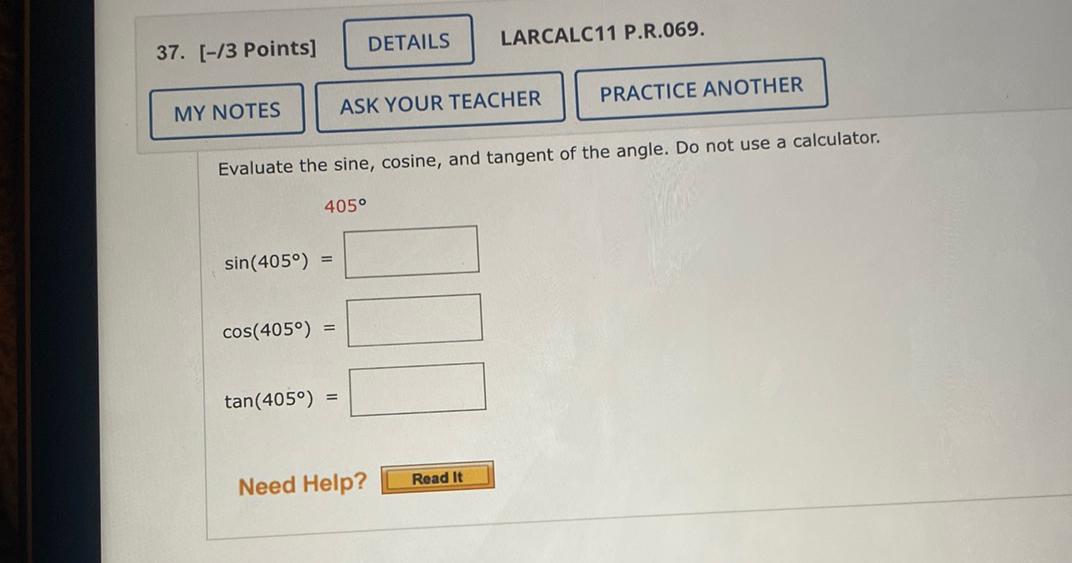
Calculus
Indefinite IntegrationEvaluate the sine, cosine, and tangent of the angle. Do not use a calculator. 405°
sin(405°) = ______
cos(405°) = ______
tan(405°) = ______

Calculus
Indefinite IntegrationConvert the degree measure to radian measure as a multiple of and as a decimal accurate to three decimal places. (-480°)
multiple of π = ____
decimal = ____
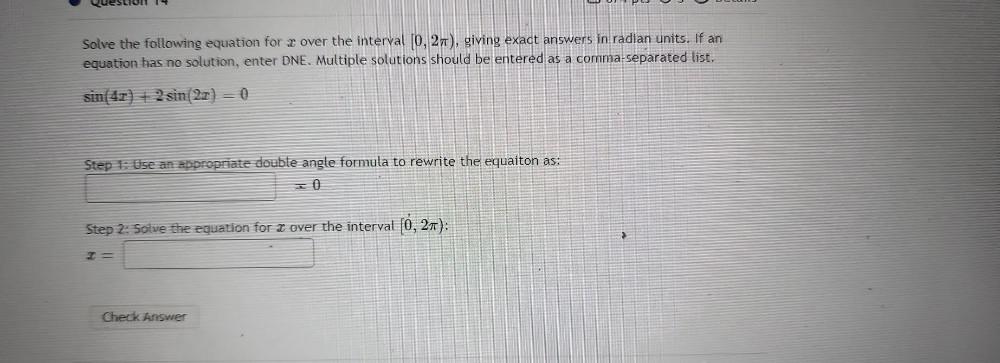
Calculus
Indefinite IntegrationSolve the following equation for over the interval [0, 2π), giving exact answers in radian units. If an equation has no solution, enter DNE. Multiple solutions should be entered as a comma-separated list.
sin(4x) + 2 sin(2x) = 0
1)Use an appropriate double angle formula to rewrite the equaiton as:
2)Solve the equation for å over the interval [0, 2π):
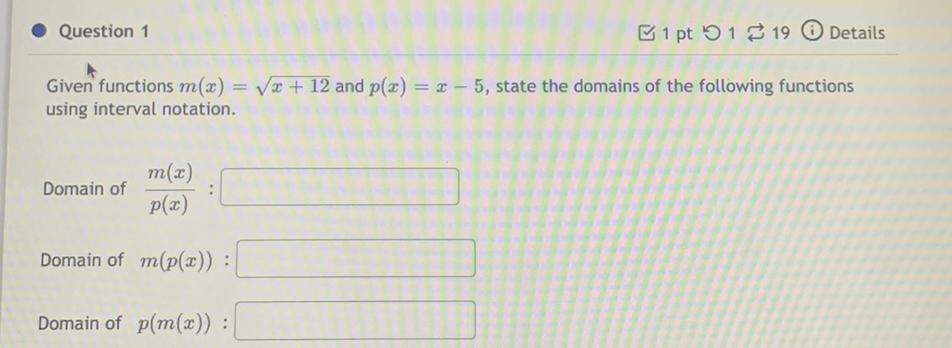
Calculus
Indefinite IntegrationGiven functions m(x) = √x+12 and p(x) = x - 5, state the domains of the following functions using interval notation.
Domain of m(x)/p(x):
Domain of m(p(x)) :
Domain of p(m(x)) :

Calculus
Indefinite IntegrationEvaluate ∫ {(9x + 25) /x² +( 6x +9)} dx using the method of Partial Fractions.
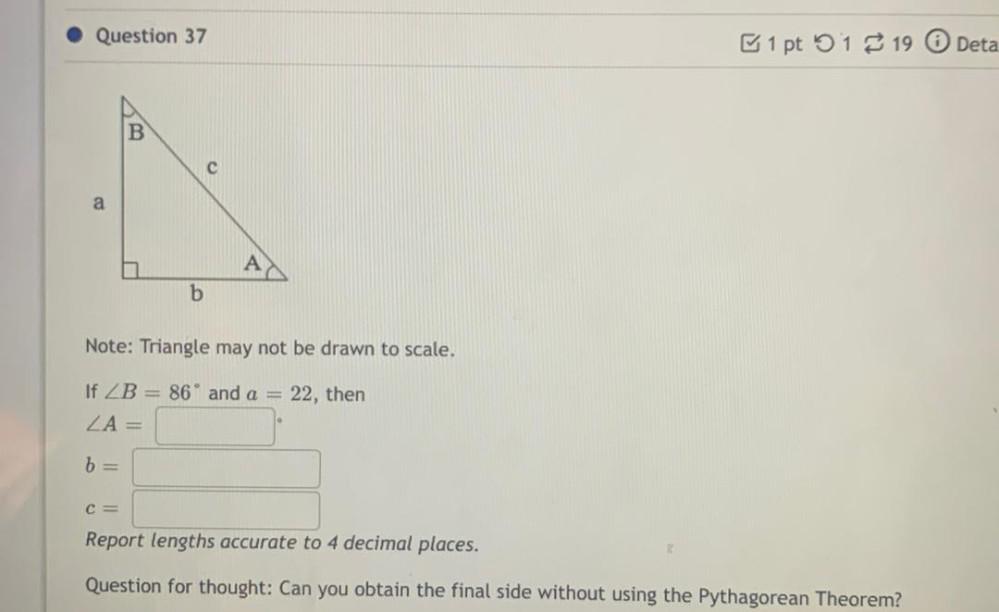
Calculus
Indefinite IntegrationNote: Triangle may not be drawn to scale.
If ∠ B = 86° and a = 22, then
Report lengths accurate to 4 decimal places.
Question for thought: Can you obtain the final side without using the Pythagorean Theorem?

Calculus
Indefinite IntegrationIce Cream Sundaes. An ice cream shop has a choice of ten toppings.
Suppose you can afford at most four toppings. How many different types of ice cream sundaes can you order?
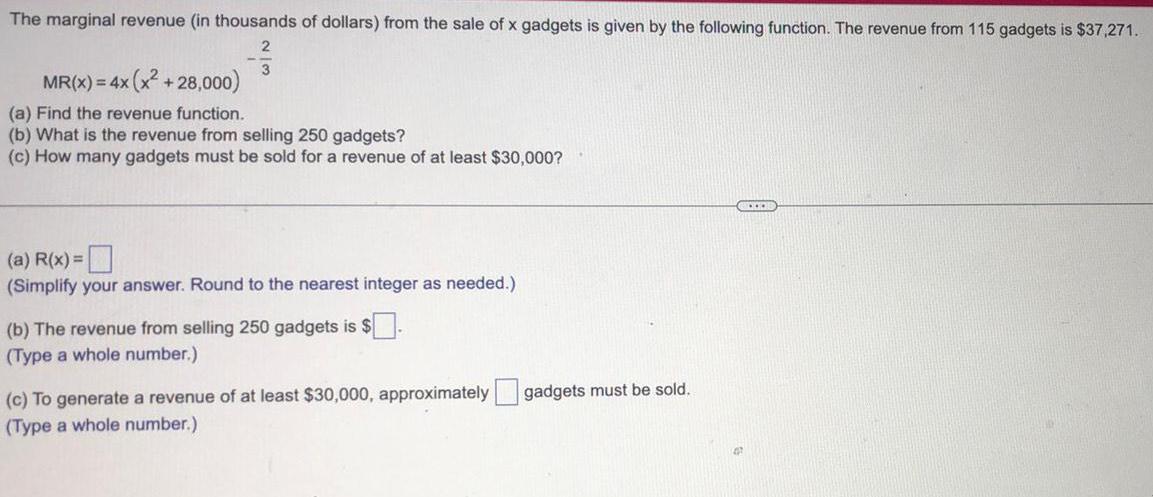
Calculus
Indefinite IntegrationThe marginal revenue (in thousands of dollars) from the sale of x gadgets is given by the following function. The revenue from 115 gadgets is $37,271.
-2/3 MR(x) = 4x (= 4x (x² +28,000)
(a) Find the revenue function.
(b) What is the revenue from selling 250 gadgets?
(c) How many gadgets must be sold for a revenue of at least $30,000?
(a) R(x) =
(Simplify your answer. Round to the nearest integer as needed.)
(b) The revenue from selling 250 gadgets is $.
(Type a whole number.)
(c) To generate a revenue of at least $30,000, approximately
(Type a whole number.)

Calculus
Indefinite IntegrationLet f(x) = log3(x-4).
a. Use transformations to graph the function.
b. Write the domain and range in interval notation.
c. Determine the vertical asymptote.

Calculus
Indefinite IntegrationEvaluate the double integral for the function f(x, y) and the given region R.
f(x, y) = y e^x^³; R is bounded by x =y/6, x = 1 and y = 0.
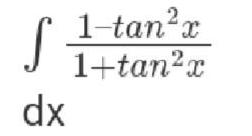
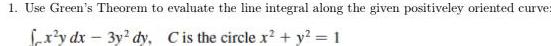
Calculus
Indefinite IntegrationUse Green's Theorem to evaluate the line integral along the given positiveley oriented curve:
∫x²y dx - 3y² dy, C is the circle x² + y² = 1
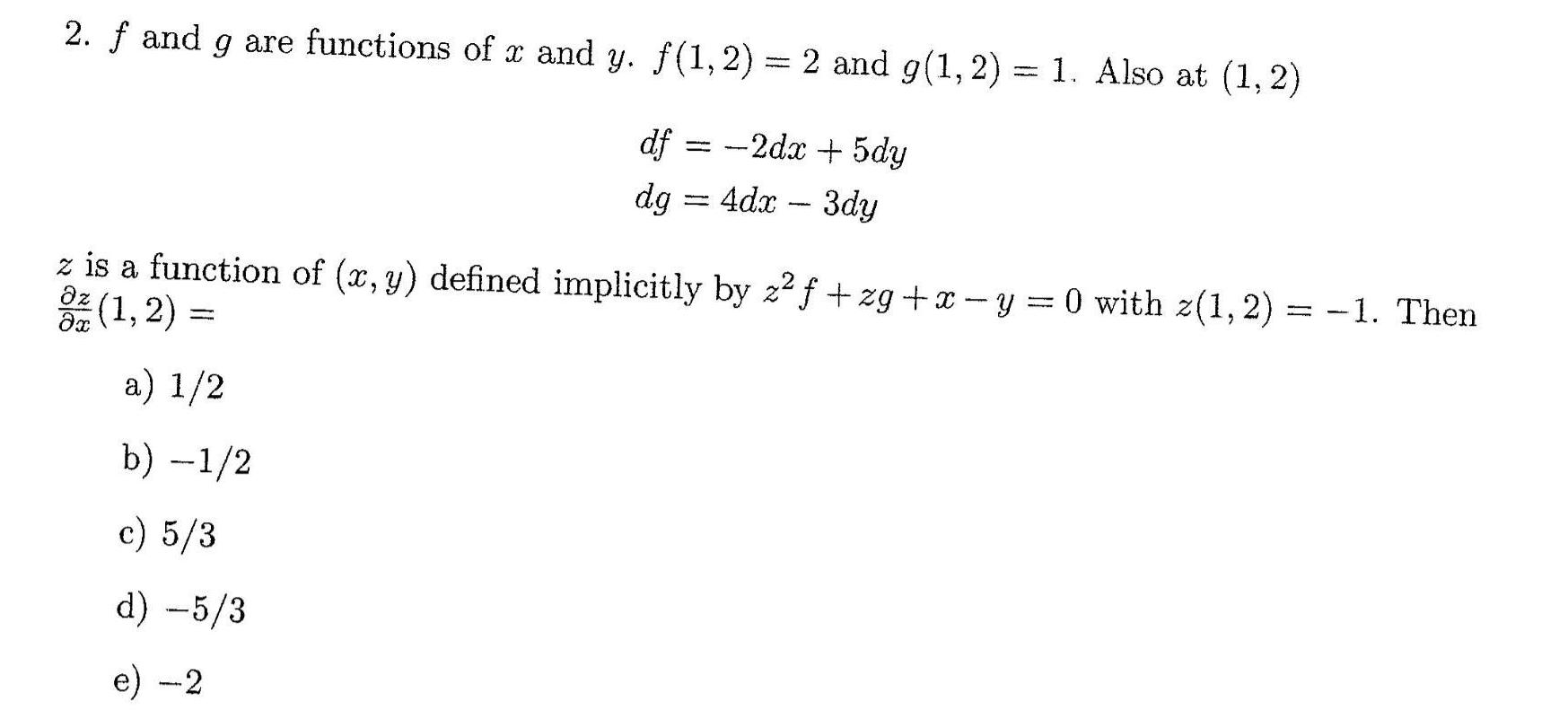
Calculus
Indefinite Integrationf and g are functions of x and y. f(1,2)= 2 and g(1,2)= 1. Also at (1,2)
df = -2dx + 5dy
dg = 4dx - 3dy
z is a function of (x,y) defined implicitly by z2f+zg+x-y=0 with z(1, 2) = -1. Then dz dx(1, 2) =
a) 1/2
b) -1/2
c) 5/3
d) -5/3
e) -2

Calculus
Indefinite Integration(a) Evaluate the following indefinite integrals. Show complete working. In particular: if you use substitution, write down the substitution that you used. Show the full working needed to make that substitution. Write your final answer in terms of a. if you use partial fraction decomposition, show the complete working that is needed to find the
appropriate partial fraction expression. if you use integration by parts, indicate which part of the integration and corresponds to corresponds to v in this formula
∫du/dx vdx= uv =-∫u dv/dx dx
(Note: the integrand is the function inside the integral that we want to integrate.)
1. ∫1/x²-1 dx
2. ∫ e^x cos h(3ex)dx
3. ∫ x ln xdx
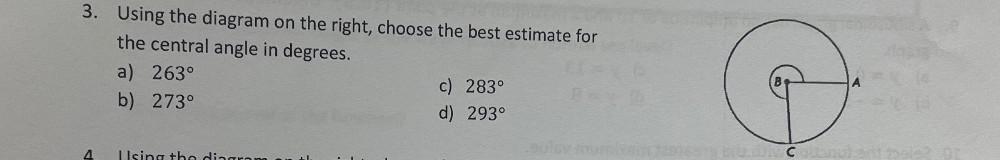
Calculus
Indefinite IntegrationUsing the diagram on the right, choose the best estimate for the central angle in degrees.
a) 263°
c) 283°
b) 273°
d) 293°

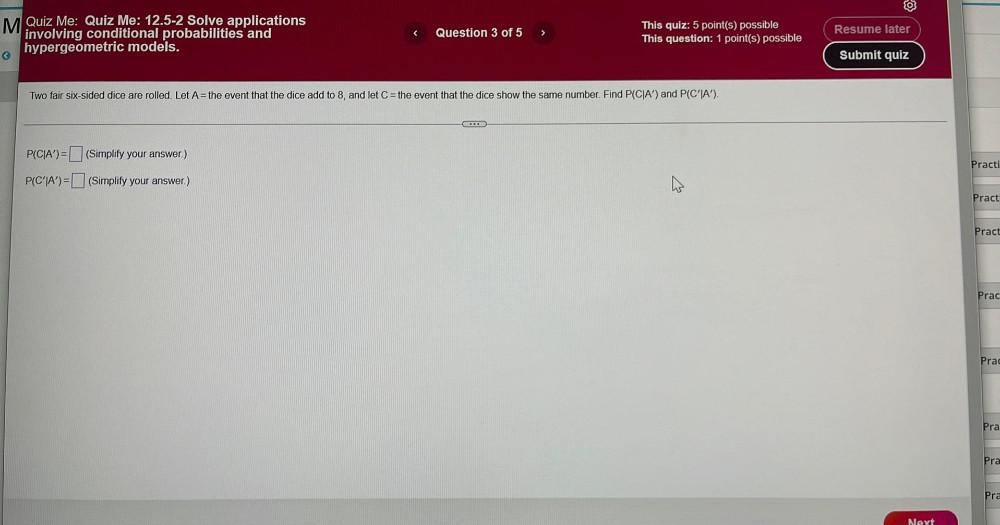
Calculus
Indefinite IntegrationTwo fair six-sided dice are rolled. Let A = the event that the dice add to 8, and let C = the event that the dice show the same number. Find P(CIA') and P(C'|A').
P(CIA')= (Simplify your answer.)
P(C'IA')= (Simplify your answer.)
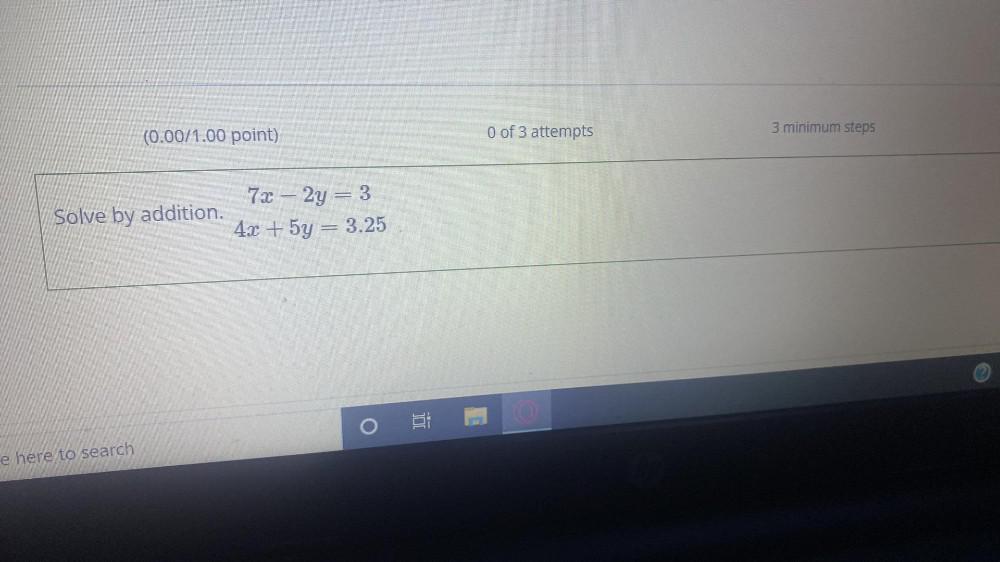
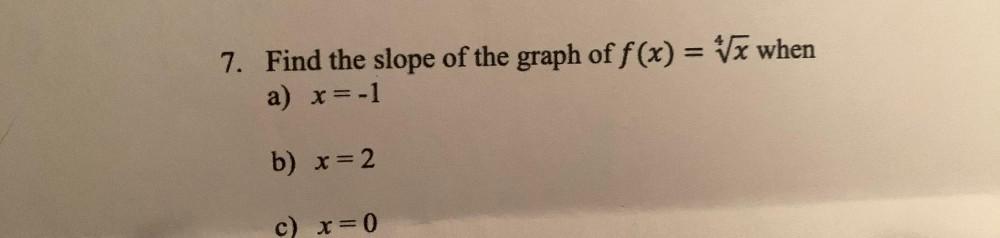
Calculus
Indefinite IntegrationFind the slope of the graph of f(x) = ∜x when
a) x = -1
b) x = 2
c) x = 0
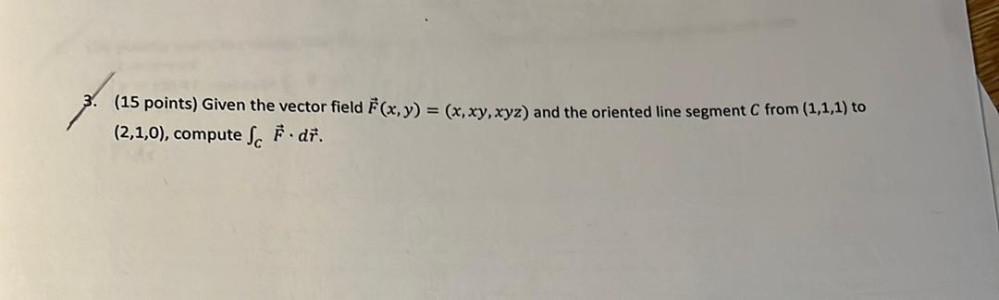
Calculus
Indefinite IntegrationGiven the vector field F(x, y) = (x, xy, xyz) and the oriented line segment C from (1,1,1) to (2,1,0), compute c∫F. dr.

Calculus
Indefinite IntegrationThe terminal side of an angle 8 in standard position intersects the unit circle at(-12/13,-5/13)
What is sin (θ)?
Write your answer in simplified, rationalized form.
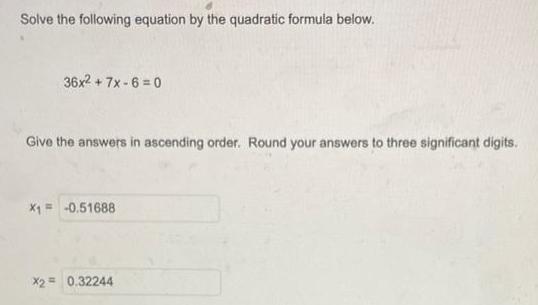
Calculus
Indefinite IntegrationSolve the following equation by the quadratic formula below.
36x² + 7x-6=0
Give the answers in ascending order. Round your answers to three significant digits.
x1 -0.51688
x2= 0.32244

Calculus
Indefinite IntegrationUse a finite approximation to estimate the area under the graph of the given function on the stated interval as instructed.
1) f(x) = x2 between x = 4 and x = 8 using the "midpoint rule" with four rectangles of equal width.
2) f(x) = x² between x = 0 and x = 1 using a lower sum with two rectangles of equal width.
Calculus
Indefinite IntegrationEach side of a square is increasing at a rate of 6 cm/s. At what rate (in cm²/s) is the area
cm²/s
Calculus
Indefinite Integrationf(x) = x² between x = 0 and x = 4 using an upper sum with two rectangles of equal width.

Calculus
Indefinite IntegrationFind the total area of the region between the curve and the x-axis.
y=1/√x; 1≤x≤ 4

Calculus
Indefinite IntegrationUse the given transformation to evaluate the integral.
∫∫3x² dA, where R is the region bounded by the ellipse 9x^2 + 25y^2 = 225; x = 5u, y = 3v

Calculus
Indefinite IntegrationEvaluate the integral by making an appropriate change of variables.
∫∫ 3 cos (9 (y-x / y+x)) dA where R is the trapezoidal region with vertices (8, 0), (10, 0), (0, 10), and (0, 8)