Indefinite Integration Questions and Answers
![Find the area of the finite part of the paraboloid y = x² + z² cut off by the plane y = 81. [Hint: Project the surface onto the xz-plane.]](https://media.kunduz.com/media/sug-question/raw/84538811-1658426307.4917405.jpeg?w=256)
Calculus
Indefinite IntegrationFind the area of the finite part of the paraboloid y = x² + z² cut off by the plane y = 81. [Hint: Project the surface onto the xz-plane.]

Calculus
Indefinite IntegrationStock Prices The weekly closing price of a corporation's stock in week t is approximated by
f(t) = 70+ 4t cos(πt 6) (0 ≤ t ≤ 15)
where f(t) is the price (in dollars) per share. Find the average weekly closing price of the stock over the 15-week period. (Round your answer to the nearest dollar.)

Calculus
Indefinite IntegrationFind the power series expansions for the following functions and specify for which x-values the expansion is valid.
(a) f(x) 1 x
Hint: Rewrite 1 x = 1 1 - (1 - x)
(b) f(x) = 1 1 - 4x²
(c) f(x) = x 2-x

Calculus
Indefinite IntegrationUse the calculator to find the following. Round your answer to 4 decimal places.
In 7

Calculus
Indefinite IntegrationSolve the following system of equations.
2a - 20b = 0
4a + 70c = 50
40b + 56c = 42
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution is
(Type an ordered triple, using integers or fractions.)
B. There are infinitely many solutions.
C. There is no solution.

Calculus
Indefinite IntegrationLet g'(y) =- 2y
Find the particular solution to the above differential equation that satisfies the following initial condition.
g(6) =-8
g(y)=

Calculus
Indefinite IntegrationFor the real-valued functions f(x) = x-4 x+1 and g(x) = 4x-5, find the composition fog and specify its domain using interval notation.

Calculus
Indefinite IntegrationFind f. (Use C for the constant of the first antiderivative and D for the constant of the second antiderivative.)
F"(x) = 32x³ - 18x² + 10x
f(x) =
Calculus
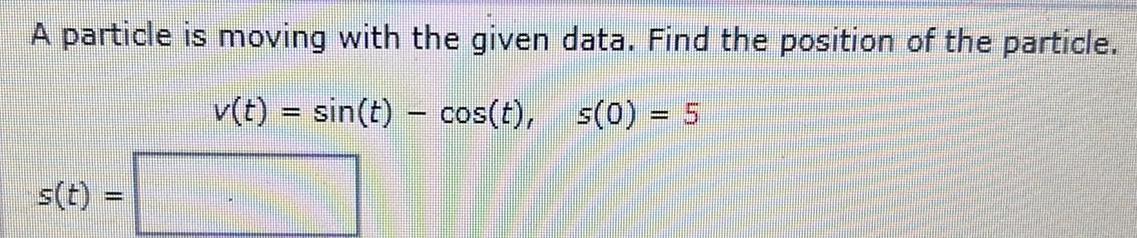
Indefinite IntegrationA particle is moving with the given data. Find the position of the particle.
v(t) = sin(t) - cos(t), s(0) = 5
s(t) =

Calculus
Indefinite IntegrationUse the formula A = P(1+ r n)nt.
Kendra invests $5800 in an account that earns 5.2% annual interest compounded quarterly. How much will be in the account after 5 years? Round to the nearest cent.
Do not enter the $ sign as part of the answer.

Calculus
Indefinite IntegrationA farmer wants to fence in a rectangular pict of land adjacent to the north wall of his bar. No fencing is needed along the barn, and the fencing along the west side of the plot is shared with a neighbor who will split the cost of that portion of the fence. If the fending costs $10 per linear foot to install and the farmer is not willing to spend more than $4000, find the dimensions for the plot that would enclose the most aren. (Enter the dimensions as a comma separated list.)

Calculus
Indefinite IntegrationFind the points on the ellipse 3x² + y² = 3 that are farthest away from the point (1, 0).
smaller y-value (x, y) =
larger y-value (x, y) =

Calculus
Indefinite IntegrationA retailer has been selling 2000 tablet computers a week at $350 each. The marketing department estimates that an additional 80 tablets will sell each week for every $10 that the price is lowered.
(a) Find the demand function.
(b) What should the price be set at in order to maximize revenue?
(c) If the retailer's weekly cost function is
C(x) = 25,000 + 170x,
what price should it choose in order to maximize its profit?

Calculus
Indefinite IntegrationUse Newton's method to find all solutions of the equation correct to six decimal places. (Enter your answers as a comma-separated list.)
arctan(x) = x2 4

Calculus
Indefinite IntegrationSolve the system of equations. You may use any method of your choice, but your method must be algebraic (not graphical). If the system is inconsistent, state there are no solutions. If the system is dependent, express the solution set by naming one coordinate as a and expressing all other coordinates in terms of a.
2(x + 2z) = 2-y
5z + 2 = y-x
2x + 4y = 2z+8

Calculus
Indefinite IntegrationThe owner of a ranch has 6000 square yards of fencing to enclose grazing land that is subdivided it into 3 parts by means of fences running parallel to the sides, as diagramed. Let x be the total width and y be the height in the diagram. Find x and y to maximize the amount of land that can be enclosed. a) Label the diagram with x and y- b) Write the function to be maximized (the objective function) in terms of x and y. c) Write the given information as an equation (the constraint equation) in terms of x and y. d) Write the function to be optimized in terms of one variable. e) Find the critical number. f) Show work to verify the critical number corresponds to a minimum. g) How should the rancher build their fences? (Round to nearest foot.) h) What is the maximum area? (Round to nearest dollar.)

Calculus
Indefinite IntegrationFind the function with the given derivative whose graph passes through the point P.
g'(x) = 2 x3 + 20x4, P(1,6)
Calculus
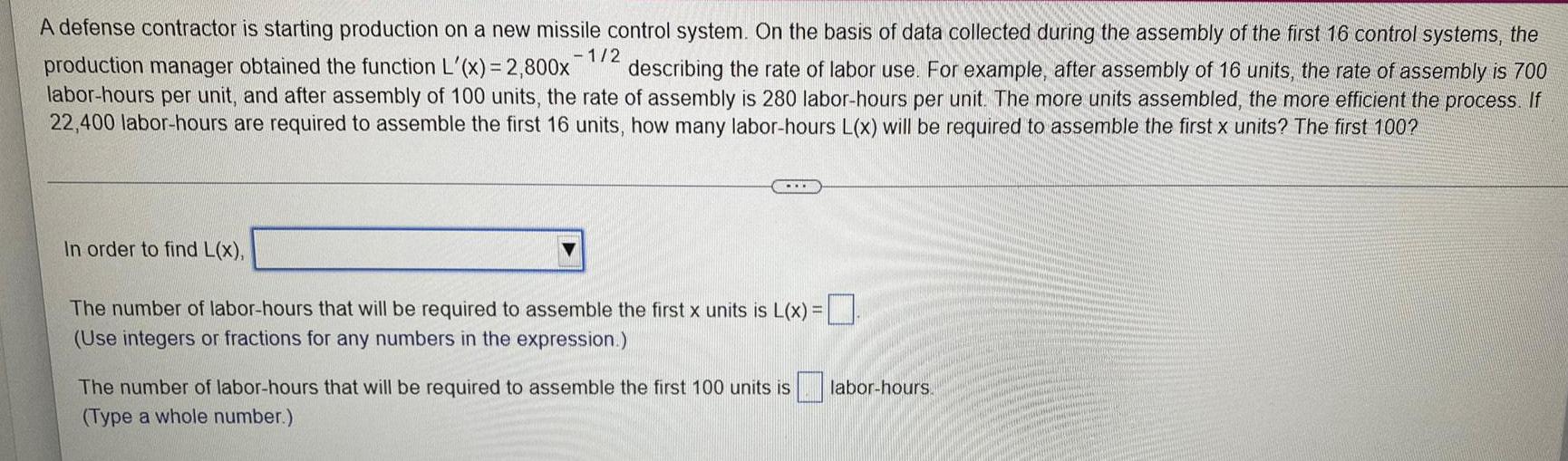
Indefinite IntegrationA defense contractor is starting production on a new missile control system. On the basis of data collected during the assembly of the first 16 control systems, the production manager obtained the function L'(x) = 2,800x1/2 describing the rate of labor use. For example, after assembly of 16 units, the rate of assembly is 700 labor-hours per unit, and after assembly of 100 units, the rate of assembly is 280 labor-hours per unit. The more units assembled, the more efficient the process. If 22,400 labor-hours are required to assemble the first 16 units, how many labor-hours L(x) will be required to assemble the first x units? The first 100?
In order to find L(x),
The number of labor-hours that will be required to assemble the first x units is L(x) =
(Use integers or fractions for any numbers in the expression.)
The number of labor-hours that will be required to assemble the first 100 units is labor-hours.
(Type a whole number.)
Calculus
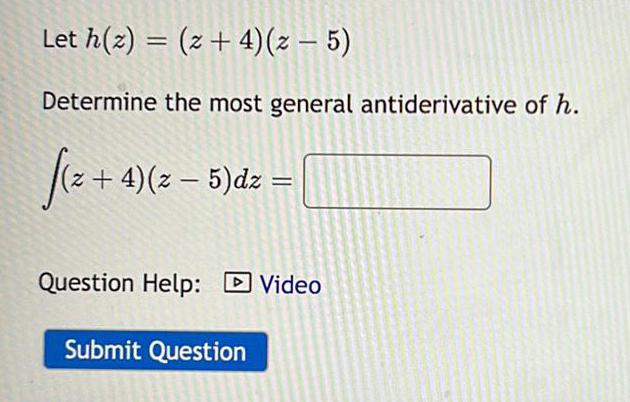
Indefinite IntegrationLet h(z) = (z + 4) (z − 5)
Determine the most general antiderivative of h.
∫(z + 4) (z − 5)dz =

Calculus
Indefinite IntegrationAn investment of $25,000 earns 2.35% annual interest and is compounded continuously. If no funds are added or removed from this account, what is the future value of the investment after 5 years?
Round your answer to the nearest penny.
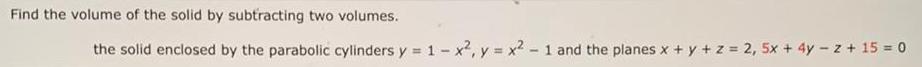
Calculus
Indefinite IntegrationFind the volume of the solid by subtracting two volumes. the solid enclosed by the parabolic cylinders y = 1 - x², y = x² - 1 and the planes x + y + z = 2, 5x + 4y - z + 15 = 0
Calculus
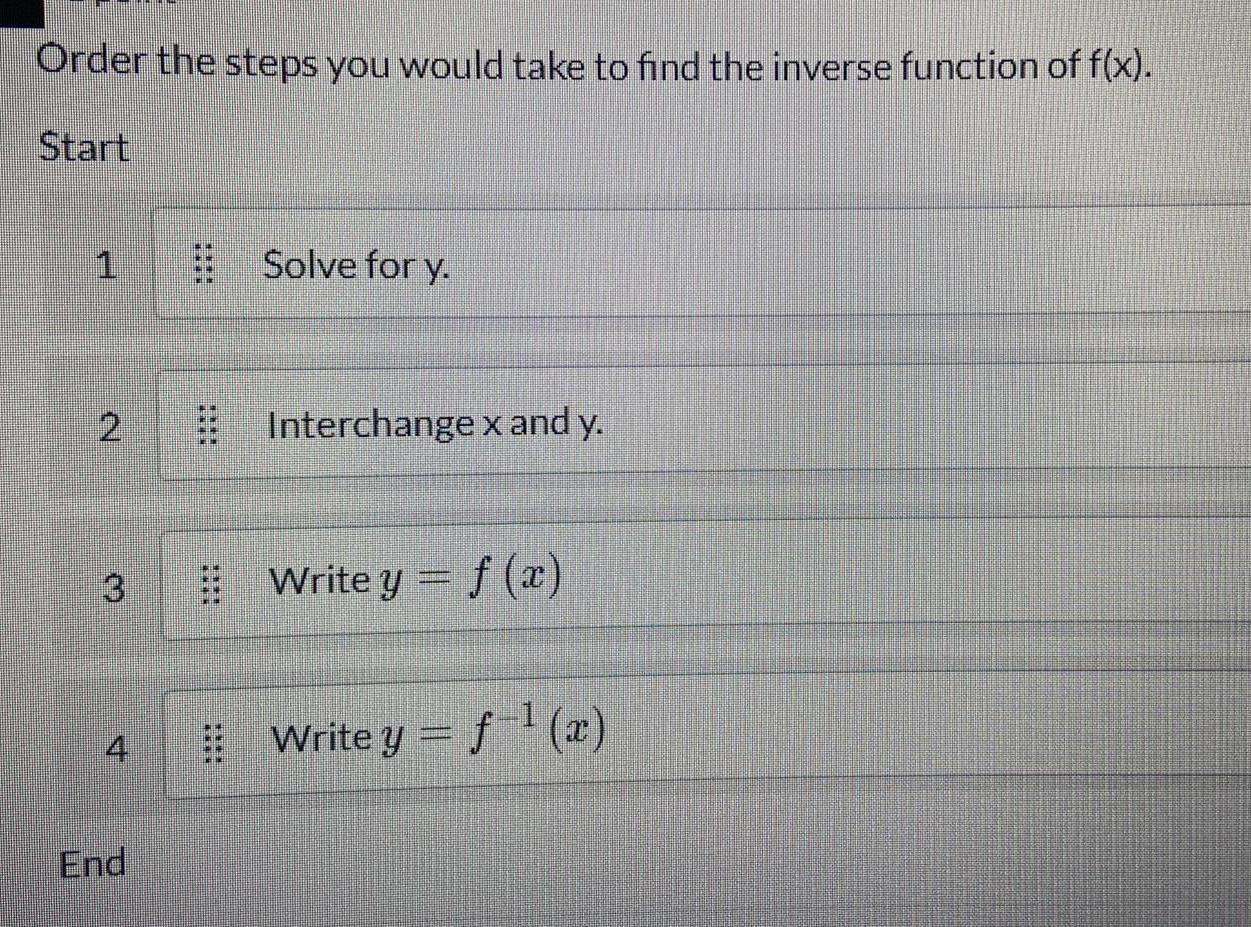
Indefinite IntegrationOrder the steps you would take to find the inverse function of f(x).
Start
1. Solve for y.
2 Interchange x and y.
Write y = f(x)
Write y = f(x)
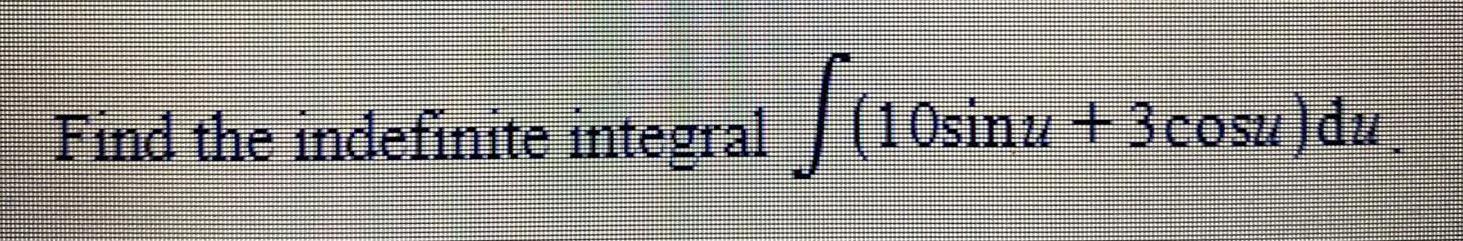

Calculus
Indefinite IntegrationDenise took out a loan to buy a She-Shed for her house. She decides to pay the loan back in full before its due date. If she's paying $165.20 monthly at 11.5% APR and still has 30 remaining scheduled payments after the payoff, find each of the following:
(a) Obtain the value of h from the table above.
(b) Use the actuarial method to find the amount of unearned interest. u = kR (h/100+h) where k is the number of remaining payments and R is the monthly payment.
(c) Find the payoff amount. Payoff amount = (k + 1)R-u
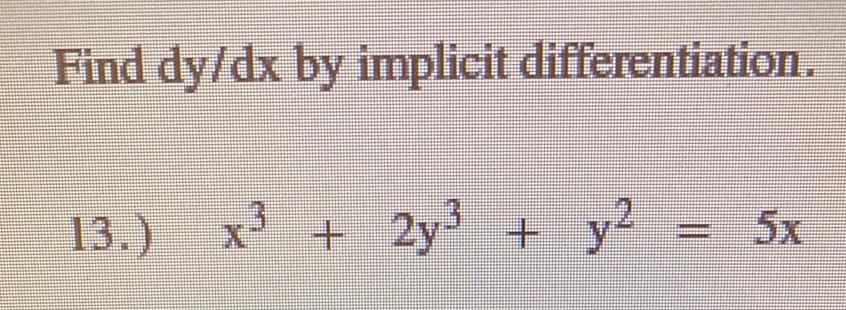

Calculus
Indefinite IntegrationA special-events promoter sells x tickets and has a marginal-profit function given by P'(x)=2x-1200, where P'(x) is in dollars per ticket. This means that the rate of change of total profit with respect to the number of tickets sold, x, is P'(x). Find the total profit from the sale of the first 340 tickets.
A. -$292400
B. $427600
C. -$584800
D. $115600

Calculus
Indefinite IntegrationA company determines that its weekly online sales, S(t), in hundreds of dollars, t weeks after online sales began can be estimated by the equation below. Find the average weekly sales for the first 8 weeks after online sales began. S(t) = 5 e^t
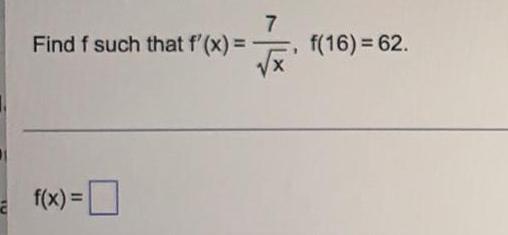

Calculus
Indefinite IntegrationFor the following function, a) give the coordinates of any critical points and classify each point as a relative maximum, a relative minimum, or neither; b) identify intervals where the function is increasing or decreasing; c) give the coordinates of any points of inflection; d) identify intervals where the function is concave up or concave down, and e) sketch the graph.
g(x)=x³-12x² +45x+7
a) What are the coordinates of the relative extrema? Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice.
A. The relative minimum point(s) is/are and the relative maximum point(s) is/are
B. The relative maximum point(s) is/are and there are no relative minimum point(s).
C. The relative minimum point(s) is/are and there are no relative maximum point(s).
D. There are no relative minimum points and there are no relative maximum points.
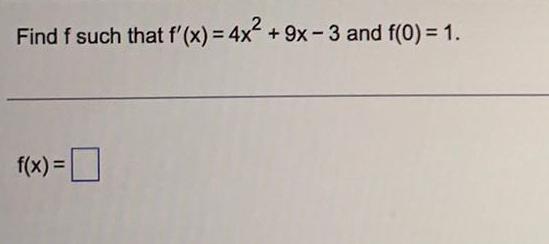

Calculus
Indefinite IntegrationLet f(x) = |x|, g(x)=x-4, and h(x)=x4.
Write N(x)=x-8 as a composition of functions.
Choose the following composition that correctly defines N(x)=x-8.
A. fogoh
B. gog
C. hog
D. goh
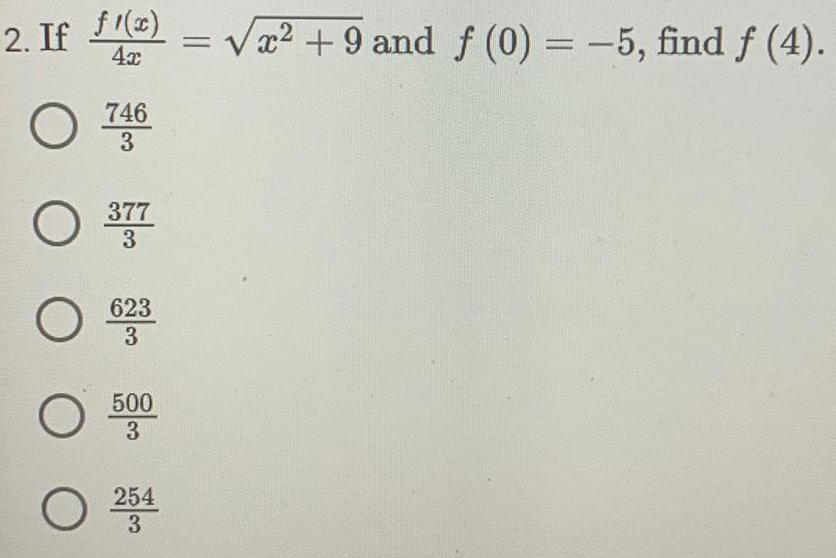
Calculus
Indefinite Integration2. If f'(x)/4x = √(x2+9) and f(0) = -5, find f(4)
A. 746/3
B. 377/3
C. 623/3
D. 500/3
E. 254/3
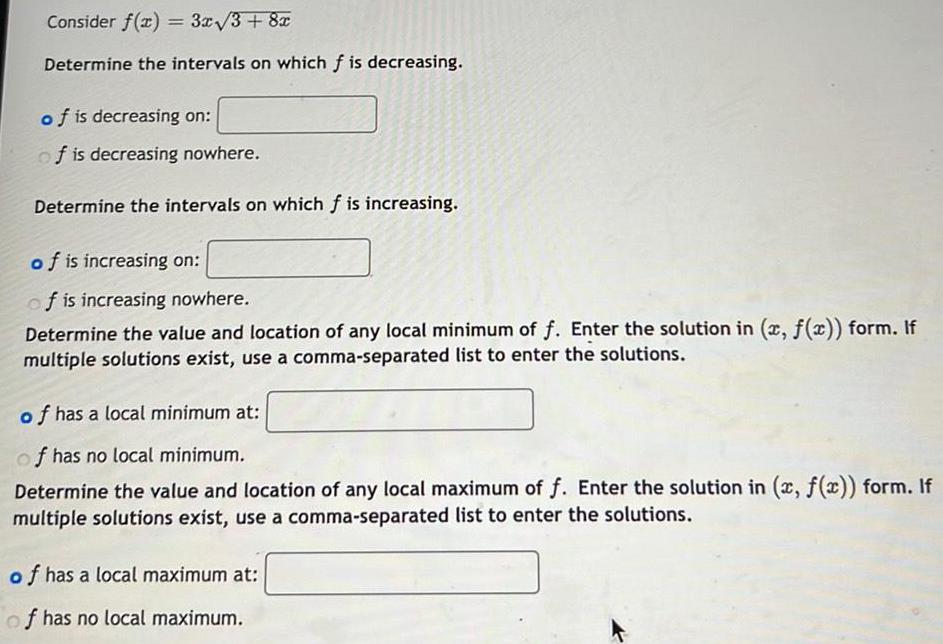
Calculus
Indefinite IntegrationConsider f(x) = 3x√(3+8x)
Determine the intervals on which f is decreasing.
f is decreasing on:
f is decreasing nowhere.
Determine the intervals on which f is increasing.
f is increasing on:
f is increasing nowhere.
Determine the value and location of any local minimum of f. Enter the solution in (x, f(x)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
f has a local minimum at:
f has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (x, f(x)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
f has a local maximum at:
f has no local maximum.

Calculus
Indefinite IntegrationConsider g(x) = -10 arcsin ( - 12x³)
Determine the intervals on which g is decreasing.
g is decreasing on:
g is decreasing nowhere.
Determine the intervals on which g is increasing.
g is increasing on:
g is increasing nowhere.
Determine the value and location of any local minimum of f. Enter the solution in (x, g(x)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
g has a local minimum at:
g has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (x, g(x)) form.
multiple solutions exist, use a comma-separated list to enter the solutions.
g has a local maximum at:
g has no local maximum.
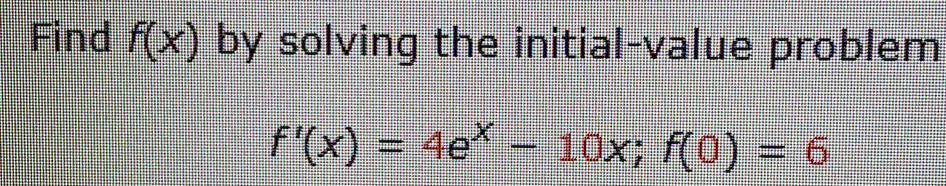
Calculus
Indefinite IntegrationFind f(x) by solving the initial-value problem
f'(x) = 4ex 10x; f(0) = 6

Calculus
Indefinite IntegrationCalculus
about the x-axis please sketch and find
volume curves x axis
Consider the given curves to do the following.
z+y-6, z=10-(y-2)²
Use the method of cylindrical shells to find the volume V of the solid obtained by rotating the region bounded by the given curves about the
V=
Sketch the region and a typical shell. (Do this on paper. Your instructor may ask you to turn in this sketch.)

Calculus
Indefinite IntegrationWhen you have watched the video and taken your notes, type the equation of a linear function whose y-intercept, is (0,
-11) in the text-box, be sure to use correct function notation and then click Submit Assignment. Many different correct
answers are possible here.

Calculus
Indefinite IntegrationSuppose you deposit $4000 at 6% interest compounded continously. Find the average value of your
account during the first 3 years.
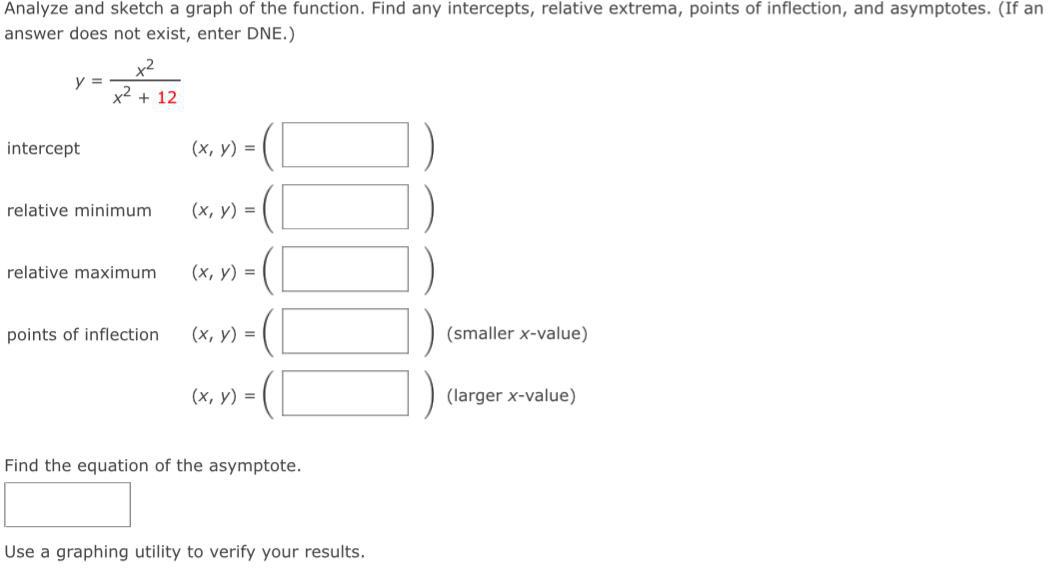
Calculus
Indefinite IntegrationAnalyze and sketch a graph of the function. Find any intercepts, relative extrema, points of inflection, and asymptotes. (If an answer does not exist, enter DNE.)
y =x²/x² + 12
intercept
relative minimum.
relative maximum
points of inflection
Find the equation of the asymptote.
Use a graphing utility to verify your results.
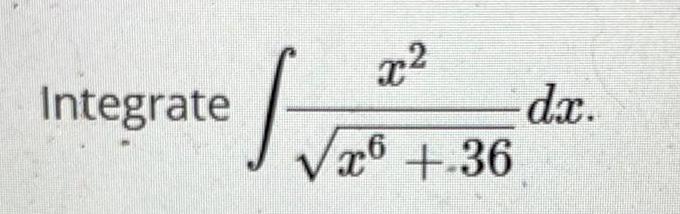
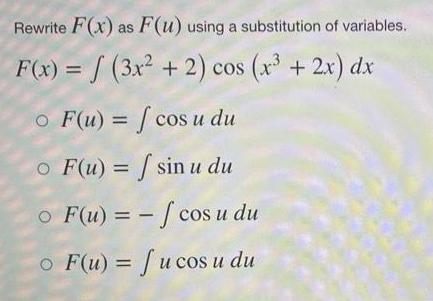
Calculus
Indefinite IntegrationRewrite F(x) as F(u) using a substitution of variables.
F(x) = ∫(3x² + 2) cos (x³ + 2x) dx
F(u) = ∫ cos u du
F(u) = ∫ sin u du
F(u) =-∫ cos u du
F(u) = ∫u cos u du
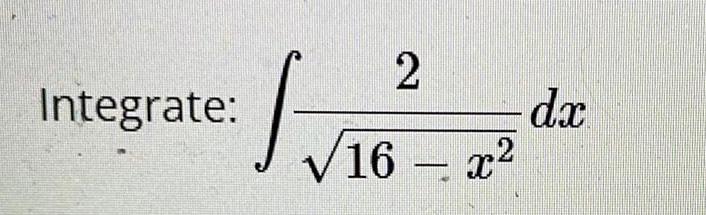

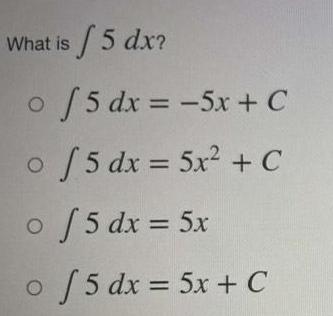
Calculus
Indefinite IntegrationWhat is ∫ 5 dx?
∫ 5 dx = -5x + C
∫5 dx = 5x² + C
∫5 dx = 5x
∫5 dx = 5x + C

Calculus
Indefinite IntegrationFind the anti-derivative of g(x) = 2x which contains the point (2, 0).
G(x) = x² - 4
G(x) = 2x + 4
G(x) = 2x - 4
G(x) = x² + 4
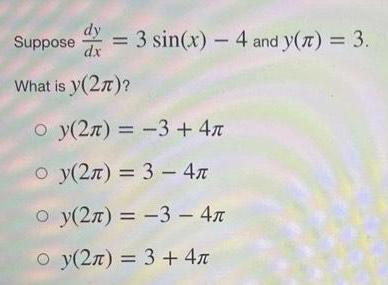
Calculus
Indefinite IntegrationSuppose = 3 sin(x) - 4 and y(z) = 3.
dy
dx
What is y(27)?
y(2л) = -3 + 4л
y(2л) = 3 4л
y(2л) = -3- 4л
y(2л) = 3 + 4л
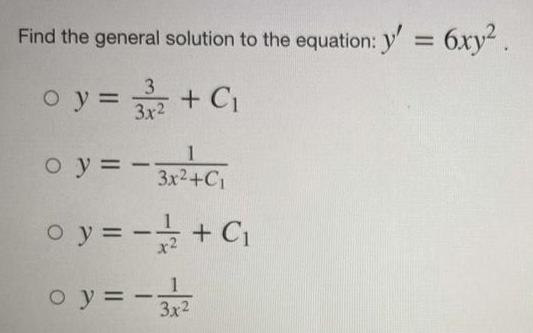
Calculus
Indefinite IntegrationFind the general solution to the equation: y' = 6xy².
y= 3/3x^2 + C1
y=-1/3x^2 +C1
y= -1/x^2 +C1
y=-1/3x^2

Calculus
Indefinite IntegrationIf the rate of change of T is proportional to (20+ T), where T> -20, and if T(0) = 2 and T(4) = 10, find T(20).
A. 86.643
B. 84.31
C. 83.652
D. 81.745