Indefinite Integration Questions and Answers
Calculus
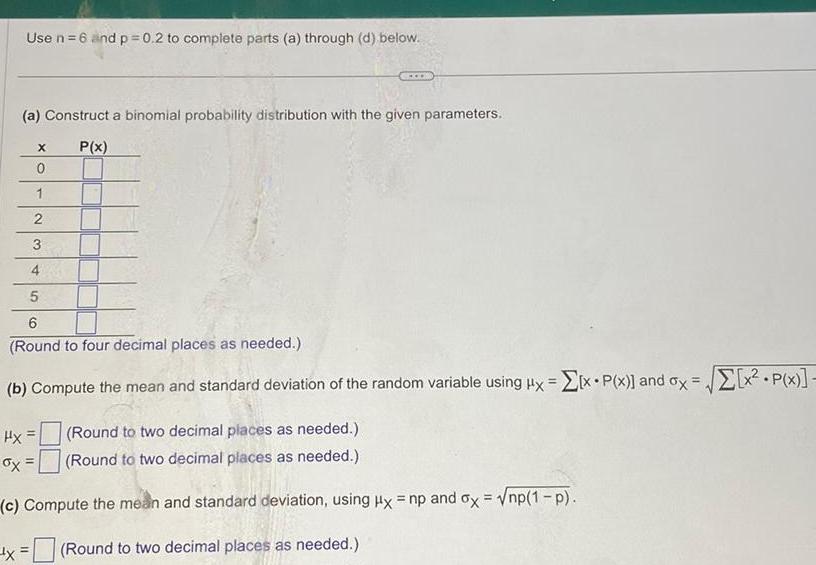
Indefinite IntegrationUse n 6 and p 0 2 to complete parts a through d below a Construct a binomial probability distribution with the given parameters P x 4 5 6 Round to four decimal places as needed b Compute the mean and standard deviation of the random variable using ux x P x and ox x P x Hx x Round to two decimal places as needed Round to two decimal places as needed c Compute the mean and standard deviation using Hx np and ox np 1 p Round to two decimal places as needed X 0 1 2 3

Calculus
Indefinite IntegrationDetermine if the following probability experiment represents a binomial experiment If not explain why If the probability experiment is a binomial experiment state the number of trials n and probability of success p An investor randomly purchases 13 stocks listed on a stock exchange Historically the probability that a stock listed on this exchange will increase in value over the course of a year is 42 The number of stocks that increase in value is recorded S www w Select the correct choice below and if necessary fill in the answer boxes to complete your answer OA Yes because the experiment satisfies all the criteria for a binomial experiment and p Type integers or decimals Do not round n OB No because the experiment is not performed a fixed number of times OC No because there are more than two mutually exclusive outcomes for each trial D No because the trials of the experiment are not independent because the PATE differs from trial to trial
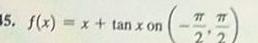

Calculus
Indefinite IntegrationTest the series for convergence or divergence Part 1 Divergence Test Evaluate the limit lim bn 71 00 Identify the corresponding positive terms b Gipss li t 00 Calea 1 n 0 n21 8 then the Divers

Calculus
Indefinite Integration4 7 Optimization Problems 1 A closed box top bottom and all four sides needs to be constructed to have a volume of 9 m and a base whose width is twice its length See Figure 1 2x T Y Figure 1 A box Use calculus to determine the dimensions length width height of such a box that uses the least amount of material Justify why your answer corresponds to a minimum not a maximum

Calculus
Indefinite Integration3 Three line segments of length 1 are joined together at endpoints to form a base and the legs of an isosceles trapezoid as in Figure 3 Let 0 in 0 2 be the common angle measurement between the legs and the line passing through the base of length 1 We want to find the angle that maximizes the area of the trapezoid 1 1 Figure 3 An isosceles trapezoid with base and legs of length 1 a Compute the area A 0 of the trapezoid The general area formula for a trapezoid ish b b where h is the height and b and b2 are the lengths of the bases Hint Break up the trapezoid into a rectangle with two right triangles at both ends Use trigonometry to compute the height and the length of the longer base in terms of 0 b Find all solutions to A 0 0 with 0 0 2 Hint Write A 0 entirely in terms of cos 0 The answer is not 0 4 45 c Verify that the area A 0 is a maximum not a minimum at the angle found in part b and compute this maximum area

Calculus
Indefinite Integration5 Consider the boundary value problem as in Q3 b y 4x 2x2y 2r2ln x ze 1 2 y 1 1 2 y 2 ln 2 1 a Write the system of first order IVP regarding y and y2 that we need to compute if we would like to apply the linear shooting method to solve the above BVP b Computational exercise Write a script to solve this problem Let h 0 1 using Euler s method to solve the system of IVP in a and compute the approximate solution to y in 0 1 DI 11 91

Calculus
Indefinite Integration1 Consider the nonlinear shooting method with Newton s algorithm We are aiming to approximate the solution to the boundary value problem y y yy 1 x 2 y 1 1 2 y 2 1 3 with h 0 5 and to 1 6 a Write down the system of first order IVP that we need to solve for each tk b Compute the value of y 2 to or y 2 to with Euler s method that you introduced in a You may round up the solution up to two decimal places c Compute t by using Newton s method to solve y b t 8 0

Calculus
Indefinite Integration2 Consider the following initial value problem of the second order y 3y 2y 6e t te 0 1 y 0 y 0 2 h 0 5 a Rewrite the above IVP into a system of first order IVPs by letting u y and u y b Compute an approximate solution to y 1 by using Euler s method to solve the system of firs order IVPs that you get in a
Calculus
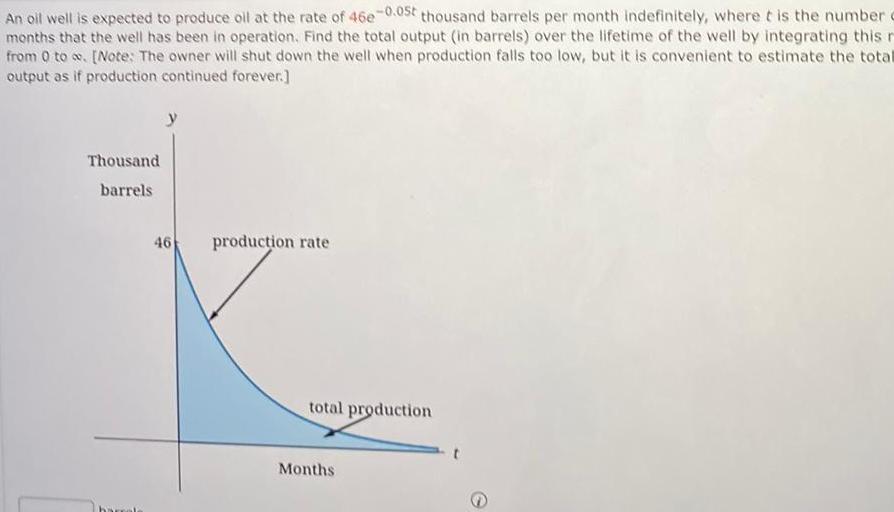
Indefinite IntegrationAn oil well is expected to produce oll at the rate of 46e 0 05t thousand barrels per month indefinitely where it is the number months that the well has been in operation Find the total output in barrels over the lifetime of the well by integrating this r from 0 to Note The owner will shut down the well when production falls too low but it is convenient to estimate the total output as if production continued forever Thousand barrels barrald 46 production rate total production Months

Calculus
Indefinite Integration11 18 Sketch the region enclosed by the given curves Decide whether to integrate with respect to x or y Draw a typical approximating rectangle and label its height and width Then find the area of the region 11 y x 2 y x 1 x 0 x 1 12 y 1 x y 2 x x 1 x 0 13 y 1 x y 1 x x 2 14 y cos x y e x 2 15 y x 2 y x 16 y x 4x y 2x 17 x 1 y x y 1
Calculus
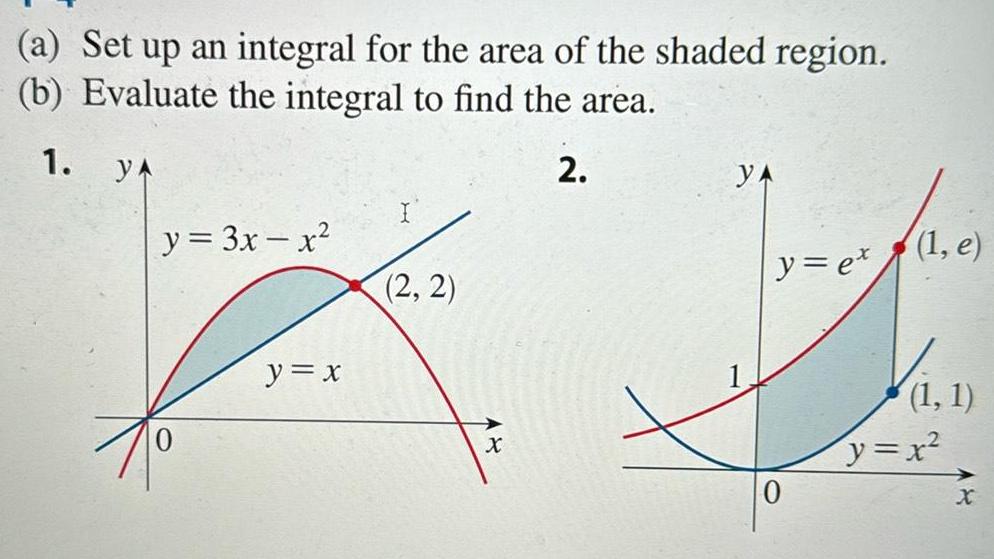
Indefinite Integrationa Set up an integral for the area of the shaded region b Evaluate the integral to find the area 1 ya 2 y 3x x y x 2 2 X YA y ex O 1 e 1 1 y x x

Calculus
Indefinite Integration4 Find a formula for the exponential function passing through the points 2 and and 2 36 y Question Help Video Message instructor
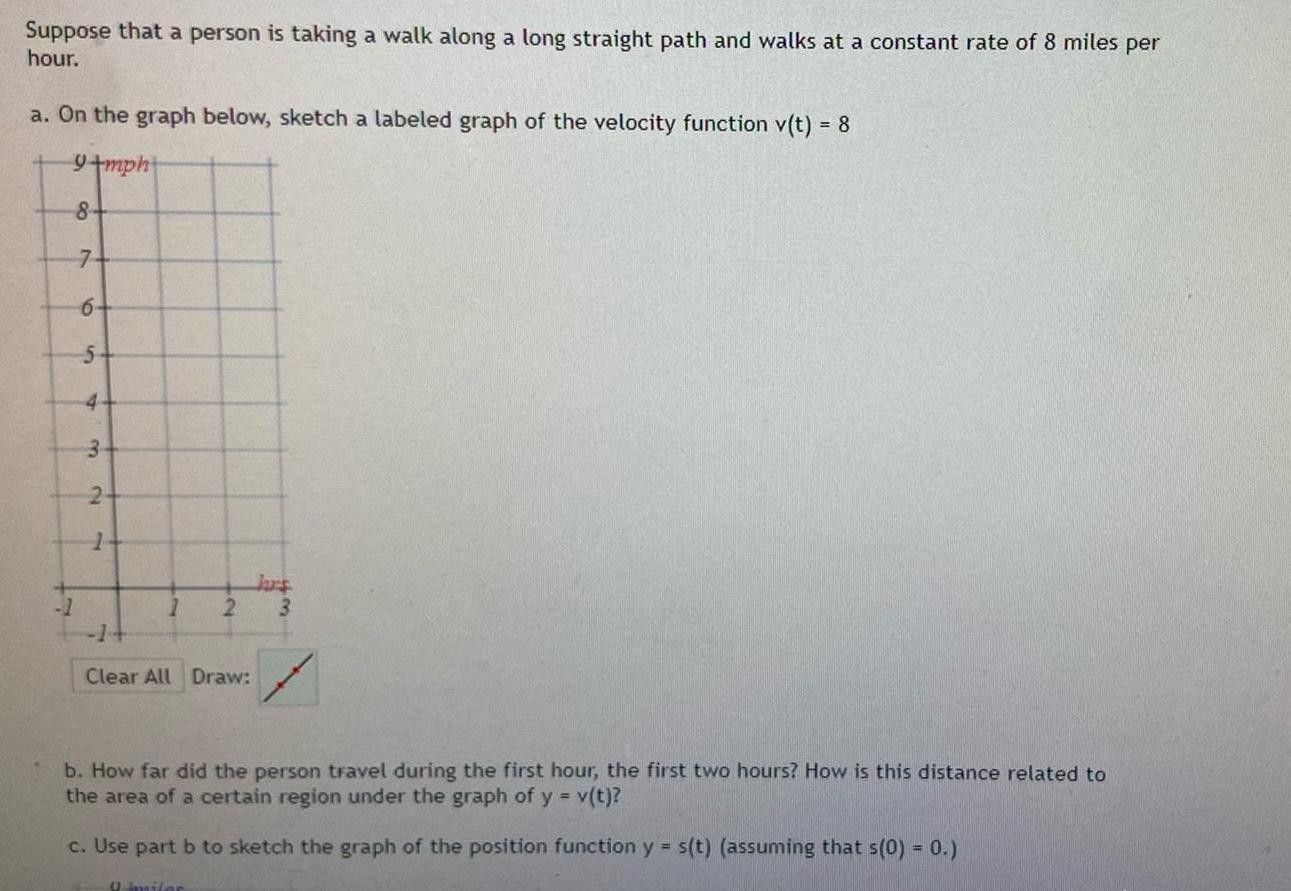
Calculus
Indefinite IntegrationSuppose that a person is taking a walk along a long straight path and walks at a constant rate of 8 miles per hour a On the graph below sketch a labeled graph of the velocity function v t 8 9 mph 8 7 6 1 5 4 3 2 1 1 2 Clear All Draw hars 3 b How far did the person travel during the first hour the first two hours How is this distance related to the area of a certain region under the graph of y v t c Use part b to sketch the graph of the position function y s t assuming that s 0 0 9 imiler

Calculus
Indefinite Integration6a 4a 6 da Do not include the constant C in your answer For example if you found the antiderivative was 2x C you would enter 2 What is
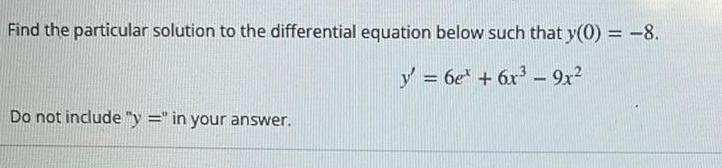
Calculus
Indefinite IntegrationFind the particular solution to the differential equation below such that y 0 8 y 6e 6x 9x Do not include y in your answer
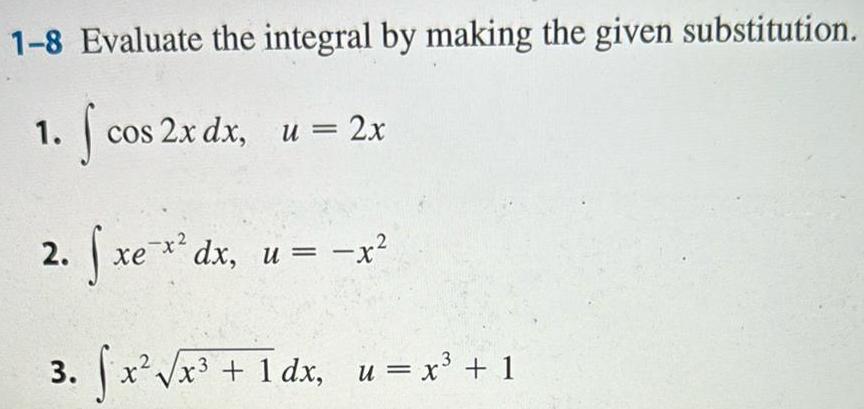
Calculus
Indefinite Integration1 8 Evaluate the integral by making the given substitution 1 fcos 2x dx u 2x xe x dx u x 3 fx x 1dx u x 1 2
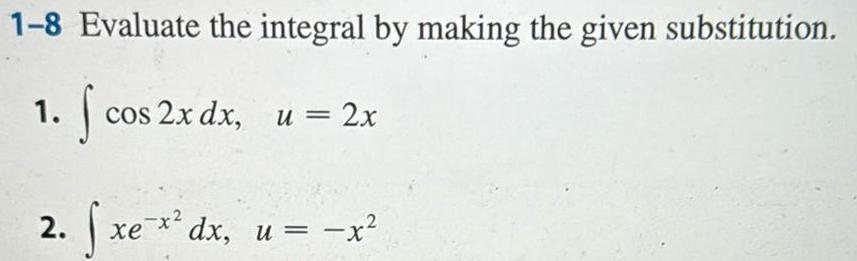
Calculus
Indefinite Integration1 8 Evaluate the integral by making the given substitution 1 cos 2x dx u 2x 2 fxe x dx u x 2
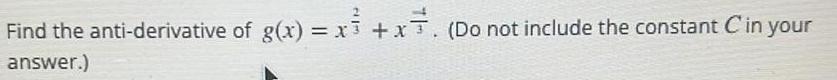
Calculus
Indefinite IntegrationFind the anti derivative of g x x x Do not include the constant C in your answer
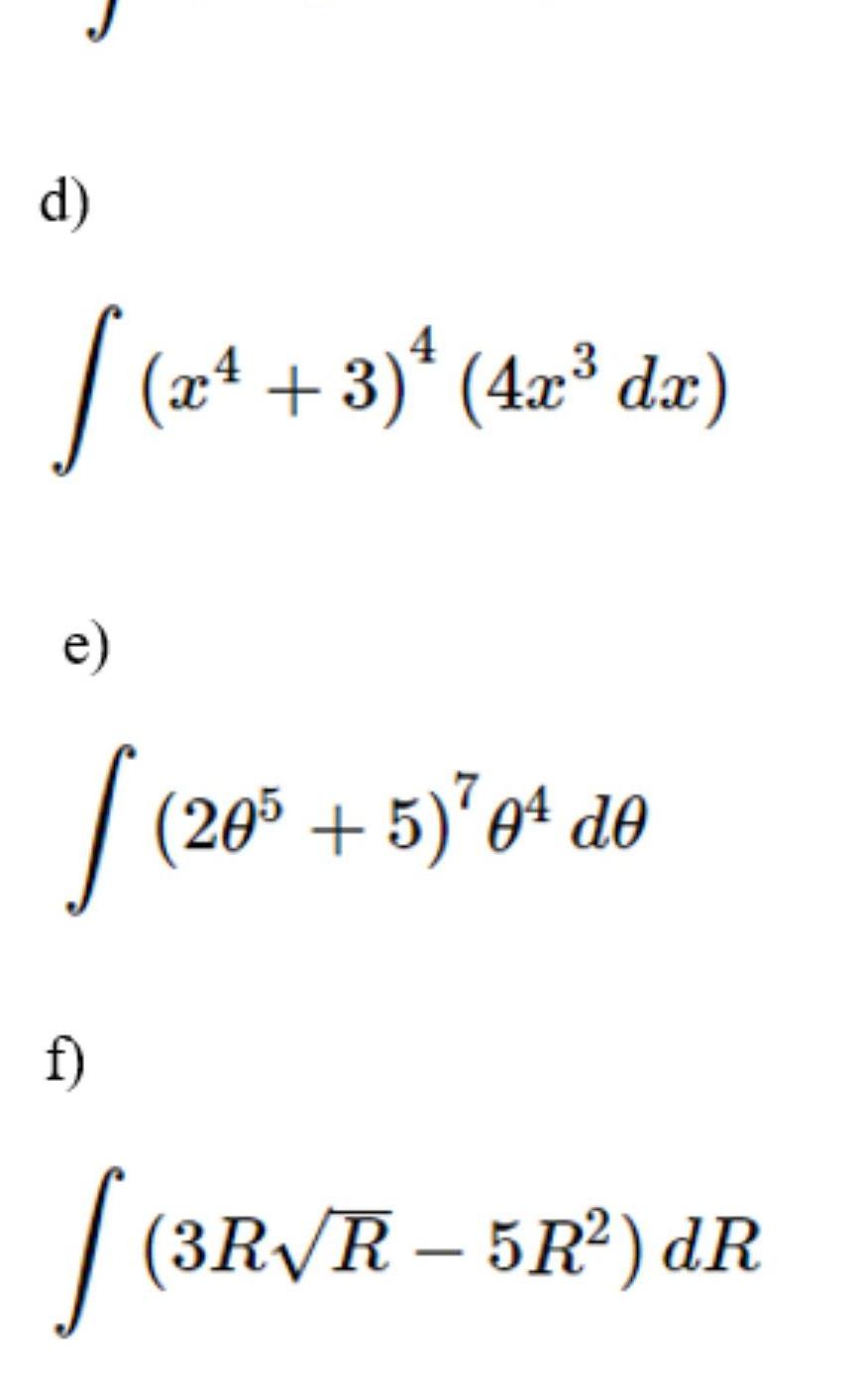
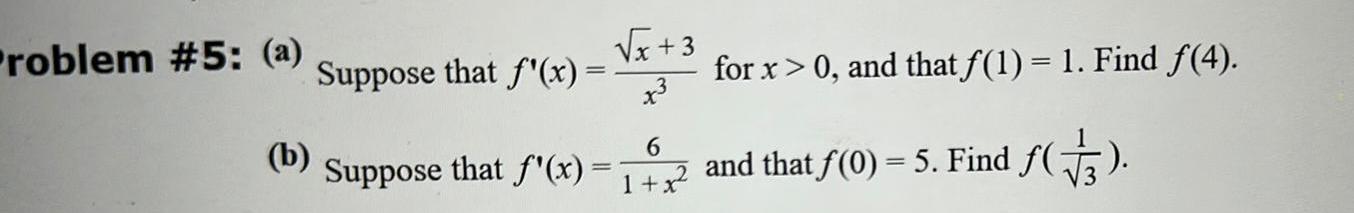
Calculus
Indefinite Integrationroblem 5 a Suppose that f x x 3 x b Suppose that f x 6 1 x for x 0 and that 1 1 Find 4 and that f 0 5 Find 3

Calculus
Indefinite IntegrationFind the following indefinite integrals 142 98 2101 dy 7 4 2 Sseek Seco tan Seed cose d

Calculus
Indefinite IntegrationFind the following indefinite integrals astias 4 2 X X 4X 5 X 14 dx df et

Calculus
Indefinite IntegrationUse a in radian mode to find approximations for cos s and sins for the number s exact values they are only approximations Then determine the quadrant in which the point or corresponding to s lies Finally find approximations for tan s cots secs and csc s sin 1 27 Round to three decimal places

Calculus
Indefinite IntegrationA company s marginal cost function is MC x xe x 2 and fixed costs are 215 Find the cost function Hint Evaluate the consta C so that the cost is 215 at x 0 C x 2e 5 4e 219 X

Calculus
Indefinite IntegrationFind the length of the parametrically defined curve x 8 cost 8t sint y 8 sin t 8t cost 0 t Use the equation editor to type your answer L

Calculus
Indefinite IntegrationSocial animals that live in groups can spend less time scanning for predators than solitary individuals However they waste time fighting with the other group members over the available food There is some group size at which the net benefit is greatest because the animals spend least time on these unproductive activities and thus can spend time on feeding mating etc Assume that for a group of size x the fraction of time spent scanning for predators is 1 x 1 and the fraction of time spent fighting with other animals over food is F x B x 1 S x A where A B are constants and A 2B Find the size of the group for which the time wasted on scanning plus time wasted on fighting is smallest
Calculus
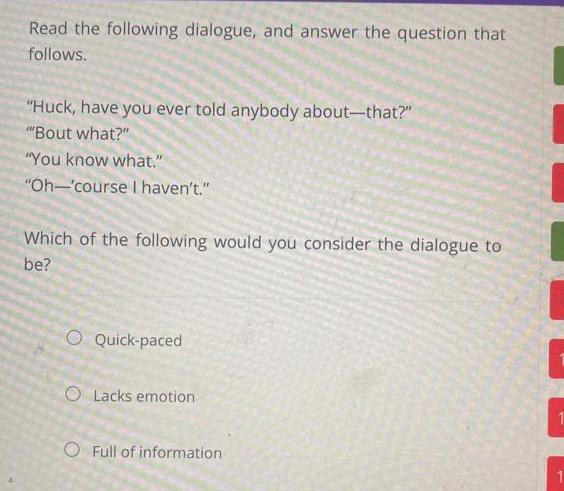
Indefinite IntegrationRead the following dialogue and answer the question that follows Huck have you ever told anybody about that Bout what You know what Oh course I haven t Which of the following would you consider the dialogue to be O Quick paced O Lacks emotion O Full of information
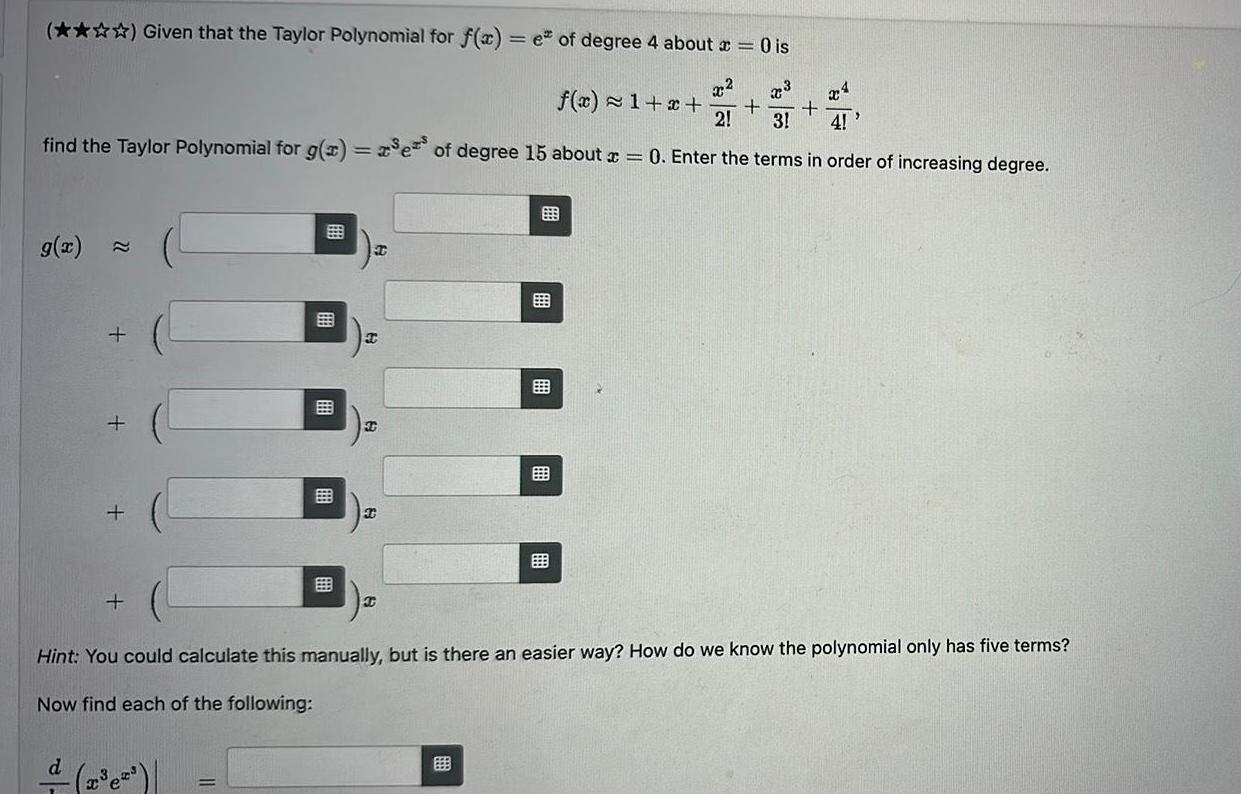
Calculus
Indefinite IntegrationGiven that the Taylor Polynomial for f x e of degree 4 about x 0 is x 2 3 2 3 4 e of degree 15 about x 0 Enter the terms in order of increasing degree find the Taylor Polynomial for g x g x 22 B 2 T 89 T C f x 1 x Hint You could calculate this manually but is there an easier way How do we know the polynomial only has five terms Now find each of the following

Calculus
Indefinite IntegrationFind the Taylor polynomial for the function f x 10x x about the point x 5 that has three nonzero terms Enter the polynomial terms in order of increasing degree 10x x x 5

Calculus
Indefinite Integration5 24 Find the general indefinite integral 5 f 3x 4x 1 dx 7 f x cos x dx 9 f x 7x 5 dx 11 5 3x x dx 13 u 4 2u 1 du 6 f 5 2 x dx x 10 x dx 12 u 2u u du 14 1 31 2 dt 8 x dx I

Calculus
Indefinite Integration5 24 Find the general indefinite integral 5 3x 4x 1 dx 7 f x cos x dx S f x 3 7x 25 dx 11 f 5 3x 3x dx 13 f u 4 2u 1 du 1 x x X 9 15 dx 6 f 5 2 x dx 1 x 1 8 dx I 10 x dx 12 f u 2u u du 14 t 3t 2 dt 16 x 1 x 1 ax dx x 1

Calculus
Indefinite IntegrationDefinition The collection of all antiderivatives of f is called the indefinite integral of f with respect to x and is denoted by f x dx Find the most general antiderivative by evaluating the following indefinite integral J 7 10x 12 dx NOTE The general antiderivative should contain an arbitrary constant NOTE To input for example the absolute value of timo lal or pho m
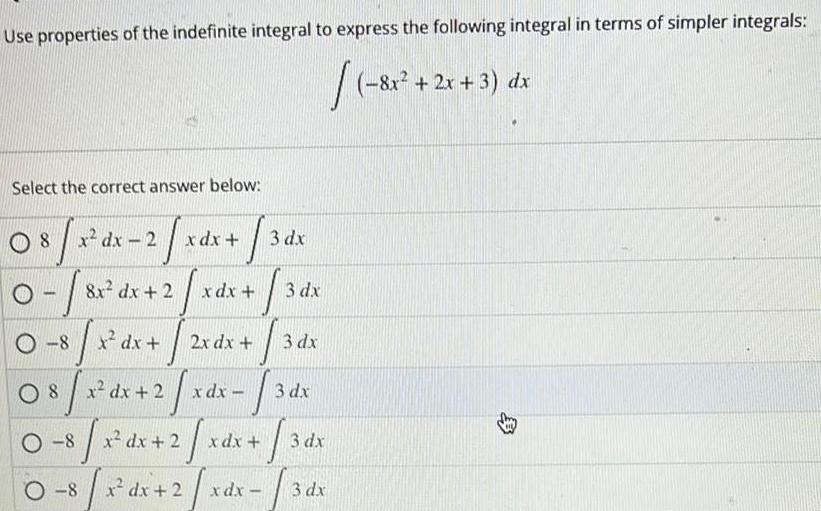
Calculus
Indefinite IntegrationUse properties of the indefinite integral to express the following integral in terms of simpler integrals 8x 2x 3 dx Select the correct answer below 08 8x dx 2 8 x dx 2 x 1 T T 8 x dx 2 2 2 0 8 x x dx 2 x 8 x dx 08 31 O 8 3 dx T 3dx T 3 dx 3 dx x dx x dx 2x dx xdx x dx x dx 2 xdx 3 dx 3 dx

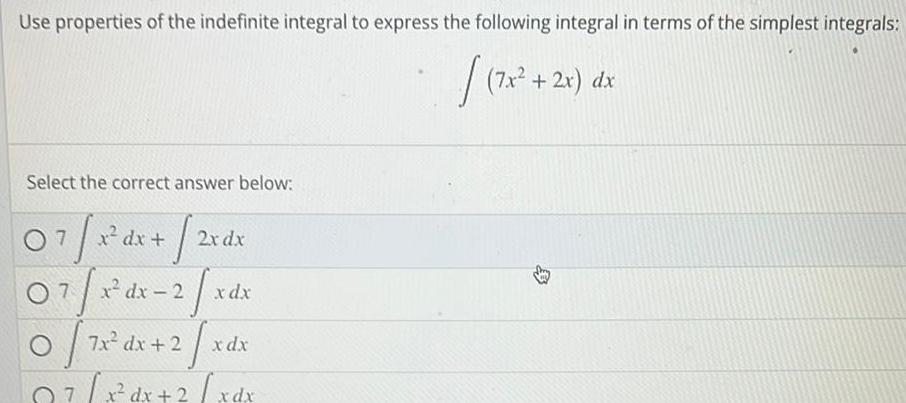
Calculus
Indefinite IntegrationUse properties of the indefinite integral to express the following integral in terms of the simplest integrals 7x Select the correct answer below 07 x dx 2x 07 1 0 7x x dx 2 2 7x dx 2 2 x0 07 x dx 2 xdx 2x dx x dx x dx 7x 2x dx
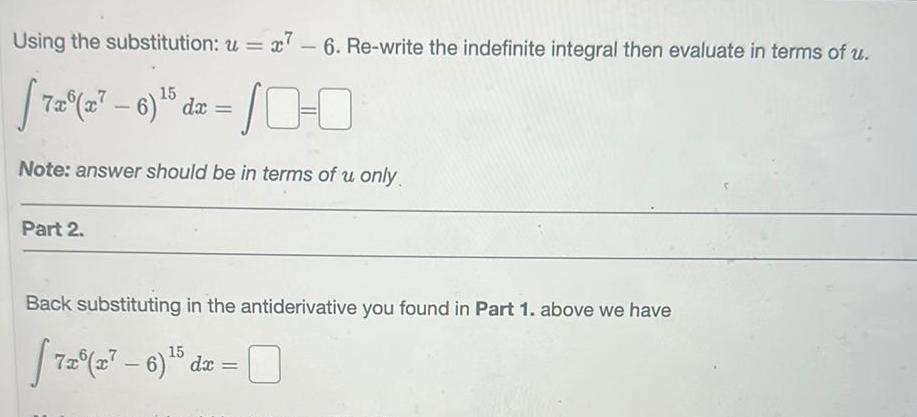
Calculus
Indefinite IntegrationUsing the substitution u 7 6 Re write the indefinite integral then evaluate in terms of u 7x x 6 5 dx 10 0 Note answer should be in terms of u only Part 2 Back substituting in the antiderivative you found in Part 1 above we have 15 7x x 6 5 dx



Calculus
Indefinite IntegrationSolve the following integral The answer can be determined by rules of antidifferentiation but some algebra may required beforehand 7 4u5 8 u 4u5 8 du du

Calculus
Indefinite Integration33 The region consisting of all points between but not on the par spheres of radius r and R centered at the origin where r R

Calculus
Indefinite Integration21 30 Describe in words the region of R represented by the ning sill equations or inequalities 21 x 5 23 y 8 22 y 2 24 x 3

Calculus
Indefinite IntegrationFinding antiderivatives Use what you know about derivatives to finc all antiderivatives of the following functions Sum Rule a f x 3x f x g x 2 1 b f x 2 1 x c f x sin x

Calculus
Indefinite IntegrationFind the absolute maximum and minimum values of each function over the indicated interval and indicate the x values at which they occur f x 3x4 2x 2 2 The absolute maximum value is at x Use a comma to separate answers as needed The absolute minimum value is at x 0 Use a comma to separate answers as needed

Calculus
Indefinite Integrationdy Write the function in the form y f u and u g x Then find as a function of x dx y 8x U Type an expression using x as the variable y Type an expression using u as the variable dy dx Type an expression using x as the variable
Calculus
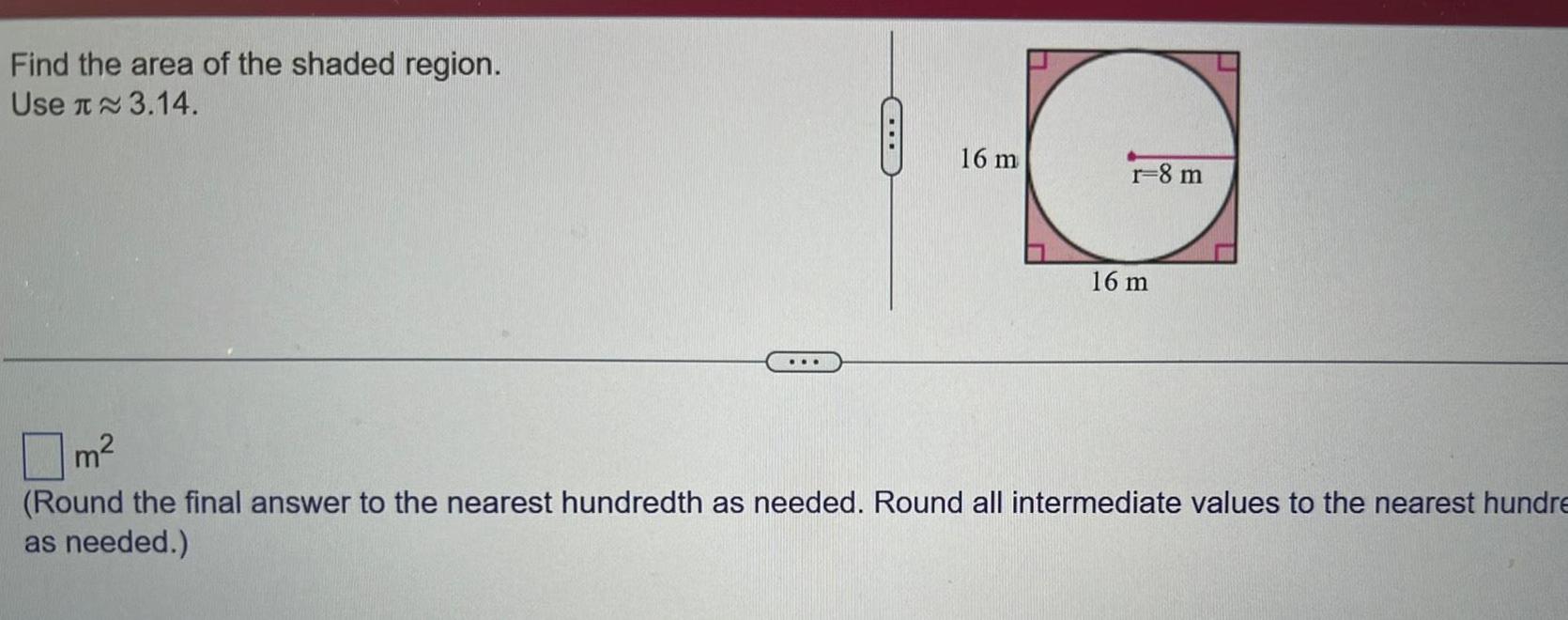
Indefinite IntegrationFind the area of the shaded region Use 3 14 16 m r 8 m 16 m m Round the final answer to the nearest hundredth as needed Round all intermediate values to the nearest hundre as needed
Calculus
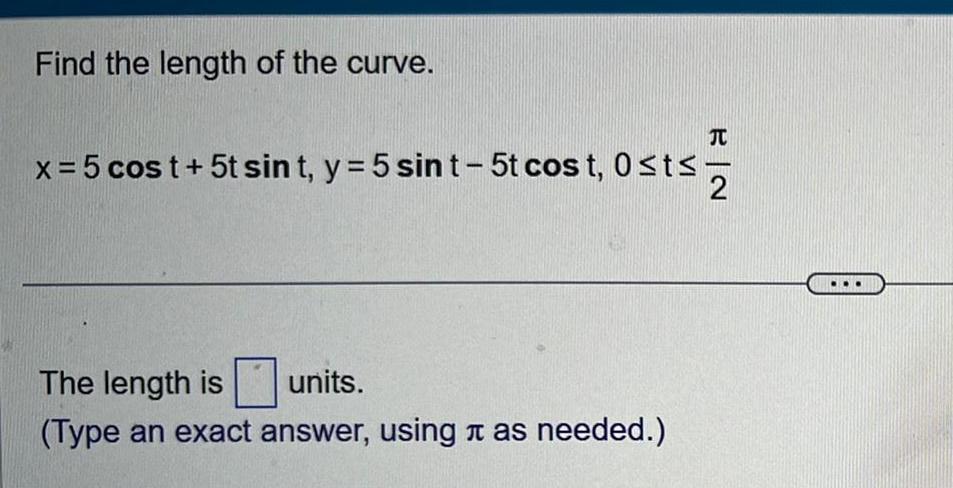
Indefinite IntegrationFind the length of the curve JU x 5 cost 5t sint y 5 sin t 5t cost 0 t 2 The length is units Type an exact answer using as needed

Calculus
Indefinite IntegrationFind the length of the following curve 2t 11 2 3 X y 5t The length of the curve is 2 0 t 4 Simplify your answer