Gauss Law Questions and Answers

Physics
Gauss LawExample 14 A point charge q is placed on the top of a cone of semi vertex angle 0 Show that the electric flux through the base of the cone is q 1 cos 0 280 HOW TO PROCEED This problem can be solved by the method of symmetry Consider a Gaussian surface a sphere with its centre at the top and radius the slant length of the cone The flux through the whole sphere is qleo Therefore the flux through the base of the cone can be calculated by using the following formula S So Here So area of whole sphere Pe H q E0

Physics
Gauss LawConsider a uniform electric field 3 x 10 i NC 1 Calculate the flux of this field through a square surface of area 10 cm when 2 i its plane is parallel to the y z plane and ii the normal to its plane makes a 60 angle with the raxis
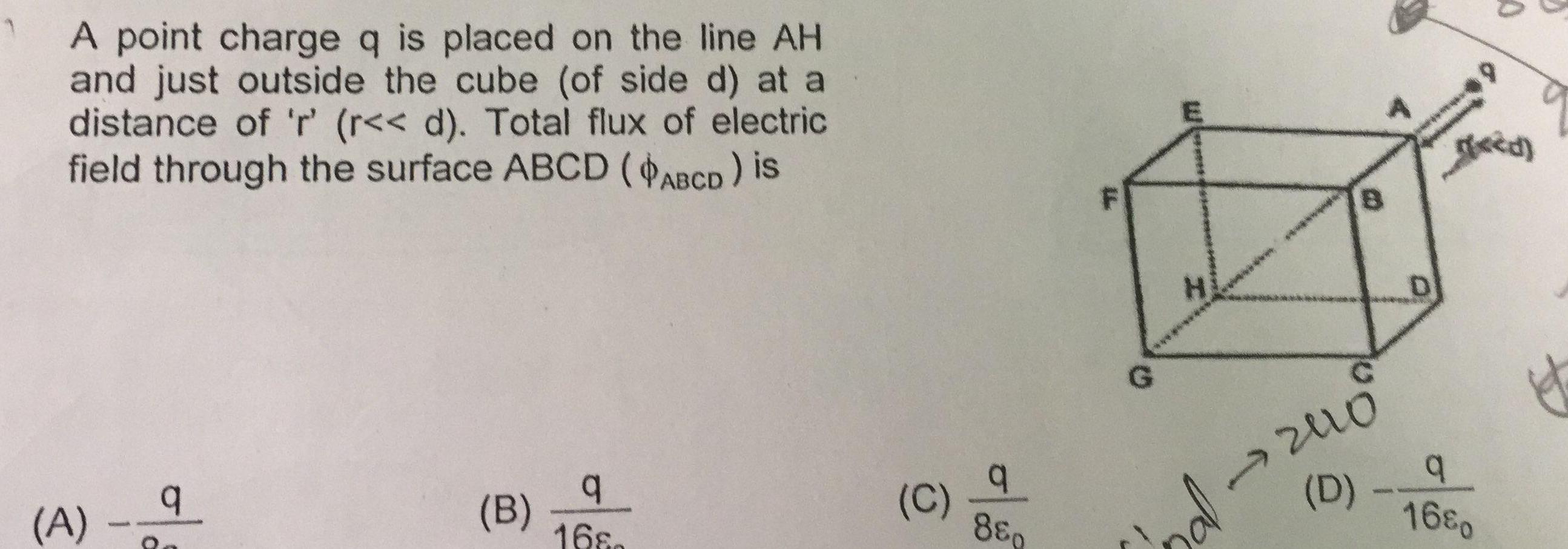
Physics
Gauss LawA point charge q is placed on the line AH and just outside the cube of side d at a distance of r r d Total flux of electric field through the surface ABCD ABCD is A q B q 168 C q 880 G H por B D 2010 D 9 q 168 goed

Physics
Gauss Law28 Three large plates A B and C are placed parallel to each other and charges are given as shown The charge that appears on the left surface of plate B is 42 30 3C 4C 5C 5L
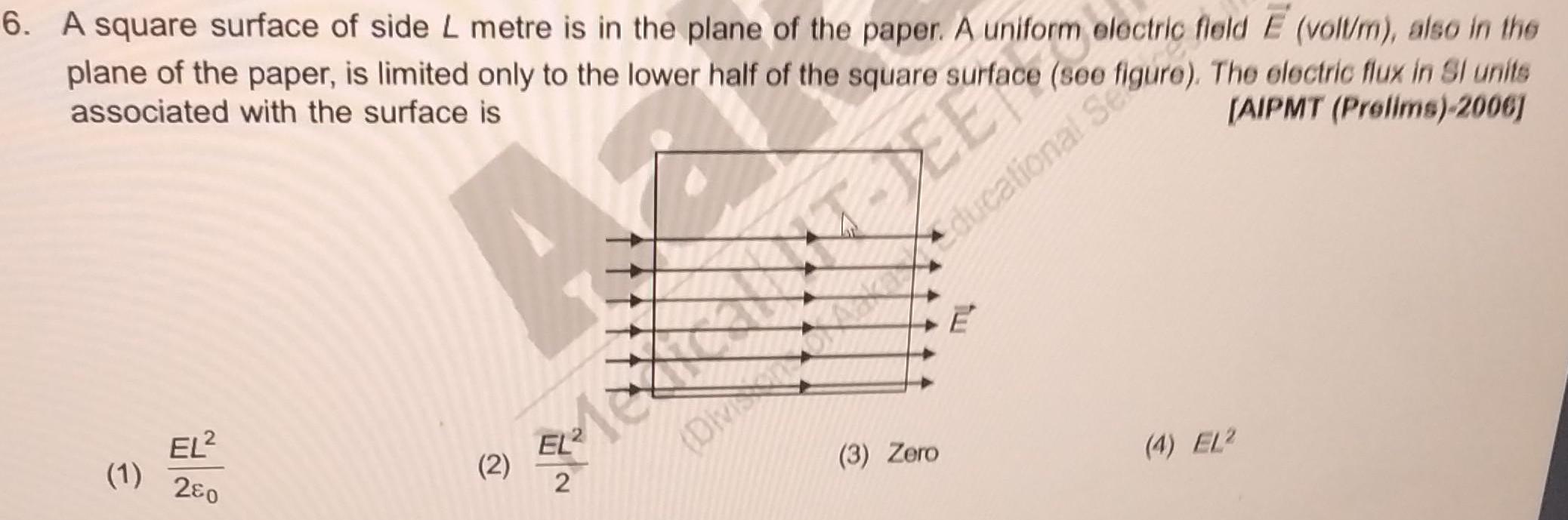
Physics
Gauss Law6 A square surface of side L metre is in the plane of the paper A uniform electric field E volt m also in the plane of the paper is limited only to the lower half of the square surface see associated with the surface is AIPMT Prelims 2006 DIVISION Educational Seguro The electric flux in Si units 1 EL 280 A 2 Me 2 3 Zero 4 EL2
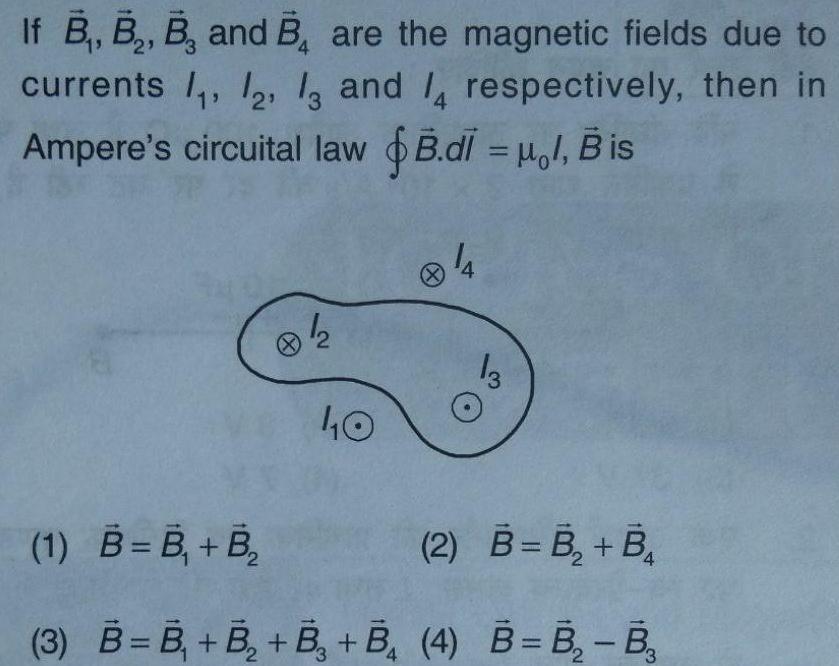
Physics
Gauss LawIf B B B and B are the magnetic fields due to currents 1 12 13 and 14 respectively then in Ampere s circuital law B di l Bis 1 2 40 14 13 1 B B B 2 B B B 3 B B B B B 4 B B B

Physics
Gauss Law9 Consider two concentric conducting spheres The outer sphere is hollow and initially has a charge 70 on it The inner sphere is solid and has a charge 20 on it a How much charge is on the outer surface and inner surface of the outer sphere b If a wire is connected between the inner and outer sphere after electrostatic equilibrium is established how much total charge is on the outer sphere How much charge is on the outer surface and inner surface of the outer sphere Does the electric field at the surface of the inside sphere change when the wire is connected

Physics
Gauss Lawa A system consists of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density P where a is a positive constant and r is the distance from the centre of the sphere Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R a 280 2 E 2 R My Answer Correct Answer

Physics
Gauss LawA plane electromagnetic wave travelling along X direction has electric field of amplitude 300 V m directed along the Y axis a What is the intensity of the wave b If the wave falls on a perfectly absorbing sheet of area 3 0 m at what rate is the momentum delivered to the sheet and what is the radiation pressure exerted on the sheet 8 854 x 10 2 C N m c 3 108 ms Take E Ans 119 529 W m2 1 195 x 106 N 3 98 x 10 7 P 1
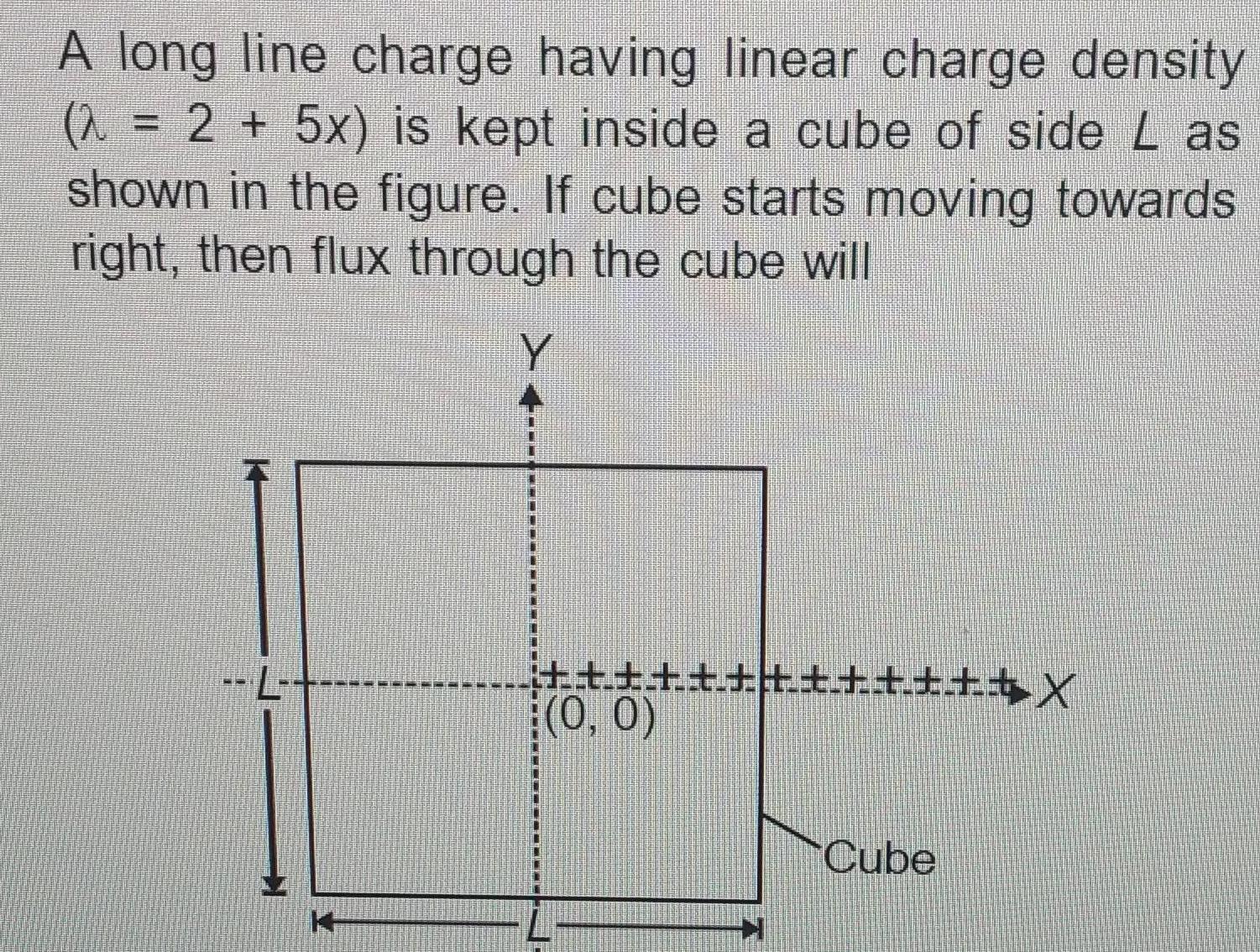
Physics
Gauss Law2 A long line charge having linear charge density 2 5x is kept inside a cube of side L as shown in the figure If cube starts moving towards right then flux through the cube will Y P 1 X 0 0 Cube

Physics
Gauss LawTwo unequal soap bubbles are formed one on each side of a tube closed in the middle by a tap What happens when the tap is opened to put the two bubbles in communication 1 No air passes in any direction as the pressure are the same on two sides of the tap 2 Larger bubble shrinks and smaller bubble increases in size till they become equal in size 3 Smaller bubble gradually collapses and the bigger one increases in size 4 None of the above and a span bubble of radius r The pressure p

Physics
Gauss LawThe electric field E A y j exists in a region where a cylinder of radius r and length L is placed with its curv surfaces parallel to y axis The charge inside the volume of the cylinder is TL A Ao o B A r L C r D 2A r L Je

Physics
Gauss LawA hollow metallic isolated sphere of inner radius R and outer radius 2R is carrying a net charge q Then the charges at the inner and the outer surface of the sphere are respectively A 0 q B q 2 q 2 C q 3 2q 3 D q 5 4q 5

Physics
Gauss LawA sphere of radius R surrounds a point charge Q Net outward flux through of semi vertical angle and of slant length R with vertex at centre is Q 250 1 cos 6 kQ cos e 450 FO 1 cos 0 200 1 cos 6 30

Physics
Gauss LawZero Marks 0 In all other cases Consider a uniform charge distribution with charge density of 2C m throughout in space If a Gaussian sphere has a variable radius which changes at the constant rate of 2 m s then value of the rate of change of total flux is proportional to r r radius of sphere Then find the value of k
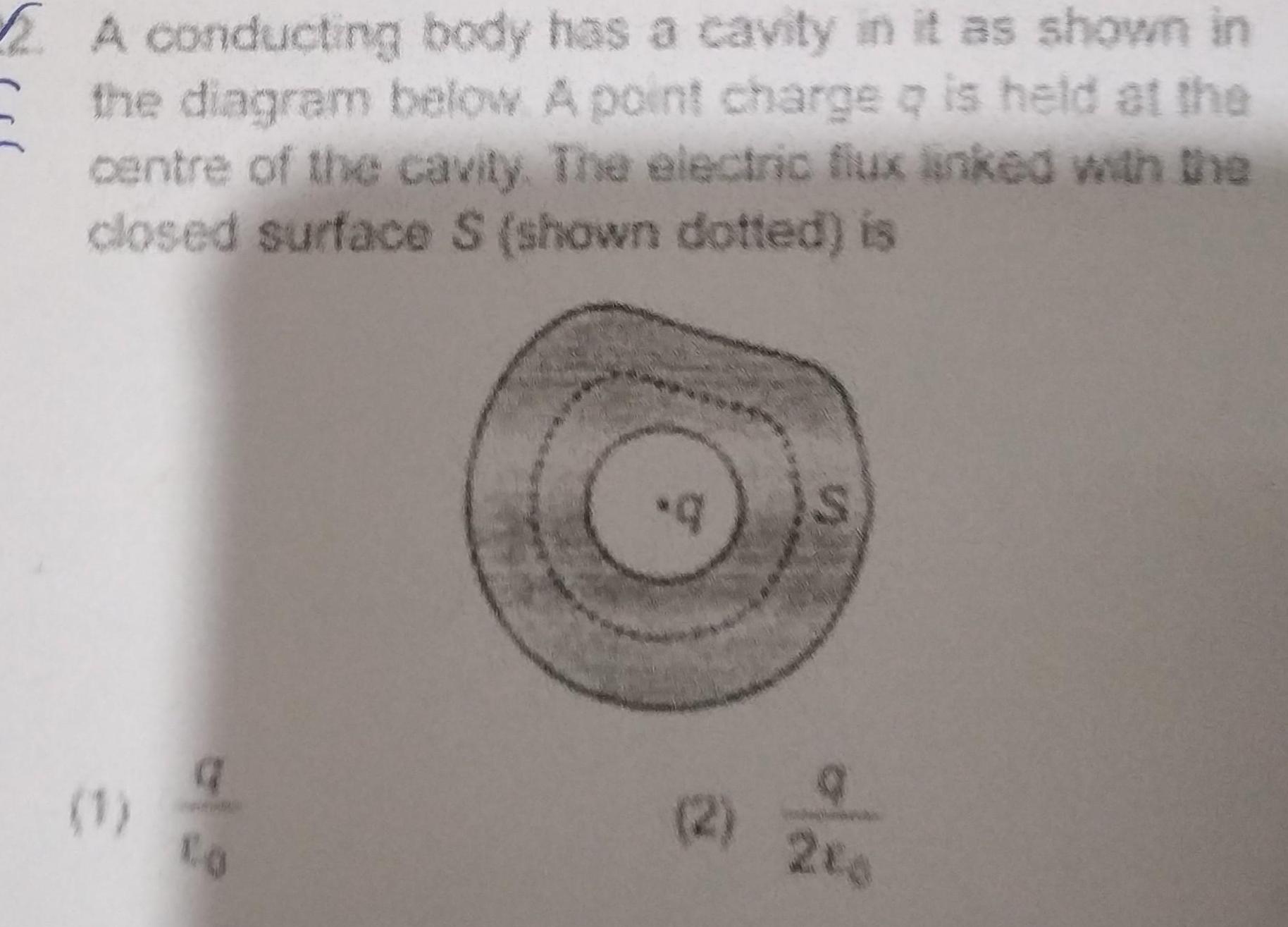
Physics
Gauss LawA conducting body has a cavity in it as shown in the diagram below A point charge is held at the centre of the cavity The electric flux linked with the closed surface S shown dotted is 1 a CO q S 2 200

Physics
Gauss LawA point charge q is kept at the centre of the circle formed by cutting a spherical shell by a plane as shown The electric flux linked with the remaining surface of the shell is then 1 p 3 Q 200 5 Q 2 g 200 a

Physics
Gauss LawProblem 2 A line charge with linear charge density 10 2 C m passes through the center of a sphere If the flux through the surface of the sphere is 1 13 10 3 Vm what is the radius R of the sphere

Physics
Gauss Law2 759 A piece of cloud is having area 25 x 106 m and electric potential of 105 volts If the height of cloud is 0 75 km then energy of electric field between earth and cloud will be 1 250 J 3 1225 J D51 4 1475 From NCERT
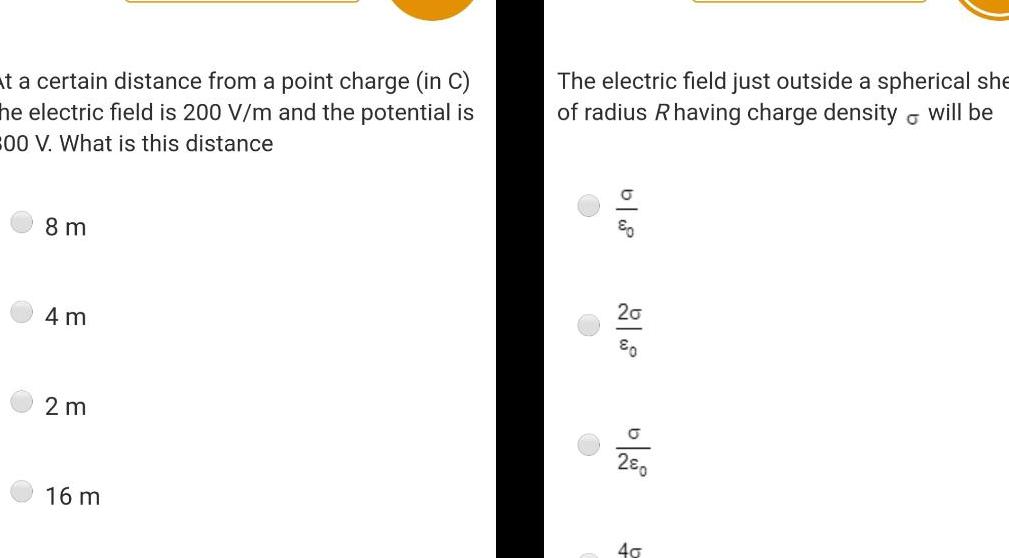
Physics
Gauss Lawat a certain distance from a point charge in C he electric field is 200 V m and the potential is 300 V What is this distance 8 m 4 m 2 m 16 m The electric field just outside a spherical she of radius R having charge density will be G b w 20 0 a 280 40

Physics
Gauss Law3 Find the expression for the electric field intensity at a point distance r apart from a charged spherica conductor Question 13

Physics
Gauss LawA charge Q is enclosed by a Gaussian spherical surface of radius R If charge and radius of Gaussian surface is doubled then outward electric flux will Becomes four times Remains same Becomes doubled Becomes half View in English
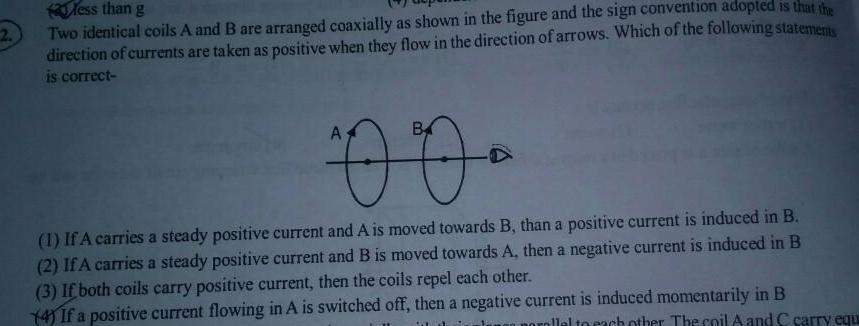
Physics
Gauss Law2 less than g Two identical coils A and B are arranged coaxially as shown in the figure and the sign convention adopted is that the direction of currents are taken as positive when they flow in the direction of arrows Which of the following statements is correct 00 1 If A carries a steady positive current and A is moved towards B than a positive current is induced in B 2 If A carries a steady positive current and B is moved towards A then a negative current is induced in B 3 If both coils carry positive current then the coils repel each other 4 If a positive current flowing in A is switched off then a negative current is induced momentarily in B orallel to each other The coil A and C carry equ

Physics
Gauss LawA circular dise of radius R carries surface charge density a r 1 7 where do is a constant and r is the distance from the center of the disc Electric flux through a large spherical surface that encloses the charged disc completely is g Electric flux through another spherical surface of radius and concentric with the disc is Then the ratio is

Physics
Gauss LawThe electric outward and is given by E Ar A charge contained in a sphere of radius a centred at the origin of the field will be given by AIPMT 2015 1 Aa 2 4 Aa 3 A a
Physics
Gauss Law55 A circular plane sheet of radius 10 cm is placed in a uniform electric field of 5 x 105 N C making an angle of 60 with the field The electric flux through the sheet is a 1 36 x 102 N m C 1 b 1 36 x 104 N m C c 0 515 x 102 N m C d 0 515 x 104 N m C 1
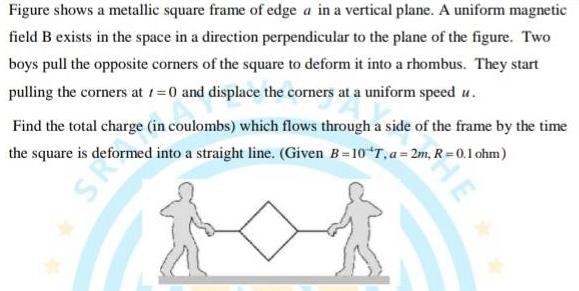
Physics
Gauss LawFigure shows a metallic square frame of edge a in a vertical plane A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure Two boys pull the opposite corners of the square to deform it into a rhombus They start pulling the corners at 1 0 and displace the corners at a uniform speed u Find the total charge in coulombs which flows through a side of the frame by the time the square is is deformed into a traightline Giv en 5 107 28 0 1 km HE
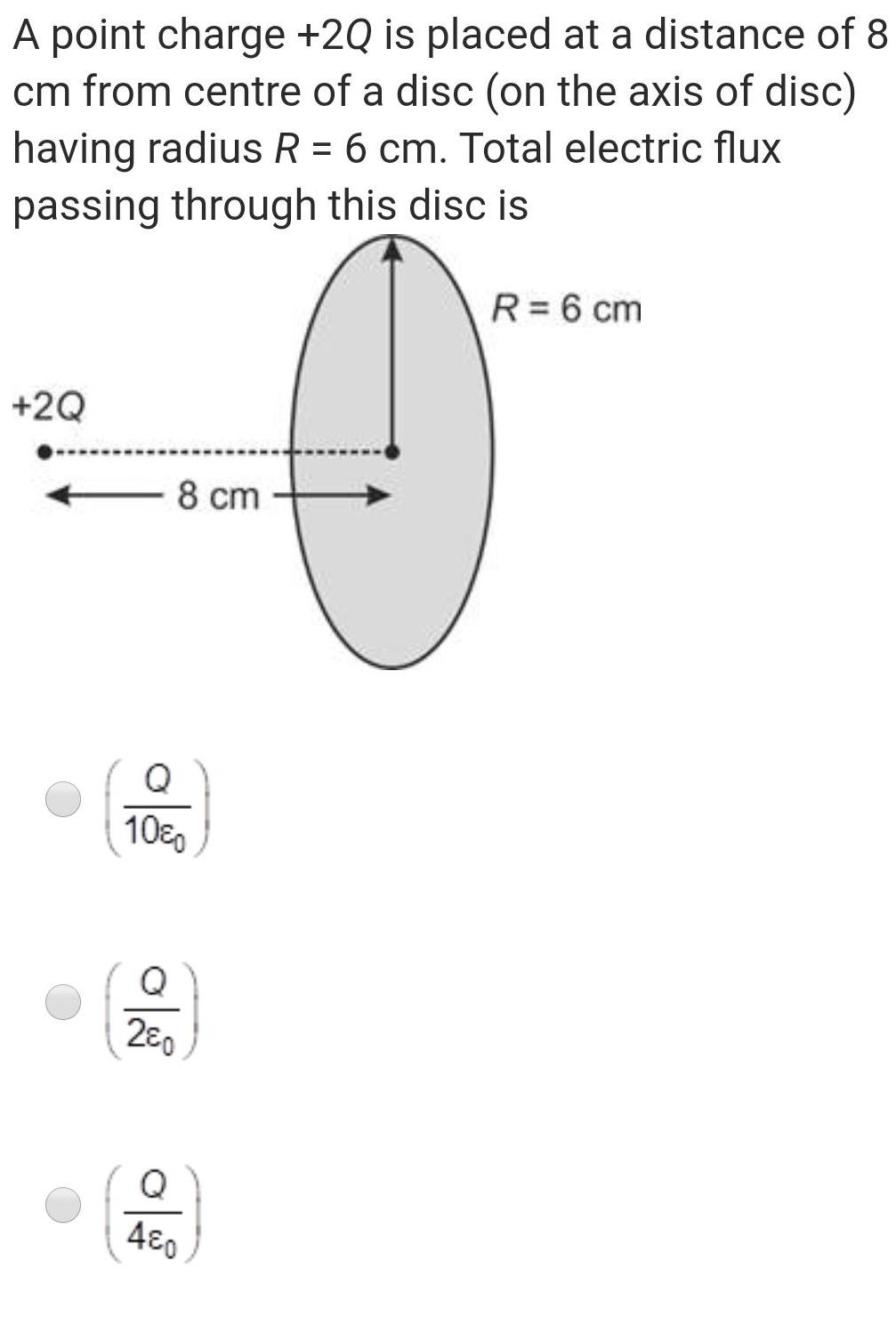
Physics
Gauss LawA point charge 2Q is placed at a distance of 8 cm from centre of a disc on the axis of disc having radius R 6 cm Total electric flux passing through this disc is 2Q 8 cm 10 Q 280 Q 480 R 6 cm
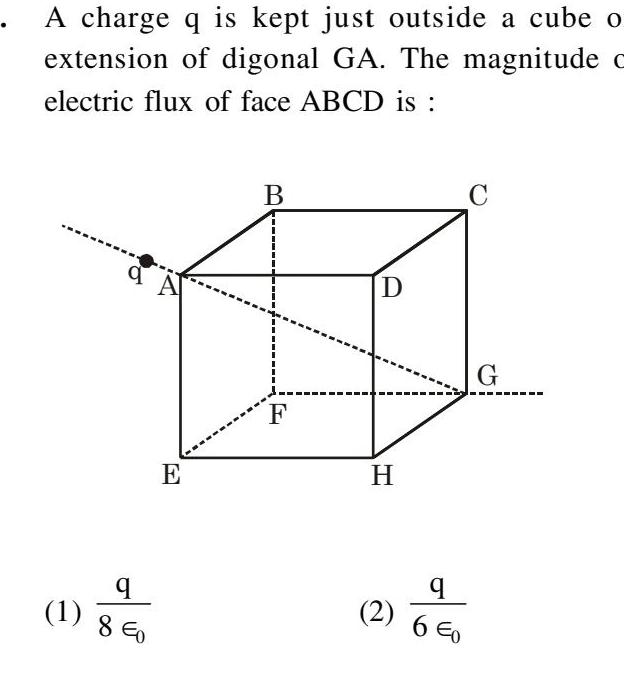
Physics
Gauss LawA charge q is kept just outside a cube o extension of digonal GA The magnitude c electric flux of face ABCD is q 1 8E0 E B F D H q 2 6 C G

Physics
Gauss Lawh Cylindrical Gaussian surface is used to calculate electric field intensity for i Point charge ii Hollow sphere iii Infinitely plane Infinitely long uniform charged wire R S
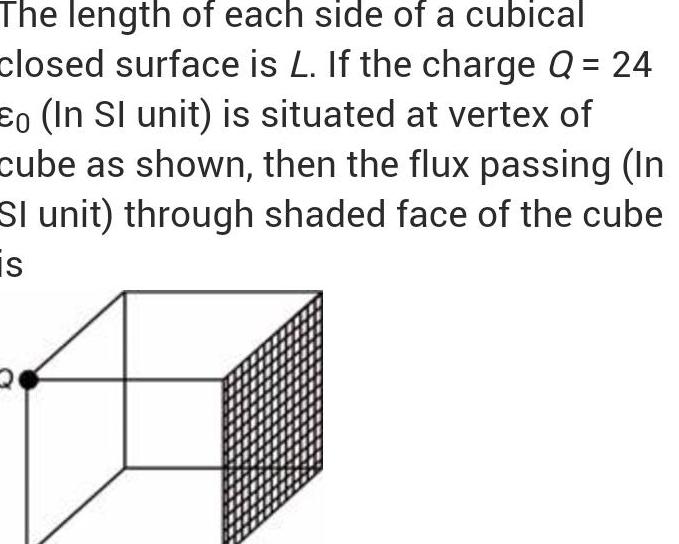
Physics
Gauss LawThe length of each side of a cubical closed surface is L If the charge Q 24 Eo In SI unit is situated at vertex of cube as shown then the flux passing In SI unit through shaded face of the cube is

Physics
Gauss Law7 If Gauss s law E ds 0 we can conclude 7 that 1 E must be zero 2 E must be perpendicular to surface 3 Total flux through the surface is zero 4 Flux is only going in the surface

Physics
Gauss LawAssignment Problem 7 A line charge with linear charge density of p 10 12 C m passes through the center of a sphere If the flux through the surface of the sphere is 1 13x10 3 Vm what is the radius R of the sphere Charged line

Physics
Gauss Law9 A point charge is placed at the center of a spherical Gaussian surface The electric flux phi is changed if 1 Point the sphore is replaced by cube of the same volume the point cage is moved to just outside the sphere the sphere is replaced by a cube of one tenth the volume
Physics
Gauss Law1 52 The electric field in a region is given by Ex 1 i Find the charge contained inside a cubical volume bounded by the surfaces x 0 x a y 0 y a z 0 and z a Take E 5 x 10 N C 1 2cm and a 1cm

Physics
Gauss Law1 51 The electric field in a region is given E axi Here a is a constant of proper dimensions Find a The total flux passing through a cube bounded by the surface x 1 x 21 y 0 y l z 0 z 1 b The charge contained inside the above cube Ans a al b a 1

Physics
Gauss Law2 39 A parallel plate capacitor with plates kept at a separation 1cm and plate area 100cm is connected across a 24V battery Find the force with wihch one plate will attract the other plates Ans 2 5 10 N

Physics
Gauss LawThe electric field a distance from the axis of a cylindrically symmetric charge distribution in vacuum of infinite length and uniform charge per unit length is 1 22 46 r a c 1 21 Ane OB O D b d 12 4m r 1 A 4neo7

Physics
Gauss Law2 The length of each side of a cubical closed surface is 1 If charge q is situated on one of the vertices of the cube then find the flux passing through shaded face of the cube
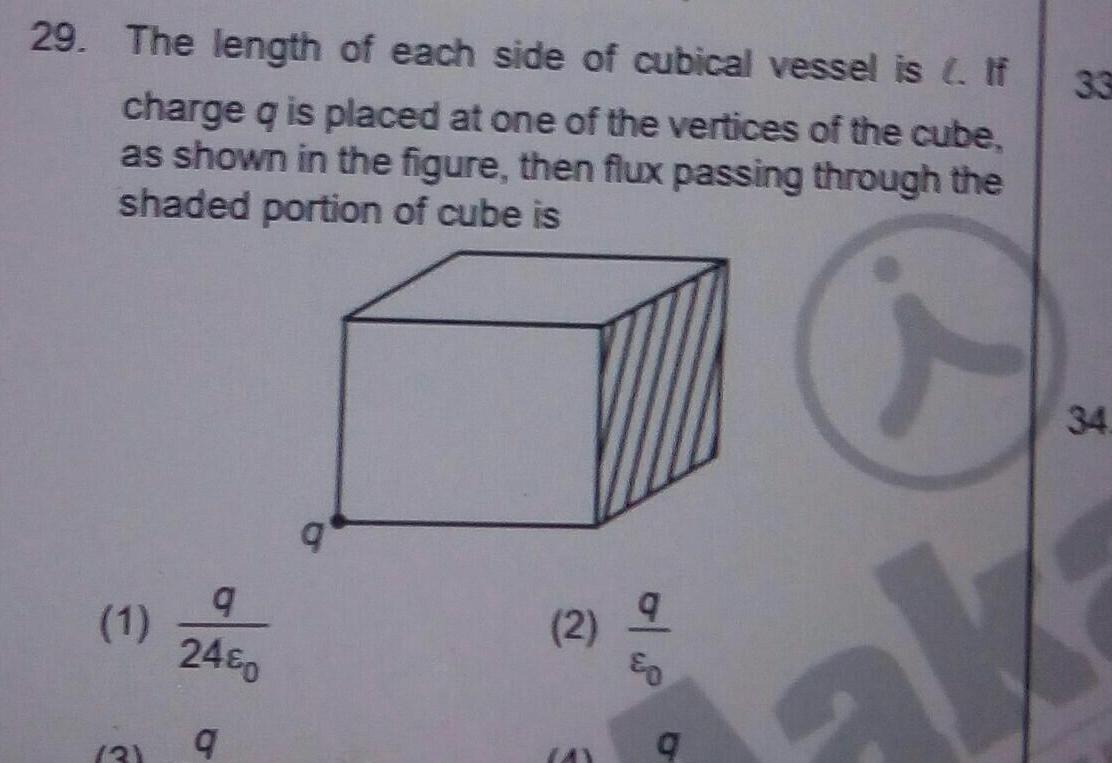
Physics
Gauss Law29 The length of each side of cubical vessel is If charge q is placed at one of the vertices of the cube as shown in the figure then flux passing through the shaded portion of cube is C 1 9 24 9 q 2 9 9 ak 33 34

Physics
Gauss Law1 25 pts As shown in the figure two particles carrying opposite charges 91 0 and 9 0 are a small distance apart from each other separated by the flat face of an insulating hemisphere of radius R The hemisphere contains only the positive charge 9 so that it is located just below the center of the flat face The charge 42 is located just above the center of the flat face What is the electric flux a through the curved surface and b through the flat face as 8 0 092 q1 R

Physics
Gauss LawElectric Charges and Fields 1 With a charge g at the centre an imaginary Gaussian sphere is constructed with a radius r The magnitude of intensity of field at any point on the Gaussian surface is E and the flux through the Gaussian surface is d If we change the radius of the Gaussian surface to 2r what happens to the values of electric field E and electric flux on the new surface A E decreases increases C E increases remains constant 2 ABC is an equilateral triangle of side L A charge q is kept at the vertex A The electric intensity at C compared to that at B has A same magnitude and same direction B different magnitude but same direction C same magnitude but different direction D different magnitude and different direction 3 When two charges each equal to 1q are arranged at the two vertices of an equilateral triangle the mutual force between them is F The magnitude of the electric intensity due to these two charges at the third vertex is 3F A C B E decreases D E increases 4 Two infinitely long thin straight wires having uniform linear charge densities 2 and 22 are arranged parallel to each other at a distance r apart The intensity of the electric field at a point midway between them is 22 r 31 2mcr D zero A not zero but positive C not zero but negative remains constant decreases 2 5 The electric flux expressed in Nm C through a sphere that has a radius of 1 0 m and has a point charge of C at its centre is nearly A 3 6x10 C 3 6x10 B 3 6x10 D 3 6x10 6 A point charge q is located on the x axis at x a and a second point charge q is located on the x axis at x a A Gaussian surface with radius r 2a is centered at the origin The flux through this Gaussian surface is B zero D 2q 8 Next

Physics
Gauss LawConsider the cube shown A point charge 8q is placed at a vertex G of the cube and another charge 4q is placed at the centre of an edge AE of the cube Electric flux through the cube is A C q o 12q o 2q o D Zero B A D 4q T E H B C F 8q G

Physics
Gauss Law26 A charge Q is placed on middle of edge of the cuber Then electric flux through cube due to field of charge Q is Q 1 BEO to Q 3 20 Q 4 40 27 Two charges each having magnitude and same Telegram

Physics
Gauss LawIf Q charge is distributed inside the material of a shell of inner and outer radii R and then non conducting R respectively Q P 1 Electric field inside shell must be zero 2 Electric field inside shell may be zero 3 Electric field inside shell is constant and non zero 4 Electric field inside shell is zero if Q is positive and non zero if Q is negative

Physics
Gauss Lawlid sphere of radius R has a charge Q distributed in its volume with a charge density p kra where k and a are constants and is the distance from its centre If the electric field at r R 2 is 1 8 times at r R find the value of a

Physics
Gauss Law3 8 N Repulsive 4 Zero R Electric field due to a non conducting sphere at 2 is same as some extemal point r r R Find the ratio of electric potential w r t infinity at internal and external point R is radius of sphere Qis charge on it 47 16 Two large conducting plates having surface 3 47 32 1 31 32 2 4 49 16 3 8 N ff stance feera fanfarr r R a far farga fava w r t infinity R Q 1 47 32 R 2 4 2 47 49 16 16 str faga s an dical are ser ve ara 3 31 32 4
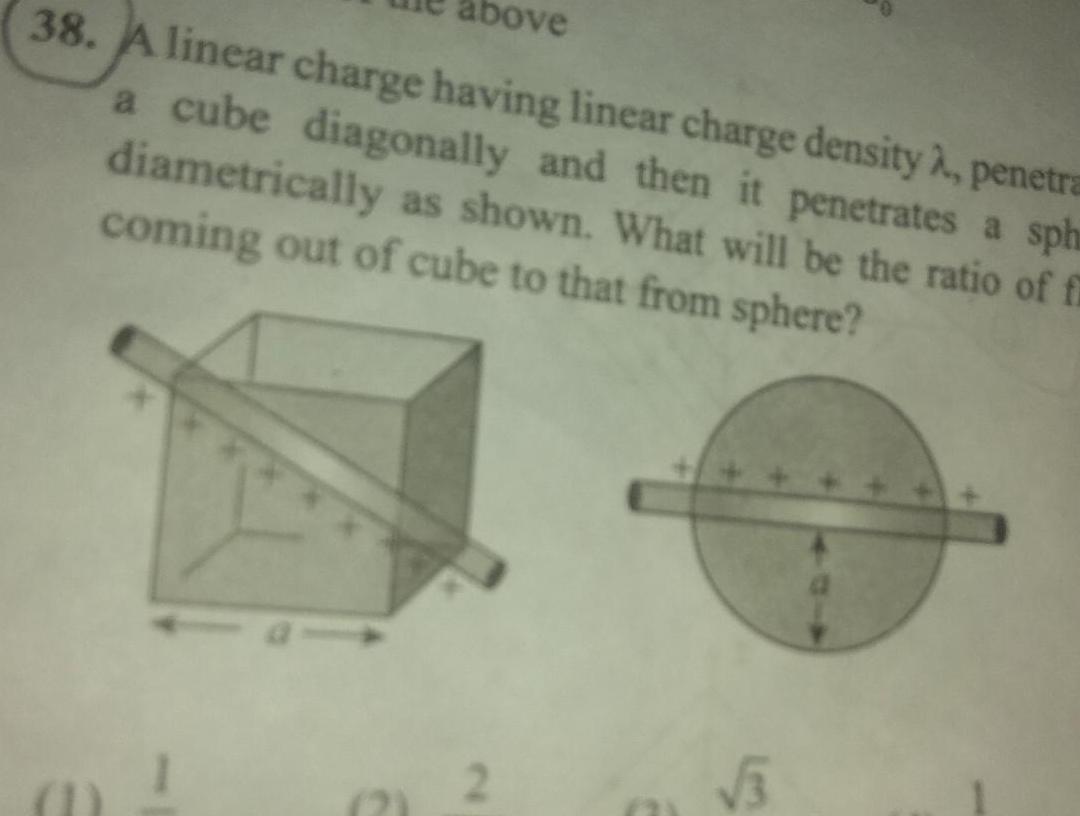
Physics
Gauss Law38 A linear charge having linear charge density penetra a cube diagonally and then it penetrates a sph diametrically as shown What will be the ratio of fi coming out of cube to that from sphere pove 2 3

Physics
Gauss LawA cylinder of radius R and length L is placed in a 45 uniform electric field E parallel to the cylinder axis The total flux from the surface of the cylinder is 1 2 R E 2 R E 3 R R E 4 zero Tea and gas de of a gen UAS UNGHA TAI 1 2TR E 2 R E 3 R R E 4

Physics
Gauss LawAssertion A A point charge is lying at the centre of a cube side The electric flux emanating from each surface of the cube is 1 6 of the total flux Reason R According to Gauss theorem total electric flux through a closed surface 1 times the enclosing a charge is equal to itud 0