Simple harmonic motion Questions and Answers

Physics
Simple harmonic motionTU If two S H M are represented by equations y 10 sin 3nt and y 5 sin 3nt 3 cos 3rt then find the ratio of their amplitudes and Solution As So Then y 5 sin 3 t 3 cos 3 t if 5 A cos and 5 3 Asino A 5 2 5 3 10 5 3 5 and tan o SO the above equation i becomes A A J SC y Acoso sin 3 t Asino cos 3 t but y 10 sin 3nt 3 3 110 b SO 3 T TU T A A 1 1 i sin 3nt n 2 difference in between t y Asin 3 t b 6 60 y 10 sin 3 t o LOCTICASSOS Y 5sin 3rt

Physics
Simple harmonic motion79 Consider a pair of identical pendulums which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2 to the right with the vertical the other pendulum makes an angle of 1 to the left of the vertical The phase difference between the pendulums is d n a RIC 2 b T c 2 T

Physics
Simple harmonic motion80 Two pendulums differ in lengths by 22 cm They oscillate at the same place so that one of them makes 30 oscillations and the other makes 36 oscillations during the same time The lengths in cm of the pendulums are a 72 and 50 c 50 and 28 b 60 and 38 d 80 and 58

Physics
Simple harmonic motionits is arily nous frequency of a driven oscillator depends on the damping 100 A block of mass m is attached to a spring of spring constant k and has a natural frequency 0 An external force F t proportional to cos cot 0 is applied to the oscillator The time displacement of the oscillator will be proportional to m 1 a b 00 00 m 0 c 1 m m d m 2

Physics
Simple harmonic motiona 2 b 2 c 4 d 3 63 Time period of oscillation of a spring is 12 s on earth What shall be the time period if it is taken to moon a 6s b 12 s c 36 s d 72 s 70 a 8 A tro conne consta its eq

Physics
Simple harmonic motiona 0 0375 J 0 125 J c 0 125 J 0 125 J SOME SYSTEMS EXECUTING SIMPLE HARMONIC MOTION 51 A body of mass m is situated in a potential field U x U 1 cosax where U and a are constants The time period of small oscillations is a 2 c 2 b 0 125 0 375 d 0 375 J 0 375 J m U m 2U m U a b 2x 2m VU a d 2n 68 F S JL T 0 re P a c

Physics
Simple harmonic motion3 An air chamber of volume V has a neck of crow sectional area a into which a light ball of mass just fits and can move up and down without friction The diameter of the ball is equal to that of the neck of the chamber The ball is pressed down a little and released If the bulk modulus of air is B the time period of the oscillation of the ball is b T 2n a T 2m Ba mV BV mB ma mV Va Ba A spring balance has a scale that reads from 0 to c T 2 d T 2r

Physics
Simple harmonic motion55 A particle executing SHM with an amplitude A The displacement of the particle when its potential energy is half of its total energy is a c d 4 56 A block of mass m is hanging vertically by spring

Physics
Simple harmonic motion2U Vua 62 The frequency of oscillations of a mass m suspended by a spring is u If the length of the spring is cut to one half the same mass oscillates with frequency U The value v v is a 2 b d 3 c 4
Physics
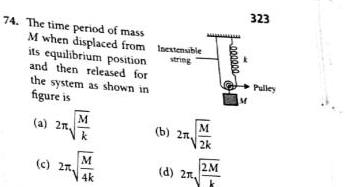
Simple harmonic motion74 The time period of mass M when displaced from Inextensible its equilibrium position string and then released for the system as shown in figure is a 2 c 2 M k M 4k b 2 d 2x M 2k 2M 000000 323 Pulley

Physics
Simple harmonic motionBOOXX XXX a I III b II III c I IV d II IV 59 When the displacement of a particle executing SHM is one fourth of its amplitude what fraction of the total energy is the kinetic energy 3 a 16 15 b 60 A block whose mass is 1 kg is fastened to a spring The spring has a spring constant of 100 Nm The block is pulled to a distance x 10 cm from its equilibrium position at x 0 on a frictionless surface from rest at t 0 The kinetic energy and potential energy of the block when it is 5 cm away from the mean position is a 0 0375 J 0 125 J b 0 125 1 0 375 J c 0 125 J 0 125 J d 0 375 J 0 375 c 2 SOME SYSTEMS EXECUTING SIMPLE HARMONIC MOTION 61 A body of mass m is situated in a potential field U x U 1 cosax where U and a are constants The time period of small oscillations is b 2 a 2 15 16 771 U m 200 771 U a 2m U a d 2n 62 The frequency of oscillations of a mass m suspended by a spring is u If the length of the spring is cut to one half the same mass oscillates with frequency U The value v v is a 2 b 2 65 In the question number 64 the maxim acceleration of the collar is b 10 ms d 20 m s a 5 ms c 15 m s 2 b 12 s c 36 s d 72 s 64 A 5 kg collar is attached to a spring of spring constant 500 N m It slides without friction over a horizontal rod The collar is displaced from its equilibrium position by 10 cm and released The time period of oscillation is 66 to a spring of spring A body of mass 20 g connected constant k executes simple harmonic motion with frequency of 5 m Hz The value of spring consta a 4 Nm b 3 Nm c 2 Nm d 5Nm 67 Two blocks each of mass m is connected to the spring of spring constant k as shown in the figure 191 in opposite If the blocks are displaced slightly directions and released they will execute simp harmonic motion The time period of oscillation m a 21 b 2x a T 2 m c T 2 000000 Ba mV mB Va a 0 5 m s c 2 ms m 2k 68 An air chamber of volume V has a neck of crow sectional area a into which a light ball of mass just fits and can move up and down without friction The diameter of the ball is equal to that of the ne of the chamber The ball is pressed down a little and released If the bulk modulus of air is B the time period of the oscillation of the ball is b T 2n c 2 m 4k d T 2n 600 Nm 43kg 600 Nm 000000 000000 27x d 2 b 1 ms d 3 ms BV ma 69 A spring balance has a scale that reads from 0 50 kg The length of the scale is 20 cm A block of mass m is suspended from this balance when displaced and released it oscillates with a period 0 5 s The value of m is Take g 10 ms a 8 kg b 12 kg c 16 kg d 20 kg c 4 d 3 63 Time period of oscillation of a spring is 12 s on 70 A trolley of mass 3 kg as shown in figure is earth What shall be the time period if it is taken to moon connected to two identical springs each of spring constant 600 N m If the trolley is displaced from its equilibrium position by 5 cm and released the maximum speed of the trolley is a 6 s mV Ba

Physics
Simple harmonic motionA block attached to a spring oscillates in simple harmonic motion with amplitude 0 2 m and period T At t 0 the block is at xo 0 1 m and is moving to the left The earliest time at which the block has velocity 0 5vmax is T 12 O 5T 12 O 7T 12 T 4

Physics
Simple harmonic motion69 A spring balance has a scale that reads from 0 50 kg The length of the scale is 20 cm A block of mass m is suspended from this balance when displaced and released it oscillates with a period 0 5 s The value of m is Take g 10 ms a 8 kg b 12 kg c 16 kg d 20 kg 70 A trolley of mass 3 kg as shown in figure is connected to two identical springs each of spring

Physics
Simple harmonic motionThe ratio of time period of oscillation of the conical pendulum to that of the simple pendulum is Assume the strings are of the same length in the two cases and 0 is the angle made by the string with the vertical in case of conical pendulum A B C D cos e cose 1 None of these

Physics
Simple harmonic motiond any diameter of reference circle 9 Figure shows the circular motion of a particle The radius of the circle the period sense of revolution and the initial position are indicated in the figure The simple harmonic motion of the x projection of the radius vector of the rotating particle Pis 7 T a x 2cos 2nt b x 2 sin 2nt d x 2 cos 2nt P 01 T 1s TL c x 2sin 2mt 1

Physics
Simple harmonic motionThe period of oscillation vibration magnetometer of a magnet in is 2 sec The period of oscillation of a magnet whose magnetic moment is four times that of the first magnet is b 4 sec d 0 5 sec a 1 sec c 8 sec

Physics
Simple harmonic motion13 Out of the following functions representing motion of a particle which represents SHM 300 A y sin wt cos wt form sit elam y sin ot B ommen sign C y 5 cos 3 3wt A Plems D y 1 ot 0 AIPMT Prelims 2011 AL 1 Only A and B 2 Only A 3 Only D does not represent SHM 1 4 18

Physics
Simple harmonic motionA particle is performing SHM according to equation y Asin et Average speed of the particle in time interval t 0 to t T will be T Time period Aco 2 4 Ao T 3 Ao 2 2A0 T

Physics
Simple harmonic motionconstant of spring is k which has been compressed by an amount xo If x is instantaneous deflection of spring from its natural length mark the correct option s 000000 m Smooth Instantaneous power developed by spring is k P kx x x 2 m INCORRECT Maximum power of spring is YOUR ANSWER k k NIF 2 Maximum power occurs at x Xo 2

Physics
Simple harmonic motiona x 0 05 c x 0 5sin5t m d x 5sin5t m 26 A non viscous liquid of density p is filled in a tube with A as the area of cross section as shown in the figure If the liquid is slightly depressed in one of the arms the liquid column oscillates with a frequency a b d 15 2n 15 PgA sin 0 0 2 111 pgA sin 8 sin0 PgA sin m pgA sin 8 sin 0 m 0 0 2 m

Physics
Simple harmonic motionspring block system is kept on a smooth horizontal surface between two vertical fixed walls Assume vacuum in the surrounding and spring to be ideal The left end of the spring is fixed to the left wall and at the right end a block is kept which may or may not be attached to the spring The distance between block and right wall initially is A 2 m Now the block is pushed slowly by a distance of A towards the left and released Given that mass of the block m 2kg spring constant k 100N m A 1m All the values given in list II are in Sl units Assume elastic collision with the wall ii mmmmm List I i Time period of the motion iii m 2kg k 200N m A Im Maximum speed attained by the block in the entire motion Speed with which block collides with the wall Speed with which block iv rebounds after colliding with the wall P List I T 1 TU Q 10 2 R 15 S 5 IG

Physics
Simple harmonic motion14 Two particles are oscillating along two close parallel straight lines side by side with the same frequency and amplitudes They pass each other moving in opposite directions when their displacement is half of the amplitude The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles The phase difference is AIPMT Mains 2011 1 T clubex 2 T FARIDAY 6 2TT

Physics
Simple harmonic motion2 A body executes SHM on a line of length 16 cm with a frequency 24 sec What will be its average velocity when it moves from mean position to half of amplitude 1 2 cm s 2 3 cm s 3 4 cm s 4 zero
Physics
Simple harmonic motion4 2x k 3 2m m 4 In a SHM resultant displacement is given by 8 7 sinot 300sest The resultant amplitude is 2 16 3 4 4 6 3

Physics
Simple harmonic motionIn one experiment the students allow the block to oscillate after stretching the spring a distance a if the potential energy stored in the spring is u0 then what is the change in kinetic energy of the block after it is released from rest and has traveled a distance of A2 u0 a 34u0 b 12u0 c 14u0

Physics
Simple harmonic motion14 180 Two waves are represented by equations y 10 sin ot kx 10 sin 3 m and y 5 sinat kx m Where x is in metre and tis in second The phase difference between the waves at position x at time tis X EIN E IT

Physics
Simple harmonic motionhen a particle of mass m is suspended from a massless spring of natural length the length of the spring becomes 21 When the same mass moves in conical pendulum as shown in figur the spring becomes L The radius of the circle of conical pendulum is K 2 m L L 1 2 L 21 00000000

Physics
Simple harmonic motionThe bob of a pendulum has mass of 40 mg and charge q 10 uC is given to it length of pendulum is 90 cm The point of suspension support also has a point charge of 10 C What is the time period of oscillation of pendulum 9 1 q O mg Support Vo 0 6T S 6 s 0 6s

Physics
Simple harmonic motionmotion of same amplitude frequency and having zero phase difference superimpose on a particle then its resultant path will be 2 A circle 4 A hyperbola of the falling represents a SHM2 A straight line 3 An ellipse C perpendicular simple harmonic motion of same amplitude frequency and having zero phase rimpose on a particle then its resultant path will be XA straight line 2 A circle 3 An ellipse 4 A SUM2
Physics
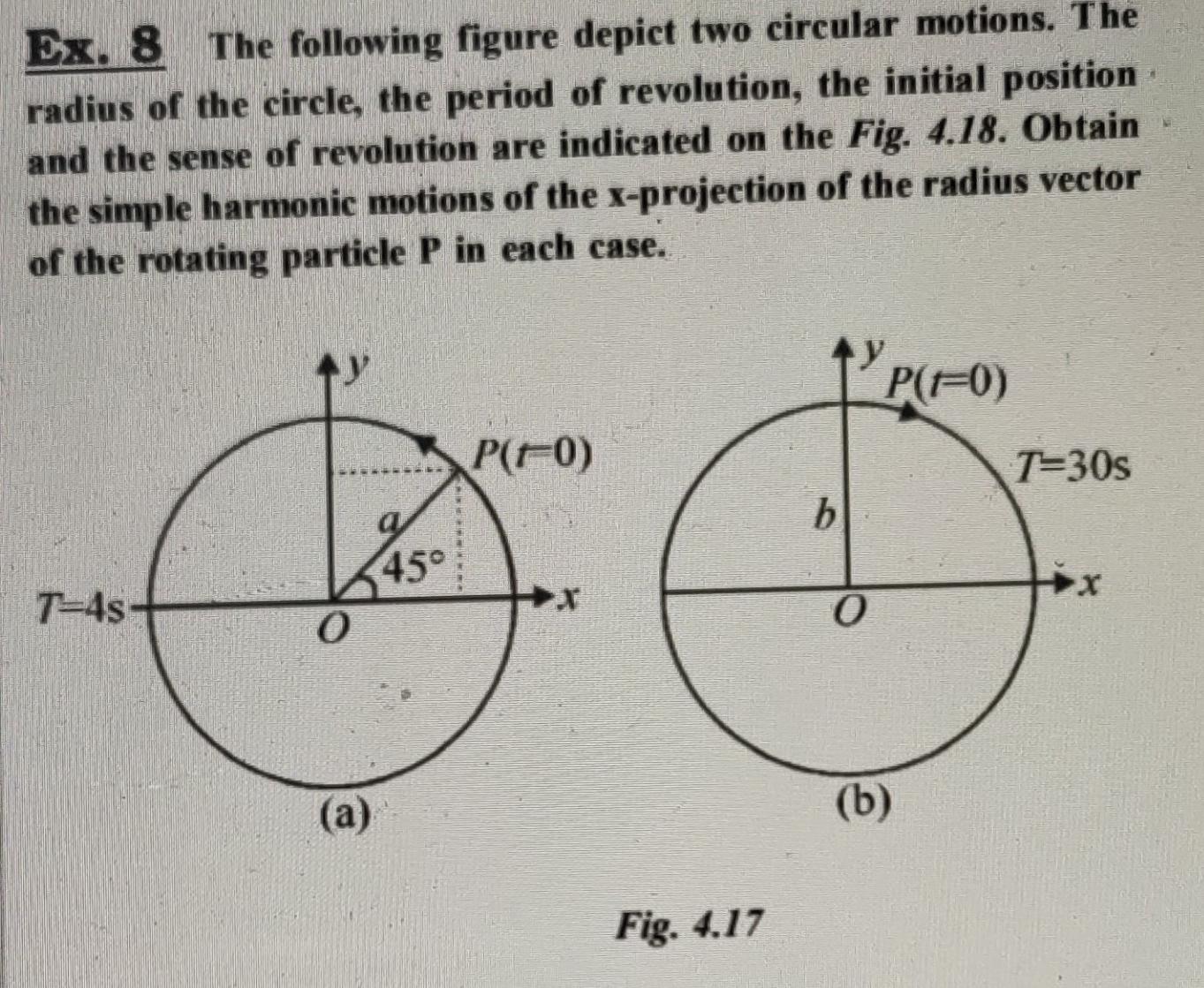
Simple harmonic motionEx 8 The following figure depict two circular motions The radius of the circle the period of revolution the initial position and the sense of revolution are indicated on the Fig 4 18 Obtain the simple harmonic motions of the x projection of the radius vector of the rotating particle P in each case T 4s 0 a 45 P r 0 Fig 4 17 b 0 P 1 0 b T 30s x

Physics
Simple harmonic motionTo check the stability slightly disturb the body from equilibrium position If on disturbing potential energy increases then equilibrium will be stable if potential energy decreases equilibrium will be unstable and if n change in potential energy then equilibrium will be neutral

Physics
Simple harmonic motionA vertical mass spring system executes simple harmonic oscillations with a period of 2s A quantity of this system which exhibits simple harmonic variation with a period of 1 second is Question Type Single Correct Type 1 Velocity 2 Potential energy 3 Phase difference between acceleration and displacement

Physics
Simple harmonic motion10 In the middle of a calm lake a radio receiver is installed on a pole at height 4 0 m above water level The receiver is used to track rad signals from a satellite orbiting the earth As the satellite rises abo the horizon intensity of the signals at the receiver varies periodical It is maximum when the satellite is 3 above the horizon and then when the satellite is 6 above the horizon Wavelength of the satell signals is closest to aga a 24 cm c 42 cm b 36 cm d 48 cm
Physics
Simple harmonic motion7180 If the amplitude of particle executing SHM is doubled then which of the following quantities will be doubled Time period Mark for Review Total energy Angular frequency Maximum acceleration

Physics
Simple harmonic motionA pendulum made of point mass m on a massless rod of length is hanging from a mass M sliding freely without friction or external forcing along a horizontal rail Write the Lagrangian of the system How many degrees of freedom does it have Solve Euler Lagrange equations and write down the nonlinear governing equations of motion Show that one of the variables is ignorable cyclic and that this leads to an integral of motion which expresses the conservation of linear momentum of the system along the rail Assume that at time zero the pendulum was slightly deflected away from vertical but nothing was moving Write the equation of infinitesimally small oscillations of the pendulum where the deflection and its rate of change are so small that powers higher than 1 of these quantities can all be neglected What is the frequency of small oscillations how different is it from the standard pendulum Discuss the limits of m M 0 m M

Physics
Simple harmonic motionAt a moment in a progressive wave the phase of a particle executing S H M is 3 Then the phase of the particle 15 cm ahead and at the time will be if the wavelength is 60 cm 7 2 3 Zero 5m

Physics
Simple harmonic motion42 An assembly of identical spring mass system is placed on a smooth horizontal surface as shown Initially the springs are relaxed The left mass is displaced to the left while the right mass is displaced to the right and released The resulting collision is elastic The time period of the oscillations of the system is a 2n c 2n 2M k IM k k 0000000 M M k voooooo b 2 d n M 2k M k

Physics
Simple harmonic motion31 A pendulum has time period T for small oscillations An obstacle P is situated below the point of suspension O at a 3 distance The pendulum is released 31 4 from rest Throughout the motion the moving string makes small angle with 11 P
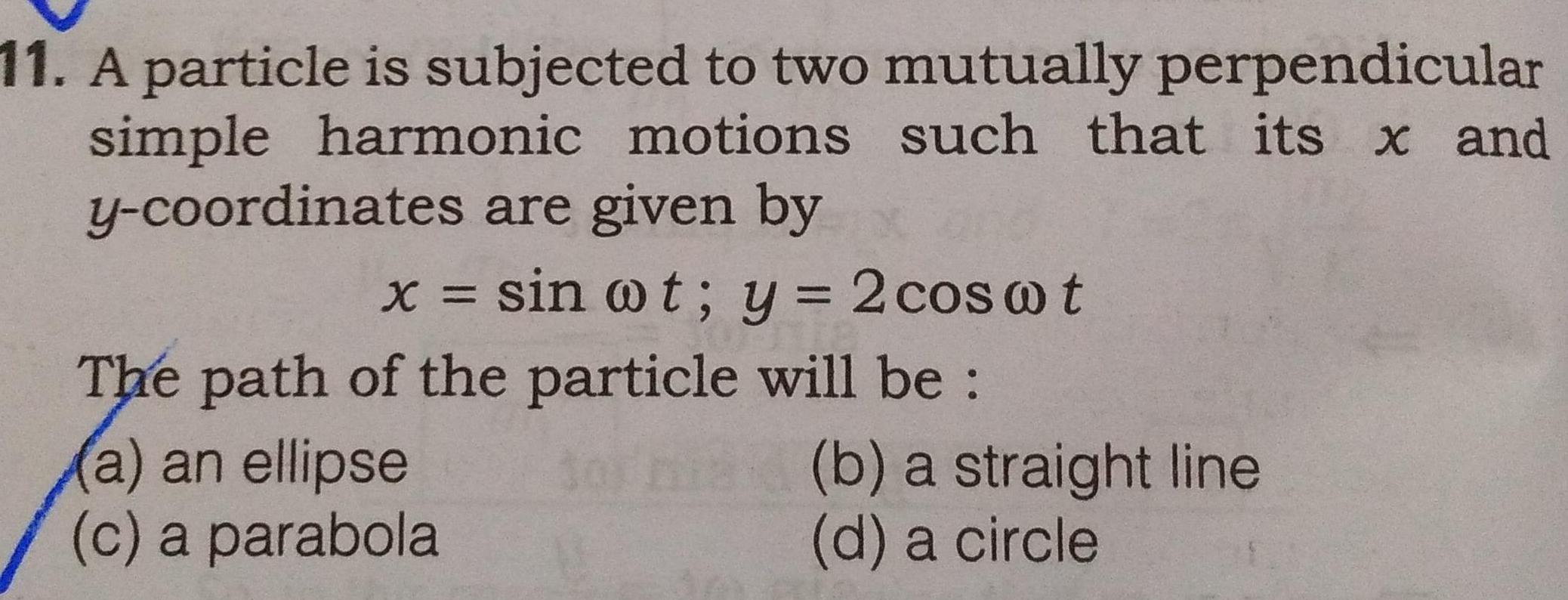
Physics
Simple harmonic motion11 A particle is subjected to two mutually perpendicular simple harmonic motions such that its x and y coordinates are given by sin ot y 2 coswt The path of the particle will be a an ellipse c a parabola torna b a straight line d a circle

Physics
Simple harmonic motion7 A sound wave of frequency 245 Hz travels with the speed of 300 ms along the positive x axis Each point of the wave moves to and fro through a total distance of 6 cm What will be the mathematical expression of this travelling wave 1 Y x t 0 03 sin 5 1 x 2 Y x t 0 06 sin 5 1 x 3 Y x t 0 06 sin 0 8 x 4 Y x t 0 03 sin 5 1 x Official Ans by NTA 4 Sol 4 2 f 1 5 x 103 6 A 2 3 cm 0 03 m 0 2 x 10 t 1 5 x 10 t 0 5 x 10 t 1 5 x 10 t

Physics
Simple harmonic motionk x 1 A student says that he had applied a force F on a particle and the particle performs in simple harmonic motion He refuses to tell whether k is a constant or not Assume that he has worked only with positive x and no other force acted on the particle a As x increase k increases b As x increases k decreases c As x increases k remains constant d The motion cannot be simple harmonic sigaid

Physics
Simple harmonic motionA block of mass 1 kg attached to a spring is made to oscillate with an initial amplitude of 12 cm After 2 minutes the amplitude decreases to 6 cm Determine the value of the damping constant for this motion take In 2 0 693 1 0 69 x 102 kg s 1 2 3 3 x 10 kg s 1 3 1 16 x 10 kg s 1 4 5 7 x 10 3 kg s 1 Official Ans by NTA NA Official Ans by ALLEN Bonus 1 A Age b x 120 2m 0 693 2 1 120 b

Physics
Simple harmonic motion13 A particle executing SHM while moving from one extremity is found at distance x x2 and x3 from the centre at the end of three successive seconds The time period of oscillation is b 2n 0 a c 0 Here 0 cos d 20 1 X1 X3 2x2
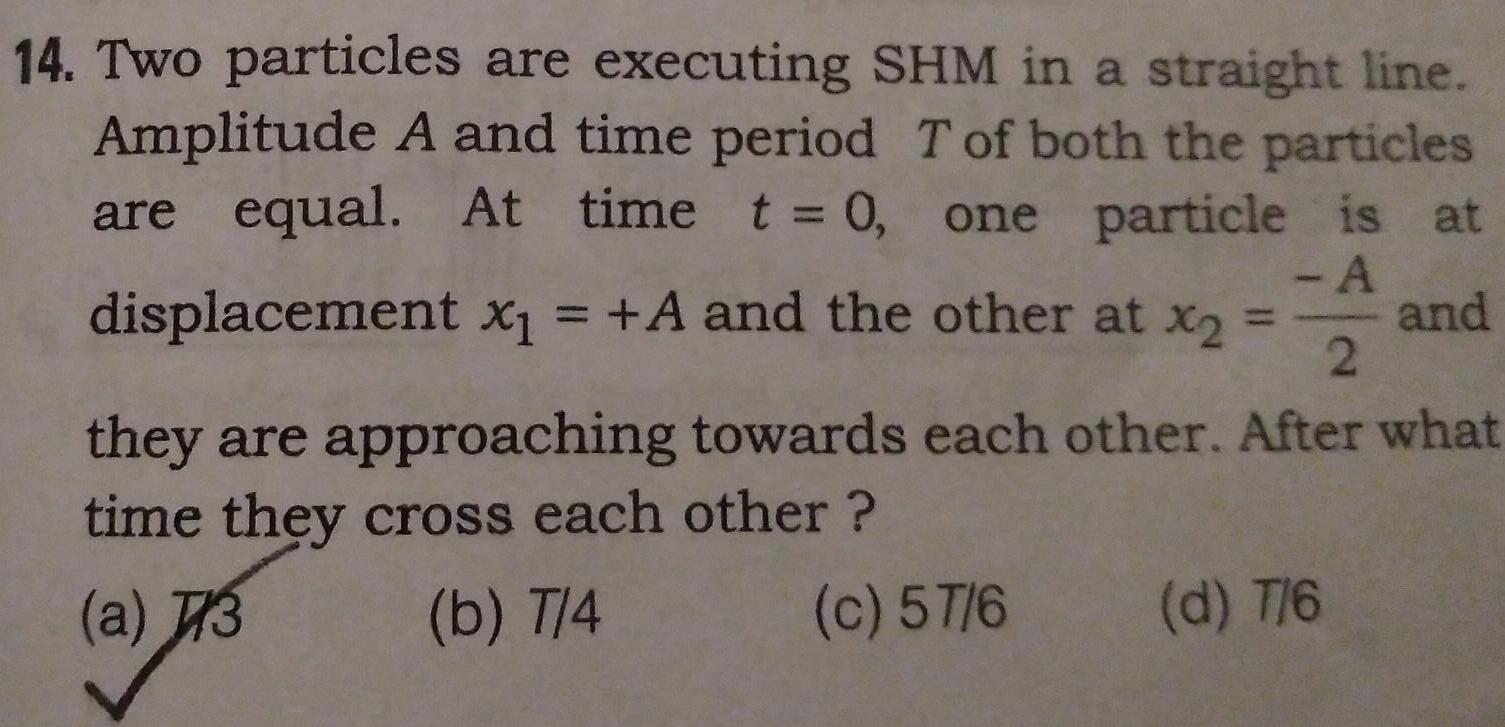
Physics
Simple harmonic motion14 Two particles are executing SHM in a straight line Amplitude A and time period T of both the particles are equal At time t 0 one particle is at displacement x 1 A and the other at x and they are approaching towards each other After what time they cross each other A 2 a 3 b T 4 c 57 6 d T 6

Physics
Simple harmonic motion9 Consider the spring block system shown in the figure initially block m is in equilibrium An impulse gives the block a velocity v upwards Find the maximum speed of the block during the motion 2 2v 3 4 5v E

Physics
Simple harmonic motionThe displacement time graph of a particle executing SHM is as T him 2 T 3T T 4 4 Which of the following statement is wrong Question Type Single Correct Type 1 2 X 3 The force is zero at t 3T 51 4 4 t t The acceleration is maximum at 4T 4 The potential energy is equal to kinetic energy T at t 2 3T

Physics
Simple harmonic motion4 A system consists of two identical cubes each of mass m linked together by the compressed weightless spring of spring constant k the cubes are connected by a thread which is burned through at a certain moment Find to what maximum height will centre of mass of this system rise if the initial compression of the spring is 7 mg k m m

Physics
Simple harmonic motionIT bodies performing S H M have same amplitude and frequency Their phases at a certain instant are as shown in the figure The phase difference between them is x x 0 5 A 2 m A 0 0 21 0 5 A A T x X 3
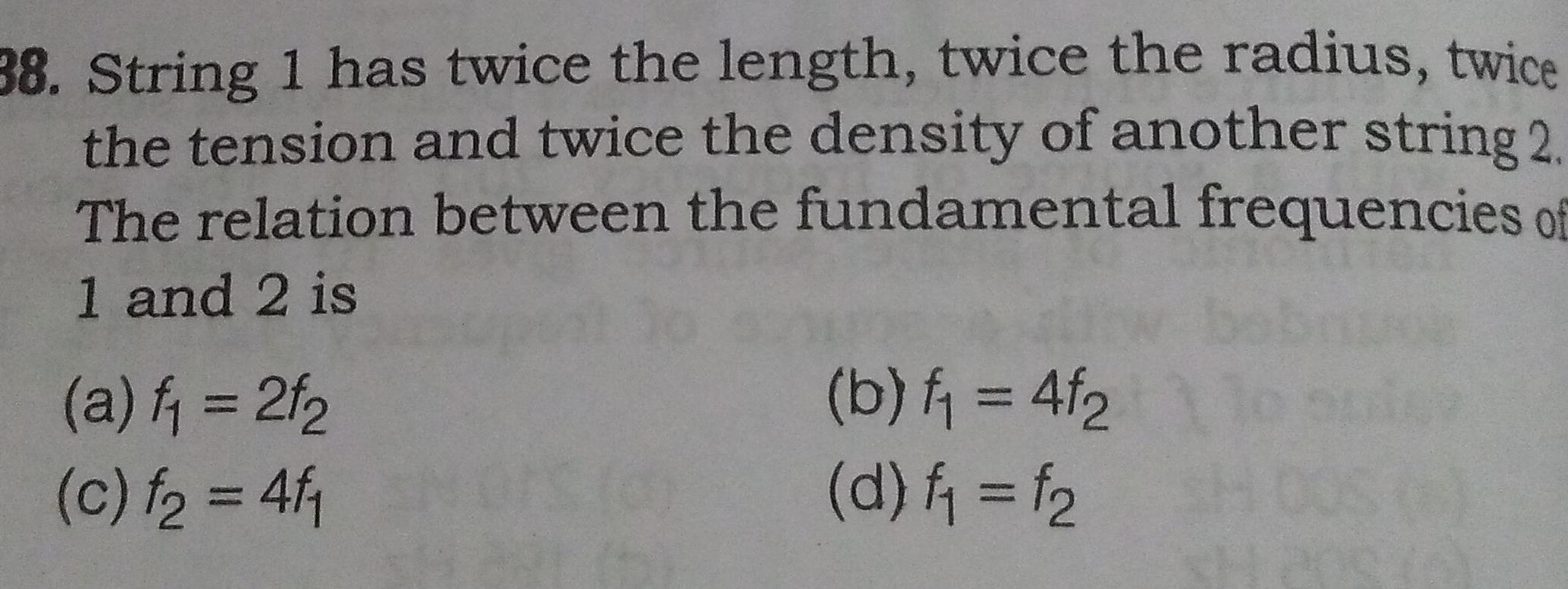
Physics
Simple harmonic motion38 String 1 has twice the length twice the radius twice the tension and twice the density of another string 2 The relation between the fundamental frequencies of 1 and 2 is a f 2f c f 4f b f 4f d f f

Physics
Simple harmonic motion18 A block with mass M rests on a frictionless surface and is connected to a horizontal spring of force constant k The other end of the spring is attached to a wall A second block with mass m rests on top of the first block The coefficient of static friction between the blocks is us a Find the maximum amplitude of oscillation such that the top block will not slip on the bottom block b Suppose the coefficient of kinetic friction between the table the block M is nonzero Mk If after 10 oscillations the amplitude decreases by 50 then what is the relation between uk and the rest of the problem e g M and k