Matrices & Determinants Questions and Answers

Algebra
Matrices & DeterminantsA 100 kg gilt (young female pig) gaining 350 grams of weight per day requires a diet containing 0.69% lysine. If you are formulating a diet using corn (0.3% lysine) and soybean meal (2.7% lysine), how many kilograms of each should be mixed together in order to get a 100 kg mixture that meets the lysine requirement? Setup a system of equations and solve. Label your answers.
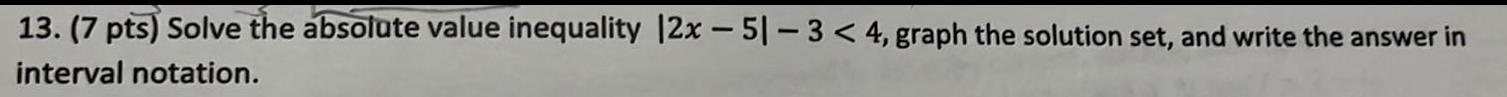
Algebra
Matrices & DeterminantsSolve the absolute value inequality |2x - 51-3 < 4, graph the solution set, and write the answer in interval notation.
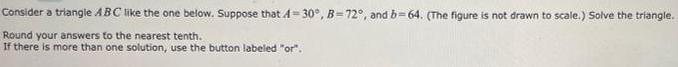
Algebra
Matrices & DeterminantsConsider a triangle ABC like the one below. Suppose that 4-30°, B-72°, and b=64. (The figure is not drawn to scale.) Solve the triangle.
Round your answers to the nearest tenth.
If there is more than one solution, use the button labeled "or".

Algebra
Matrices & DeterminantsSuppose that the following system of inequalities represents the constraints in a linear programming application. Graph the feasible region on paper, then
answer the questions that follow.
9x-3y 27
-3x+6y≤ 36
x≥0
y≥0
List the corner points of the feasible region:
Now, suppose that the following function is the objective function corresponding to the constraints listed above.
z = -3x+8y.
Test the corner points to find minimum value of the objective function:
• The "winning" corner point is
• The minimum value of the objective function is

Algebra
Matrices & DeterminantsLet T: R² → R² be a linear transformation such that T(x₁, x₂) = (x₁ + x₂, 4x₁ + 5x₂).
Find x such that T(x) = (3,8).

Algebra
Matrices & DeterminantsSketch the three planes and comment on the existence of the solution System of linear equations.
-2x - 3y + 2z = 3
3x + 2y - z = 2
2x + 3y - 2z = 4
Algebra
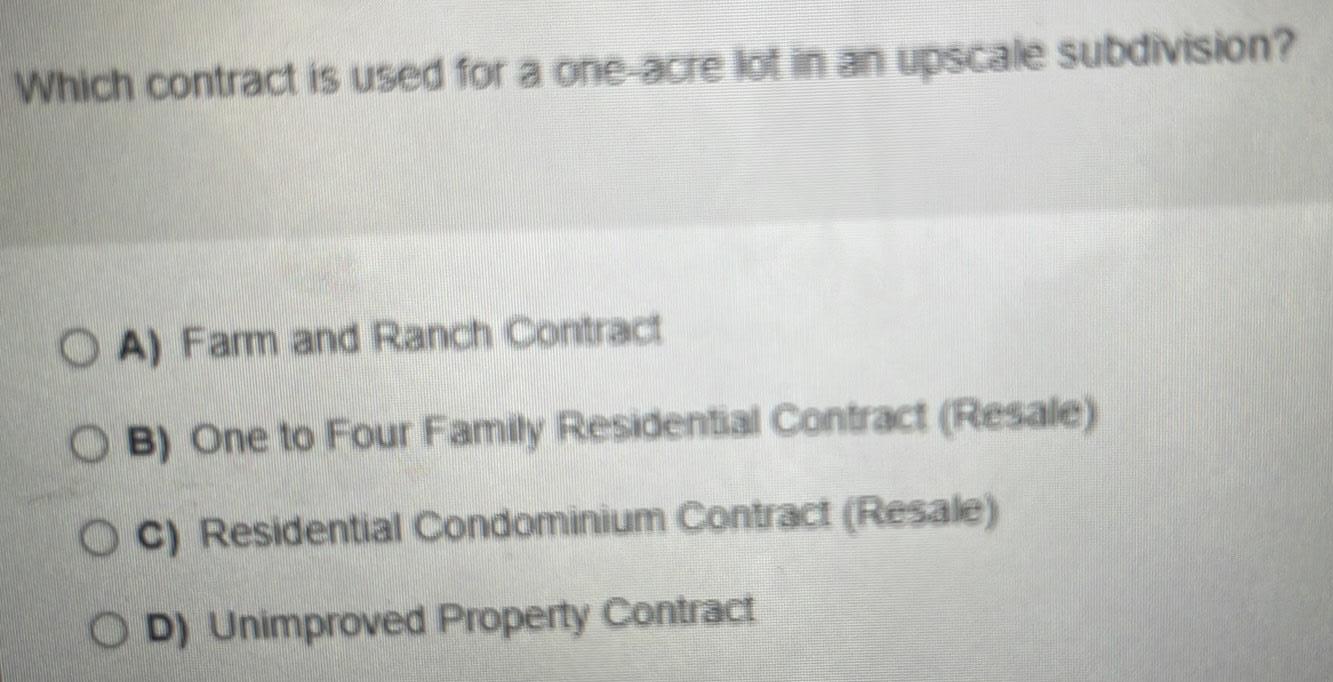
Matrices & DeterminantsWhich contract is used for a one-acre lot in an upscale subdivision?
A) Farm and Ranch Contract
B) One to Four Family Residential Contract (Resale)
C) Residential Condominium Contract (Resale)
D) Unimproved Property Contract
Algebra
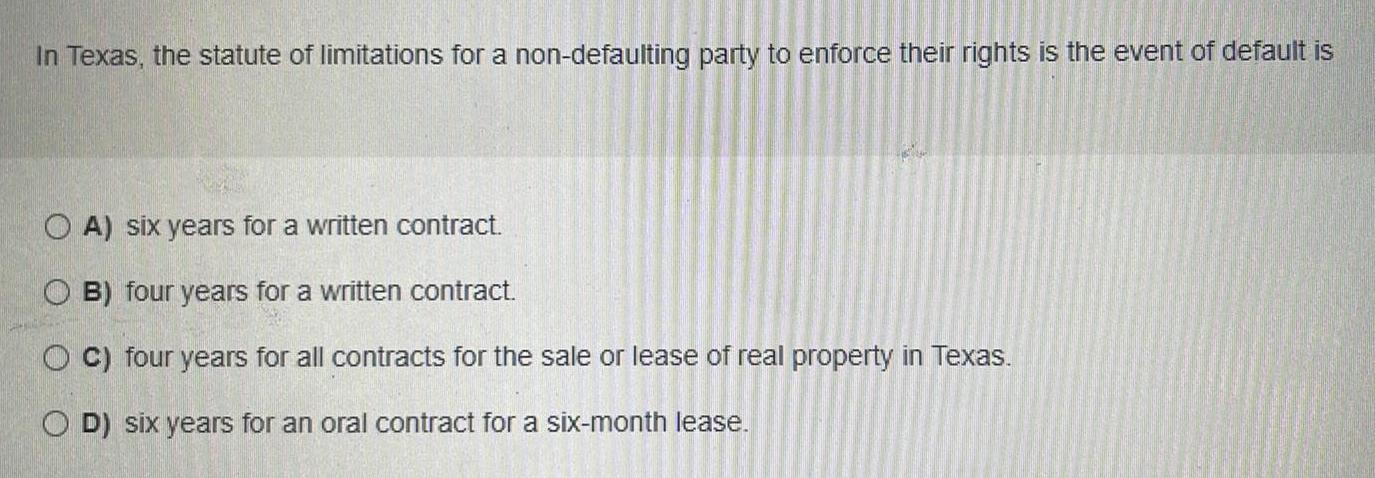
Matrices & DeterminantsIn Texas, the statute of limitations for a non-defaulting party to enforce their rights is the event of default is
A) six years for a written contract.
B) four years for a written contract.
C) four years for all contracts for the sale or lease of real property in Texas.
D) six years for an oral contract for a six-month lease.
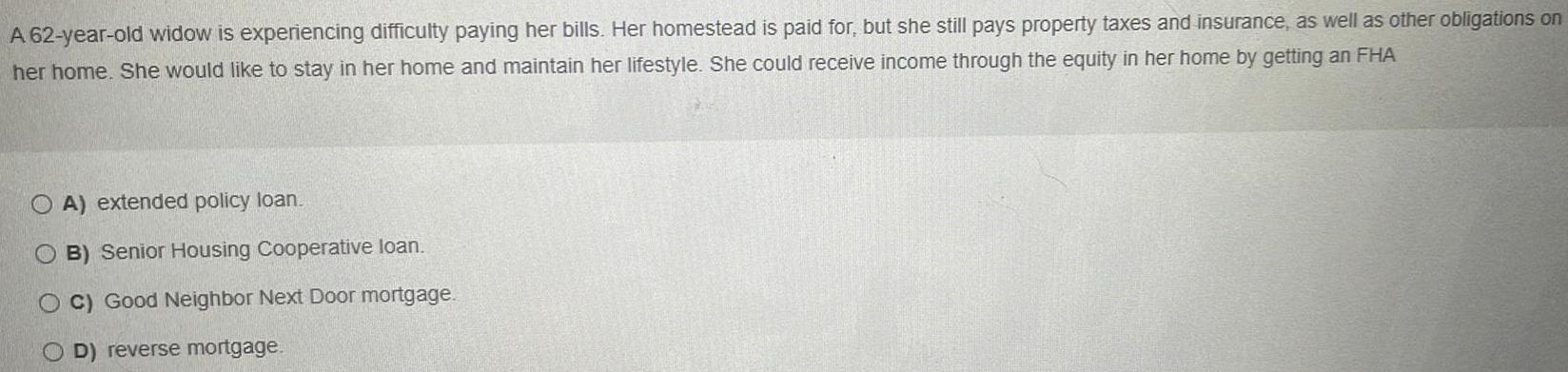
Algebra
Matrices & DeterminantsA 62-year-old widow is experiencing difficulty paying her bills. Her homestead is paid for, but she still pays property taxes and insurance, as well as other obligations on her home. She would like to stay in her home and maintain her lifestyle. She could receive income through the equity in her home by getting an FHA
A) extended policy loan.
B) Senior Housing Cooperative loan.
C) Good Neighbor Next Door mortgage.
D) reverse mortgage.
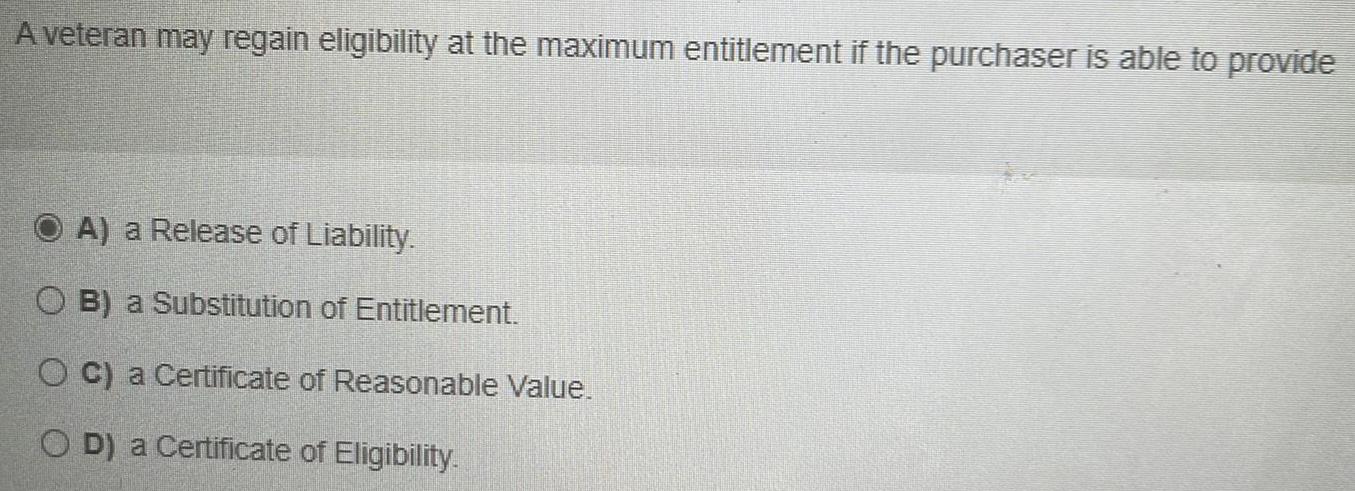
Algebra
Matrices & DeterminantsA veteran may regain eligibility at the maximum entitlement if the purchaser is able to provide
A) a Release of Liability.
B) a Substitution of Entitlement.
C) a Certificate of Reasonable Value.
D) a Certificate of Eligibility.

Algebra
Matrices & DeterminantsAn aeroplane moves forward in x, sideways in y and upwards in z. Pitch is the rotation around its y-axis. Derive the rotation matrix that describes the typical 30° upward pitch of a glider being launched by a winch..
![3.) Which of the following statements accurately describes the system represented by the matrix [ 12-73016 -20004]?
A) The system has one solution.
B) The system has infinitely many solutions.
C) The number of systems cannot be determined.
D) The system has no solution](https://media.kunduz.com/media/sug-question/raw/84390830-1657362369.0611138.jpeg?w=256)
Algebra
Matrices & Determinants3.) Which of the following statements accurately describes the system represented by the matrix [ 12-73016 -20004]?
A) The system has one solution.
B) The system has infinitely many solutions.
C) The number of systems cannot be determined.
D) The system has no solution
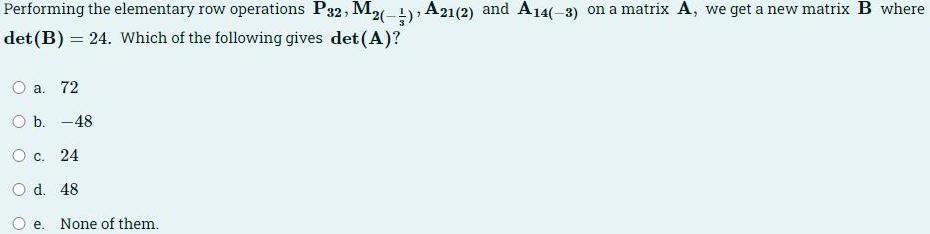
Algebra
Matrices & DeterminantsPerforming the elementary row operations P32, M₂(-) A21(2) and A14(-3) on a matrix A, we get a new matrix B where det (B) = 24. Which of the following gives det(A)?
a. 72
b. -48
c. 24
d. 48
e. None of them.
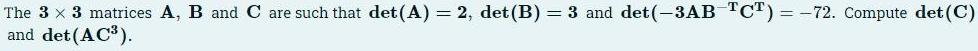
Algebra
Matrices & DeterminantsThe 3 × 3 matrices A, B and C are such that det(A) = 2, det (B) = 3 and det(-3AB -TCT) = -72. Compute det (C) and det (AC³).

Algebra
Matrices & DeterminantsIn triangle RST, angle S is a right angle, RS = 24 and cos R = 12/13. Find the value of cos T.
Select one:
a. 12/5
b. 13/5
c. 5/13
d. 12/13

Algebra
Matrices & DeterminantsThe linear system
mx + 3y - z = m
2x -z = 1
-2x - 3y + mz = 0
is inconsistent for m = 0.
True
False

Algebra
Matrices & DeterminantsFind the domain of the function.
f(x) =10/x+8
What is the domain of f?
A. (-∞,∞)
B. (-∞, -8)U(-8,0)U(0,∞)
C. (-∞0,0)U(0,∞)
D. (-∞, -8)U(-8,∞)

Algebra
Matrices & DeterminantsThe number of cans of soft drinks sold in a machine each week is recorded below. Develop forecasts using Exponential Smoothing with a alpha value of 0.30. FI-338.
338, 219, 276, 265, 314, 323, 299, 257, 287, 302
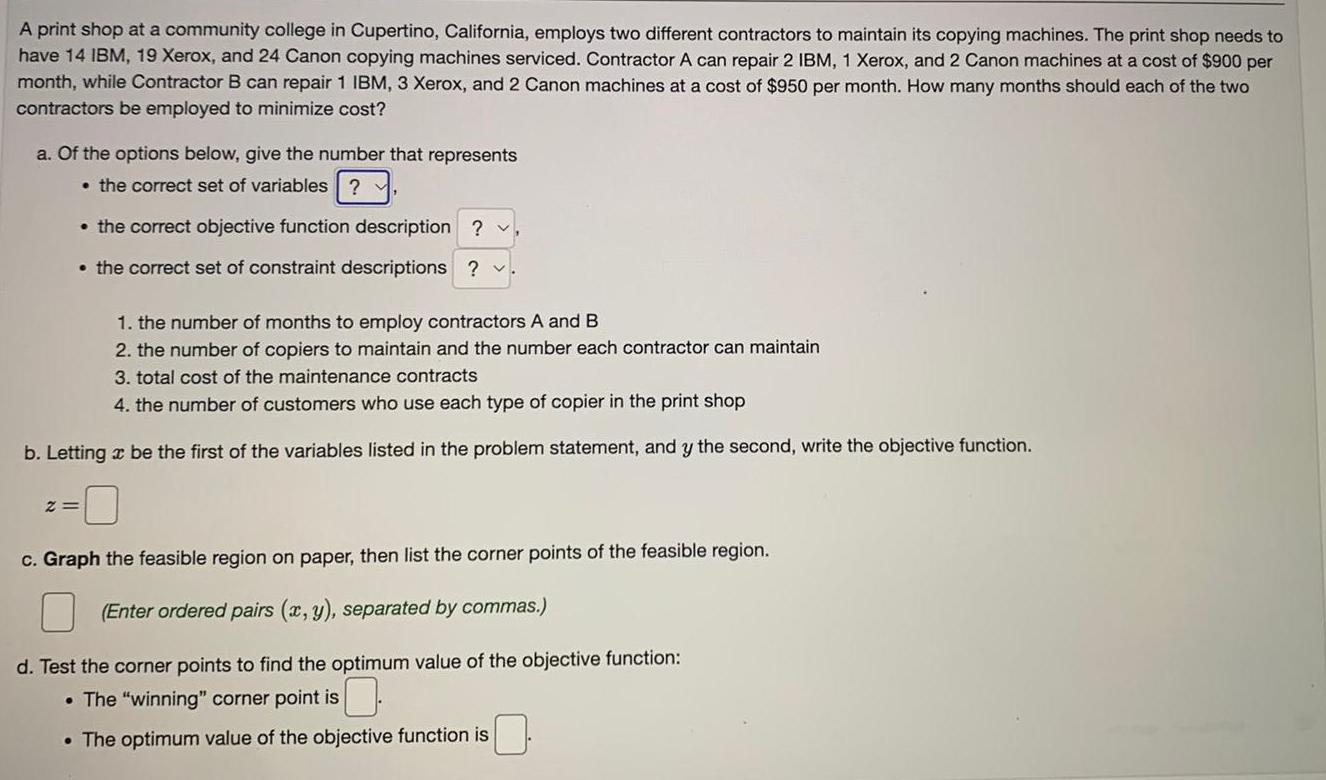
Algebra
Matrices & DeterminantsA print shop at a community college in Cupertino, California, employs two different contractors to maintain its copying machines. The print shop needs to have 14 IBM, 19 Xerox, and 24 Canon copying machines serviced. Contractor A can repair 2 IBM, 1 Xerox, and 2 Canon machines at a cost of $900 per month, while Contractor B can repair 1 IBM, 3 Xerox, and 2 Canon machines at a cost of $950 per month. How many months should each of the two contractors be employed to minimize cost?

Algebra
Matrices & DeterminantsIf A is a 5 x 7 matrix with rank 3, which one of the following statements is true:
A) The column space of A has dimension 2.
B) The row space of A has dimension 4.
C) The null space of A has dimension 4.
D) Ax = 0 has only the trivial solution.
E) A-¹ can be written as a multiplication of elementary matrices.
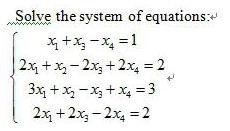
Algebra
Matrices & DeterminantsSolve the system of equations:
x₁+x3-x4 = 1
2x₁ + x₂ - 2x3+2x4 = 2
3x1 + x₂-x3+ x4 = 3
2x1 + 2x3 - 2x₂ = 2

Algebra
Matrices & DeterminantsConsider the following reduced matrix. This matrix represents a solution to a system of linear equations. What is the x, y, and z values for this solution?
1 0 0 7
0 1 2 1
0 0 0 0
x=7
y = 1-2t
z = t for any t
x = 7
y=2
2=0
No solution
x = 2
y = 1
z=0
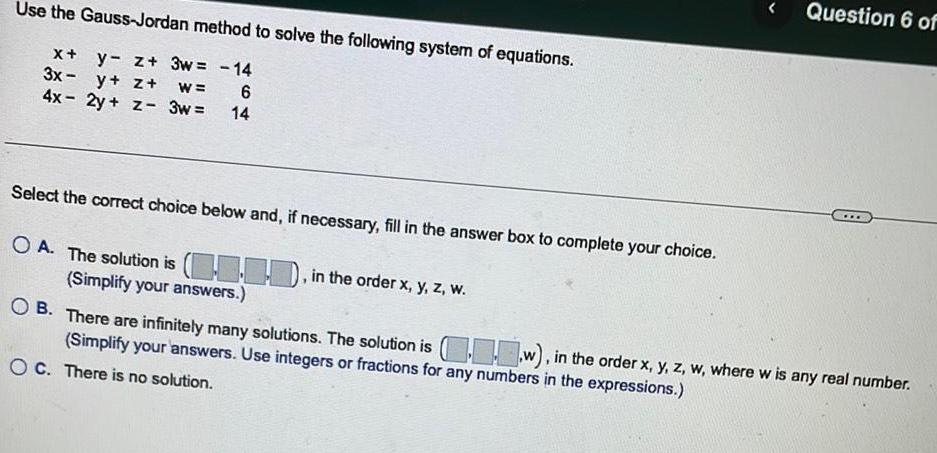
Algebra
Matrices & DeterminantsUse the Gauss-Jordan method to solve the following system of equations.
x+y- z+ 3w= -14
3x-y+z+w = 6
4x - 2y + z- 3w= 14
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution is ..., in the order x, y, z, w.
B. There are infinitely many solutions. The solution is (...w), in the order x, y, z, w, where w is any real number.
(Simplify your answers. Use integers or fractions for any numbers in the expressions.)
C. There is no solution.
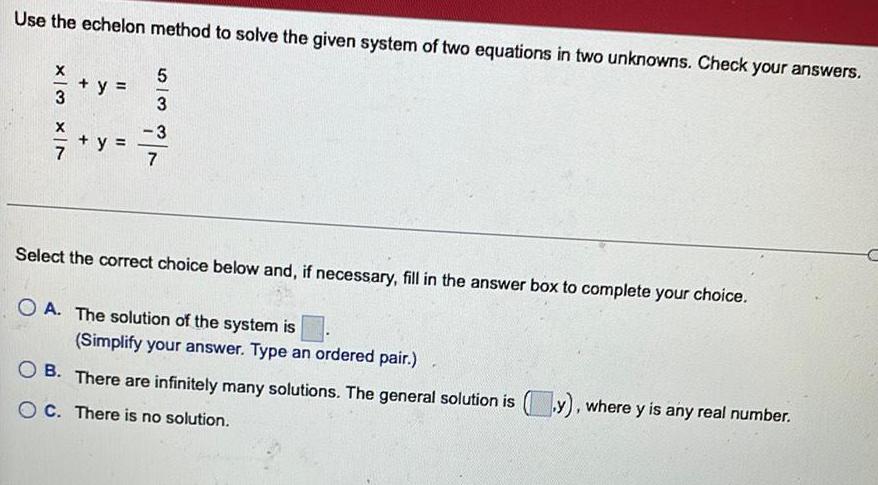
Algebra
Matrices & DeterminantsUse the echelon method to solve the given system of two equations in two unknowns. Check your answers.
X/3 + y = 5/3
x/7 + y =-3/7
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution of the system is
(Simplify your answer. Type an ordered pair.)
B. There are infinitely many solutions. The general solution is y), where y is any real number.
OC. There is no solution.

Algebra
Matrices & DeterminantsA plane traveled 4760 miles with the wind in 8.5 hours and 4420 miles against the wind in the same amount of time. Find the speed of the plane in still air and the speed of the wind.

Algebra
Matrices & DeterminantsAt a concession stand, five hot dog(s) and four hamburger(s) cost $14.50; four hot dog(s) and five hamburger(s) cost $14.75. Find the cost of one hot dog and the cost of one hamburger.
What is the cost of one hot dog?

Algebra
Matrices & DeterminantsFind all subsets of the set
S = {(1, 0), (0, 1), (-1,-1)}
that form a basis for R2. (Select all that apply.)
{(0, 1))
{(1, 0), (0, 1), (-1, -1)}
{(1, 0), (0, 1)}
((-1,-1)}
{(1, 0), (-1, -1)}
{(0, 1), (-1, -1)}
{(1, 0))

Algebra
Matrices & DeterminantsSketch a right triangle with θ as the measure of one acute angle. Find the other five trigonometric ratios of θ.
sin θ = 5/7
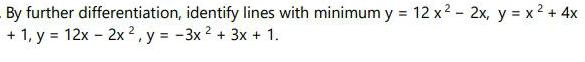
Algebra
Matrices & DeterminantsBy further differentiation, identify lines with minimum y = 12 x² - 2x, y = x² + 4x + 1, y = 12x - 2x2, y = -3x² + 3x + 1.

Algebra
Matrices & DeterminantsUse a graphing calculator to find the values of cosine and sine of each angle. Round your answers to the nearest hundredth.
a. -95⁰
b. 154⁰

Algebra
Matrices & DeterminantsA sports drink was offered for sale at $3.95 at Feng's Store. At Abreu Menezes' Store, the regular
selling price of a similar sports drink was $4.35.
What rate of markdown would Abreu Menezes' Store have to offer to sell the drink at the same
price as Feng's Store?
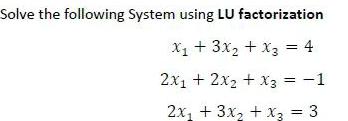
Algebra
Matrices & DeterminantsSolve the following System using LU factorization
x₁ + 3x₂ + x3 = 4
2x₁ + 2x₂ + x3 = -1
2x₁ + 3x₂ + x3 = 3

Algebra
Matrices & DeterminantsSolve the following System using x=A¹ b
X₁ + 3x₂ + x3 = 4
2x₁ + 2x₂ + x3 = -1
2x₁ + 3x2 + x3 = 3

Algebra
Matrices & DeterminantsFind a basis for the kernel of the linear operator:
T(x, y) = (3x-y, -12x + 4y)
NOTE: Using the parameter t, complete the following solution.

Algebra
Matrices & DeterminantsUse a system of three equations in three variaties to solve the problem,
A woman invested a $23,000 rollover IRA account in three banks paying 5%, 0%, and 7% annual interest. She invested $1.000 more at 6s than a The Smal
interest she earned was 11,486. How much did she invest at each rate?
amount invested at 5% $
amount invested at 6%
amount invested at 7
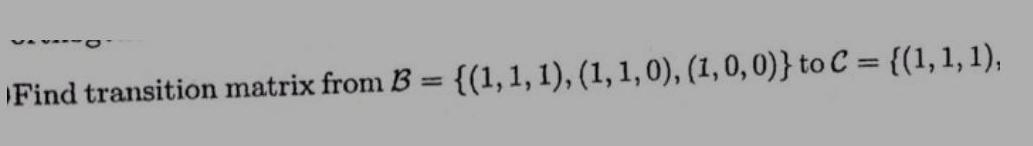
Algebra
Matrices & DeterminantsFind transition matrix from B = {(1, 1, 1), (1, 1, 0), (1, 0, 0)} to C = {(1, 1, 1),

Algebra
Matrices & DeterminantsRecall that Rm denotes the set of all m x n matrices with real number entries.
How many of the following assertions are correct?
(i) In a product of matrices AB the matrix B maps rows of A to rows of AB.
(ii) In a product of matrices AB rows of A are multiplied by columns of B.
(iii) A matrix A of size m x n maps n-columns x to m-columns Ax.
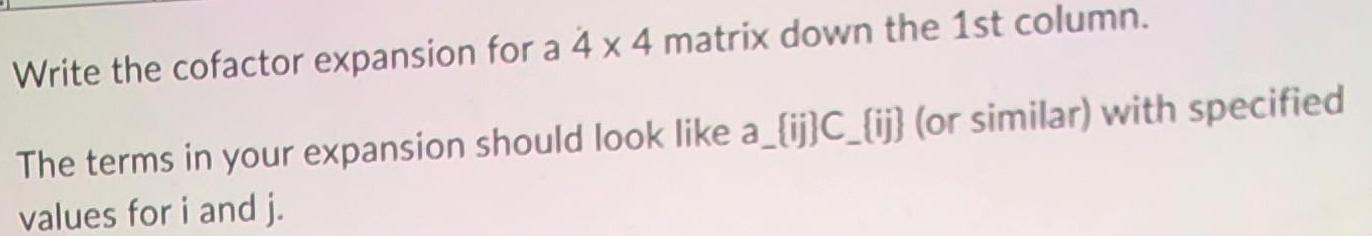
Algebra
Matrices & DeterminantsWrite the cofactor expansion for a 4 x 4 matrix down the 1st column.
The terms in your expansion should look like a_{ij}C_{ij} (or similar) with specified
values for i and j.

Algebra
Matrices & DeterminantsFind the dimension and a basis for the solution space. (If an answer does not exist, enter DNE for the dimension and in any cell of the vector.)
x₁ + x2 - 4x3 = 7
2x13x₂ + 2x3 = 19

Algebra
Matrices & DeterminantsConsider the line parameterized by x=5-2t, y = 3+ 8t, z= 10t. Find an equation of a plane so that the plane is perpendicular to the line and through the point (4, 3, 3).

Algebra
Matrices & DeterminantsSolve the linear equation system, find its particular solution and the fundamental solution of its corresponding homogeneous linear system. Find the general solution.
2x14x2 + 5x3 + 3x4 = 1
3x16x2 + 4x3 + 2x4 = 3
4x18x2 + 17x3 + 11x4 = -1

Algebra
Matrices & DeterminantsA building that is the nearest 50.65 feet. tall has a shadow 55.48 feet long. Find the angle of the Sun to the Sen elevation of hundreth of a degree.

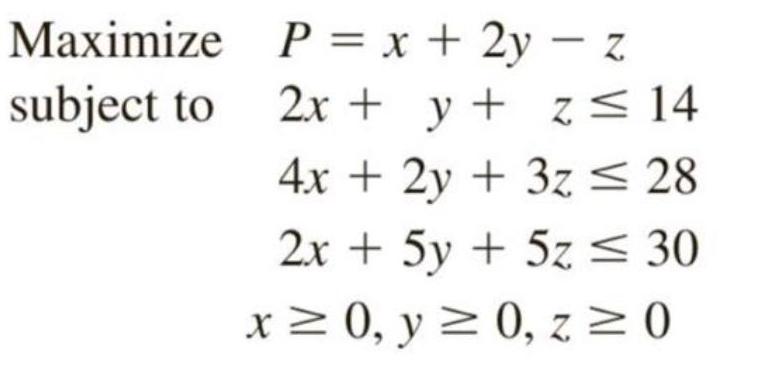
Algebra
Matrices & DeterminantsMaximize P = x + 2y - z
subject to
2x + y + z ≤ 14
4x + 2y + 3z ≤ 28
2x + 5y + 5z ≤ 30
x ≥ 0, y ≥ 0, z ≥ 0
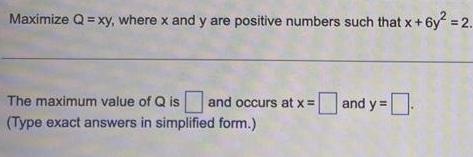
Algebra
Matrices & DeterminantsMaximize Q = xy, where x and y are positive numbers such that x+6y² = 2.

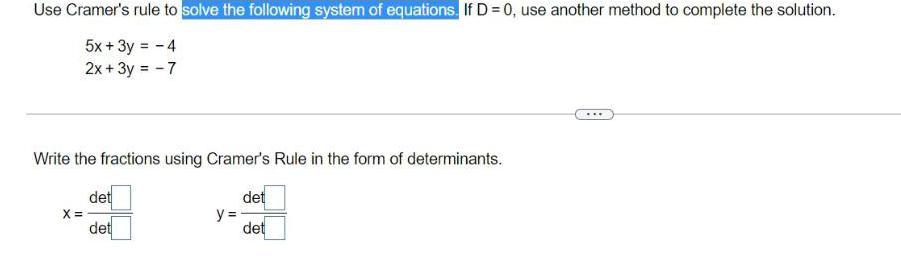
Algebra
Matrices & DeterminantsUse Cramer's rule to solve the following system of equations. If D = 0, use another method to complete the solution.
5x + 3y = - 4
2x + 3y = -7
Write the fractions using Cramer's Rule in the form of determinants.
det
det
det
det
X =
y =
***

Algebra
Matrices & DeterminantsDetermine whether the statement is true or false.
x + 2 is a factor of P(x) = x³ + 2x² - x - 2.

Algebra
Matrices & DeterminantsLet A = 1 -2 Q = 1/√2 -1/√2
1 4 1/√2 1/√2
We obtained the column vectors of Q by applying the Gram-Schmidt process to the column vectors of A.
Find a QR-decomposition of the matrix A.
NOTE: Enter exact answers.
Q=
R=

Algebra
Matrices & DeterminantsThe matrix A= 1 -1
1 1
defines a transformation of R². Select all true statements about this transformation. A
A rotates every vector by 45° anti-clockwise.
A halves the area. have an inverse?
A rotates every vector by 45° clockwise.
A stretches every vector by the same factor.
For which value or values of a does the matrix
A= x -x
-x x
○ x = -1,0,1
O No values of a
O x = 0
O x = = 1