Matrices & Determinants Questions and Answers

Algebra
Matrices & DeterminantsUse the inner product
< p,q>= p(-1)q(−1) +p(0)q(0) + p(3)q(3) in P₃ to find the orthogonal projection of p(x) = 4x² + 5x - 7 onto the line L spanned by q(x) = 4x²-3x - 2.
projL(p) =
![Given A= [-2 -3] and B= [5 2]
[5 2] [1 -1]
use the Frobenius inner product and the corresponding induced norm to determine the value of each of the following:
(A, B): =_____
||A||F= _________
||B||F= ___________-
θA,B=______radians.](https://media.kunduz.com/media/sug-question/raw/82955830-1658658117.9840238.jpeg?w=256)
Algebra
Matrices & DeterminantsGiven A= [-2 -3] and B= [5 2]
[5 2] [1 -1]
use the Frobenius inner product and the corresponding induced norm to determine the value of each of the following:
(A, B): =_____
||A||F= _________
||B||F= ___________-
θA,B=______radians.

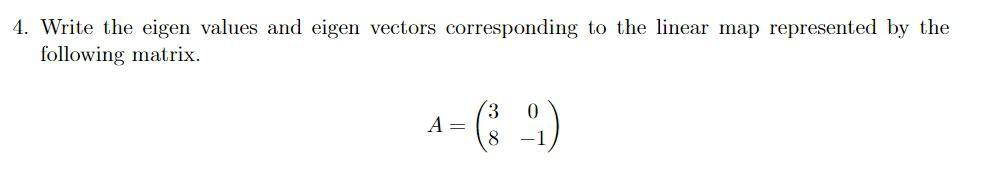
Algebra
Matrices & DeterminantsWrite the eigen values and eigen vectors corresponding to the linear map represented by the following matrix.
A = 3 0
8 -1

Algebra
Matrices & Determinants4. Determine whether the given matrix is invertible without computing its determinant.
-1 -3 0 1
3 5 8 -3
-2 -6 3 2
0 -1 2 1

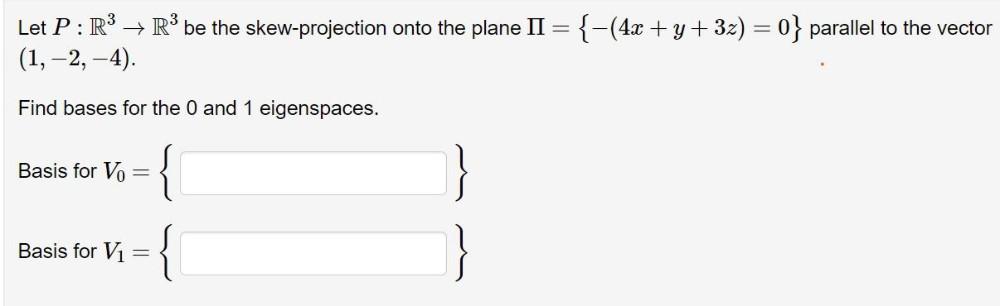
Algebra
Matrices & DeterminantsLet P : R³ → R³ be the skew-projection onto the plane II = {-(4x + y + 3z) = 0} parallel to the vector (1, −2, –4).
Find bases for the 0 and 1 eigenspaces.
Basis for V0=
Basis for V₁=
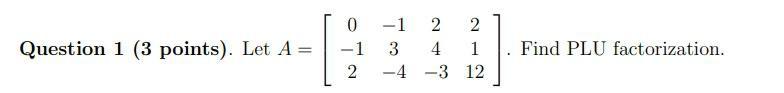

Algebra
Matrices & DeterminantsUse Gauss Jordan to find the solution of system of Linear equations. Use elementary row operations in your solution.
x -2y+ z = -1
x + 3z=-11
-4x + 7y + 4z = 3

Algebra
Matrices & DeterminantsConsider
3x + 3y + 3z=- 3k²
4y + 8z= -4
x + 4y +7z = 4k
a) Using Gaussian elimination method find all value(s) of k such that the system becomes consistent.
b) Using part (a), write down the solution(s) of the system if k = -1.

Algebra
Matrices & Determinants3) Find the values of x and y using pseudoinverse.
X + 3y =17
5x + 7y =19
11x + 13y =23
Algebra
Matrices & DeterminantsPlot the ordered pair (1,-1). State in which quadrant or on which axis the point lies.
Plot the ordered pair on the graph to the right.
In which quadrant, or on which axis, does the point lie?
I
III
II
on the x-axis
on the y-axis
IV
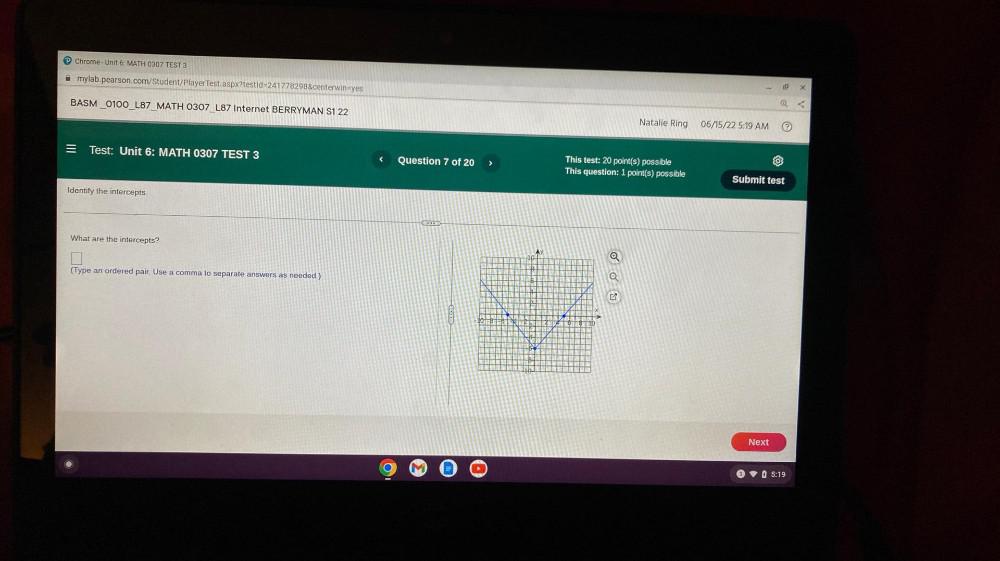
Algebra
Matrices & DeterminantsIdentify the intercepts.
What are the intercepts?
(Type an ordered pair. Use a comma to separate answers as needed.)
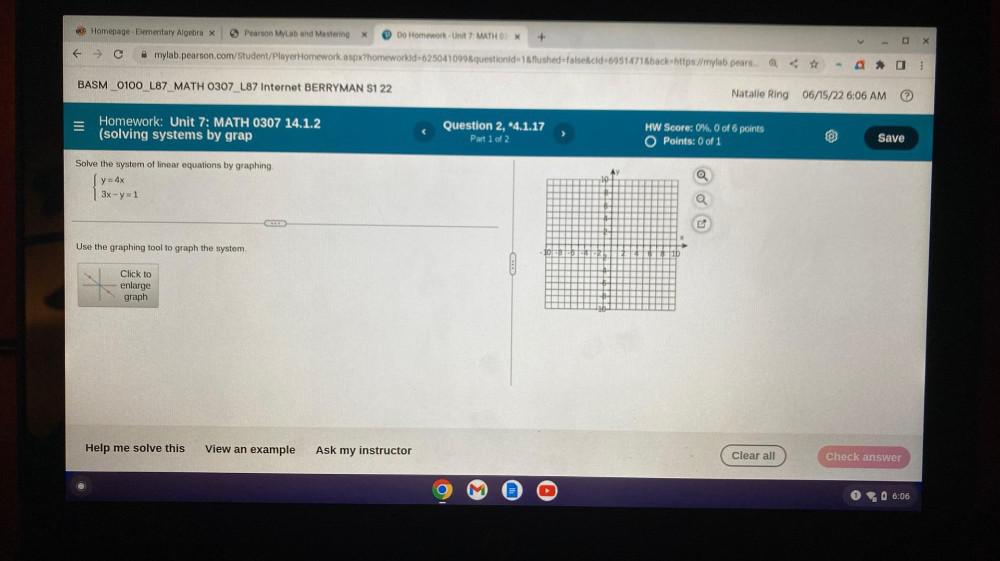
Algebra
Matrices & DeterminantsSolve the system of linear equations by graphing.
y = 4x
3x-y=1
Use the graphing tool to graph the system.
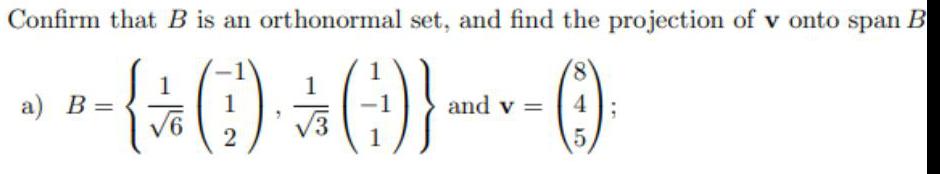
Algebra
Matrices & DeterminantsConfirm that B is an orthonormal set, and find the projection of v onto span B
B= 1/√6 -1 , 1/√3 1 and v= 8
1 -1 4
2 1 5
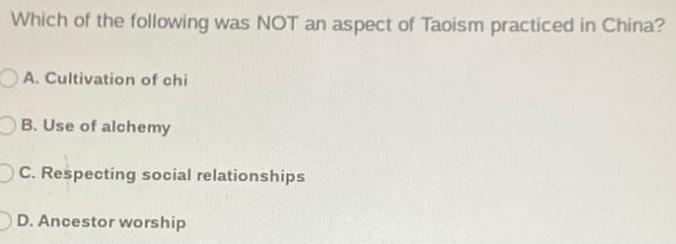
Algebra
Matrices & DeterminantsWhich of the following was NOT an aspect of Taoism practiced in China?
A. Cultivation of chi
B. Use of alchemy
C. Respecting social relationships
D. Ancestor worship

![3. Complete the following questions using the following planes T₁: 2x + 4y-6z -2 = 0 T₂: 7x+14y-21z-7=0 R3: 4x+8y-11z +5=0 a) Determine the normal vectors for each of the three planes [1K] b) Are any of the planes parallel? Show your work (If yes, determine the scalar multiple. If no, show that they are not multiples) [27] c) Are the normals for the three planes coplanar? [2A]](https://media.kunduz.com/media/sug-question/raw/84622471-1658606070.7671928.jpeg?w=256)
Algebra
Matrices & Determinants3. Complete the following questions using the following planes T₁: 2x + 4y-6z -2 = 0 T₂: 7x+14y-21z-7=0 R3: 4x+8y-11z +5=0 a) Determine the normal vectors for each of the three planes [1K] b) Are any of the planes parallel? Show your work (If yes, determine the scalar multiple. If no, show that they are not multiples) [27] c) Are the normals for the three planes coplanar? [2A]

Algebra
Matrices & DeterminantsFind the 3x3 matrix that produces the described composite 2D transformation below, using homogeneous coordinates. Rotate points through 45° about the point (6,9).

Algebra
Matrices & DeterminantsConsider T(x,y) = (2x-y, -4x+2y), is T invertible? Why or why not? If so, compute the inverse, T-1, and compute the image of 8 under the inverse map. ie. Compute T^-1

Algebra
Matrices & Determinants6-Which of the following statements is true
(a) det A = det A-¹
(b)det(A + B)=det(A)+det(B)
![Perform the indicated operation, if possible.
[4 8 5 -9 + [ 7 1 -11 3
6 -1 12 1] - 3 8-10 9]
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The resulting matrix is
B. The matrices cannot be added.](https://media.kunduz.com/media/sug-question/raw/84585210-1658592239.298367.jpeg?w=256)
Algebra
Matrices & DeterminantsPerform the indicated operation, if possible.
[4 8 5 -9 + [ 7 1 -11 3
6 -1 12 1] - 3 8-10 9]
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The resulting matrix is
B. The matrices cannot be added.
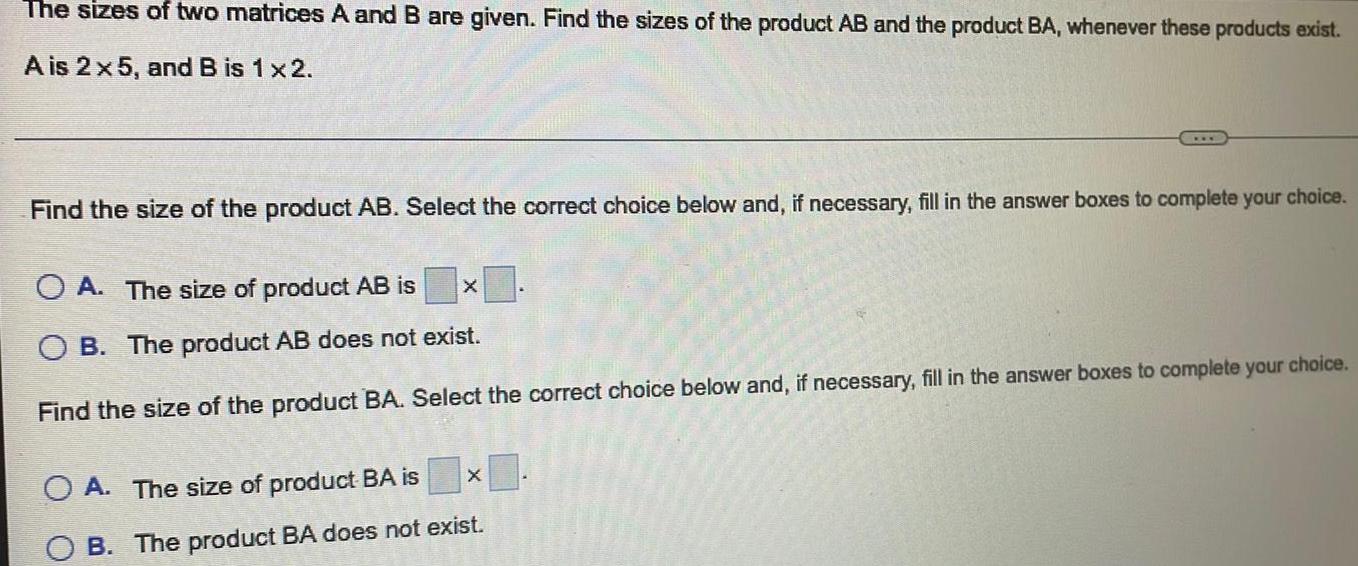
Algebra
Matrices & DeterminantsThe sizes of two matrices A and B are given. Find the sizes of the product AB and the product BA, whenever these products exist.
A is 2 x 5, and B is 1 x 2.
Find the size of the product AB. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The size of product AB is
B. The product AB does not exist.
Find the size of the product BA. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The size of product BA is
B. The product BA does not exist.
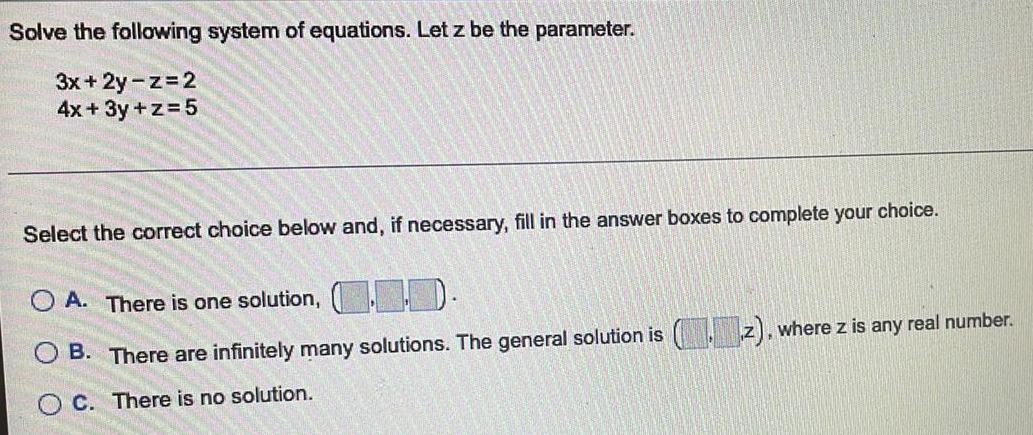
Algebra
Matrices & DeterminantsSolve the following system of equations. Let z be the parameter.
3x+2y-z=2
4x + 3y +z = 5
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. There is one solution, ..
B. There are infinitely many solutions. The general solution is (z), where z is any real number.
C. There is no solution.
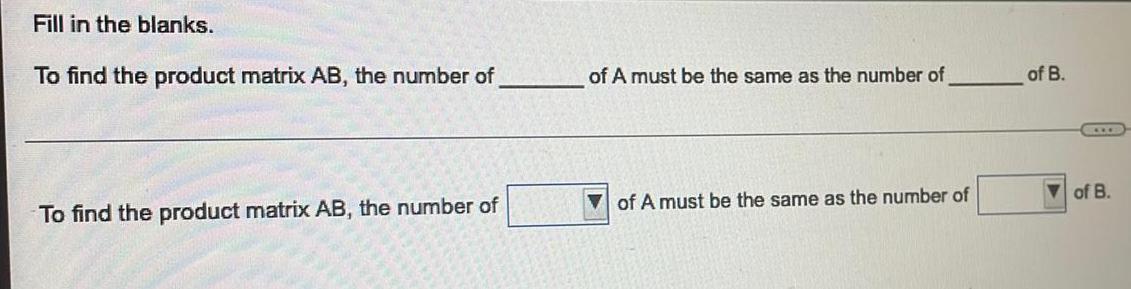
Algebra
Matrices & DeterminantsTo find the product matrix AB, the number of of A must be the same as the number of of B.
To find the product matrix AB, the number of of A must be the same as the number of of B.
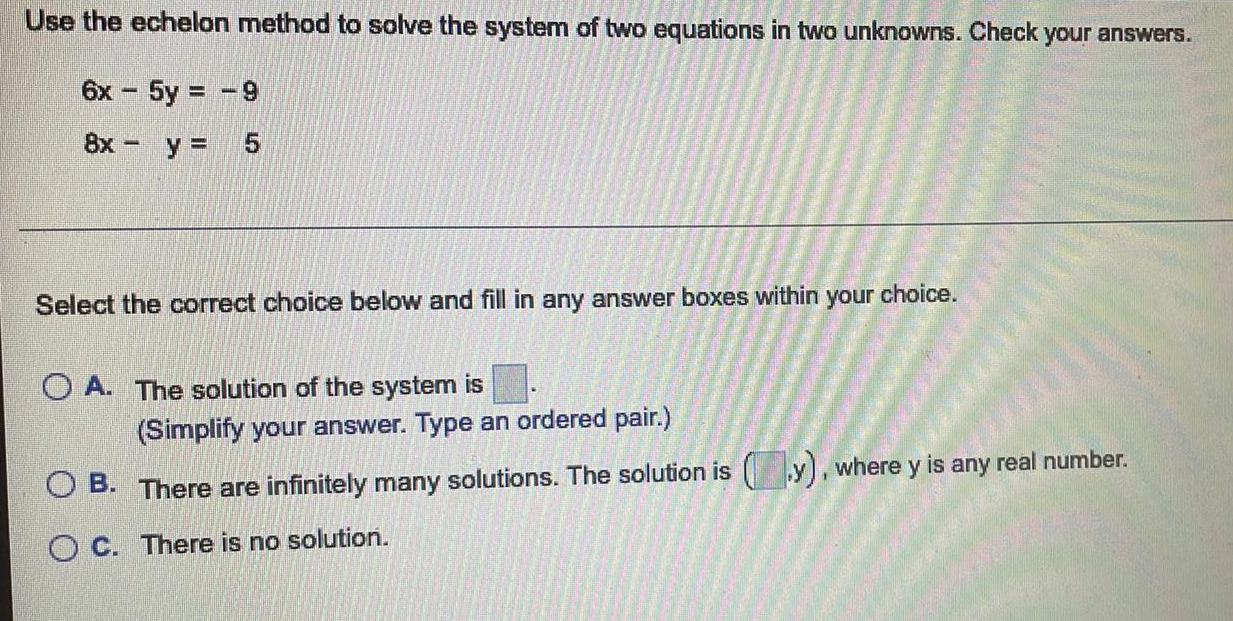
Algebra
Matrices & DeterminantsUse the echelon method to solve the system of two equations in two unknowns. Check your answers.
6x - 5y = -9
8x - y = 5
Select the correct choice below and fill in any answer boxes within
A. The solution of the system is
B. There are infinitely many solutions. The solution is (y), where y is any real number.
C. There is no solution.
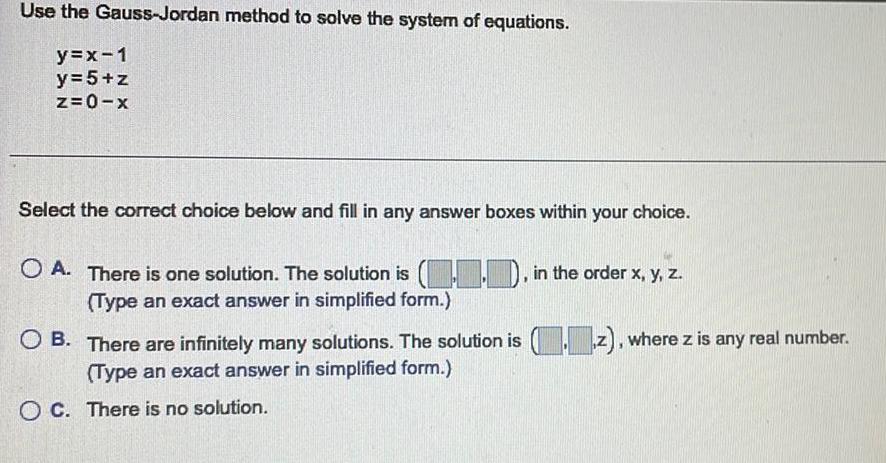
Algebra
Matrices & DeterminantsUse the Gauss-Jordan method to solve the system of equations.
y=x-1
y=5+z
z=0-x
Select the correct choice below and fill in any answer boxes within your choice.
A. There is one solution. The solution is (..), in the order x, y, z.
B. There are infinitely many solutions. The solution is z), where z is any real number.
C. There is no solution.

Algebra
Matrices & DeterminantsFill in the blank with the correct answer that completes the following sentence.
on a matrix correspond to transformations of a system of equations.
on a matrix correspond to transformations of a system of equations.

Algebra
Matrices & DeterminantsSolve the following equations:
a) tan (x-72) = -1 on the interval (-∞,∞).
b) 2cos (x/3) + 1 = 0 on the interval [0,27).
c) 2cos^2(x) -3cos(x) +1 = 0 on the interval
[0,2π)
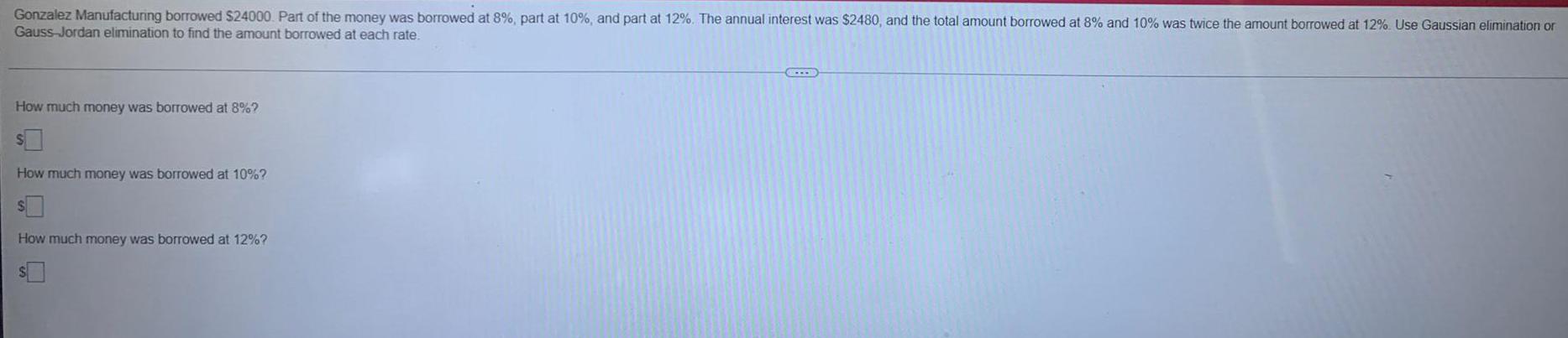
Algebra
Matrices & DeterminantsGonzalez Manufacturing borrowed $24000. Part of the money was borrowed at 8%, part at 10%, and part at 12%. The annual interest was $2480, and the total amount borrowed at 8% and 10% was twice the amount borrowed at 12%. Use Gaussian elimination or Gauss-Jordan elimination to find the amount borrowed at each rate.
How much money was borrowed at 8%?
How much money was borrowed at 10%?
How much money was borrowed at 12%?
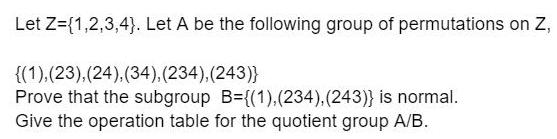
Algebra
Matrices & DeterminantsLet Z={1,2,3,4}. Let A be the following group of permutations on Z,
{(1), (23),(24),(34),(234),(243)}
Prove that the subgroup B={(1), (234), (243)} is normal.
Give the operation table for the quotient group A/B.

Algebra
Matrices & DeterminantsSuppose v₁, v2, v3 is an orthogonal set of vectors in R5. Let w be a vector in Span(v₁, v₂, v3) such that
v₁.v₁ = 18, v₂.v2=131, v3.v3=16,
w.v₁ 90, w.v₂=524, w.v3=-32,
then w= v₁+ V₂+ v3.
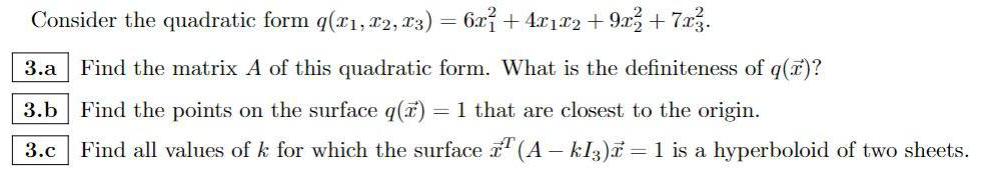
Algebra
Matrices & DeterminantsConsider the quadratic form q(x₁, x2, x3) = 6x1² + 4x1x2 +9x2² + 7x3².
3.a Find the matrix A of this quadratic form. What is the definiteness of q(x)?
3.b Find the points on the surface q(x) =1 that are closest to the origin.
3.c Find all values of k for which the surface x^T(A-kI3)x = 1 is a hyperboloid of two sheets.

Algebra
Matrices & DeterminantsMatrix A is singular. True or false?
A= 1 2 -1
2 -1 3
3 1 2
TRUE
FALSE

![Find a) the characteristic equation and (b) the eigenvalues and eigenvectors of A below, then decide whether or not A is diagonalizable. If not, explain why not.
A= [5 8 16]
[4 1 8]
[-4 -4 -11]](https://media.kunduz.com/media/sug-question/raw/84606293-1658498950.0623271.jpeg?w=256)
Algebra
Matrices & DeterminantsFind a) the characteristic equation and (b) the eigenvalues and eigenvectors of A below, then decide whether or not A is diagonalizable. If not, explain why not.
A= [5 8 16]
[4 1 8]
[-4 -4 -11]

Algebra
Matrices & DeterminantsWrite an augmented matrix for the following system of equations, and state the dimension of the augmented matrix.
3x-2y+3z = -1
3x-9y+7z = 7
9y-9z = -2
![The subset in the form [x y], where x and y are real numbers, is a subspace of R2 if
Select one:
x = 0 and y ≠ x.
None of these
x ∈ R and y ≤ 0.
x = -y and y ≥ 0.
x ≠ 0 and y ∈ R.](https://media.kunduz.com/media/sug-question/raw/84583631-1658340379.8743434.jpeg?w=256)
Algebra
Matrices & DeterminantsThe subset in the form [x y], where x and y are real numbers, is a subspace of R2 if
Select one:
x = 0 and y ≠ x.
None of these
x ∈ R and y ≤ 0.
x = -y and y ≥ 0.
x ≠ 0 and y ∈ R.

Algebra
Matrices & DeterminantsSolve the linear system by Gaussian elimination:
x- y + 2z - w = -1
2x - y-2z- 2w = -2
-x+2y-4z + w = 1
3x + 2aw = -3
Determine for which values of a the system is consistent, and if so whether the solution is unique.
Answer "inconclusive" if there is not enough information to make a decision.

Algebra
Matrices & DeterminantsProvide the missing information.
Explain the meaning of the notation R₂ = R3.

Algebra
Matrices & DeterminantsThe real zeros" can be described as follows (if the zero is not an integer, type the fraction form, not the decimal form
A real zero is Does the graph cross the x-axis or bounce off it at
this zero? Does the graph "flatten out" at this zero?
Another real zero is Does the graph cross the x-axis or bounce
off it at this zero? Does the graph "flatten out" at this zero?
Another real zero is Does the graph cross the x-axis or bounce
off it at this zero? Does the graph "flatten out" at this zero?

Algebra
Matrices & DeterminantsConstruct the equation of a 4th degree polynomial with real coefficients that has the following characteristics:
• the only zeros are 1/3, -4, and 2
• the graph should "bounce off" the x-axis at x = -4
• the y-intercept is (0, 32)
Please, you do not have to spend time multiplying out the polynomial. Factored form is completely acceptable.
![Question 1 [20 pts] Let W be the set of polynomials of the form
at² + b²t + c².
a) Does p(t) = t² + 4t - 4 belongs to W?
b) Is W a subspace of P2?](https://media.kunduz.com/media/sug-question/raw/84578700-1658331644.5581686.jpeg?w=256)
Algebra
Matrices & DeterminantsQuestion 1 [20 pts] Let W be the set of polynomials of the form
at² + b²t + c².
a) Does p(t) = t² + 4t - 4 belongs to W?
b) Is W a subspace of P2?
![Question2: (20 points): Let v₁ = [2 -2] and v₂ = [3 -2] be two vectors in R2.
(a) [10 pts] Determine whether v = [2 -2] belongs to span {v₁, v₂}
(b) [10 pts] Determine whether (v₁, v₂} span R².](https://media.kunduz.com/media/sug-question/raw/84579353-1658331597.5721042.jpeg?w=256)
Algebra
Matrices & DeterminantsQuestion2: (20 points): Let v₁ = [2 -2] and v₂ = [3 -2] be two vectors in R2.
(a) [10 pts] Determine whether v = [2 -2] belongs to span {v₁, v₂}
(b) [10 pts] Determine whether (v₁, v₂} span R².

Algebra
Matrices & DeterminantsLet A and B be row-equivalent matrices.
(a) Show that the dimension of the column space of A is equal to the dimension of the column space of B.
(b) Are the column spaces of A and B necessarily the same? Justify your answer.

Algebra
Matrices & DeterminantsSolve the system of equation by the method of your choice. If the the system has a unique solution, type in that answer as an ordered triple. If the system is inconsistent or dependent, type in "no solution".
-2x - 5y + 4z = 21
-5x - 5y + z = 21
- 4y - 4z = 8.
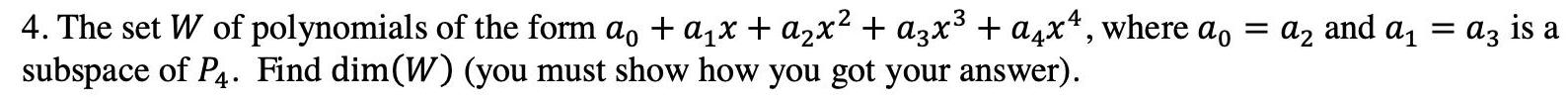
Algebra
Matrices & Determinants4. The set W of polynomials of the form a₁ + a₁x + a₂x² + α3x³ + α₁x4, where a = a₂ and a₁ = a3 is a
subspace of P4. Find dim(W) (you must show how you got your answer).

Algebra
Matrices & DeterminantsAlgebra
S = {(6,-7,8,6),(4,6,-4,1)}
(a) u = (-42,113,-112,-60)
check whether the set S is a basis or not
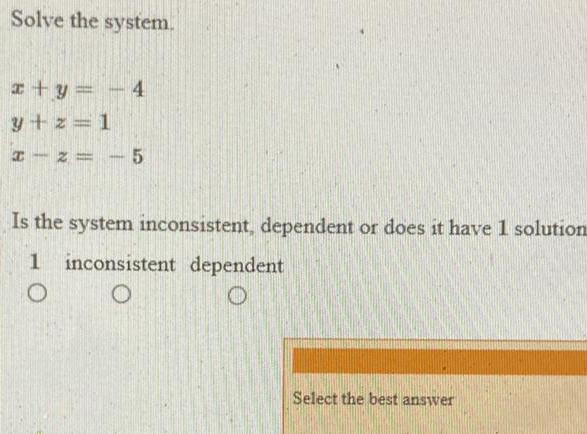
Algebra
Matrices & DeterminantsSolve the system.
x+y = -4
y+z=1
x-z = -5
Is the system inconsistent, dependent or does it have 1 solution
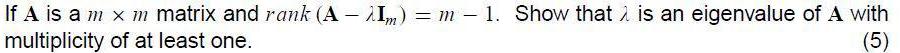
Algebra
Matrices & DeterminantsIf A is a m x m matrix and rank (A - Im) = m - 1. Show that is an eigenvalue of A with multiplicity of at least one.