Quadratic equations Questions and Answers

Algebra
Quadratic equationsEvaluate the determinants in Exercises 1 and 2 1 2 5 2 i 3 If A 82 cos 0 sin 0 4 iii 4 If A 0 1 8 If i 4 sin 0 cos e MATHEMATICS 6 IfA 2 5 Evaluate the determinants 3 1 2 i 0 0 1 3 5 0 A 6 2 X 2 18 X of be rep 004 1 0 2 1 0 3 2 3 0 1 1 54 9 7 Find values of x if 2 4 5 1 2 then show that 2A 4 A T 2 3 N 6 2x 4 4 X 6 2 18 6 ii then show that 3 A 27 A find A x x 1 x 1 B 6 11 Rationalised 2023 24 then x is equal to 2 iv 0 3 1 2 3 1 4 TK ber 5 1 2 2 1 3 5 0 4 3 Area of a Triangle In earlier classes we have studied that the area of 2 13 31 12 x x y 1 X 3 1 X Y x 1 x 35 2x 5 olished triangle whose vertices a x 3 x vz V x y x y and x y is given by the expression x3 Now this expression can be written in the form of a determinant as Remarks i Since area is a positive quantity we always take the absolute value of th 1

Algebra
Quadratic equations80 a31 a32 a 1 a 2 a33 a32 a 13 a22 a 1 a23 a 1 a32 a3 a A a 1 a 12 a33 a21 932 913 a23 a31 a12 a11 a22 a33 913 931 922 Expansion along first Column C By expanding along C we get A a 1 1 922 MATHEMATICS a11 912 a13 A a21 922 923 a31 a32 A33 iii Let A 923 a32 a33 t to me jepub 2 2 23 4 0 a12 a21 a33 a12 923 a31 and B 921 1 1 Rationalised 2023 24 1 20 a31 a 13 a 12 a13 931 1 1 922 923 a 1 a 2 a33 a23 a32 a21 a 12 a 33 a 3 a32 a31 a 12 a23 a13 a22 13 a22 a31 a 13 A a a22 a33 a 11 a23 a32 a21 a 12 a33 a31 a 13 a22 a 1 a 22 a33 a 11 a 23 a32 a 12 a21 A33 A 2 A23 A31 a 13 a21 a32 12 A 0 8 8 and B 0 2 2 Observe that A 4 2 2 B or A square matrices A and B 912 a13 a32 a33 1 24 3 0 4 1 0 a23 a11 a32 a13 a31922 3 Clearly values of A in 1 2 and 3 are equal It is left as an exercise to the reader to verify that the values of A by expanding along R C and C are equal to the value of A obtained in 1 2 or 3 Hence expanding a determinant along any row or column gives same value Remarks i For easier calculations we shall expand the determinant along that row or column which contains maximum number of zeros Example 3 Evaluate the determinant A 1 a13 a21 a32 a21 a 13 a32 ii While expanding instead of multiplying by 1 we can multiply 1 or 1 according as i j is even or odd 2 a31 a 12 a23 verify that A 2B Also In general if A kB where A and B are square matrices of order n then A k B where n 1 2 3 where n 2 is the order of

Algebra
Quadratic equationsand Now So II 1 i 18 3 7 21 25 21 25 4 3 22 M32 M 33 ON62 12 1 31 10 545 1 0 0 2 1 0 1 0 00 1 30 0 30 0 5 If A 21 14 5 19 a11 912 12 0 12 CERT 8 30 22 0 18 18 ii be requalis a 2 a 2 3 a 3 5 A 12 A2 22 A 18 12 13 31 a 1 A31 a12 A32 a13 A33 2 12 3 22 5 18 24 66 90 0 a13 1 0 4 ii 35 1 0 1 2 EXERCISE 4 3 Write Minors and Cofactors of the elements of following determinants 2 4 0 3 a b d a31 a32 a33 A a A a A a 4 4 1 2 2 19 19 A23 1 3 13 13 Rationalised 2023 24 A 1 12 12 A32 1 3 2 22 22 B A33 1 3 18 18 4 Using Cofactors of elements of third column evaluate 5 3 8 3 Using Cofactors of elements of second row evaluate A 20 1 3 DETERMINANTS ignas yz A a A a A ZX Z xy 87 then value of A is given by


Algebra
Quadratic equationsAs x y O 0 oo Question 19 1 point What are the x intercepts of y x x 3 x 3 0 3 3 3 0 3

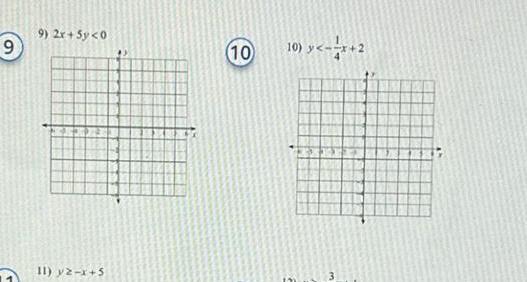
Algebra
Quadratic equationsUse the vertex formula to find the vertex of the quadratic function f x x 4x 7 The vertex is Type an ordered pair Simplify your answer

Algebra
Quadratic equationsSelect the correct answer The quadratic function which has a vertex h k 1 4 and contains the point x y 2 6 IS Of 2 2 x 1 4 Of x 2x 4x 6 Of x x 1 4 Of x 2 x 1 4 f x x 3x 2

Algebra
Quadratic equationsA ball is thrown directly upward from a height of 5 ft with an initial velocity of 20 ft sec The function s t 16t 20t 5 gives the height of the ball in feet t seconds after it has been thrown Determine the time at which the ball reaches its maximum height and find the maximum height The ball reaches its maximum height of Type integers or decimals ft sec s after the ball is thrown C

Algebra
Quadratic equationsWrite an equation for a parabola with x intercepts 2 0 and 5 0 which passes through the point 3 30 Write the equation 7
Algebra
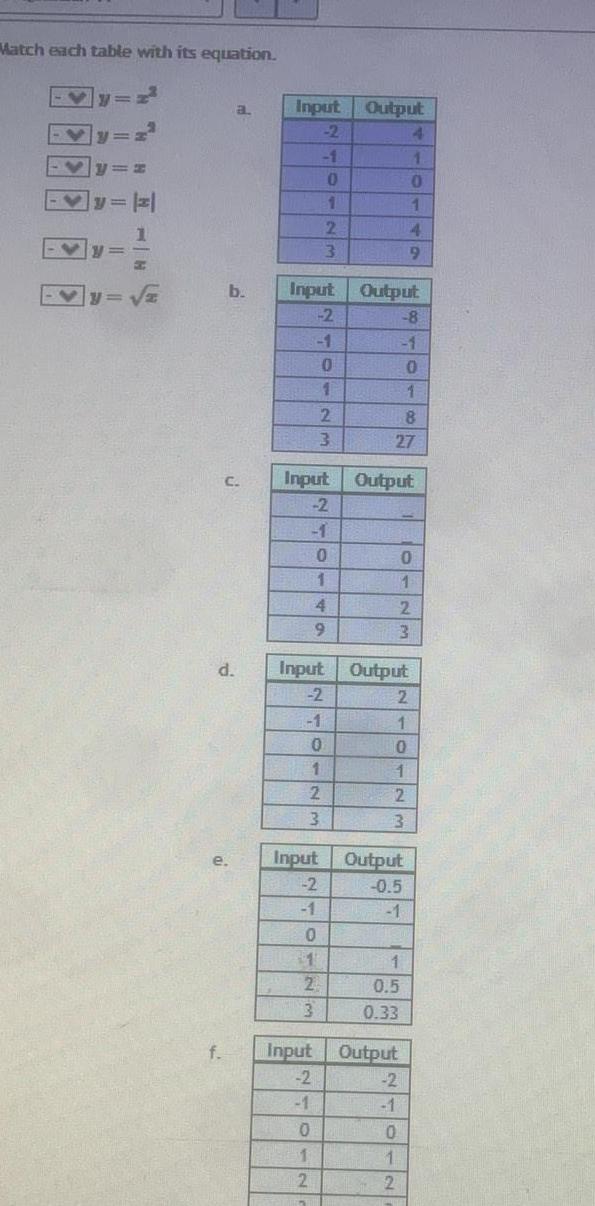
Quadratic equationsMatch each table with its equation A E A 11 d e f a b Input 2 1 0 1 2 3 Input 2 1 1 0 1 2 3 0 1 4 Input 2 1 0 1 2 3 Input 2 1 Input Output 2 0 1 2 3 Input 2 1 0 1 2 Output 4 1 0 Output 8 0 1 8 27 1 4 9 1 0 1 2 3 Output 2 1 0 1 12 3 Output 0 5 1 0 5 0 33 Output 2 1 0 1 2

Algebra
Quadratic equationsMicah found the vertex for the function y 9 5x 47 5x 63 as shown Find and correct Micah s error X X X b 2a 47 5 2 9 5 47 5 19 x 2 5 x 2 5 y 9 5 2 5 47 5 2 5 63 y 59 375 118 75 63 y 115 125 Explain the error O A Micah should have found a positive value when he simplified the 9 5 2 5 term B Micah used the wrong sign for b in the formula x b 2a C Micah should have evaluated the function with x 0 to find the y coordinate OD Micah did not use the correct order of operations dividing 47 5 by 2 9 5 The correct vertex is Type an ordered pair


Algebra
Quadratic equationsm 4 The distance s that an object falls varies directly with the square of the time t of the fall If an object falls 16 feet in one second how long for it to fall 144 feet Follow these steps to help you solve the question a Write a function s t and use k as the proportionality constant b Find the constant of proportionality k and write the function s t If necessary round the value of k to two decimal places c Use your function from part b to answer the question



Algebra
Quadratic equationsQuestion 8 Suppose f x 22 2x 7 Compute the following A f 4 f 4 B f 4 f 4 Question Help Video

Algebra
Quadratic equationsZ at Q 20000 6000 8 20000 7 6000 202000 Z at R 10500 34500 8 x 10500 7 34500 325500 Z at S 5000 40000 8 5000 7 40000 320000 Z at T 0 40000 7 40000 280000 Now observe that the profit is maximum at x 10500 and y 34500 and the maximum profit is 325500 Hence the manufacturer should produce 10500 bottles of M medicine and 34500 bottles of M medicine in order to get maximum profit of 325500 Example 6 Suppose a company plans to produce a new product that incur some costs fixed and variable and let the company plans to sell the product at a fixed price Prepare a mathematical model to examine the profitability Solution Step 1 Situation is clearly identifiable 204 MATHEMATICS Rationalised 2023 24 Step 2 Formulation We are given that the costs are of two types fixed and variable The fixed costs are independent of the number of units produced e g rent and rates while the variable costs increase with the number of units produced e g material Initially we assume that the variable costs are directly proportional to the number of units produced this should simplify our model The company earn a certain amount of money by selling its products and wants to ensure that it is maximum For convenience we assume that all units produced are sold immediately The mathematical model Let x number of units produced and sold C total cost of production in rupees I income from sales in rupees P profit in rupees Our assumptions above state that C consists of two parts i fixed cost a in rupees ii variable cost b rupees unit produced Then C a bx Also income I depends on selling price s rupees unit Thus I Sx The profit P is then the difference between income and costs So s b x a ott be published independent dependent 1 3 We now have a mathematical model of the relationships 1 to 3 between the variables x C I P a b s These variables may be classified as 2 X C I P parameters a b s The manufacturer knowing x a b s can determine P Step 3 From 3 we can observe that for the break even point i e make neither profit units a nor loss he must have P 0 i e x s b Stens 4 and 5 In view of the break even point one may conclude that if the company

Algebra
Quadratic equationsMacmillan Learning Follow the four step process to sketch the graph of the rational function R x Use the graphing utility to plot zeros graph asymptotes and create a sign diagram for the given rational function R x x 1 x x 1 x 2 1 Plot any zeros Select the zero button then click the graph to place a apro if th Reset step x 1 x x 1 x 2 10 Next step


Algebra
Quadratic equations26 Represent the above information in the form of a 3 2 matrix What does the entry in the third row and second column represent 38 MATHEMATICS Solution The information is represented in the form of a 3 x 2 matrix as follows 30 25 A 25 31 27 26 The entry in the third row and second column represents the number of women workers in factory III Rationalised 2023 24 Example 2 If a matrix has 8 elements what are the possible orders it can have Solution We know that if a matrix is of order m n it has mn elements Thus to find all possible orders of a matrix with 8 elements we will find all ordered pairs numbers whose product is 8 Thus all possible ordered pairs are 1 8 8 1 4 2 2 4 Hence possible orders are 1 8 8 1 4 2 2 4 Now Example 3 Construct a 3 2 matrix whose elements are by aj Solution In general a 3 2 matrix is given by Therefore 21 11 i 3j i 1 a11 13 3 11 0 3 and j 1 2 912 1 3 2 a32 921 922 a31 a32 2 12 3 11 4 12 3 21 2 Hence the required matrix is given by A 21 2 H 0 52 2 3x2 2 1 11 3 3x2 noxto be ravishe 3 i 3jl

Algebra
Quadratic equationsDallas needs 4 liter of milk for a recipe and there is 10 of a liter of milk left in the carton How much is left after Dallas makes his recipe

Algebra
Quadratic equationsx 5 2 The general geometric series is a ar ar n Write out the first few terms of the geometric series n 0 series Then express the inequality r 1 in terms of x and find the values of x for which the inequality holds and the series converges ar arm to find a and r and find the sum of the 3 What is the first term of the given series

Algebra
Quadratic equationsIndicate whether the series converges or diverges If it converges find its sum k k k 1 106k Select the correct choice below and if necessary fill in the answer box within your choice OA The series diverges because it is a geometric series with r 1 O B The series converges because it is a geometric series with r 1 The sum of the series is Type an integer or a simplified fraction O C O D k k 106k The series diverges because lim 0 or fails to exist k k 106k The series converges because lim 0 The sum of the series is

Algebra
Quadratic equationsThen the sum of the two matrices A and B is defined as a matrix C c c a b for all possible values of i and j Example 6 Given A 1 3 she A B defined 1 5 1 1 1 5 and B KARN Since A B are of the same order 3 Therefore addition of A and B is defined and is given by 2 3 2 2 3 3 0 2 5 1 1 2 3 2 3 B Note 1 We emphasise that if A and B are not of the same order then A B is not xample if A 1 5 0 1 2 This can be represented in the matrix 6 10 Rationalised 2023 24 23 e 31 2 We may observe that addition of matrices is an example of binary operation on the set of matrices of the same order 3 4 2 Multiplication of a matrix by a scalar Now suppose that Fatima has doubled the production at a factory A in all categories refer to 3 4 1 Girls 60 65 85 where then A B is not defined Previously quantities in standard units produced by factory A were Boys 80 75 90 Revised quantities produced by factory A are as given below Boys Girls 1 2 80 2x 60 2 2x75 2 65 32x90 2x85 MATRICES 170 olshed 45 We observe that the new matrix is obtained by multiplying each element of the previous matrix by 2 In general we may define multiplication of a matrix by a scalar as follows if A a is a matrix and k is a scalar then kA is another matrix which is obtained by multiplying each element of A by the scalar k mx n

Algebra
Quadratic equationsDetermine whether the series n 0 DIR OB The series diverges because lim n O C converges or diverges If it converges find its sum Select the correct choice below and if necessary fill in the answer box within your choice The series converges because it is a geometric series with r 1 The sum of the series is Type an exact answer O A The series converges because lim n T T 0 or fails to exist n 0 The sum of the series is Type an exact answer OD The series diverges because it is a geometric series with r 21

Algebra
Quadratic equationsExample 9 Find X and Y if X Y or Solution We have X Y X Y or Also or or 1 or 20 8 10 4 25 6 5 12 or or or i e X X Y Y X Y X Y 2 2x 3 10 4 14 1 2y 6 2 X 2x 3 7 N 2x 7 3 4 2 x 2 5 2 0 9 Y 5 GSH Y 3 0 5 2 8 3 9 88 8 113 52 3 0 9 2 6 X X X Y 5 3 2 1 0 188 210 Example 10 Find the values of x and y from the following equation and and 12 14 31 7 and X Y and and 7 6 15 14 2X 3 4 3 4 210 731 60 2 0 10 Rationalised 2023 24 6 9 6 9 Solution We have 5 4 7 6 2x 10 3 6 H 2 6 1 2 4 4 7 y 3 15 2y 6 2Y 15 6 1 0 2 5 6 14 y 2x 3 6 2y 4 15 2y 4 14 2y 18 4 y 9 18 2 31 7 3 3 14 3 T 41 10 what to shed 7 7 6 1 is 14 15 Why MATRICES 6 49 Example 11 Two farmers Ramkishan and Gurcharan Singh cultivates only three varieties of rice namely Basmati Permal and Naura The sale in Rupees of these varieties of rice by both the farmers in the month of September and October are given hu the follo A ond R

Algebra
Quadratic equationsRamkishan Gurcharan Singh Thus in October Ramkishan receives 100 200 and 120 as profit in the sale of each variety of rice respectively and Grucharan Singh receives profit of 400 200 and 200 in the sale of each variety of rice respectively 5 8 10 11 100 400 3 4 5 Multiplication of matrices Suppose Meera and Nadeem are two friends Meera wants to buy 2 pens and 5 story books while Nadeem needs 8 pens and 10 story books They both go to a shop to enquire about the rates which are quoted as follows Pen 5 each story book 50 each How much money does each need to spend Clearly Meera needs 5 2 50 5 that is 260 while Nadeem needs 8 x 5 50 10 that is 540 In terms of matrix representation we can write the above information as follows Requirements Prices per piece in Rupees Money needed in Rupees 260 5 50x50 340 50 200 200 2 5 8 10 2 5 8 10 120 200 Suppose that they enquire about the rates from another shop quoted as follows pen 4 each story book 40 each de f Now the money required by Meera and Nadeem to make purchases will be respectively 4 2 40 5 208 and 8 4 10 40 432 Rationalised 2023 24 4 40 5x2 5x50 8x5 10x50 5 4 50 40 Again the above information can be represented as follows Requirements Prices per piece in Rupees Money needed in Rupees MATRICES 51 Now the information in both the cases can be combined and expressed in terms of matrices as follows Requirements Prices per piece in Rupees Money needed in Rupees 208 8 4 10 40 432 260 208 5x2 5x50 4x2 40 5 8x5 10x50 8 4 10 40 The above is an example of multiplication of matrices We observe that for multiplication of two matrices A and B the number of columns in A should be equal to the number of rows in B Furthermore for getting the elements of the product matrix we take rows of A and columns of B multiply them element wise and take the sum Formally we define multiplication of matrices as follows HOUT The product of two matrices A and B is defined if the number of columns of A is equal to the number of rows of B Let A a be an m n matrix and B b be an nxp matrix Then the product of the matrices A and B is the matrix C of order m p To get the i k th element c of the matrix C we take the ith row of A and kth column of B multiply them elementwise and take the sum of all these products In other words if A almx B bl xp then the ith row of A is a a a and the kth column of

Algebra
Quadratic equationsYour business requests a 3 month loan for 500 000 What will be the interest paid at the end of the term if the business risk percentage is assessed at 2 0 and LIBOR is at 1 8 interest paid

Algebra
Quadratic equationsO Macmillan Learning Graph the rational function R x follow R x x 3x x3 3x2 9 y 8 7 6 5 4 3 18x 40 18x 40 using the graphing utility Use the graph to answer the questions that PAR 201

Algebra
Quadratic equationsIdentify the graph of a rational function consistent with the given information There is more than one correct answer Vertical asymptotes x 4 and x 4 and no horizontal asymptote 4 3 y 6 3 0 3 6 9 0 4 8 3 4 6 8 9 12 8 4 Y 12 0 12 8 0 4 4 8 8 12 x x
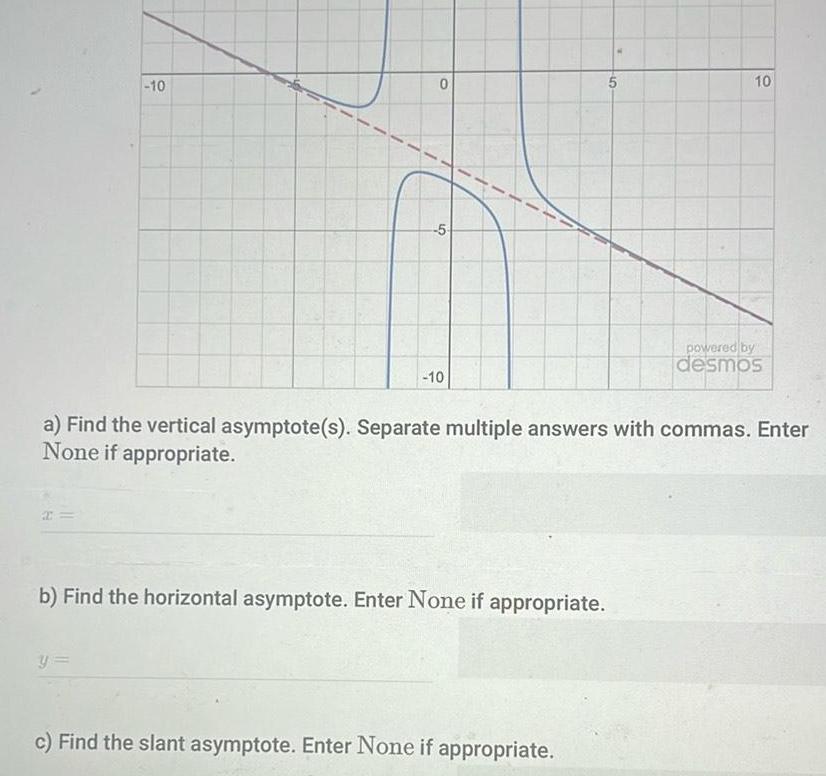
Algebra
Quadratic equations2 10 O y 5 10 b Find the horizontal asymptote Enter None if appropriate a Find the vertical asymptote s Separate multiple answers with commas Enter None if appropriate 10 c Find the slant asymptote Enter None if appropriate 10 powered by desmos
Algebra
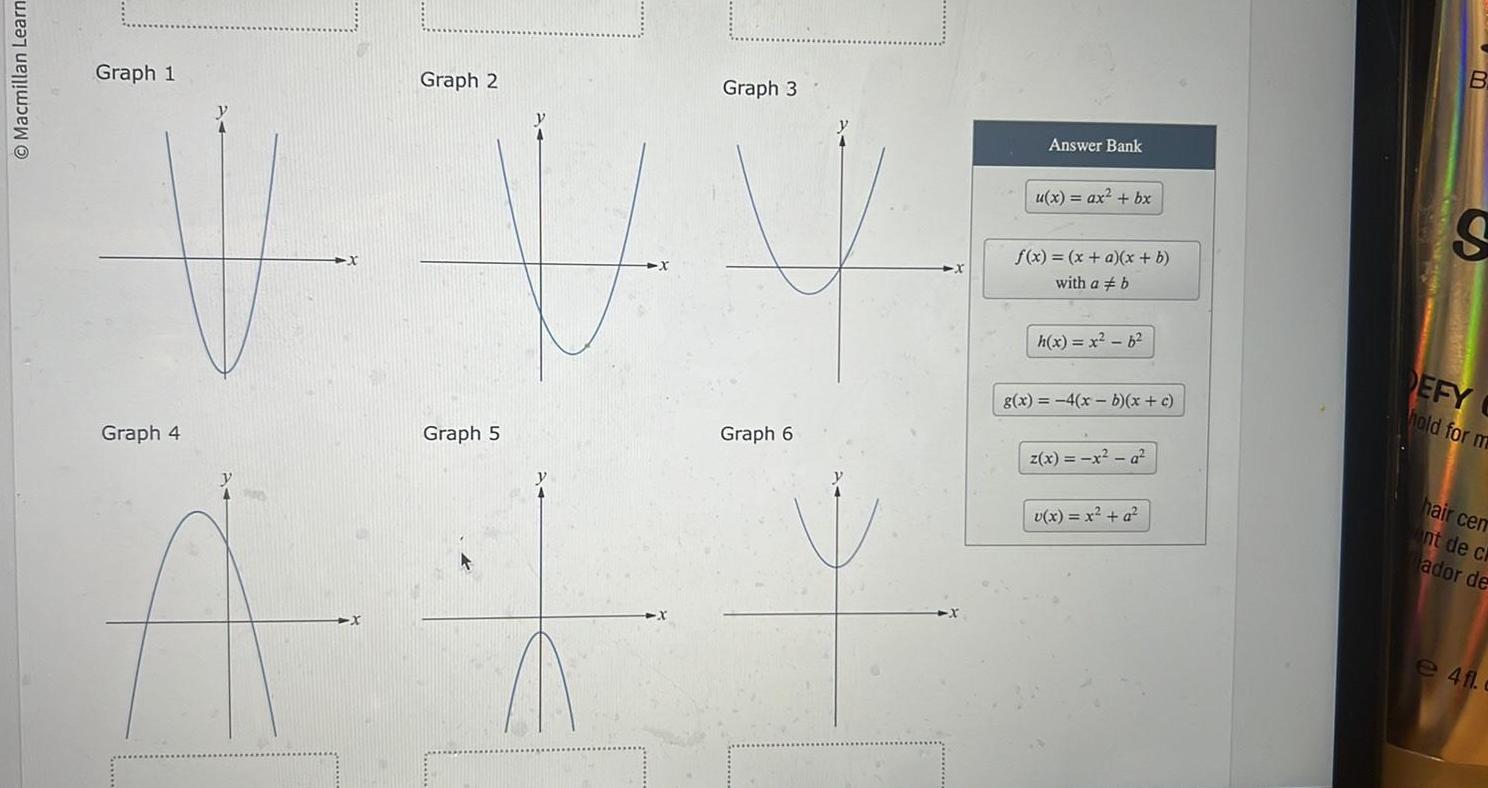
Quadratic equationsO Macmillan Learn Graph 1 Graph 4 Graph 2 Graph 5 Graph 3 Graph 6 Answer Bank u x ax bx f x x a x b with a b h x x b g x 4 x b x c z x x a v x x a m B S DEFY hold for m hair cem ent de ch ador de e 4fl c

Algebra
Quadratic equationsFind the limit of the given rational function as x o and the limit as x co R x X x 3 Express numbers in exact form Use symbolic notation and fractions where needed as x o R as x o R

Algebra
Quadratic equationsO Macmillan Learnir x 1 x 7 R x x x 7 Determine the domain Give your answer as an interval in the form Use the symbol co for infinity U for combining intervals and an appropriate type of parenthesis depending on whether the interval is open or closed Enter if the interval is empty Express numbers in exact form Use symbolic notation and fractions where needed domain Identify any poles Give your answer in the form of a comma separated list if needed Express numbers in exact form Use symbolic notation and fractions where needed Enter DNE if poles do not exist
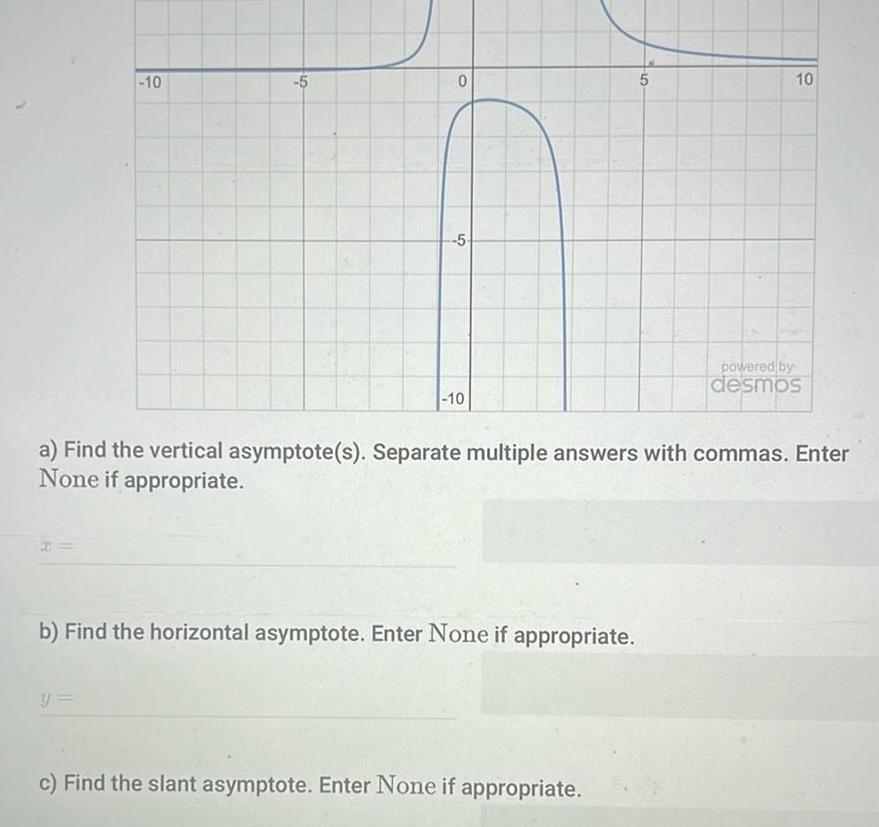
Algebra
Quadratic equations10 5 y 0 5 10 b Find the horizontal asymptote Enter None if appropriate 5 a Find the vertical asymptote s Separate multiple answers with commas Enter None if appropriate c Find the slant asymptote Enter None if appropriate 10 powered by desmos

Algebra
Quadratic equationsUse a calculator to evaluate the expression to the nearest tenth of a degree sin 0 1302
Algebra
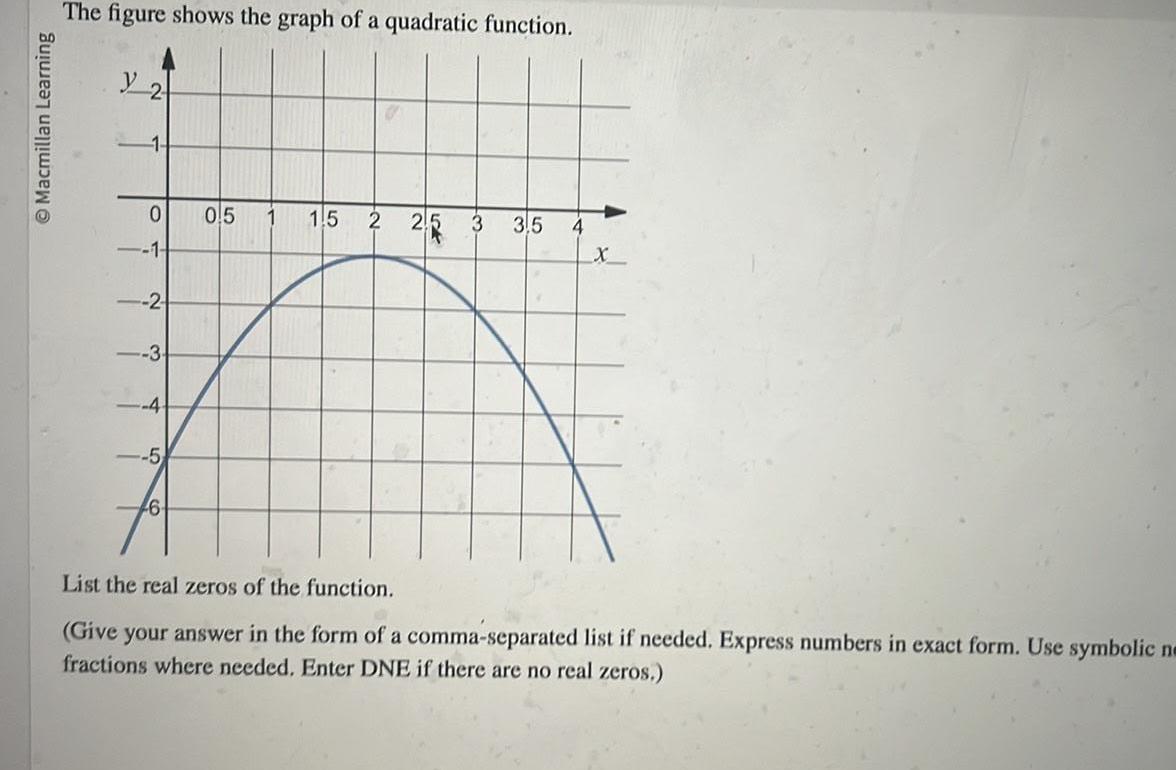
Quadratic equationsMacmillan Learning The figure shows the graph of a quadratic function y 2 1 0 1 2 3 4 5 6 0 5 1 5 2 25 3 3 5 4 X List the real zeros of the function Give your answer in the form of a comma separated list if needed Express numbers in exact form Use symbolic ne fractions where needed Enter DNE if there are no real zeros
Algebra
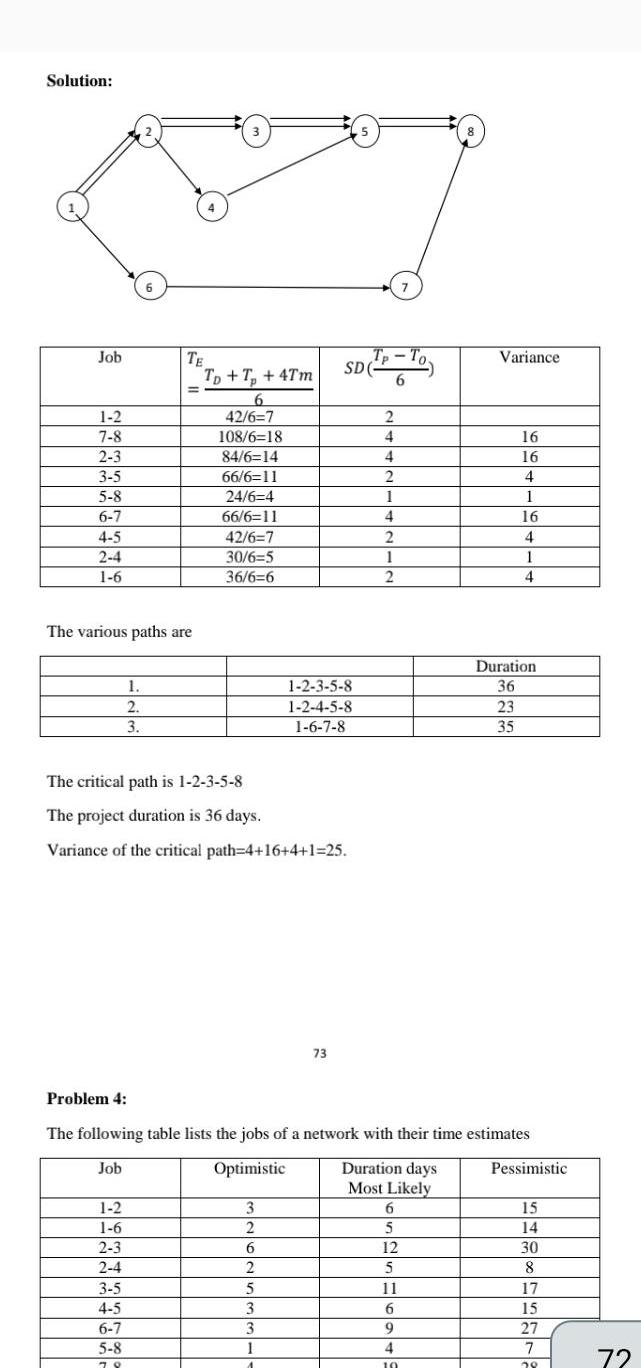
Quadratic equationsSolution Job 1 2 7 8 2 3 3 5 5 8 6 7 4 5 2 4 1 6 6 1 2 3 TE The various paths are 1 2 1 6 2 3 2 4 3 5 4 5 6 7 5 8 78 TD Tp 4Tm 6 42 6 7 108 6 18 84 6 14 66 6 11 24 6 4 66 6 11 42 6 7 30 6 5 36 6 6 The critical path is 1 2 3 5 8 The project duration is 36 days Variance of the critical path 4 16 4 1 25 3 2 1 2 3 5 8 1 2 4 5 8 1 6 7 8 6 2 5 3 3 1 A 73 5 SD Tp 6 2 4 4 2 1 4 2 1 2 6 7 Problem 4 The following table lists the jobs of a network with their time estimates Job Optimistic Duration days Most Likely 5 12 5 11 6 9 4 10 Variance 16 16 4 1 16 4 1 4 Duration 36 23 35 Pessimistic 15 14 30 8 17 15 27 7 25 72
Algebra
Quadratic equationsO Macmillan Learning A child tosses a baseball upward and catches it as it falls back The height above the ground of the ball t seconds after the toss is given by h 16t 24t 3 where h is measured in feet How high above the ground is the ball when it is tossed Give your answer as a whole number initial height feet How long is the ball in the air The ball is caught when its height above the ground is the same as at the moment it is tossed Use decimal notation Give your answer to one decimal place time the ball is in the air seconds

Algebra
Quadratic equationsMacmillan Learning Consider the polynomial function P x 8 2x x Find its real zeros Give your answer in the form of a comma separated list if needed Express numbers in exact form Use symbolic notation and fractions where needed Enter DNE if there are no real zeros real zeros Find the vertex of the graph Give your answer in the form Express numbers in exact form Use symbolic notation and fractions where needed vertex

Algebra
Quadratic equationsMacmillan Learning Calculate the discriminant of the quadratic function y x 3x 4 Give an exact answer Use symbolic notation and fractions where needed discriminant What does the discriminant tell you about the zeros The equation has one real zero Otwo real zeros no real zeros

Algebra
Quadratic equationsMultiply the factors and simplify the expression x 6 i x 6 i Suggestion Use the fact that A B A B A B Express numbers in exact form Use symbolic notation and fractions where needed Simplify your answer completely x 6 i x 6 i

Algebra
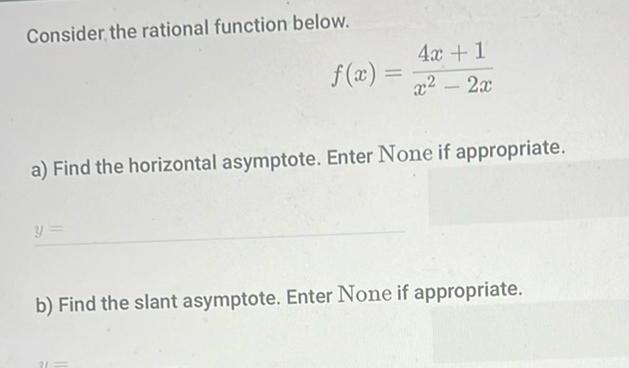
Quadratic equationsConsider the rational function below f x 4x 1 x 2x a Find the horizontal asymptote Enter None if appropriate b Find the slant asymptote Enter None if appropriate

Algebra
Quadratic equationsDetermine the domain of the rational function below Enter your answer in interval notation and use the union symbol U to combine multiple intervals f x C 6
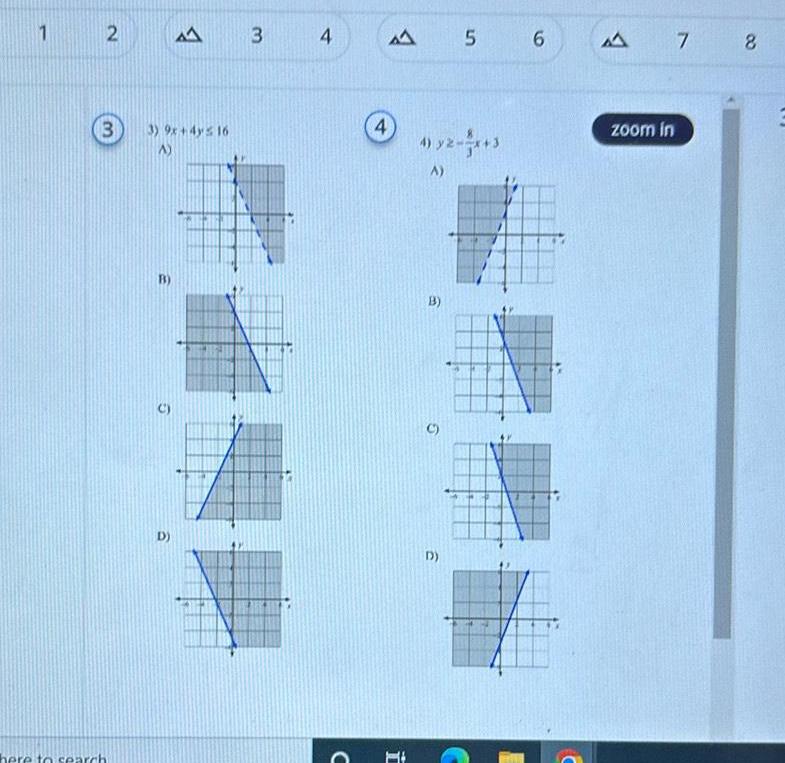
Algebra
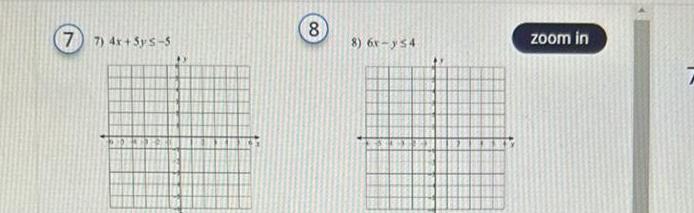
Quadratic equations1 2 3 here to search 3 9x 4y5 16 A B 5 A D 3 4 C 4 A 5 6 4 2 3x 3 A A zoom in 7 8