Quadratic equations Questions and Answers


Algebra
Quadratic equationsDivide using synthetic division 3 2 6w 41w 31w 4 W W 1 6 6w 41w 2 31w 4 3 1

Algebra
Quadratic equationsWrite an equation for a parabola with x intercepts 2 0 and 3 0 which passes through the point 2 20 Write the equation
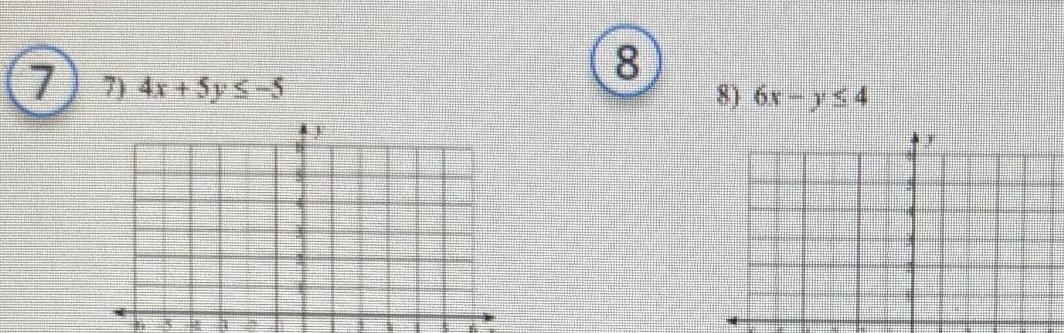
Algebra
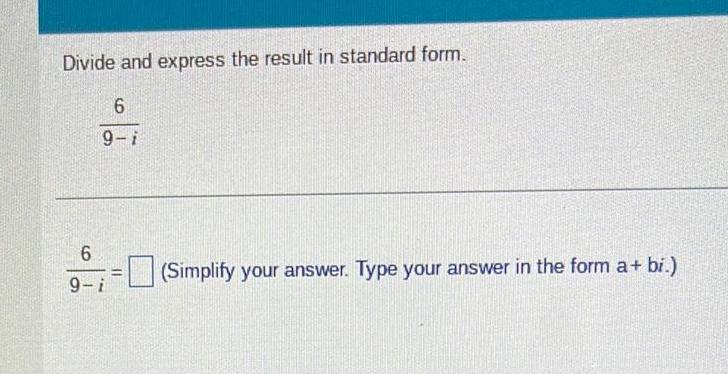
Quadratic equationsDivide and express the result in standard form 6 9 i 6 9 i Simplify your answer Type your answer in the form a bi

Algebra
Quadratic equationsSimplify the expression 8 i 3 5i The simplified expression is Type your answer in the form a bi

Algebra
Quadratic equationsService Service centre 3 Departures Queuing theory is concerned with the statistical description of the behavior of queues with finding e g the probability distributed of the number in the queue from which the mean and variance of queue length an probability distribution of waiting time for a customer or the distribution of a server s busy periods can be found In operational research problems involving queues investigators must measure the existing system to make an objective assessment of its characteristics and must determine how changes may be made to the system what effects of various system s kinds of changes in the system s characteristics would be and whether in the light of the queuing system under study must be constructed in this kind of analysis and the results of queuing theory are required to obtain the characteristics of the model and to assess the effects such as the addition of an extra server or a reduction in mean service time Arriving units QUEUEING SYSTEM A queuing system can be completely described by a The input or arrival pattern b The service mechanism or service pattern c The queue discipline and d Customer s behavior Queuing System Service Centre Queue or waiting time Servicing Station 0 41 system Departures a The input or arrival pattern The input describes the way in which the customers arrive and join the system Generally the customers arrive in a more or less random fashion which is not worth making the prediction Thus the arrival patteren can best be described in terms of probabilities and consequently the probability distribution for inter arrival times the time between two successive arrivals or the distribution of number customers arriving in unit time must be defined
Algebra
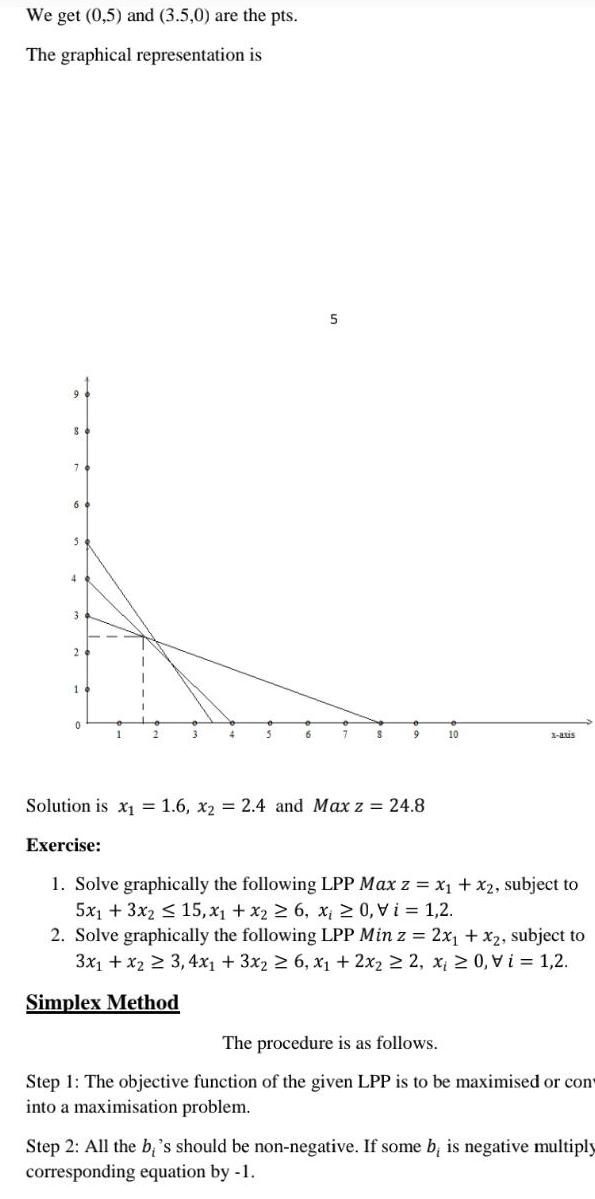
Quadratic equationsWe get 0 5 and 3 5 0 are the pts The graphical representation is 3 6 5 S 9 10 1 aus Solution is x 1 6 x 2 4 and Max z 24 8 Exercise 1 Solve graphically the following LPP Max z x x2 subject to 5x1 3x2 15 x x 6 x 0 Vi 1 2 2 Solve graphically the following LPP Min z 2x x2 subject to 3x1 x2 3 4x 3x 6 x 2x 2 x 0 Vi 1 2 Simplex Method The procedure is as follows Step 1 The objective function of the given LPP is to be maximised or con into a maximisation problem Step 2 All the bi s should be non negative If some b is negative multiply corresponding equation by 1
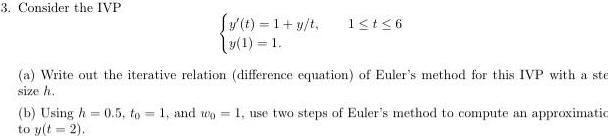
Algebra
Quadratic equations3 Consider the IVP y t 1 y t 3 1 1 1 t 6 a Write out the iterative relation difference equation of Euler s method for this IVP with a ste size h b Using h0 5 to 1 and wo to y t 2 1 use two steps of Euler s method to compute an approximatio

Algebra
Quadratic equationsproblem has no solution using graphical method 2 If the maximum value of z appears only at o then the problem has unbounded solution 3 If the maximum value of z appears at 2 points there exists infinite number of solutions to the LPP Problem 4 Find the maximum value of z to the following LPP using graphical method Max z 5x 7x2 subject to x x2 4 3x1 8x2 24 10x 7x 35 and x 0 Vi 1 2 Solution The given problem contains only two variables x and x So graphical method is possible Consider the equations we get X X 4 3x 8x 24 Now to find the points Consider x x 4 Put x 0 x 4 10x 7x 35 and x 0 x 4 Therefore 0 4 and 4 0 are the pts Similarly consider 3x 8x 24 We get 0 3 and 8 0 are the pts Consider 10x 7x 35 We get 0 5 and 3 5 0 are the pts The graphical representation is

Algebra
Quadratic equationsA shop has 4 workers and 4 works to be performed The estimate of time man hours each man will take to perform each project is given in the following table How should the works to be allotted so as to optimise the total work 1 2 3 4 1 2 3 1 4 19 2 3 4 Solution Step 1 Given matrix is 1 1 8 2 13 3 4 38 19 8 13 38 19 26 0 9 23 28 4 26 9 26 24 10 Step 2 Here the given matrix is a square matrix Hence the assignment problem is a balanced problem Subtracting minimum cost of each row of the cost matrix we obtain the following matrix 17 2 3 4 11 26 17 11 18 15 28 4 26 1 2 3 4 19 18 15 26 24 10 18 24 4 16 9 3 0 22 3 0 28 14 0 Step 3 Subtracting minimum cost of each column of the modified cost matrix we obtain the following matrix 12 3 4
Algebra
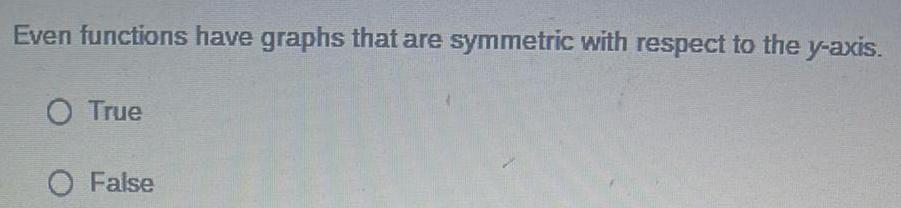
Quadratic equationsEven functions have graphs that are symmetric with respect to the y axis O True O False
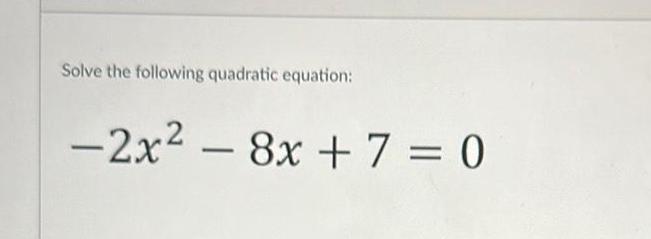

Algebra
Quadratic equationsDescribe how to transform x5 into an expression with a rational exponent Make sure you respond with complete sentences CCC CO
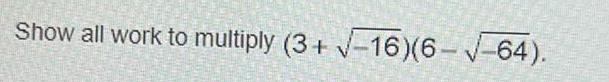

Algebra
Quadratic equationsSolve the equation x 6 2 6 for the variable Show each step of your solution process
Algebra
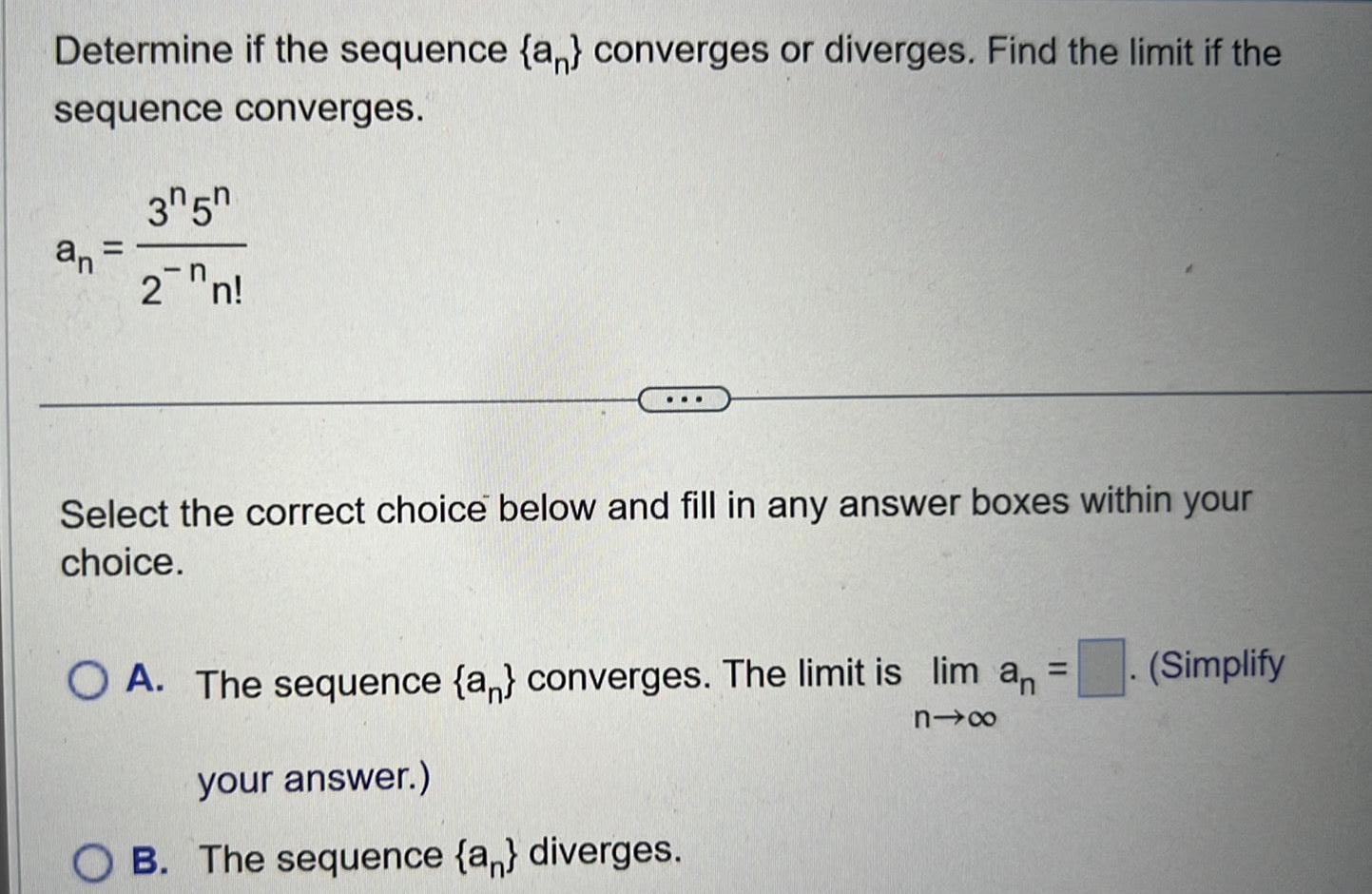
Quadratic equationsDetermine if the sequence an converges or diverges Find the limit if the sequence converges 35 an 2n Select the correct choice below and fill in any answer boxes within your choice OA The sequence a converges The limit is lim a n your answer OB The sequence a diverges Simplify

Algebra
Quadratic equationspoint For the function f x f x h f x h f w f x W X h 0 14x 7h 9 7 x2 simplify each expression as much as possible x w

Algebra
Quadratic equationsIs the function defined by 2x 3 if x 2 2x 3 if x 2 6 f x x 8 f x x 0 continuous at x 0 At x 1 At x 2 Find all points of discontinuity off where fis defined 10 f x if x 0 if x 0 NO x 1 if x 1 x 1 if x 1 x 0 1 if x 1 12 f x if x 1 13 Is the function defined by a continuous function f x User uden she f x x if x 1 2 if x 1 16 f x 2x if 1 x 1 2 if x 1 5 if x 1 x 3 if x 3 f x 2x if 3 x 3 6x 2 if x 3 11 f x 9 f x x x 5 if x 1 x 5 if x 1 Rationalised 2023 24 x if x 0 1 1 if x 0 x 3 if x 2 x 1 if x 2 CONTINUITY AND DIFFERENTIABILITY Discuss the continuity of the function f where fis defined by 3 if 0 x 1 14 f x 4 if 1 x 3 5 if 3 x 10 2x if x 0 15 f x 0 if 0 x 1 4x if x 1 is continuous at x 3 18 For what value of 2 is the function defined by 17 Find the relationship between a and b so that the function f defined by ax 1 if x 3 f x bx 3 if x 3 2 x 2x if x 0 4x 1 117 olished f x continuous at x 0 What about continuity at x 1 19 Show that the function defined by g x x x is discontinuous at all integral points Here x denotes the greatest integer less than or equal to x 20 Is the function defined by f x x sin x 5 continuous at x

Algebra
Quadratic equationsThe table shows the percent of each type of doughnut sold at a bakery A store clerk put all of the cream filled and powdered sugar doughnuts on a display in the front of the store Both of these types of doughnuts completely sold out on Tuesday morning rt A If the clerk put 108 doughnuts in the front of store how many doughnuts were there in all at beginning of the day on Tuesday Type of Doughnut Cream Filled Glazed Maple Bacon Powdered Sugar Percen t 20 45 10 25
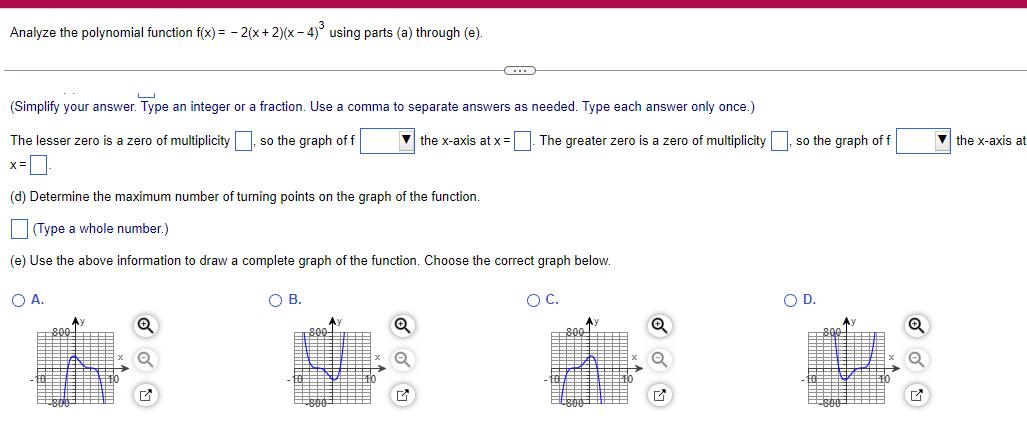
Algebra
Quadratic equationsAnalyze the polynomial function f x 2 x 2 x 4 using parts a through e Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once The lesser zero is a zero of multiplicity so the graph of f the x axis at x The greater zero is a zero of multiplicity x d Determine the maximum number of turning points on the graph of the function Type a whole number e Use the above information to draw a complete graph of the function Choose the correct graph below O C OA Ay OB 800 C Ay G so the graph of f O D Q the x axis at

Algebra
Quadratic equationsFind the average rate of change for the function f x x 3 3 between xa and x a h 0 8 of 64

Algebra
Quadratic equationsett a he 9 Find the angle between the hands of the och in sch figure 9 00 am 1 00 pm 10 te in the given figure the angle mease 20 Look at the same figure through a magnifying Dose change angle becomes laiger Does the suk of the angle 200 Measure and classify each angis CACH CADC Doc DOR 2008 Exercise 5 5 Me 6 00 pm a The adjacent edges of a table tap b The lines of a railway track c The line segments forming the leta 1 d The letter V from 1 Which of the following are modelsforperpendicular lines LR PLUS Pperverse to the the night Land XV esact in the peshtA Wer measure of Y 1 There are two ses ages in your the measures of the angles that a S comen Do they have any angle mat i perpine somman dy the digrom The is GE EGY b Door PE bes CO c dentify any e segments for which P Herpendicular tisector AC FG CD GHBC H Exercise 5 6 t Nams the types of owing ge a Tiangle with length of sides 7 cm 8 mand by BC with AB 87 cm AC 7 om and BC c APOR the PQ OR PR S5om id ADEF with eD 90 n SKYZ with mY 90 and XYYZ ALMN with 1 30 mM 70 and mN 80 Match the following Measure of Triangle 3 sides of equal lengt a Scale 8 2 sides of equal length b iscsperes right Types of Triangle angled Al sides of different Otae angled lingh v 3 acute anges v 1 night angin vi 1 obtuse angle vejt nght angle with two sides of equal length 0 Right angled e Equilateral Acute angled gosceias 3 Nemesach of the folowing triangies in two difer ways You may judge the nature of angle t obation MI Try to construct triangles ung machacks Some are shown here Can you make a tangle with a 3 matchto e 5 matates 1 6 matchwo Remember you have to use the matchats in each case i Nams the type of trade think of reasons for you cannot matang think of masons for b 4 match Exercise 5 7 1 Say true or false a Each angle of rectangle ght ange b The opposite sides of a rectangle an equal m lingh ght of a 10 Souess scans a d At the side of a mombus se of equal length 0 All the sides of a paralelogram are of soul length 4 Sepas pieselwigram 3 Ap regard d length and wipes angun meur Can you identify the requ The opposite sides of a trapanum um paralle 2 Give reasons for the following a Asquare can be thought of as a special rectangle A rectangle can be thought of special paralelogram mamb Exercise 5 8 Examine wheme the og epolygons among these say wh M 2 Namech polygon Make two more examples of each of the c The diagonale of a squarere perpendicular to 3 Draw a rough skich of a regular hexagon Connectin one another any time of vertices throw thangle identify th type of the triangle you uveden Drawough skach of a regula octagun Um aquared paper if you wan D rectangle joiningscy four of the vertices of the antagon 5 Adagol segment that joins any two vertic polygon arut is e side of the polygon Dram rough sch of a pentagon and draw is diegonale

Algebra
Quadratic equationsThe table represents a quadratic function Write an equation of the function in standard form x 9 7 5 3 8 y 0 2 8 0

Algebra
Quadratic equationsWrite a quadratic function in standard form whose graph has the given characteristics vertex 2 5 passes through 4 4

Algebra
Quadratic equationsO Macmillan Learning If x 5 and x 8 are zeros of a quadratic function with leading coefficient 3 then the quadratic function factors as Enter the answer in factored form f x

Algebra
Quadratic equations1 2 3 The critical path is 1 2 3 5 8 and 1 6 7 8 The project duration is 36 days Variance of the critical path 4 16 16 36 Exercises 1 A project consists of 12 jobs Draw a project network and determine the critical path Job 1 2 2 3 2 4 3 4 3 5 4 6 5 8 Activity 1 2 1 3 3 5 3 4 4 6 5 6 6 7 1 2 4 5 8 1 2 3 5 8 1 6 7 8 6 8 7 8 8 9 Duration 2 7 3 3 5 3 5 2 Consider the following project whose activities along with PERT time estimates the optimistic time a most likely time m and the pessimistic time b are given as follows a days 12 7 4 36 12 6 9 6 4 8 Job 6 7 6 10 7 9 8 9 9 10 75 23 36 36 m days 14 10 6 40 15 8 12 10 5 10 Duration 8 4 4 1 7 b days 21 16 10 60 24 12 18 15 7 14
Algebra
Quadratic equationsConsider the polynomial function f x 44 25x 27 5x5 6 5x 5 1 25x 3 22x 39 What is the degree of this polynomial Identify the constant term Identify the leading coefficient Identify the leading term
Algebra
Quadratic equationsAnalyze the polynomial function f x x 2x 3x Answer parts a through e Hint First factor the polynomial The y intercept is 0 Type an integer or a simplified fraction c Determine the zeros of the function and their multiplicity Use this information to determine whether the graph crosses or touches the x axis at each x intercept The zero s of f is are 0 3 1 Type an integer or a simplified fraction Use a comma to separate answers as needed Type each answer only once The smallest zero is of multiplicity multiplicity so the graph of f so the graph of f the x axis at x The middle zero is of the x axis at x The largest zero is of multiplicity so the graph
Algebra
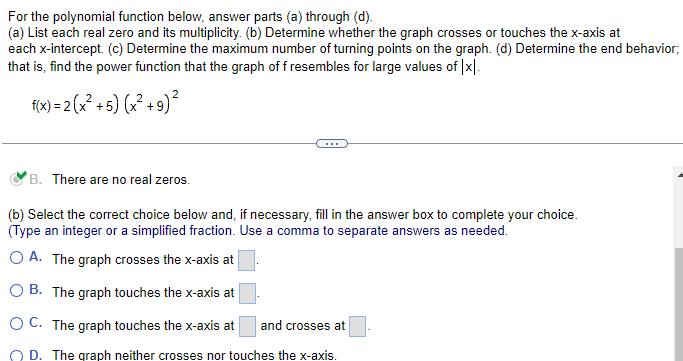
Quadratic equationsFor the polynomial function below answer parts a through d a List each real zero and its multiplicity b Determine whether the graph crosses or touches the x axis at each x intercept c Determine the maximum number of turning points on the graph d Determine the end behavior that is find the power function that the graph of f resembles for large values of x f x 2 x 5 x 9 B There are no real zeros b Select the correct choice below and if necessary fill in the answer box to complete your choice Type an integer or a simplified fraction Use comma to separate answer as needed OA The graph crosses the x axis at B The graph touches the x axis at OC The graph touches the x axis at and crosses at OD The graph neither crosses nor touches the x axis

Algebra
Quadratic equationsAnalyze the polynomial function f x 6x x 4 x 3 using parts a through e c Determine the real zeros of the function and their multiplicity Use this information to determine whether the graph crosses or touches the x axis at each x intercept The zero s off is are 0 2 2 3 Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once Starting from least to greatest the first zero of the function is of multiplicity 1 so the graph of f crosses the x axis at x 3 The second zero of the function is of multiplicity 1 so the graph of f crosses the x axis x 2 The third zero of the function is of multiplicity 1 so the graph of f crosses the x axis at x 0 The fourth zero of the function is of multiplicity 1 so the graph of f crosses the x axis at x 2 d Determine the maximum number of turning points on the graph of the function 2 Type a whole number
Algebra
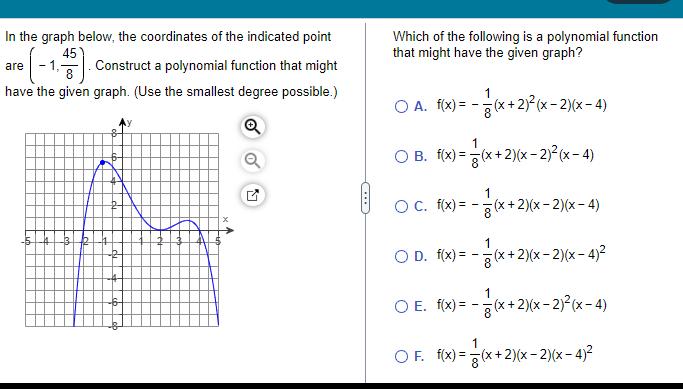
Quadratic equationsIn the graph below the coordinates of the indicated point are 1 1 45 Construct a polynomial function that might have the given graph Use the smallest degree possible Q 13 R Ly Which of the following is a polynomial function that might have the given graph O A f x x 2 x 2 x 4 1 O B f x x 2 x 2 x 4 1 OC f x x 2 x 2 x 4 O D f x O E f x x 2 x 2 x 4 1 x 2 x x 2 x 2 x 4 OF f x x 2 x 2 x 4
Algebra
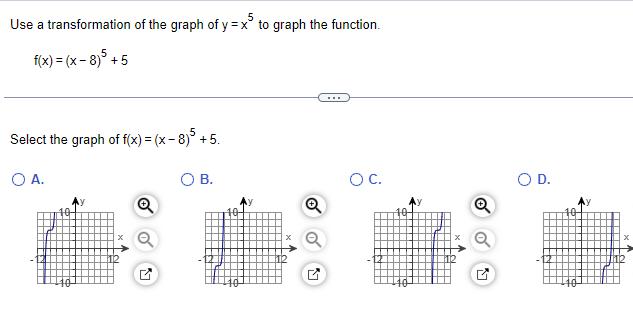
Quadratic equationsUse a transformation of the graph of y x5 to graph the function f x x 8 5 5 Select the graph of f x x 8 5 5 O A Q O B Q O C
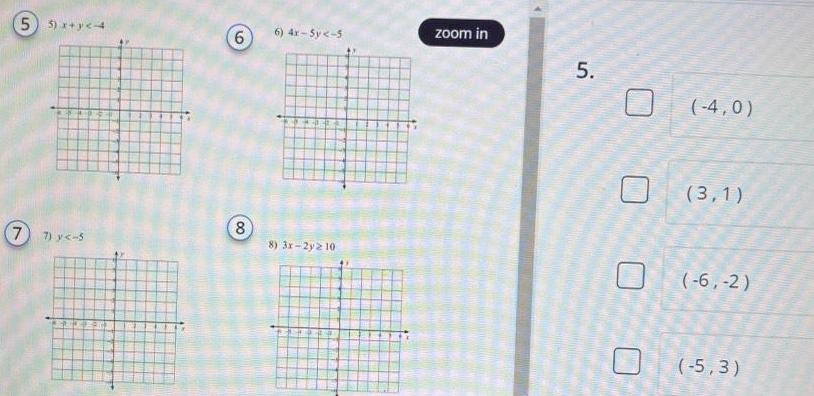
Algebra
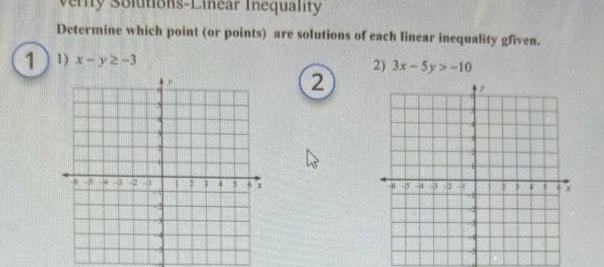
Quadratic equationsInequality Determine which point or points are solutions of each linear inequality given 1 1 x y2 3 2 3x 5y 10 2 27 0436 AT

Algebra
Quadratic equationsWhich phrase identifies the importance of the elastic clause in Article 1 Provides a loophole to make laws without the approval of the executive branch O Gives Congress powers that stretch beyond the other branches of government ORemoves flexibility to legislate on topics not listed in the Constitution O Allows Congress to make laws not specifically stated in the Constitution

Algebra
Quadratic equationsA pole with a length of 120 meters is placed vertically in the ground at point K whose altitude is 84 Since the altitude of point M is 132 point Lis What is the altitude of the border K 84 M 132 A 24 B 18 C 16 D 12

Algebra
Quadratic equationsDirections Solve each equation for the variable SHOW YOUR WORK FOR CRED 13 56d 7d 4 15 7f 6 116 3f 16 4 2g 5g 66 19 4j 26 50 6j 22 3q 7 7q 13 14 4e 4 e 4 17 5h 3 3h 11 20 2k 36 6k 12 23 21 r 87 2r 18 5i 4 14 4i 21 L 21 L 87 24 2s 54 s 21
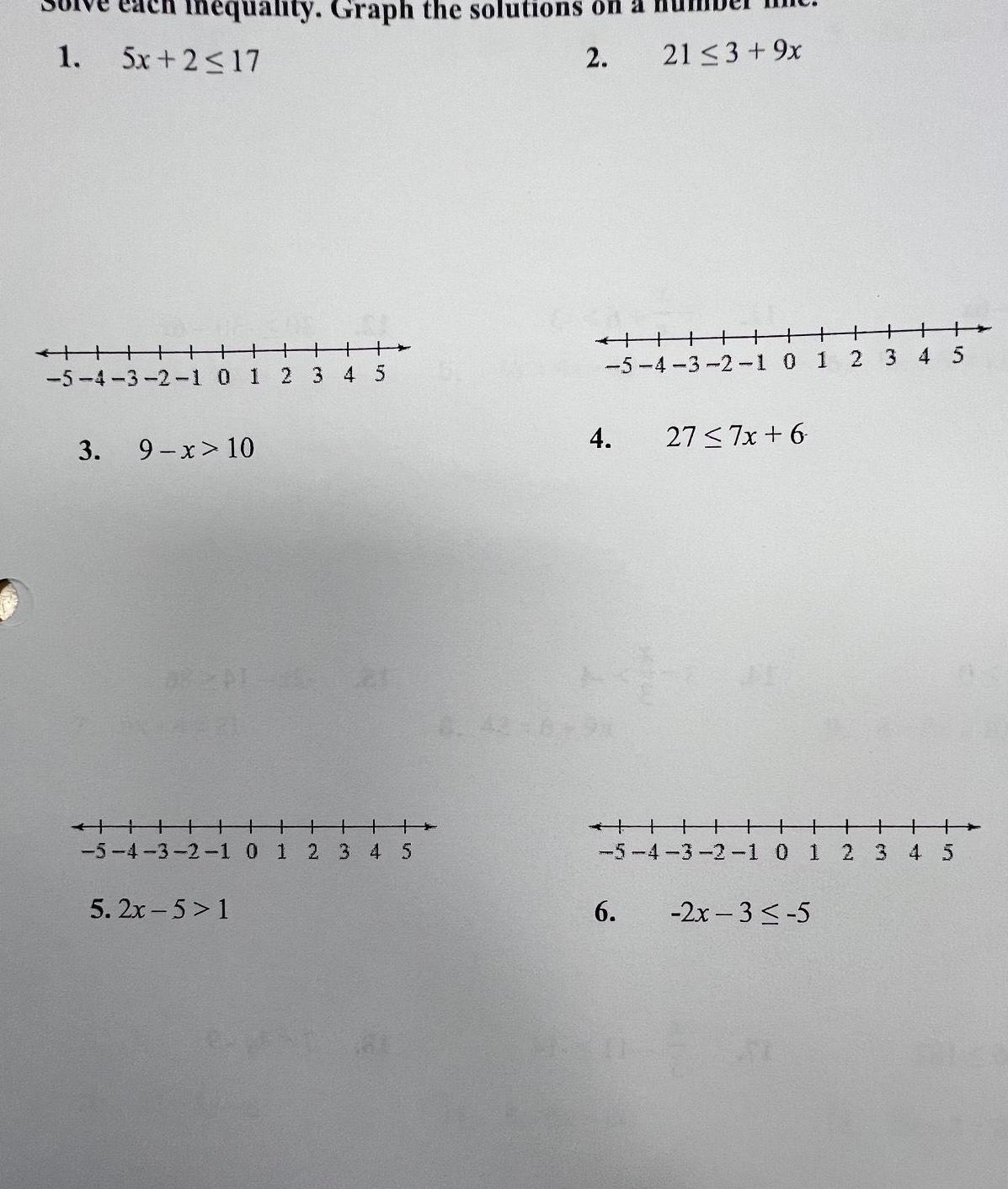
Algebra
Quadratic equations1 nequality Graph the solutions on 2 5x 2 17 TH1 5 4 3 2 1 0 1 2 3 4 5 3 9 x 10 5 4 3 2 1 0 1 2 3 4 5 5 2x 5 1 HHHHH 21 3 9x 5 4 3 2 1 0 1 2 3 4 5 4 6 27 7x 6 5 4 3 2 1 0 1 2x 3 5 2 3 4 5
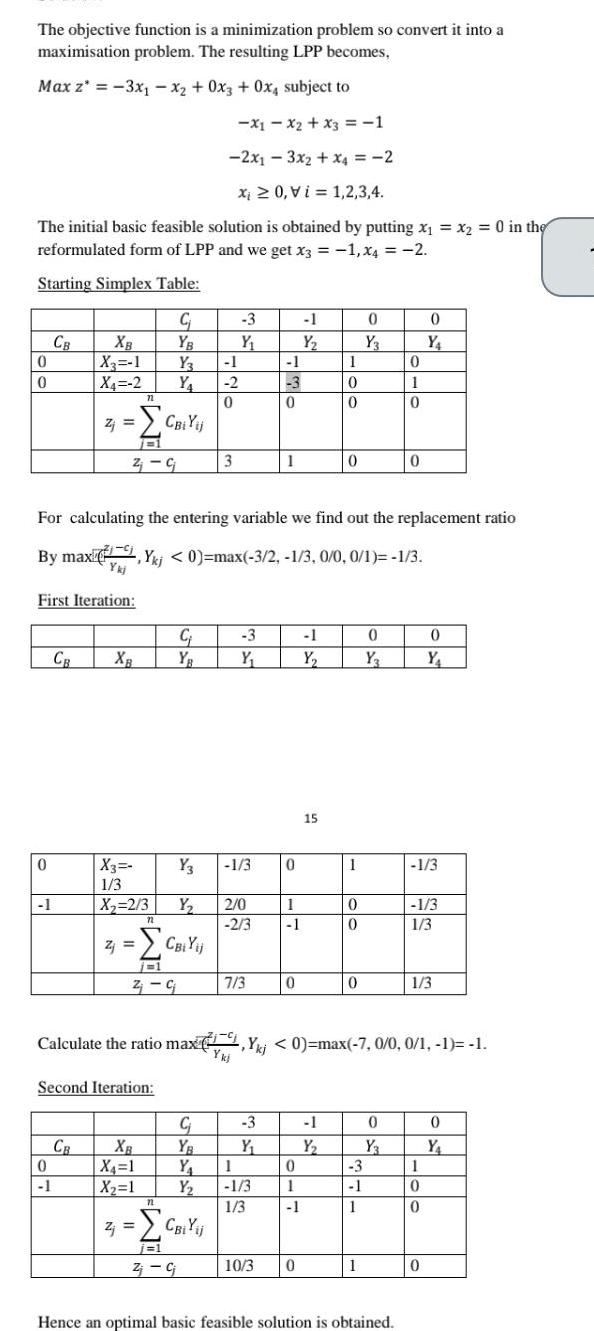
Algebra
Quadratic equationsThe objective function is a minimization problem so convert it into a maximisation problem The resulting LPP becomes Max z 3x x2 0x3 0x4 subject to X1X2 x3 1 2x13x2 x4 2 Xi 0 Vi 1 2 3 4 The initial basic feasible solution is obtained by putting x x2 0 in the reformulated form of LPP and we get x3 1 x4 2 Starting Simplex Table 0 0 0 CB 1 XB X 1 X4 2 First Iteration CB 0 1 Zj Z CB 71 n 7731 Z C XB X3 1 3 X 2 3 Second Iteration C YB Y Y Y3 Y Z CBi Yij j 1 2 G 72 XB X 1 X 1 CBi Yij For calculating the entering variable we find out the replacement ratio By max kj 0 max 3 2 1 3 0 0 0 1 1 3 72 C 1 2 0 3 3 Y Z CBiYij j 1 Z cj 3 Y 1 3 2 0 2 3 7 3 C YB Y 1 Y 1 3 1 3 3 Y 1 3 0 1 10 3 0 1 1 0 1 Y 0 1 1 0 1 Y 15 1 0 0 0 1 Y 1 7 9 Calculate the ratio max kj 0 max 7 0 0 0 1 1 1 Ykj 0 0 0 0 Y3 3 1 1 1 0 Y 0 1 0 0 Y3 0 Hence an optimal basic feasible solution is obtained 0 Y 1 3 0 Y 1 3 1 3 1 3 1 0 0 0 0 Y
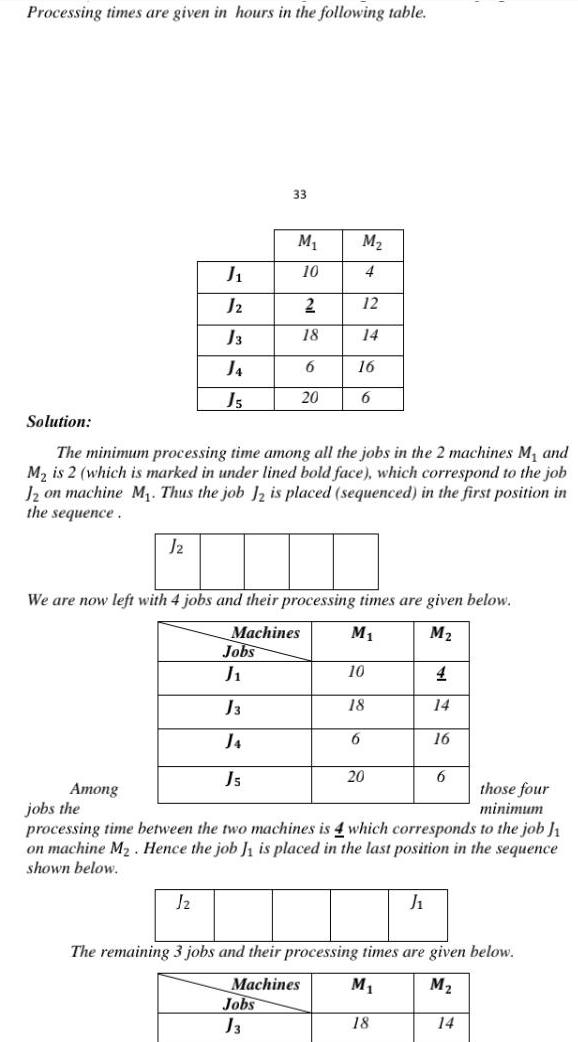
Algebra
Quadratic equationsProcessing times are given in hours in the following table J2 J J2 J3 Among J5 J Jobs J J3 33 Js M 10 2 al 2 Jobs J3 18 6 Solution The minimum processing time among all the jobs in the 2 machines M and M is 2 which is marked in under lined bold face which correspond to the job 12 on machine M Thus the job J2 is placed sequenced in the first position in the sequence 20 We are now left with 4 jobs and their processing times are given below Machines M M M 4 12 16 6 6 10 18 20 those four minimum jobs the processing time between the two machines is 4 which corresponds to the job J on machine M Hence the job J is placed in the last position in the sequence shown below 4 14 J 18 16 6 The remaining 3 jobs and their processing times are given below Machines M M 14
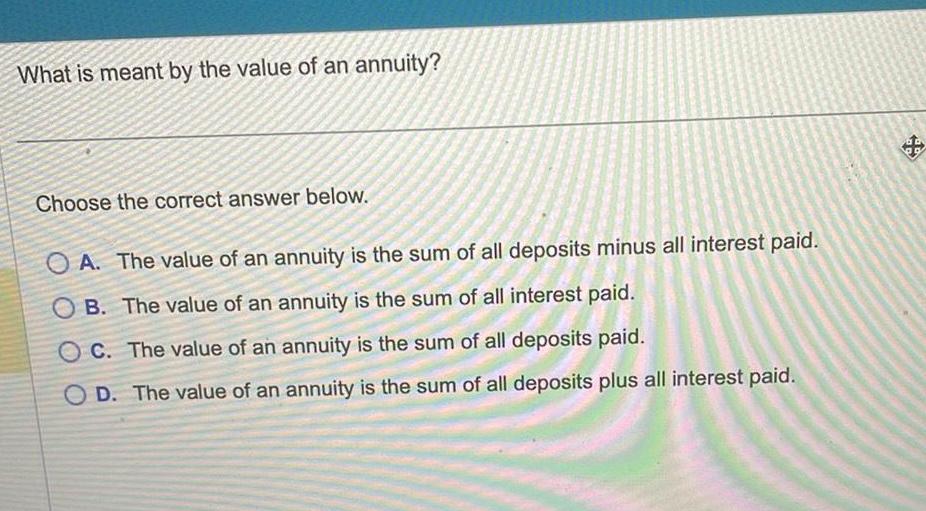
Algebra
Quadratic equationsWhat is meant by the value of an annuity Choose the correct answer below OA The value of an annuity is the sum of all deposits minus all interest paid OB The value of an annuity is the sum of all interest paid OC The value of an annuity is the sum of all deposits paid OD The value of an annuity is the sum of all deposits plus all interest paid
Algebra
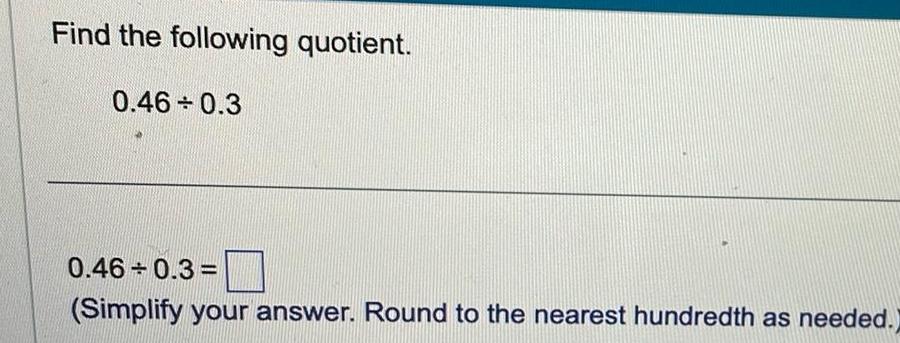
Quadratic equationsFind the following quotient 0 46 0 3 0 46 0 3 Simplify your answer Round to the nearest hundredth as needed

Algebra
Quadratic equationsFind a polynomial function P of the lowest possible degree having real coefficients a leading coefficient of 1 and with the given zeros 2 21 2 and 1 The polynomial of lowest degree is P x
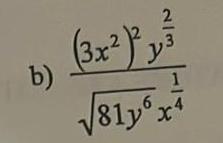
Algebra
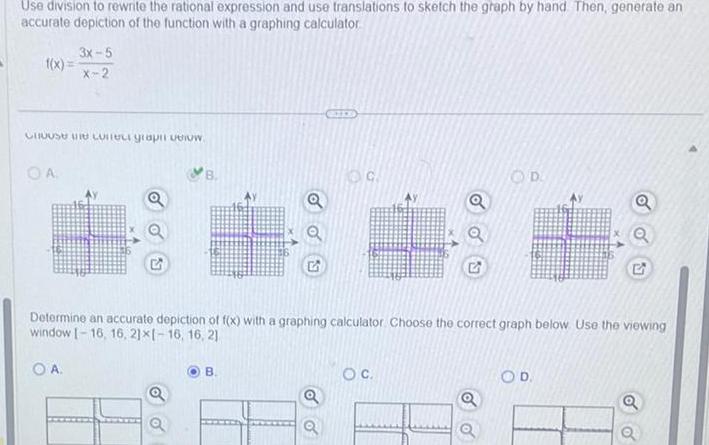
Quadratic equationsUse division to rewrite the rational expression and use translations to sketch the graph by hand Then generate an accurate depiction of the function with a graphing calculator 3x 5 X 2 Choose the corect grapi celow OA B Q G OC OD Determine an accurate depiction of f x with a graphing calculator Choose the correct graph below Use the viewing window 16 16 21x1 16 16 21 OA OD Q G o O

Algebra
Quadratic equationsCreate a 3rd degree polynomial with real coefficients and a leading coefficient of 1 which has the roots below 2 2 3i Put your answer in the expanded form ax3 bx cx d

Algebra
Quadratic equationsNASA launches a rocket at t 0 seconds Its position height in meters above sea level as a function of time t is given by s t 4 9t 67t 290 Use this position function to answer the following questions Round solutions to three decimal places if necessary Assuming that the rocket will splash down into the ocean at what time does splashdown occur The rocket splashes down after seconds How many seconds after the launch does the rocket reach its peak height The rocket reaches its peak height seconds after launch How high above sea level does the rocket get at its peak The rocket peaks at meters above sea level
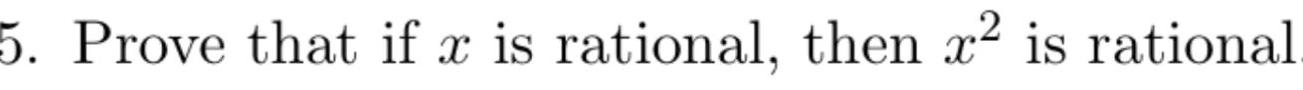

Algebra
Quadratic equationsIn the electric currect flow it is found that the resistance measured in the units called ohms offered by a fixed length of wire of a given material varies inversely as the square of the diameter of the wire If a wire 0 01 in in diameter has a resistance of 0 427 ohm what is the resistance of a wire of the same length and material with diameter 0 0249 in to the nearest ten thousandth The resistance of a wire is sohm Round your answer to the nearest ten thousandth C