Application of derivatives Questions and Answers

Calculus
Application of derivativesFind the polar coordinates of the following rectangular coordinates 12 1 01


Calculus
Application of derivativesFind the rectangular coordinates of the following polar coordinates 10 7 5 110
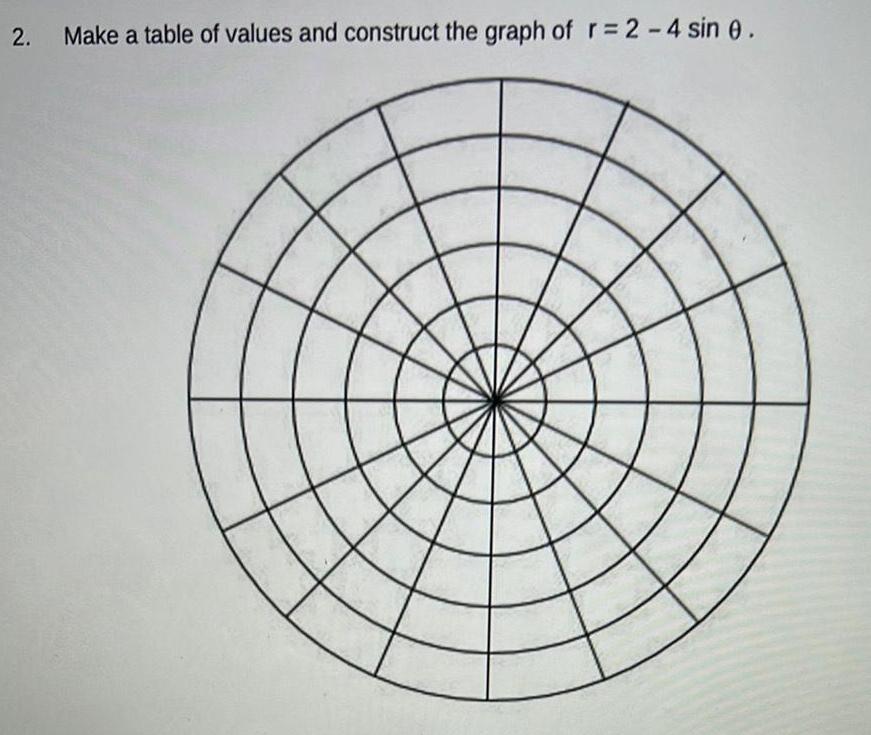
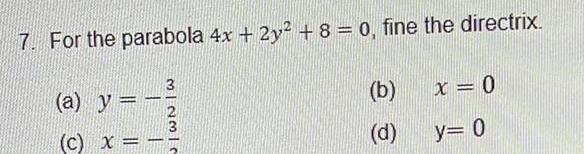
Calculus
Application of derivatives7 For the parabola 4x 2y 8 0 fine the directrix a y c x 3 J WN W b d x 0 y 0

Calculus
Application of derivativesFor which positive integers is the following series convergent Enter your answer as an inequalit 01
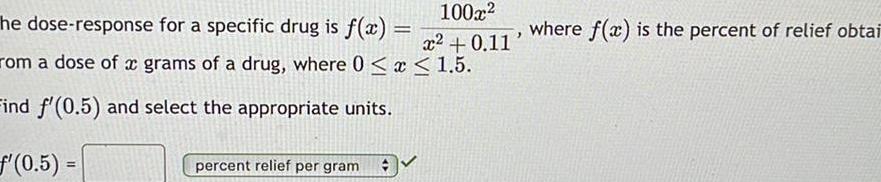
Calculus
Application of derivatives100x he dose response for a specific drug is f x x 0 11 rom a dose of a grams of a drug where 0 x 1 5 Find f 0 5 and select the appropriate units f 0 5 percent relief per gram where f x is the percent of relief obtai
Calculus
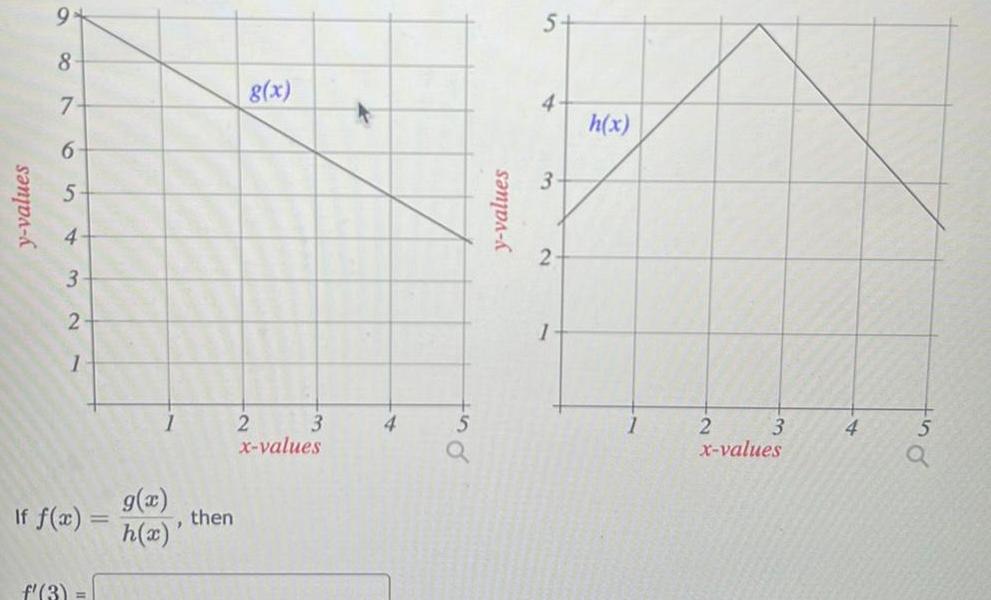
Application of derivativesy values 9 8 7 6 5 4 3 2 1 If f x f 3 1 g x h x then g x 2 3 x values y values 5 B 3 2 1 h x 2 3 x values 4 5
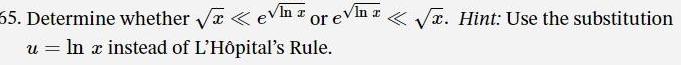
Calculus
Application of derivativesIn z 55 Determine whether evn or e x Hint Use the substitution u ln x instead of L H pital s Rule

Calculus
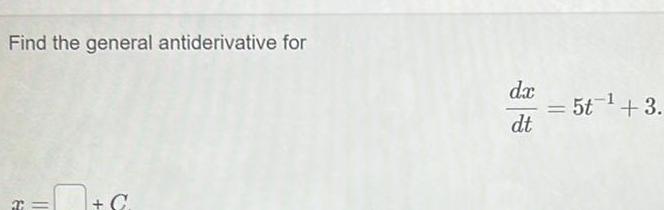
Application of derivativesFind the particular antiderivative that satisfies the following conditions dy 52 4 dx x y y 1 5

Calculus
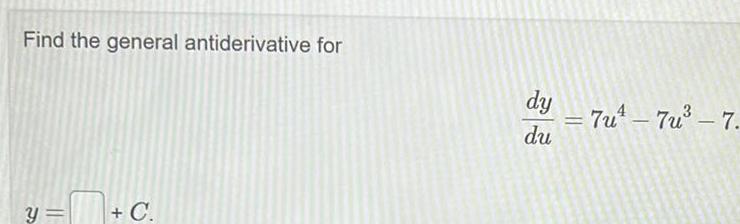
Application of derivativesConsider the function f t 6 sec t 10t Let F t be the antiderivative of f t with F 0 0 Then F t equals

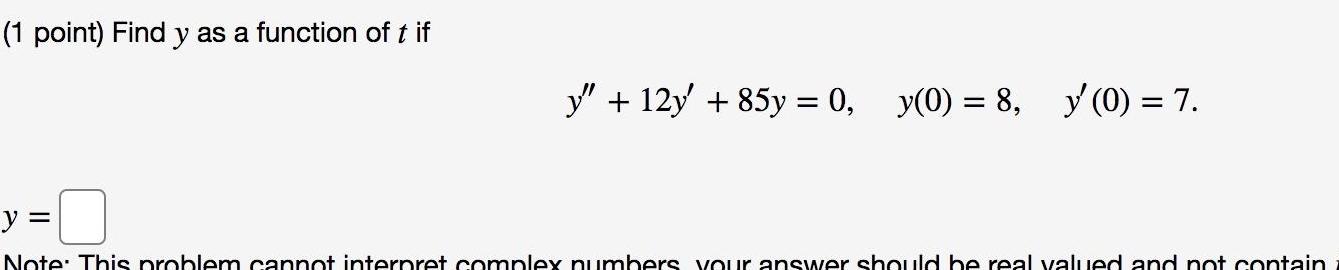
Calculus
Application of derivatives1 point Find y as a function of t if 12y 85y 0 y 0 8 y 0 7 y Note This problem cannot interpret complex numbers your answer should be real valued and not contain

Calculus
Application of derivativesFind the indicated value 2 3 f 5 1 if f x y 9x y 3xy f 5 1 Type an integer or a simplified fraction
Calculus
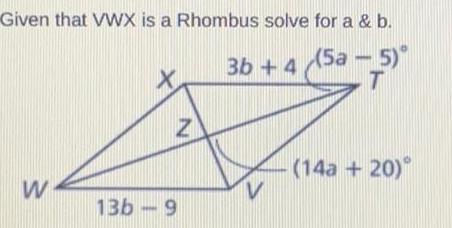
Application of derivativesGiven that VWX is a Rhombus solve for a b 3b 4 5a 5 T W X Z 13b 9 V 14a 20

Calculus
Application of derivatives1 1 x 2 SS S 1 0 0 1 1 x 2 S S S 1 1 x 1 2 2 1 x y dz dy dx 2 dz dy dx 1 0 0 Type an exact answer using as needed

Calculus
Application of derivatives20 1 pt 03 299 Details Find the maximum and minimum values of the function g 0 70 8 sin on the interval 0 Minimum value Maximum value Enter exact values or round to the nearest 0 001

Calculus
Application of derivatives399 Detai Find the point on the line y 8x 3 closest to the point 10 2 A function s x giving the distance between the point 10 2 and a point x 8x 3 on the line is s x The point closest to the line is Enter the coordinates of the point Be sure to include commas and parentheses as required

Calculus
Application of derivativesylinder shaped can needs to be constructed to hold 350 cubic centimeters of soup The materia for the sides of the can costs 0 02 cents per square centimeter The material for the top and bottor of the can need to be thicker and costs 0 07 cents per square centimeter Find the dimensions for the can that will minimize production cost To minimize the cost of the can use T h The minimum cost of this can would be C Round your answers to the nearest hundredth Helpful information h height of can r radius of can Volume of a cylinder V h Area of the sides A 2 rh Area of the cents

Calculus
Application of derivativeshy the gift According to the shipping regulation of a may not exceed 124 inches where by girth we mean the perimeter of the smallest end What is the largest possible volume of a rectangular parcel with a square end that can be sent by mail What are the dimensions of the package of largest volume a Suppose a box has two square ends and other faces are rectangles Let a represent the length of one side of the square end and y the length of the longer side Draw the box and label the sides b Find a formula for the volume of the box in terms of x and y V c The problem statement tells us that the parcel s girth plus length may not exceed 124 inches In order to maximize volume we assume that we will actually need the girth plus length to equal 124 inches What equation does this produce involving and y d Solve the equation you found in c for one of a or y whichever is easier e Now use your work in b and d to determine a formula for the volume of the parcel so that this formula is a function of a single variable Simplify your answer V f Over what domain should we consider this function Note that both x and y must be positive how does the constraint that girth plus length is 124 inches produce intervals of possible values for x and y g Find the absolute maximum of the volume of the parcel on the domain you established in f and hence also determine the dimensions of the box of greatest volume C y in in

Calculus
Application of derivatives24 Simplify and express your answer in exponential form Assume x 0 y 0 x y x y 16 34

Calculus
Application of derivatives20 Simplify the following complex fraction 8x 17 8x 10 x 17 x 10 17 10 17 7x 10 7x None of the above X x 10 X 7 7

Calculus
Application of derivatives23 Simplify the following expression 15y8 15y15 245 243y15 45 243245 None of the above 3x9 23

Calculus
Application of derivatives12 The expression a 3a 1 5 is equivalent to which of the following a 5 3 a 5 a 5 3 a 5 3a8 5 all s 5 3 a 5 a 1 3a 5
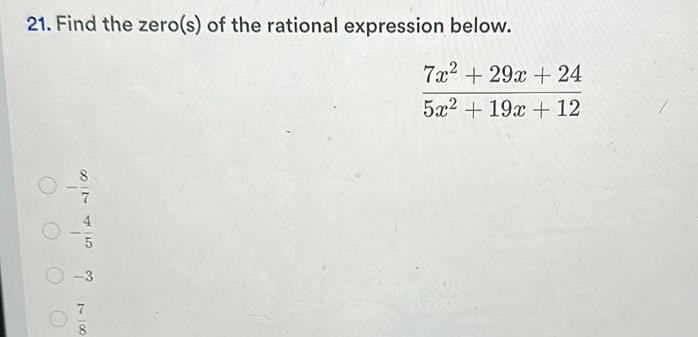
Calculus
Application of derivatives21 Find the zero s of the rational expression below O 8 7 do A 78 7x 29x 24 5x2 19x 12

Calculus
Application of derivatives6 Suppose y t 30e t 9 represents the number of bacteria present at time t minutes At what time will the population reach 100 bacteria Note Answers are expressed in terms of the natural logarithm In 100 In 9 3 ln 30 In 91 mins 1 90 91 In 3 30 In 91 3 In 30 mins mins mins None of the above

Calculus
Application of derivatives16 Find the equation s of all the vertical and horizontal asymptotes for the function f x 4x 1 5x 1 x 9 Vertical asymptote s a x 45 horizontal asymptote s y 20 Vertical asymptote s x 3 x 3 horizontal asymptote s none Vertical asymptote s x 3 x 3 horizontal asymptote s y 20 Vertical asymptote s x 3 x 3 horizontal asymptote s y 4 3 1 Vertical asymptote s z 5 horizontal asymptote s none 1 5


Calculus
Application of derivatives8 Consider the polynomials p x 21x 4x and g x 5 Find the x coordinate s of the point s of intersection of these two polynomials What is the sum of these x If there is only one point of intersection give the corresponding x coordinates coordinate 19 4 21 4 18
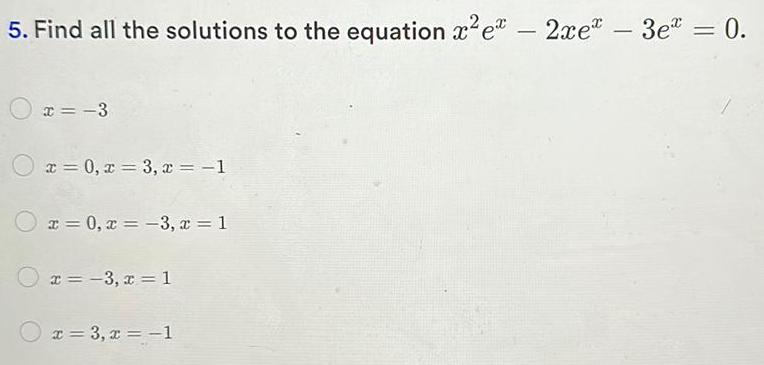
Calculus
Application of derivatives5 Find all the solutions to the equation x e 2xe 3e 0 x 3 x 0 x 3 x 1 x 0 x 3 x 1 x 3 x 1 x 3 x 1
Calculus
Application of derivativesConsider the one parameter family of functions given by p x 5x3 ax 2 where a 0 Determine p x p x The function p x has exactly two critical points The leftmost critical point is at x and the rightmost critical point is at a Determine p x p x The function p x has exactly one inflection point at x A where A p x is Select an answer for A and Select an answer for z A If the value of a is increased what happens to the location of the critical numbers and the inflection point O Both critical points and the inflection point move left O Both critical points and the inflection point move right O One critical point and the inflection point move left The other critical point stays fixed One critical point and the inflection point move right The other critical point stays fixed O it is impossible to tell in general how the location of these points will
Calculus
Application of derivativesLet a h and k be arbitrary real numbers with a 0 and let f be the function f x a x h k What familiar type of function is f Select an answer What information do you know about fjust by looking at its form There is no information that be gained simply by looking at the function f x in this form Parabola opens up if a 0 and opens down if a 0 Oh and k are the input and output of the parabola s vertex Next we use some calculus to develop familiar ideas from a different perspective To start treat a h and k as constants and compute f x f x Find all critical numbers of f These will depend on at lest one of a h and k X Assume a 0 Construct a first derivative sign chart for f Interval s where is negative Interval s where is positive Based on the information you ve found above classify the critical values of fas maxima or minima The critical value s at x
Calculus
Application of derivativesGiven the function g x 4x 18x g x Notice that g x 0 when x Find the second derivative g x g x Evaluate g 5 g 5 Now we want to know whether there is a local minimum or local maximum at x 5 so we will use the second derivative test At x 5 the graph of g x is O concave down concave up 120x find the first derivative g x At x 5 there is a local O minimum maximum 5 That is g 5 0 Based on the sign of this number does this mean the graph of g x is concave up or concave down at x 5 Based on the concavity of g x at x 5 does this mean that there is a local minimum or local maximum at x 5

Calculus
Application of derivativesA piece of cardboard measuring 11 inches by 9 inches is formed into an open top box by cutting squares with side length x from each corner and folding up the sides Find a formula for the volume of the box in terms of V x Find the value for x that will maximize the volume of the box Round your answer to the nearest hundredth X
Calculus
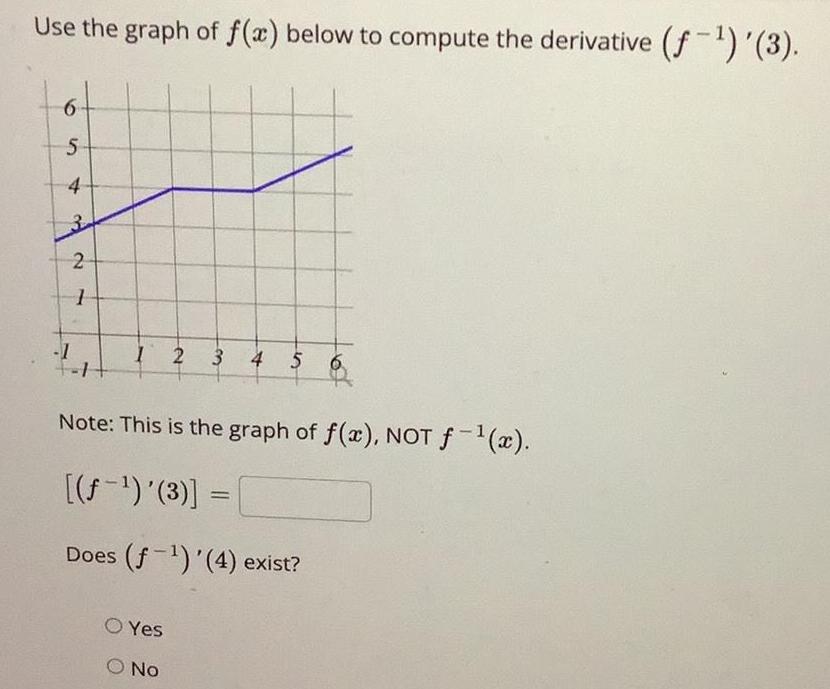
Application of derivativesUse the graph of f x below to compute the derivative f 3 6 5 4 3 2 1 1 1 2 3 4 5 6 Note This is the graph of f x NOT f x f 3 Does f 4 exist Yes No
Calculus
Application of derivativesConsider the function f x Find the derivative f x f x 2x 21x 180x 7 on the interval 10 4 This function has an absolute minimum value equal to This function has an absolute maximum value equal to
Calculus
Application of derivativesConsider the function f x x 147 0 x 9 The absolute maximum of f x on the given interval is at x and the absolute minimum of f x on the given interval is at x

Calculus
Application of derivativesUse L H pital s rule to determine the following limit Use exact values cos 8x 0 1 cos 7x lim 1

Calculus
Application of derivativesConsider the function f x 2x 8x 6 defined on 0 9 Find the derivative f x f x The function f x has exactly one critical point The critcal point is located at x The absolute maximum of f x on 0 9 occurs at x The absolute minimum of f x on 0 9 occurs at x Question a 99
Calculus
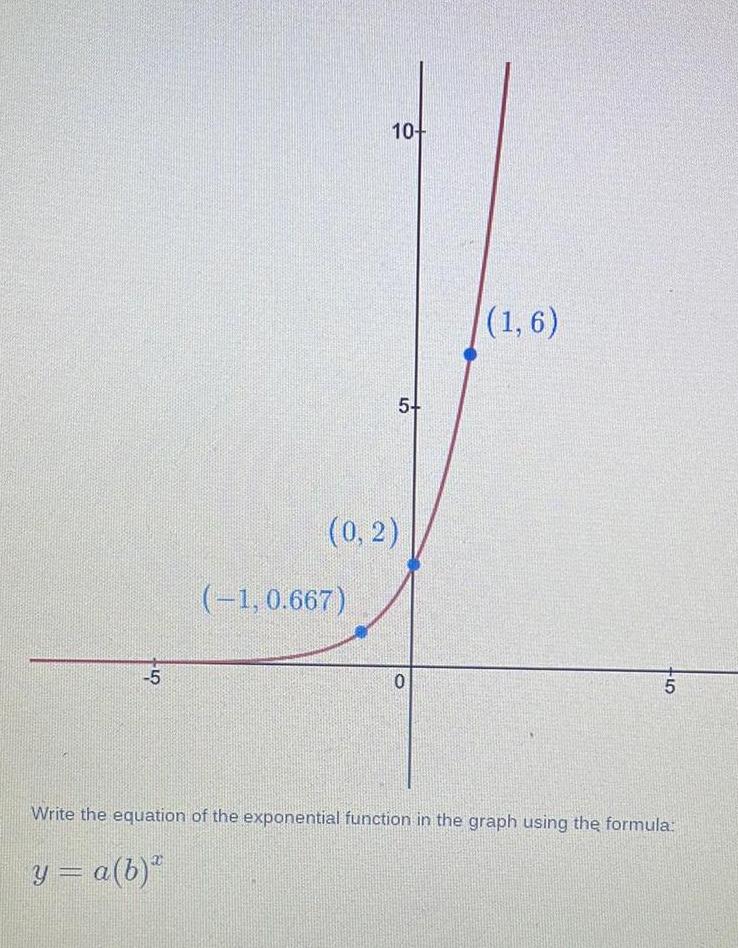
Application of derivatives5 y a b 10 1 0 667 5 0 2 0 1 6 5 Write the equation of the exponential function in the graph using the formula

Calculus
Application of derivativesIdentify a pair of alternate interior angles in the diagram Name th
Calculus
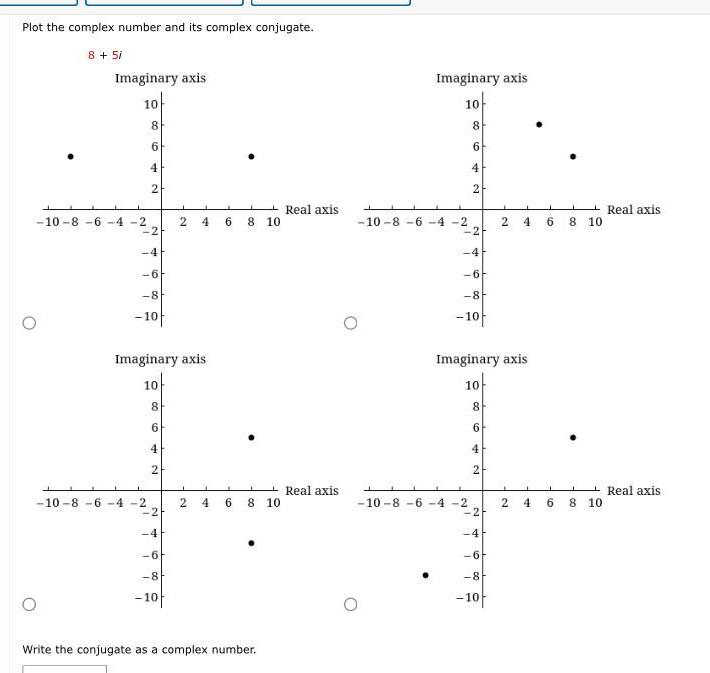
Application of derivativesPlot the complex number and its complex conjugate 8 5i Imaginary axis 10 10 8 6 4 2 L 8 6 1 4 2 2 6 8 10 10 8 6 4 2 Imaginary axis 10 8 6 4 2 2 4 6 2 4 8 10 2 4 6 6 8 10 8 10 Write the conjugate as a complex number Real axis Real axis Imaginary axis 10 T 8 6 10 8 6 4 2 2 2 6 8 10 10 8 6 4 2 Imaginary axis 10 8 6 4 2 2 4 L 2 6 8 10 4 2 J 6 4 6 8 10 8 10 Real axis Real axis

Calculus
Application of derivatives7 Write the matrix equation as a system of equations 1 6 H 2 1 0 3 2 1 3 3 4 2
Calculus
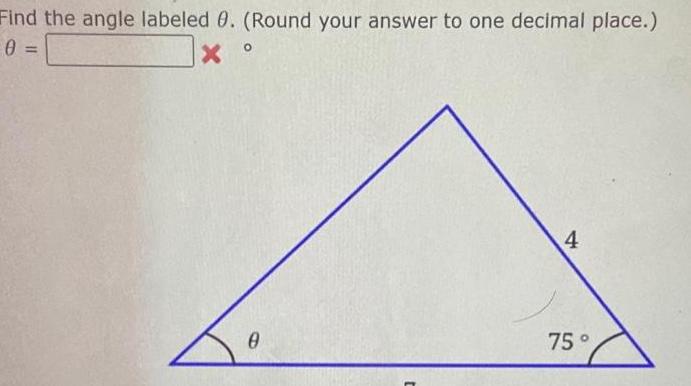
Application of derivativesFind the angle labeled 0 Round your answer to one decimal place 0 X 0 4 75