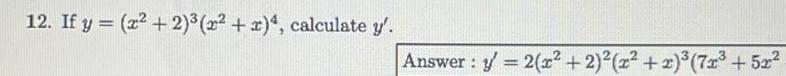Application of derivatives Questions and Answers
Calculus
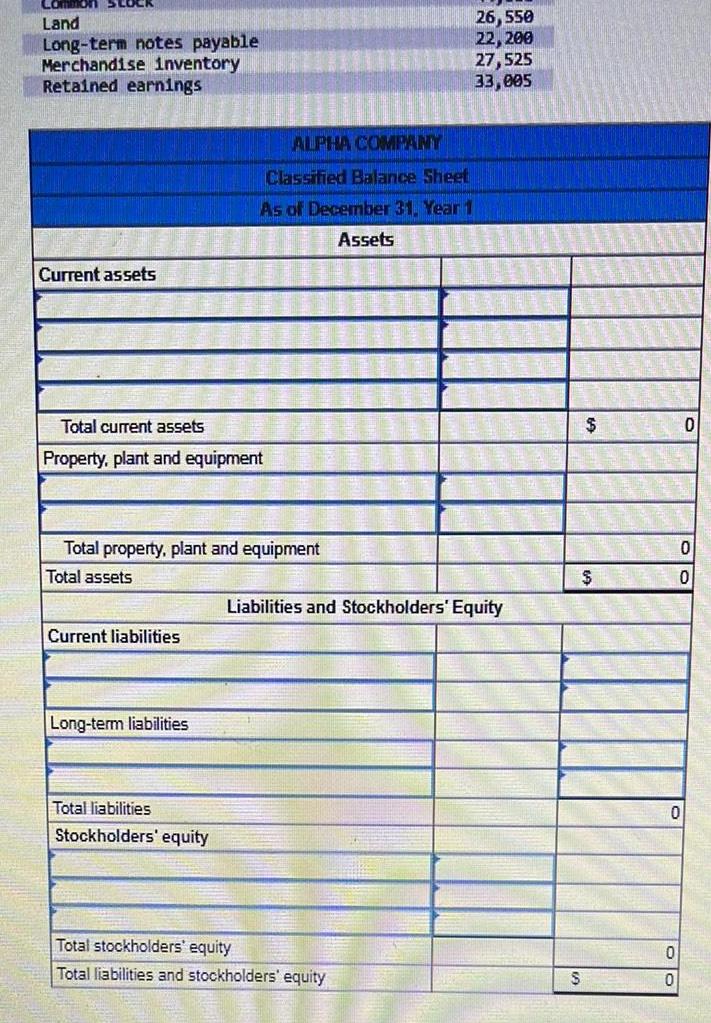
Application of derivativesLand Long term notes payable Merchandise inventory Retained earnings Current assets Total current assets Property plant and equipment Total property plant and equipment Total assets Current liabilities Long term liabilities ALPHA COMPANY Classified Balance Sheet As of December 31 Year 1 Assets Total liabilities Stockholders equity 26 550 22 200 27 525 33 005 Liabilities and Stockholders Equity Total stockholders equity Total liabilities and stockholders equity S 0 0 0 0 0
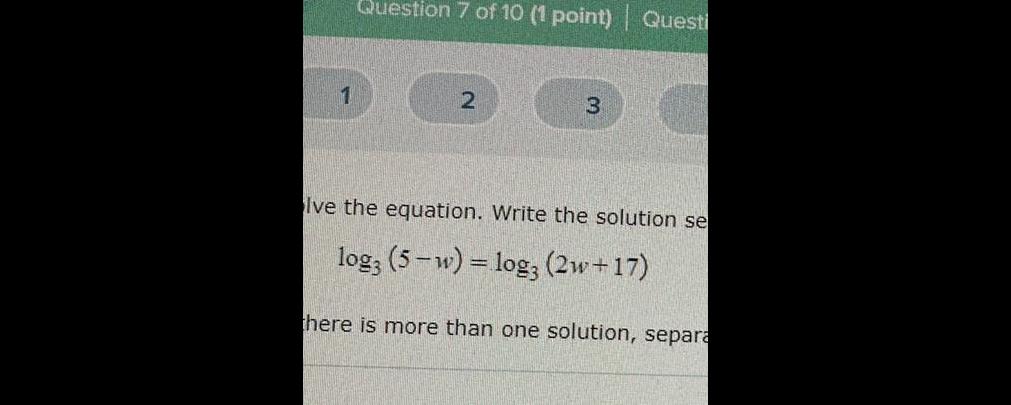
Calculus
Application of derivatives1 Question 7 of 10 1 point Questi 2 3 Ive the equation Write the solution se log3 5 w log3 2w 17 there is more than one solution separa

Calculus
Application of derivativesKevin is an auto mechanic He spends 3 hours when he replaces the shocks on a car and 2 hours when he replaces the brakes He works no more than 36 hours a week He routinely completes at least 2 shocks replacements and 6 brake replacements a week If he charges 450 for labor replacing shocks and 200 in labor for replacing brakes how many jobs of each type should he complete a week to maximize his income Kevin should do shock replacements and brake replacements every week to maximize his weekly income
Calculus
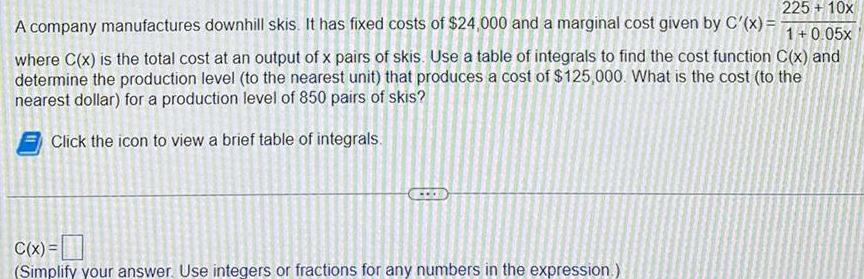
Application of derivatives225 10x 1 0 05x where C x is the total cost at an output of x pairs of skis Use a table of integrals to find the cost function C x and determine the production level to the nearest unit that produces a cost of 125 000 What is the cost to the nearest dollar for a production level of 850 pairs of skis Click the icon to view a brief table of integrals A company manufactures downhill skis It has fixed costs of 24 000 and a marginal cost given by C x C x Simplify your answer Use integers or fractions for any numbers in the expression

Calculus
Application of derivativesFind the slope of the tangent line to the graph of the polar equation at the point specified by the value of 8 0 r cos 8
Calculus
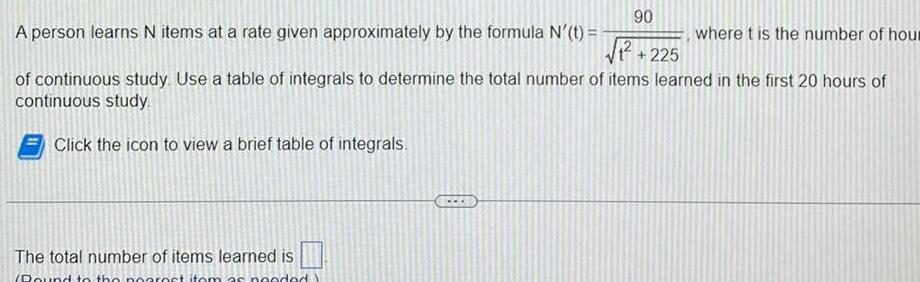
Application of derivatives90 A person learns N items at a rate given approximately by the formula N t of continuous study Use a table of integrals to determine the total number of items learned in the first 20 hours of continuous study Click the icon to view a brief table of integrals The total number of items learned is Pound to the nearest item as needed 225 where t is the number of hour

Calculus
Application of derivativesUse the trapezoidal rule with n 5 to approximate 2x dx and use the fundamental theorem of calculus to find the 2 exact value of the definite integral The approximate value of the integral from the trapezoidal rule is Simplify your answer

Calculus
Application of derivativesUse Simpson s rule with n 1 so there are 2n 2 subintervals to approximate 6 1 x dx The approximate value of the integral from Simpson s rule is Round the final answer to two decimal places as needed Round all intermediate values to four decimal place as needed
Calculus
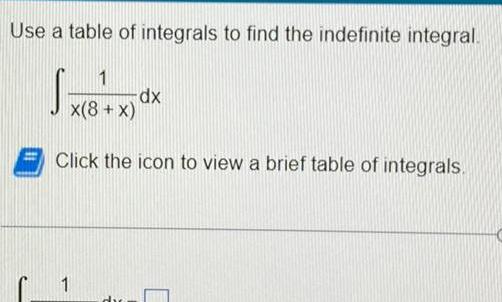
Application of derivativesUse a table of integrals to find the indefinite integral S 1 x 8 x Click the icon to view a brief table of integrals 1 dx
Calculus
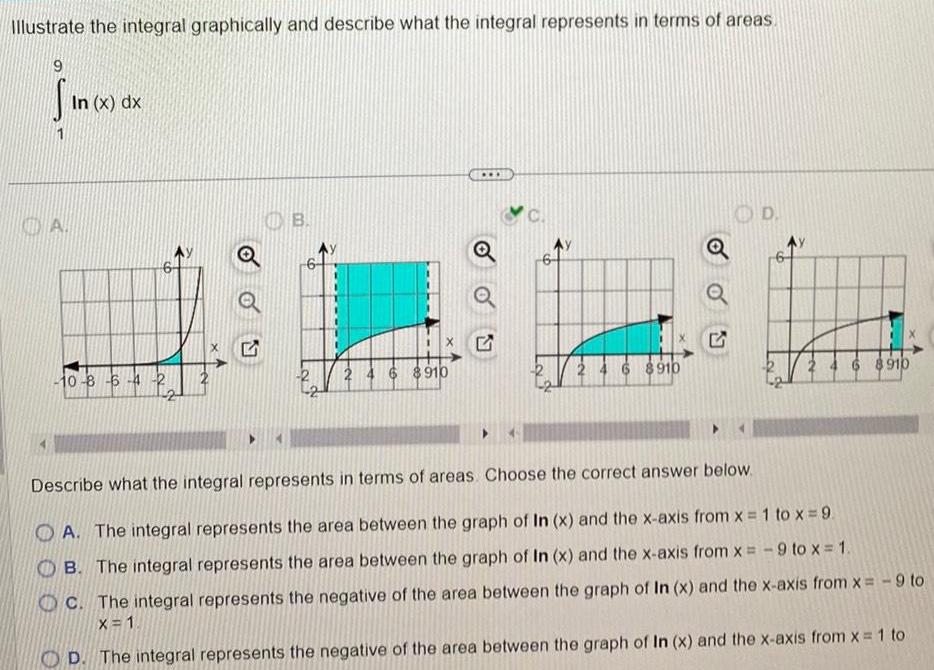
Application of derivativesIllustrate the integral graphically and describe what the integral represents in terms of areas 9 A In x dx 10 8 6 4 2 S OB 2 2 4 6 8910 Q 2 4 6 8910 OD 6 8910 Describe what the integral represents in terms of areas Choose the correct answer below A The integral represents the area between the graph of In x and the x axis from x 1 to x 9 B The integral represents the area between the graph of In x and the x axis from x 9 to x 1 OC The integral represents the negative of the area between the graph of In x and the x axis from x 9 to X 1 D The integral represents the negative of the area between the graph of In x and the x axis from x 1 to

Calculus
Application of derivativesFind the distance between the points with polar coordinates 2 7 and 4 27 3
Calculus
Application of derivativesBrightspace O TRIGONOMETRIC FUNCTIONS Using a calculator to approxi se the ALEKS calculator to evaluate ve your answers in radians und them to the nearest hundredt
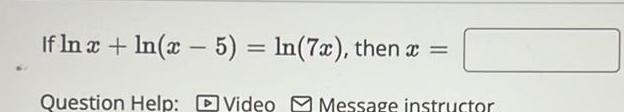
Calculus
Application of derivativesIf In x ln x 5 ln 7x then x Question Help Video Message instructor

Calculus
Application of derivativesFor each of the following integrals determine whether it converges and if it does evaluate it Make sure to i set up the improper integral using a limit ii determine whether or not this integral converges If converges finds its value Clearly show and justify your steps for each parts 11 a S 1 11 dr note that 1 1 is x 1 1 b 1 dx

Calculus
Application of derivativesSketch the parabola and label the focus vertex and directrix y 1 12 x 4

Calculus
Application of derivativesFind the equation of a hyperbola that satisfies the given conditions Vertices 0 2 0 2 asymptotes y 2 3 x

Calculus
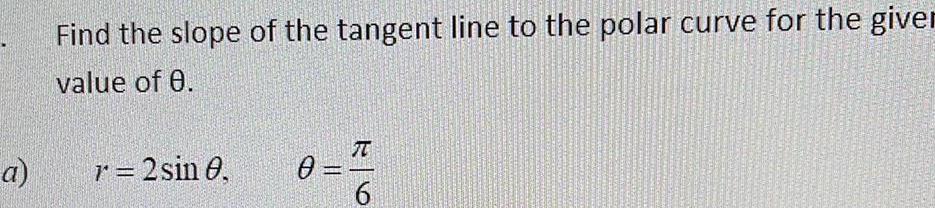
Application of derivativesa Find the slope of the tangent line to the polar curve for the giver value of 0 r 2 sin 0 0 K 6

Calculus
Application of derivativesSuppose that a volcano is erupting and readings of the rate r t at which solid materials are spewed into the atmosphere are given in the table The time t is measured in seconds and the units for are tonnes metric tons per second Use 6 equal subintervals t 0 1 2 3 4 6 r t 2 12 18 36 46 56 60 a Give upper and lower estimates for the total quantity Q 6 of erupted materials after 6 seconds Q 6 tonnes lower estimate Q 6 tonnes upper estimate b Use the Midpoint Rule to estimate Q 6 Use 3 equal subintervals

Calculus
Application of derivativesSolve the differential equation by variation of parameters 3 y 3y 2y e2x 1 ex

Calculus
Application of derivativesBased on census data the population of Freedonia is modeled by the function P t 277t 26710 peop where t represents the number of years after 1990 Use this function to determine how fast the population was increasing at the end of the year 1996 people per year
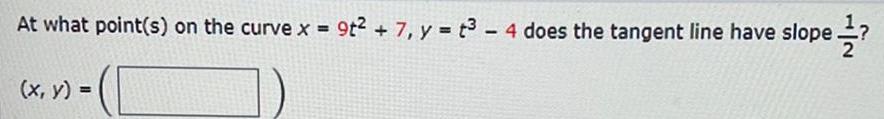
Calculus
Application of derivativesAt what point s on the curve x 9t 7 y t 4 does the tangent line have slope t3 x y
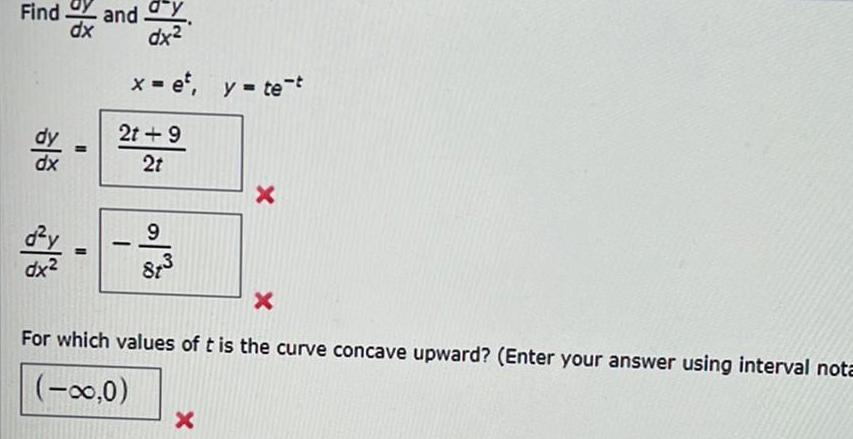
Calculus
Application of derivativesFind dx d y dx dx and dy dx x et y te t 2t 9 2t 9 2 3 X X For which values of t is the curve concave upward Enter your answer using interval nota 0 X

Calculus
Application of derivativesIn Exercises 15 24 use the fundamental identities and appropriate algebraic Operations to simplify each expression 15 1 tan x 1 tan x sec x 16 sec x 1 sec x 1 tan x 17 sec x tan x sec x tan x sec x 4 18 sec x 2 19 csc x cot4 X 20 sin cos tan cot x sec x csc x sin x cos x 21 sec 22 23 24 1 csc x 1 tan x csc x 1 x 2 tan x sec x csc x 1 3 tan x 1 tan x sec x 1 1
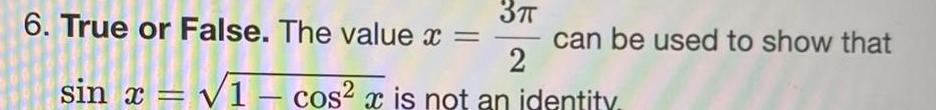
Calculus
Application of derivatives3 6 True or False The value x e or False 2 sin x 1 cos x is not an identity can be used to show that

Calculus
Application of derivativesk A offers 8 interest compounded annually and Bank B offers 7 2 interest compounded annually At the end of 6 years how much more money will be in Bank A than Bank B with
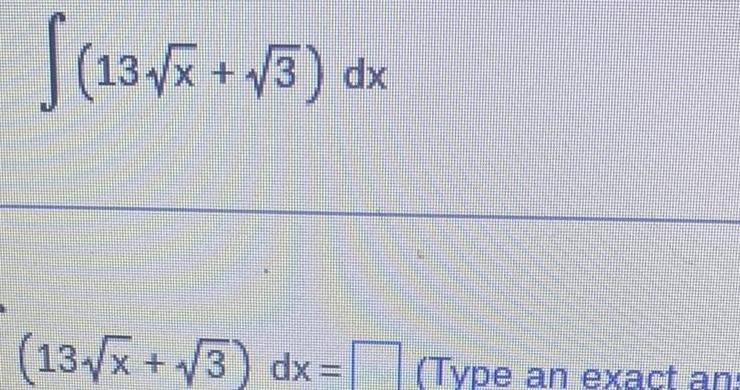
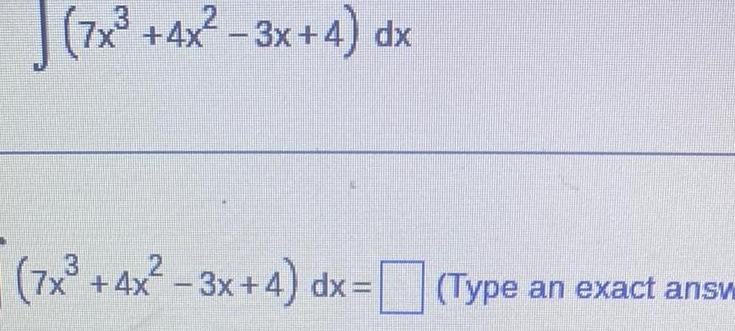

Calculus
Application of derivatives4 Sketch a possible graph of a function f x that satisfies the following conditions f x 0 on 1 f x 0 on 2 2 f x 0 on 1 lim f x 2 8118 f x 0 on 2 and 2 lim f x 0 818
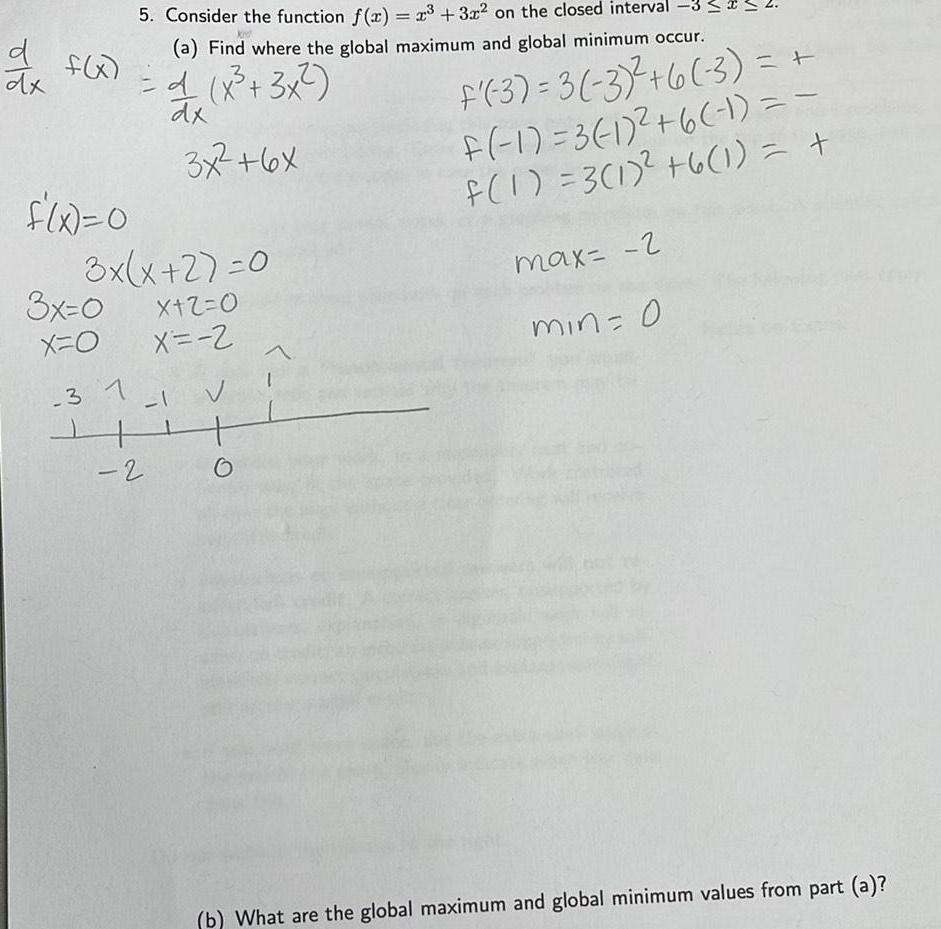
Calculus
Application of derivativesd dx f x f x 0 3x x 2 0 X 2 0 X 2 3x 0 x 0 5 Consider the function f x x 3x on the closed interval a Find where the global maximum and global minimum occur 3 4 x 3x dx 3x 6x 3 1 1 V 6 2 F 3 3 3 6 3 F 1 3 1 6 1 f 1 3 1 6 1 max 2 min 0 b What are the global maximum and global minimum values from part a

Calculus
Application of derivativeselevation to the top of from the base of the plateau Finding the Reach of a Ladder A 22 foot extension ladder leaning against a building makes a 70 angle with the ground How far up the building does the ladder touch

Calculus
Application of derivatives45 lighthouse OR 18 mi land Movement of a Minute Hand The minute hand of a clock is 6 inches long How far does the tip of the minute hand move in 15 minutes How far does it move in 25 minutes Round answers to two decimal places
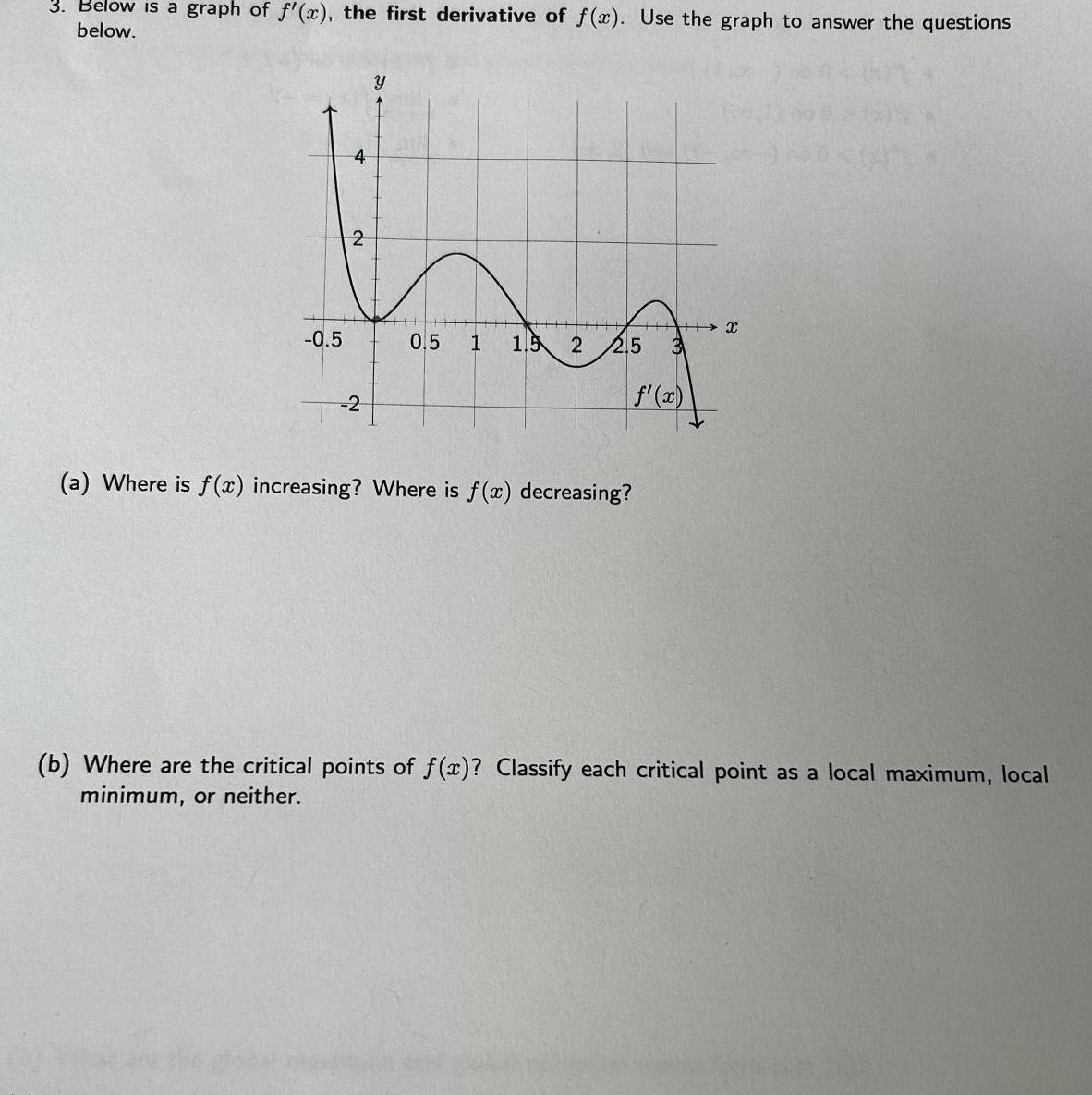
Calculus
Application of derivatives3 Below is a graph of f x the first derivative of f x Use the graph to answer the questions below 0 5 4 2 2 Y 0 5 1 1 5 2 2 5 f x a Where is f x increasing Where is f x decreasing X b Where are the critical points of f x Classify each critical point as a local maximum local minimum or neither

Calculus
Application of derivatives3 Do 3 of these 4 problems SHOW work even if you use a calculator to do the calculations 2 points e points total Find a positive conterminal angle to 1260 degrees Convert 20 56 degrees to degrees minutes seconds Find a negative conterminal angle to n 9 Convert 110 6 36 to decimal degrees 5 Matchir 1 y sin 2x 3 y 2 sin


Calculus
Application of derivativesd If f x tan x then the Mean Value Theorem guarantees that f c 0 for some c in the interval 0 TRUE FALSE

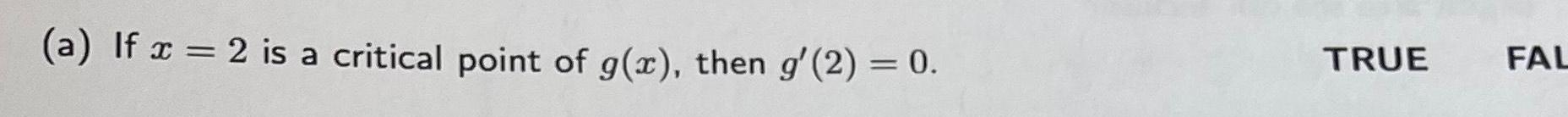
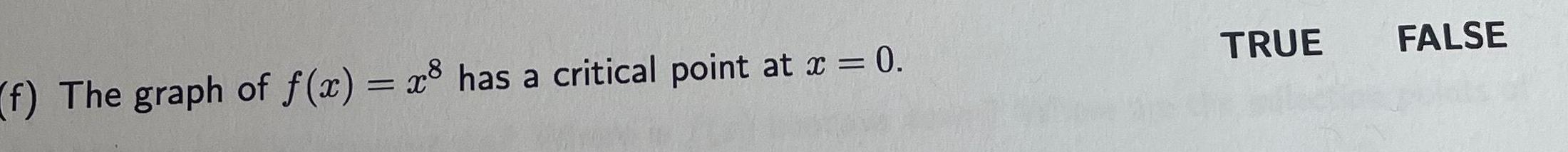
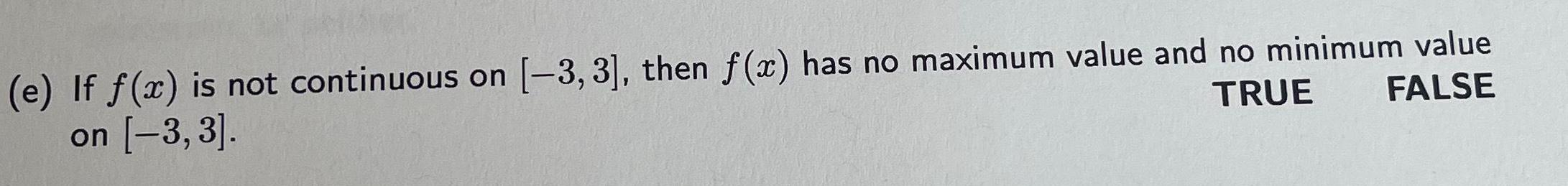
Calculus
Application of derivativese If f x is not continuous on 3 3 then f x has no maximum value and no minimum value TRUE FALSE on 3 3
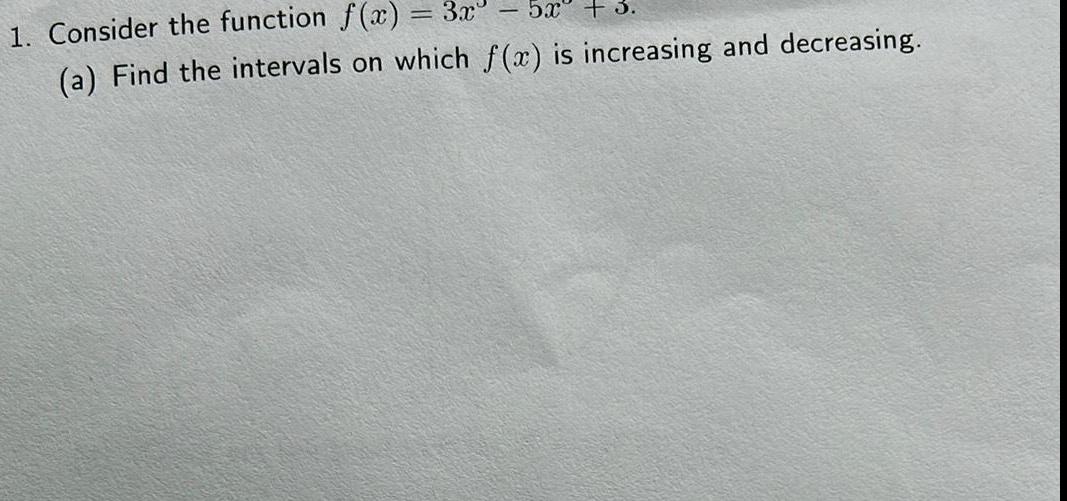
Calculus
Application of derivatives1 Consider the function f x 3x 52 3 a Find the intervals on which f x is increasing and decreasing


Calculus
Application of derivatives20 8 e 4x 20 18 Solve for x ex 15e 8 0 19 8pts Determine whether each equation is true or false for all possible values of the variables Ignore values of the variables for which any term is undefined Write T or F to the left of each problem log v log y b log x y log H log a a log c log log a log b d log 2 log 2 e log P log Q log P log Q log a log b log y 2 log b g log 7 x log 7 h log a a a The natural logarithm has base b The common logarithm has base
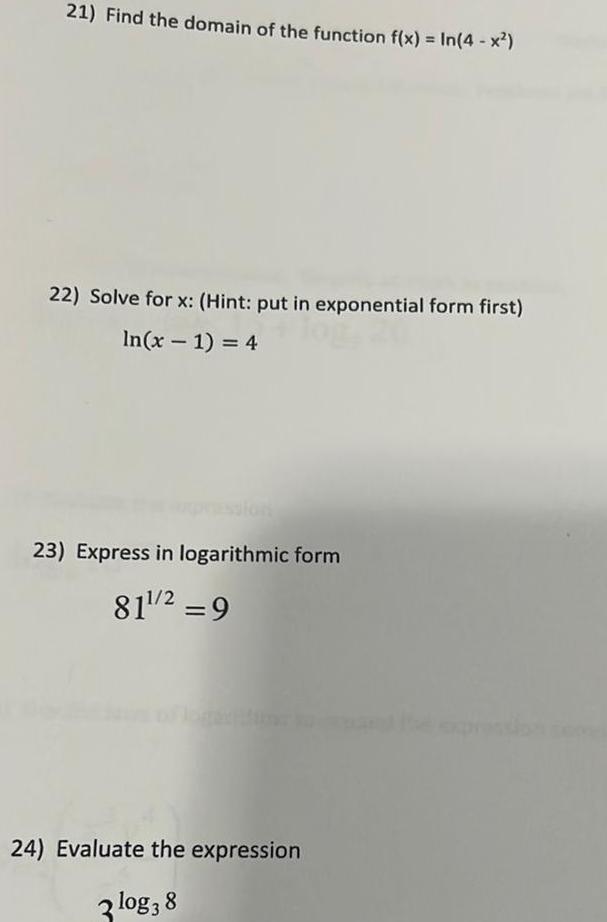
Calculus
Application of derivatives21 Find the domain of the function f x In 4 x 22 Solve for x Hint put in exponential form first In x 1 4 23 Express in logarithmic form 81 2 9 24 Evaluate the expression 3 log 3 8

Calculus
Application of derivatives3 The rate at which photosynthesis takes place for a certain plant species is modeled by the function P 1004 L 0 where P represents photosynthesis rate and L represents light intensity L 4 For what light intensity L is the photosynthesis rate P a maximum Your work must clearly show how you know your answer gives a maximum
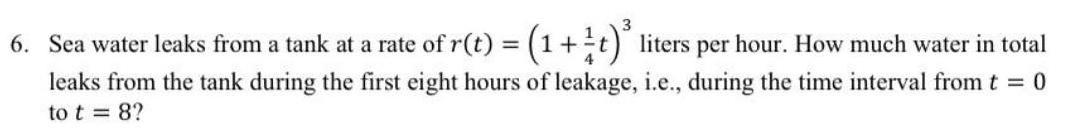
Calculus
Application of derivatives6 Sea water leaks from a tank at a rate of r t 1 t liters per hour How much water in total leaks from the tank during the first eight hours of leakage i e during the time interval from t 0 to t 8

Calculus
Application of derivatives11 Match the exponential function with it s graph Roman Numeral a f x 2 b f x 2 c f x 2 d f x 2 12 Solve the Equation a b c d 3xex x ex 0 13 Find the exponential function f x a Whose graph is given to the to the right 14 State the domain and range of f x 3 15 Solve for x log x 5 log x 3 1 n Domain Range 21 0 3 X Beed red mathesalvonnas