Application of derivatives Questions and Answers
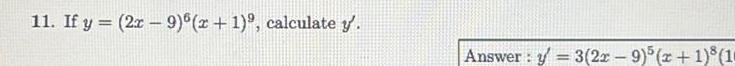
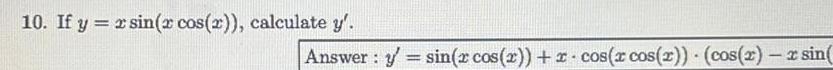
Calculus
Application of derivatives10 If y x sin x cos x calculate y Answer y sin x cos x x cos x cos x cos 2 xsin

Calculus
Application of derivatives16 If y cos x cos 3 calculate y 3 Int Answer y sin 2 cos 3 cos x 1


Calculus
Application of derivativesEstimate 26 by using a linear approximation of f x about the value 27 Round your answer to four decimal places if necessary Provide your answer bol
Calculus
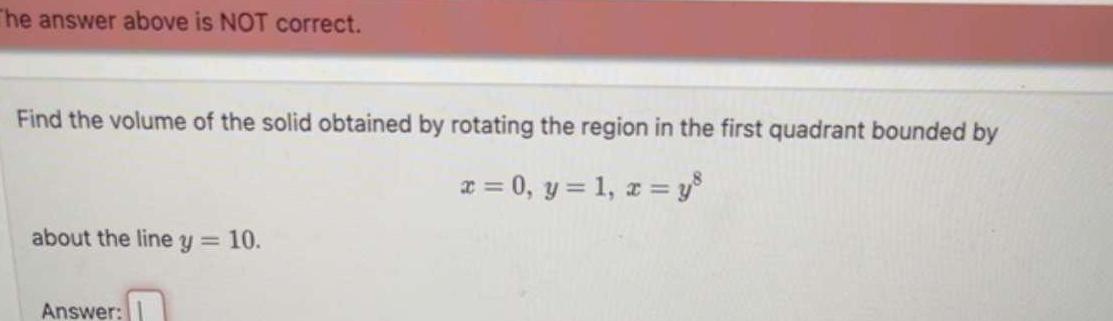
Application of derivativesThe answer above is NOT correct Find the volume of the solid obtained by rotating the region in the first quadrant bounded by x 0 y 1 x y about the line y 10 Answer
Calculus
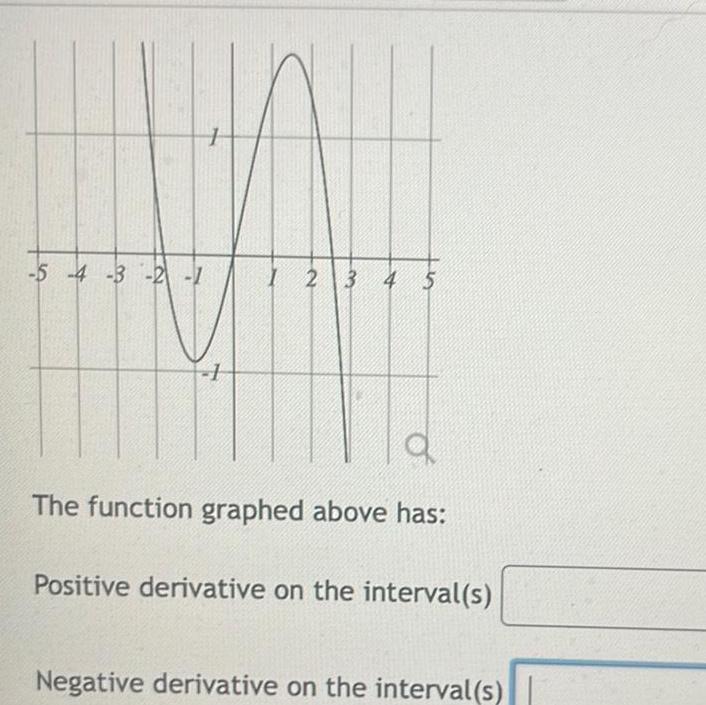
Application of derivatives5 4 3 2 1 1 2 3 4 5 o The function graphed above has Positive derivative on the interval s Negative derivative on the interval s
Calculus
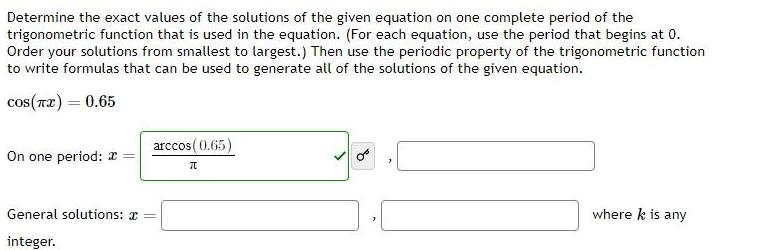
Application of derivativesDetermine the exact values of the solutions of the given equation on one complete period of the trigonometric function that is used in the equation For each equation use the period that begins at 0 Order your solutions from smallest to largest Then use the periodic property of the trigonometric function to write formulas that can be used to generate all of the solutions of the given equation cos x 0 65 On one period General solutions integer arccos 0 65 70 where k is any

Calculus
Application of derivativesSolve the logarithmic equation for x Enter your answers as a comma separated list log2 x log2 x 7 3

Calculus
Application of derivativesConsider the following 6 X 7 a Find the exact solution of the exponential equation in terms of logarithms X b Use a calculator to find an approximation to the solution rounded to six decimal places X
Calculus
Application of derivativessignment 11 Problem 9 ious Problem Problem List Next Problem nt Answer the following questions for the function ed on the interval 6 7 x is concave down on the open interval x is concave up on the open interval e minimum for this function occurs at

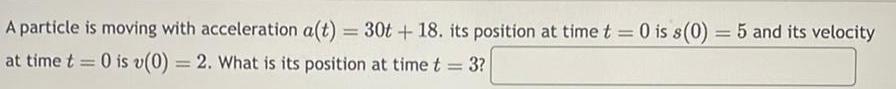
Calculus
Application of derivativesA particle is moving with acceleration a t 30t 18 its position at time t 0 is s 0 5 and its velocity at time t 0 is v 0 2 What is its position at time t 3

Calculus
Application of derivativesQuestion 2 The function h z z 1 can be expressed in the form f g 2 where f z z and g ar is defined below
Calculus
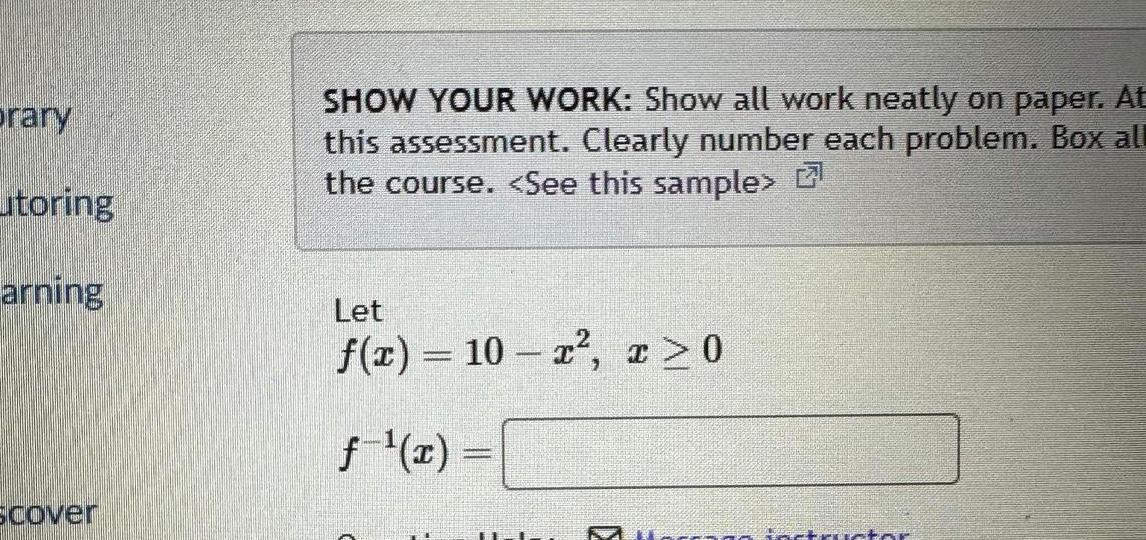
Application of derivativesbrary itoring arning scover SHOW YOUR WORK Show all work neatly on paper At this assessment Clearly number each problem Box all the course See this sample Let f x 10 x x 0 f x fastructor


Calculus
Application of derivativesme the focal length of a diverging lens which produces a virtual image 12 9 cm from the lens when the object is 32 4 cm from the lens

Calculus
Application of derivativesb Find the actual speed and direction of the airplane 12 A 3000 lb car is parked on a street that makes an angle of 16 with the horizontal Find the force required to keep the car from rolling down the hill
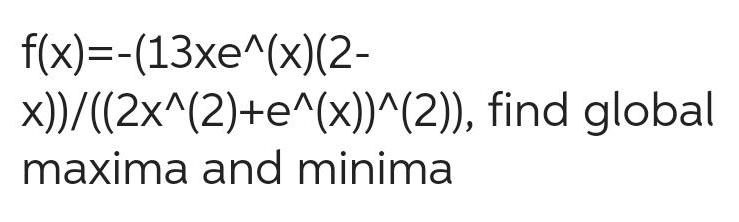
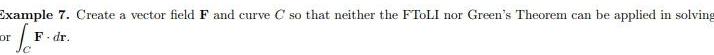
Calculus
Application of derivativesExample 7 Create a vector field F and curve C so that neither the FTOLI nor Green s Theorem can be applied in solving F or F dr
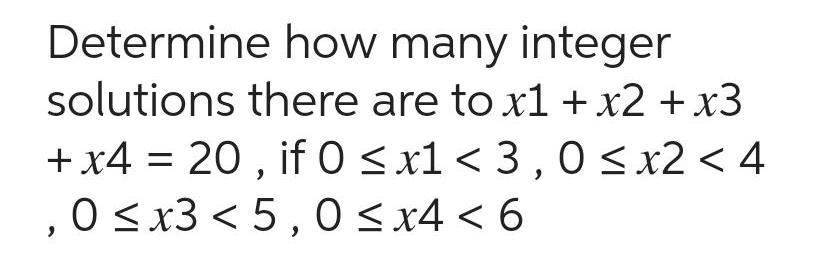
Calculus
Application of derivativesDetermine how many integer solutions there are to x1 x2 x3 x4 20 if 0 x1 3 0 x2 4 0 x3 5 0 x4 6

Calculus
Application of derivatives35 Let r denote the total rainfall in Portland on the jth day of the year in 2009 Interpret rj

Calculus
Application of derivatives3 Find a a unit vector in the direction of AB and b a vector of magnitude 3 in the opposite direction I A 4 0 B 2 1 4 Find a the direction angle

Calculus
Application of derivatives7 Eliminate the parameter rand identify the graph a x 4 t y 8 5t 3 t 5 b x 3cost y 3sint
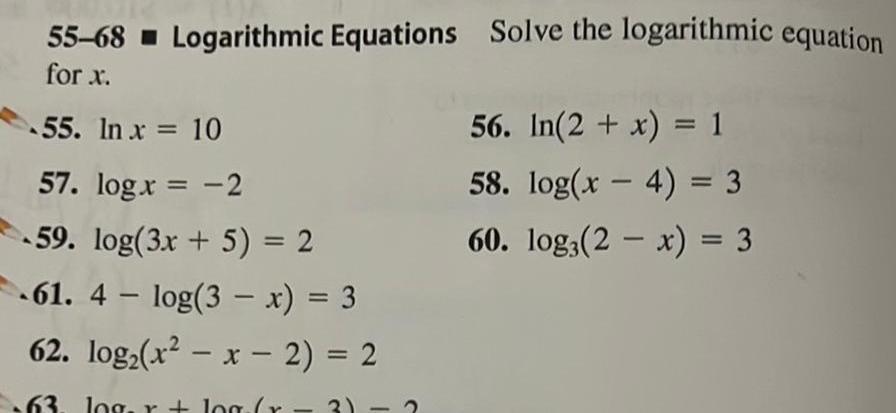
Calculus
Application of derivatives55 68 Logarithmic Equations Solve the logarithmic equation for x 55 In x 10 57 log x 2 59 log 3x 5 2 61 4 log 3 x 3 62 log x x 2 2 63 log r log r 3 2 56 In 2 x 1 58 log x 4 3 60 log 2x 3
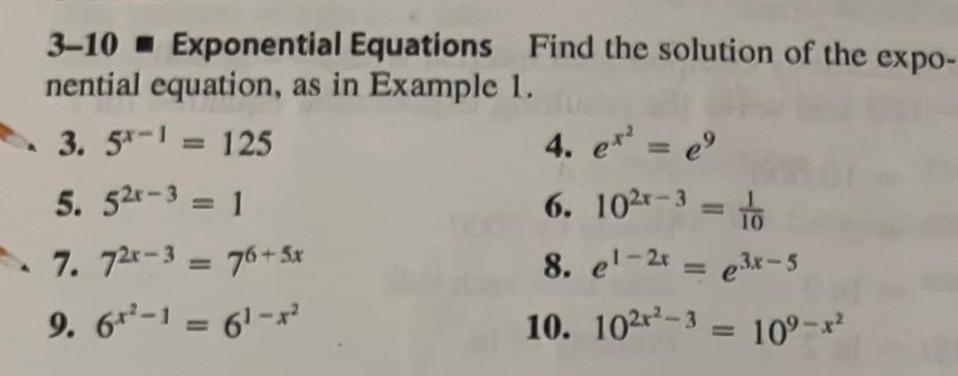
Calculus
Application of derivatives3 10 Exponential Equations Find the solution of the expo nential equation as in Example 1 3 5 1 125 5 52 31 7 72x 3 76 5x 9 6 1 61 x 4 e e 6 10 x 3 10 8 el 2x e3x 5 10 102 3 10
Calculus
Application of derivativesthe fractal dimension of t rging any portion of the c dimension is
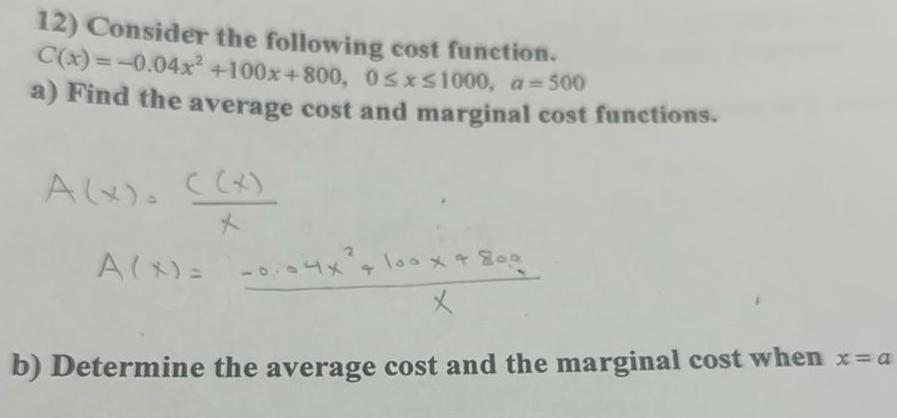
Calculus
Application of derivatives12 Consider the following cost function C x 0 04x 100x 800 0 x 1000 a 500 a Find the average cost and marginal cost functions A x x X A X 0104x 1x 4 100 x 800 x b Determine the average cost and the marginal cost when x a
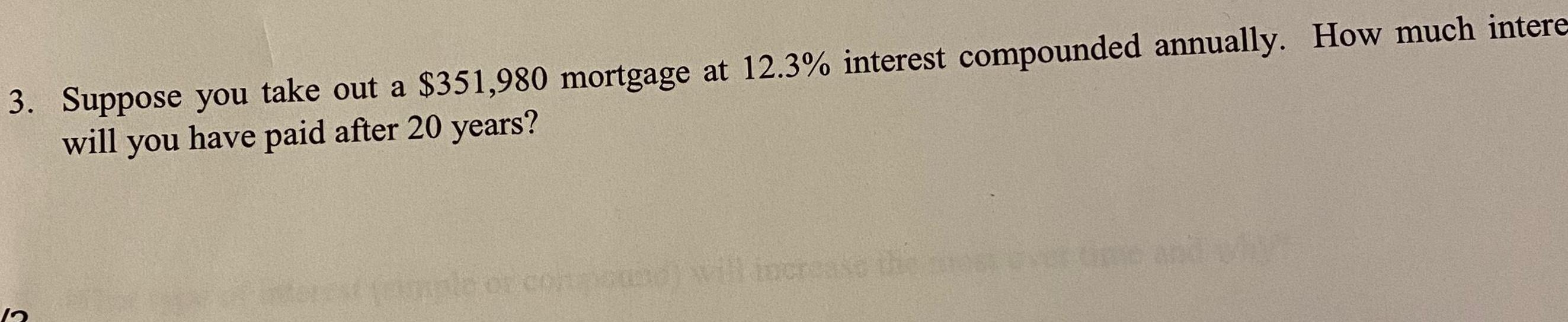
Calculus
Application of derivatives3 Suppose you take out a 351 980 mortgage at 12 3 interest compounded annually How much intere will you have paid after 20 years conmound will increase the

Calculus
Application of derivatives2 How much interest simple will you pay after 12 years at 3 3 on a loan of 763 000

Calculus
Application of derivatives248 Pre Health students put in their applications for their programs of choice 123 students applied to the nursing program 45 applied to the dental program 22 applied to the fitness program It has been reported that 28 students applied to the nursing program and to the dental program It has also been reported that 8 students applied to the fitness program and to the dental program Use Venn Diagrams to solve the following problems a What is the probability of picking at random a student who applied to the nursing program given that they also applied to the dental program Convert to percent then round to 2 significant figures DO NOT INPUT THE SYMBOL b What is the probability of picking at random a student who applied to the fitness program given that they also applied to the dental program Convert to percent then round to 2 significant figures DO NOT INPUT THE SYMBOL
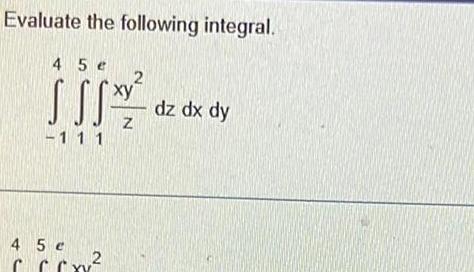
Calculus
Application of derivativesEvaluate the following integral 4 5 e 2 S SS 11 1 4 5 e CCCxv 2 dz dx dy
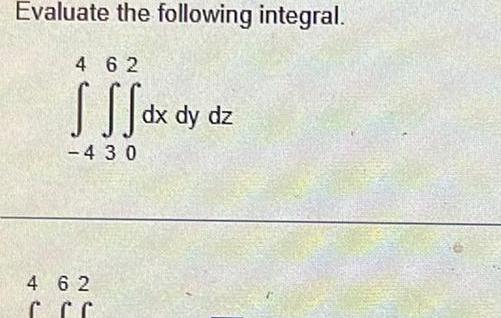
Calculus
Application of derivativesenMain Forums Calendar Grad ring 2023 Precalculus M Rational Inequa 2 answered

Calculus
Application of derivativesUse a graphing calculator to graph the equation over the indicated interval and fin the area between the curve and the x axis over that interval Find the answer to tw decimal places y x 4 ln x 1 x 8 2 14 10 42 6 14 8 28

Calculus
Application of derivativesFind the interest earned at 5 compounded continuously for two years by a continuous income stream with rate flow of f t 1250 Round answer to the nearest dollar 22 621 2379 129 2629

Calculus
Application of derivativesEvaluate the definite integral to two decimal places 5 1 e t dt 147 41 O 0 99 0 36 145 69


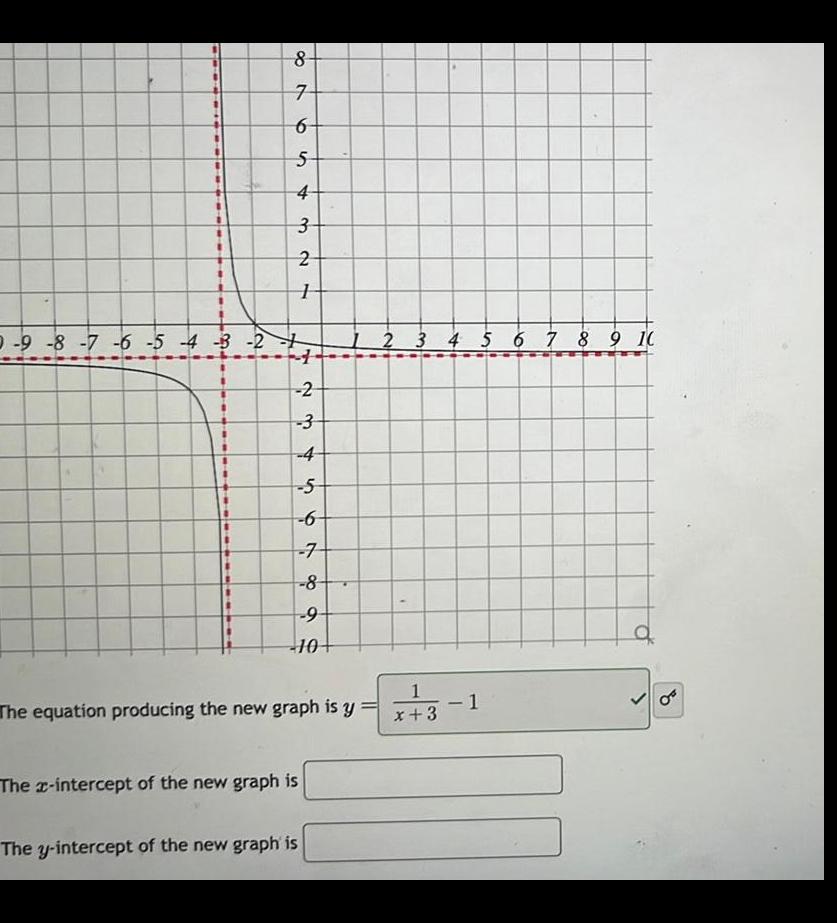
Calculus
Application of derivatives0 9 8 7 6 5 4 3 2 8 7 6 5 4 3 32 2 234 4 5 6 7 8 9 10 The equation producing the new graph is y The x intercept of the new graph is The y intercept of the new graph is 3 4 5 6 7 8 9 10 1 x 3 1 B
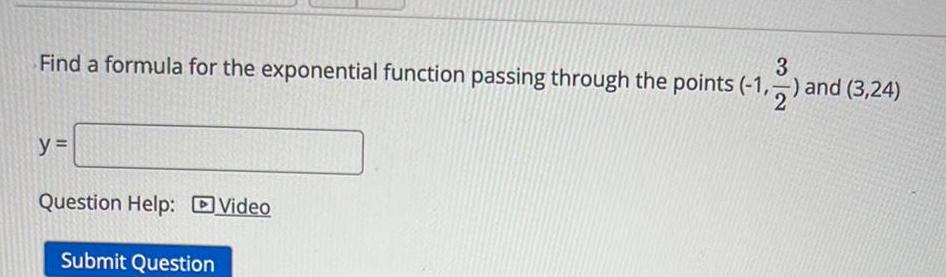
Calculus
Application of derivatives3 Find a formula for the exponential function passing through the points 1 1 2 and 3 24 y Question Help Video Submit Question
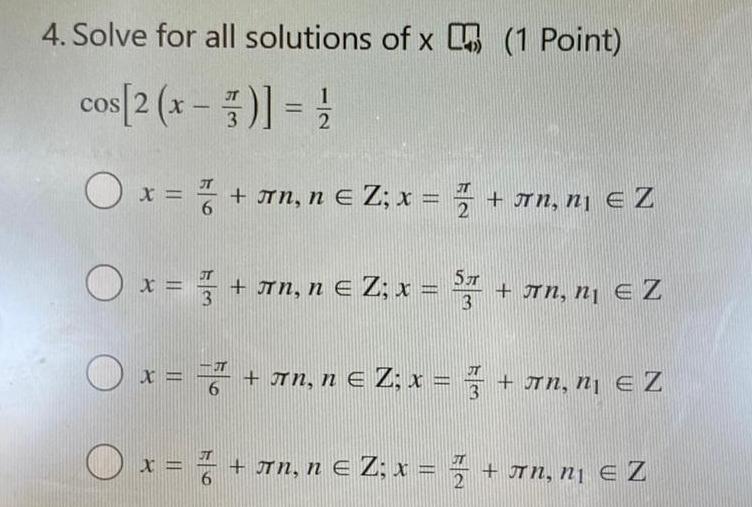
Calculus
Application of derivatives4 Solve for all solutions of x 1 Point cos 2 x 7 1 O x n n Z x 2 Jn n eZ x JnneZ x n n Z x 5JT 3 n n EZ O x y rn n e Z x Jn n eZ 6 3 x n n Z x n n e Z
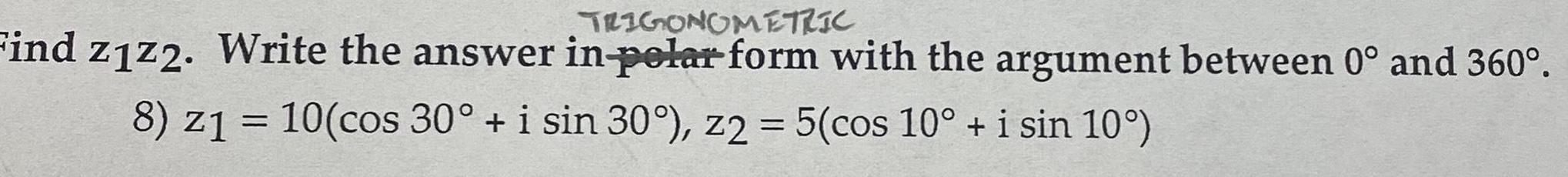
Calculus
Application of derivativesTRIGONOMETRIC Find z1z2 Write the answer in pelar form with the argument between 0 and 360 8 z1 10 cos 30 i sin 30 z2 5 cos 10 i sin 10
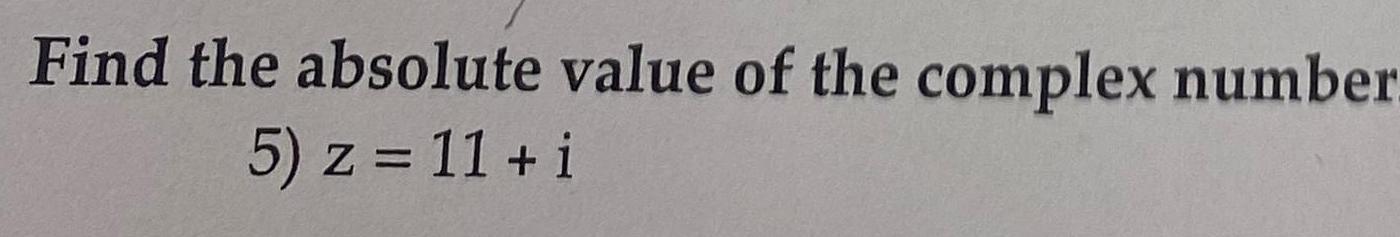

Calculus
Application of derivativesWilliam has put 5 000 of savings into a bank that will collect a 1 annua interest rate Suppose he does not deposit any additional money how muc interest will he earn in 6 months Recall I Prt and in this case t 6 12
Calculus
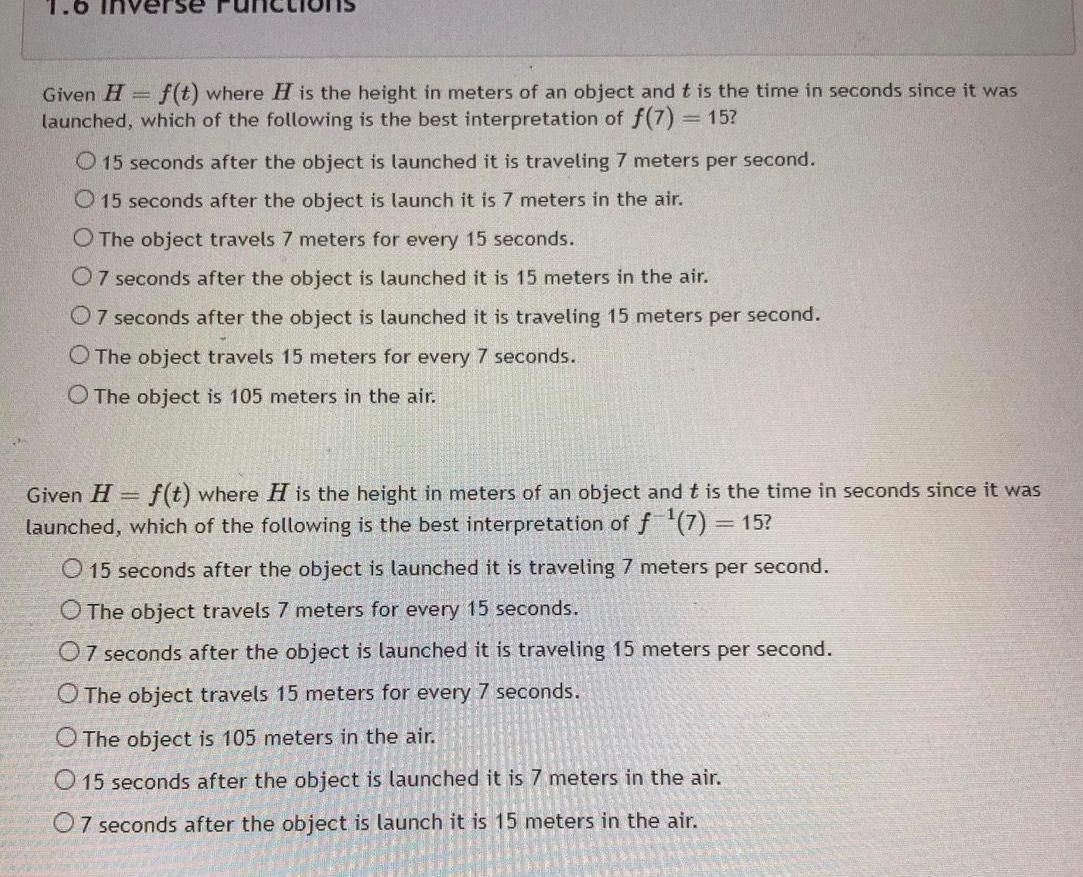
Application of derivativesGiven H f t where H is the height in meters of an object and t is the time in seconds since it was launched which of the following is the best interpretation of f 7 15 O 15 seconds after the object is launched it is traveling 7 meters per second O 15 seconds after the object is launch it is 7 meters in the air O The object travels 7 meters for every 15 seconds 07 seconds after the object is launched it is 15 meters in the air 07 seconds after the object is launched it is traveling 15 meters per second O The object travels 15 meters for every 7 seconds O The object is 105 meters in the air Given H f t where H is the height in meters of an object and t is the time in seconds since it was launched which of the following is the best interpretation of f 7 15 O 15 seconds after the object is launched it is traveling 7 meters per second O The object travels 7 meters for every 15 seconds 07 seconds after the object is launched it is traveling 15 meters per second O The object travels 15 meters for every 7 seconds O The object is 105 meters in the air O 15 seconds after the object is launched it is 7 meters in the air 07 seconds after the object is launch it is 15 meters in the air
Calculus
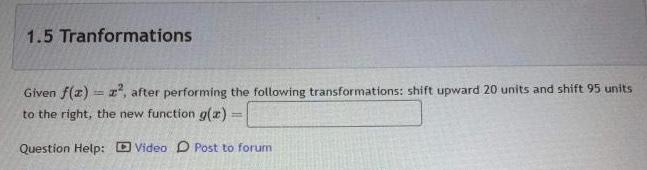
Application of derivatives1 5 Tranformations Given f x x after performing the following transformations shift upward 20 units and shift 95 units to the right the new function g x Question Help Video Post to forum

Calculus
Application of derivativesExpress the function h x g x x a g x b f x VI z 1 in the form x fog x where f x x and