Application of derivatives Questions and Answers

Calculus
Application of derivativesCalculate the following derivative Use symbolic notation and fractions where needed Kaminubleth d dx 7e 4x 2e 10x 10

Calculus
Application of derivativesCompute the derivative y cos te Express numbers in exact form Use symbolic notation and fractions where needed POLECEN

Calculus
Application of derivativesFind the derivative of y using the appropriate rule or combination of rules y x cos x Express numbers in exact form Use symbolic notation and fractions where needed dy dx
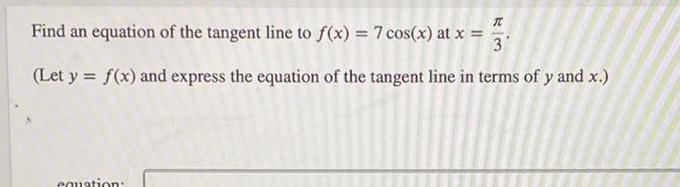
Calculus
Application of derivativesT Find an equation of the tangent line to f x 7 cos x at x 3 Let y f x and express the equation of the tangent line in terms of y and x equation
Calculus
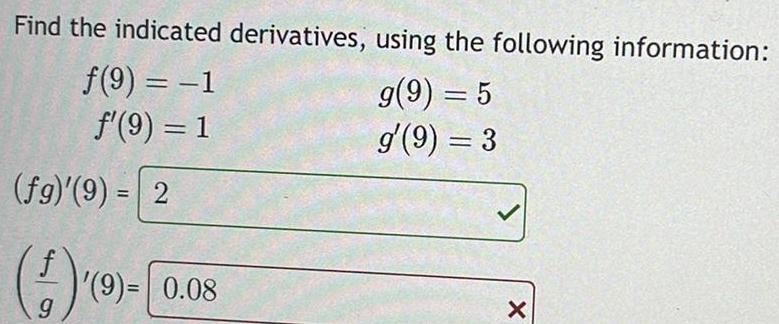
Application of derivativesFind the indicated derivatives using the following information f 9 1 f 9 1 g 9 5 g 9 3 fg 9 2 f 9 9 0 08 X

Calculus
Application of derivativesIf f x 2x 5x 3 find f 4 21 Use this to find the equation of the tangent line to the parabola y 2x 5x 3 at the poi 4 55 The equation of this tangent line can be written in the form y mx b where m is 21 X and where b is 139 X

Calculus
Application of derivativesA large koi pond is filled from a garden hose at the rate of 14 gal min Initially the pond contains 400 gal of water a Find a linear function V that models the volume of water in the pond at any time t V t b If the pond has a capacity of 1604 gal how long does it take to completely fill the pond min
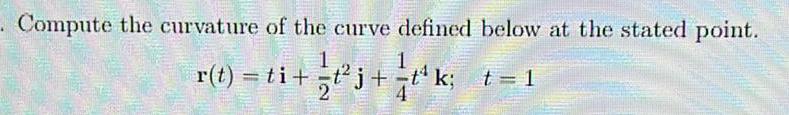
Calculus
Application of derivativesCompute the curvature of the curve defined below at the stated point r t ti j t k t 1
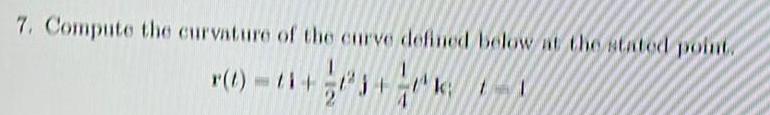
Calculus
Application of derivatives7 Compute the curvature of the curve defined below at the stated point k 11
Calculus
Application of derivatives9 Consider the curve defined below Find T t and N t to the curve at the given point r t ln sin t i j tk t 6
Calculus
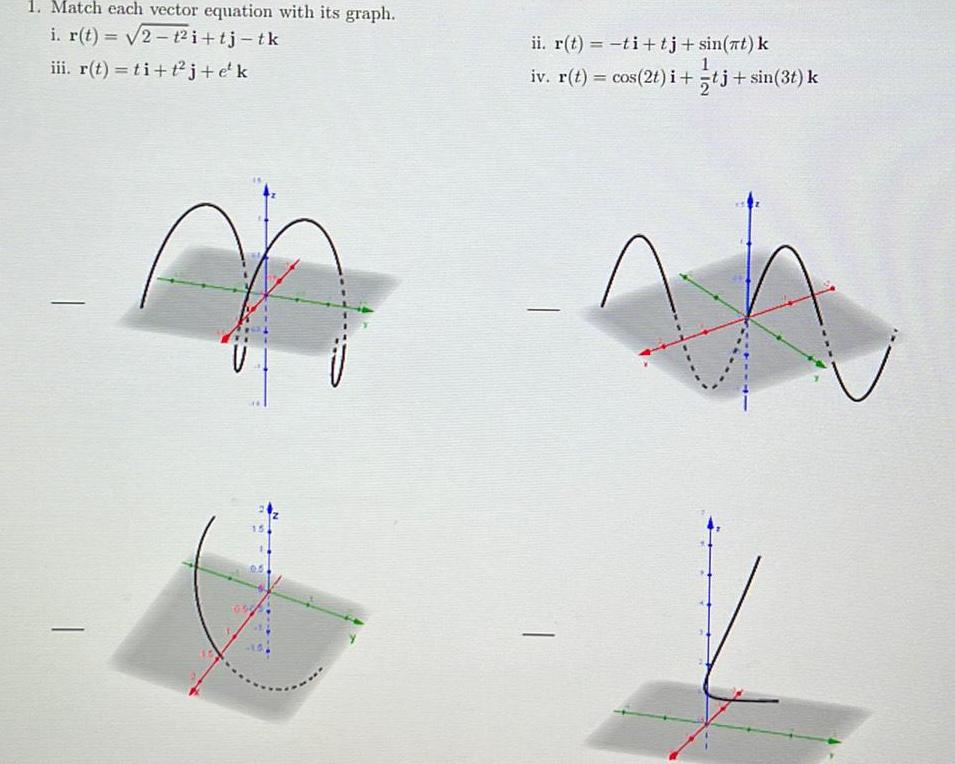
Application of derivatives1 Match each vector equation with its graph i r t 2 i tj tk iii r t ti t j ek U ii r t ti tj sin at k iv r t cos 2t i tj sin 3t k

Calculus
Application of derivativesse Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraint If an answer does not exist enter DNE f x y z x y z x4 y 24 7 maximum minimum
Calculus
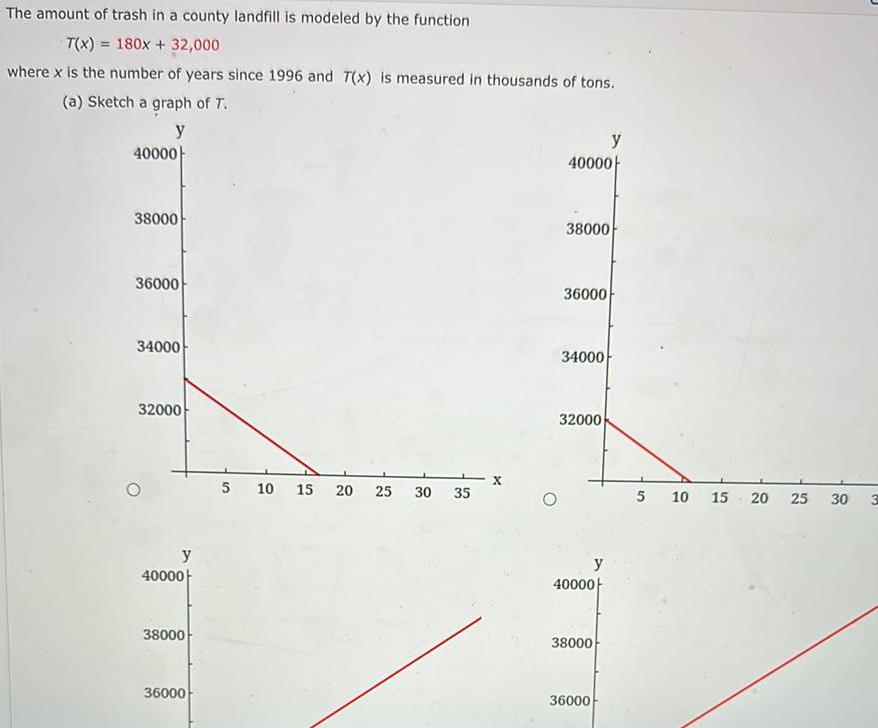
Application of derivativesThe amount of trash in a county landfill is modeled by the function T x 180x 32 000 where x is the number of years since 1996 and 7 x is measured in thousands of tons a Sketch a graph of T y 40000H 38000 36000 34000 32000 y 40000 38000 36000 5 10 15 20 25 30 35 40000 38000 36000 34000 32000 y 40000 38000 36000 y 5 10 15 20 25 30 3

Calculus
Application of derivativestomework Decide whether the given is an ic 0 3 x 3 0 5 x 3 0 2x equation 0 6
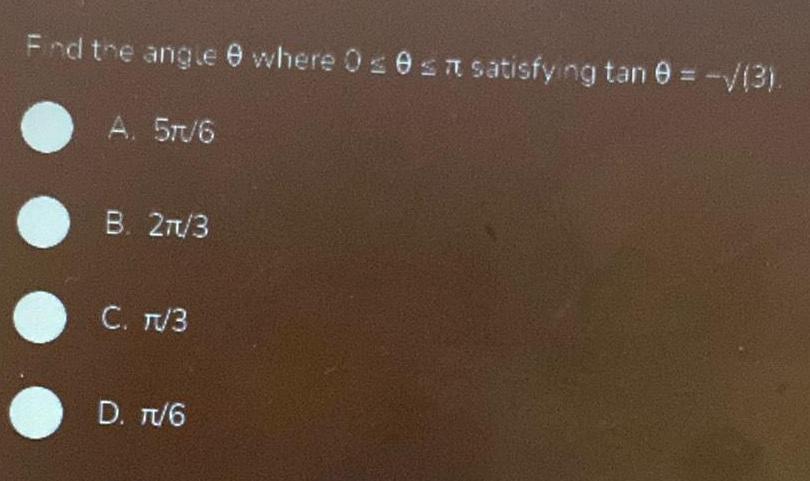
Calculus
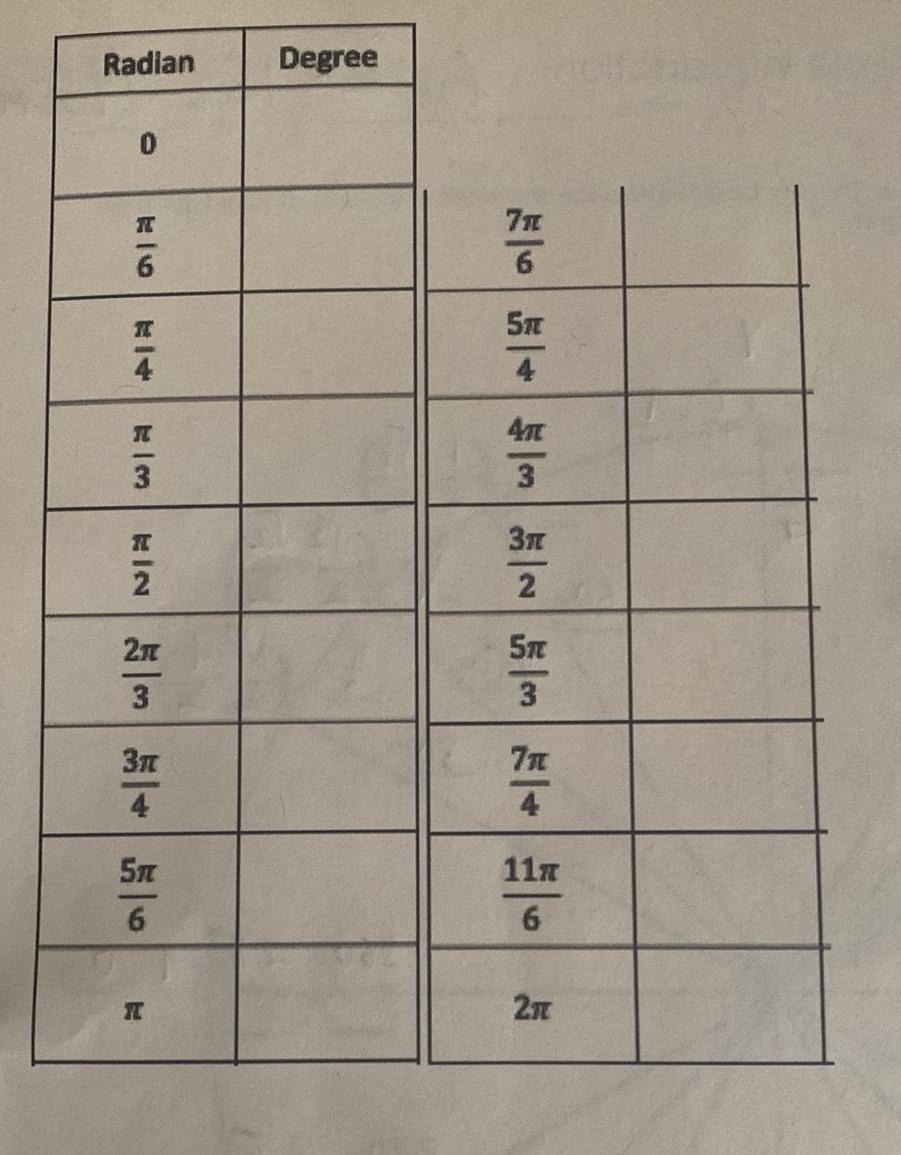
Application of derivativesFind the angle 9 where 0 0 satisfying tan 9 3 A 5 6 B 27 3 C TV3 D T 6

Calculus
Application of derivatives1 2 Terminal Points A point P x y is given a Show that P is on the unit circle b Suppose that P is the terminal point determined by t Find sin t cos t and tan t 3 1 P 1 1 2 2 3 t 3 6 Reference Number and Terminal Point A real number t is given a Find the reference number for 1 b Find the terminal point P x y on the unit circle determined by t c Find the six trigonometric functions of t 2 3 11T 4 J5J bol 2 P 5 t 5 4 t 0 6 t 5 T 3 7T 6
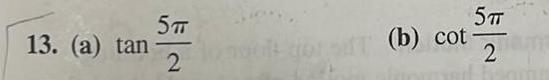

Calculus
Application of derivatives4 1kg 10 9 8 7 6 5 4 3 2 1 0 1 2 T 4 2kg 3 4 5 6 4kg 7 As shown above there are 3 masses located in a line at the positions shown in meters At what position would the center of mass be located for this system of 3 masses 8 9 10

Calculus
Application of derivativesLet C be the CCW unit circle centered at the origin In each case do the following i Find the domain of F ii Calculate F T ds by hand C iii Calculate f F Tds using Green s Theorem C iv Compare your answers to Parts ii and iii Use Part i to explain the difference if applicable a F y x I F b F
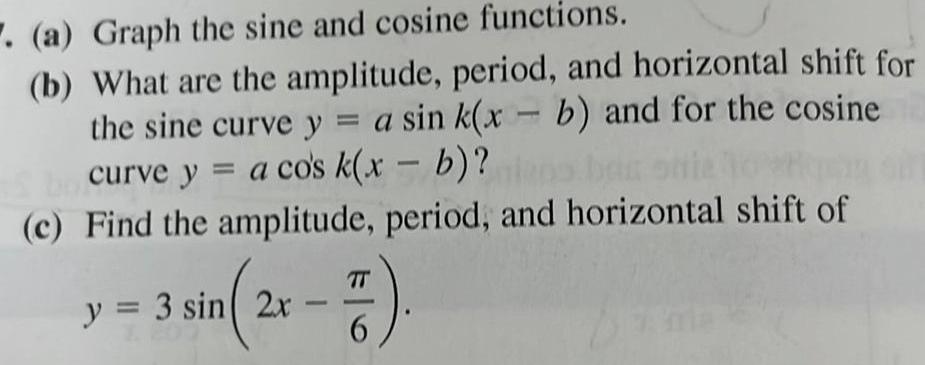
Calculus
Application of derivativesa Graph the sine and cosine functions b What are the amplitude period and horizontal shift for the sine curve y a sin k x b and for the cosine curve y a co s k x b c Find the amplitude period and horizontal shift of y 3 sin 2x sin 2 TT

Calculus
Application of derivatives11 a What is simple harmonic motion b What is damped harmonic motion c Give real world examples of harmonic motion
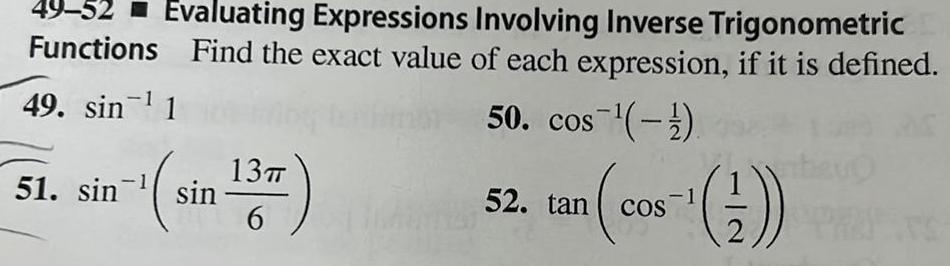
Calculus
Application of derivatives49 52 Evaluating Expressions Involving Inverse Trigonometric Functions Find the exact value of each expression if it is defined 49 sin 1 50 cos 51 sin sin 13T 6 11141 52 tan cos 2 COS RET

Calculus
Application of derivatives5 a What is an even function and what is an odd function b Which trigonometric functions are even Which are odd c If sin t 0 4 find sin t d If cos s 0 7 find cos s

Calculus
Application of derivatives29 36 Horizontal Shifts A trigonometric function is given a Find the amplitude period and horizontal shift of the func tion b Sketch the graph 29 y 10 cos x 31 y sin x 33 y 3 sin 2x 2 35 y cos 6 30 y 4 sin 27x 32 y TT m x 7 4 2 sin x TT 34 y cos 2 x 2 cos x 36 y 10 sin 2x
Calculus
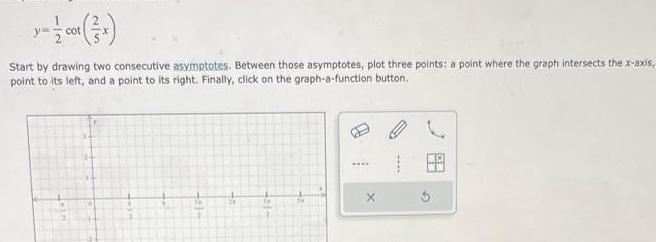
Application of derivativescot Start by drawing two consecutive asymptotes Between those asymptotes plot three points a point where the graph intersects the x axis point to its left and a point to its right Finally click on the graph a function button X
Calculus
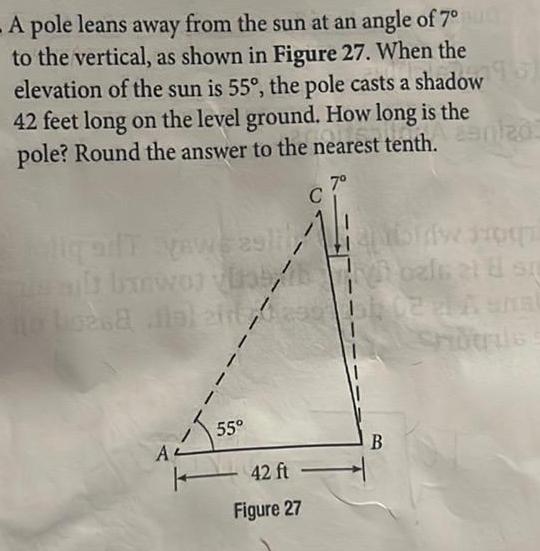
Application of derivativesA pole leans away from the sun at an angle of 7 to the vertical as shown in Figure 27 When the elevation of the sun is 55 the pole casts a shadow 42 feet long on the level ground How long is the pole Round the answer to the nearest tenth anlad 7 e alt banworth 0268 A 1 I 55 42 ft Figure 27 oals at 8 st 102 2 Anal B

Calculus
Application of derivativesA projectile is fired from a cliff 190 feet above the water at an inclinati 32x h x x 190 45 where x is the horizontal distance of the projectile from the face of the

Calculus
Application of derivatives3 10 Evaluating Inverse Trigonometric Functions Find the exact value of each expression if it is defined 3 a sin 1 b sin V3 2 c sin 2
Calculus
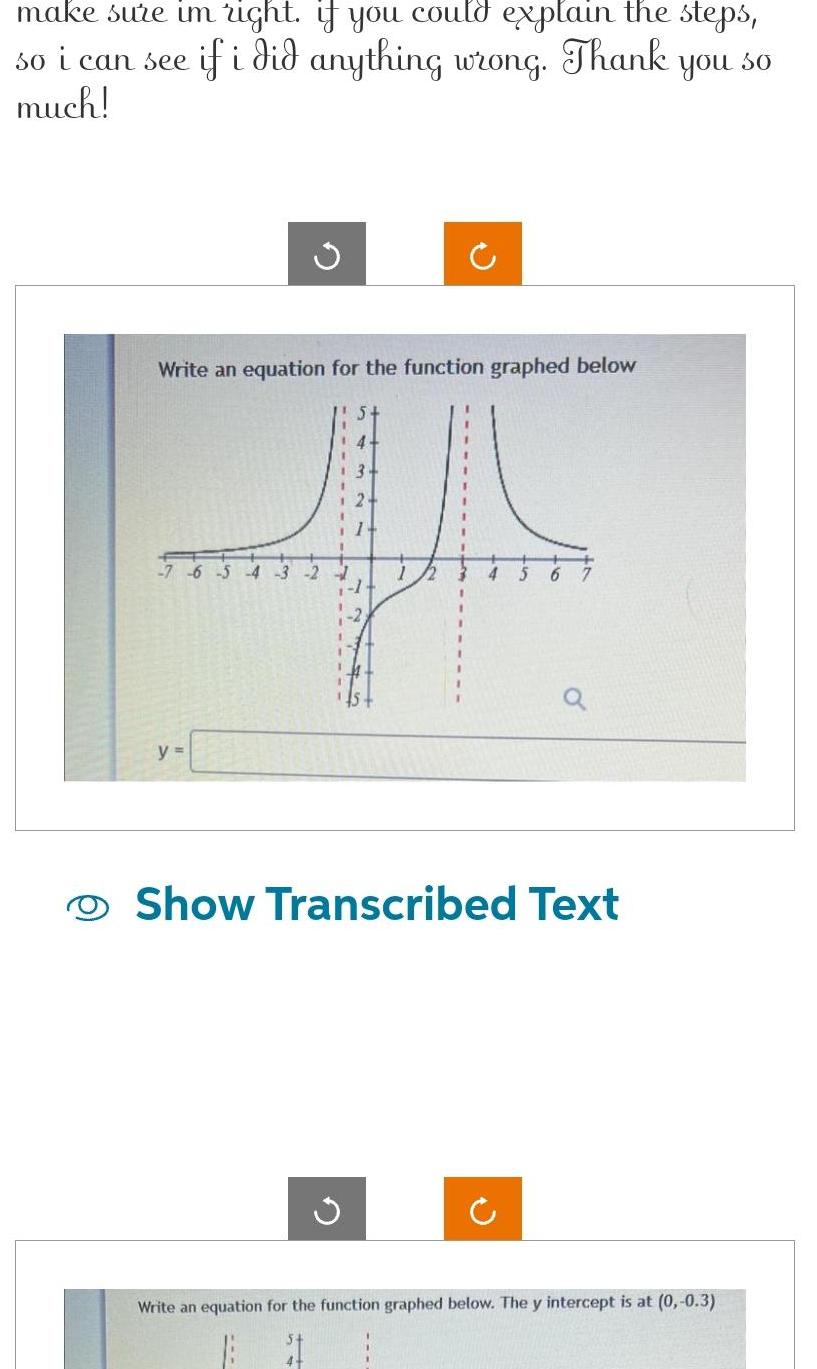
Application of derivativesmake sure im right if you could explain the steps so i can see if i did anything wrong Thank you 30 much Write an equation for the function graphed below J 7 y 6 5 4 5 Show Transcribed Text G Write an equation for the function graphed below The y intercept is at 0 0 3
Calculus
Application of derivativesQuestion 6 A person leaves home and walks 4 miles west then 6 miles southwest How far from home is she miles In what direction must she walk to head directly home degrees North of East
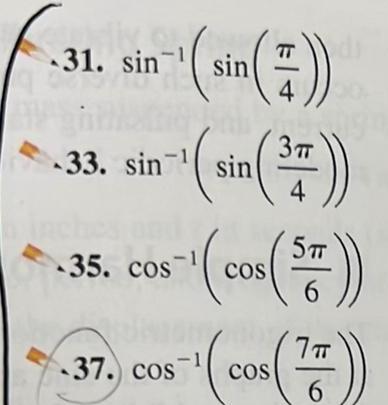
Calculus
Application of derivativesScore 20 100 1 12 answered Question 3 4 miles Southeast 3 miles South A person starts walking from home and walks 3 miles East 2 miles Southwest 3 miles East This person has walked a total of Find the total displacement vector for this walk If this person walked straight home they d have to walk Question Help Video miles miles
Calculus
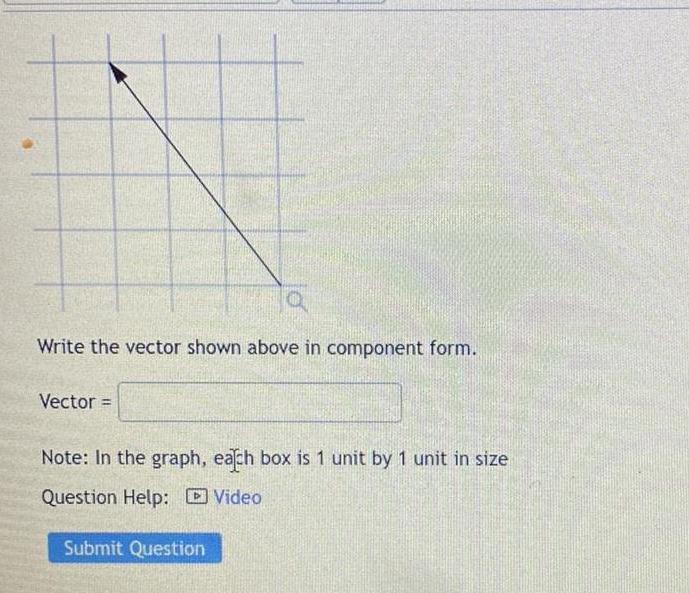
Application of derivativesWrite the vector shown above in component form Vector 0 Note In the graph each box is 1 unit by 1 unit in size Question Help Video Submit Question
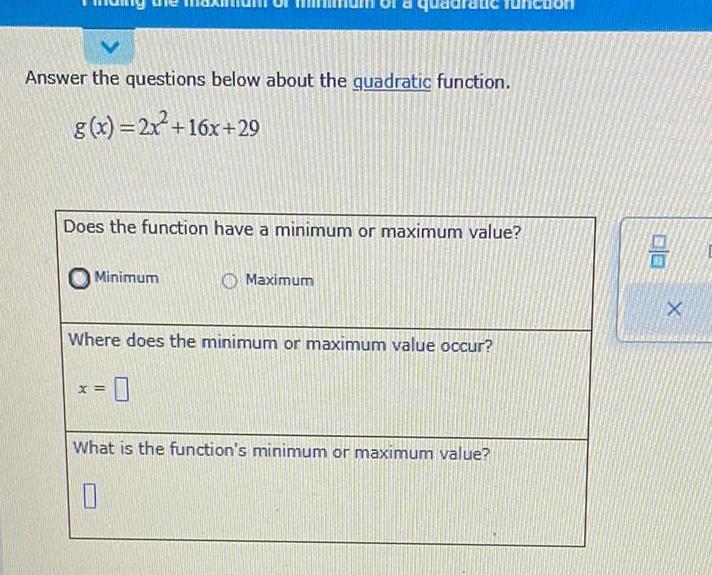
Calculus
Application of derivativesAnswer the questions below about the quadratic function g x 2x 16x 29 Does the function have a minimum or maximum value Jadratic Minimum x Maximum Where does the minimum or maximum value occur 0 What is the function s minimum or maximum value 0 00 X

Calculus
Application of derivativespt tails A maintenance worker fills a swimming pool with water m at a rate of 4 minute Suppose at t 0 the swimming pool is filled with 70 m of water How much water will be in the swimming pool at t 12 minutes A function giving the volume V of water in the swimming pool after t minutes is V t m When will the swimming pool contain 190 m of water minutes
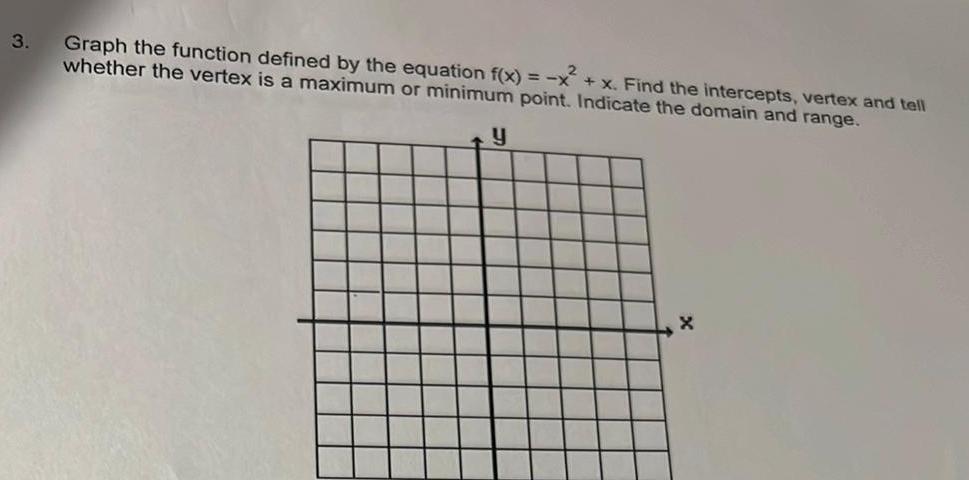
Calculus
Application of derivatives3 Graph the function defined by the equation f x x x Find the intercepts vertex and tell whether the vertex is a maximum or minimum point Indicate the domain and range y X
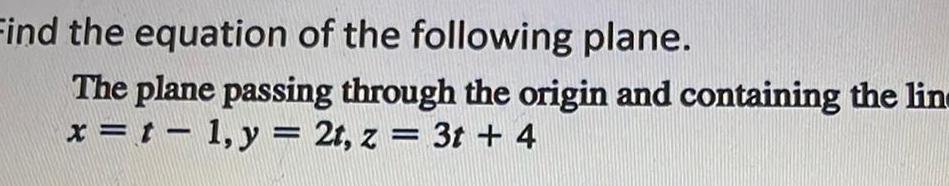
Calculus
Application of derivativesFind the equation of the following plane The plane passing through the origin and containing the line x t 1 y 2t z 3t 4
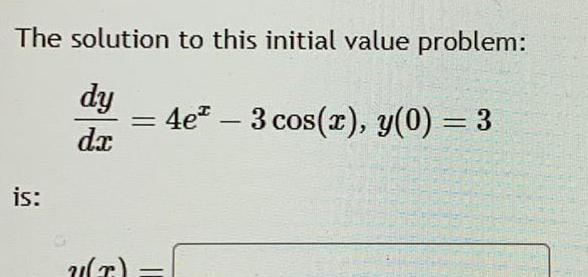
Calculus
Application of derivativesThe solution to this initial value problem dy dx is U T 4e 3 cos x y 0 3

Calculus
Application of derivativesI point Suppose x y z 1 2 2 P 3 3 2 Find the gradient of f af i j Hote Your answers should be expressions of x y and z e g 3x 4y 5 What is the maximum rate of change of f at the point P lote Your answer should be a number

Calculus
Application of derivativesFind both the vector equation and the parametric equations of the line through 0 0 6 in the direction of the vector v 2 6 0 where t 0 corresponds to the given point The vector equation is x y z
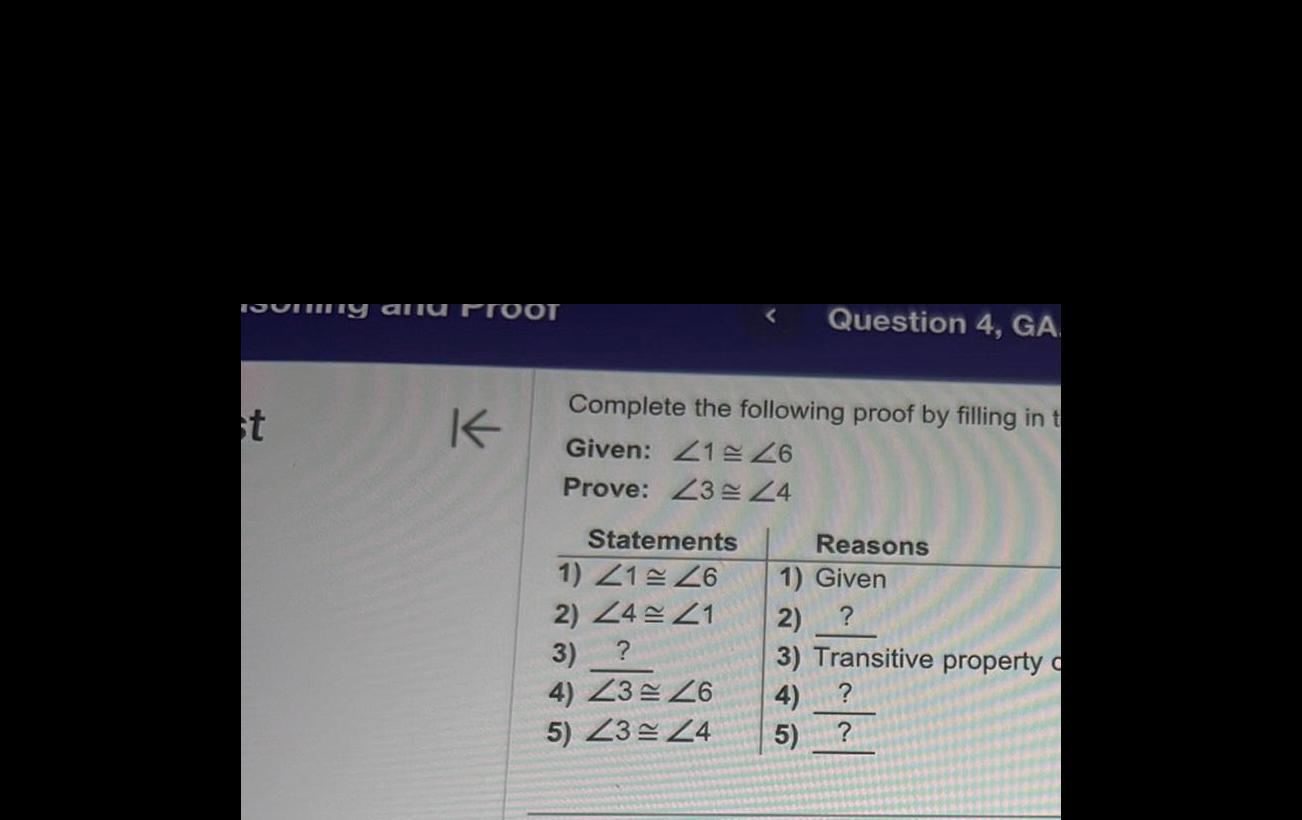
Calculus
Application of derivativestooning and PTOOT st K Complete the following proof by filling in t Given 126 Prove Z3 Z4 Statements Question 4 GA 1 41 26 2 Z4 21 3 4 23 46 5 23 24 Reasons 1 Given 2 3 Transitive property o 4 5
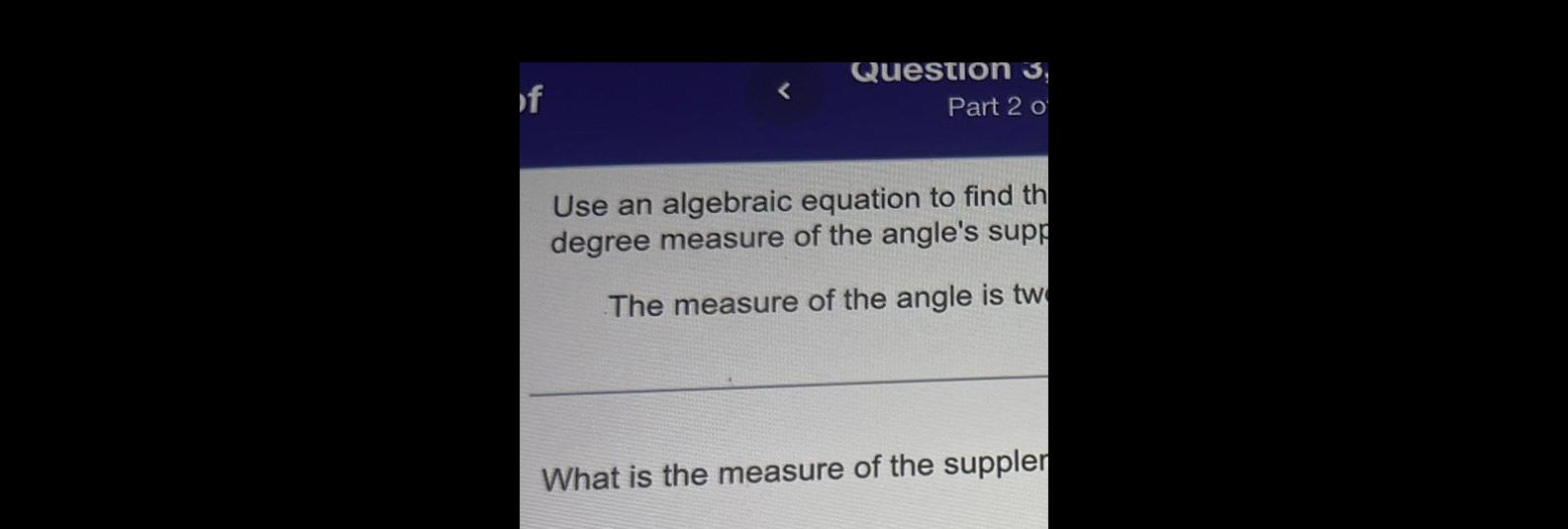
Calculus
Application of derivativesof Question 3 Part 2 o Use an algebraic equation to find th degree measure of the angle s supp The measure of the angle is tw What is the measure of the suppler
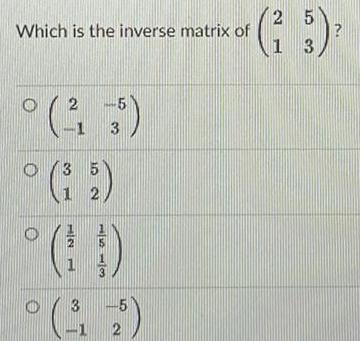
Calculus
Application of derivativesWhich is the inverse matrix of 2 13 3 15 2 121 3 1513 5 1 2 25 1 3

Calculus
Application of derivativesTranslate the sentence into a mathematical equation The total revenue derived from selling x dishwashers is 190 per dishwasher times the number of dishwashers sold Let R represent the revenue and x the number of dishwashers sold R
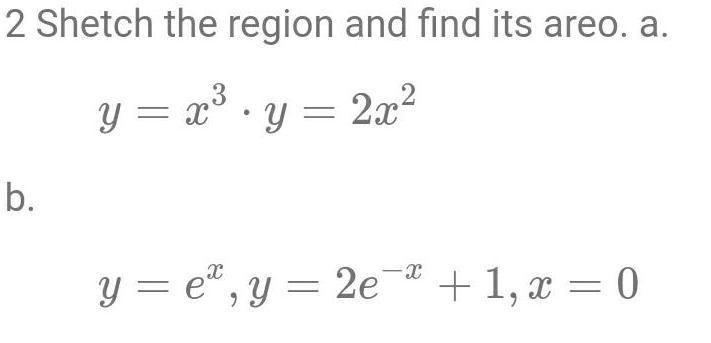

Calculus
Application of derivativesAll edges of a cube are expanding at a rate of 7 centimeters per second a How fast is the volume changing in cm sec when each edge is 4 centimeter s cm sec b How fast is the volume changing in cm sec when each edge is 15 centimeters cm sec

Calculus
Application of derivativesFind the derivative of the trigonometric function y cos 5x y x 5 sin 5x X

Calculus
Application of derivativesFind the derivative of the function using the limit process a t 3 6t