Application of derivatives Questions and Answers

Calculus
Application of derivativesFind the limit L L Use the 8 8 definition to prove that the limit is L Given 0 assume f x L then E lim x 3 X 7 x 3 x 3 X Let 8 E If 0 x C E D when 8 you have x 0 E x 3
Calculus
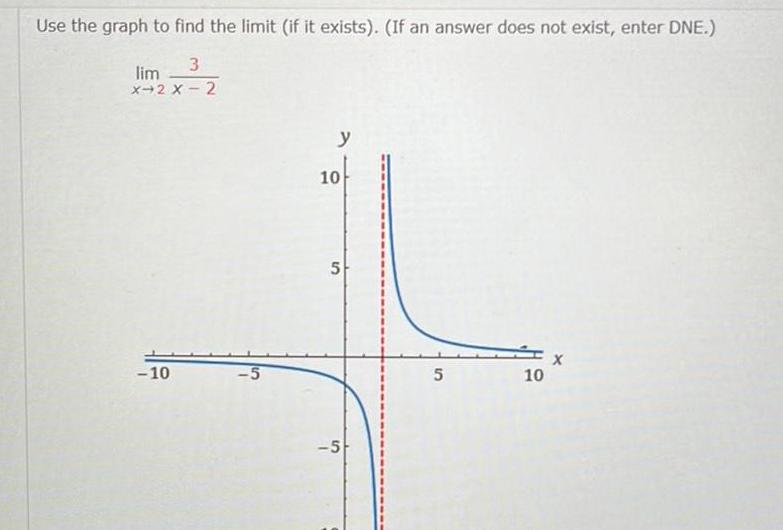
Application of derivativesUse the graph to find the limit if it exists If an answer does not exist enter DNE 3 lim X 2 X 2 10 5 y 10 5 5 5 10 X

Calculus
Application of derivativesConsider the normed linear spaces L1 L2 and Loo Let c0 be the subset of consisting of all sequences that converges to O Prove that we have following proper set inclusions L1 C L2 C COC L o
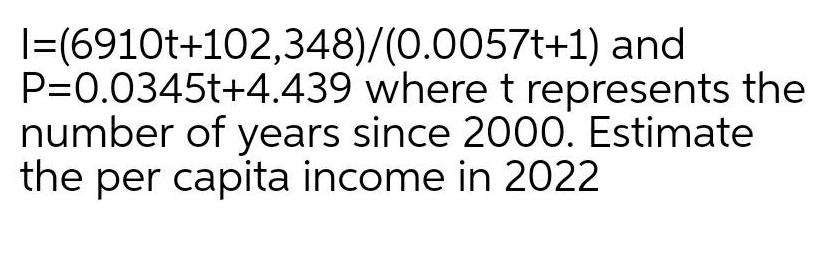
Calculus
Application of derivatives6910t 102 348 0 0057t 1 and P 0 0345t 4 439 where t represents the number of years since 2000 Estimate the per capita income in 2022

Calculus
Application of derivativesGiven f x cos x and g x cos x give exact answers for all parts a Plot the functions on the x interval 0 5 Find the volume when the region between the two curves is rotated about the line x b Find the area of the region 1 x f x g x dx A a cb 1 1 and y I x g x dx with A the area between the curves Find the x A coordinate of the center of mass of the region In a print statement explain why this answer makes sense based on the graph in part a c The center of mass of a region a b is the point x y where cb d When the region rotates about the line x how far does the center of mass travel Multiply this value by the area What do you notice when you compare your answer to part a

Calculus
Application of derivativesComplete the following steps for the given function interval and value of n a Sketch the graph of the function on the given interval b Calculate Ax and the grid points x X Xn c Illustrate the left and right Riemann sums Then determine which Riemann sum underestima d Calculate the left and right Riemann sums f x 3x for 2 5 n 6 a Sketch the graph of f x 3x on the interval 2 5 Choose the correct graph below A Q B 0 Q Q

Calculus
Application of derivativesAn inverted cone base above the vertex is 5 m high and has a base radius of 1 2 m If the tank is full how much work is required to pump the water to a level 4 m above the top of the tank Set up the integral to find the work required to pump all of the liquid 4 m above the cone assuming the vertex of the cone is the origin W int 0 infty p g d y Type an exact answer using as needed Use integers or fractions for any numbers in the expression
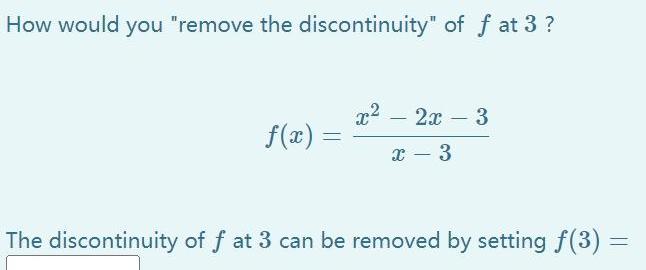
Calculus
Application of derivativesHow would you remove the discontinuity of f at 3 f x x 2x 3 X 3 The discontinuity of f at 3 can be removed by setting f 3


Calculus
Application of derivativesIf the region bounded by x 3 y 4 2 is rotated by the axis y 3 then find the volume of the generated solid a 0 28 b 2477 d 28 e 04
Calculus
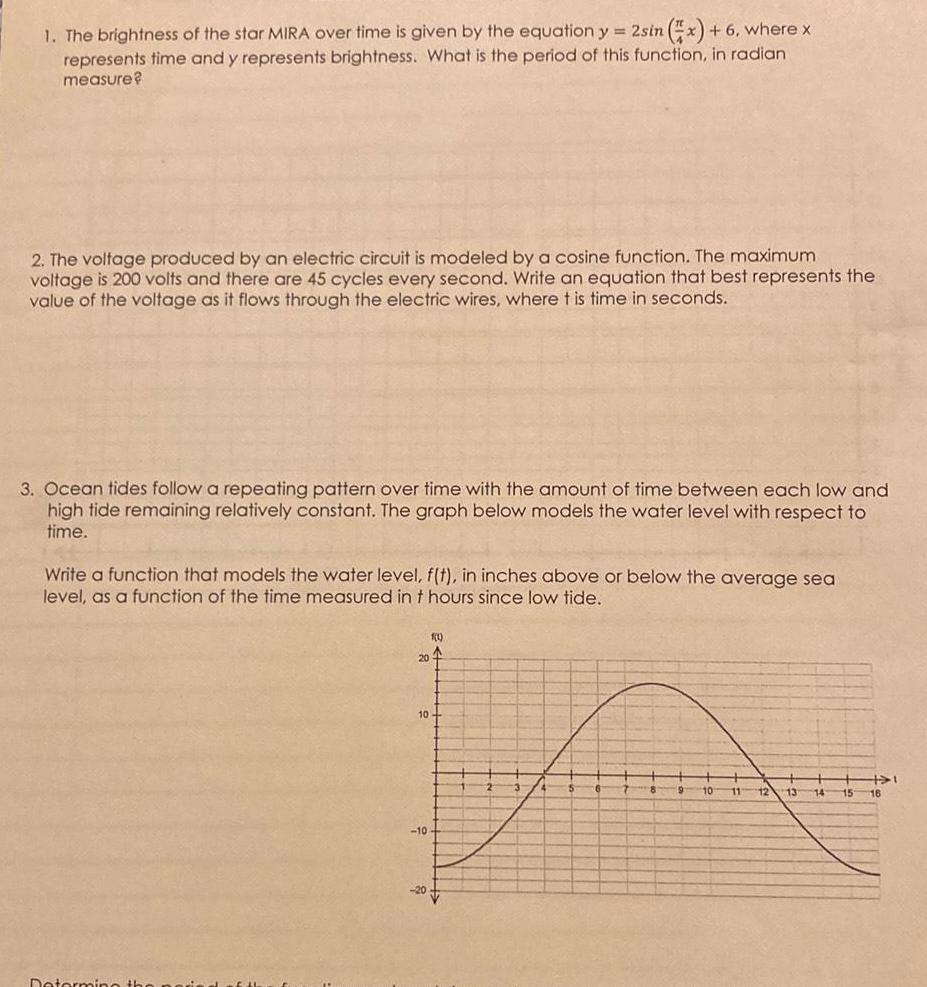
Application of derivatives1 The brightness of the star MIRA over time is given by the equation y 2sin x 6 where x represents time and y represents brightness What is the period of this function in radian measure 2 The voltage produced by an electric circuit is modeled by a cosine function The maximum voltage is 200 volts and there are 45 cycles every second Write an equation that best represents the value of the voltage as it flows through the electric wires where t is time in seconds 3 Ocean tides follow a repeating pattern over time with the amount of time between each low and high tide remaining relatively constant The graph below models the water level with respect to time Write a function that models the water level f t in inches above or below the average sea level as a function of the time measured in t hours since low tide Determine the 20 10 10 1 1 20 9 10 11 12 13 15 1 16


Calculus
Application of derivativesFind the exact value of the expression if it is defined If an answer is undefined enter UNDEFINED cos cos 3
Calculus
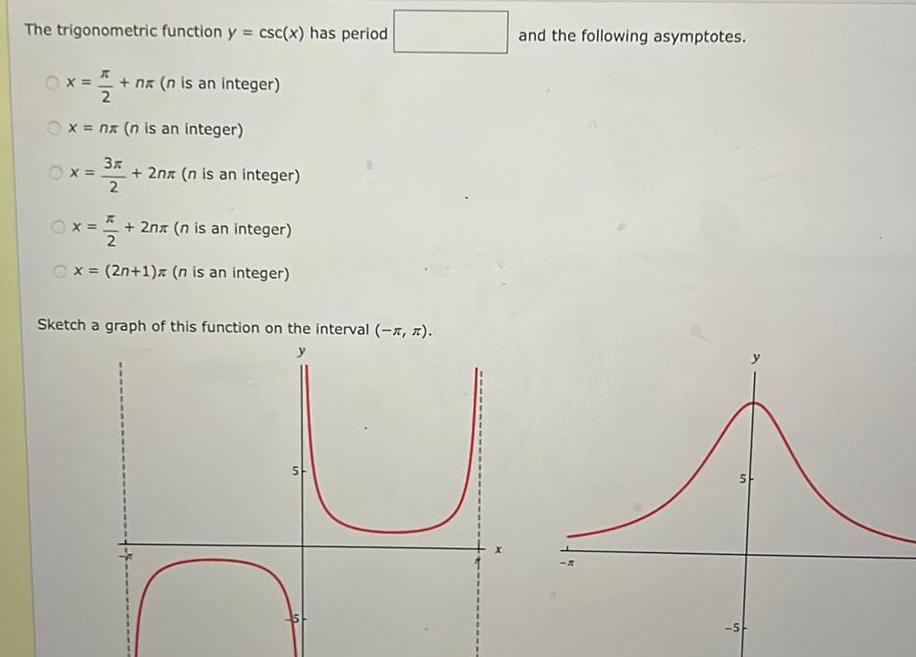
Application of derivativesThe trigonometric function y csc x has period n n is an integer x 2 x n n is an integer Ox 3 2 2n n is an integer 2nx n is an integer 2 x 2n 1 x n is an integer Sketch a graph of this function on the interval 5 and the following asymptotes 5 5

Calculus
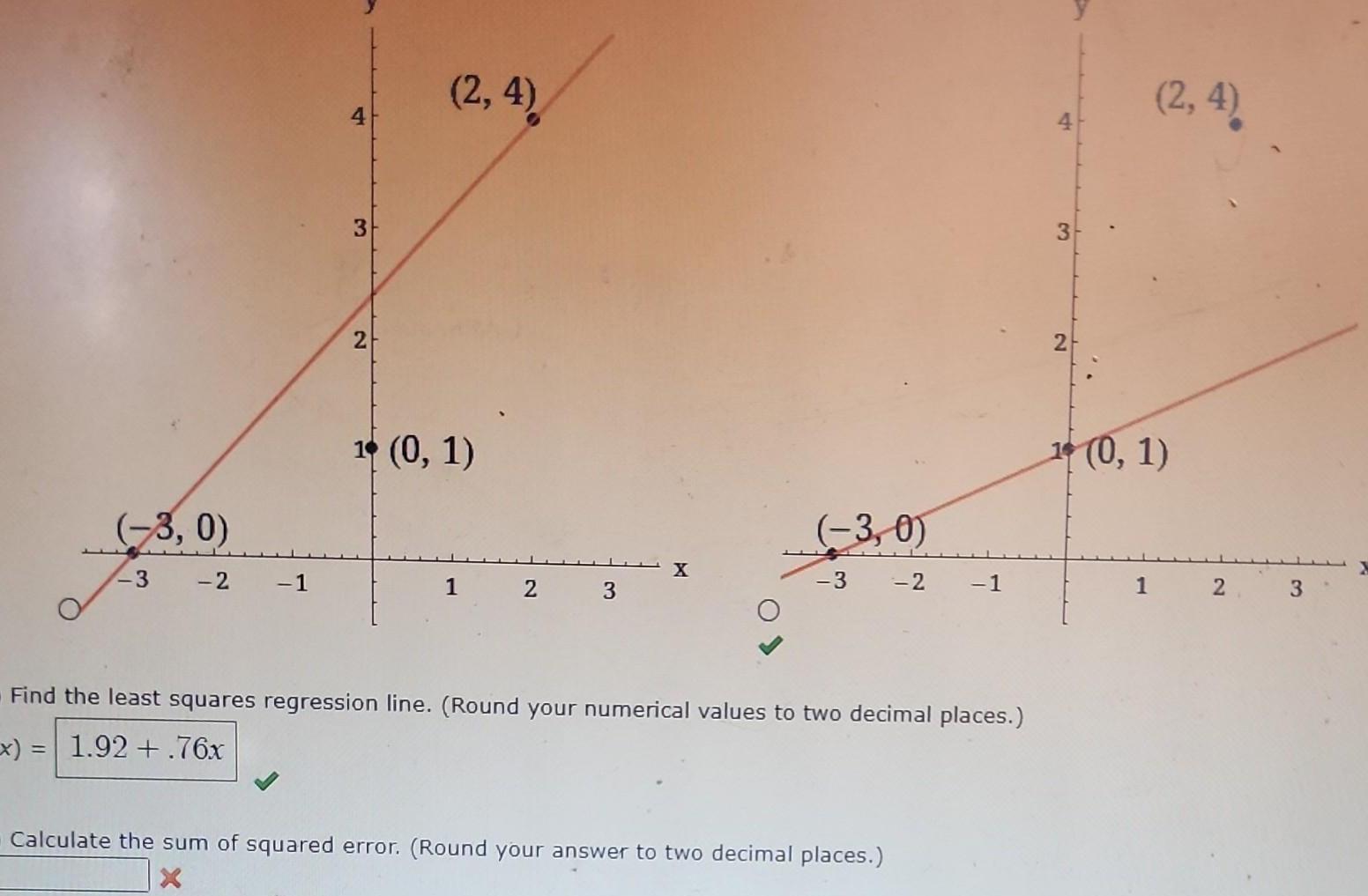
Application of derivatives3 0 3 2 1 3 2 2 4 1 0 1 1 2 3 X 3 0 3 2 Calculate the sum of squared error Round your answer to two decimal places 1 Find the least squares regression line Round your numerical values to two decimal places x 1 92 76x 2 2 4 1 0 1 1 2 3
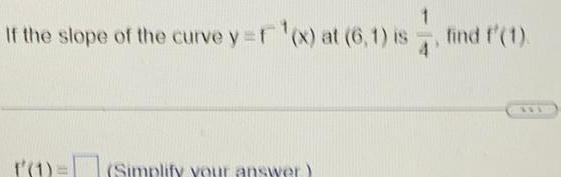
Calculus
Application of derivativesIf the slope of the curve y f x at 6 1 is 1 Simplify your answer find f 1 111
Calculus
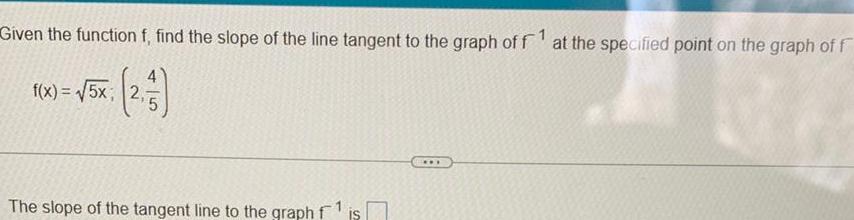
Application of derivativesGiven the function f find the slope of the line tangent to the graph of f1 at the specified point on the graph of f 2 53 f x 5x 2 The slope of the tangent line to the graph f is

Calculus
Application of derivativesWhat is the multiplicative for the exponential rate of change function f x 2 5 2 x 0 4 0 6 1 5 2 5

Calculus
Application of derivativesThe half life of an antibiotic in the bloodstream is 12 hr If an initial dose of 20 mg is administered the quantity left after thours is modeled by Q t 20e 0 0578t for t 0 a Find the instantaneous rate of change of the amount of antibiotic in the bloodstream for 0 st 12 hr b How fast is the amount of antibiotic changing at t 0 hr At t 2 hr c Evaluate and interpret lim Q t and lim Q t 1 1 0 a Find the instantaneous rate of change of the amount of antibiotic in the bloodstream for 0 st 12 hr Q t Type an exact answer in terms of e Round to four decimal places as needed
Calculus
Application of derivativesQuestion 9 4 2 19 GC Part 3 of 6 ssor wanted to find a linear model that relates the number of hours a student plays video each week h to the cumulative grade point average G of the student He obtained a random of 10 full time students at his college and asked each student to disclose the number of hours playing video games and the student s cumulative grade point average ete parts a through f below 5 Cumulative grade point average is being used to predict the number of hours C The number of hours is directly related to the cumulative grade point average D The number of hours and the cumulative grade point average are unrelated Use a graphing utility to draw a scatter diagram Choose the correct scatter diagram below CO H Hou
Calculus
Application of derivativesQuestion 8 4 2 17 Part 3 of 6 lowing data represent the weight in grams of Candy Bar candy bars and the corresponding number of Bar A S Bar B Bar C Bar D Bar E Weig 49 59 4 5 56 raw a scatter diagram of the data treating weight as the independent variable Choose th
Calculus
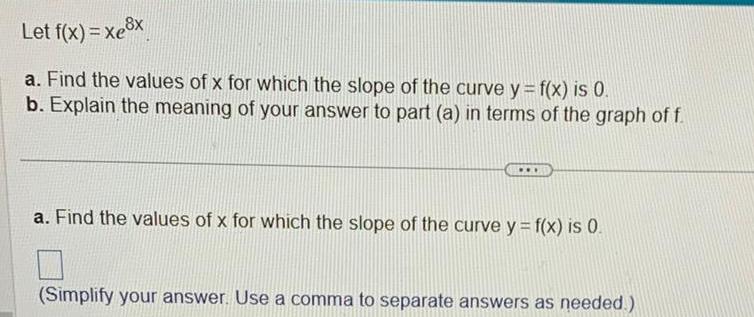
Application of derivativesLet f x xe x a Find the values of x for which the slope of the curve y f x is 0 b Explain the meaning of your answer to part a in terms of the graph of f a Find the values of x for which the slope of the curve y f x is 0 Simplify your answer Use a comma to separate answers as needed
Calculus
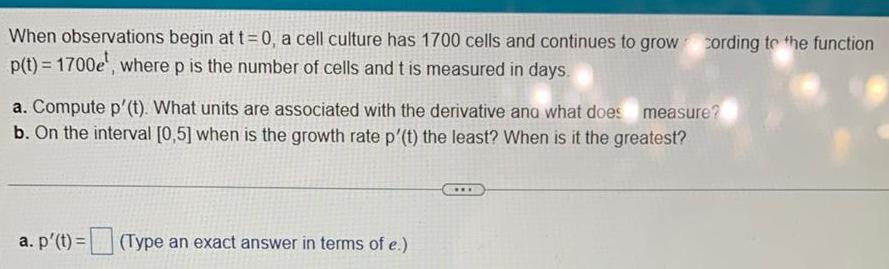
Application of derivativesWhen observations begin at t 0 a cell culture has 1700 cells and continues to grow p t 1700e where p is the number of cells and t is measured in days a Compute p t What units are associated with the derivative and what does measure b On the interval 0 5 when is the growth rate p t the least When is it the greatest a p t Type an exact answer in terms of e cording to the function www

Calculus
Application of derivativesExercise 4 Consider a monotonically strictly increasing function i e a function f x whose graph is going up that is if x y then Let f x f y a b Order the following three quanities in increasing magnitude 1 f x dx R100 L100

Calculus
Application of derivativesX 28 Mr Baddie is trying to shoot Mr Spy with a laser gun Mr Spy is underwater at a depth of 1m swimming horizontally at a speed of 2ms Mr Baddie is stationary on the surface of the water Mr Baddie has to fire the laser at an angle a to the horizontal Mr Spy starts vertically underneath Mr Baddie Find the rate of change of a when a 30
Calculus
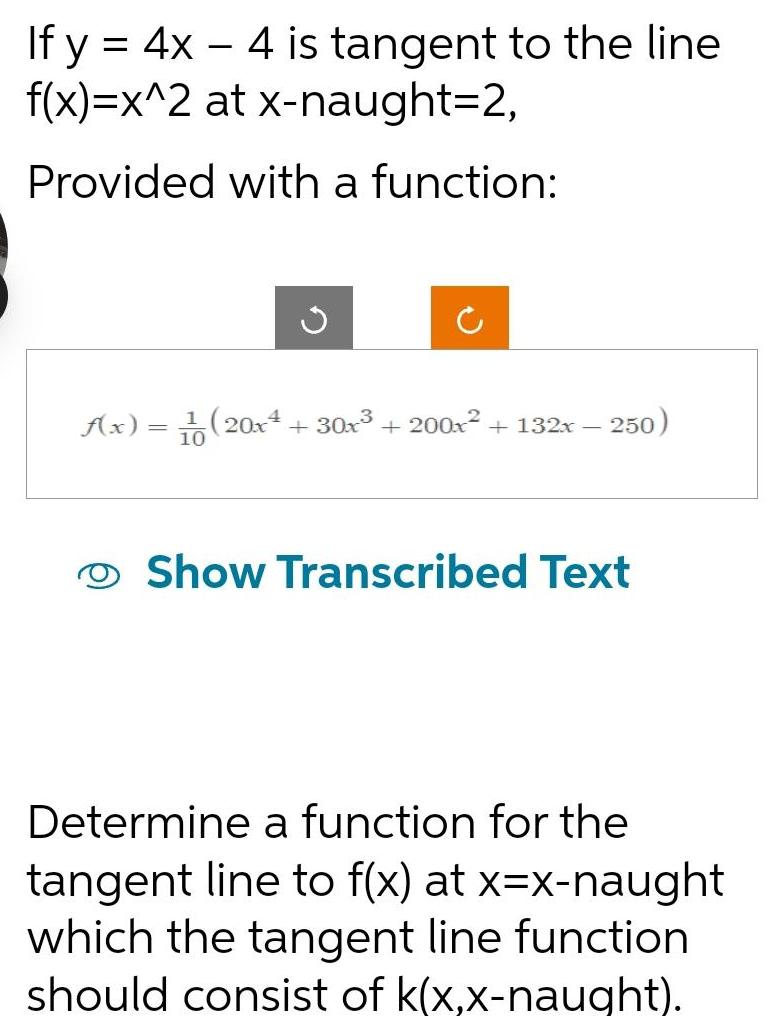
Application of derivativesIf y 4x4 is tangent to the line f x x 2 at x naught 2 Provided with a function Ax 1 20x 30x 200x 132x 10 250 Show Transcribed Text Determine a function for the tangent line to f x at x x naught which the tangent line function should consist of k x x naught
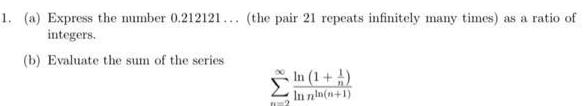
Calculus
Application of derivatives1 a Express the number 0 212121 the pair 21 repeats infinitely many times as a ratio of integers b Evaluate the sum of the series In 1 1 In nln n 1
Calculus
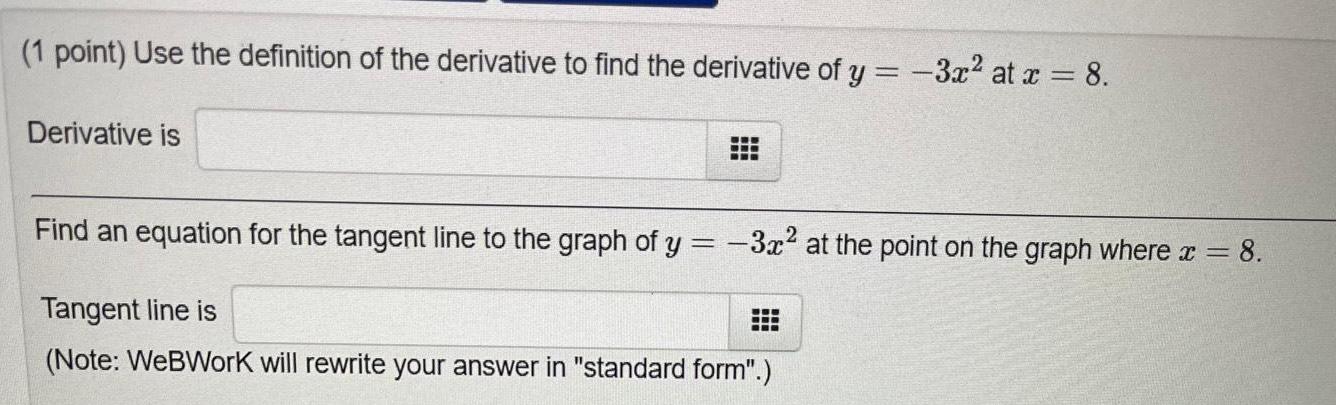
Application of derivatives1 point Use the definition of the derivative to find the derivative of y 3x at x 8 Derivative is Find an equation for the tangent line to the graph of y 3x at the point on the graph where x 8 Tangent line is Note WeBWork will rewrite your answer in standard form
Calculus
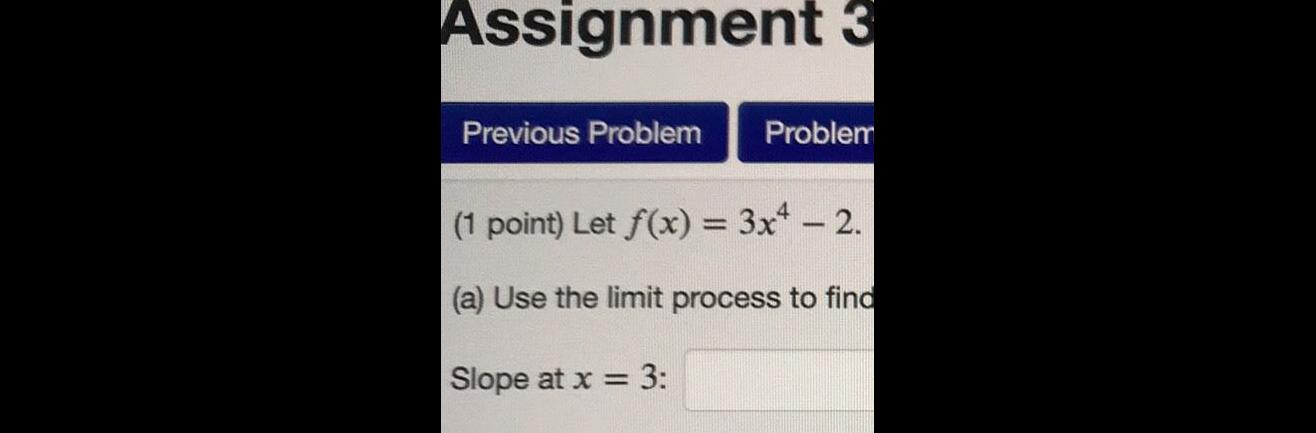
Application of derivativesAssignment 3 Previous Problem Problem 1 point Let f x 3x 2 a Use the limit process to find Slope at x 3

Calculus
Application of derivativesBDWORK main 200 gnment 3 Problem 3 Problem List Next Problem The point P 25 7 lies on the curve y x 2 the slope of the secant line PQ for the following va s Problem

Calculus
Application of derivativesFind the x value of all points where the function has relative extrema Sketch a graph or labe number line to show positive negative intervals Label each extremum as a max or min and state the associated y value c y x x d v lnx x 0

Calculus
Application of derivativesA rectangle initially has width 8 meters and length 6 meters and is expanding so that the area increases at a rate of 3 square meters per hour If the width increases by 20 centimeters per hour how quickly does the length increase initially hint Using the product rule if you know any two of the derivatives you can work out the third one Here you know A L W and A and W centimeters per hour
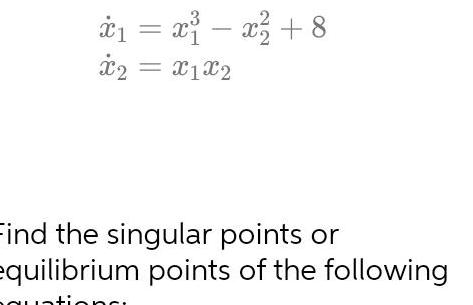
Calculus
Application of derivatives1 x x 8 x2 x1x2 Find the singular points or equilibrium points of the following quations
Calculus
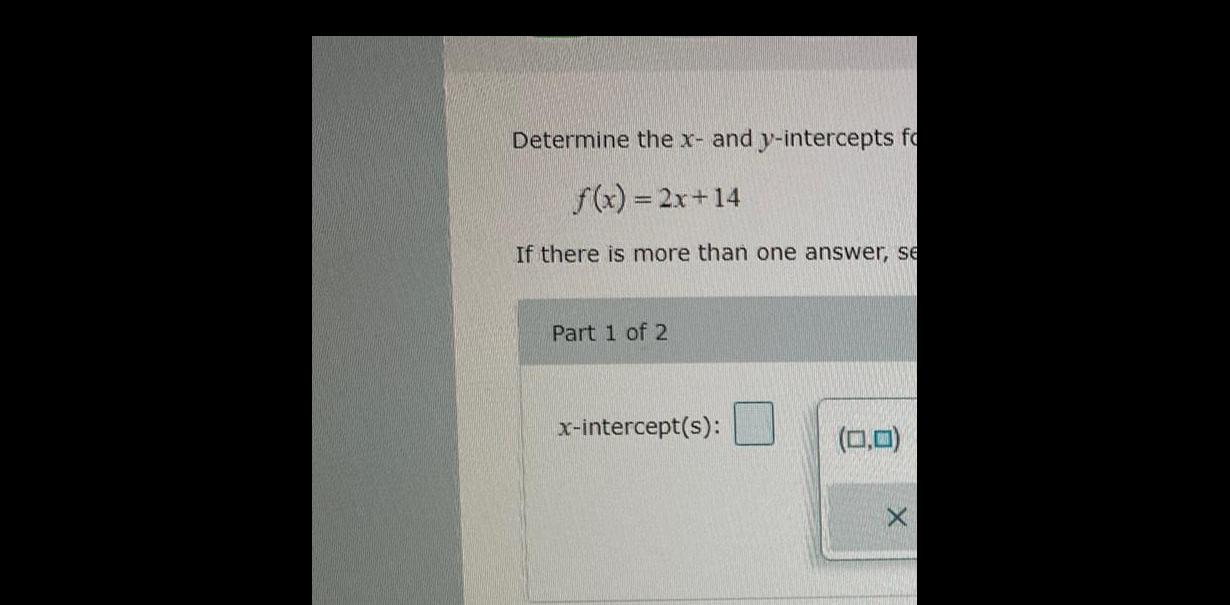
Application of derivativesDetermine the x and y intercepts fo f x 2x 14 If there is more than one answer se Part 1 of 2 x intercept s 0 0 X

Calculus
Application of derivativesf x y Explore x x y y x 2y lim f x y x y 0 0 either proving it does not exist or hypothesizing its value If it seems that it does exist prove your hypothesis Graph the function in Geogebra and get a few print screen shots organized on a single page one sided word document to print and attach
Calculus
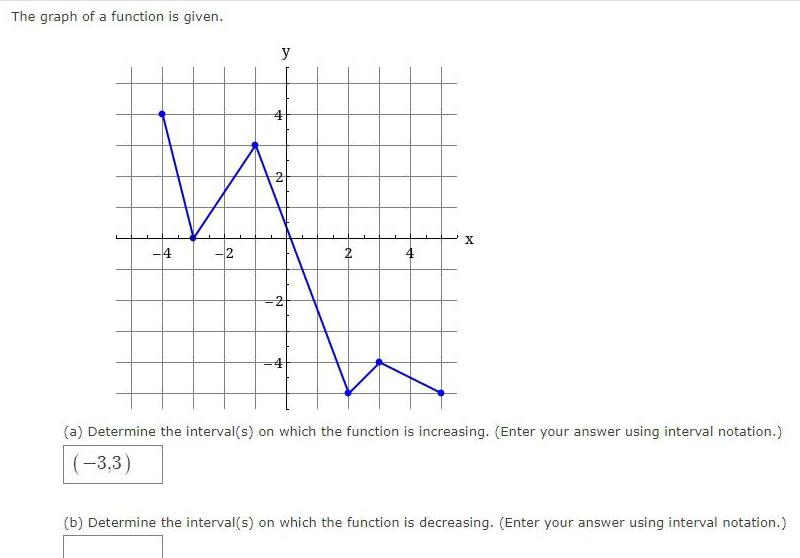
Application of derivativesThe graph of a function is given 4 2 y 4 2 2 X a Determine the interval s on which the function is increasing Enter your answer using interval notation 3 3 b Determine the interval s on which the function is decreasing Enter your answer using interval notation


Calculus
Application of derivativese the model for projectile motion assuming there is no air resistance and g 32 Teet per second per second pale ejector consists of two variable speed belts at the end of a baler Its purpose is to toss bales into a trailing wagon In loading the back of a wagon a bale must be thrown to a position 8 feet above a et behind the ejector a Find the minimum initial speed of the bale v and the corresponding angle 8 at which it must be ejected from the baler Round your answers to two decimal places V ft sec 0 0 b The ejector has a fixed angle of 45 Find the initial speed v required ft ser

Calculus
Application of derivativesb Find lim f x If the limit does not exist explain why x 2 c Based on your work in parts a and b does the graph of f x have any If so find the equations of the vertical asymptotes
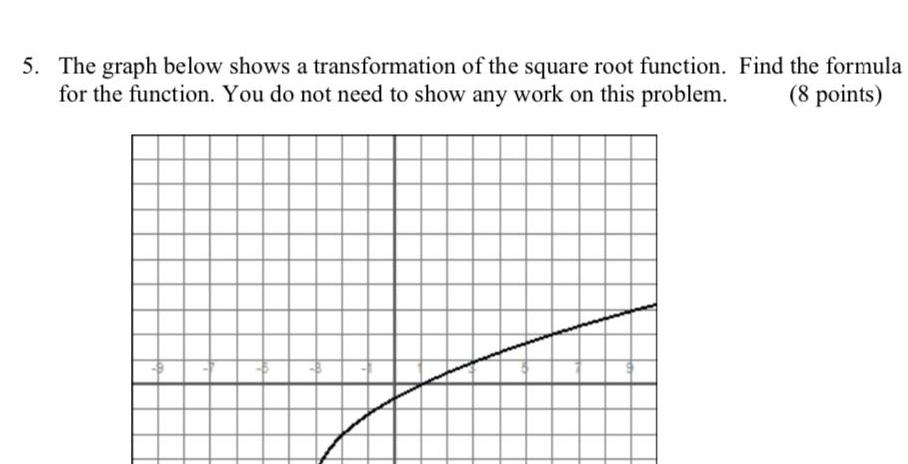
Calculus
Application of derivatives5 The graph below shows a transformation of the square root function Find the formula for the function You do not need to show any work on this problem 8 points

Calculus
Application of derivatives6 Suppose fis a 1 1 function and f 3 7 You do not need to show any work on this 10 pts problem a What is f 7 b Evaluate f 1 of 5 c Iffis even what is f 7 d Iffis odd what is f 7 e If the point 3 6 is on the graph off what is ff 7

Calculus
Application of derivativesd the inverse f 1 of f x sin 1 x 5 6 se integers or fractions for any numbers in the expre e range of f x is 1 11
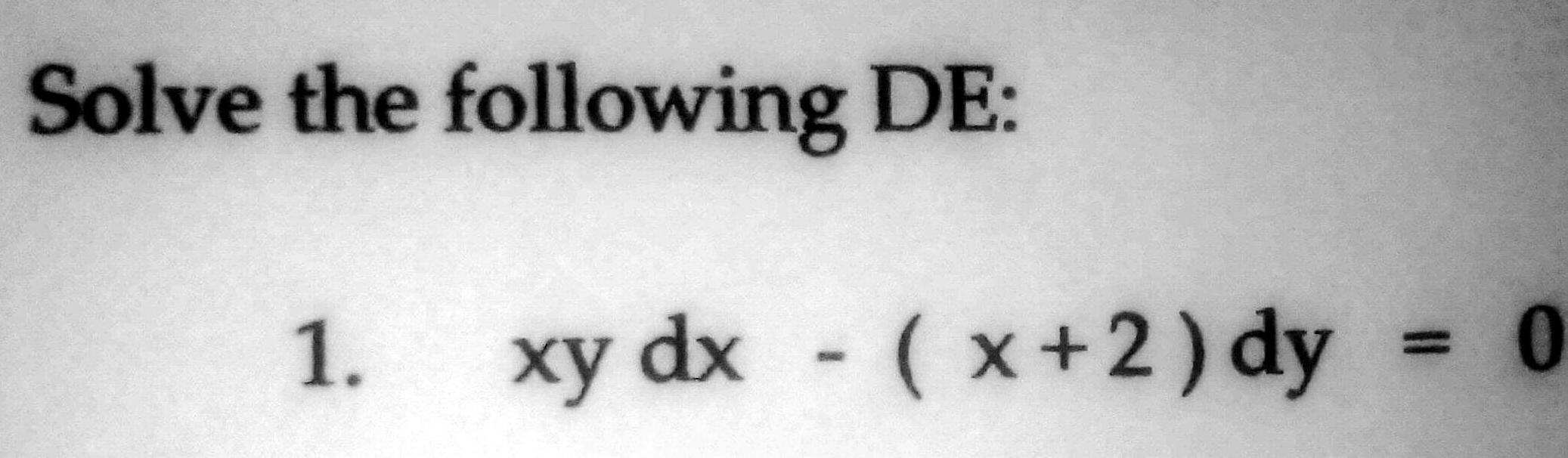
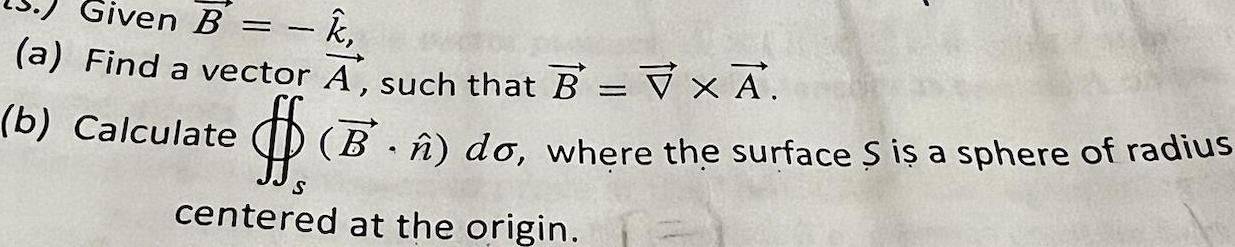
Calculus
Application of derivativesGiven B k a Find a vector A such that B V x A b Calculate B do where the surface S is a sphere of radius S centered at the origin
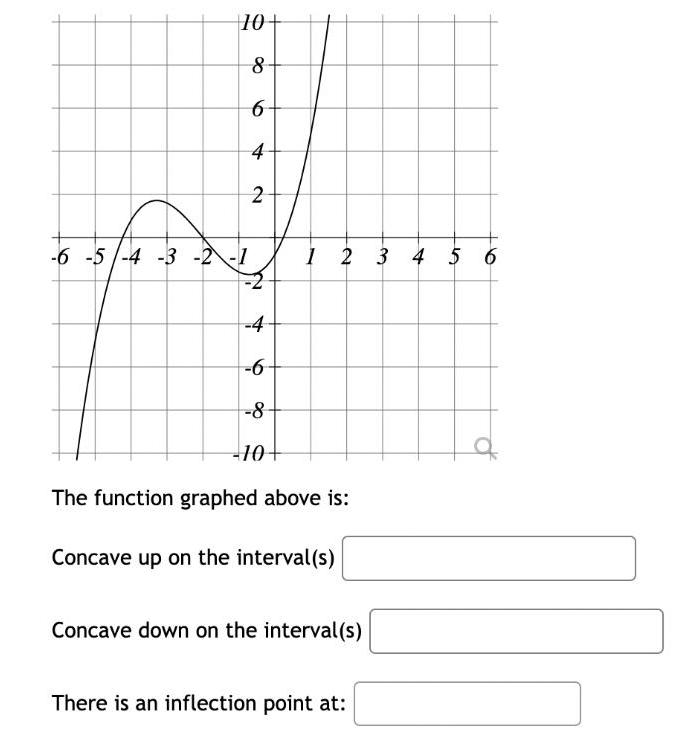
Calculus
Application of derivatives10 8 6 4 2 6 5 4 3 2 1 1 2 3 4 5 6 4 6 8 10 The function graphed above is Concave up on the interval s Concave down on the interval s There is an inflection point at

Calculus
Application of derivativesThe cancellation property sin sin x x is valid for x in what interval Enter your answer using interval notation Which of the following is not true Select all that apply sin sin sin 57 5 3 7 sin sin 4 3 sin sin


Calculus
Application of derivativesLCULATOR 3 Find the value of 1 i 6 giving your answer in the form a bi