Application of derivatives Questions and Answers

Calculus
Application of derivatives75057 20 sos Choose the correct graph below O A 5 AY 5 5 OB 5 5 O C O D 5 5 5

Calculus
Application of derivativesFind the slope of the curve below at the given points Sketch the curve along with its tangent lines at these points r 9 9 cos 0 0 The slope at the point 0 Simplify your answer B TU RIN 2 is

Calculus
Application of derivativesThe figure below gives the behavior of the derivative of a function g x on 2 x 2 Notice that no scale is given on the y axis on the graph a At what x values does the graph of g x have inflection points X minimum at x b What x values give the global maxima and minima of g on 2 2 maximum at x Graph of g x Click on the graph to get a larger version Enter your answer as a comma separated list of values or enter none if there are none c If g 2 5 what are possible values for g 0 653 g 0 is in Enter your answer as an interval or union of intervals giving the possible values Thus if you know 3 g 0 1 enter 3 1 Enter infinity for co the interval 3 3 to indicate a single point d How is the value of g 2 related to the value of g 0

Calculus
Application of derivativesLet f x Find the domain and range of f 1 Is it possible to do this without finding the expression for f Explain 1 x 5

Calculus
Application of derivativesNote If you are asked for value s give your answer as a single value e g 17 or a comma separated list e g 1 2 3 or NONE If you are asked for an interval give your answer in interval notation Type INF for oo and INF for Let which has the following derivatives f x 2xe x 4 e f x 2e 2xe 2xe x 4 e a Find the locations the x values of the points of inflection b Determine the x intervals on which f is concave up or down The left most interval is The middle interval is The right most interval is f x x 4 e and on this interval f is and on this interval f is I and on this interval f Concave Down


Calculus
Application of derivatives2 The graph of y f x is shown below on the ay plane for 6 6 Is fa one to one function on its domain Explain 10

Calculus
Application of derivativesOwners of a bike rental company that charges customers between 5 and 25 per day have determined that the number of bikes rented per day n can be modeled by the linear function n p 200 8p where p is the daily rental charge How much should the company charge each customer per day to maximize revenue Do not include units or a dollar sign in your answer

Calculus
Application of derivativesConsider the following graph of a derivative f a At what a values do the points of inflection of f occur Click on the graph to enlarge it Enter your answer as a value or a comma separated list of values or NONE b On which interval s is f concave down Enter your answer using interval notation

Calculus
Application of derivativesConsider the function f x 2 sin x 3 2 This function has two inflection points which occur at the x values A and B where 0 A B 2T A and B In the interval 0 A the function fis Concave up Concave down In the interval A B the function fis Concave up Concave down In the interval B 2T the function fis Concave up Concave down x

Calculus
Application of derivativesNote If you are asked for value s give your answer as a single value e g 17 or a comma separated list e g 1 2 3 or NONE If you are asked for an interval give your answer in interval notation Type INF for co and INF for 00 Let A Use interval notation to indicate where f x is increasing Increasing for a in B Use interval notation to indicate where f x is decreasing Decreasing for a in C List the values of all local maxima of f values of local maxima D List the values of all local minima of f values of local minima 4 f x 4x

Calculus
Application of derivativesA company plans to manufacture a rectangular bin with a square base an open top and a volume of 800 cm The cost of the material for the base is 0 1 cents per square centimeter and the cost of the material for the sides is 0 5 cents per square centimeter Determine the dimensions of the bin that will minimize the cost of manufacturing it What is the minimum cost Round any calculations and the final answer to the nearest hundredth if necessary

Calculus
Application of derivatives1 QUESTION 6 2 points Let F be an antiderivataive of f x 2 e such that F 0 3 Then find F 4


Calculus
Application of derivativesQUESTION 5 2 points Consider the function f x 23 24x 2 defined on the closed bounded interval 3 3 Find its Global absolute maximum and find its Global absolute minimum

Calculus
Application of derivativesQUESTION 6 2 points Let F be an antiderivataive of f x 1 antiderivataive of f x e find F 4 e 1 such that F 0 3 Then

Calculus
Application of derivativesoblem 5 a Find the value of c that satisfies the conclusion of the Mean Value Theorem for the function f x ln x on the interval 2 16 b If f 1 4 and f x 9 for 1 x 9 then according to the Mean Value Theorem what is the smallest possible value for f 9 c Let f be the function whose graph is shown below y 3 2 0 0 N 3 4 1 2 5 6 7 8 X Estimate the two values of c that satisfy the conclusion of the Mean Value Theorem on the interval 2 7

Calculus
Application of derivativesblem 4 Consider the function f given below x 1 if 1 x 2 x 3 4 if 2 x 5 Which of the following statements is true f x A f has both an absolute maximum and an absolute minimum B f has an absolute maximum but no absolute minimum C f has an absolute minimum but no absolute maximum D f has no absolute maximum and no absolute minimum

Calculus
Application of derivativesAn inverted cylindrical cone 24 m deep and 12 m in diameter across the top is being filled with water at a constant rate of 16 m min At what rate is the water rising in the tank when the depth of the water is 1 meter Answer 10 meters Answer 23 meters Answer

Calculus
Application of derivatives5 0 5 5 Shown above is the graph of two functions Both are defined for a 0 a The red line shows the function 3 10 or f x 10g 2 b Find the three values of a at which f x g x Give your answers in order from smallest to largest and g z log z or c Find the two values of a at which f x and g x have parallel tangent lines Give your answers in order from smallest to la

Calculus
Application of derivativesroblem 7 Let f x x In x On what interval is f concave down A e72 17 0 B 0 el7 72 C 0 e72 17 D 0 E e 17 72 0 F 0 e 17 72 G H e 72 17 00 7 72

Calculus
Application of derivatives1 x 1 You may use the following derivatives Let y 3 Find the values of x for which y is increasing most rapidly and decreasing most rapidly y x 2x x 1 is where y is increasing most rapidly is where y is decreasing most rapidly and y x 2 3x 1 x 1
Calculus
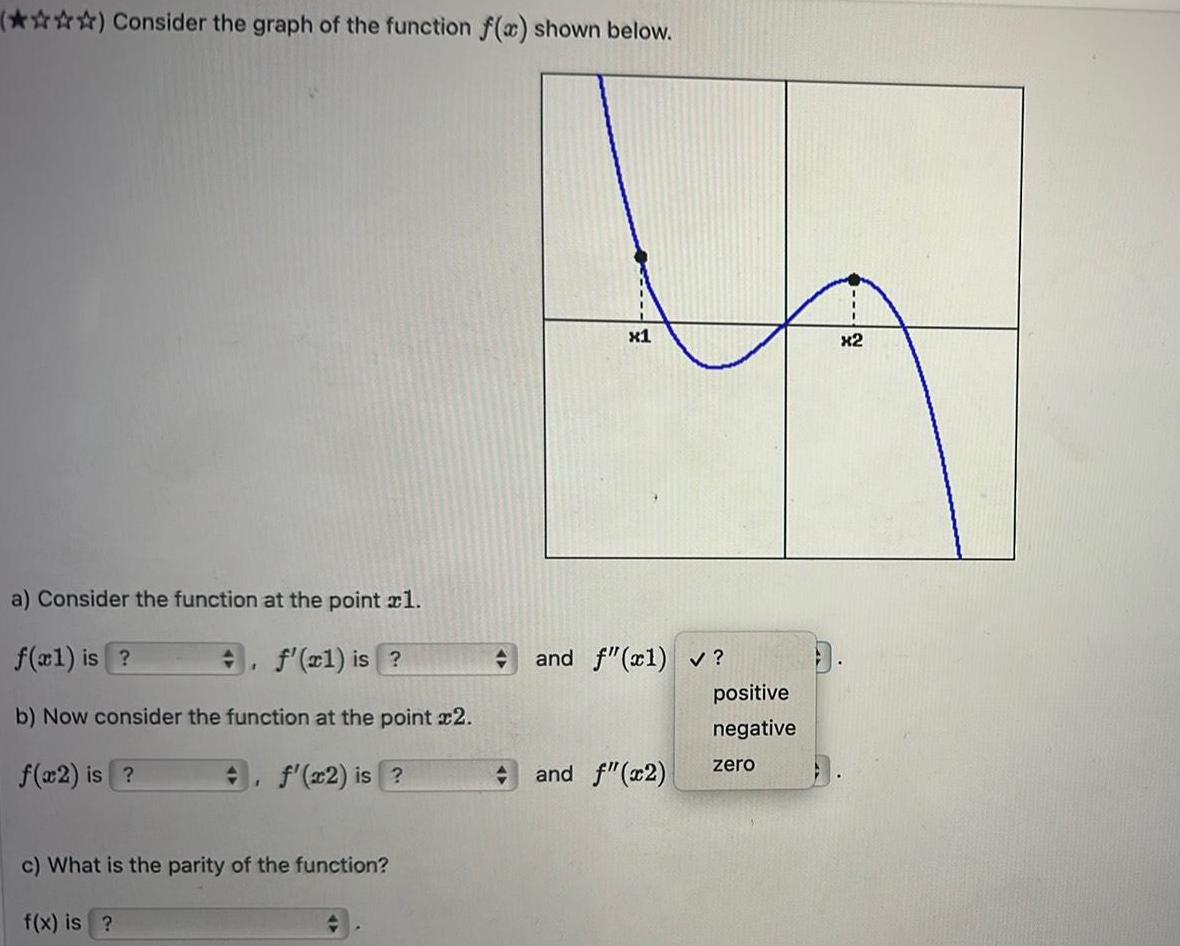
Application of derivativesConsider the graph of the function f x shown below a Consider the function at the point xl f xl is f xl is b Now consider the function at the point x2 f x2 is f x2 is 1 c What is the parity of the function f x is x1 and f x1 and f x2 positive negative zero x2

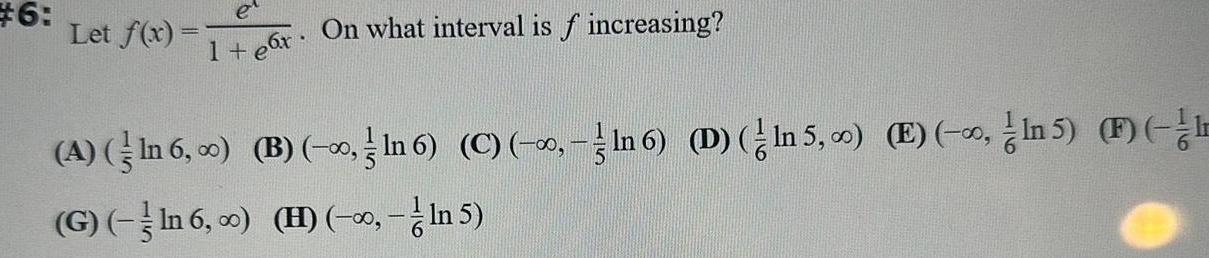
Calculus
Application of derivatives6 e 1 e x Let f x On what interval is f increasing B ln 6 C ln 6 D ln 5 E In 5 F A In 6 G In 6 0 H In 5
Calculus
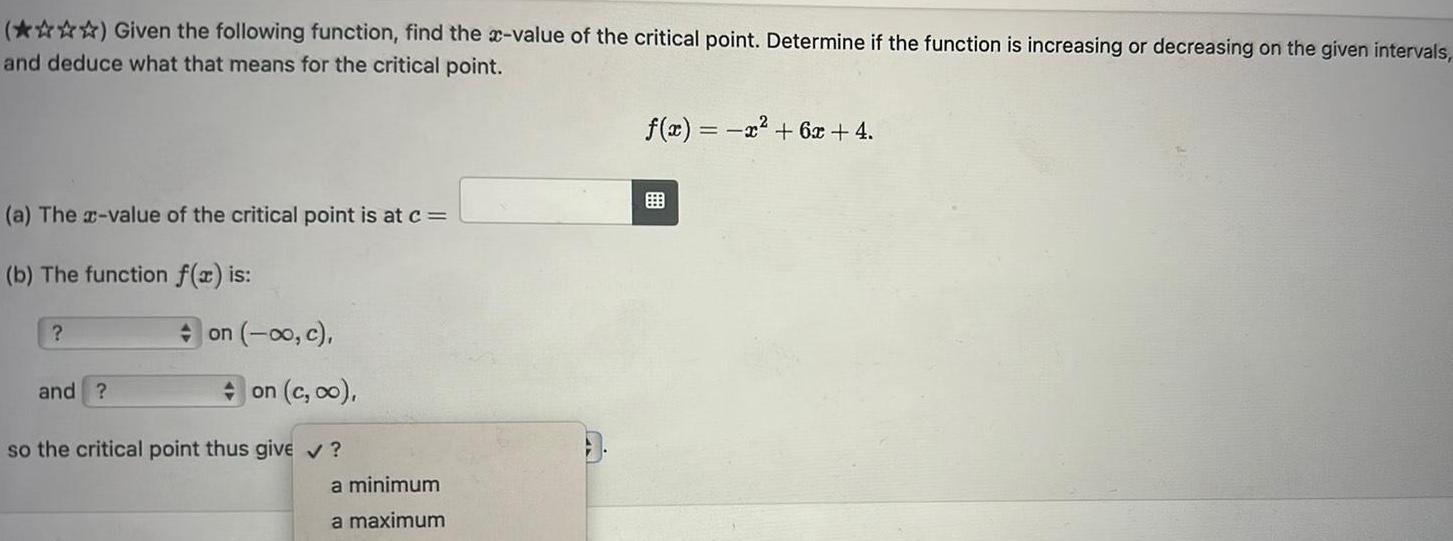
Application of derivativesGiven the following function find the x value of the critical point Determine if the function is increasing or decreasing on the given intervals and deduce what that means for the critical point a The x value of the critical point is at c b The function f x is on o c and on c oo so the critical point thus give a minimum a maximum f x x 6x 4

Calculus
Application of derivativesNewton s Law of Gravitation says that the magnitude F of the force exerted by a body of mass m on a body of mass Mis GmM 72 where G is the gravitational constant and r is the distance between the bodies F a Find d F dr What does the minus sign mean b Suppose it is known that Earth attracts an object with a force that decreases at a rate of 2 N km when 7 20000 km How fast does this force change when r 10000 km The force changes at a rate of N km

Calculus
Application of derivativesThe length of a rectangle is increasing at a rate of 6cm s and its width is increasing at a rate of 5cm s When the length is 30cm and the width is 25cm how fast is the area of the rectangle increasing The area of the rectangle is increasing at a rate of

Calculus
Application of derivativesThe pressure P and volume V of an expanding gas are related by the formula PV C where b and Care constants this model assumes adiabatic expansion without heat gain or loss Find if b 1 2 P 6kPa V 150cm and 80cm min d P dt kPa min

Calculus
Application of derivativesIn 1905 a Bohemian farmer accidentally allowed several muskrats to escape an enclosure Their population grew and spread occupying increasingly larger areas throughout Europe In a classical paper in ecology it was shown by the scientist Skellam 1951 that the square root of the occupied area increased at a constant rate k Determine the rate of change of the distance from the site of release that the muskrats had spread For simplicity you may assume that the expanding area of occupation is circular with radius r t Simplify your answer so that it only depends on k r t
Calculus
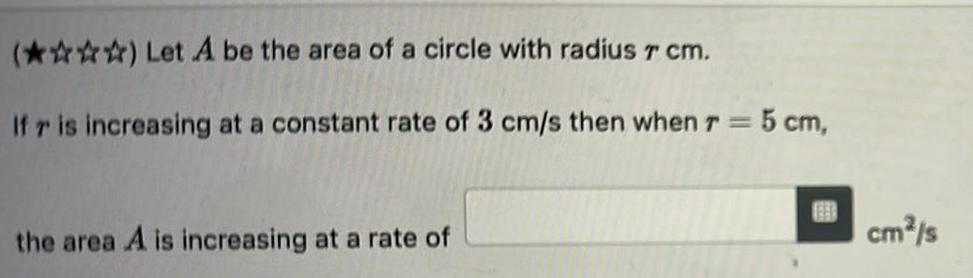
Application of derivativesLet A be the area of a circle with radius 7 cm If r is increasing at a constant rate of 3 cm s then when r 5 cm the area A is increasing at a rate of cm s
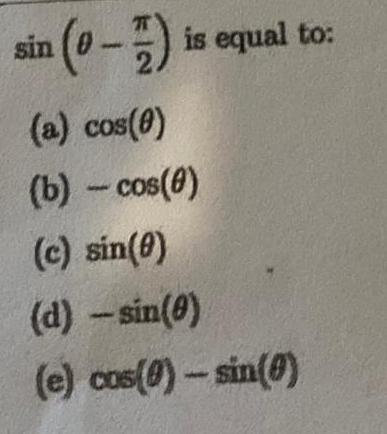
Calculus
Application of derivativessin 0 1 is equal to a cos 0 b cos 8 c sin 0 d sin 0 e cos 0 sin 0 3 E

Calculus
Application of derivativesQuestion 2 2 3 5 points a 2 points Suppose a curve is described implicitly by the equation y sin x e cos y Find the equation of the tangent line to this curve at the point 0 2

Calculus
Application of derivativesA 16 foot ladder is leaning against a wall If the top of the ladder slides down the wall at a rate of 3 feet per second how fast is the bottom of the ladder moving along the ground when the bottom of the ladder is 4 feet from the wall Leave your answer in exact form simplified as much as possible Do not include units

Calculus
Application of derivativesA company plans to manufacture a rectangular box with a square base an open top and a volume of 458 in The cost of the material for the base is 0 5 cents per square inch and the cost of the material for the sides is 0 4 cents per square inch Determine the dimensions of the box that will minimize the cost of manufacturing it What is the minimum cost per box rounded to the nearest cent Round any calculations and the final answer to the nearest hundredth if necessary C

Calculus
Application of derivativesA box with a square base and open top must have a volume of 2500 cm What is the minimum possible surface area in cm of this box Round to the nearest whole number and omit units

Calculus
Application of derivativesA rectangular bin is going to be made with a volume of 492 in The base of the bin will be a square and the top will be open The cost of the material for the base is 0 8 cents per square inch and the cost of the material for the sides is 0 6 cents per square inch Determine the dimensions of the bin that will minimize the cost of manufacturing it What is the minimum cost Round any calculations and the final answer to the nearest hundredth if necessary Provide your answer below
Calculus
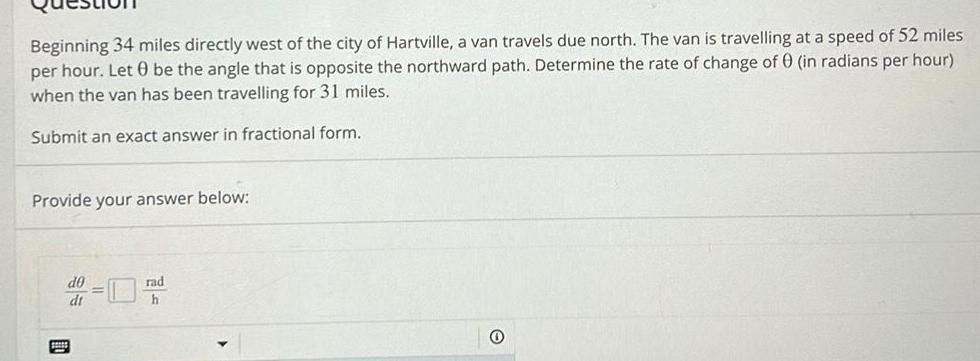
Application of derivativesBeginning 34 miles directly west of the city of Hartville a van travels due north The van is travelling at a speed of 52 miles per hour Let 0 be the angle that is opposite the northward path Determine the rate of change of 0 in radians per hour when the van has been travelling for 31 miles Submit an exact answer in fractional form Provide your answer below d0 dt rad h 0

Calculus
Application of derivativesA cylindrical can is partially filled with sand The radius of the cylindrical can is 15 cm The height of the cylindrical can is 14 cm If the volume of the sand is increasing at a rate of 555 cubic cm per second what is the rate in cm per second at which the height of the sand is changing when the height of the sand is 5 cm Submit an exact simplified answer Remember that the volume of a cylinder is V r h Provide your answer below
Calculus
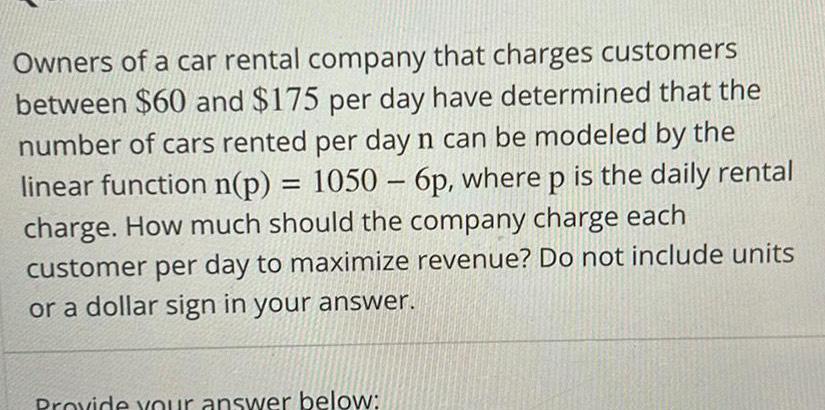
Application of derivativesOwners of a car rental company that charges customers between 60 and 175 per day have determined that the number of cars rented per day n can be modeled by the linear function n p 1050 6p where p is the daily rental charge How much should the company charge each customer per day to maximize revenue Do not include units or a dollar sign in your answer Provide your answer below

Calculus
Application of derivativesQuestion the A cylindrical can is partially filled with water The radius of the cylindrical can is 8 inches and its height is 9 inches If volume of the water is decreasing at a rate of 527 cubic inches per minute what is the rate in inches per minute at which the height of the water is changing when the height of the water is 5 inches Submit an exact answer Do not forget to include a negative sign if the height is decreasing Remember that the volume of a cylinder is V r h Provide your answer below

Calculus
Application of derivativesA circle has a radius that is decreasing at a rate of 18 mm per minute What is the rate of change of the area of the circle when the radius is 4 mm Do not include the units in your answer

Calculus
Application of derivativesUse the parent function f x b and transformation techniques to graph h x 4 2 2 Also indicate which transformation s is are applied Determine the domain range and horizontal asymptote of h Select all transformations that apply Shift the graph of f 2 units to the left Shift the graph of f 2 units down Shift the graph of f 2 units up Reflect the graph of f about the y axis Horizontally stretch the graph of f by a factor of 2 Reflect the graph of f about the x axis Vertically stretch the graph of f by a factor of 2 Shift the graph of f 2 units to the right Vertically compress the graph of f by a factor of 2 Horizontally compress the graph of f by a factor of 2

Calculus
Application of derivativesQuestion A triangle has a base that is decreasing at a rate of 16 cm per hour with the height being held constant What is the rate o change of the area of the triangle if the height is 9 cm Do not include the units in your answer Provide your answer below

Calculus
Application of derivativesFor a dosage of x cubic centimeters cc of a certain drug the resulting blood pressure B is approximated by the function below Find the maximum blood pressure and the dosage at which it occurs B x 355x 1420x 0 x 0 25 The maximum is obtained for a dosage of 0 17 Round to two decimal places as needed The maximum blood pressure obtained is Round to two decimal places as needed

Calculus
Application of derivativesFor a dosage of x cubic centimeters cc of a certain drug the resulting blood pressure B is approximated by the function below Find the maximum blood pressure and the dosage at which it occurs B x 355x 1420x 0 x 0 25 The maximum is obtained for a dosage of Round to two decimal places as needed
Calculus
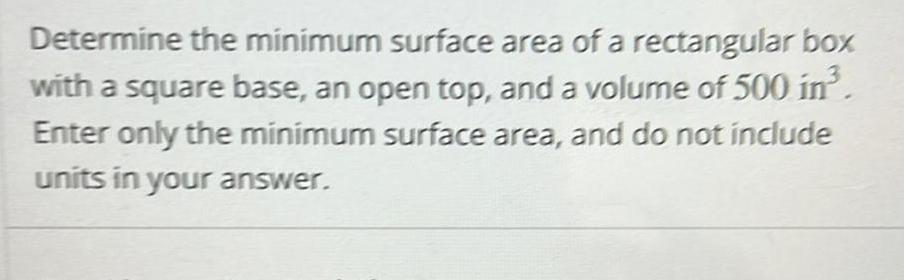
Application of derivativesDetermine the minimum surface area of a rectangular box with a square base an open top and a volume of 500 in Enter only the minimum surface area and do not include units in your answer

Calculus
Application of derivativesA lifeguard needs to rope off a rectangular swimming area in front of Long Lake Beach using 800 yd of rope and floats What dimensions of the rectangle will maximize the area What is the maximum area Note that the shoreline is one side of the rectangle Let x be the length of a side of the rectangle perpendicular to the shoreline Write the objective function for the area in terms of x A x Type an expression using x as the variable The length of the shorter side of the rectangular region is The length of the longer side of the rectangular region is The maximum area of the rectangular region is
Calculus
Application of derivativesQuestion A circle has an area that is decreasing at a rate of 555 square feet per second Determine the rate of change of the radius when the radius is 6 feet Do not include the units in your answer Provide your answer below 7 8 9 4 5 6 X X X y X x X
Calculus
Application of derivativesA box is partially filled with sand The length of the box is 8 mm The width of the box is 17 mm If the volume of the sand is decreasing at a rate of 562 cubic mm per minute what is the rate in mm per minute at which the height of the sand is changing when the height of the sand is 2 mm Submit an exact answer Do not forget to include a negative sign if the height is decreasing Provide your answer below dh dt 1 mm min Y