Application of derivatives Questions and Answers
Calculus
Application of derivativesA rectangular bin is going to be made with a volume of 646 cm The base of the bin will be a square and the top will be open The cost of the material for the base is 0 5 cents per square centimeter and the cost of the material for the sides is 0 3 cents per square centimeter Determine the dimensions of the bin that will minimize the cost of manufacturing it What is the minimum cost Round any calculations and the final answer to the nearest hundredth if necessary Provide your answer below

Calculus
Application of derivativesAn employee s monthly productivity M in number of units produced is found to be a function of the number t of years of service For a certain product a productivity function is shown below Find the maximum productivity and the year in which it is achieved M t 3t 1441 140 0st 40

Calculus
Application of derivativesAn inverted cone has a height of 11 inches and an initial radius of 18 inches The volume of the inverted cone is decreasing at a rate of 541 cubic inches per second with the height being held constant What is the rate of change of the radius in inches per second when the radius is 5 inches Submit an exact answer Do not forget to include a negative sign if the radius is decreasing Remember that the volume of a cone is V r h Provide your answer below

Calculus
Application of derivativesOf all numbers that add to 82 find the pair that has the maximum product That is maximize the objective function Q xy subject to the constraint x y 82 The values of x and y that have the maximum product are x Type integers or simplified fractions The maximum product of x and y is Q Type an integer or a simplified fraction and y B

Calculus
Application of derivativesAn employee s monthly productivity M in number of units produced is found to be a function of the number t of years of service For a certain product a productivity function is shown below Find the maximum productivity and the year in which it is achieved M t 3t 144t 140 0 t 40 The maximum productivity is achieved in year The maximum productivity is units

Calculus
Application of derivativesQuestion A circle has a radius that is increasing at a rate of JT second What is the rate of change of the area of the circle when the radius is 3 feet Do not include the units in your answer feet per

Calculus
Application of derivatives5 km Coral reef 15 km 1 Provide your answer below Tent Shoreline A visitor is staying in a tent that is 15 kilometers east of the closest point on a shoreline to a coral reef The coral reef is 5 kilometers due south of the shoreline The visitor plans to travel from the tent to the coral reef by running and swimming If the visitor runs at a rate of 9 kmph and swims at a rate of 5 kmpl how far should the visitor run to minimize the time it takes to reach the coral reef Round to two decimal places
Calculus
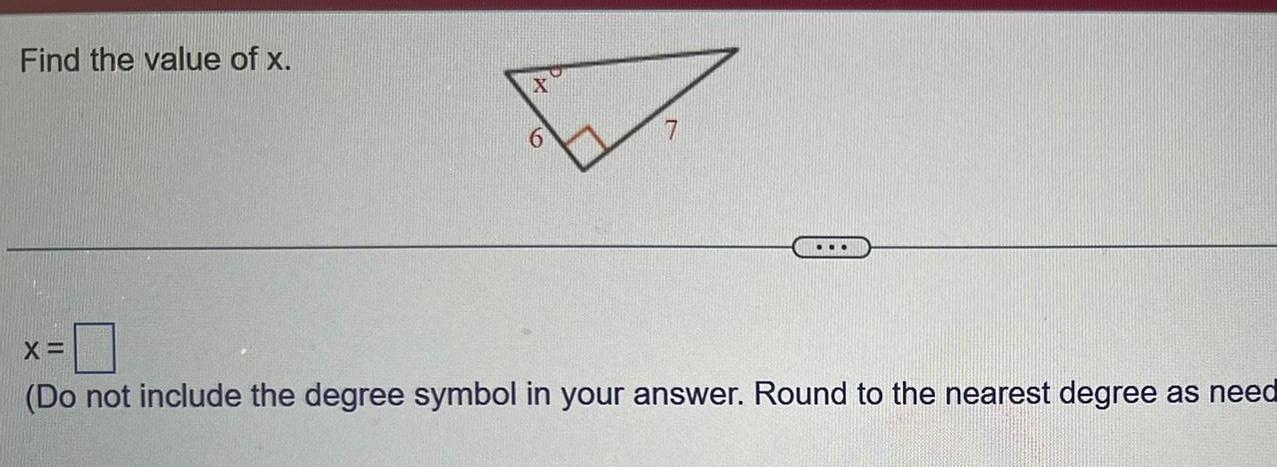
Application of derivativesFind the value of x X Do not include the degree symbol in your answer Round to the nearest degree as need

Calculus
Application of derivativesQuestion A Use implicit differentiation to find the equation of the tangent line to the function defined implicitly by the equation below at the point 1 1 3x 4x 10 2y y Give your answer in the form y mx b
Calculus
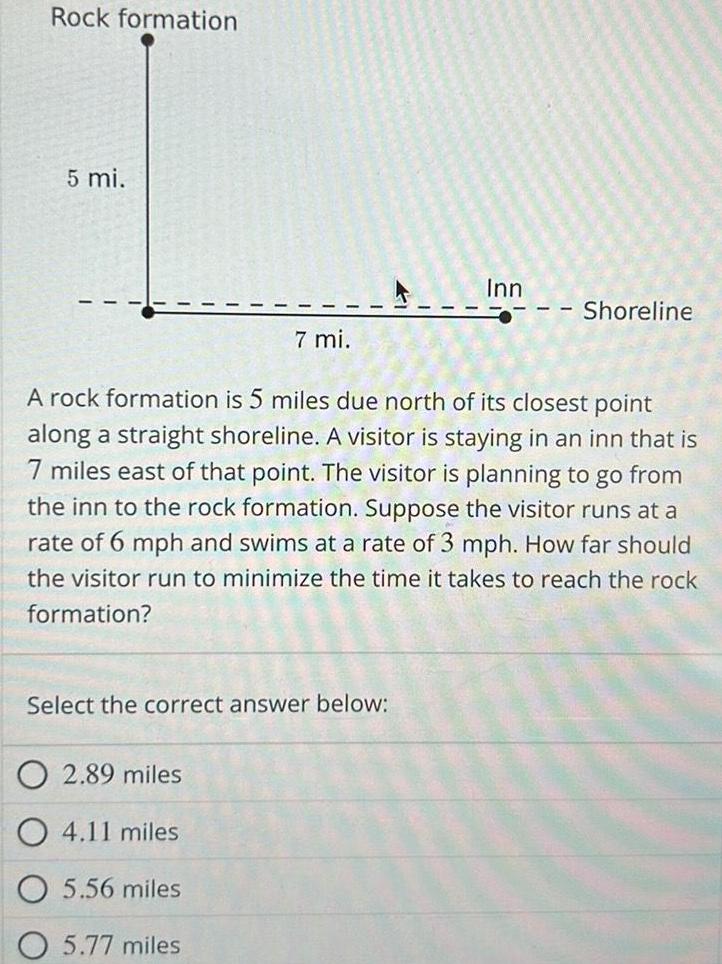
Application of derivativesRock formation 5 mi Select the correct answer below 2 89 miles 4 11 miles 7 mi A rock formation is 5 miles due north of its closest point along a straight shoreline A visitor is staying in an inn that is 7 miles east of that point The visitor is planning to go from the inn to the rock formation Suppose the visitor runs at a rate of 6 mph and swims at a rate of 3 mph How far should the visitor run to minimize the time it takes to reach the rock formation 5 56 miles 5 77 miles Inn Shoreline

Calculus
Application of derivativesFind an equation for the line tangent to the curve at the point defined by the given value of t Also find the value o d y 2 dx at this point x 41 10 y t t 1 Write the equation of the tangent line

Calculus
Application of derivativesnd the quotient Leave the result in trigonometric form Let 0 0 2 9 cos 4 4 i sin 4 4 7 cos 1 5 i sin 1 5

Calculus
Application of derivativesFind all absolute maximum and minimum values for the function y 3x 6x 9 on the interval 5 1 enter NONE if there are none help numbers enter NONE if there are none help numbers a Absolute maximum is b Absolute minimum is

Calculus
Application of derivativesAbsolute Extreme Values Find the absolute maximum and minimum values of the function f x e on the interval 4 7 Absolute maximum value Absolute minimum value
Calculus
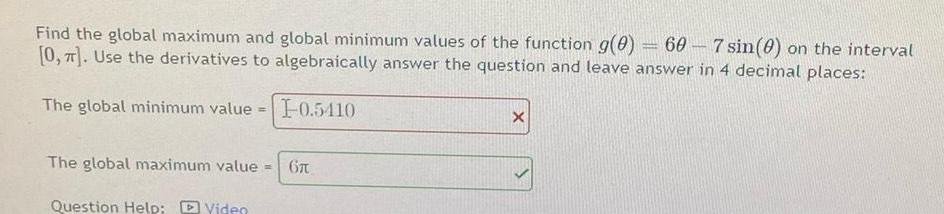
Application of derivativesFind the global maximum and global minimum values of the function g 0 60 7 sin 0 on the interval 0 Use the derivatives to algebraically answer the question and leave answer in 4 decimal places The global minimum value I 0 5410 The global maximum value 6 Question Help Video X
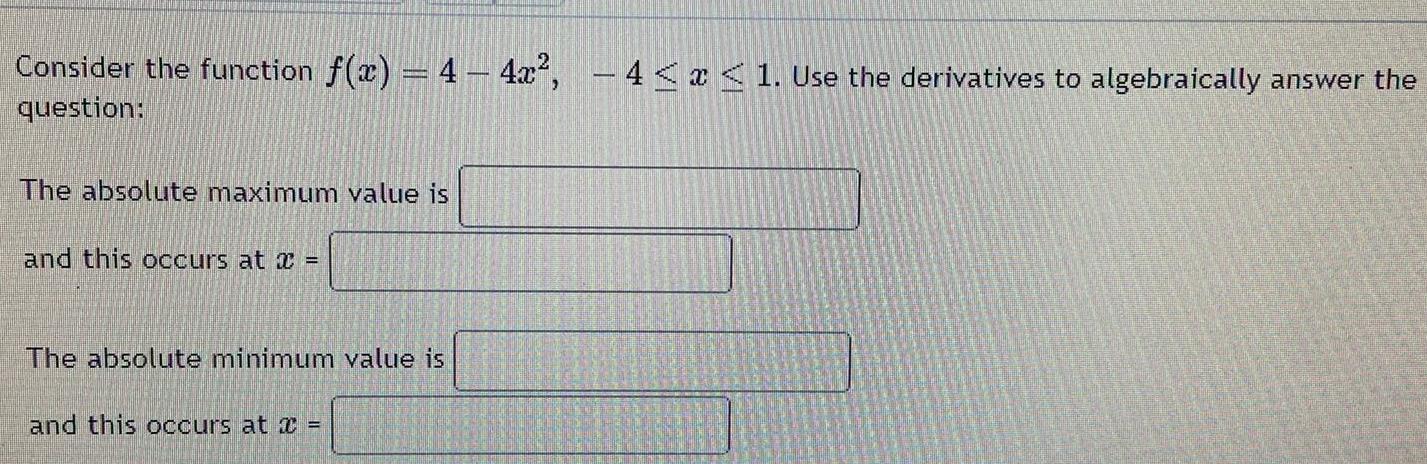
Calculus
Application of derivativesConsider the function f x 4 4x question The absolute maximum value is and this occurs at x The absolute minimum value is and this occurs at x 4 x 1 Use the derivatives to algebraically answer the

Calculus
Application of derivativesConsider the sequence Describe the behavior of the sequence Is the sequence monotone Monotone decreasing for all n Is the sequence bounded an 2 5 0 9 Bounded Determine whether the sequence converges or diverges If it converges find the value it converges to diverges enter DIV
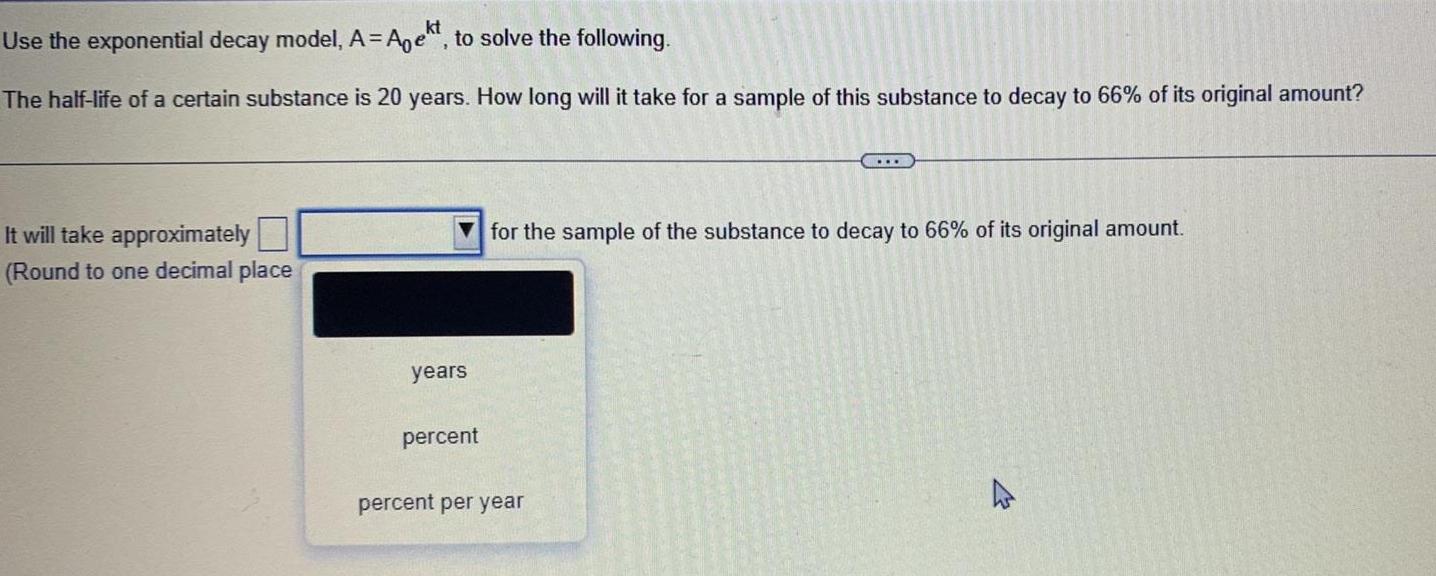
Calculus
Application of derivativesUse the exponential decay model A Aekt to solve the following The half life of a certain substance is 20 years How long will it take for a sample of this substance to decay to 66 of its original amount It will take approximately Round to one decimal place years percent for the sample of the substance to decay to 66 of its original amount percent per year
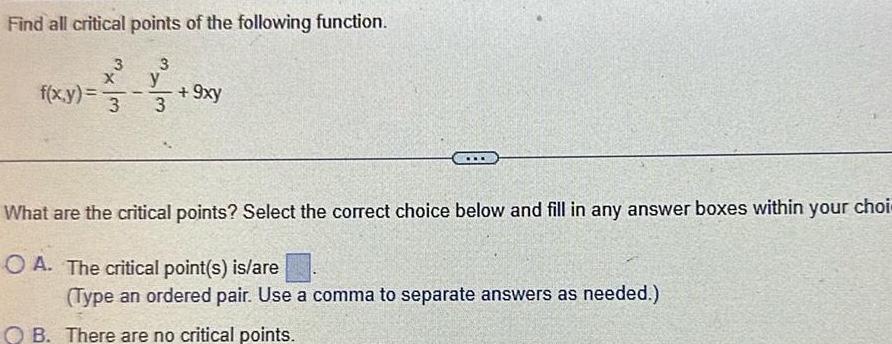
Calculus
Application of derivativesFind all critical points of the following function f x y 3 X 3 3 y 3 9xy What are the critical points Select the correct choice below and fill in any answer boxes within your choi OA The critical point s is are Type an ordered pair Use a comma to separate answers as needed OB There are no critical points

Calculus
Application of derivativesSome questions make use of the Interactive Graphing Tool to draw a basic graph and then use interactions to edit special graph values in order to complete the graph Click the icon to view instructions for the Interactive Graphing Tool 2 Use the x cubed tool to graph the x cubed function Update the function to have a Vertical Stretch of 3 a Horizontal Stretch of 1 a Vertical Shift of 0 a Horizontal Shift of 5 and a Reflection over the x axis Use the x cubed tool button on the graphing palette to place the function on the graph Then update the Vertical Stretch Horizontal Stretch Vertical Shift Horizontal Shift and Reflect over x axis interactions to have the values noted above Click to enlarge
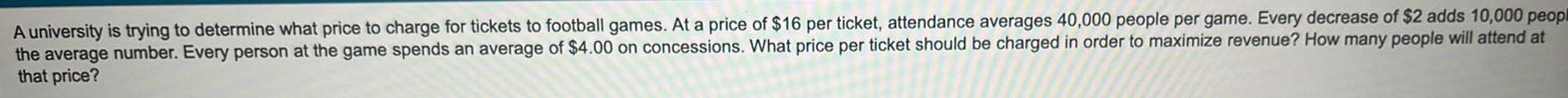
Calculus
Application of derivativesA university is trying to determine what price to charge for tickets to football games At a price of 16 per ticket attendance averages 40 000 people per game Every decrease of 2 adds 10 000 peopl the average number Every person at the game spends an average of 4 00 on concessions What price per ticket should be charged in order to maximize revenue How many people will attend at that price
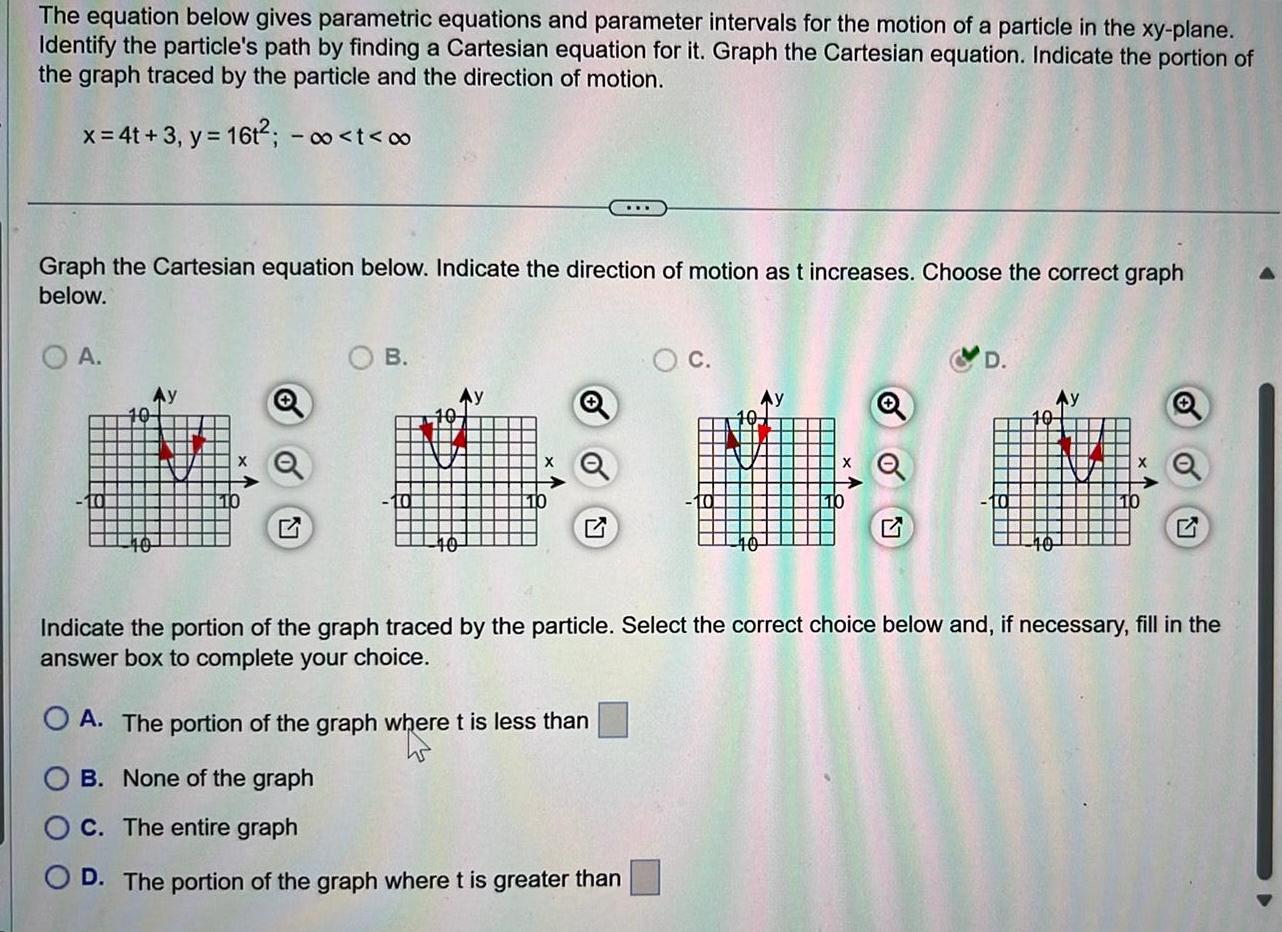
Calculus
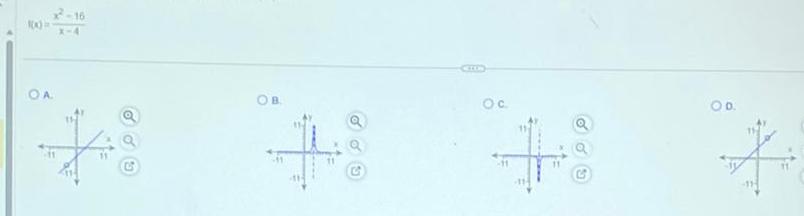
Application of derivativesThe equation below gives parametric equations and parameter intervals for the motion of a particle in the xy plane Identify the particle s path by finding a Cartesian equation for it Graph the Cartesian equation Indicate the portion of the graph traced by the particle and the direction of motion x 4t 3 y 16t t Graph the Cartesian equation below Indicate the direction of motion as t increases Choose the correct graph below A Q B 40 C OA The portion of the graph where t is less than B None of the graph C The entire graph O D The portion of the graph where t is greater than Y G Indicate the portion of the graph traced by the particle Select the correct choice below and if necessary fill in the answer box to complete your choice
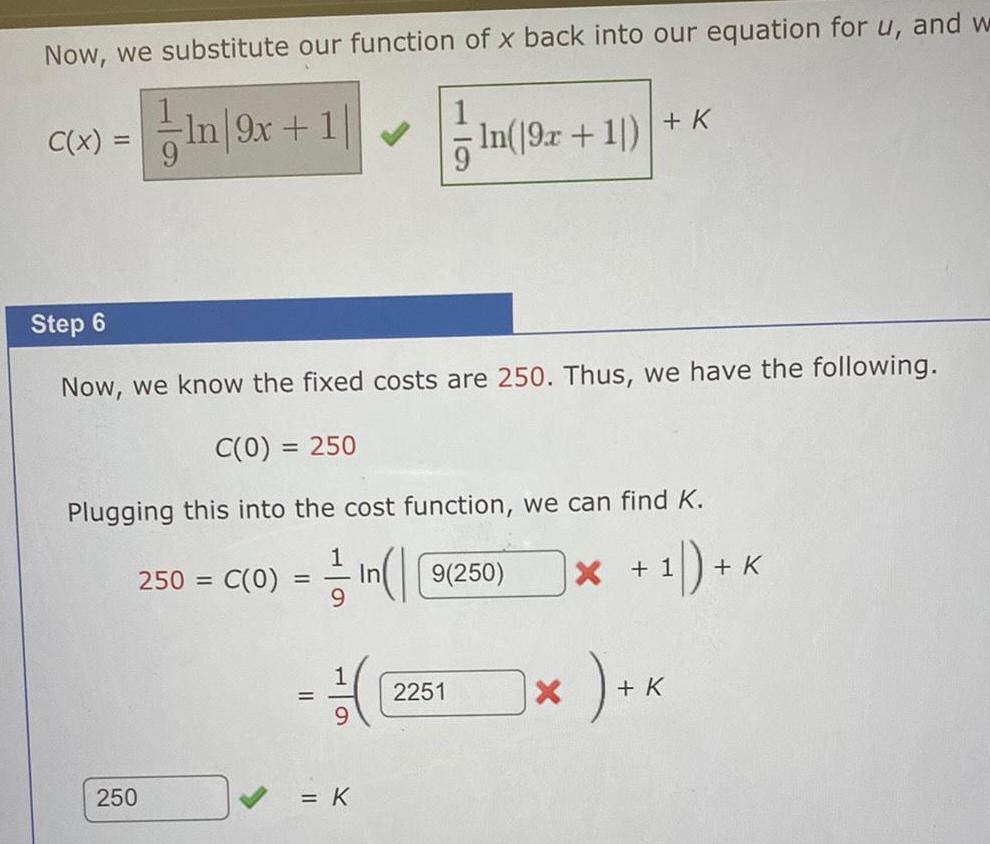
Calculus
Application of derivativesNow we substitute our function of x back into our equation for u and w In 9x 1 1 C x Step 6 Now we know the fixed costs are 250 Thus we have the following C 0 250 Plugging this into the cost function we can find K 250 C 0 n 9 250 1 K 250 1 K In 9x 1 K 2251 X 1 K
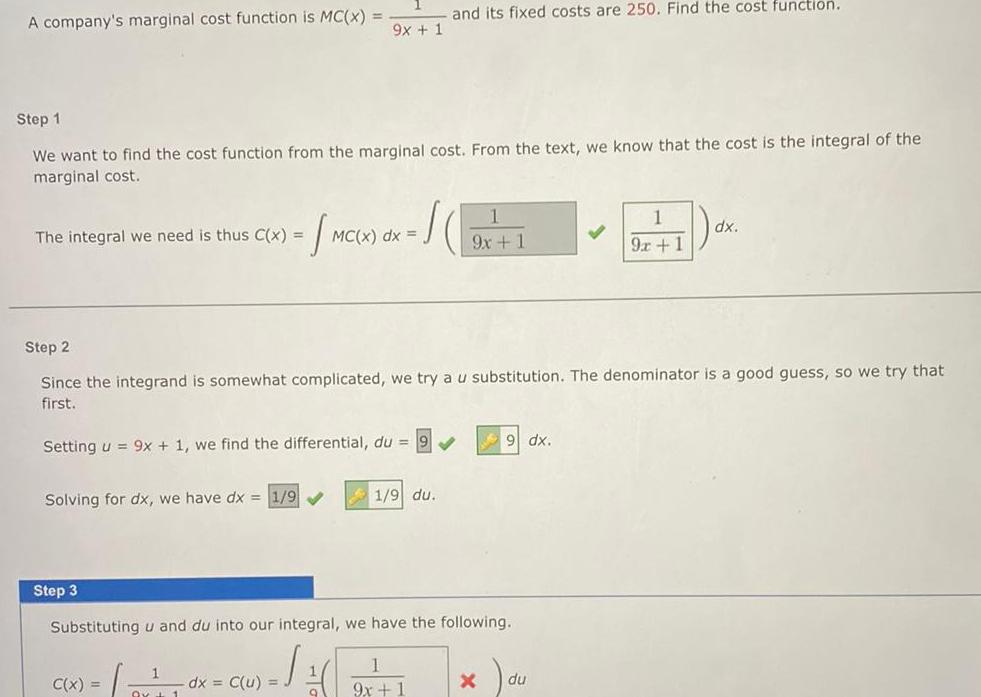
Calculus
Application of derivativesA company s marginal cost function is MC x The integral we need is thus C x Step 1 We want to find the cost function from the marginal cost From the text we know that the cost is the integral of the marginal cost Solving for dx we have dx 1 9 Step 3 Setting u 9x 1 we find the differential du 9x 1 C x dx C u MC x dx Step 2 Since the integrand is somewhat complicated we try a u substitution The denominator is a good guess so we try that first o and its fixed costs are 250 Find the cost function 1 1 9 du Substituting u and du into our integral we have the following 9x 1 9x 1 X du 1 9x 1 dx dx
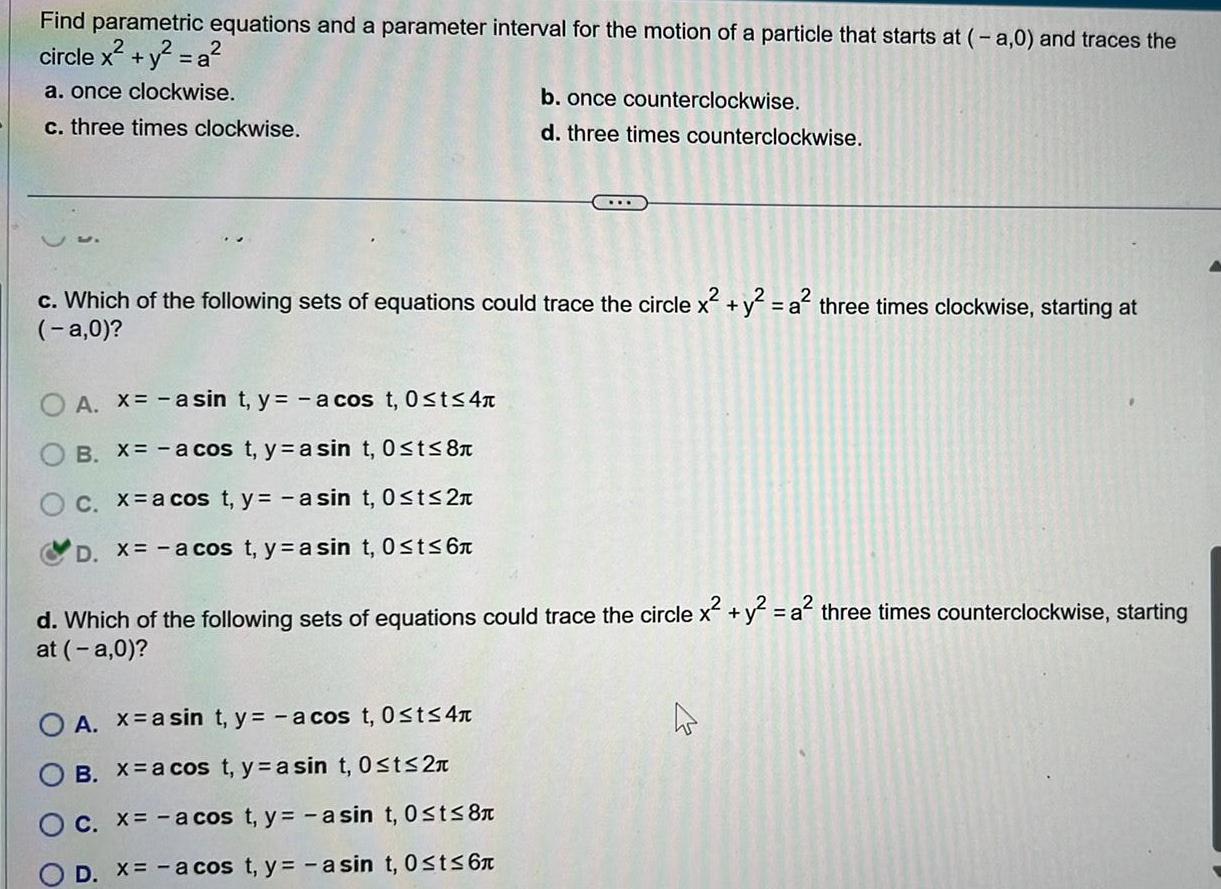
Calculus
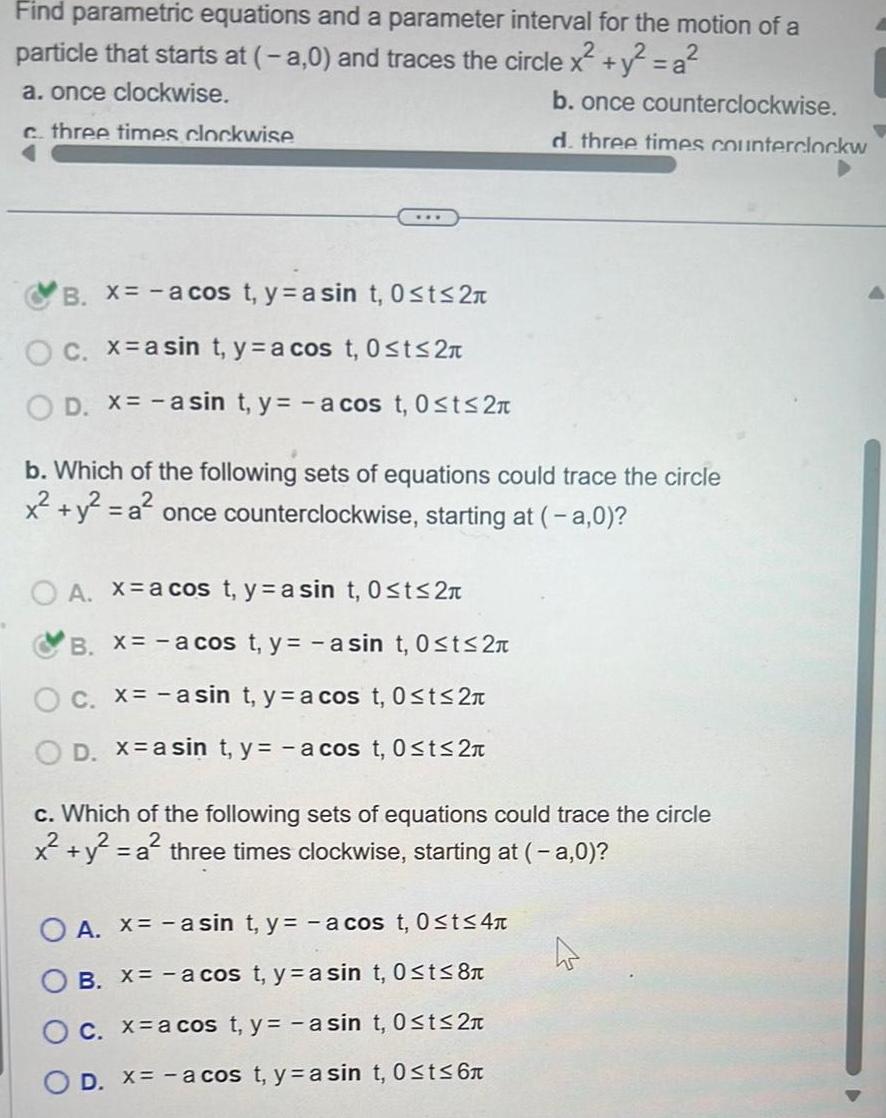
Application of derivativesFind parametric equations and a parameter interval for the motion of a particle that starts at a 0 and traces the circle x y a a once clockwise c three times clockwise c Which of the following sets of equations could trace the circle x y a three times clockwise starting at a 0 O A x asin t y a cos t 0 t 4 B X a cos t ya sin t 0 t 8 O c x a cos t y a sin t 0 t 2 D x a cos t yasin t 0 t 6 b once counterclockwise d three times counterclockwise d Which of the following sets of equations could trace the circle x y a three times counterclockwise starting at a 0 O A x asin t y a cos t 0 t 4 OB X a cos t y a sin t 0 t 2n O c x a cos t y a sin t 0 t 8 D X a cos t y asin t 0 t 6
Calculus
Application of derivativesFind the fixed point of the function f A fixed point of a function f is a real number c such that f c c Round your answer to three decimal places f x cos 2x CM radians

Calculus
Application of derivativesUse a graphing utility to approximate the solutions of the equation in the interval 0 2x by collecting all terms on one side graphing the new equation and using the zero or root feature to approximate the x intercepts the graph Round your answers to four decimal places Enter your answers as a comma separated list If there is no solution enter NO SOLUTION 2 sec x tan x 3 X

Calculus
Application of derivativesA company s marginal cost function is MC x given below where x is the number o Find the total cost of the first hundred units 6e 0 022 MC x

Calculus
Application of derivatives5 Find the equa 6 To find the derivative of h x x 2e 6 would require the chain rule What functions f x and g x could you use to find h x if h x f g x

Calculus
Application of derivativesSolve the equation for x cot r 1 0 STEP 1 Subtract the constant from both sides cot x 1 0 cot x STEP 2 The term cot x is now isolated in the equation Find a particular solution on the interval 0 0 x X STEP 3 On 00 00 there are an infinite number of solutions Write the general form of the solution Use n as an integer con X
Calculus
Application of derivatives5 Find the equation of the tangent line to f x 10x 6 when x 1 6 ohoin rule What functions f x and g x

Calculus
Application of derivativesSolve the multiple angle equation Enter your answers as a comma separated list Let n be any integer sin 7x X 3 2
Calculus
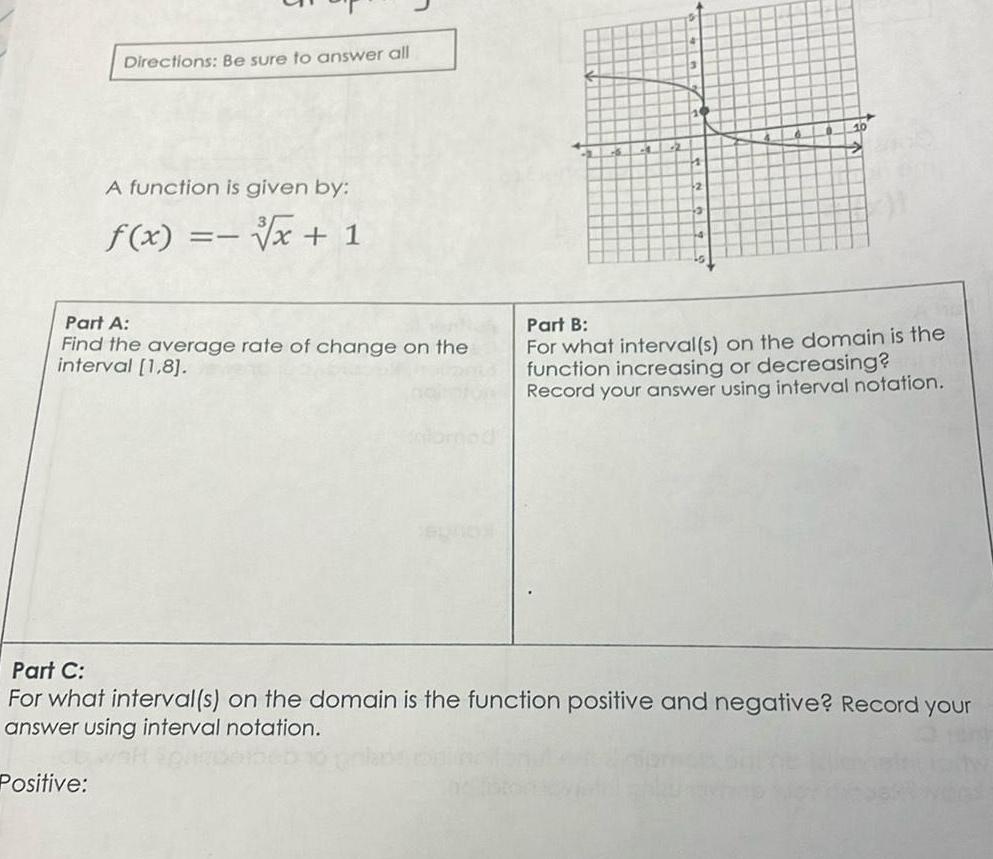
Application of derivativesDirections Be sure to answer all A function is given by x 1 Positive f x Part A Find the average rate of change on the interval 1 8 AL 10 Part B For what interval s on the domain is the function increasing or decreasing Record your answer using interval notation Part C For what interval s on the domain is the function positive and negative Record your answer using interval notation

Calculus
Application of derivativesFind the slope of the tangent line to the ellipse slope 1 at the point x y Are there any points where the slope is not defined Enter them as semicolon separated ordered pairs e g 1 3 2 5 Enter none if there are no such p slope is undefined at
Calculus
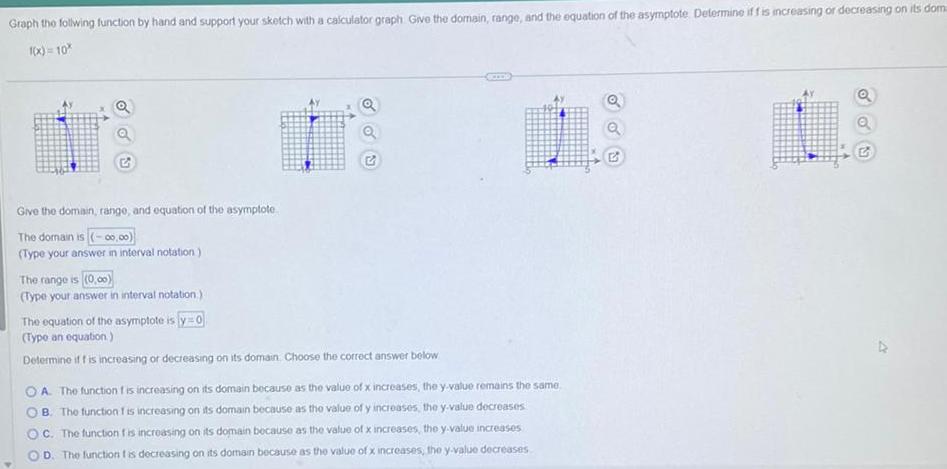
Application of derivativesGraph the follwing function by hand and support your sketch with a calculator graph Give the domain range and the equation of the asymptote Determine if f is increasing or decreasing on its dom 1 x 10 sur Give the domain range and equation of the asymptote The domain is 00 00 Type your answer in interval notation The range is 0 00 Type your answer in interval notation The equation of the asymptote is y 0 Type an equation Determine if f is increasing or decreasing on its domain Choose the correct answer below OA The function is increasing on its domain because as the value of x increases the y value remains the same B The function is increasing on its domain because as the value of y increases the y value decreases OC The function is increasing on its domain because as the value of x increases the y value increases D The function t is decreasing on its domain because as the value of x increases the y value decreases Q Q

Calculus
Application of derivativesAn open top bin is to be made from a 15 centimeter by 40 centimeter piece of plastic by removing a square from each corner of the plastic and folding up the flaps on each side What size square should be cut out of each corner to get a bin with the maximum volume Enter an exact answer for the area of the square

Calculus
Application of derivativesA car rental company charges its customers p dollars per day to rent a car where 35 SPS 120 The number of cars rented per day can be modeled by the linear function p 1200 10p How much should the company charge each customer per day to maximize revenue Do not include units or a dollar sign in your answer

Calculus
Application of derivativesA bike rental company charges its customers p dollars per day to rent a bike where 5 p 30 The number of bikes rented per day can be modeled by the linear function n p 300 10p How much should the company charge each customer per day to maximize revenue Do not include units or a dollar sign in your answer

Calculus
Application of derivativesSuppose that the elasticity of demand at a given price level is E p 0 8 What does that mean Select both the correct answer to elastic unit or inelastic as well as what the company should do to increase revenue Since 0 E p 1 demand is inelastic The company should lower prices to raise revenue The company should raise prices to raise revenue Since 0 E p 1 demand is elastic Since 0 E p 1 demand is unit The company should leave prices alone as the revenue is currently maximized

Calculus
Application of derivativesa Evaluate the Riemann sum for f x 1 x 1 x 2 with four terms taking the sample points to be right end points Give your answer correct to six decimal places Explain what the Riemann sum represents with the aid of a sketch b Repeat part a with midpoints as the sample points


Calculus
Application of derivativest MY NOTES A drug response curve describes the level of medication in the bloodstream after a drug is administered A surge function S t AtPe kt where t 0 is often used to model the response curve reflecting an initial surge in the drug level and then a more gradual decline If for a particular drug A 0 03 p 4 k 0 08 and t is measured in minutes estimate the times t corresponding to the inflection points Round your answers to two decimal places min smaller value min larger value t PRACTICE ANOTHER
Calculus
Application of derivativesFind parametric equations and a parameter interval for the motion of a particle that starts at a 0 and traces the circle x y a a once clockwise b once counterclockwise c three times clockwise d three times counterclockw B x a cos t y asin t 0 t 2 O c x a sin t y a cos t 0 t 2 D x asin t y a cos t 0 t 2n b Which of the following sets of equations could trace the circle x y a once counterclockwise starting at a 0 OA xa cos t y a sin t 0 t 2 B x a cos t y asin t 0 ts 2 C x a sin t ya cos t 0 t 2 D x a sint y a cos t 0 t 2 c Which of the following sets of equations could trace the circle x y a a three times clockwise starting at a 0 O A x asin t y a cos t 0 t 4 B X a cos t y a sin t 0 t 8 C x a cos t y asin t 0 t 2 D x a cos t y a sin t 0 t 6 4 D

Calculus
Application of derivatives5 a Estimate the prea under the graph of f x 1 x from x 1 to x 2 using three rectangles and right end points Then improve your estimate by using six rect angles Sketch the curve and the approximating rectangles b Repeat part a using left endpoints c Repeat part a using midpoints d From your sketches in parts a c which estimate appears to be the most accurate

Calculus
Application of derivativesWhich of the following would represent an approximation of R 51 using information from R x OR 51 R 51 R 51 OR 51 R 50 OR 51 R 50 OR 51 R 50 R 50

Calculus
Application of derivativesIf h x f g x and f 1 7 f 1 10 g 1 1 and g 1 5 find h 1 O 14 ONot enough information O 350 O 50 O 35

Calculus
Application of derivativesIf C x 3000 10x 0 05x then find the marginal average cost function Cave x O Cave x 10 0 1x 3000 O O O Cave x Cave Cave x Cave x OC 3000 C 10 x 0 05 10 0 05x 0 1 3000 10x 0 05x
Calculus
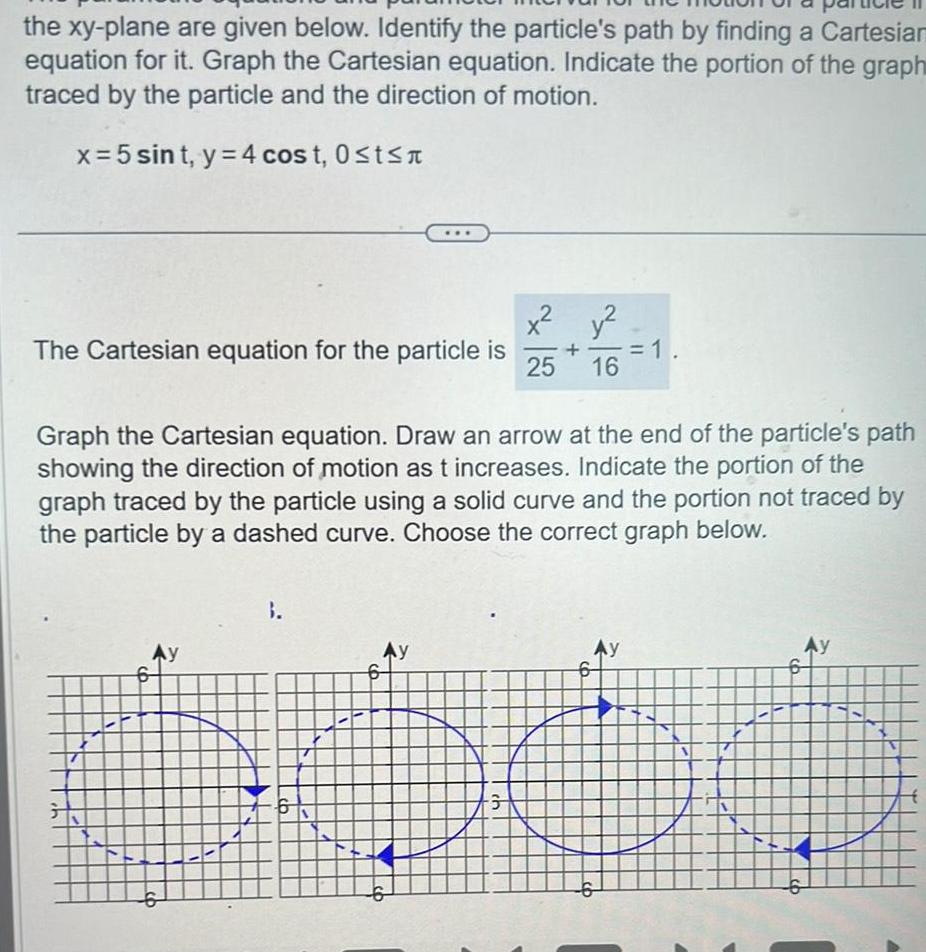
Application of derivativesthe xy plane are given below Identify the particle s path by finding a Cartesian equation for it Graph the Cartesian equation Indicate the portion of the graph traced by the particle and the direction of motion x 5 sint y 4 cost 0 t The Cartesian equation for the particle is Ay 9 3 Graph the Cartesian equation Draw an arrow at the end of the particle s path showing the direction of motion as t increases Indicate the portion of the graph traced by the particle using a solid curve and the portion not traced by the particle by a dashed curve Choose the correct graph below Ay 6 25 ch y 16 1 Ay AY

Calculus
Application of derivativesFind the derivative of y 3x5 4x 2 g x O None of the other choices is correct O 1524 g 2 g x 3x 4x 2 O 15244 g x g x 3x 4x 2 O 1524 4 g x O 1544 g x g x 3x 4x 2