Application of derivatives Questions and Answers

Calculus
Application of derivativessuppose that the price p in dollars and the weekly sales x in thousands of units of a certain commodity satisfy the demand equation 8p3 x 8100 Determine the rate at which sales are hanging at a time when x 10 p 10 and the price is falling at the rate of 10 per week The rate at which sales are changing is thousand units per week

Calculus
Application of derivativesA solid is formed by adjoining two hemispheres to the ends of a right circular cylinder The total volume of the solid is 10 cubic centimeters Find the radius of the cylinder that produces the minimum surface area Round your answer to th 15 2 cm Need Help Read It Master it MY NOTES ASK YOUR TEACH
Calculus
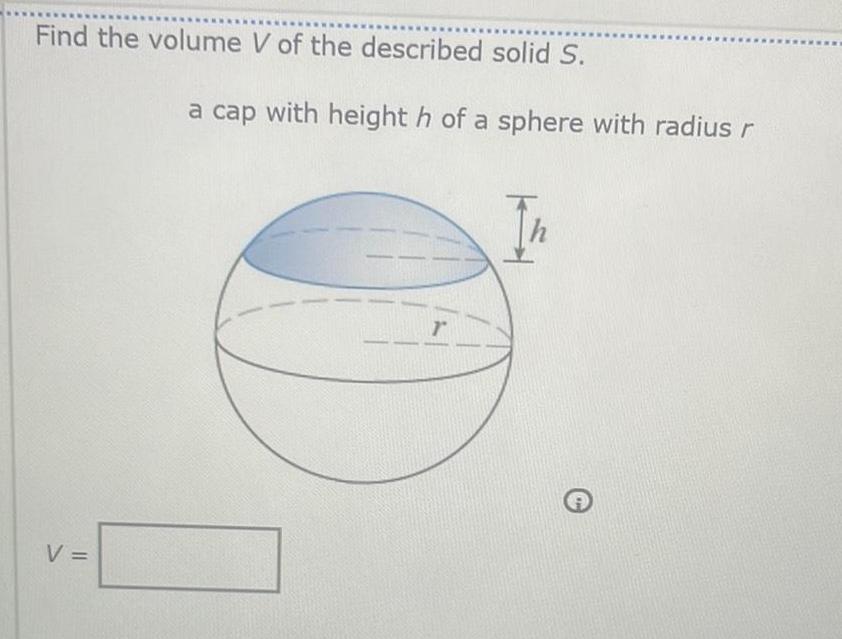
Application of derivativesFind the volume V of the described solid S V a cap with height h of a sphere with radius r r
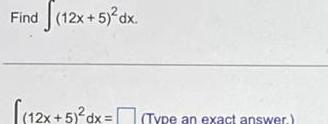

Calculus
Application of derivativesA Norman window is constructed by adjoining a semicircle to the top of an ordinary rectangular window see fig dimensions of a Norman window of maximum area if the total perimeter is 30 feet X y 56 4 28 4 T X ft X ft 3

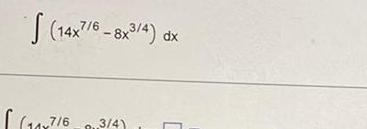

Calculus
Application of derivativesGiven that x and y are functions of time find the indicated rate of change dy dt Find dx dit dx when x 5 y 2 and dt 4 given that xy x y Round to one decimal place as needed

Calculus
Application of derivativesSet up an integral representing the area A of the region enclosed by the given curves x y x 2 y 1 D x 2 3 ov A dy

Calculus
Application of derivativesAn offshore oil well is 2 kilometers off the coast The refinery is 6 kilometers down the coast see figure Laying pipe in ocean is twice as expensive as on land What path should the pipe follow in order to minimize the cost X 2 ASK YOUR TEACH km

Calculus
Application of derivativesUse differentials to approximate the value of the expression Compare your answer with that of a calculator Round yo answers to four decimal places 2 99 3 using differentials using a calculator
Calculus
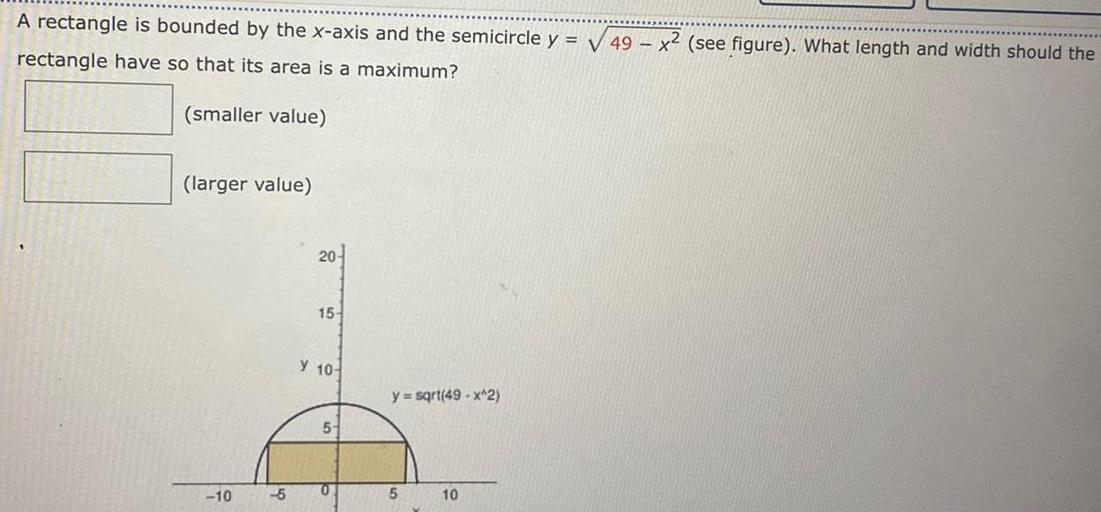
Application of derivativesA rectangle is bounded by the x axis and the semicircle y 49 x2 see figure What length and width should the rectangle have so that its area is a maximum smaller value larger value 10 5 20 15 Y 10 5 0 y sqrt 49 x 2 5 10
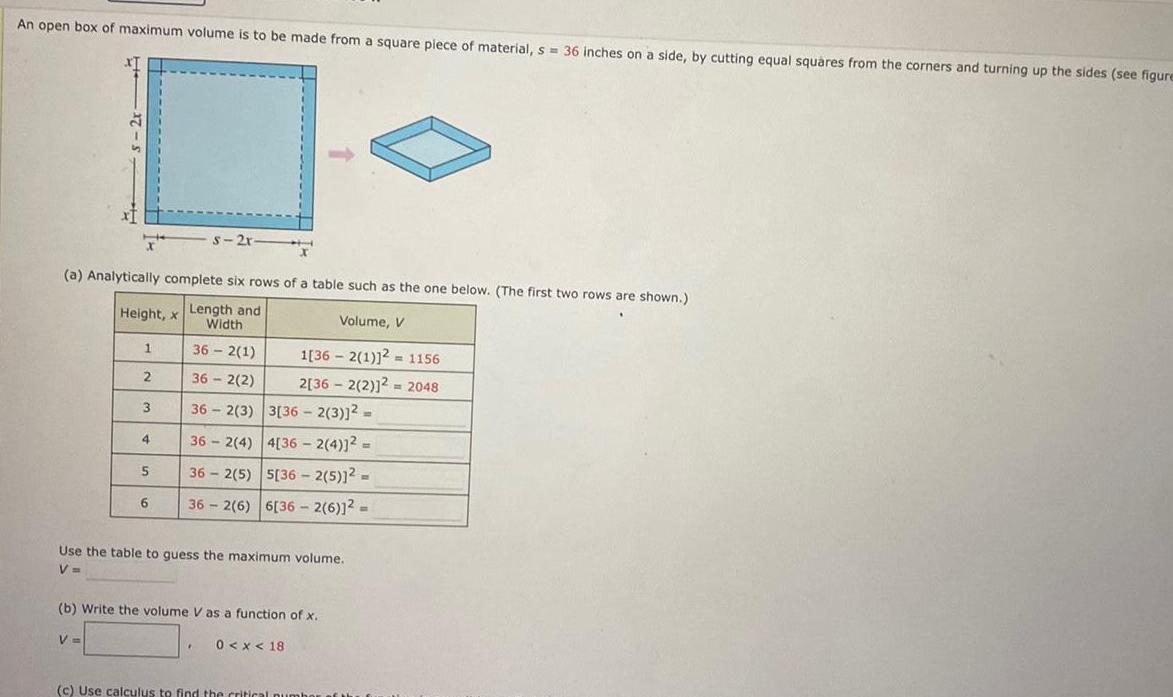
Calculus
Application of derivativesAn open box of maximum volume is to be made from a square piece of material s 36 inches on a side by cutting equal squares from the corners and turning up the sides see figure a Analytically complete six rows of a table such as the one below The first two rows are shown Height x Length and Volume V Width 362 1 36 2 2 3 36 2 3 3 36 2 3 362 4 4 36 2 4 362 5 5 36 2 5 2 362 6 6 36 2 6 12 1 2 V 4 5 6 s 2r 1 362 1 2 1156 2 362 2 2 2048 Use the table to guess the maximum volume V b Write the volume V as a function of x 0 x 18 E c Use calculus to find the critical number of the f
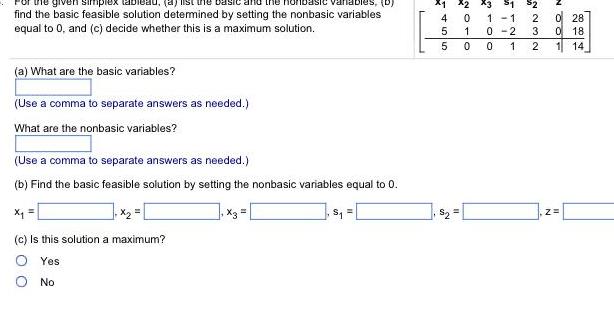
Calculus
Application of derivativesvariables D find the basic feasible solution determined by setting the nonbasic variables equal to 0 and c decide whether this is a maximum solution a What are the basic variables Use a comma to separate answers as needed What are the nonbasic variables Use a comma to separate answers as needed b Find the basic feasible solution by setting the nonbasic variables equal to 0 c Is this solution a maximum Yes O No x3 S 4 455 X1 X2 X3 1 0 1 0 11 0 2 0 1 723 2 0 28 0 18 1 14 Z
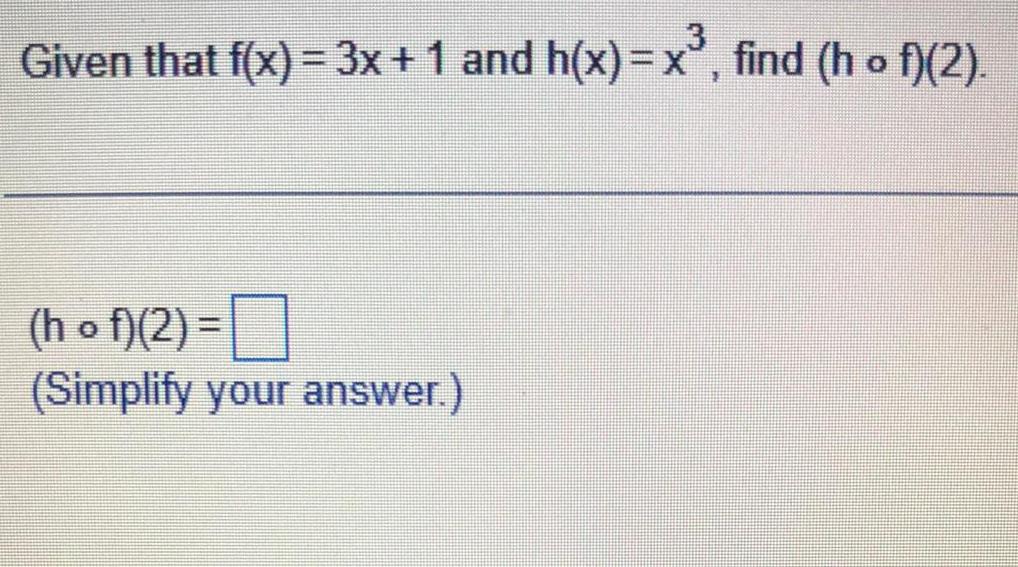
Calculus
Application of derivativesGiven that f x 3x 1 and h x x find h o f 2 hof 2 Simplify your answer
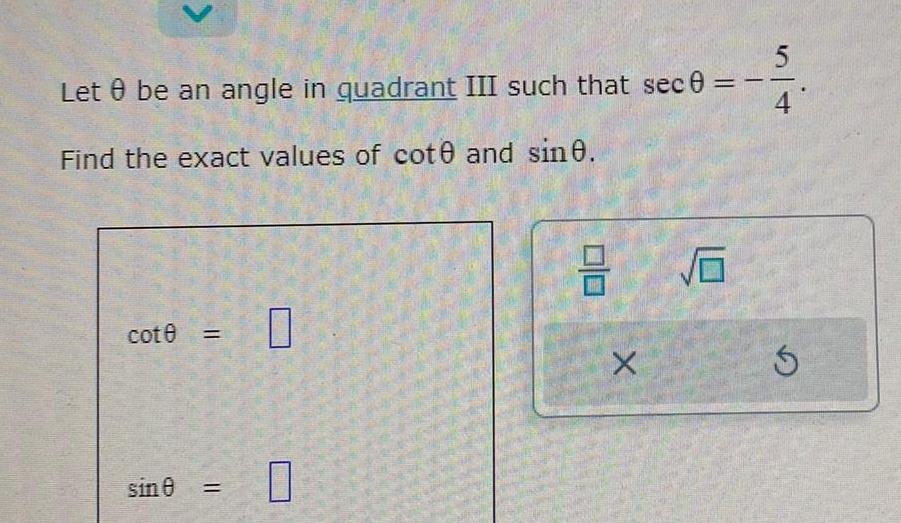
Calculus
Application of derivativesLet be an angle in quadrant III such that sec 0 Find the exact values of cote and sin0 cot0 sin 0 0 3 16 X 5 4
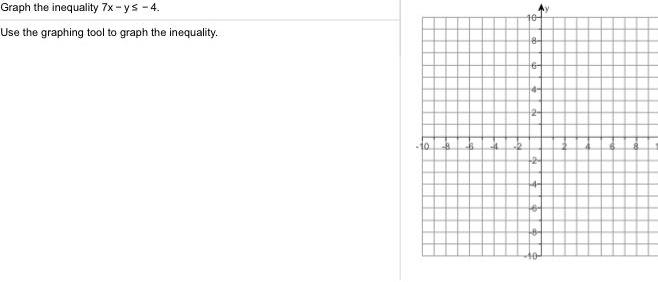
Calculus
Application of derivativesGraph the inequality 7x ys 4 Use the graphing tool to graph the inequality 10 8 B 4 32 104 18 164 44 2 24 40
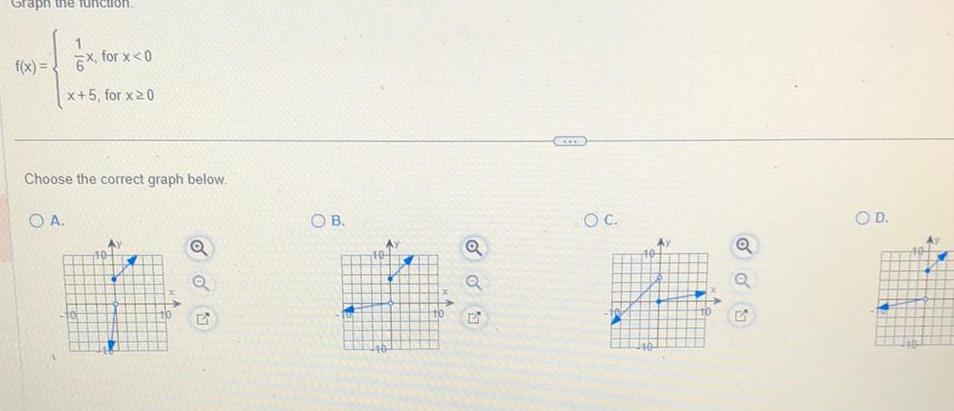
Calculus
Application of derivativesGraph the function f x 6x for x 0 x 5 for x 20 Choose the correct graph below O A G OB 40 10 Q EV O C 2 10 Q L O D
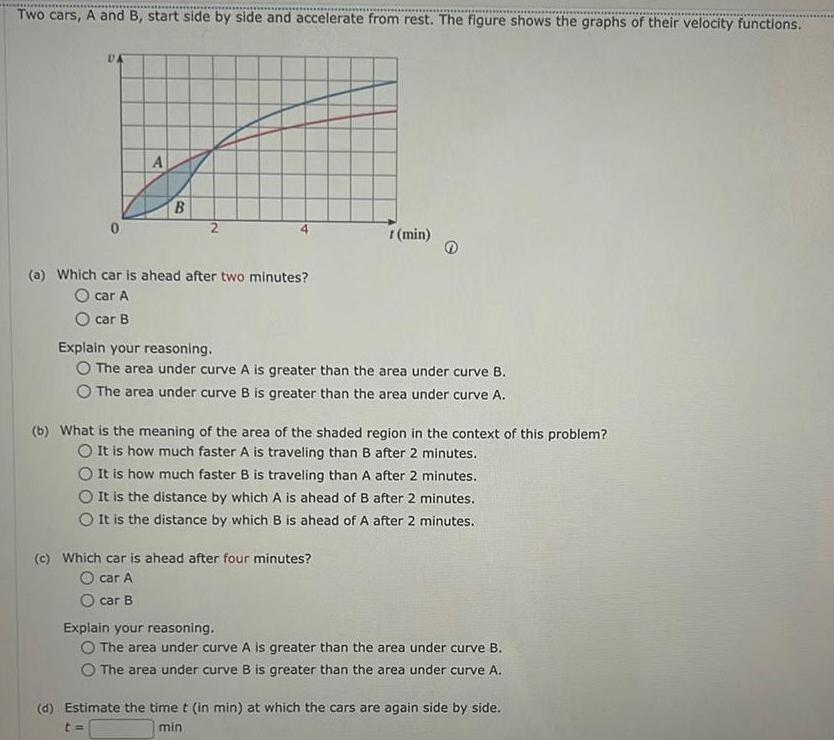
Calculus
Application of derivativesTwo cars A and B start side by side and accelerate from rest The figure shows the graphs of their velocity functions DA 0 A B 2 a Which car is ahead after two minutes O car A O car B r min Explain your reasoning O The area under curve A is greater than the area under curve B The area under curve B is greater than the area under curve A b What is the meaning of the area of the shaded region in the context of this problem O It is how much faster A is traveling than B after 2 minutes O It is how much faster B is traveling than A after 2 minutes It is the distance by which A is ahead of B after 2 minutes O It is the distance by which B is ahead of A after 2 minutes c Which car is ahead after four minutes O car A car B Explain your reasoning O The area under curve A is greater than the area under curve B The area under curve B is greater than the area under curve A d Estimate the time t in min at which the cars are again side by side t min
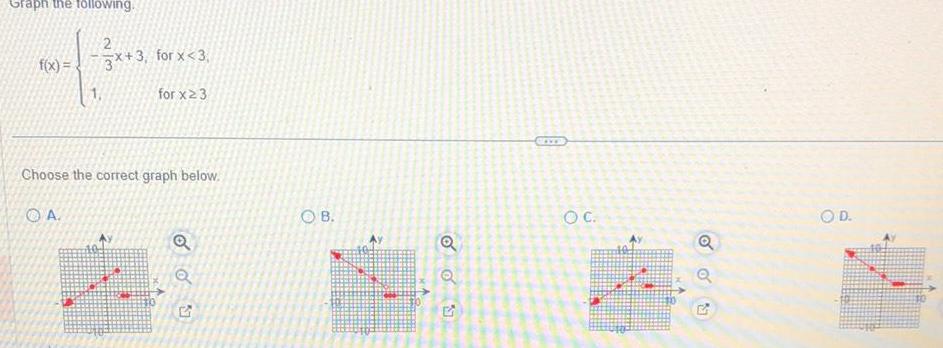
Calculus
Application of derivativesGraph the following f x 2 3x 3 for x 3 for x 23 Choose the correct graph below A Q OB Q Q OC 4 OD
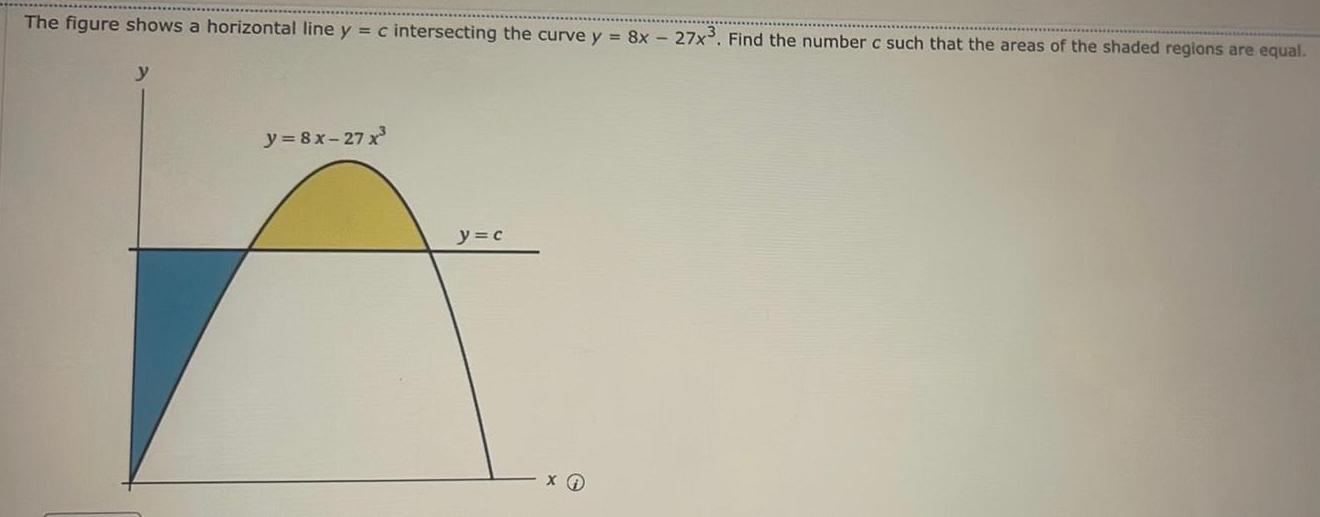
Calculus
Application of derivativesThe figure shows a horizontal line y c intersecting the curve y 8x 27x Find the number c such that the areas of the shaded regions are equal y y 8x 27x y c X
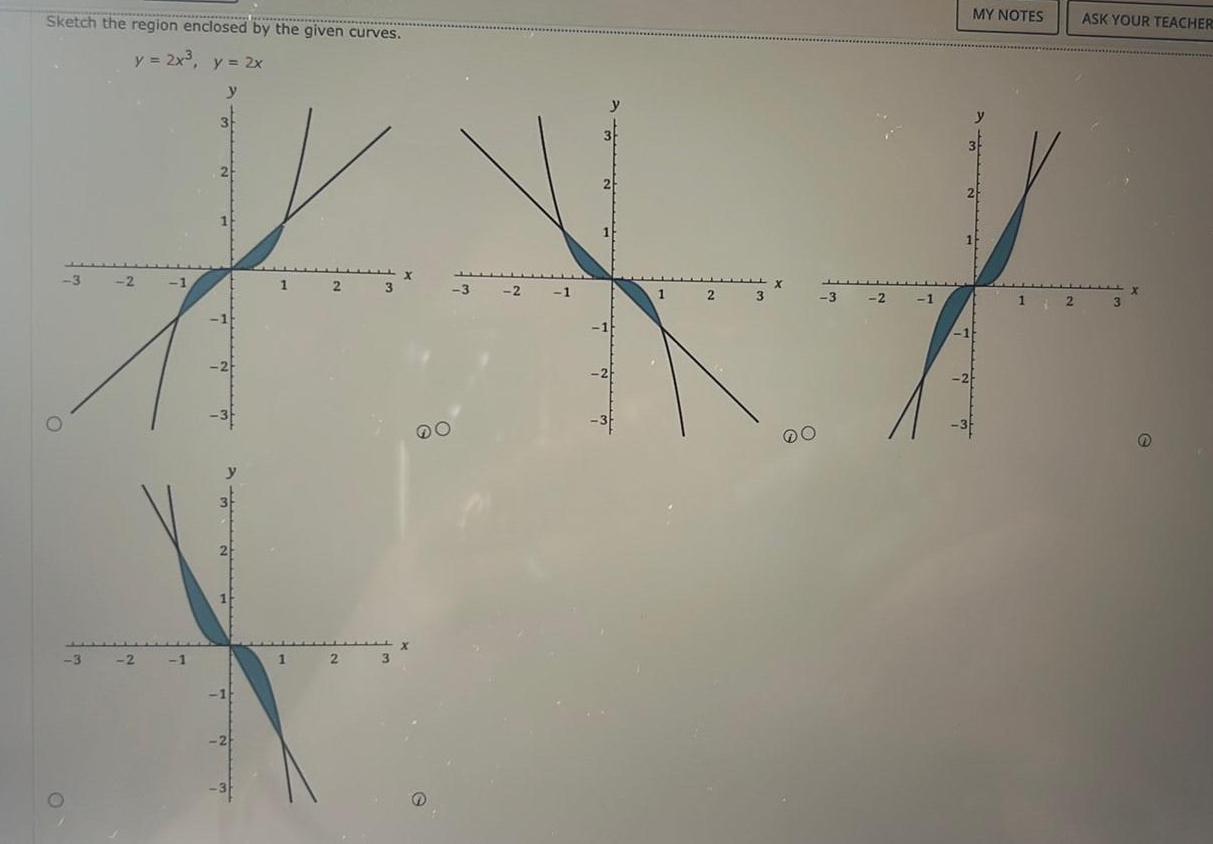
Calculus
Application of derivativesSketch the region enclosed by the given curves y 2x y 2x y 3 3 2 2 1 1 1 2 3 O 2 1 2 3 2 MY NOTES 12 ASK YOUR TEACHER 3
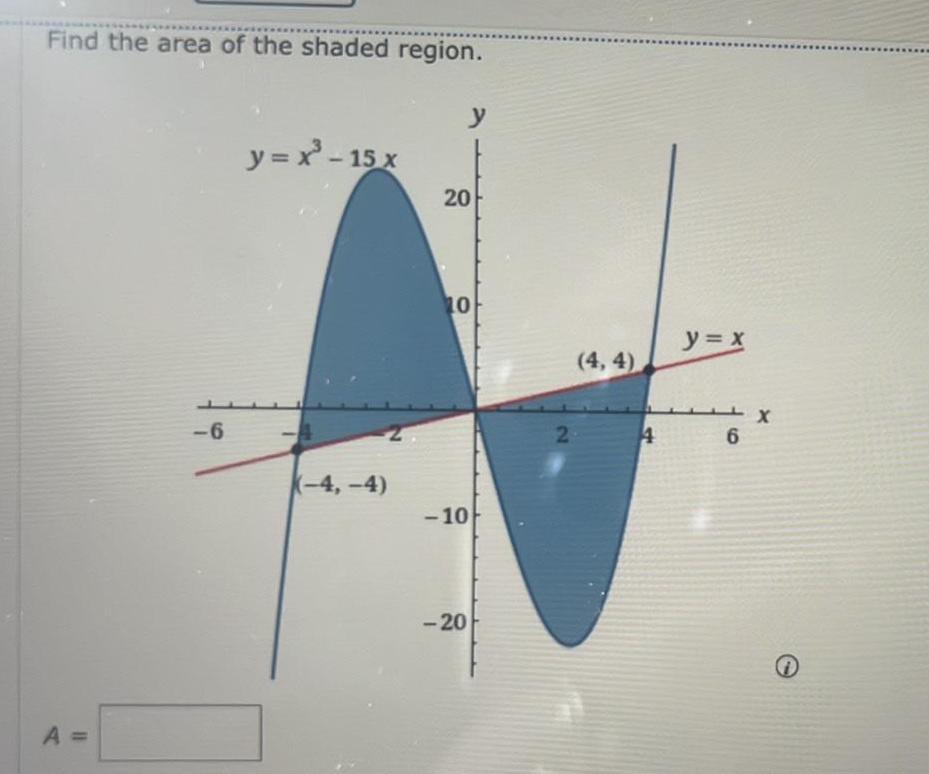
Calculus
Application of derivativesFind the area of the shaded region A 6 y x 15x 2 4 4 y 20 10 10 20 2 4 4 4 y x 6 X
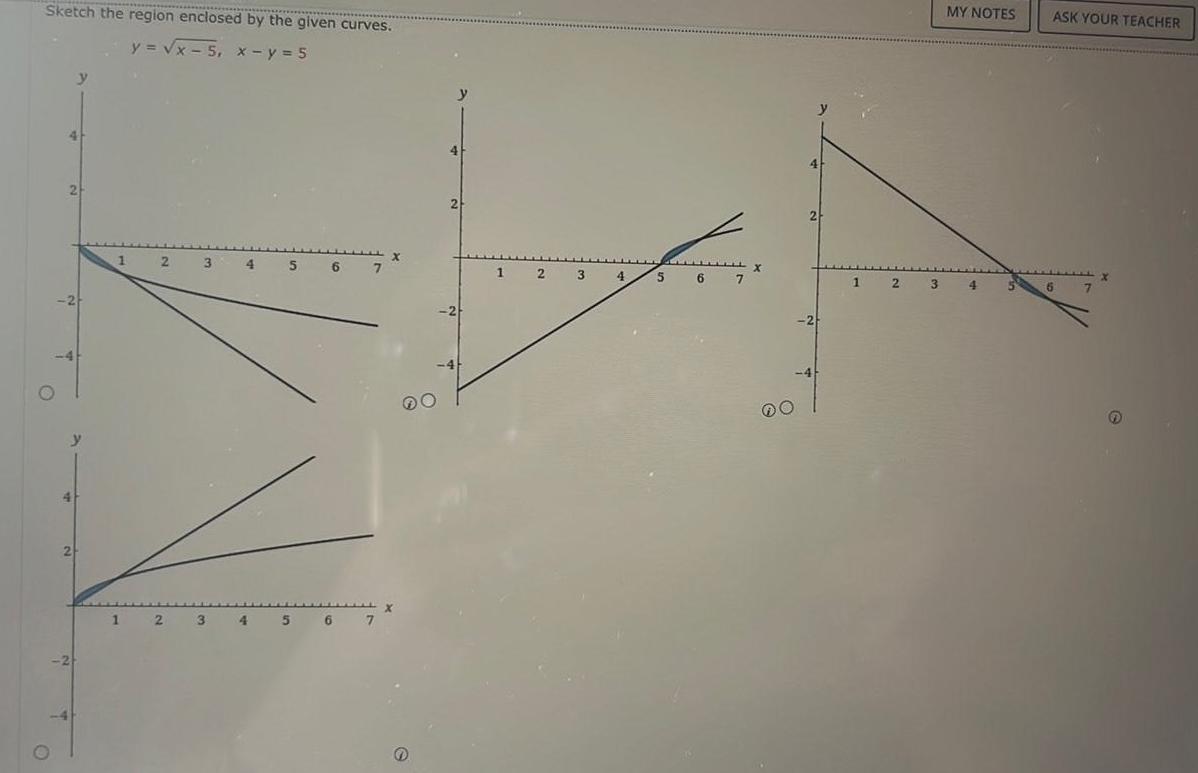
Calculus
Application of derivativesSketch the region enclosed by the given curves y x 5 x y 5 4 2 2 y y 4 2 1 1 2 2 3 3 4 4 5 6 7 5 6 7 X y 4 2 1 2 3 4 7 O 1 2 3 MY NOTES 4 5 ASK YOUR TEACHER 6
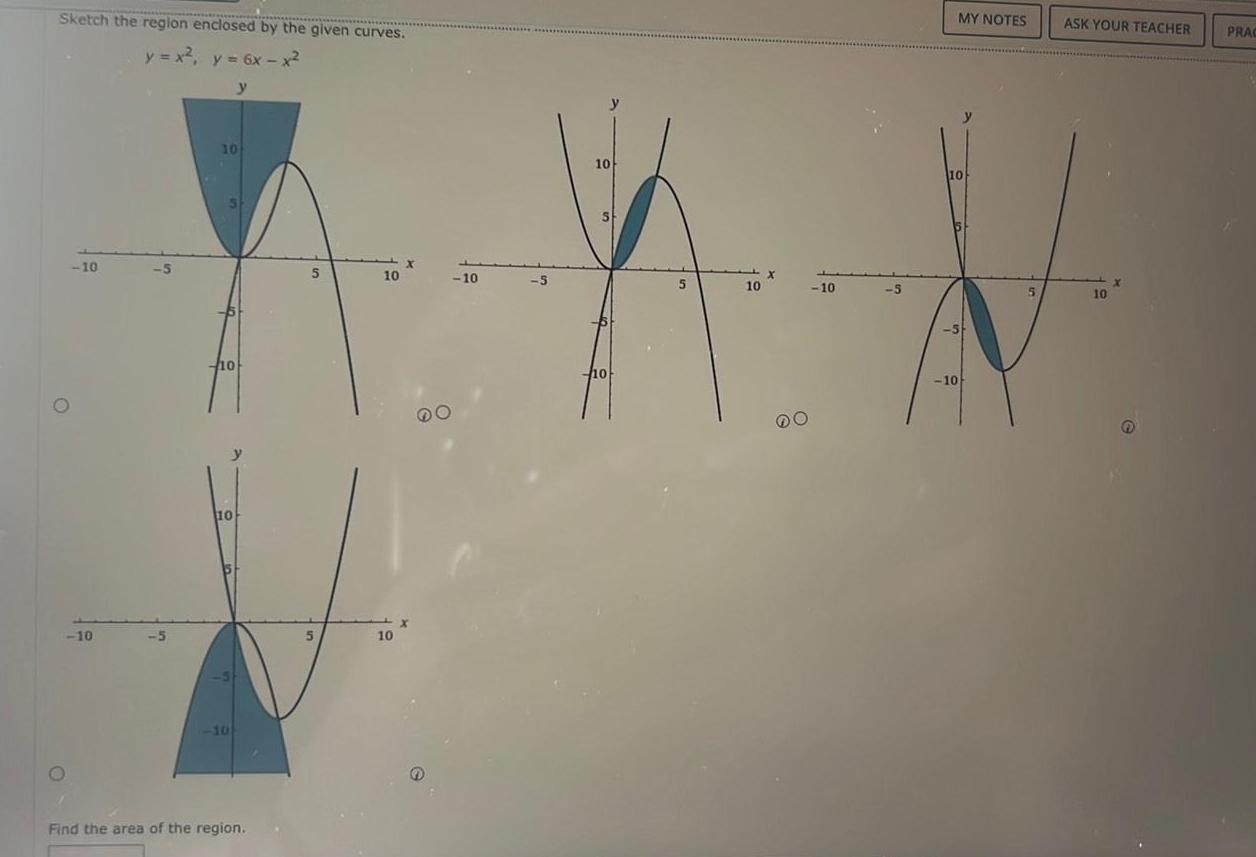
Calculus
Application of derivativesSketch the region enclosed by the given curves y x y 6x x y 10 10 5 5 10 5 10 10 B 10 Find the area of the region 5 5 10 10 X X 10 5 10 S 10 5 10 DO 10 5 MY NOTES 10 5 10 ASK YOUR TEACHER 10 x PRAC
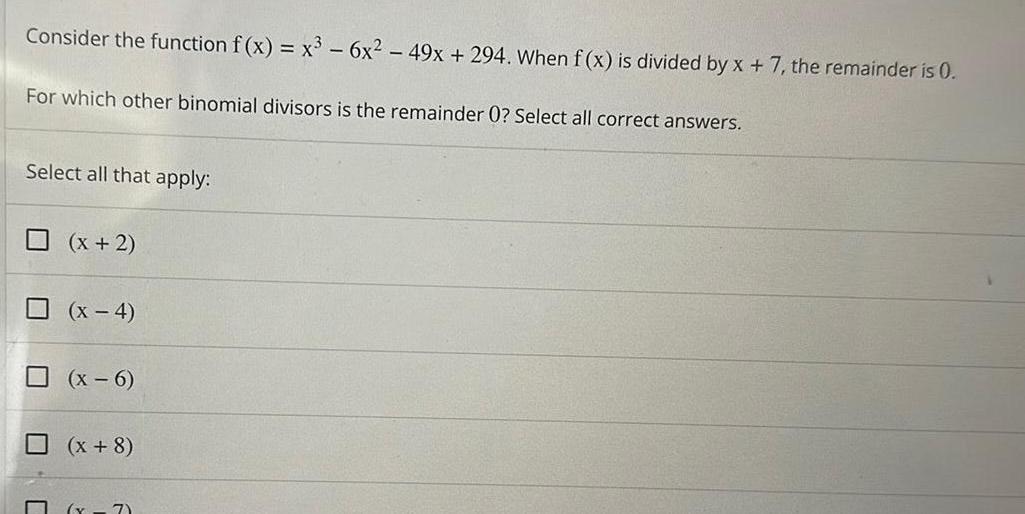
Calculus
Application of derivativesConsider the function f x x 6x 49x 294 When f x is divided by x 7 the remainder is 0 For which other binomial divisors is the remainder 0 Select all correct answers Select all that apply x 2 x 4 x 6 x 8 7
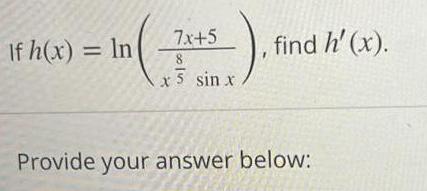

Calculus
Application of derivativesUsing the rational zero theorem which is a rational zero of f x x 5x 7x 3 Select the correct answer below 3 1 5 3 1 5 2 0 2
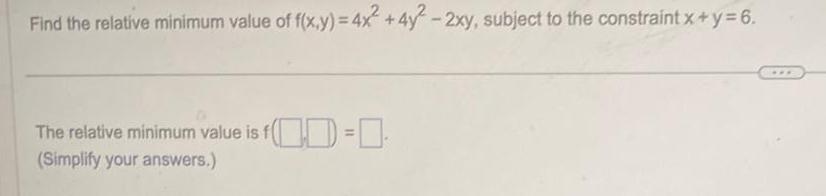
Calculus
Application of derivativesFind the relative minimum value of f x y 4x 4y 2xy subject to the constraint x y 6 The relative minimum value is f Simplify your answers

Calculus
Application of derivativesThe total revenue in hundreds of dollars from the sale of x spas and y solar heaters is approximated by R x y 15 114x 141y 3x2 4y2 5xy Find the number of each that should be sold produce maximum revenue Find the maximum revenue Find the derivatives R Ry and Ry R R y R y Selling spas and solar heaters gives the maximum revenue of Simplify your answers
Calculus
Application of derivativesFind the local maxima Select the correct choice below and if necessary fill in the answer box to complete your choice OA There are local maxima located at Simplify your answers Type ordered pairs Use a comma to separate answers as needed OB There are no local maxima Find the local minima Select the correct choice below and if necessary fill in the answer box to complete your choice OA There are local minima located at Simplify your answers Type ordered pairs Use a comma to separate answers as needed OB There are no local minima Find the saddle points Select the correct choice below and if necessary fill in the answer box to complete your choice OA There are saddle points located at Simplify your answers Type ordered pairs Use a comma to separate answers as needed OB There are no saddle points

Calculus
Application of derivativesFind the quotient and write it in rectangular form 40 cos 365 i sin 365 5 cos 140 isin 140 40 cos 365 i sin 365 5 cos 140 isin 140 Do not factor
Calculus
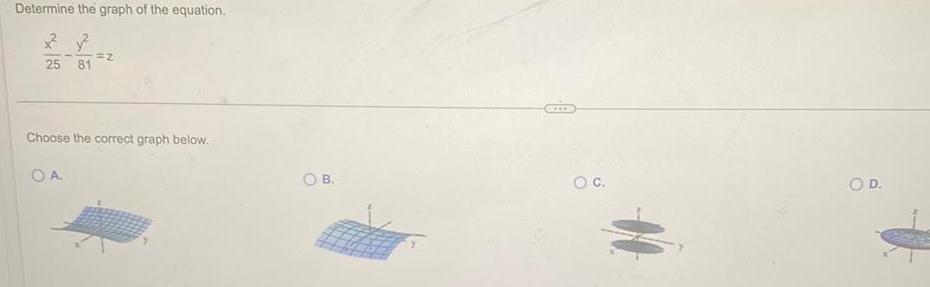
Application of derivativesDetermine the graph of the equation x y 25 81 Z Choose the correct graph below OA O B O C OD

Calculus
Application of derivativesStep 3 We are given that the length is increasing at a rate of 4 cm s and the width is increasing at a rate of 9 cm s Therefore we have the following dl X dt dw dt 9 8 X Furthermore we are given that the length is 8 cm when the width is 6 cm In other words when 8 we have the following W 9 X

Calculus
Application of derivativesTwo cars start moving from the same point One travels south at 48 mi h and the other travels west at 20 mi h At what rate in mi h is the distance between the cars increasing for later mi h
Calculus
Application of derivativesa a 2a 4b 32 a c 9 2 3 What is the solution Select the correct choice below and fill in any answer boxes within your choice A There is one solution Type exact answers in simplified form OB The system is dependent OC There is no solution
Calculus
Application of derivativesFind the average rate of change for the given function f x x 7x between x 0 and x 9 The average rate of change is Simplify your answer
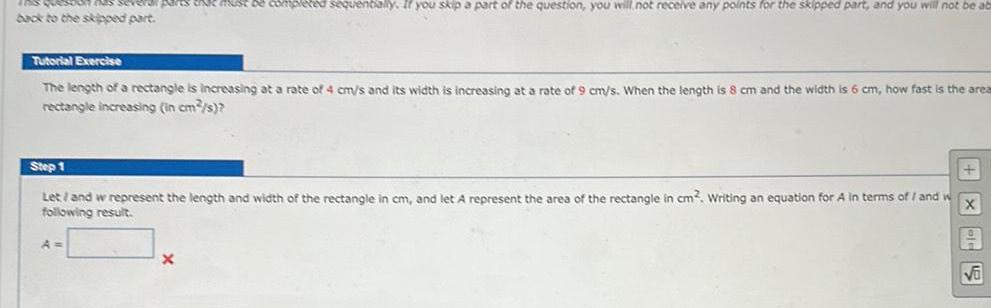
Calculus
Application of derivativesIf parts tak must be completed sequentially If you skip a part of the question you will not receive any points for the skipped part and you will not be ab back to the skipped part Tutorial Exercise The length of a rectangle is increasing at a rate of 4 cm s and its width is increasing at a rate of 9 cm s When the length is 8 cm and the width is 6 cm how fast is the area rectangle increasing in cm s Step 1 X Let and w represent the length and width of the rectangle in cm and let A represent the area of the rectangle in cm Writing an equation for A in terms of I and w following result A

Calculus
Application of derivativesUse a linear approximation or differentials to estimate the given number e 0 015 Step 1 To estimate e 0 015 we ll find the linearization for f x ex at a 0 We have the following f x

Calculus
Application of derivativesEach side of a square is increasing at a rate of 3 cm s At what rate in cm s is the area of the square increasing when the area of the square is 36 cm x cm s Enter an exact number Enhanced Feedback Please try again keeping in mind that the area of square of side a is a xa A a2 Differentiate this equation with respect to time t using the Chain Rule to find the equation for at which the area is increasing da Then use the values from the exercise to evaluate the rate of change of the area of the square paying close attention to the signs of the rates dt change of the side nositive when in

Calculus
Application of derivativesTutorial Exercise The length of a rectangle is increasing at a rate of 4 cm s and its width is increasing at a rate of 9 cm s When the length is 8 cm and the width is 6 cm how fast is the area of the rectangle increasing in cm s Step 1 Let and w represent the length and width of the rectangle in cm and let A represent the area of the rectangle in cm Writing an equation for A in terms of and w gives the following result A

Calculus
Application of derivativesA bank in Houston loans 90 000 to a business at 13 5 annual simple interest for 9 months How much interest will the bank earn The bank will earn Round to the nearest dollar in interest

Calculus
Application of derivativesFind the following product and write the product in rectangular form using exact values 8 cos 90 i sin 90 3 cos 120 i sin 120 8 cos 90 i sin 90 3 cos 120 i sin 120 Type your answer in the form a bi
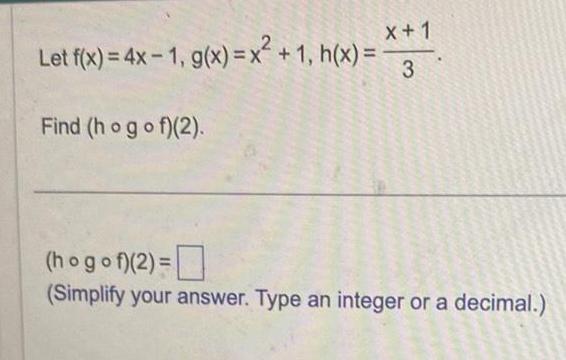
Calculus
Application of derivativesX 1 Let f x 4x 1 g x x 1 h x 3 Find ho gof 2 hogof 2 Simplify your answer Type an integer or a decimal
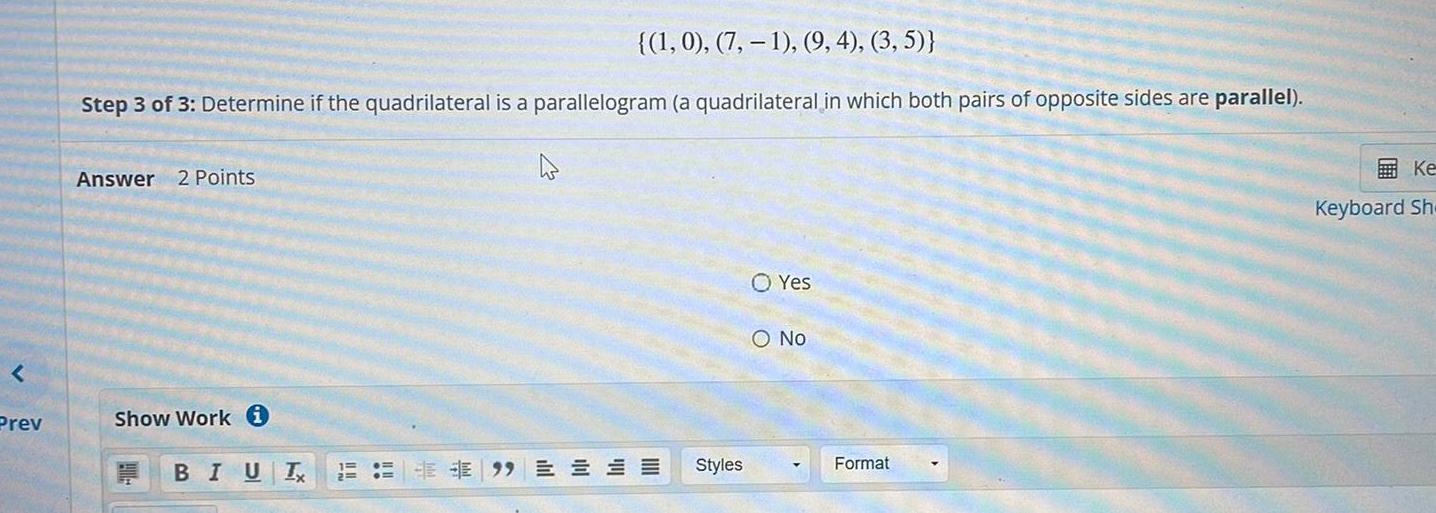
Calculus
Application of derivativesPrev 1 0 7 1 9 4 3 5 Step 3 of 3 Determine if the quadrilateral is a parallelogram a quadrilateral in which both pairs of opposite sides are parallel Answer 2 Points Show Work i BIUT O Yes O No Styles EE 99EE Format Ke Keyboard Sh
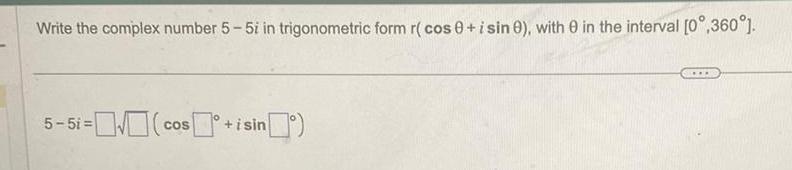
Calculus
Application of derivativesWrite the complex number 5 5i in trigonometric form r cos 0 i sin 0 with 0 in the interval 0 360 5 5i cos isin

Calculus
Application of derivativesFind the exact value in radians of the expression 3 sin 3 Type an intege sin



Calculus
Application of derivativesExpress as a sum or difference of logarithms without exponents 5 log c 9 X 5 9 y z The answer is Simplify your answer Use integers or fractions for any numbers in the expression