Application of derivatives Questions and Answers

Calculus
Application of derivativesA fence must be built to enclose a rectangular area of 45 000 ft Fencing material costs 1 per foot for the two sides facing north and south and 2 per foot for the other two sides Find the com the least expensive fence The cost of the least expensive fence is Simplify your answer

Calculus
Application of derivativesFind the location of the absolute maximum and absolute minimum of the function on the interval 4 4 B 6 Ah x 20 16 124 18 8 12 16 20 Q Q G The absolute minimum occurs at x Use a comma to separate answers as neede

Calculus
Application of derivativesFind the limit If the limit is infinite enter o or as appropriate If the limit does not otherwise exist enter DNE 9 x lim 3 x

Calculus
Application of derivativesA hot air balloon is rising vertically above a level straight road at a constant rate of 1 feet per second A the moment when the balloon is 65 feet above the road a bicycle moving at a constant rate of 17 feet per second passes directly under it Determine the rate of change of the distance betweeen the hot air baloon and the bycicle 3 seconds later Hot Air Balloon feet p t per second Question Help P Video Bike
Calculus
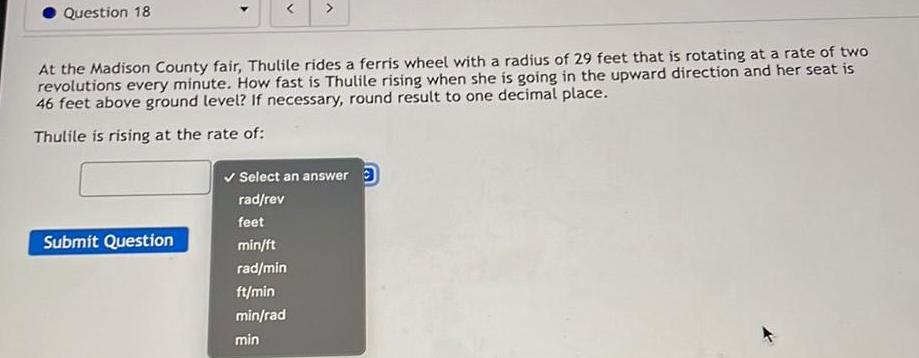
Application of derivativesQuestion 18 A At the Madison County fair Thulile rides a ferris wheel with a radius of 29 feet that is rotating at a rate of two revolutions every minute How fast is Thulile rising when she is going in the upward direction and her seat is 46 feet above ground level If necessary round result to one decimal place Thulile is rising at the rate of Submit Question Select an answer rad rev feet min ft rad min ft min min rad min
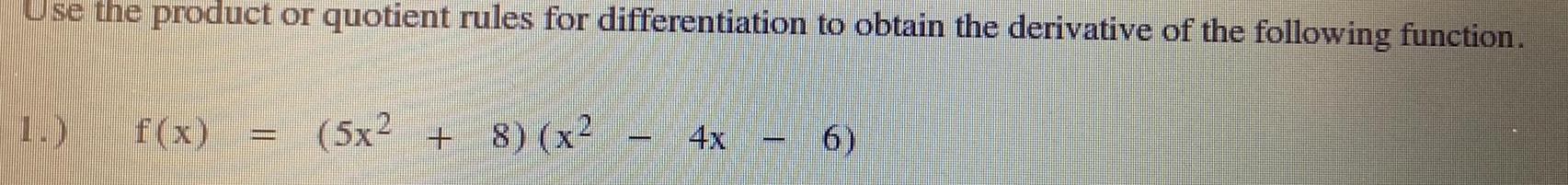
Calculus
Application of derivativesUse the product or quotient rules for differentiation to obtain the derivative of the following function 1 f x 5x 8 x 4x 6
Calculus
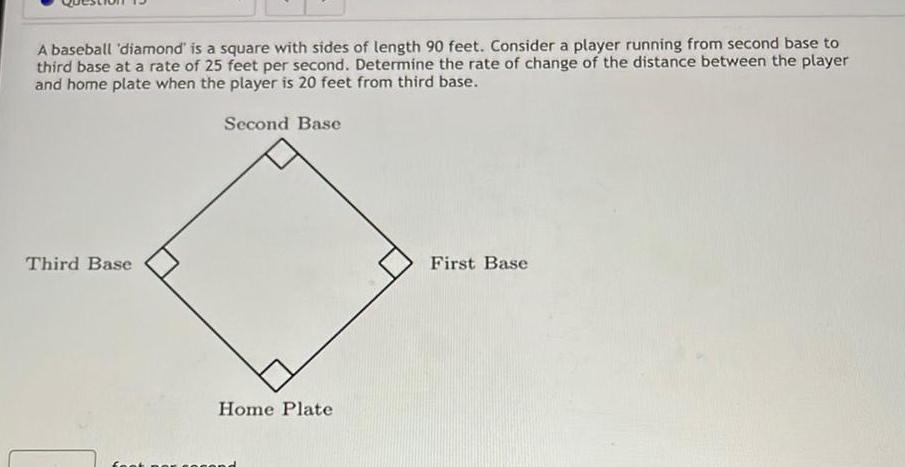
Application of derivativesA baseball diamond is a square with sides of length 90 feet Consider a player running from second base to third base at a rate of 25 feet per second Determine the rate of change of the distance between the player and home plate when the player is 20 feet from third base Second Base Third Base Home Plate First Base
Calculus
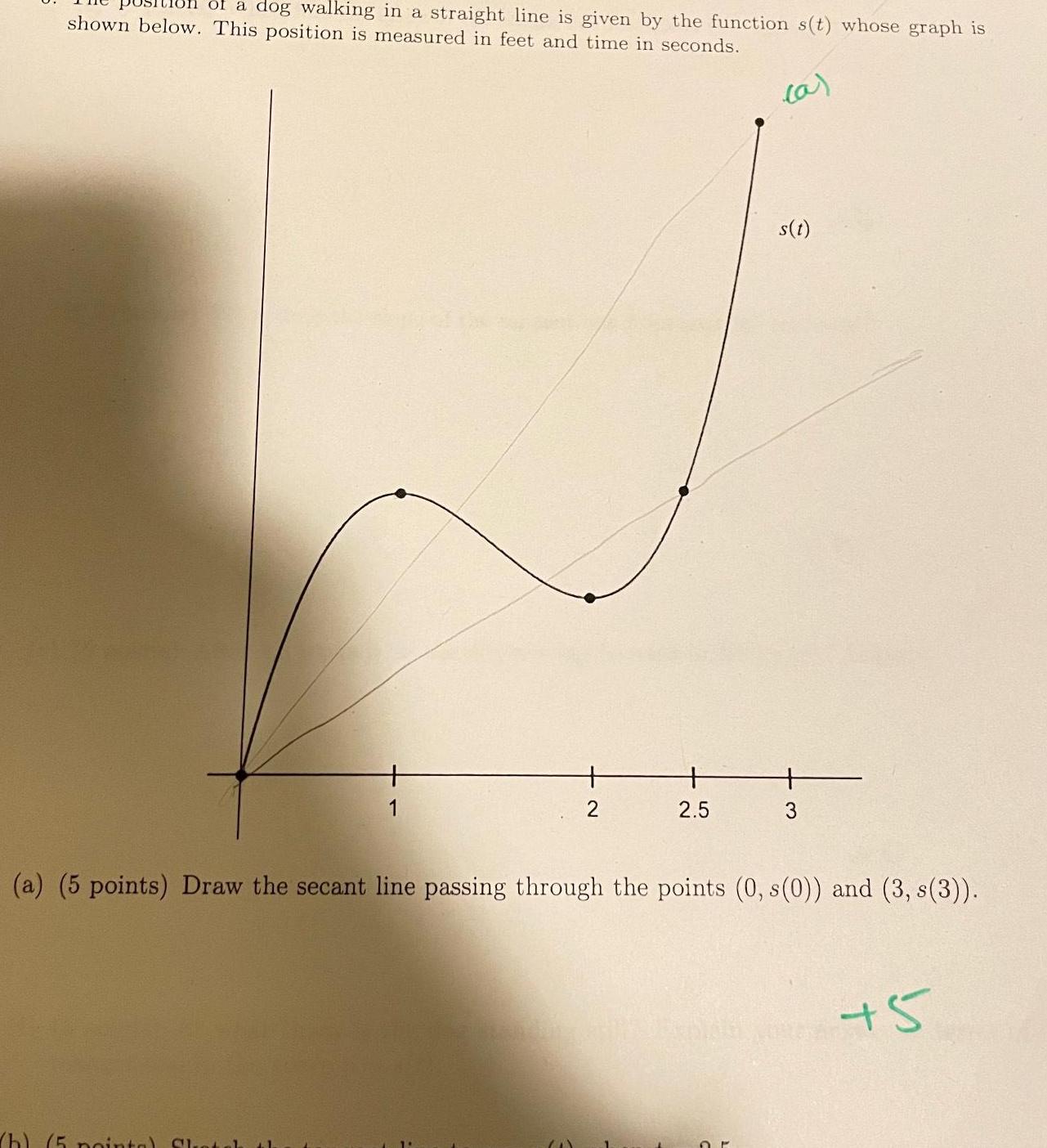
Application of derivativesof a dog walking in a straight line is given by the function s t whose graph is shown below This position is measured in feet and time in seconds a 1 h 5 pointa Sletak 1 2 2 5 s t a 5 points Draw the secant line passing through the points 0 s 0 and 3 s 3 3 5
Calculus
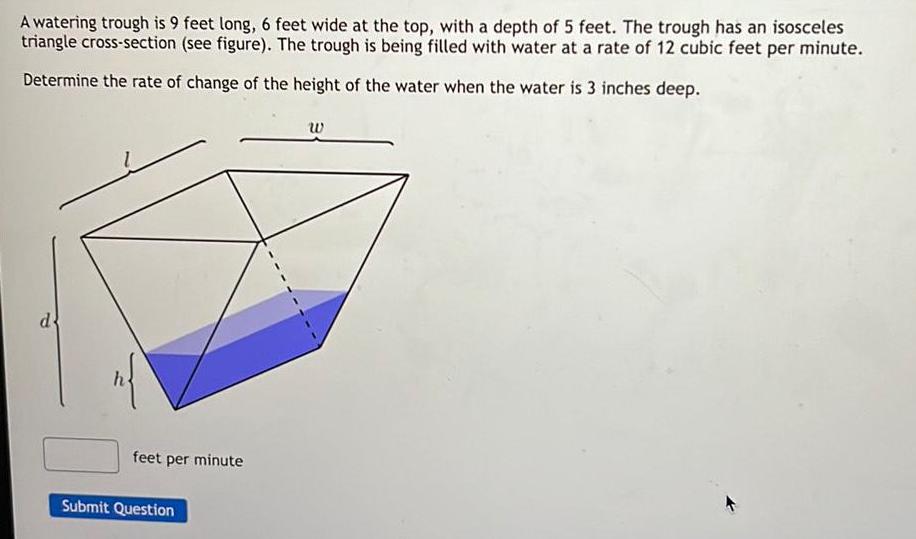
Application of derivativesA watering trough is 9 feet long 6 feet wide at the top with a depth of 5 feet The trough has an isosceles triangle cross section see figure The trough is being filled with water at a rate of 12 cubic feet per minute Determine the rate of change of the height of the water when the water is 3 inches deep d n feet per minute Submit Question W
Calculus
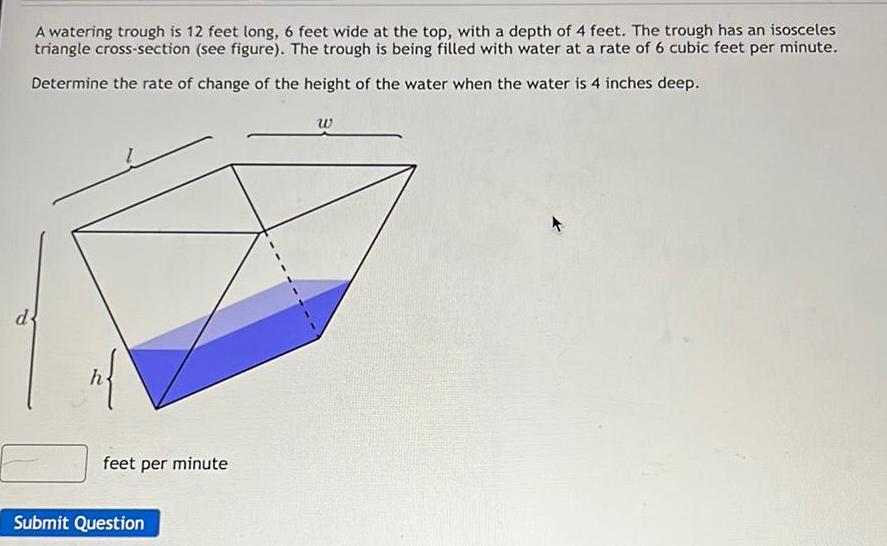
Application of derivativesd A watering trough is 12 feet long 6 feet wide at the top with a depth of 4 feet The trough has an isosceles triangle cross section see figure The trough is being filled with water at a rate of 6 cubic feet per minute Determine the rate of change of the height of the water when the water is 4 inches deep n feet per minute Submit Question W
Calculus
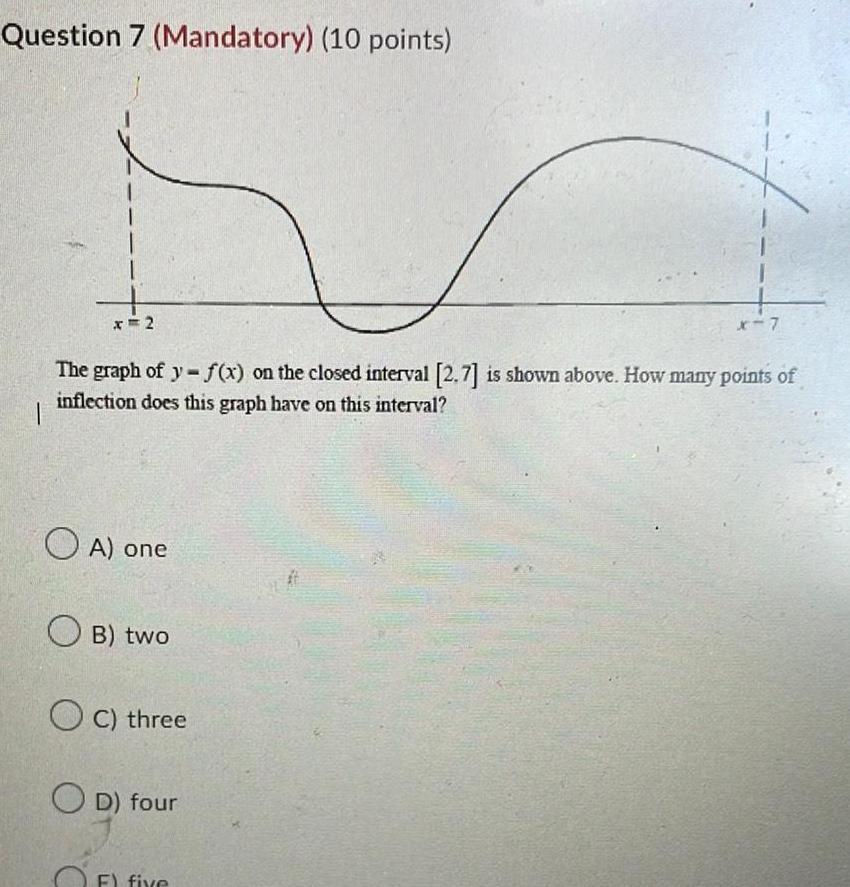
Application of derivativesQuestion 7 Mandatory 10 points x 2 The graph of y f x on the closed interval 2 7 is shown above How many points of inflection does this graph have on this interval OA one OB two OC three OD four F five X 7 6
Calculus
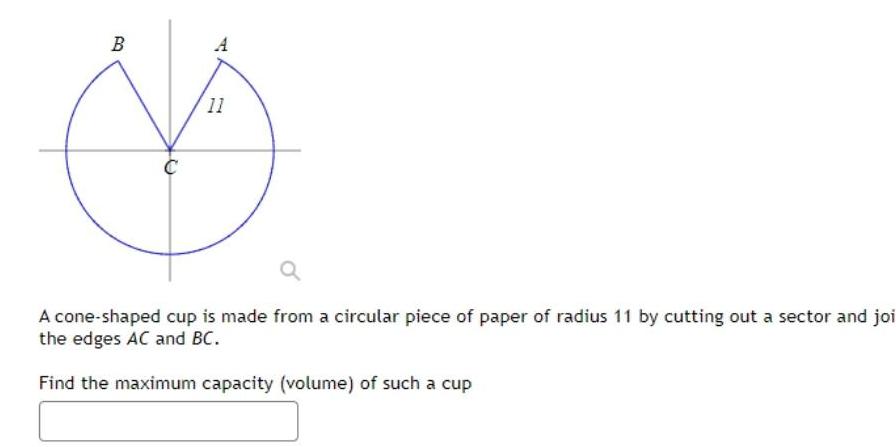
Application of derivativesB D A 11 A cone shaped cup is made from a circular piece of paper of radius 11 by cutting out a sector and joi the edges AC and BC Find the maximum capacity volume of such a cup
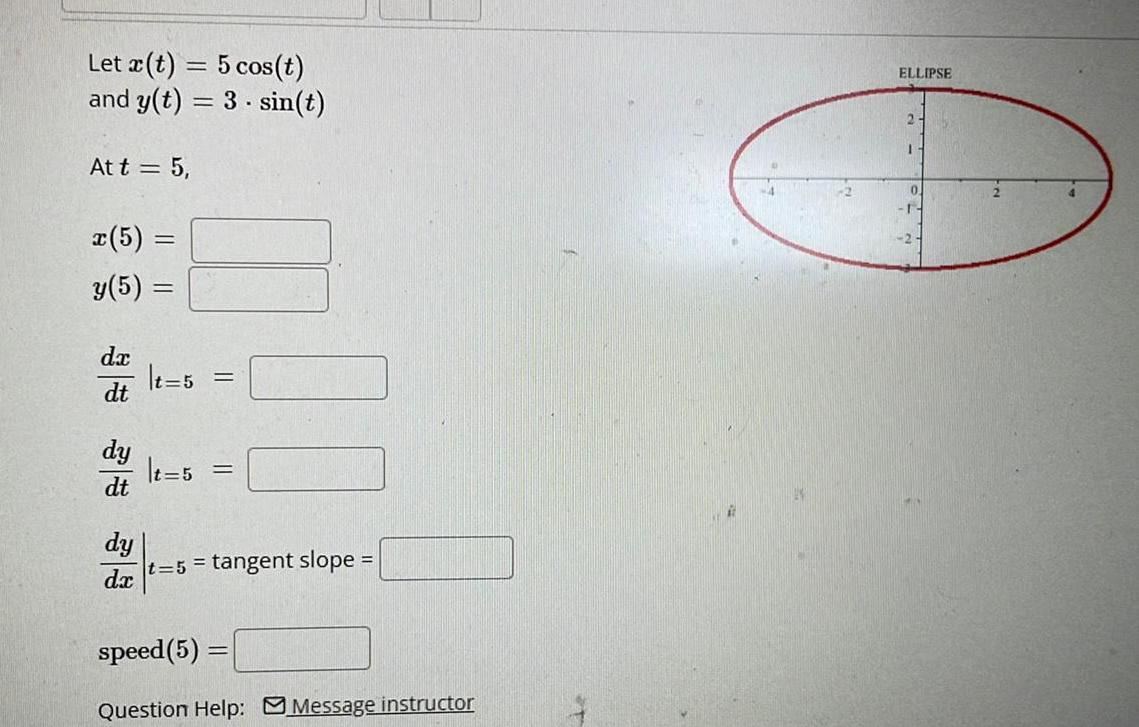
Calculus
Application of derivativesLet x t 5 cos t and y t 3 sin t At t 5 x 5 y 5 dx dt dy dt dy dx t 5 t 5 t 5 tangent slope speed 5 Question Help Message instructor ELLIPSE 2 1 0

Calculus
Application of derivativesFind the local and absolute extreme values for the function on the given interval f x x 1 x 1 1
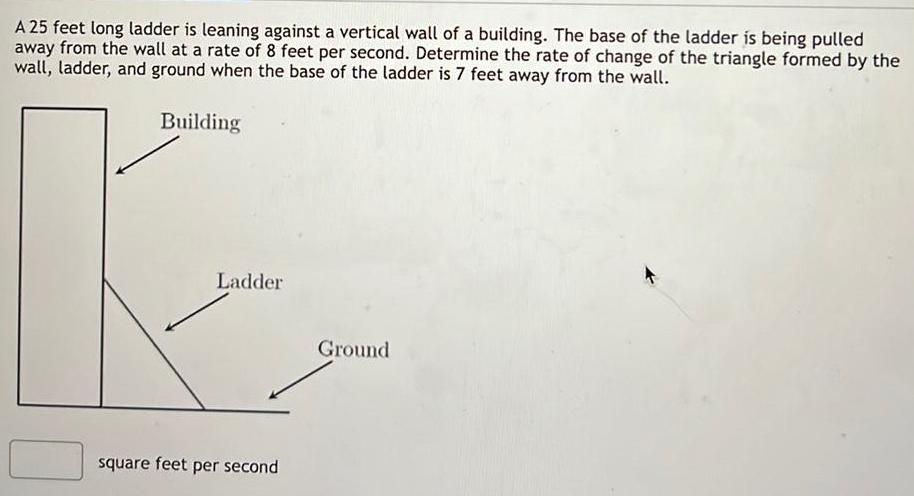
Calculus
Application of derivativesA 25 feet long ladder is leaning against a vertical wall of a building The base of the ladder is being pulled away from the wall at a rate of 8 feet per second Determine the rate of change of the triangle formed by the wall ladder and ground when the base of the ladder is 7 feet away from the wall Building Ladder square feet per second Ground
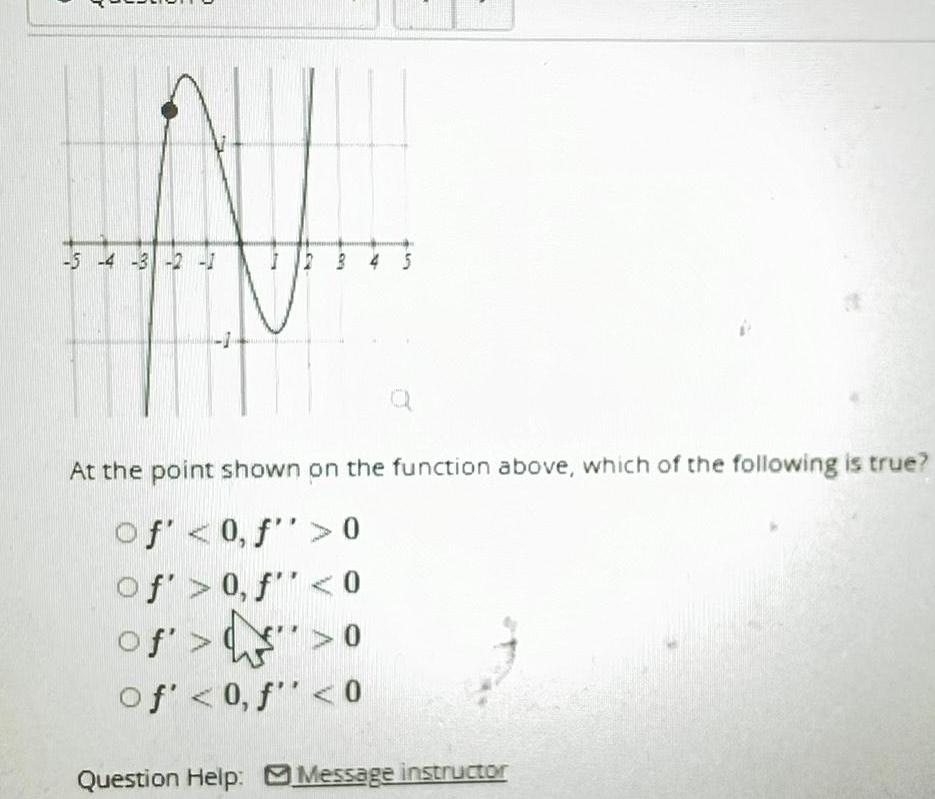
Calculus
Application of derivatives5 4 3 2 1 At the point shown on the function above which of the following is tru of 0 f 0 of 0 f 0 of 0 of 0 f 0 Question Help Message instructor
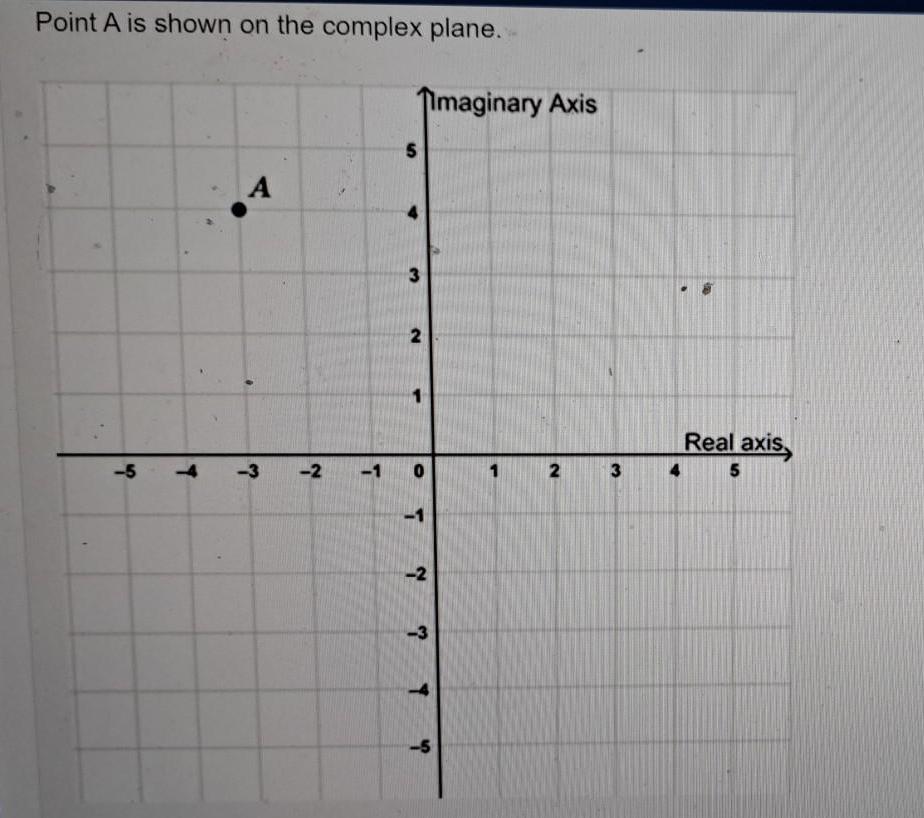
Calculus
Application of derivativesPoint A is shown on the complex plane 5 A 3 2 1 S Imaginary Axis 3 T 2 3 2 3 Real axis 4 5

Calculus
Application of derivativesA 50 feet long ladder is leaning against a vertical wall of a building The base of the ladder is being pulled away from the wall at a rate of 3 feet per second Determine the rate of change of the triangle formed by the wall ladder and ground when the base of the ladder is 14 feet away from the wall Building Ladder square feet per second Ground
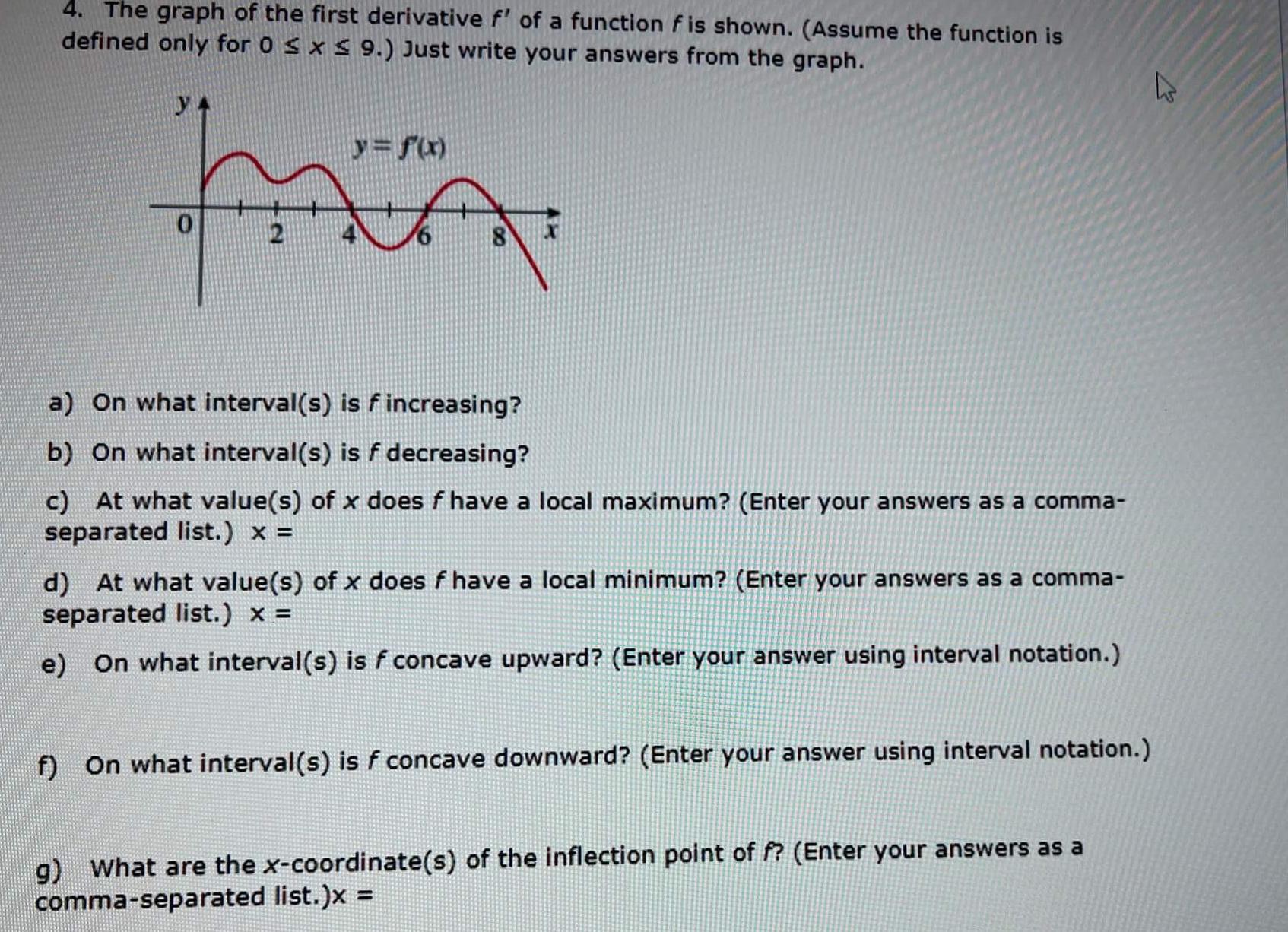
Calculus
Application of derivatives4 The graph of the first derivative f of a function f is shown Assume the function is defined only for 0 x 9 Just write your answers from the graph YA y f x ma a On what interval s is f increasing b On what interval s is f decreasing c At what value s of x does f have a local maximum Enter your answers as a comma separated list x d At what value s of x does f have a local minimum Enter your answers as a comma separated list x e On what interval s is f concave upward Enter your answer using interval notation f On what interval s is f concave downward Enter your answer using interval notation g What are the x coordinate s of the inflection point of f Enter your answers as a comma separated list x E
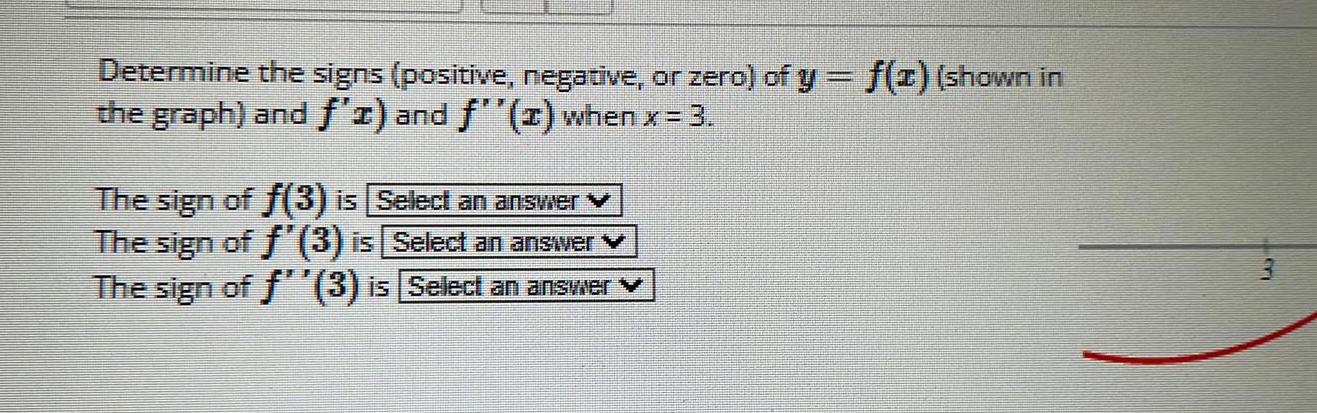
Calculus
Application of derivativesDetermine the signs positive negative or zero of y f x shown in the graph and f x and f x when x 3 The sign of f 3 is Select an answer The sign of f 3 is Select an answer The sign of f 3 is Select an answer LAD 3
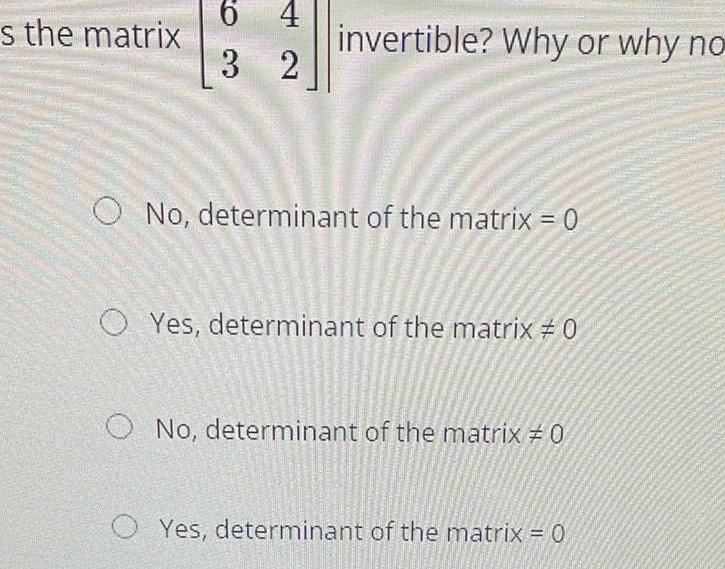
Calculus
Application of derivativess the matrix 6 42 3 2 invertible Why or why no O No determinant of the matrix 0 OYes determinant of the matrix 0 O No determinant of the matrix 0 O Yes determinant of the matrix 0

Calculus
Application of derivatives8 ln x 3 x 3 Let f x Determine the absolute extrema of f on 2 2 If multiple such values exist enter the solutions using a comma separated list The absolute minimum of f is 8 The absolute maximum of f is Submit All Parts and it occurs at x and it occurs at x
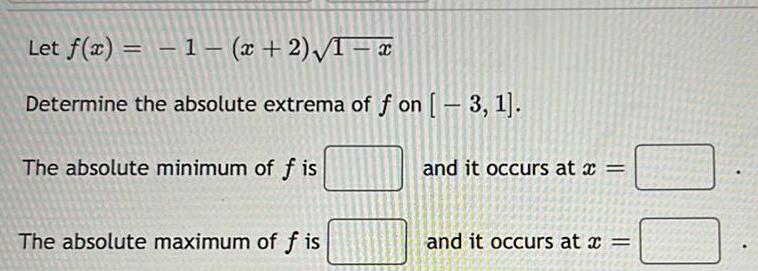
Calculus
Application of derivativesLet f x 1 x 2 1 x Determine the absolute extrema of f on 3 1 The absolute minimum of fis The absolute maximum of fis and it occurs at x and it occurs at x
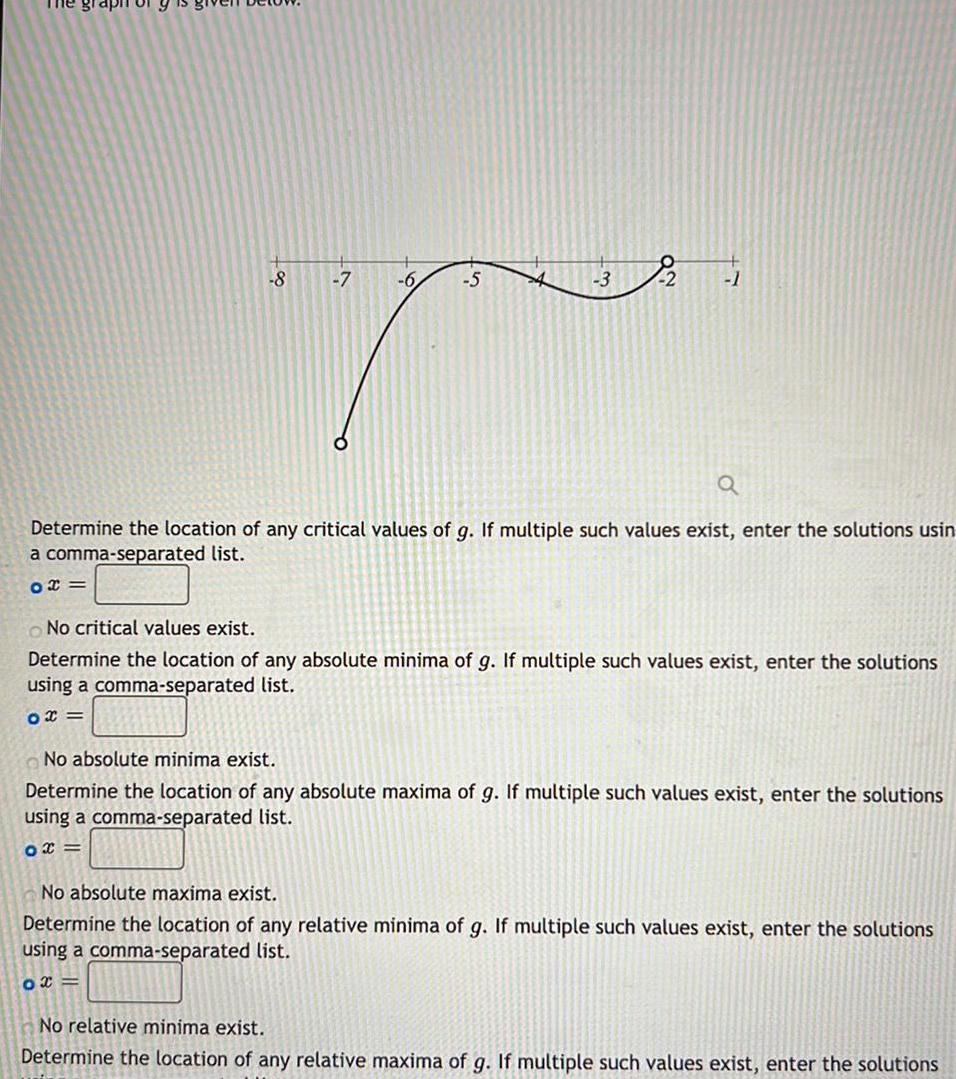
Calculus
Application of derivativesThe graph 8 5 3 1 Determine the location of any critical values of g If multiple such values exist enter the solutions usin a comma separated list 02 No critical values exist Determine the location of any absolute minima of g If multiple such values exist enter the solutions using a comma separated list 0x No absolute minima exist Determine the location of any absolute maxima of g If multiple such values exist enter the solutions using a comma separated list 0x No absolute maxima exist Determine the location of any relative minima of g If multiple such values exist enter the solutions using a comma separated list 0x No relative minima exist Determine the location of any relative maxima of g If multiple such values exist enter the solutions
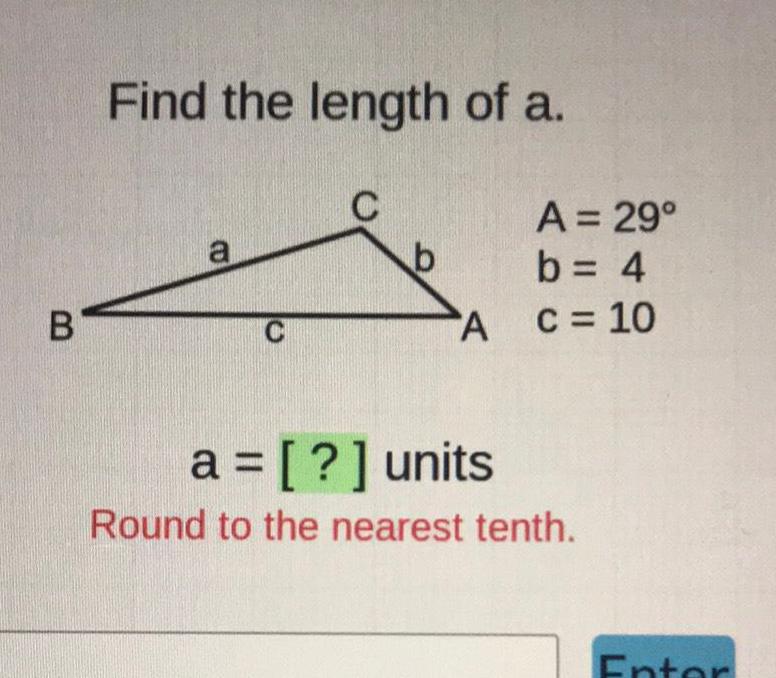
Calculus
Application of derivativesB Find the length of a a C C b A A 29 b 4 c 10 a units Round to the nearest tenth Entor
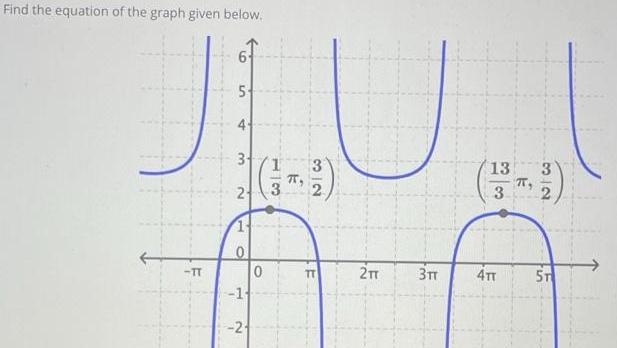
Calculus
Application of derivativesFind the equation of the graph given below TT 5 3 2 Lored O 1 2 0 3 TT 2TT 3TT 13 3 4TT TT 2 ST
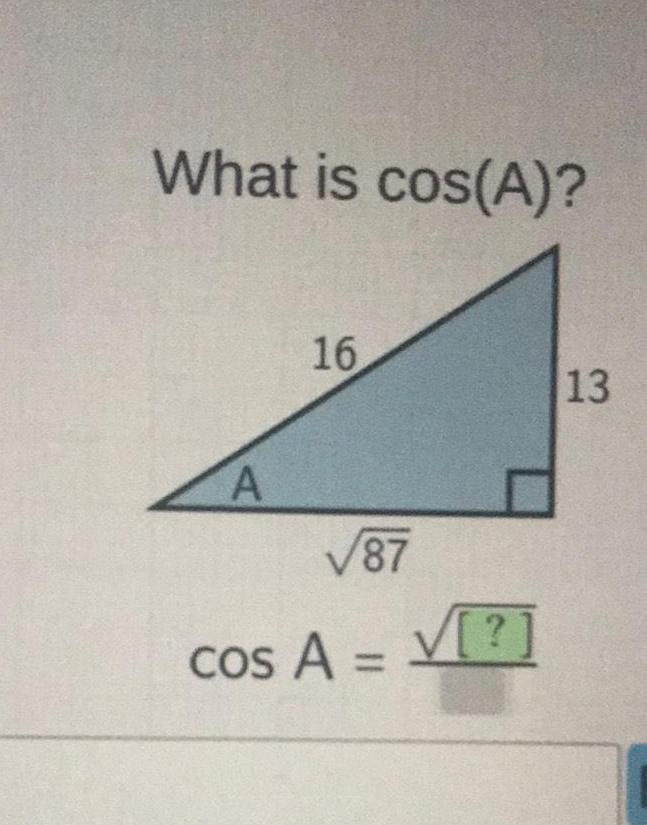

Calculus
Application of derivativesEXAMPLE B Find the absolute maximum and minimum values of the function below ra ti 4 14 SOLUTION Since fis continuous on F x x 3x 1 F 0 Since Fix exists for all x the only critical numbers of foccur when The values of fat these critical numbers are we can use the Clesed Interval Method that is Notice that each of these critical numbers lies in K 0 and 2 The values off at the endpoints of the interval are 0 and 4 Comparing these four numbers we see that the absolute masimum value is 4 and the absolute minimum value is 2 Note that in this example the absolute maximum occurs at an endpoint whereas the absolute minimum occurs at a critical number The graph of fis sketched in the

Calculus
Application of derivativesAn 80 foot rope is attached to a boat 7 feet above the water level as shown and a boy jumps over the wake while wakeboarding What is the distance between his hands and the water level ft 80 ft 10 87 Round to the nearest hundredth Enter

Calculus
Application of derivativesWhich expression uses the associative property to make it easier to evaluate 8 O A 4 3 O B 8 O c 8 1 O D 8
Calculus
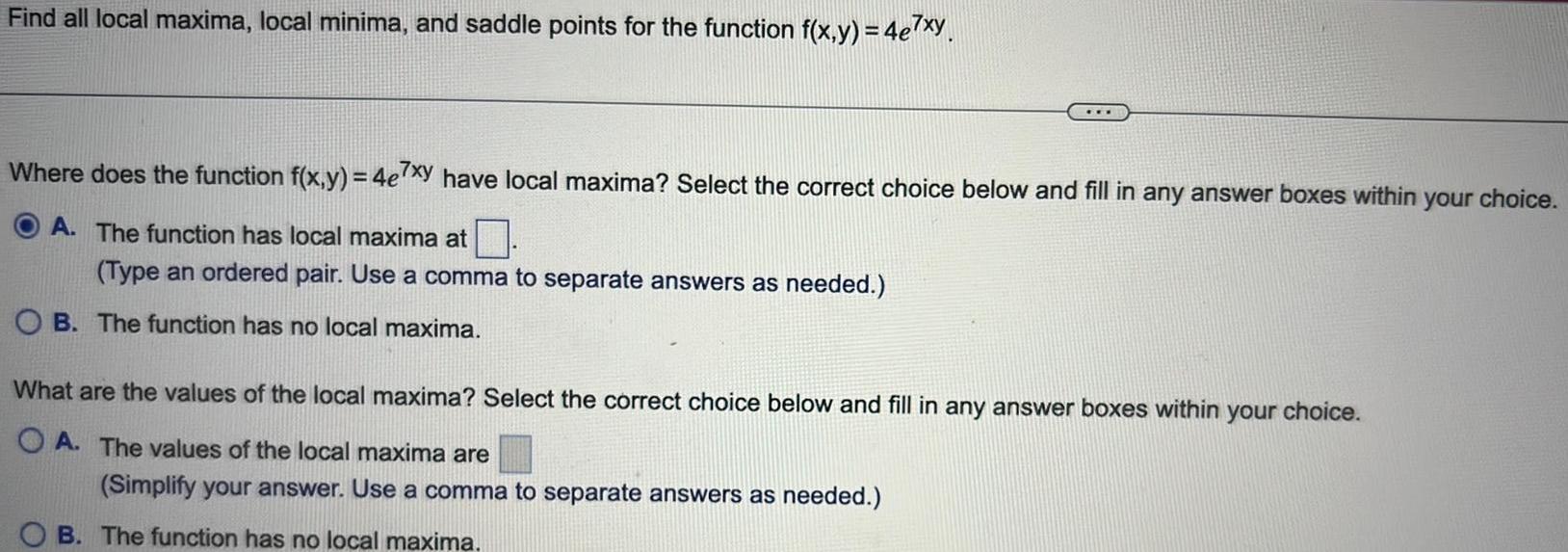
Application of derivativesFind all local maxima local minima and saddle points for the function f x y 4e7xy Where does the function f x y 4e7xy have local maxima Select the correct choice below and fill in any answer boxes within your choice A The function has local maxima at Type an ordered pair Use a comma to separate answers as needed OB The function has no local maxima What are the values of the local maxima Select the correct choice below and fill in any answer boxes within your choice OA The values of the local maxima are Simplify your answer Use a comma to separate answers as needed B The function has no local maxima
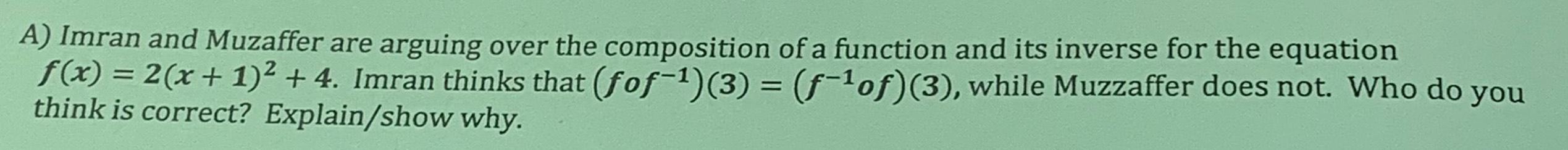
Calculus
Application of derivativesA Imran and Muzaffer are arguing over the composition of a function and its inverse for the equation f x 2 x 1 4 Imran thinks that fof 3 f of 3 while Muzzaffer does not Who do you think is correct Explain show why

Calculus
Application of derivatives2 Find the directional derivative of the function f x y 2xy 3y2 at Po 5 5 in the direction of u 4i 3j a 4 b 4 0 U d 12 8
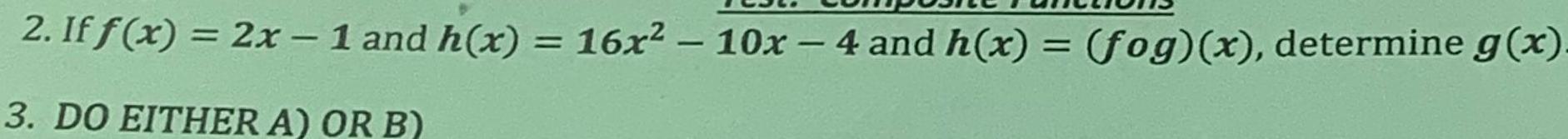
Calculus
Application of derivatives2 If f x 2x 1 and h x 16x 10x 4 and h x fog x determine g x 3 DO EITHER A OR B
Calculus
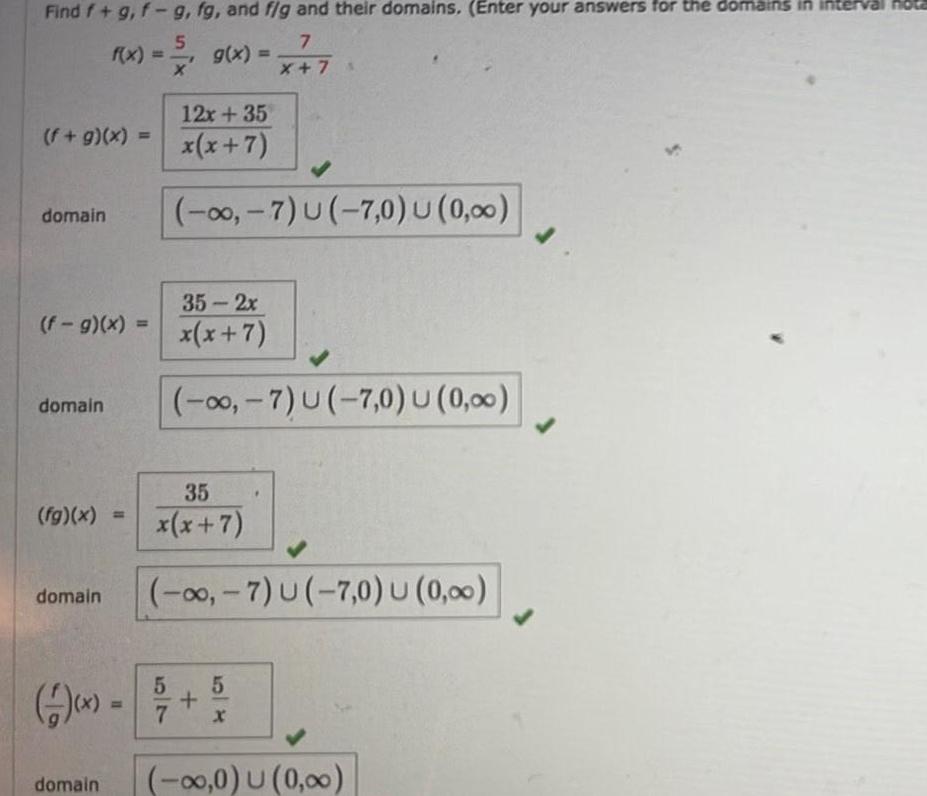
Application of derivativesFind f g f g fg and f g and their domains Enter your answers for the domains in interval nota 7 X 7 f g x domain 5 f x g x X f g x domain fg x 12x 35 x x 7 0 7 U 7 0 U 0 00 35 x x 7 domain 0 7 U 7 0 U 0 00 domain 35 2x x x 7 0 7 U 7 0 U 0 00 5 7 x 5 7 0 0 U 0 00
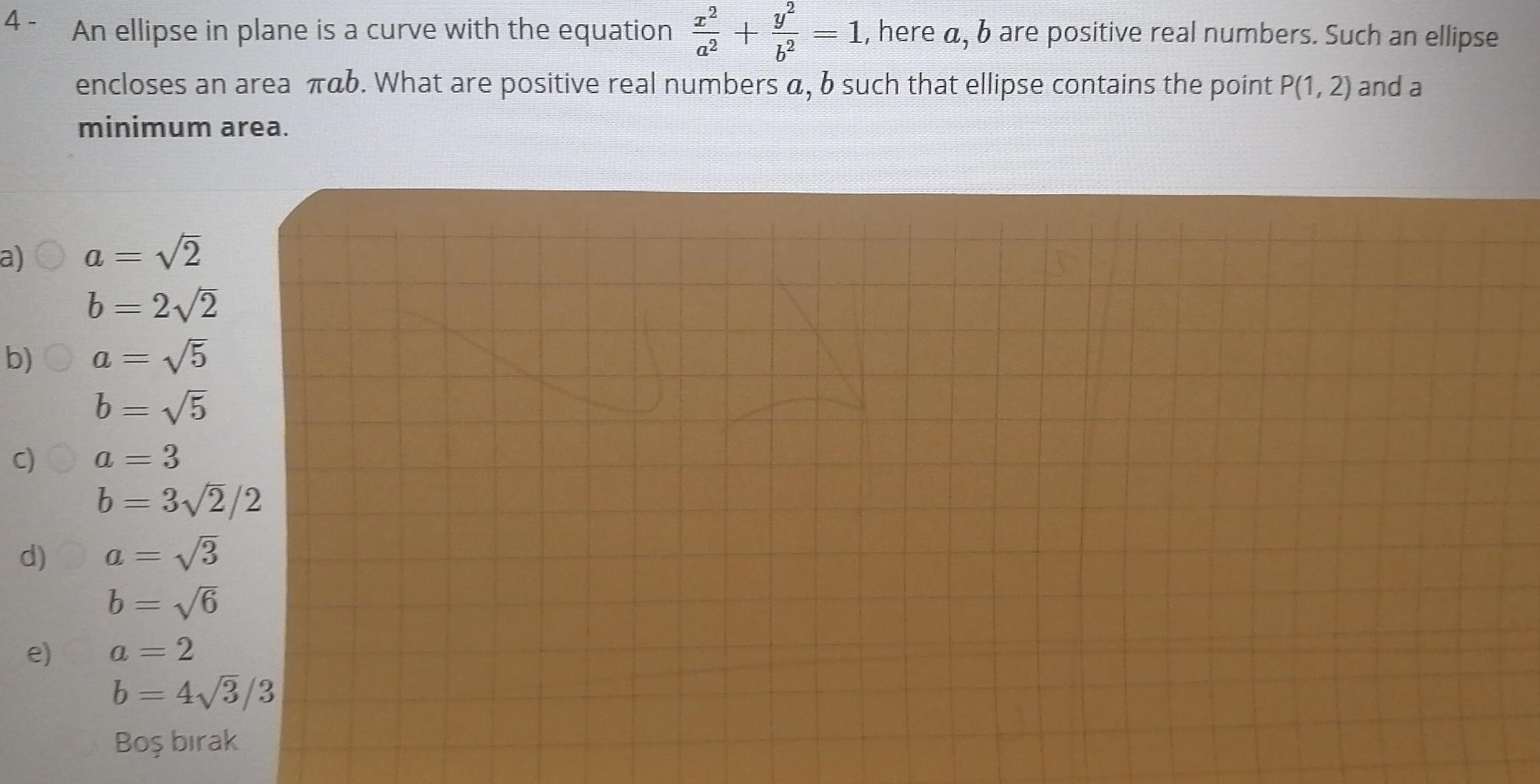
Calculus
Application of derivatives4 a a 2 b 2 2 b a 5 b 5 a 3 c y bare positive real numbers Such an ellipse An ellipse in plane is a curve with the equation q2 6 encloses an area Tab What are positive real numbers a b such that ellipse contains the point P 1 2 and a minimum area e b 3 2 2 a 3 b 6 a 2 b 4 3 3 Bo b rak 1 here a

Calculus
Application of derivatives8 Which statement s on the function f x y z x xy xy z z is true I f has exactly one critical point namely a local minimum II f has exactly one critical point namely a local maximum III f has exactly one critical point namely a saddle point IV has multiple critical points a D I C IV 11 None d

Calculus
Application of derivatives6 a b c d e Which one of the functions satisfies the three dimensional Laplace equation given below The three dimensional Laplace equation 4 4 4 1 f x y z x y z f x y z x y z f x y z x y 2 f x y z x y 2 f x y z x y 22 Bo b rak
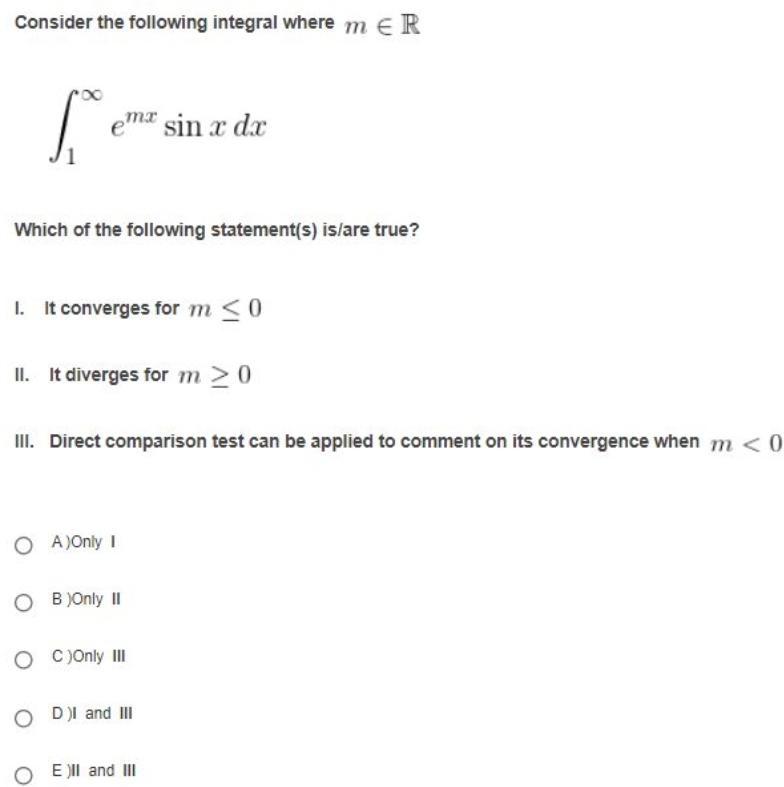
Calculus
Application of derivativesConsider the following integral where m ER fo emx sin x dx Which of the following statement s is are true 1 It converges for m 0 II It diverges for m 20 III Direct comparison test can be applied to comment on its convergence when m 0 O A Only I OB Only II OC Only III OD I and III E II and III

Calculus
Application of derivativesWhat type of partial fractions is used to evaluate the integral x 2x x 2 x 1 x x 2 x 1 OA A x O BA X O CA X O DIA X O E A 2 B x 2 B x B x 2 X B C 72 73 Ca D x 1 C Bx C 2 2 C x 2 2 Dx E 2 Ex F Ga H x 1 x x 2 D x Da E x 1 2 Dx E x 1 dx Fx G x 1 Ex F x 1 Fx G Hx I 2 x 1 x x 2 Fx G 2 1 Ga H x 1 Hx I Jx K x 1 x x 2 H x 1 I x 1

Calculus
Application of derivativesf x 5dx 32x x then find the domain of the function f x O AX 3 U 1 OB 3 U 3 1 U 1 O c 3 U 3 O D 1 U 1 O EX 3 1

Calculus
Application of derivativesRevenue and elasticity The price demand equation for hamburgers at a fast food restaurant is x 400p 3 000 Currently the price of a hamburger is 3 00 If the price is increased by 10 will revenue increase or decrease Revenue and elasticity Refer to Problem 85 If the current price of a hamburger is 4 0 will a 10 price increase cause revenue to increase or decrease
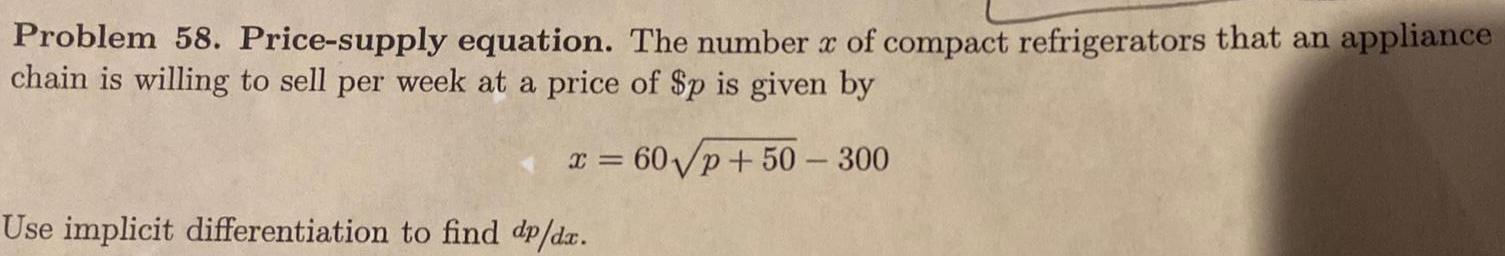
Calculus
Application of derivativesProblem 58 Price supply equation The number x of compact refrigerators that an appliance chain is willing to sell per week at a price of p is given by p 50 300 X 60 Use implicit differentiation to find dp dx
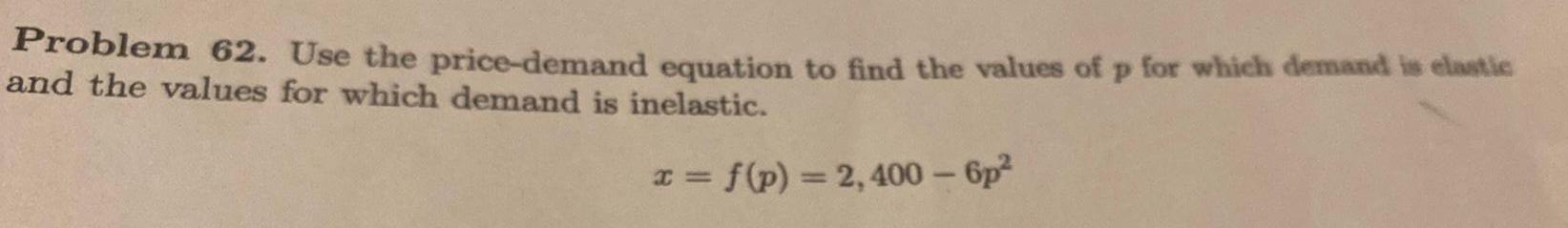
Calculus
Application of derivativesProblem 62 Use the price demand equation to find the values of p for which demand is elastic and the values for which demand is inelastic x f p 2 400 6p
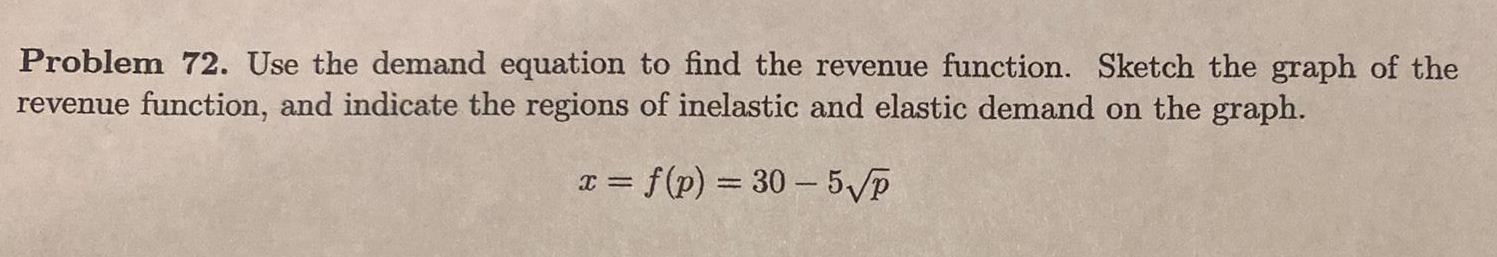
Calculus
Application of derivativesProblem 72 Use the demand equation to find the revenue function Sketch the graph of the revenue function and indicate the regions of inelastic and elastic demand on the graph x f p 30 5 P

Calculus
Application of derivativesI see that you mentioned there are identical transformations using 1 2 and 2 For what function is this true Is it true for every function For example do those values result in the same graph for the cubed function f x x3

Calculus
Application of derivatives0 5 0 0 5 25 15 30 45 75 90 120 135 150 165 180 195 Question 14 Percentage of R enantiomer UNKNOWN 2

Calculus
Application of derivativesA function R x measures the revenue of a company in millions when producing x items Explain in your words the meaning of R 3200 1 25 For the toolbar press ALT F10 PC or ALT FN F10 Mac

Calculus
Application of derivativests to put a rectangular garden on her property using 64 meters of fencing There is a river that runs through her property so she decides to increase the size of the garden by using the river as one side of the Fencing is then needed only on the other three sides Let x represent the length of the side parallel to the river Express the garden s area as a function of x full points show your work for this problem on your scratch paper
