Application of derivatives Questions and Answers

Calculus
Application of derivativesA line goes through the points 2 2 and 1 6 a Write the equation of the line in point slope form b Write the equation of the line in y intercept form Write the equation of the line in standard form n
Calculus
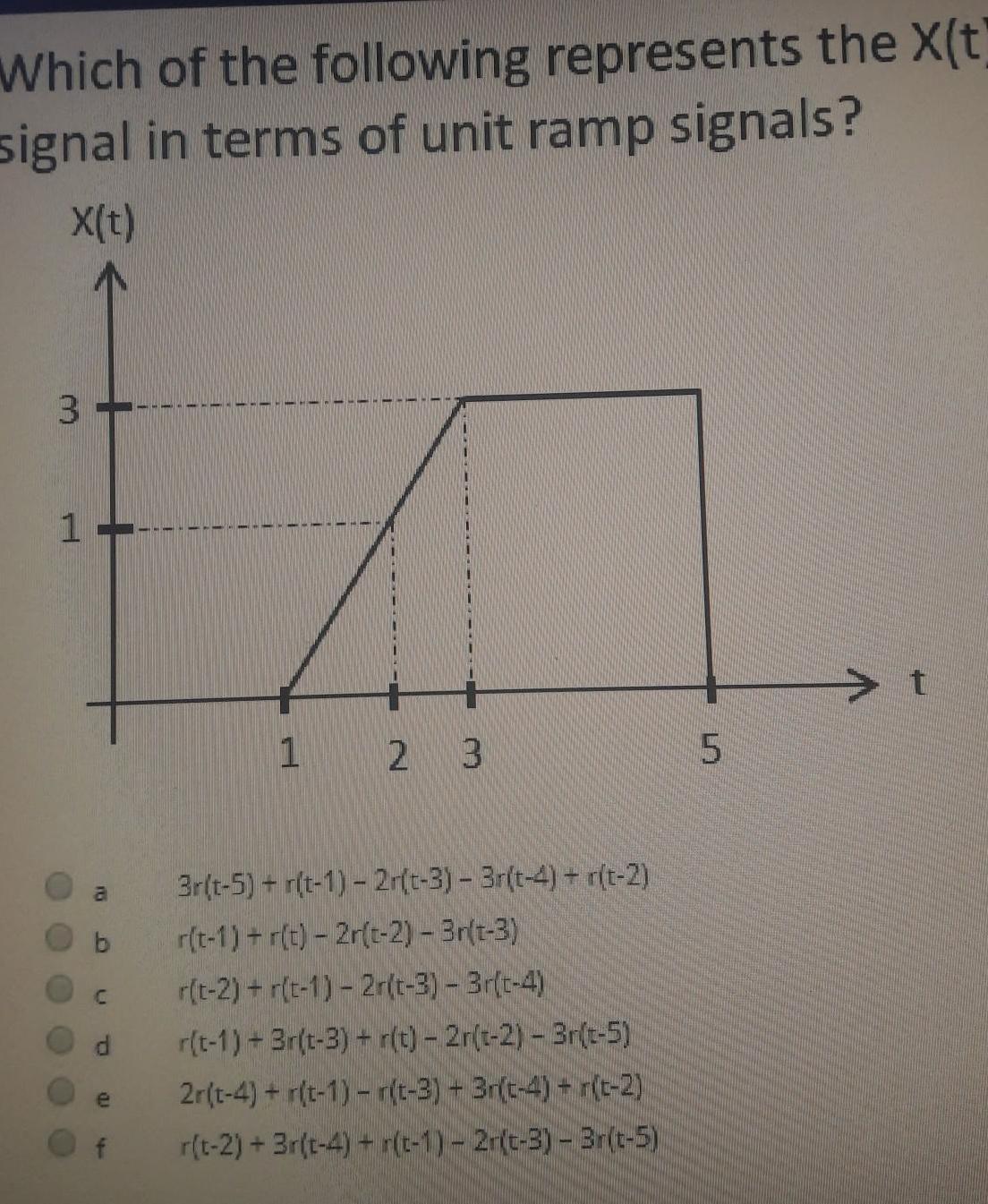
Application of derivativesWhich of the following represents the X t signal in terms of unit ramp signals X t 3 1 a C e 1 2 3 3r t 5 r t 1 2r t 3 3r t 4 r t 2 r t 1 r t 2r t 2 3r t 3 r t 2 r t 1 2r t 3 3r t 4 r t 1 3r t 3 r t 2r t 2 3r t 5 2r t 4 r t 1 r t 3 3r t 4 r t 2 r t 2 3r t 4 r t 1 2r t 3 Br t 5 5 t
Calculus
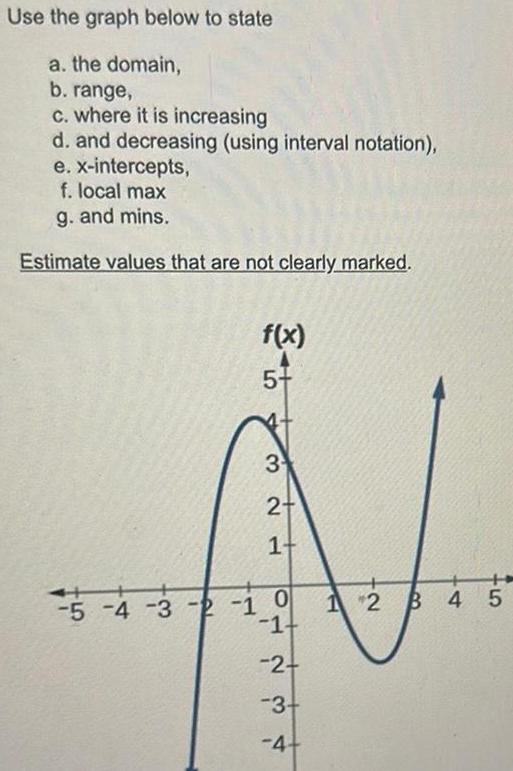
Application of derivativesUse the graph below to state a the domain b range c where it is increasing d and decreasing using interval notation e x intercepts f local max g and mins Estimate values that are not clearly marked f x 5 3 2 1 5 4 3 2 1 0 1 2 3 4 12 B 45

Calculus
Application of derivativesConsider the equation f x x 2 5 Identify the parent function and describe ALL the transformations shifts stretches etc
Calculus
Application of derivativesFind the length of the major axis of Earth s orbit using Kepler s third law and the fact that Earth s orbital period is 365 256 days Use G 6 6726 10 Nm kg M 1 99 x 1030 kg and 3 14 Recall that 1 N 1 kg m s 11 The length of the major axis of Earth s orbit is km Do not round until the final answer Then round to the nearest thousand as needed
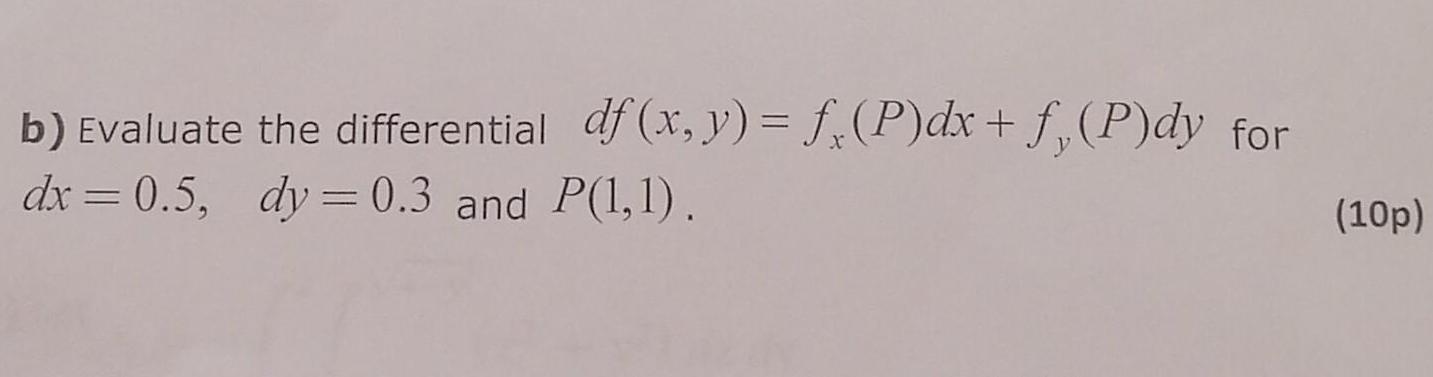
Calculus
Application of derivativesb Evaluate the differential df x y f P dx f P dy for dx 0 5 dy 0 3 and P 1 1 10p
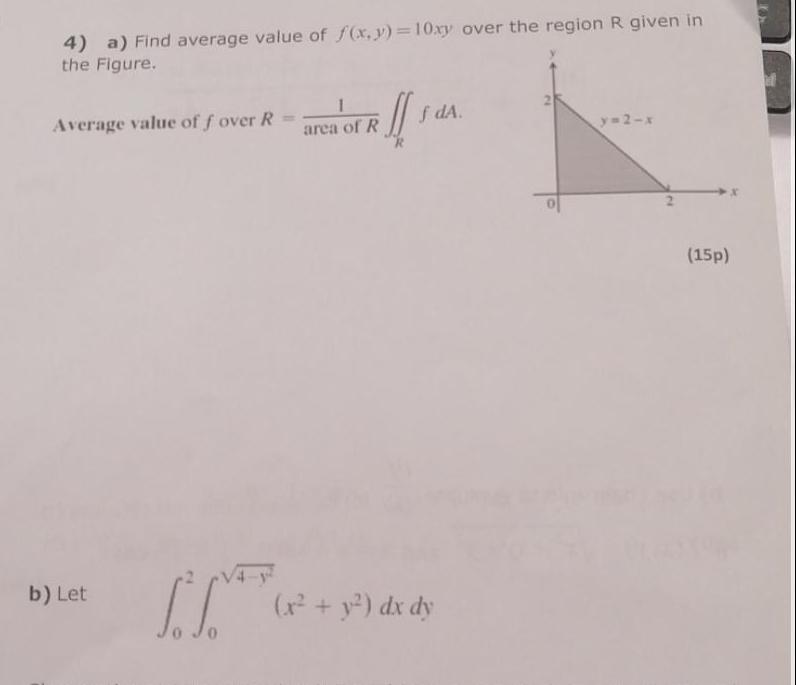
Calculus
Application of derivatives4 a Find average value of f x y 10xy over the region R given in the Figure Average value of f over R b Let I ill 1 area of R f dA x y dx dy y 2 x 15p
Calculus
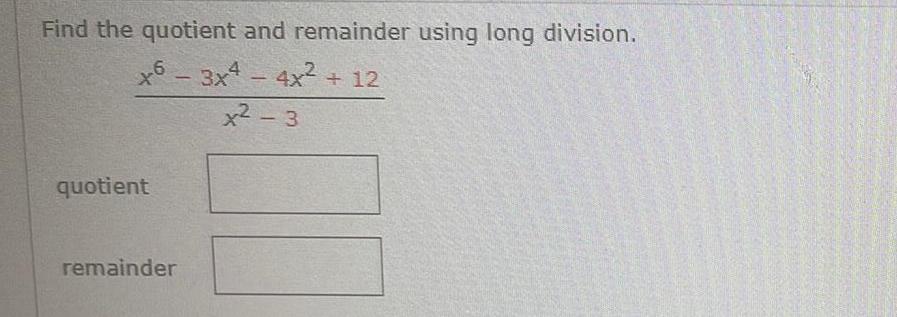
Application of derivativesFind the quotient and remainder using long division 6 x6 3x4 4x x2 3 quotient remainder 12


Calculus
Application of derivativesThinking about transformations most basic functions can be thought of in the following forms where the lower case letters a through d have the same meaning y a bx c d y asin bx c d y ae bx c d Match each of the lowercase letters with their role v b VC vd 1 left right shift II horizontal compression stretch III vertical compression stretch IV up down shift

Calculus
Application of derivatives5 We have accidentally introduced a new bacteria in our pond and their growth rate can be described using an exponential model a Given that their population is 5 times the initial population after 2 days what is the exponential growth constant k b How many days will it take to reach 20 times the initial population

Calculus
Application of derivativesThe square region with vertices 13 0 26 13 13 26 and 0 13 is revolved about the x axis to generate a solid Find the volume and surface area of the solid

Calculus
Application of derivativesHow many license plates can be made using either three uppercase English letters followed by three digits or four uppercase English lettem followed by two digits
Calculus
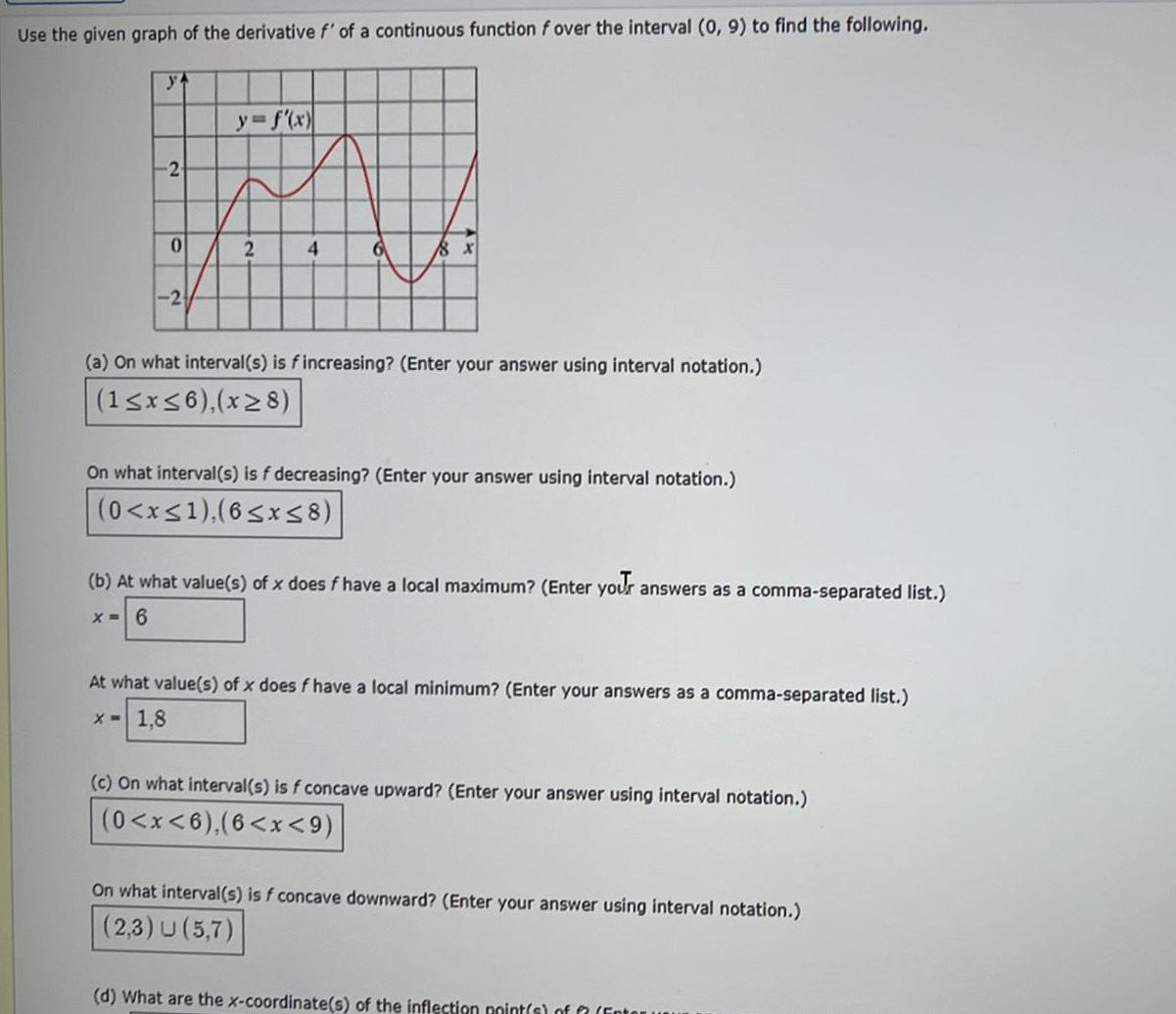
Application of derivativesUse the given graph of the derivative f of a continuous function f over the interval 0 9 to find the following ya 2 0 2 y f x 2 4 6 18 x a On what interval s is fincreasing Enter your answer using interval notation 1 x 6 x 8 On what interval s is f decreasing Enter your answer using interval notation 0 x 1 6 x 8 b At what value s of x does f have a local maximum Enter your answers as a comma separated list x 6 At what value s of x does f have a local minimum Enter your answers as a comma separated list x 1 8 c On what interval s is f concave upward Enter your answer using interval notation 0 x 6 6 x 9 On what interval s is f concave downward Enter your answer using interval notation 2 3 U 5 7 d What are the x coordinate s of the inflection point s of Enter
Calculus
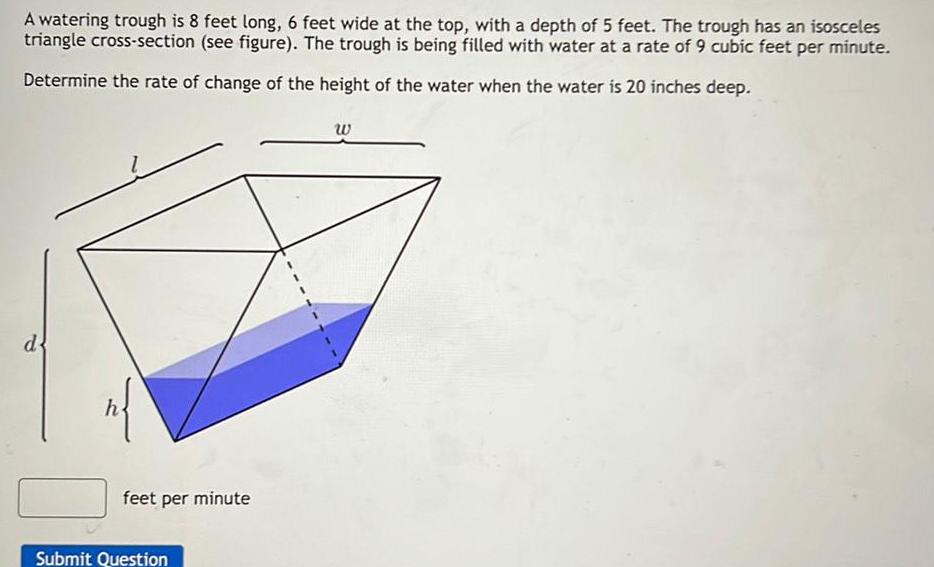
Application of derivativesA watering trough is 8 feet long 6 feet wide at the top with a depth of 5 feet The trough has an isosceles triangle cross section see figure The trough is being filled with water at a rate of 9 cubic feet per minute Determine the rate of change of the height of the water when the water is 20 inches deep d n feet per minute Submit Question W

Calculus
Application of derivativesLet h t 4 log sin 4 log sin Ot Determine the critical values of h If multiple such values exist enter the solutions using a comma separated list No critical values exist 11 t 0 Submit Question
Calculus
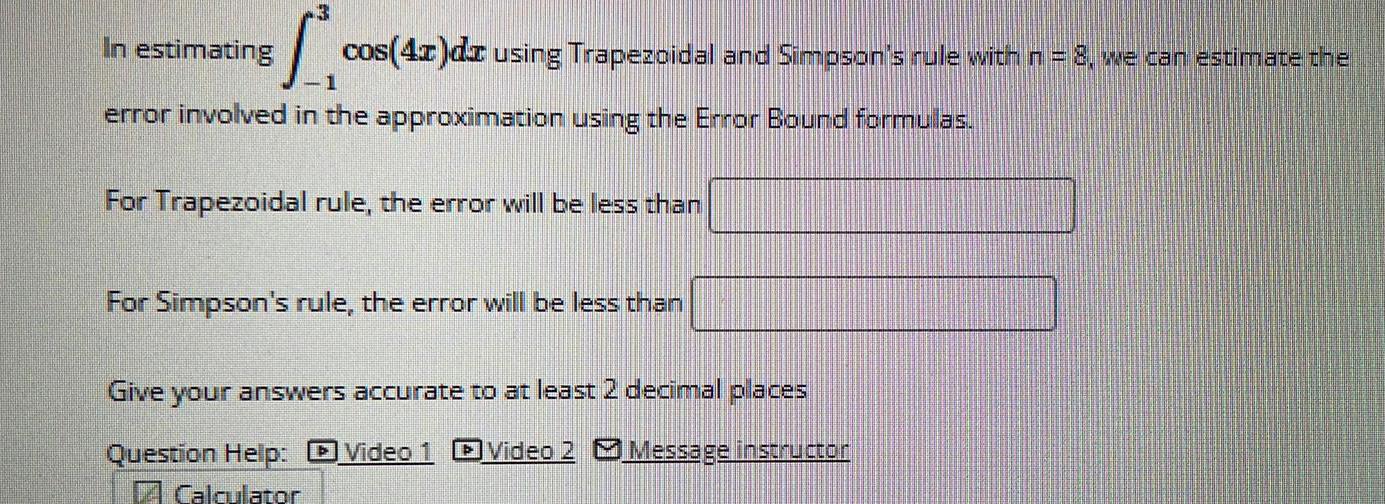
Application of derivatives3 In estimating 1 error involved in the approximation using the Error Bound formulas cos 4x dx using Trapezoidal and Simpson s rule with n 8 we can estimate the For Trapezoidal rule the error will be less than For Simpson s rule the error will be less than Give your answers accurate to at least 2 decimal places Question Help Video 1 Video 2 Message instructor Calculator

Calculus
Application of derivativespoints possible graded For the given function f evaluate f 3 f 2 f 1 and f 0 f 3 2 f 1 f 0 f x x 4 2x 3 if x 2 if x 2
Calculus
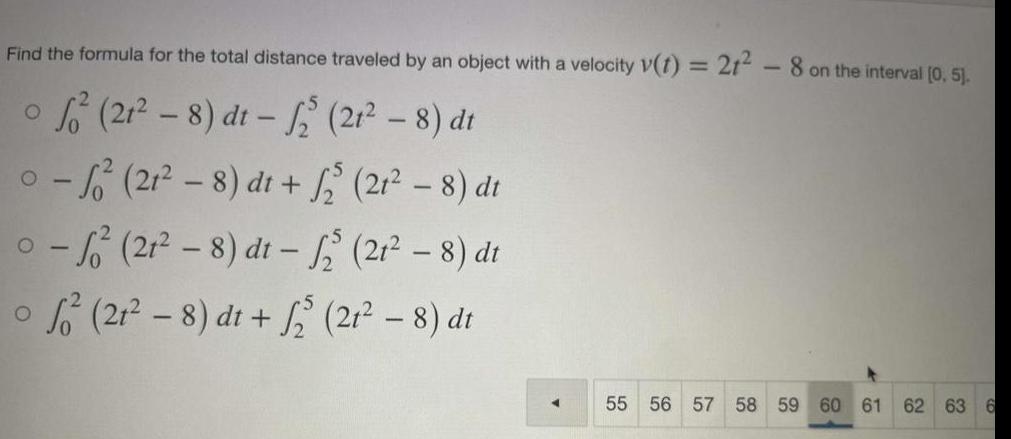
Application of derivativesFind the formula for the total distance traveled by an object with a velocity v t 21 8 on the interval 0 5 21 8 dt 21 8 dt 0 21 8 dt 2 21 8 dt O 0 21 8 dt 21 8 dt 21 8 dt 21 8 dt 55 56 57 58 59 60 61 62 63 6

Calculus
Application of derivativesFind the area of this triangle 155 260 175 Round to the nearest whole number

Calculus
Application of derivatives0 A survey found that women s heights are normally distributed with mean 63 6 in and standard deviation 2 2 in A branch of the military requires women s heights to be between 58 in and 80 in a Find the percentage of women meeting the height requirement Are many women being denied the opportunity to join this branch of the military because they are too short or too tall b If this branch of the military changes the height requirements so that all women are eligible except the shortest 1 and the tallest 2 what are the new height requirements Click to view page 1 of the table Click to view page 2 of the table a The percentage of women who meet the height requirement is 99 46 Round to two decimal places as needed Are many women being denied the opportunity to join this branch of the military because they are too short or too tall OA Yes because a large percentage of women are not allowed to join this branch of the military because of their height OB Yes because the percentage of women who meet the height requirement is fairly large C No because only a small percentage of women are not allowed to join this branch of the military because of their height OD No because the percentage of women who meet the height requirement is fairly small b For the new height requirements this branch of the military requires women s heights to be at least most in Round to one decimal place as needed in and at
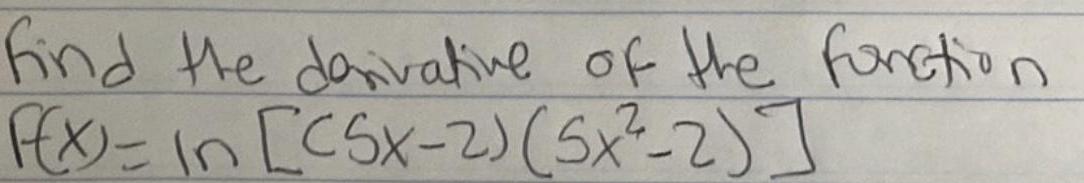

Calculus
Application of derivativesIn this last step we are going to go back to our first reflection We asked the question Are vertical stretches shrinks and horizontal stretches shrinks basically the same thing Yes that s right we re asking the first question again This time apply the following sequence of transformations to your chosen function f x Graph Transformations f x x2 The vertical stretch by 4 then a vertical shift by 2 A horizontal shrink by 2 and then a vertical shift by 2 A vertical shift by 2 then a vertical stretch by 4 A vertical shift by 2 then a horizontal shrink by 2
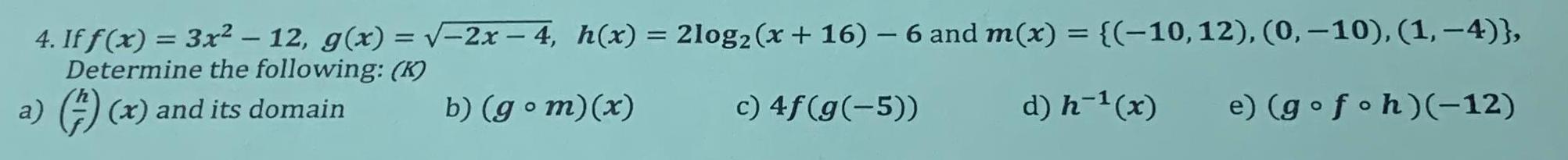
Calculus
Application of derivatives4 If f x 3x 12 g x 2x 4 h x 2log2 x 16 6 and m x 10 12 0 10 1 4 Determine the following K a x and its domain b gom x c 4f g 5 d h x e gofoh 12

Calculus
Application of derivatives6 In a laboratory culture the number N d of bacteria in thousands at temperature d degrees Celsius is given 90 by the function N d 20 for 4 d 32 The temperature D t at time t hours after start time is given by the function d t 3t 4 for 0 t 14 A d 1 a Write an expression for the number of bacteria in terms of t b Determine the initial temperature and number of bacteria in the culture c Determine the number of bacteria after 6 hours d Determine the number of bacteria after 10 hours
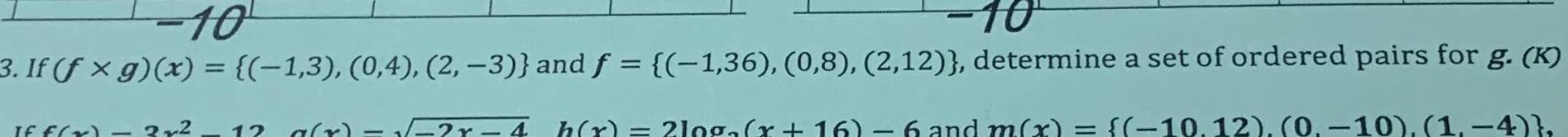
Calculus
Application of derivatives10 10 3 If fx g x 1 3 0 4 2 3 and f 1 36 0 8 2 12 determine a set of ordered pairs for g K If f x 3x 12 a r h r 10g x 16 6 and m x 10 12 0 10 1 4 2r 4



Calculus
Application of derivativesf x 2x 3x 12x 2 Junction Then use the second derivative test on each critical number to determine whether it leads to a local maximum or minimum OB The critical number s is are x What is the second derivative of f x f x Find all critical numbers and determine whether they lead to a local maximum or minimum Select the correct choice below and if necessary fill in the answer box es to complete your choice A The critical number s is are x There is no local maximum There is a local minimum at x Use a comma o separate answers as needed There is a local maximum at x Use comma to separate answers as needed SICCOS OC The critical number s is are x There is a local maximum at x Use a comma to separate answers as needed There is a local minimum at x There is no local minimum D The critical number s is are x There is no local maximum and no local minimum Use a comma to separate answers as needed OE There are no critical numbers

Calculus
Application of derivativesThe function s t 13 27t 8 gives the distance from a starting point at time t of a particle moving along a line Find the velocity and acceleration functions Then find the velocity and acceleration at t 0 and t 3 Assume that time is measured in seconds and distance is measured i centimeters Velocity will be in centimeters per second cm sec and acceleration in centimeters per second per second cm sec The velocity function is v t 3t 27 Simplify your answer The acceleration function is a t 6t Simplify your answer The velocity at t 0 is v 0 27 cm sec Simplify your answer The velocity at t 3 is v 3 0 cm sec Simplify your answer The acceleration at t 0 is a 0 0 cm sec Simplify your answer The acceleration at t 3 is a 3 18 cm sec GELOD
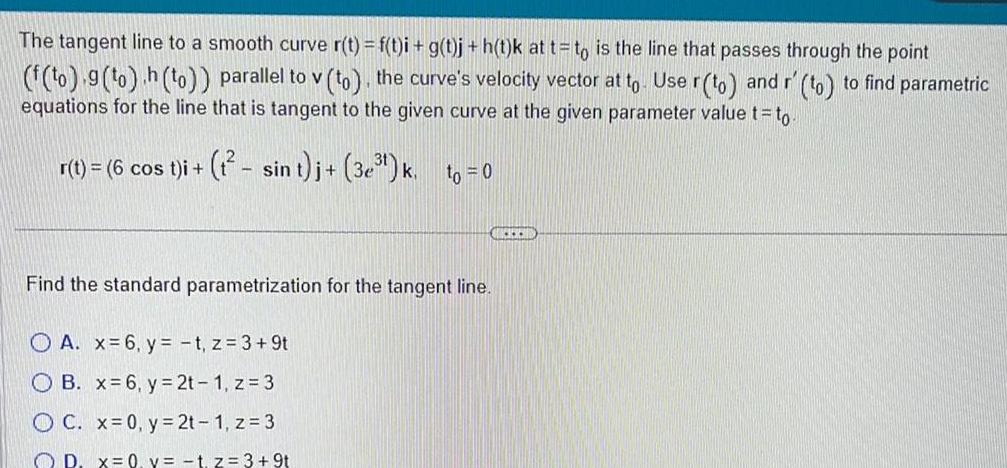
Calculus
Application of derivativesThe tangent line to a smooth curve r t f t i g t j h t k at t to is the line that passes through the point f to 9 to h to parallel to v to the curve s velocity vector at to Use r to and r to to find parametric equations for the line that is tangent to the given curve at the given parameter value t to r t 6 cos t i t sin t j 3e k to 0 Find the standard parametrization for the tangent line A x 6 y t z 3 9t OB x 6 y 2t 1 z 3 OC x 0 y 2t 1 z 3 OD x 0 y t z 3 9t

Calculus
Application of derivativesA rectangular auditorium seats 2494 people The number of seats in each row exceeds the number of rows by 15 Find the number of seats in each row

Calculus
Application of derivativesThe function s t 27t 8 gives the distance from a starting point at time t of a particle moving along a line Find the velocity and acceleration functions Then find the velocity and acceleration at t 0 and t 3 Assume that time is measured in seconds and distance is measured in centimeters Velocity will be in centimeters per second cm sec and acceleration in centimeters per second per second cm sec The velocity function is v t Simplify your answer The acceleration function is a t Simplify your answer The velocity at t 0 is v 0 cm sec Simplify your answer The velocity at t 3 is v 3 cm sec Simplify your answer The acceleration at t 0 is a 0 cm sec Simplify your answer The acceleration at t 3 is a 3 cm sec CEIXE

Calculus
Application of derivativesFind the acceleration function a t if s t 7t 61 8t 7 O A a t 42t 8 OB a t 21t 12t 8 OC a t 42t 12 OR 002

Calculus
Application of derivativesa starting point at time t of a particle moving along a line Find the velocity and acceleration functions Then find the velocity and acceleration a t 0 and t 5 Assume that time is measured in seconds and distance is measured in centimeters Velocity will be in centimeters per second cm sec and acceleration in centimeters per second p second cm sec The velocity function is v t Simplify your answer The acceleration function is a t Simplify your answer The velocity at t 0 is v 0 cm sec Simplify your answer The velocity at t 5 is v 5 cm sec Simplify your answer The acceleration at t 0 is a 0 cm sec Simplify your answer The acceleration at t 5 is a 5 cm sec
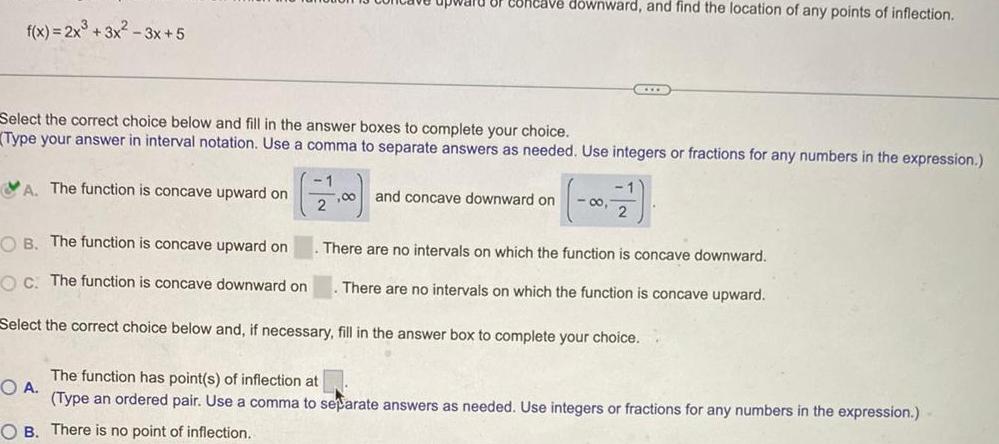
Calculus
Application of derivativesf x 2x 3x 3x 5 A The function is concave upward on OF Concave downward and find the location of any points of inflection Select the correct choice below and fill in the answer boxes to complete your choice Type your answer in interval notation Use a comma to separate answers as needed Use integers or fractions for any numbers in the expression 00 and concave downward on 2 OA 00 CITE 2 OB The function is concave upward on OC The function is concave downward on Select the correct choice below and if necessary fill in the answer box to complete your choice There are no intervals on which the function is concave downward There are no intervals on which the function is concave upward The function has point s of inflection at Type an ordered pair Use a comma to separate answers as needed Use integers or fractions for any numbers in the expression OB There is no point of inflection
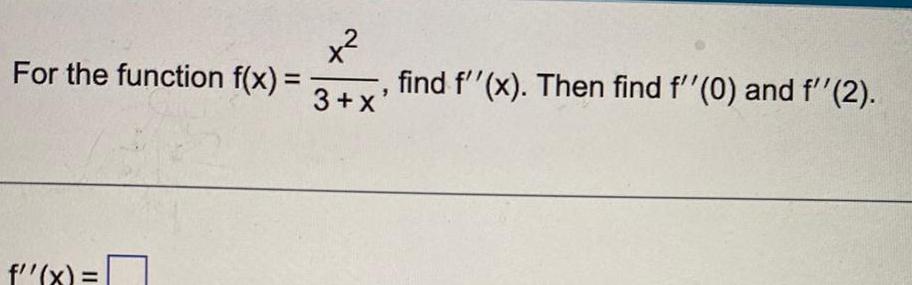

Calculus
Application of derivativesLast week Jeff noted that 100 of the 200 flights to airport A flying out of airport B departed on time During the next week 500 flights left airport B for airport A If the same ratio holds how many of those flights would he expect to depa on time Jeff would expect flights to depart on time

Calculus
Application of derivativesFor the function f x In 3x 2 find f x f 0 f 2 and f 1 f x 0 Use integers or fractions for any numbers in the ex tion
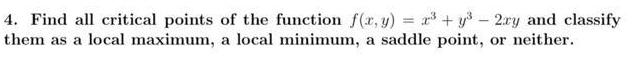
Calculus
Application of derivatives4 Find all critical points of the function f x y x y 2ry and classify them as a local maximum a local minimum a saddle point or neither


Calculus
Application of derivatives1 25 pt Sketch the region of integration for the following integral and evaluate the integral 22 2 0 0 Te2y 2 y dy dr 2 25 pt Find the value of Zer at the point 1 1 0 where yz x y e 3 25 pt Test the function below for local maxima local minima and saddle points Find the value of the function at these points f x y x y 2xy y 3y 4 25 pt Identify the symmetries of the curves r 12 cos 0 and r 4 4 cos 0 Make a table for r values corresponding to values Draw the curves on the same plane Then find the area of the region shared by these curves
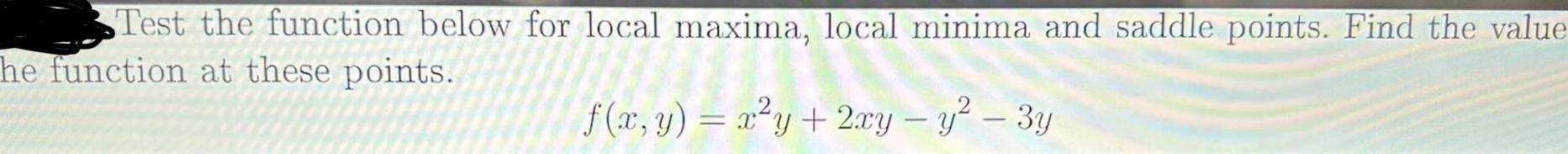
Calculus
Application of derivativesTest the function below for local maxima local minima and saddle points Find the value he function at these points f x y x y 2xy y 3y
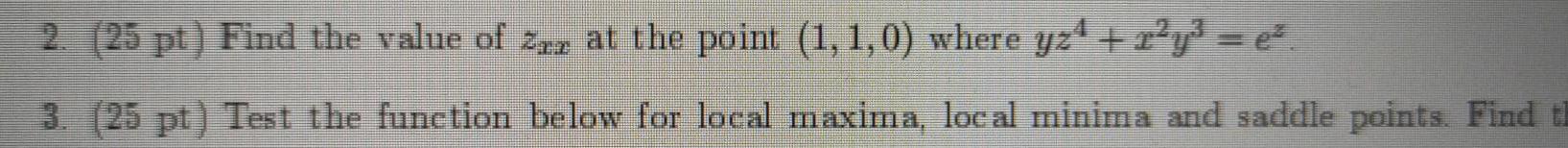
Calculus
Application of derivatives2 25 pt Find the value of at the point 1 1 0 where y24 2 y e 3 25 pt Test the function below for local maxima local minima and saddle points Find t
Calculus
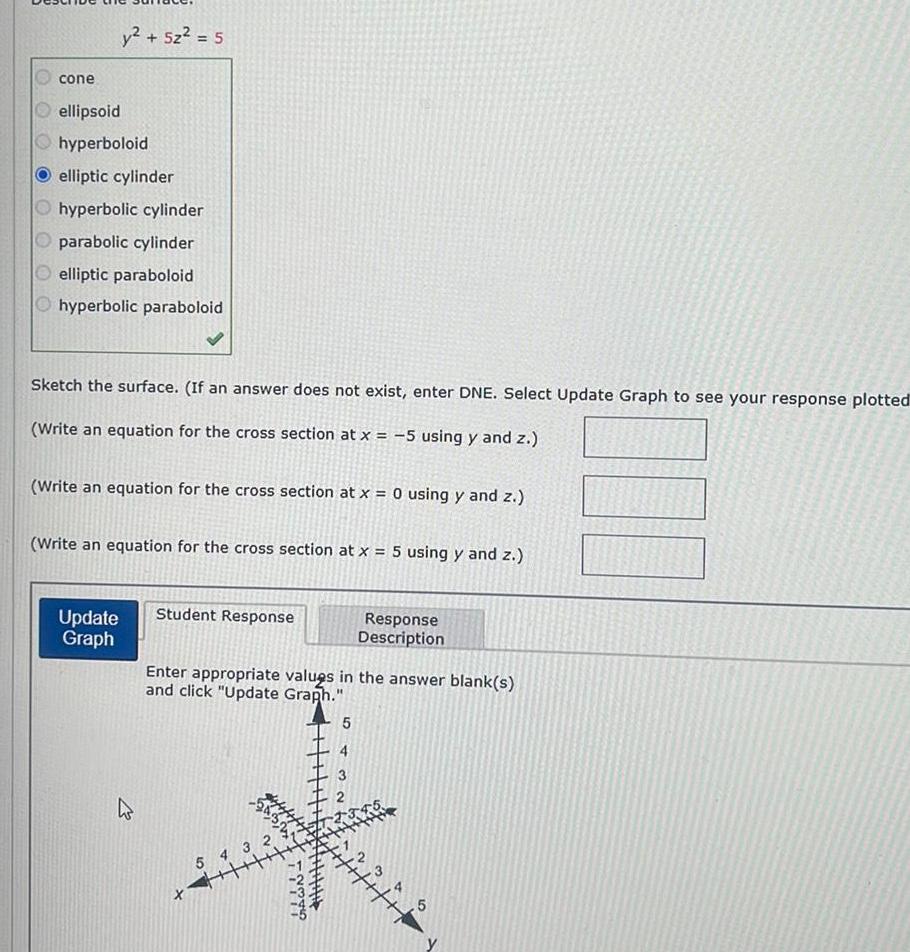
Application of derivativescone y 5z 5 ellipsoid hyperboloid elliptic cylinder Ohyperbolic cylinder Oparabolic cylinder elliptic paraboloid hyperbolic paraboloid Sketch the surface If an answer does not exist enter DNE Select Update Graph to see your response plotted Write an equation for the cross section at x 5 using y and z Write an equation for the cross section at x 0 using y and z Write an equation for the cross section at x 5 using y and z Update Graph Student Response Enter appropriate values in the answer blank s and click Update Graph Xx 5 4 3 GAWN Response Description 5 2 1345 5

Calculus
Application of derivativesSolve the general 1 D heat equation with the given boundary values and initial conditions a uxx ut u 0 t 0 u L t 0 u x 0 f x 0 x L t 0
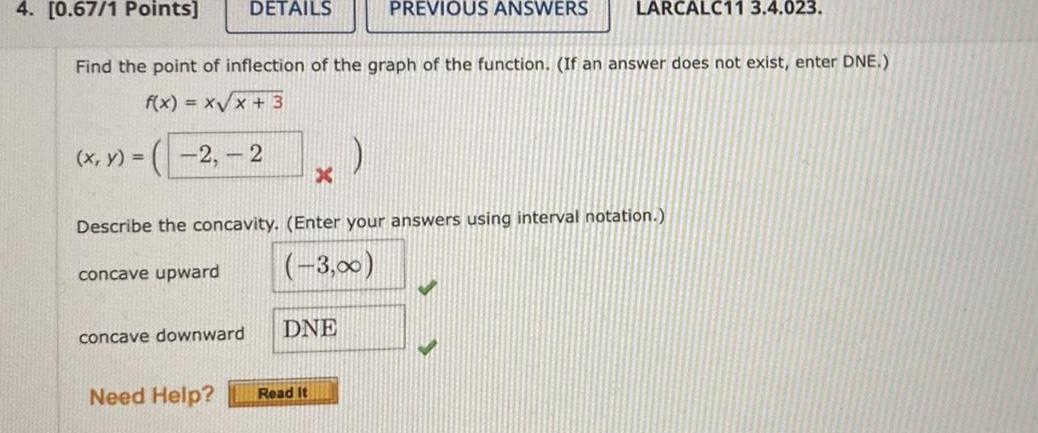
Calculus
Application of derivatives4 0 67 1 Points Find the point of inflection of the graph of the function If an answer does not exist enter DNE f x x x 3 2 2 x y DETAILS concave downward X DNE Need Help Read It Describe the concavity Enter your answers using interval notation concave upward 3 0 PREVIOUS ANSWERS LARCALC11 3 4 023
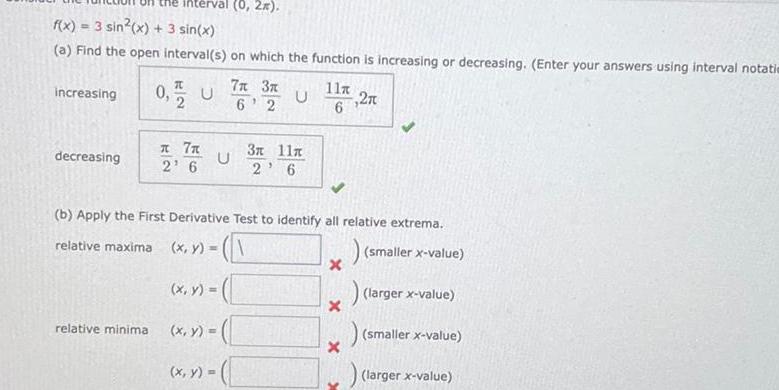
Calculus
Application of derivativesf x 3 sin x 3 sin x a Find the open interval s on which the function is increasing or decreasing Enter your answers using interval notatie increasing decreasing interval 0 2 relative minima 0 U 7x 2 6 U 7x 3x U 6 2 x y b Apply the First Derivative Test to identify all relative extrema relative maxima x y smaller x value larger x value smaller x value 3x 11x 2 6 x y x y 11 27 6 x X X larger x value

Calculus
Application of derivativesDevelop your own optimization application question of any type or description Try to make it something that interests you That might make it fun Complete the following 1 State your optimization problem 2 Provide the context story that motivates the question why is this question being asked 3 Explain how to or who can use this problem solution in a real world context 4 Provide the worked solution Please note the following You should use your class notes or textbook as reference as you work on your solution Your teacher recognizes the value that comes from discussing problems with your classmates There are several different examples you can use for optimization It is very easy for each student to produce their own unique optimization problem You can use any of the questions and examples from the textbook as a quide if that problem interests you

Calculus
Application of derivatives2 A function is continuous on the closed interval 3 3 such that f 3 4 and f 3 1 The functions f x and f x have the properties given in the table below x f x f x 3 1 x 1 1 1 x 1 1 3 Positive Fails to exist Negative Zero Negative Positive Fails to exist c On the axes provided sketch a graph of f x Positive Zero Negative a What are the x coordinates of absolute maximum and minimum points of on the interval 3 3 Justify your answer b What are the x coordinates of all points of inflection on the interval 3 3 Justify your answer ty