Definite Integrals Questions and Answers
Calculus
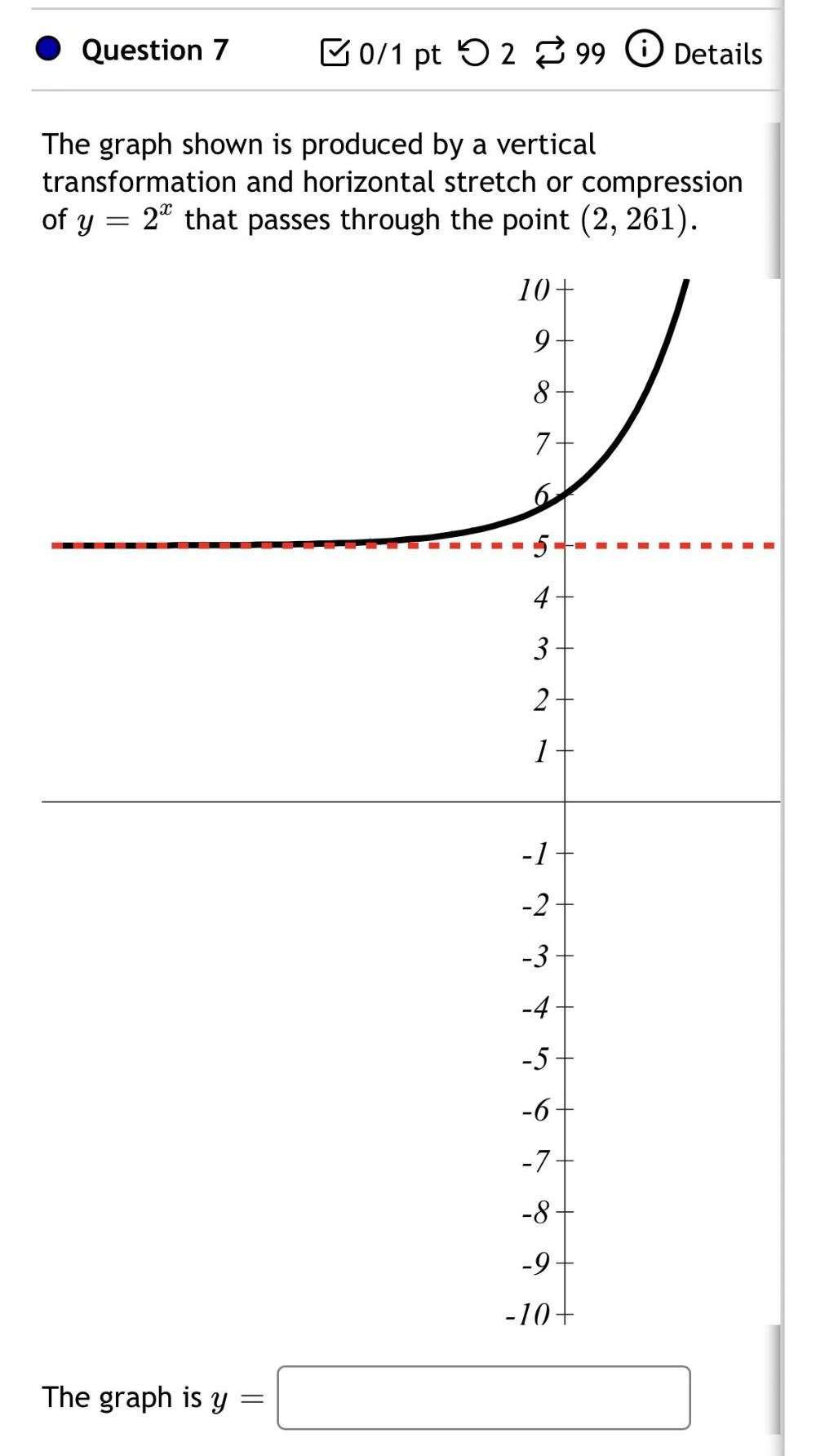
Definite IntegralsThe graph shown is produced by a vertical transformation and horizontal stretch or compression of y = 2 that passes through the point (2, 261).
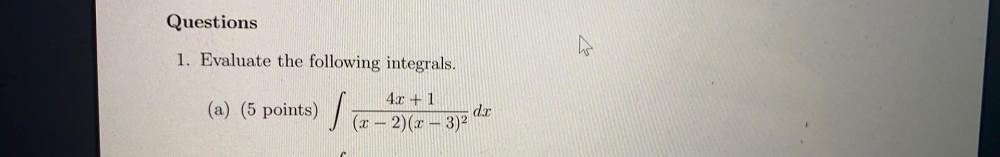

Calculus
Definite IntegralsSuppose the graphs of y=4x²-10x-9 and y=x³ + bx²-21 intersect at
x =2.
Find all intersection points.__________
(Enter your answer(s) as ordered pairs, separated by commas)
Calculus
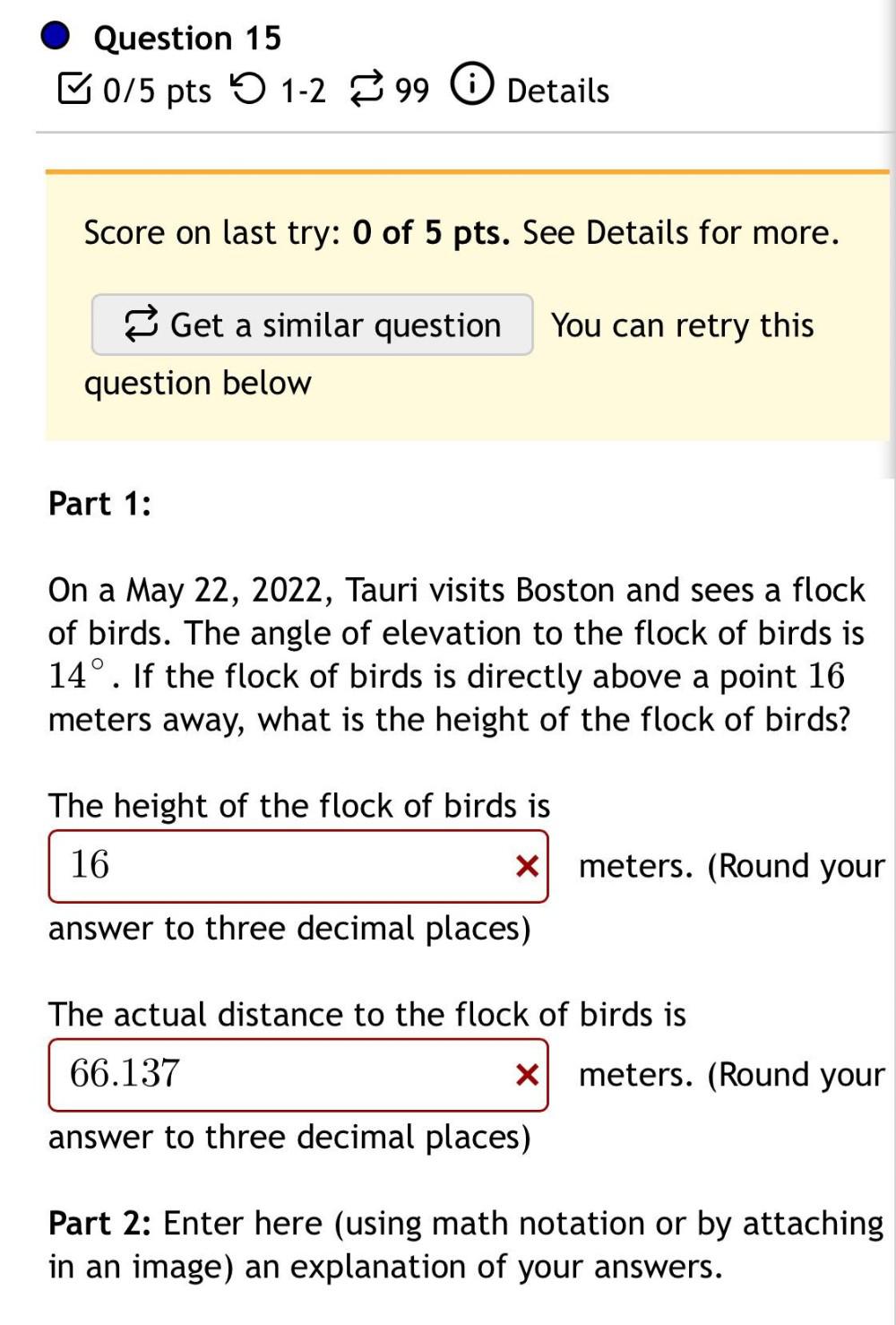
Definite IntegralsPart 1:
On a May 22, 2022, Tauri visits Boston and sees a flock of birds. The angle of elevation to the flock of birds is 14°. If the flock of birds is directly above a point 16 meters away, what is the height of the flock of birds?
The height of the flock of birds is _______ meters. (Round your answer to three decimal places)
The actual distance to the flock of birds is _______ meters. (Round your answer to three decimal places)
Part 2: Enter here (using math notation or by attaching in an image) an explanation of your answers.

Calculus
Definite IntegralsA publisher for a promising new novel figures fixed costs (overhead, advances, promotion, copy editing, typesetting, and so on) at $56,000, and variable costs (printing, paper, binding, shipping) at $1.90 for each book produced. If the book is sold to distributors for $14 each, how many must be produced and sold for the publisher to break even?
books to break even.
The publisher must produce and sell________books to break even.
(Round to the nearest integer as needed.)
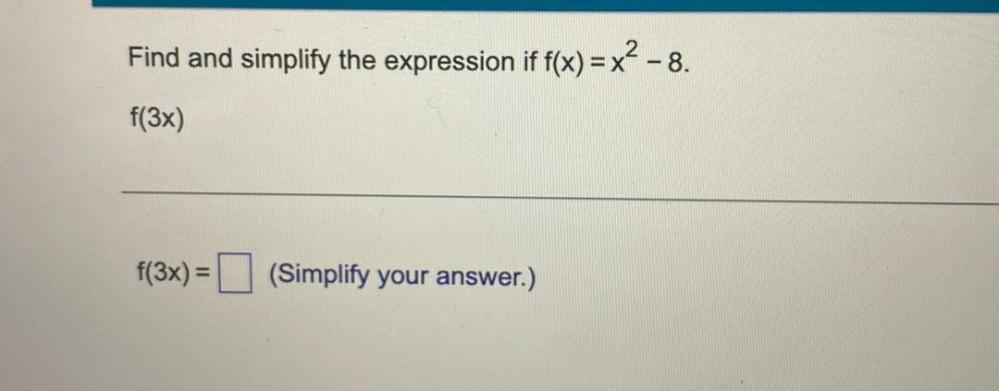
Calculus
Definite IntegralsFind and simplify the expression if f(x) = x² - 8.
f(3x)= ________ (Simplify your answer.)
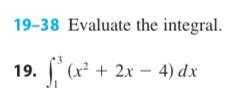
Calculus
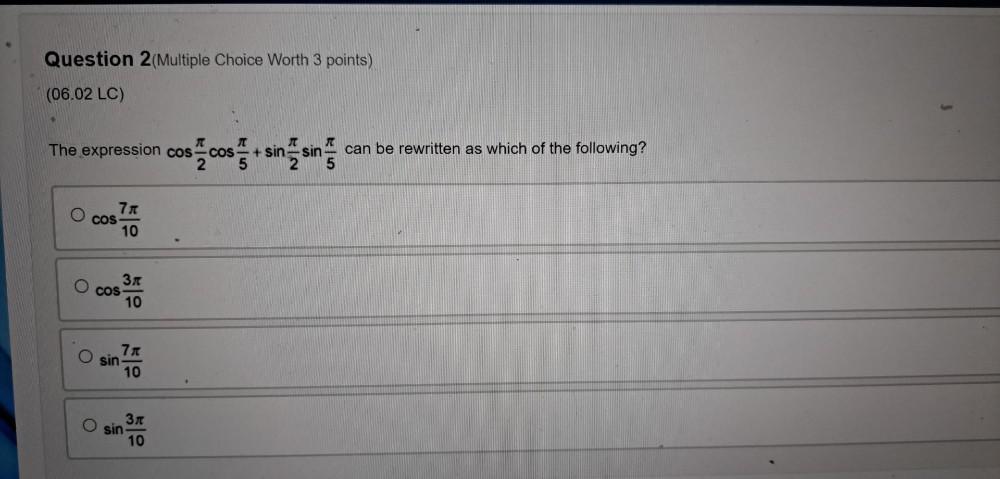
Definite IntegralsThe expression cos(π/2)cos(π/5) + sin(π/2)sin(π/5) can be rewritten as which of the following?
A) cos(7π/10)
B) cos(3π/10)
C) sin(7π/10)
D) sin(3π/10)
Calculus
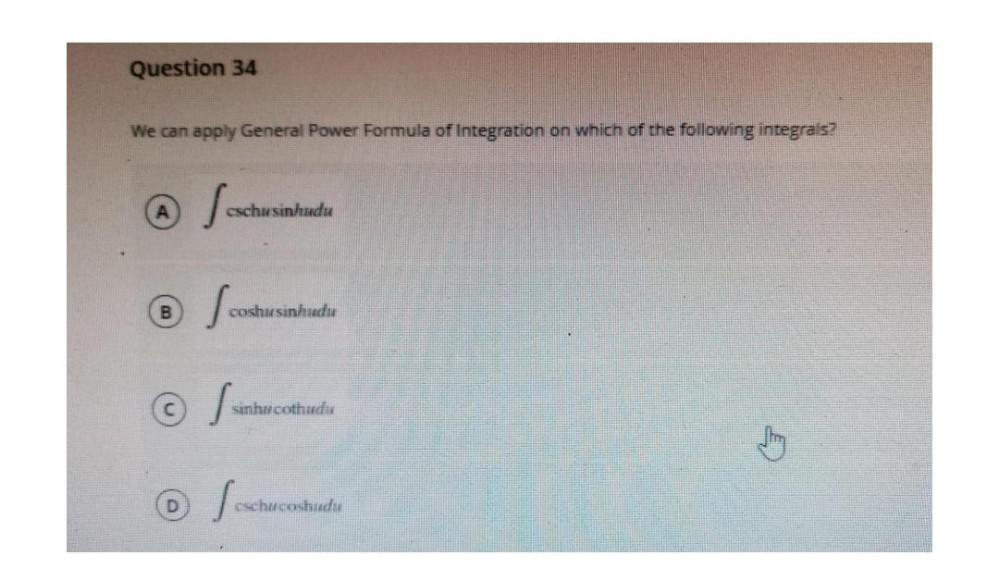
Definite IntegralsWe can apply General Power Formula of Integration on which of the following integrals?
(A) cschu sinhu du
(B) coshu sinhu du
(C) sinhu cothu du
(D) cschu coshu du

Calculus
Definite IntegralsUse a graph to give a rough estimate of the area of the region that lies beneath the given curve. Then find the exact area.
43. y = 3√x, 0 ≤ x ≤ 27
44. y = x^(-4), 1 ≤ x ≤ 6
45. y = sin x, 0 ≤ x ≤ π
46. y = (sec^2)x, 0 ≤ x ≤ π/3
![Express the limit as a definite integral on the given interval.
lim Σ(sinxi/(1+xi))Δx , [0,π ]](https://media.kunduz.com/media/sug-question/raw/79905411-1660162716.6883883.jpeg?w=256)
Calculus
Definite IntegralsExpress the limit as a definite integral on the given interval.
lim Σ(sinxi/(1+xi))Δx , [0,π ]

Calculus
Definite IntegralsThe area satisfying inequality is divided into three parts with the same area. What is the value of the area of this entire area? The inequality is 3-3sin0<=r<=2+sin30
(a)3^(1/2)-pi/3
(b)4*(3)^(1/2)-4pi/3
(c)2* (3)^(1/2)-2pi/3
(d)5*(3)^(1/2)-5pi/3


Calculus
Definite IntegralsEvaluate the definite integral.
0∫1 cos(πt/2) dt
0∫ 1 (1 + 7x)^(1/3) dx
0∫ π/6 sint/cos²tdt

Calculus
Definite IntegralsSketch the region enclosed by the curves and find its area: y = 12 - x², y = x² - 6
![Evaluate the ∫(2+x)/∛x² dx [1,8] integral
A particle moves along a line so that its velocity at time t is v(t) = t²-2t-3, 2≤t≤4](https://media.kunduz.com/media/sug-question/raw/80073592-1660161836.5536475.jpeg?w=256)
Calculus
Definite IntegralsEvaluate the ∫(2+x)/∛x² dx [1,8] integral
A particle moves along a line so that its velocity at time t is v(t) = t²-2t-3, 2≤t≤4
Calculus
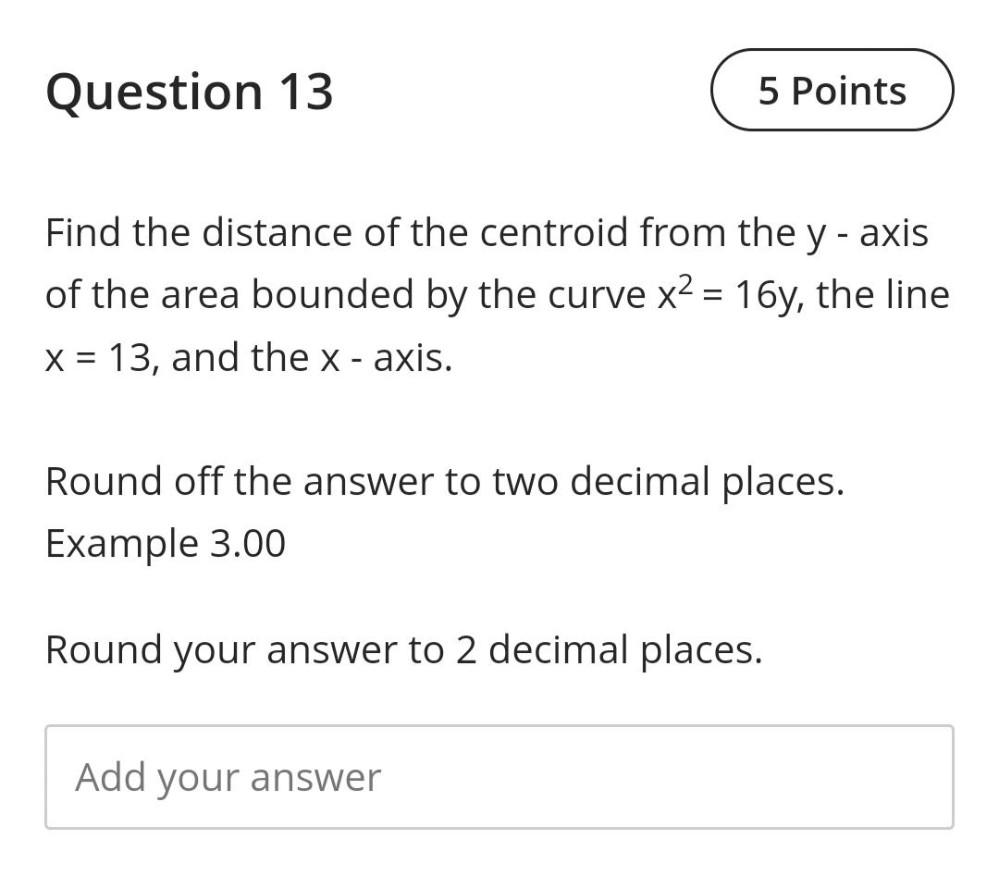
Definite IntegralsFind the distance of the centroid from the y - axis of the area bounded by the curve x² = 16y, the line x = 13, and the x - axis. Round off the answer to two decimal places. Example 3.00Round your answer to 2 decimal places.
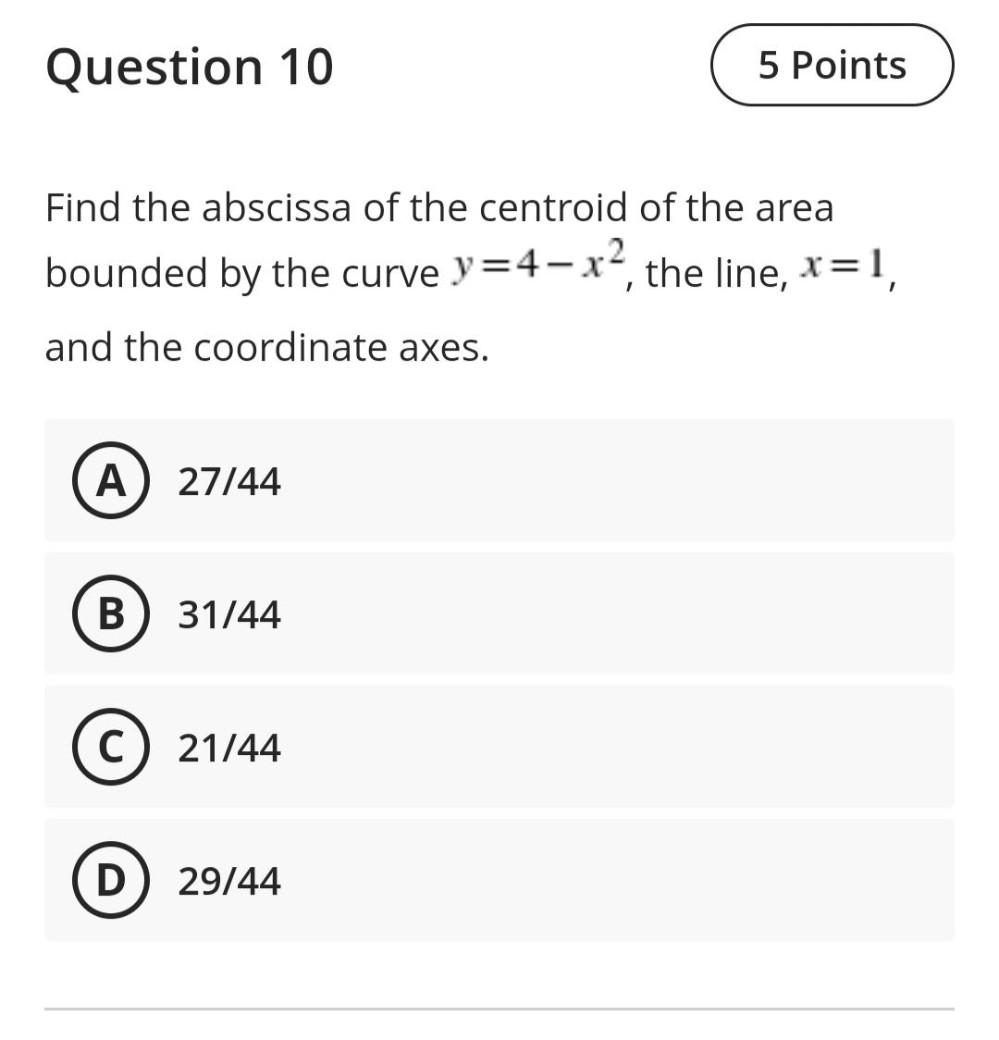
Calculus
Definite IntegralsFind the abscissa of the centroid of the area bounded by the curve y=4-x², the line, x=1, and the coordinate axes.
A) 27/44
B) 31/44
C) 21/44
D) 29/44

Calculus
Definite IntegralsMichelle has 19 coins in her pocket. She has $2.00 made up of nickels, dimes and quarters. She has twice as many nickels as dimes. Write a system of equations and then use matrices to determine how many of each coin Michelle has.
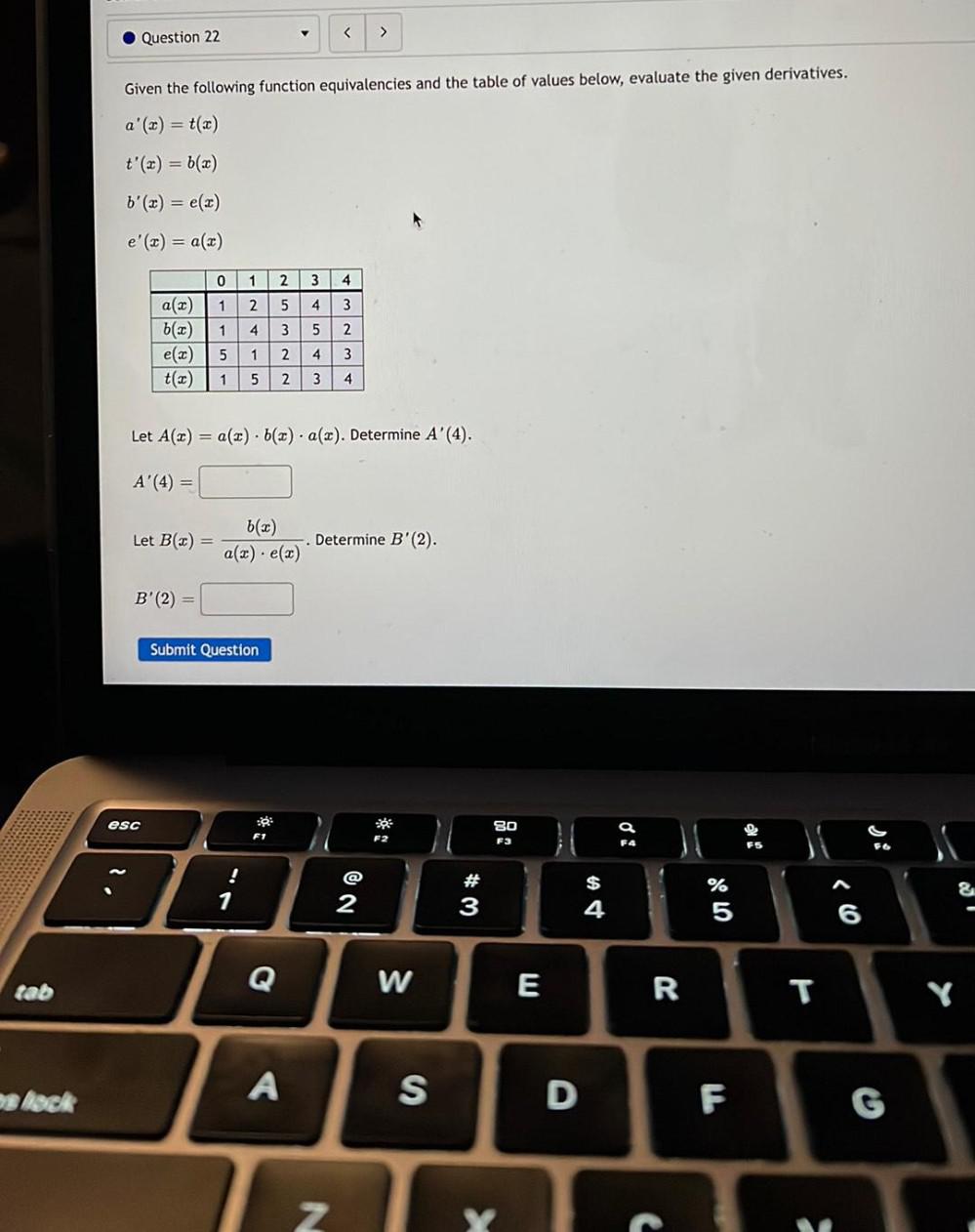
Calculus
Definite IntegralsGiven the following function equivalencies and the table of values below, evaluate the given derivatives.
a'(x) = t(x)
t'(x) = b(x)
b'(x) = e(x)
e'(x) = a(x)
0 1 2 3 4
a(x) 1 2 5 4 3
b(x) 1 4 3 5 2
e(x) 5 1 2 4 3
t(x) 1 5 2 3 4
Let A(x) = a(x) * b(x) * a(x). Determine A'(4).
A'(4) =
Let B(x) = b(x)/a(x) * e(x)
Determine B'(2).
B' (2) =

Calculus
Definite IntegralsFind the volume V of the solid obtained by rotating the region bounded by the given curves about the specified line.
2x = y², x = 0, y = 5; about the y-axis
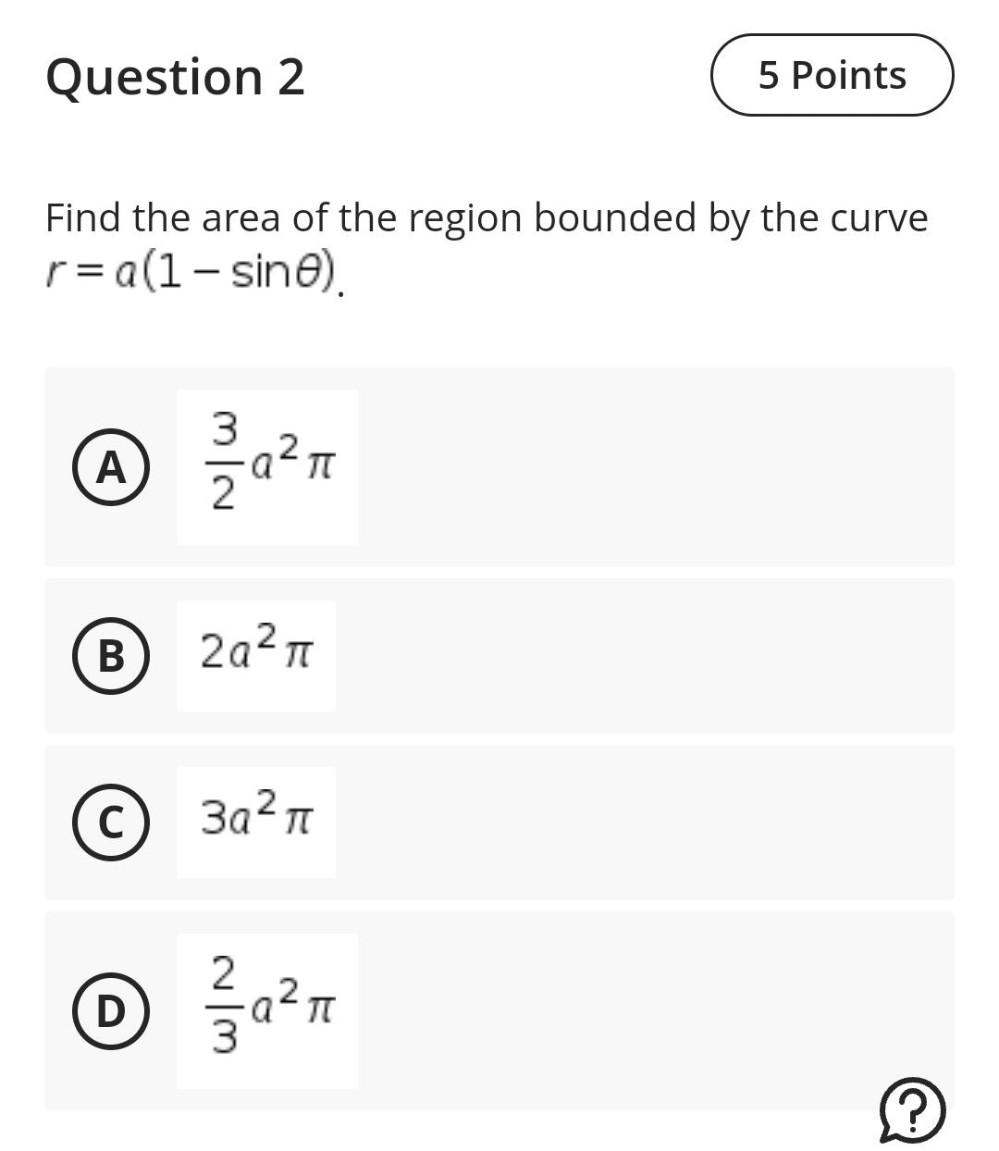
Calculus
Definite IntegralsFind the area of the region bounded by the curve r = a (1-sinθ).
A) (3/2)a²π
B) 2a²π
C) 3a²π
D)(2/3)a²π
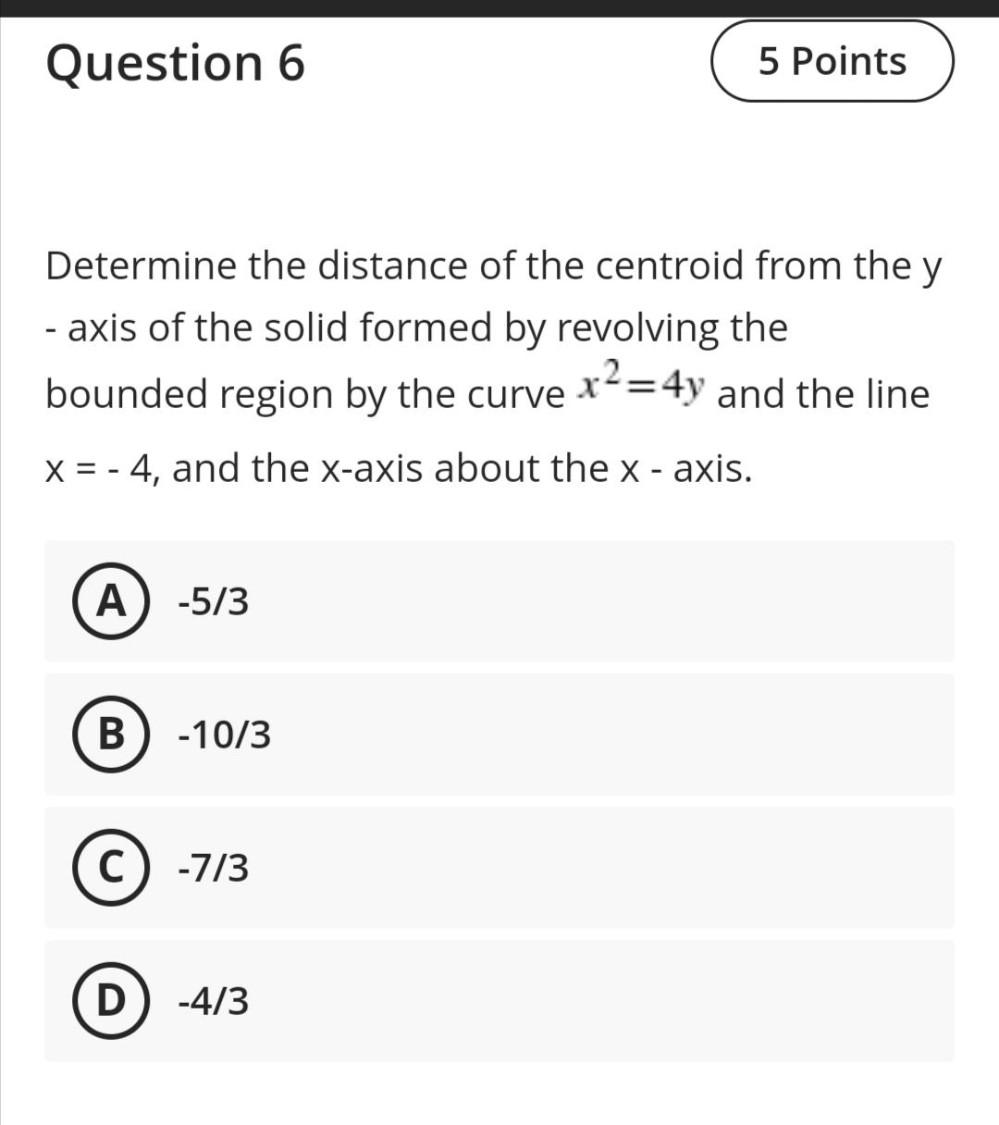
Calculus
Definite IntegralsDetermine the distance of the centroid from the y - axis of the solid formed by revolving the bounded region by the curve x²=4y and the line x = - 4, and the x-axis about the x - axis.
(A) -5/3
(B) -10/3
(C) -7/3
(D) -4/3
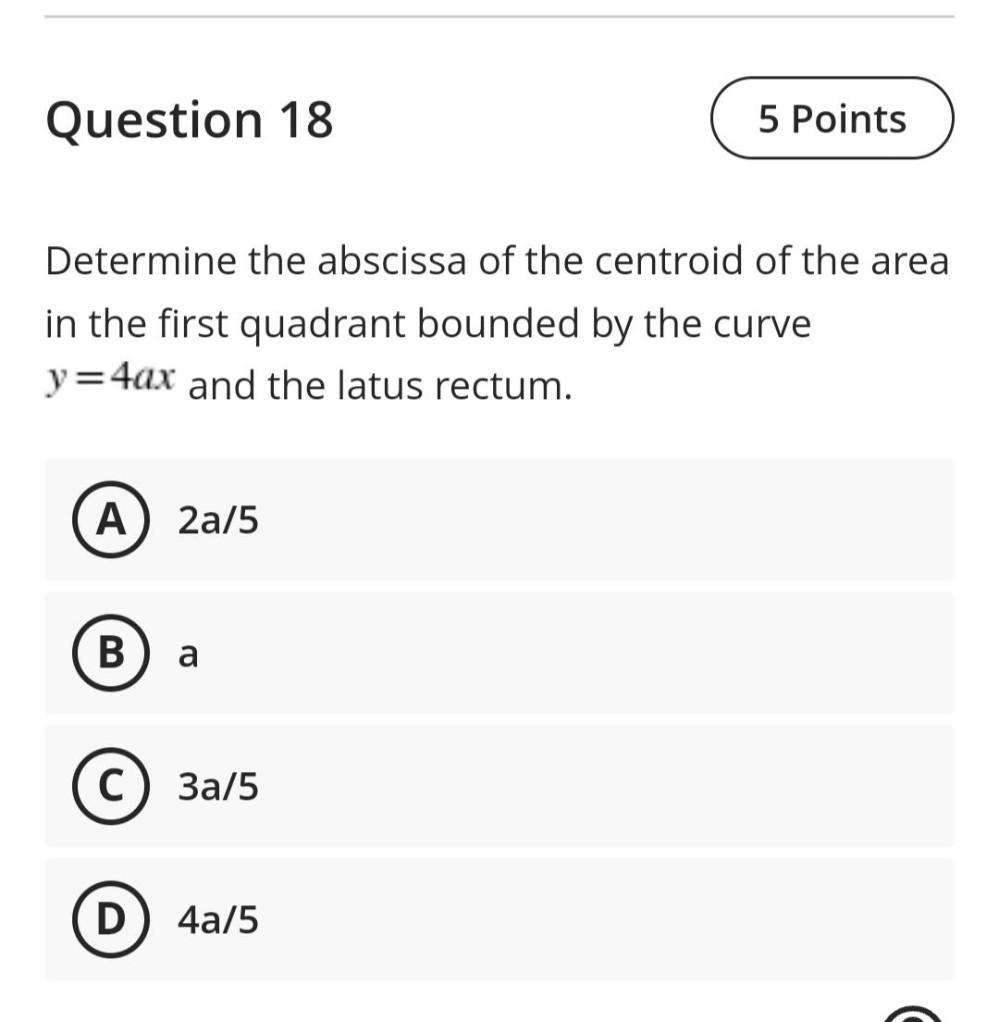
Calculus
Definite IntegralsDetermine the abscissa of the centroid of the area in the first quadrant bounded by the curve y=4ax and the latus rectum.
A) 2a/5
B) a
C) 3a/5
D) 4a/5

Calculus
Definite IntegralsA building has 100 apartments. When the rent is $1600 per month, all the apartments are occupied. However, when rent is $1700 per month, only 90 apartments are occupied. Assume the relationship between the rent, r, and the number of apartments rented (the demand, d) is linear. Write a linear equation that gives the demand d in terms of the rent.
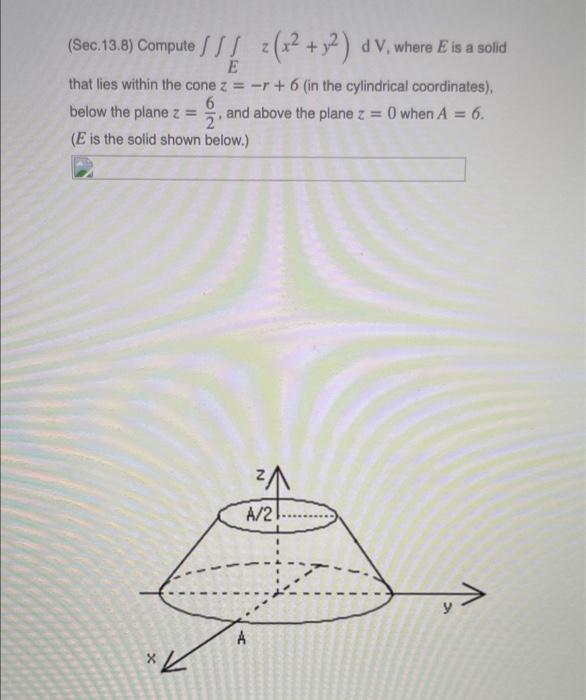
Calculus
Definite IntegralsCompute∫ ∫ ∫ z(x² + y2) d V, where E is a solid that lies within the cone
z = -r +6 (in the cylindrical coordinates),below the plane z = 6/2and above the plane z = 0 when A = 6.
Calculus
Definite IntegralsThe angle between 0° and 360° that is coterminal with the 1962° angle is ______ degrees.
Calculus
Definite IntegralsFind an equation of the circle that has center (5, -1) and passes through (1, -6).

Calculus
Definite IntegralsConsider a 10 in x 10 in squared piece of paper. We want to cut off squares from the corners to make a topless box,
1. If the squares have side x, write a function f(x) that gives the volume of the box.
2. Find the critical points of f(x).
3. Find the maximum of f(x).

Calculus
Definite IntegralsLet S be the square in the x y-plane shown in the figure below, oriented with the normal pointing in the positive z-direction. Estimate
∫∫F. dS where F is a vector field whose values at the labeled points are
F(A) =(4,1,-2)
F(B)= (1,6,9)
F(C)=(6,-3,-5)
F(D)= (9,3,9)

Calculus
Definite IntegralsDetermine the anti-derivative of e³ˣ + 5x - 2
a) e³ˣ + 5x² - 2x + c
b) e³ˣ/3 + 5x²/2 - 2 + c
c) e³ˣ/3 + 5x² - 2x + c
d) e³ˣ/3 + 5x²/2 - 2x + c
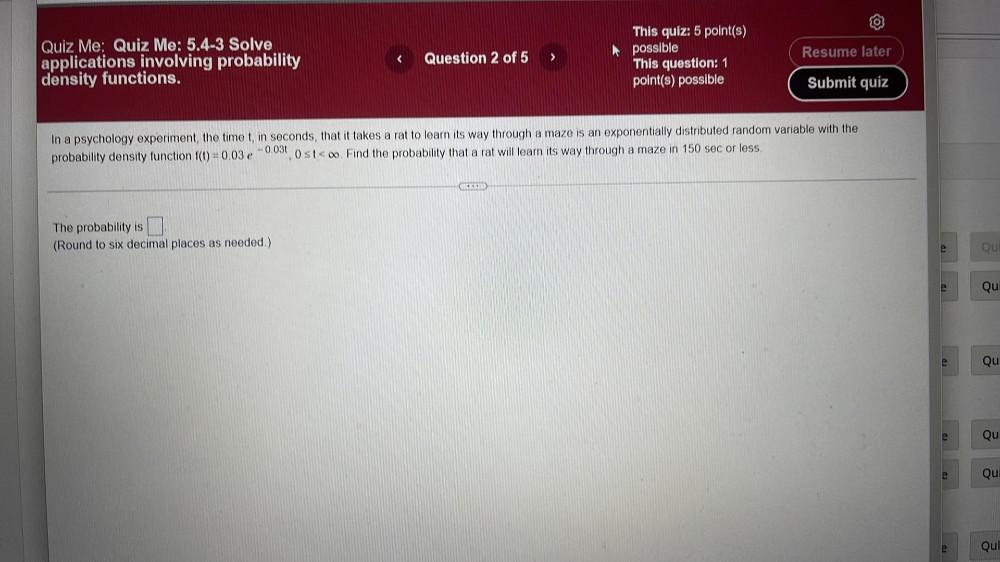
Calculus
Definite IntegralsIn a psychology experiment, the time t, in seconds, that it takes a rat to learn its way through a maze is an exponentially distributed random variable with the probability density function f(t) = -0.03e‾⁰⁰³ᵗ , 0≤t<∝. Find the probability that a rat will learn its way through a maze in 150 sec or less.
The probability is ______
(Round to six decimal places as needed.)
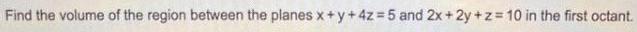
Calculus
Definite IntegralsFind the volume of the region between the planes x+y+4z=5 and 2x+2y+z=10 in the first octant.
![For the given probability density function, over the stated interval, find the requested value.
f(x)=(1/3)x², over the interval [-2.1]. Find E(x²).
A. 7/3
B.-5/4
* C. -31/15
D. 11/5](https://media.kunduz.com/media/sug-question/raw/82019713-1660069668.1715121.jpeg?w=256)
Calculus
Definite IntegralsFor the given probability density function, over the stated interval, find the requested value.
f(x)=(1/3)x², over the interval [-2.1]. Find E(x²).
A. 7/3
B.-5/4
* C. -31/15
D. 11/5
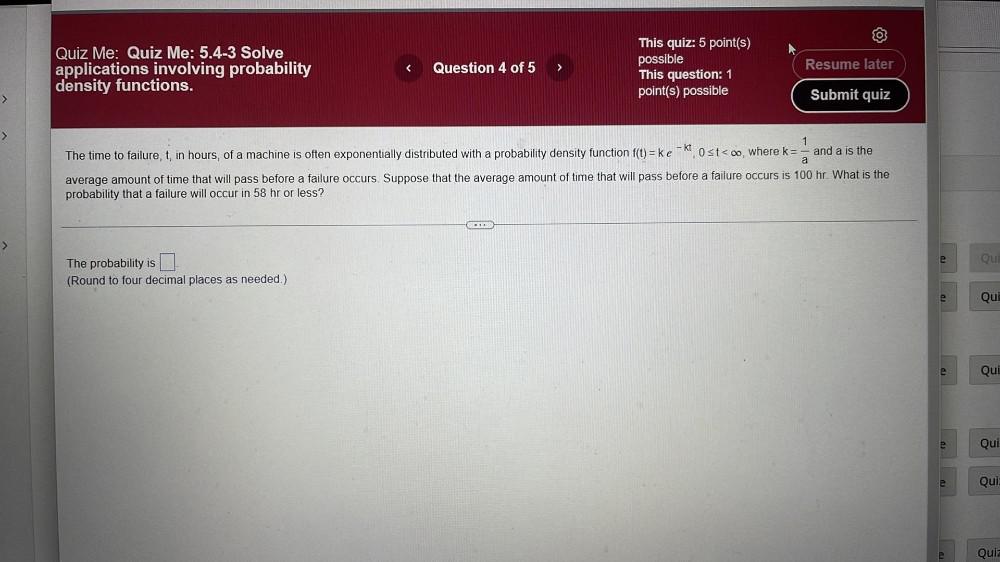
Calculus
Definite IntegralsThe time to failure, t, in hours, of a machine is often exponentially distributed with a probability density function f(t) = ke⁻ᵏᵗ, 0≤t<∞, where k=1/a and a is the average amount of time that will pass before a failure occurs. Suppose that the average amount of time that will pass before a failure occurs is 100 hr. What is the probability that a failure will occur in 58 hr or less? The probability is____ (Round to four decimal places as needed.)

Calculus
Definite IntegralsUse the washer method to find the volume of revolution generated by revolving the region bounded by the graphs of y = 2x²,y = 8, and the y-axis about the x-axis.
(Express numbers in exact form. Use symbolic notation and fractions where needed.)
![A number x is selected at random from the interval [4,20]. The probability density function for x is given by the following function. Find the probability that a number selected is in the subinterval [6,15]. 1 16 f(x) = for 4 ≤x≤20. How is the probability that a number selected is in the subinterval [6,15] calculated? A. Integrate B. Evaluate C. Evaluate D. Integrate The probability is 1 twice, then evaluate the integral over the limits 6 and 15. 16 1 over the limits 6 and 15, then add. 16 1 over the limits 6 and 15, then subtract. 16 1 then evaluate the integral over the limits 6 and 15. 16](https://media.kunduz.com/media/sug-question/raw/84763861-1659864784.7234569.jpeg?w=256)
Calculus
Definite IntegralsA number x is selected at random from the interval [4,20]. The probability density function for x is given by the following function. Find the probability that a number selected is in the subinterval [6,15]. 1 16 f(x) = for 4 ≤x≤20. How is the probability that a number selected is in the subinterval [6,15] calculated? A. Integrate B. Evaluate C. Evaluate D. Integrate The probability is 1 twice, then evaluate the integral over the limits 6 and 15. 16 1 over the limits 6 and 15, then add. 16 1 over the limits 6 and 15, then subtract. 16 1 then evaluate the integral over the limits 6 and 15. 16

Calculus
Definite IntegralsThis question: 1 point(s) possible The distance x, in feet, between successive cars on a certain stretch of highway has the following probability density function, where k = 1/a and a is the average distance, in feet, between successive cars over some period of time. f(x)=ke -kx for 0≤x<co A transportation planner determines that the average distance between cars on a certain highway is 60 ft. What is the probability that the distance between two successive cars, chosen at random, is 40 ft or less? P(0≤x≤40)= (Round the final answer to four decimal places as needed. Round all intermediate values to four decimal places as needed.)
![A dart is thrown at a number line in such a way that it always lands in the interval [0,10]. Let x represent the number that the dart hits. Suppose that the probability density function for x is given by the following function. f(x)= -x, for 0 ≤x≤ 10 1 50 Find P(8≤x≤ 9), the probability that the dart lands in [8,9]. How is the probability that the dart lands in [8,9] found? 1 A. Evaluate the expression 50x over the limits 8 and 9, then add. 1 B. Integrate x twice, then evaluate the integral over the limits 8 and 9. 50 1 50 -x over the limits 8 and 9, then subtract. D. Integrate C. Evaluate the expression 1 50 -x, then evaluate the integral over the limits 8 and 9. P(8≤x≤9)= (Type an integer or a simplified fraction.)](https://media.kunduz.com/media/sug-question/raw/84763425-1659863604.7356806.jpeg?w=256)
Calculus
Definite IntegralsA dart is thrown at a number line in such a way that it always lands in the interval [0,10]. Let x represent the number that the dart hits. Suppose that the probability density function for x is given by the following function. f(x)= -x, for 0 ≤x≤ 10 1 50 Find P(8≤x≤ 9), the probability that the dart lands in [8,9]. How is the probability that the dart lands in [8,9] found? 1 A. Evaluate the expression 50x over the limits 8 and 9, then add. 1 B. Integrate x twice, then evaluate the integral over the limits 8 and 9. 50 1 50 -x over the limits 8 and 9, then subtract. D. Integrate C. Evaluate the expression 1 50 -x, then evaluate the integral over the limits 8 and 9. P(8≤x≤9)= (Type an integer or a simplified fraction.)

Calculus
Definite IntegralsSolve the rational equation.
3/X + 3/ X-6 = 3X-15/X-6
{- , 5/2,1/3)
θ
{1}
{1,6}

Calculus
Definite IntegralsFind the cumulative density function for the given probability density function.
1
f(x)=, for 4 ≤x≤8
F(x)=, for 4 ≤x≤8
![Let g(u) = 2 + 12u
Determine the average value, g(c), of g over [1, 2].
g(c) =
Determine the value(s) of c in [1, 2] guaranteed by the Mean Value Theorem.](https://media.kunduz.com/media/sug-question/raw/84726645-1659833906.829607.jpeg?w=256)
Calculus
Definite IntegralsLet g(u) = 2 + 12u
Determine the average value, g(c), of g over [1, 2].
g(c) =
Determine the value(s) of c in [1, 2] guaranteed by the Mean Value Theorem.
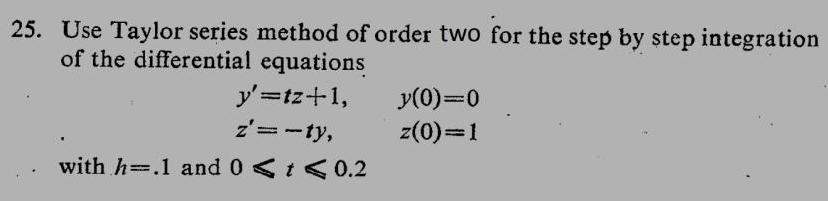
Calculus
Definite IntegralsUse Taylor series method of order two for the step by step integration of the differential equations
y'=tz+1, y(0)=0
z'= -ty, z(0)=1
with h= .1 and 0 < t < 0.2

Calculus
Definite IntegralsEvaluate the double integral
∫∫Rf(x, y) dA
for the function f(x, y) and the region R.
f(x, y) = 5x²y2; R is bounded by x = 0, x = 1, y = x², and y = x³.

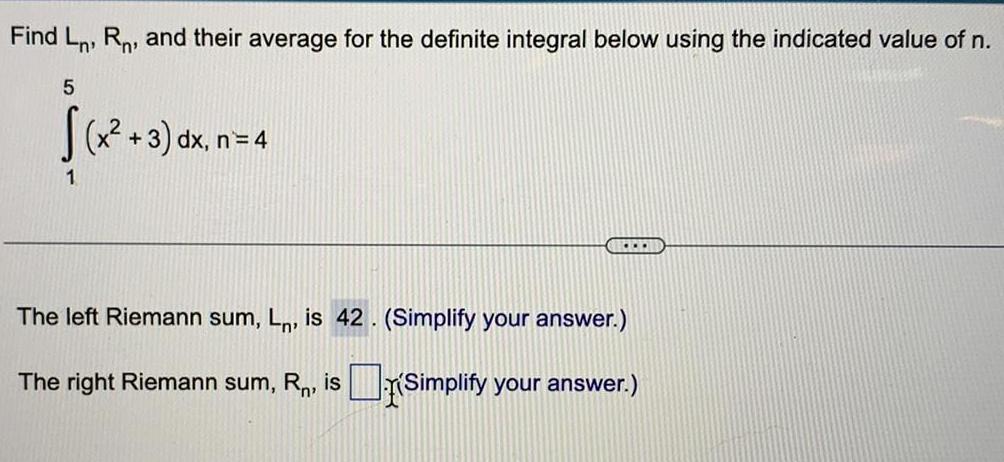
Calculus
Definite IntegralsFind Ln, Rn, and their average for the definite integral below using the indicated value of n.
5
∫(x²+3) dx, n = 4
1
The left Riemann sum, Ln, is (Simplify your answer.)
The right Riemann sum, R₁, is (Simplify your answer.)

Calculus
Definite IntegralsFind the derivative of the function f(x) = -4 -4 cos(x).
f'(x) = -4x+4 sin(x)
f'(x) = -8x+4 sin(x)
f'(x) = -8x + 4 cos(x)
f'(x) = -8x - 4 sin(x)
f'(x) = -8x-4 cos(x)
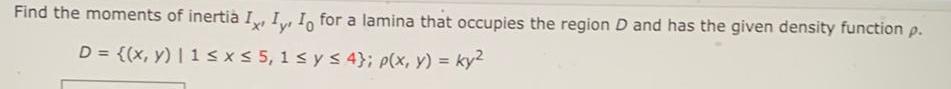
Calculus
Definite IntegralsFind the moments of inertia Ix, Iy, I0 for a lamina that occupies the region D and has the given density function p.
D = {(x, y) | 1 ≤ x ≤ 5, 1 ≤ y ≤ 4}; p(x, y) = ky²

Calculus
Definite IntegralsFind the average value of f over the region D.
f(x, y) = 4xy, D is the triangle with vertices (0, 0), (1, 0), and (1, 6)
