Definite Integrals Questions and Answers

Calculus
Definite IntegralsEvaluate the double integral by first identifying it as the volume of a solid. ∫∫D (3x +2y+6)dA where D = {(x, y)| -1 ≤ x ≤ 1,-2 ≤ y ≤ 2}.

Calculus
Definite IntegralsGiven that f(x, y) = -x + 1 and D is the triangular region with vertices
(0, 0), (0, 2), (6, 2), set up two integrals which evaluate the volume between the region D and the surface f(x, y) in two different ways.
Do not evaluate these two integrals.

Calculus
Definite IntegralsEvaluate the first partial derivatives of the function at the given point.
f(x, y) = 8ex In(y); (0, e)
f(0, e) =
f(0, e) =
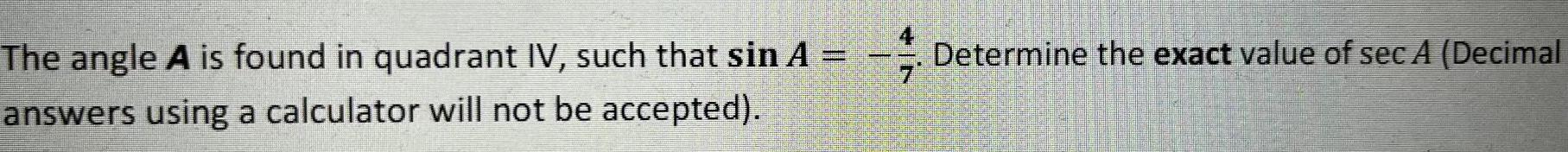
Calculus
Definite IntegralsThe angle A is found in quadrant IV, such that sin A = -4 7 Determine the exact value of sec A (Decimal answers using a calculator will not be accepted).
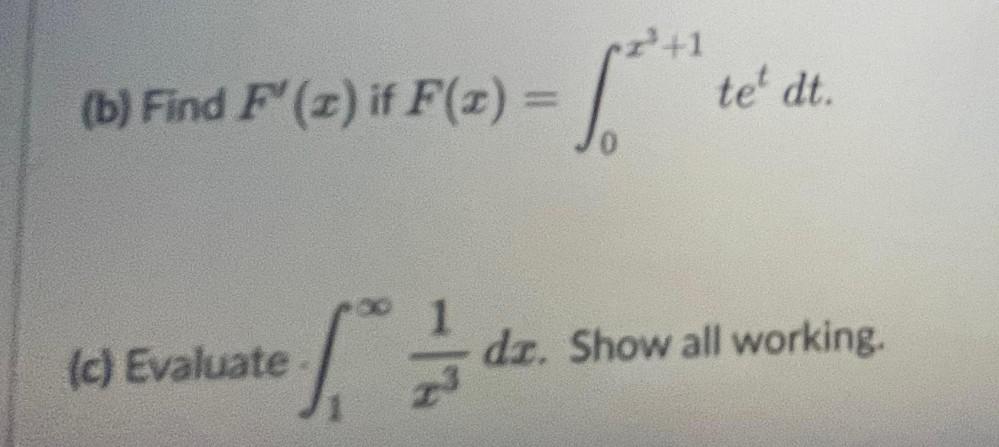
Calculus
Definite IntegralsFind F' (x) if F(x) = ₀∫x²+1 teᵗ dt.
Evaluate 1∫∞ 1/x³ dx. Show all working.
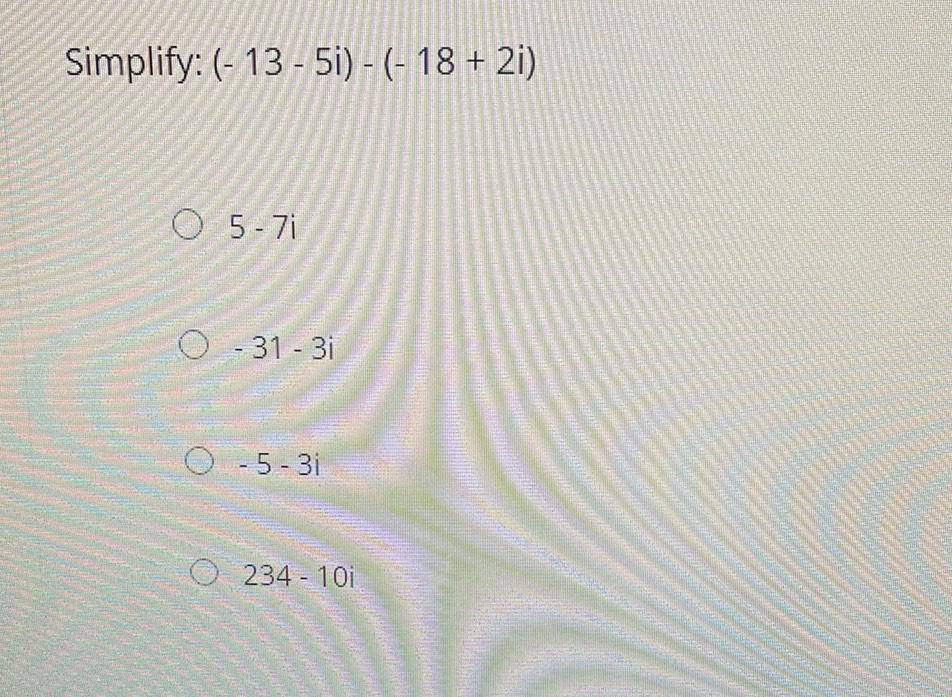

Calculus
Definite IntegralsUse the disk method to find the volume of the solid of revolution formed by revolving the region underneath y = 2x² around the x-axis from z = 0 to z = 4. Draw a sketch.

Calculus
Definite IntegralsSet up (but do not compute) the integrals that would represent the area of the region bounded between the two curves y = x³ and y = x² + x. Set the two functions equal to each other to determine the limits of integration. Use a graphing software or calculator to see a picture of the situation. Note that the upper and lower function will change along the interval!
Note: I am just having you set up and not compute the integrals because you should notice that the limits of integration are not particularly nice for this question!

Calculus
Definite IntegralsIf A = 2yzi - (x + 3y − 2)j + (x² + z)k, evaluate ∫∫(▽ x A). n dS, over surface of intersection of the cylinders x² + y² = a², x² + z² = a², which is included in the first octant.

Calculus
Definite IntegralsPlease estimate the area under the curve c(x) = 1 - x³ for 0 ≤ x ≤ 1 using 4 rectangles with width 1/4.
Please show a sketch of the curve, the rectangles, and calculations. (A calculator is allowed.)
![Determine a particular solution for the differential equation
dy/dt + 2y = 2/π ₀∫∞ [sin(3ω) - 3ω cos(3ω) / ω²] sin(ωt) dω.](https://media.kunduz.com/media/sug-question/raw/83925019-1658664914.4968534.jpeg?w=256)
Calculus
Definite IntegralsDetermine a particular solution for the differential equation
dy/dt + 2y = 2/π ₀∫∞ [sin(3ω) - 3ω cos(3ω) / ω²] sin(ωt) dω.
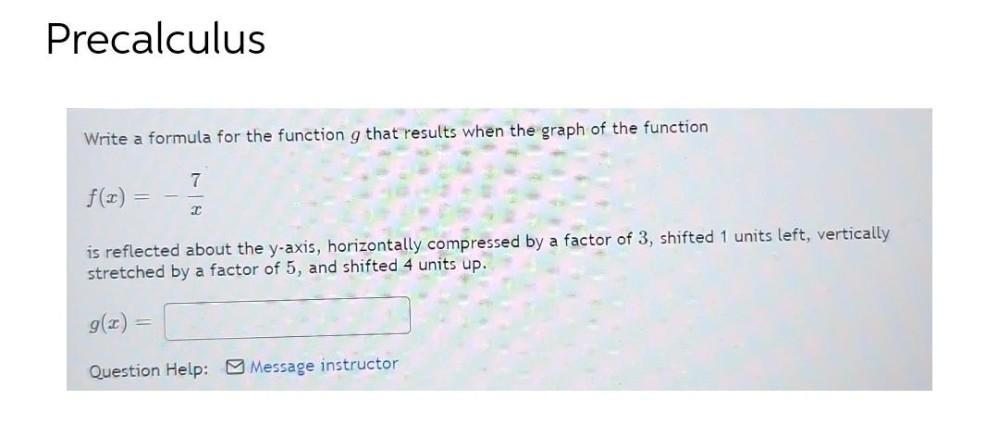
Calculus
Definite IntegralsWrite a formula for the function g that results when the graph of the function
f(x)=-7/x
is reflected about the y-axis, horizontally compressed by a factor of 3, shifted 1 units left, vertically stretched by a factor of 5, and shifted 4 units up.
g(x) =

Calculus
Definite IntegralsCompute ∫c F .dr where F(x, y) = (-y³, x³) and C is the counterclockwise oriented unit circle.
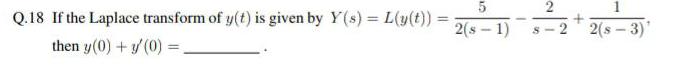
Calculus
Definite IntegralsQ.18 If the Laplace transform of y(t) is given by Y(s) = L(y(t)) = 5/2(s-1)-2/(s-2)+1/2(s-3)
then y(0) + y'(0) =
![2 For the given probability density function, over the stated interval, find the requested value.
f(x) = x, over the interval [1,3]. Find E(x).
A. 13/6
B. 25/12
C. 9/4
D. 5/8](https://media.kunduz.com/media/sug-question/raw/84567173-1658663490.4479268.jpeg?w=256)
Calculus
Definite Integrals2 For the given probability density function, over the stated interval, find the requested value.
f(x) = x, over the interval [1,3]. Find E(x).
A. 13/6
B. 25/12
C. 9/4
D. 5/8
![Determine whether or not the function is a probability density function over the given interval.
f(x) = 1/5x, [1,4]
Yes
No](https://media.kunduz.com/media/sug-question/raw/84567205-1658663422.978497.jpeg?w=256)
Calculus
Definite IntegralsDetermine whether or not the function is a probability density function over the given interval.
f(x) = 1/5x, [1,4]
Yes
No
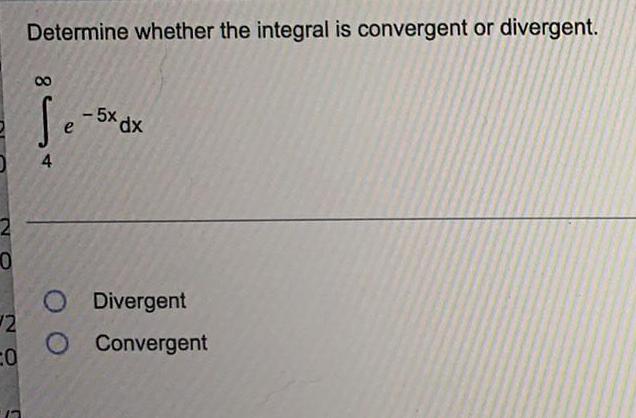
Calculus
Definite IntegralsDetermine whether the integral is convergent or divergent.
∫e^-5x dx (4 to ∞)
Divergent
Convergent
![Use a definite integral to find an expression that represents the area of the region between the given curve and the x-axis on the interval [0, b].
15) y = 6x
Compute the definite integral as the limit of Riemann sums.](https://media.kunduz.com/media/sug-question/raw/84616852-1658661095.1126306.jpeg?w=256)
Calculus
Definite IntegralsUse a definite integral to find an expression that represents the area of the region between the given curve and the x-axis on the interval [0, b].
15) y = 6x
Compute the definite integral as the limit of Riemann sums.

Calculus
Definite IntegralsA curve, described by x² + y² + 6y = 0, has a point A at (-3, -3) on the curve.
Part A: What are the polar coordinates of A? Give an exact answer.
Part B: What is the polar form of the equation? What type of polar curve is this?
Part C: What is the directed distance when θ: 4π/3? Give an exact answer.

Calculus
Definite IntegralsLet ∫ h(x)dx = 252 ∫ h(x) dx = − 144
Use the given definite integrals above to evaluate each definite integral below.
∫ - 2h(x) dx =
∫ - 3h(x) dx
∫ h(x)/9 dx
∫ h(x) dx =

Calculus
Definite IntegralsConsider
∫g(x)dx (1to-9) - ∫g(x)dx(-8to-9)
Use properties of definite integrals to rewrite the expression above as a single definite integral.

Calculus
Definite IntegralsLet g(x) = ∫2dt (x to-2)
Use the limit definition of the definite integral to evaluate the following expressions.
g(-2) =
g(-4)=
g(5) =
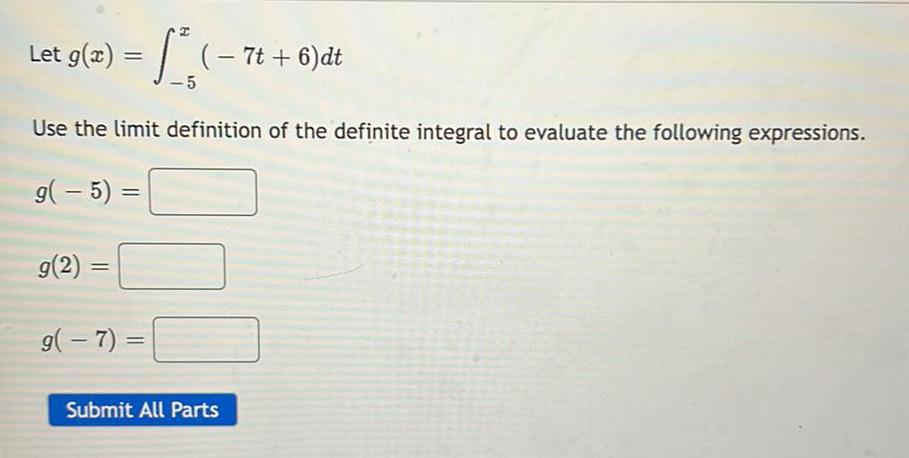
Calculus
Definite IntegralsLet g(z) = ∫( − 7t + 6)dt
Use the limit definition of the definite integral to evaluate the following expressions.
g(-5)=
g(2)=
g(-7)=

Calculus
Definite IntegralsUse cylindrical coordinates.
Find the mass and center of mass of the S solid bounded by the paraboloid z= 10x^2 + 10y2 and the plane z = a (a > 0) if S has constant density K.
m=
![Find E(x), E(x²), the mean, the variance, and the standard deviation of the random variable whose probability density function is given below. f(x) = 1/72x, [0,12]](https://media.kunduz.com/media/sug-question/raw/84606428-1658499706.6557586.jpeg?w=256)
Calculus
Definite IntegralsFind E(x), E(x²), the mean, the variance, and the standard deviation of the random variable whose probability density function is given below. f(x) = 1/72x, [0,12]
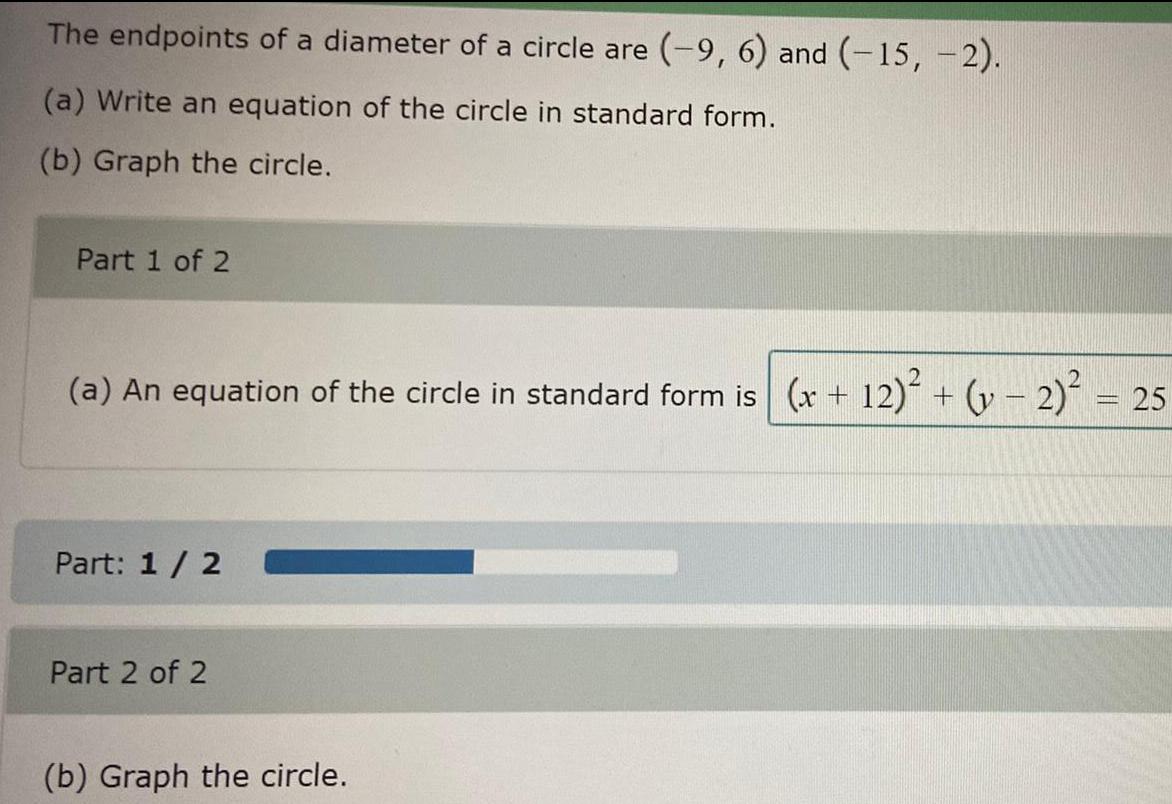
Calculus
Definite IntegralsThe endpoints of a diameter of a circle are (-9, 6) and (-15, -2).
(a) Write an equation of the circle in standard form.
(b) Graph the circle.
Part 1 of 2
(a) An equation of the circle in standard form is
Part: 1 / 2
Part 2 of 2
(b) Graph the circle.
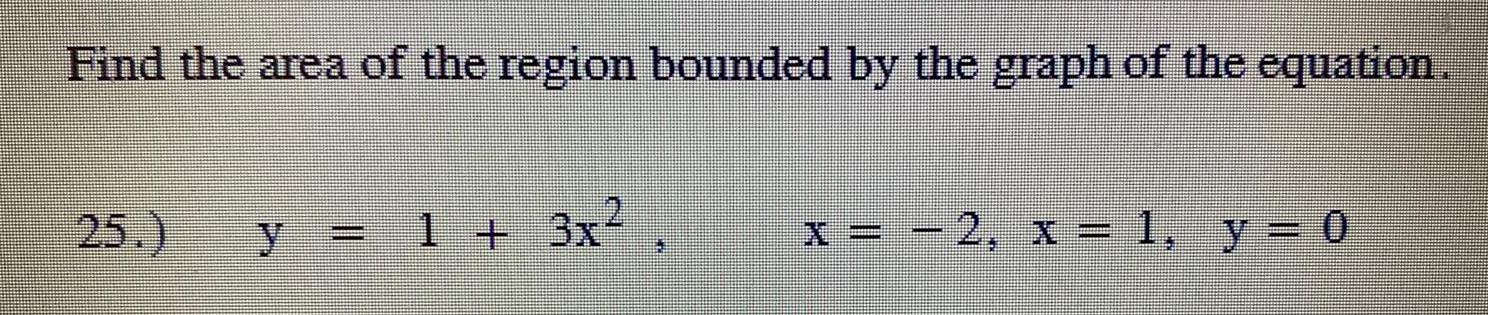
Calculus
Definite IntegralsFind the area of the region bounded by the graph of the equation.
25.) y = 1 + 3x² x = -2, x = 1, y = 0
Calculus
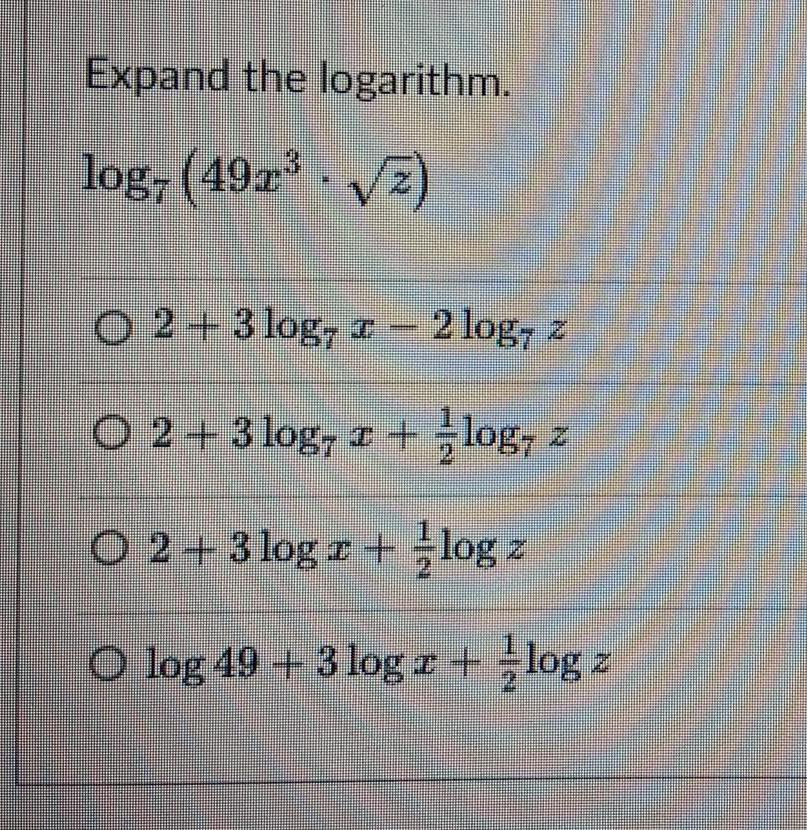
Definite IntegralsExpand the logarithm.
log7(49x³-√z)
2+3 log7 x - 2 log7 z
2+3 log7 x + 1 2log7 z
2+3 log x + 1 2log z
log 49 + 3 log x + 1 2log z
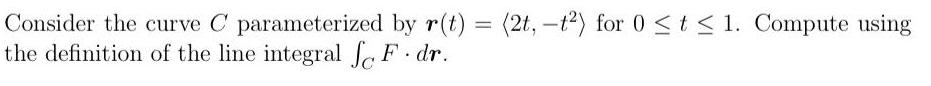
Calculus
Definite IntegralsConsider the curve C parameterized by r(t) = (2t, -t2) for 0 ≤ t ≤ 1. Compute using the definition of the line integral ∫cF.dr.
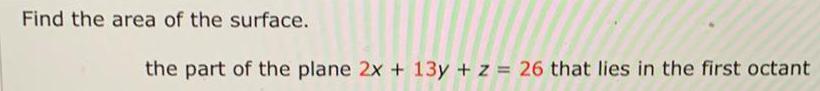
Calculus
Definite IntegralsFind the area of the surface.
the part of the plane 2x + 13y + z = 26 that lies in the first octant

Calculus
Definite Integrals(Coding) In this problem we will find the exponential of best fit (y = c1ec2t) through the points
(1, 2), (2, 2), (3, 7), (4, 10), (5. 17).
(a) Find the vector of equations r and the Jacobian Dr.
(b) Determine (with justification) some initial guess x0
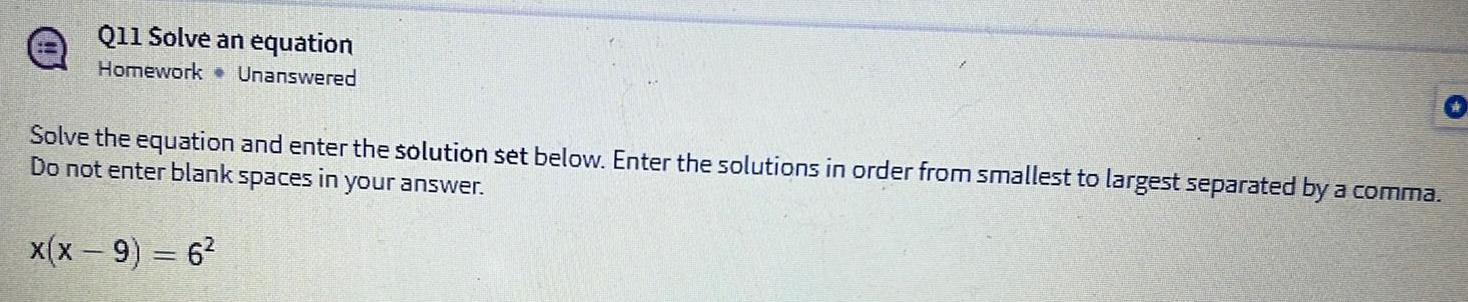
Calculus
Definite IntegralsSolve the equation and enter the solution set below. Enter the solutions in order from smallest to largest separated by a comma. Do not enter blank spaces in your answer.
x(x - 9) = 6²2

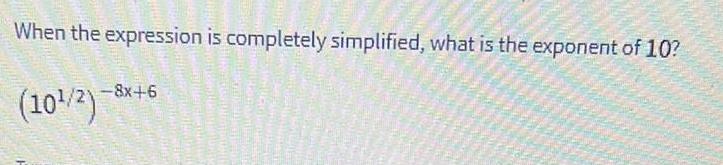
Calculus
Definite IntegralsWhen the expression is completely simplified, what is the exponent of 10?
(10¹/2)
-8x+6
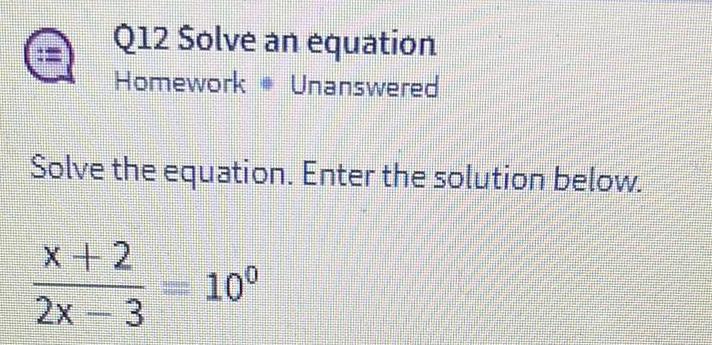

Calculus
Definite IntegralsSimplify the expression. What exponent of 3 results? Do not enter any blank spaces i in your answer.
(3-4)3-x

Calculus
Definite IntegralsFind the standard equation for the positions of a body moving with a constant acceleration a along a coordinate
The following properties are known:
i. d²s dt² = a,
ii. ds dt = v0 when t = 0, and
iii. s = s0 when t = 0,
where t is time, s0 is the initial position, and v0 is the initial velocity.
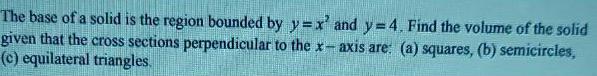
Calculus
Definite IntegralsThe base of a solid is the region bounded by y=x' and y=4. Find the volume of the solid given that the cross sections perpendicular to the x-axis are: (a) squares, (b) semicircles, (c) equilateral triangles.

Calculus
Definite IntegralsConsider the following function.
f(x) = cos (8x 9)
Find the derivative of the function.
Use the derivative to determine whether the function is strictly monotonic on its entire domain and therefore has an inverse function.
The given function is f(x) = cos(8x 9) Differentiate f(x) with respect to x.
The function f(x) is strictly monotonic, if f '(x) is f '(x) > 0 or f '(x) < 0✔ f'(x) > 0 or f '(x) < 0 on the domain of f(x). Also to be strictly monotonic, the function f(x) should not take the same value for different values of x. That is,
f(x₁) = f(x₂) if X₁ ≠ X2

Calculus
Definite IntegralsFind the volume of the solid E described by the solution of this system of inequalities:
x² + y² ≤ 1
x² +2² ≤1
y² +z²≤1

Calculus
Definite IntegralsFind the moments of inertia I, I, Io for a lamina in the shape of an isosceles right triangle with equal sides of length a if the density at any point is proportional to the square of the distance from the vertex opposite the hypotenuse. (Assume that the coefficient of proportionality is k, and that the lamina lies in the region bounded by x = 0, y = 0, and y = a - x).
Ix =
Iy=
Io=
![Find E(x), E(x²), the mean, the standard deviation and variance, over the given interval, of the random variable whose probability density function is given below.
f(x) = 1 4, [3,7]](https://media.kunduz.com/media/sug-question/raw/84513655-1658279129.8822439.jpeg?w=256)
Calculus
Definite IntegralsFind E(x), E(x²), the mean, the standard deviation and variance, over the given interval, of the random variable whose probability density function is given below.
f(x) = 1 4, [3,7]

Calculus
Definite IntegralsUse Newton's method to approximate the indicated solution of the equation correct to six decimal places.
the positive solution of e³x = x + 8
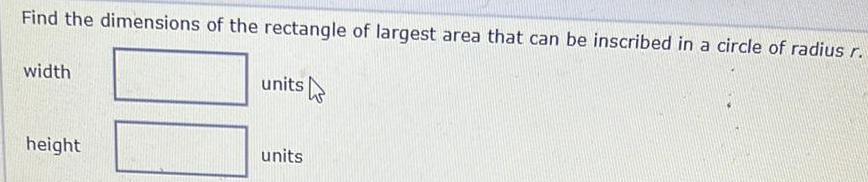
Calculus
Definite IntegralsFind the dimensions of the rectangle of largest area that can be inscribed in a circle of radius r.

Calculus
Definite IntegralsUse a double integral to find the area of the region.
one loop of the rose r = 5 cos(3θ)
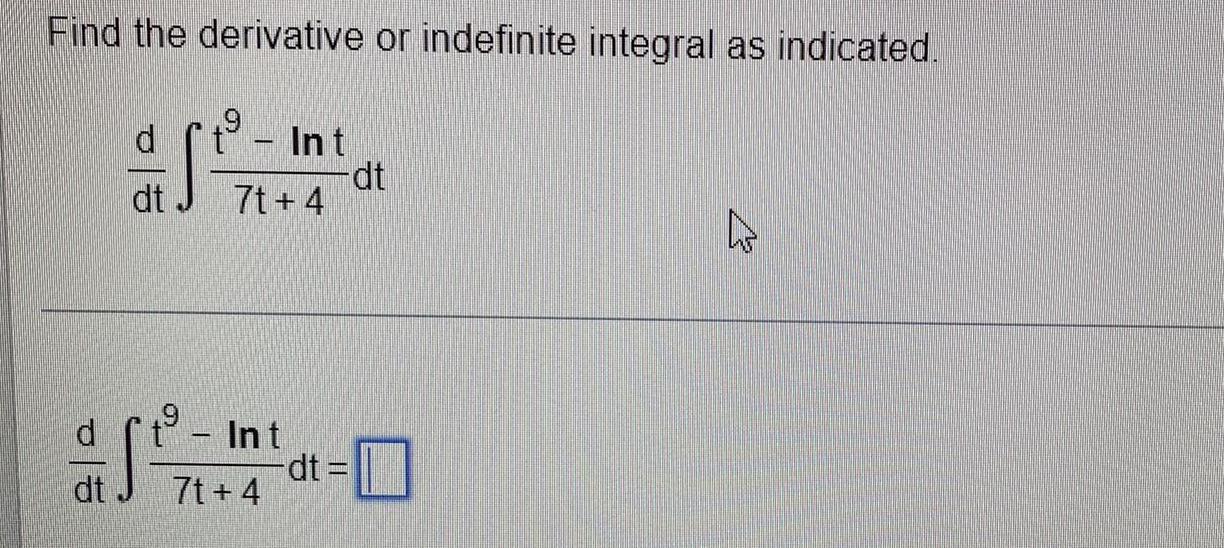
Calculus
Definite IntegralsFind the derivative or indefinite integral as indicated.
d/dt ∫ t9 - lnt 7t+4 dt
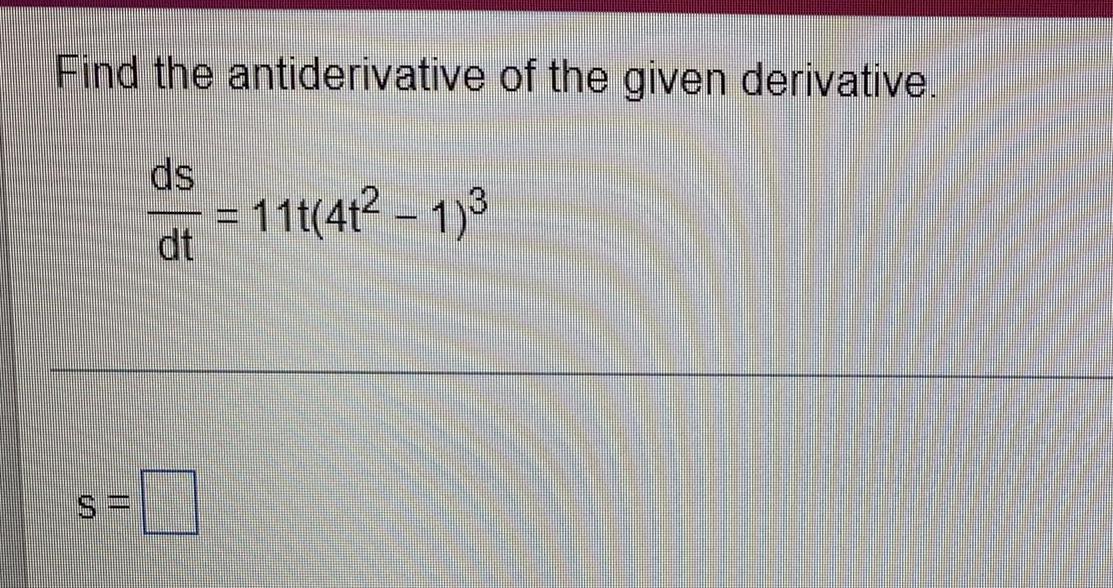

Calculus
Definite IntegralsFind the volume of the given solid. under the plane 9x + 2y - z = 0 and above the region enclosed by the parabolas y = x² and x = y²

Calculus
Definite IntegralsLet f (x) = − 4x + 1.
Find the inverse of f (x).
f¹(x)=-x+1/4
f¹(x) = -4x – 1
Does not exist
f¹(x) = -4x+1
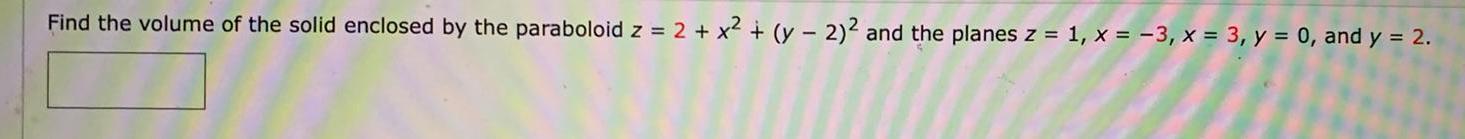
Calculus
Definite IntegralsFind the volume of the solid enclosed by the paraboloid z = 2 + x² + (y - 2)2 and the planes z = 1, x = -3, x = 3, y = 0, and y = 2.