Differential equations Questions and Answers
Calculus
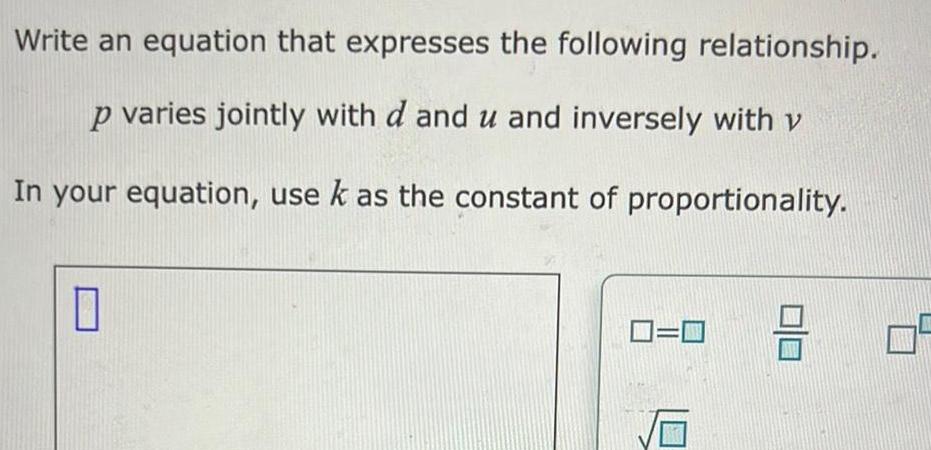
Differential equationsWrite an equation that expresses the following relationship p varies jointly with d and u and inversely with v In your equation use k as the constant of proportionality 0 0 0 3
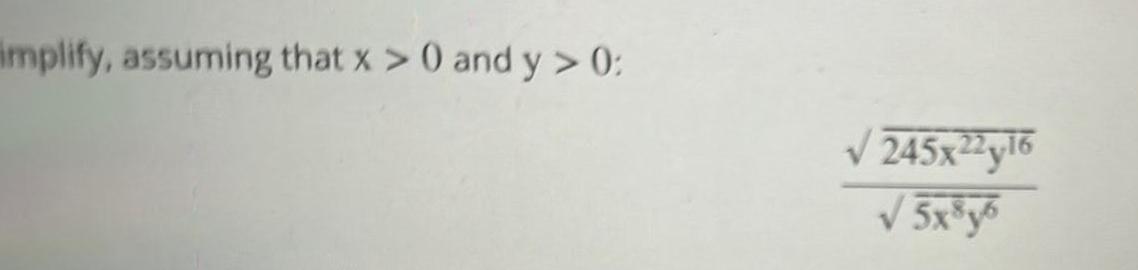
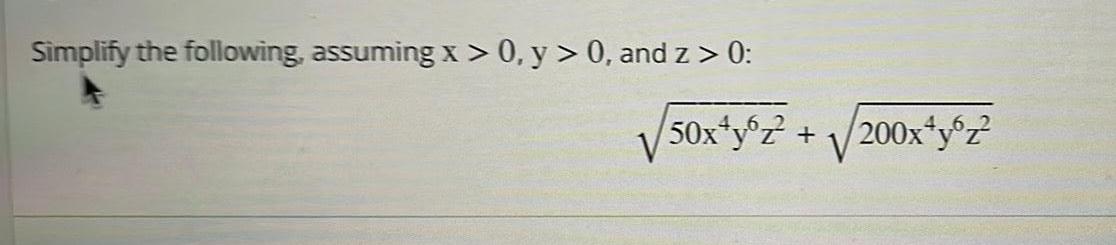
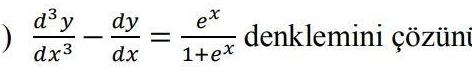
Calculus
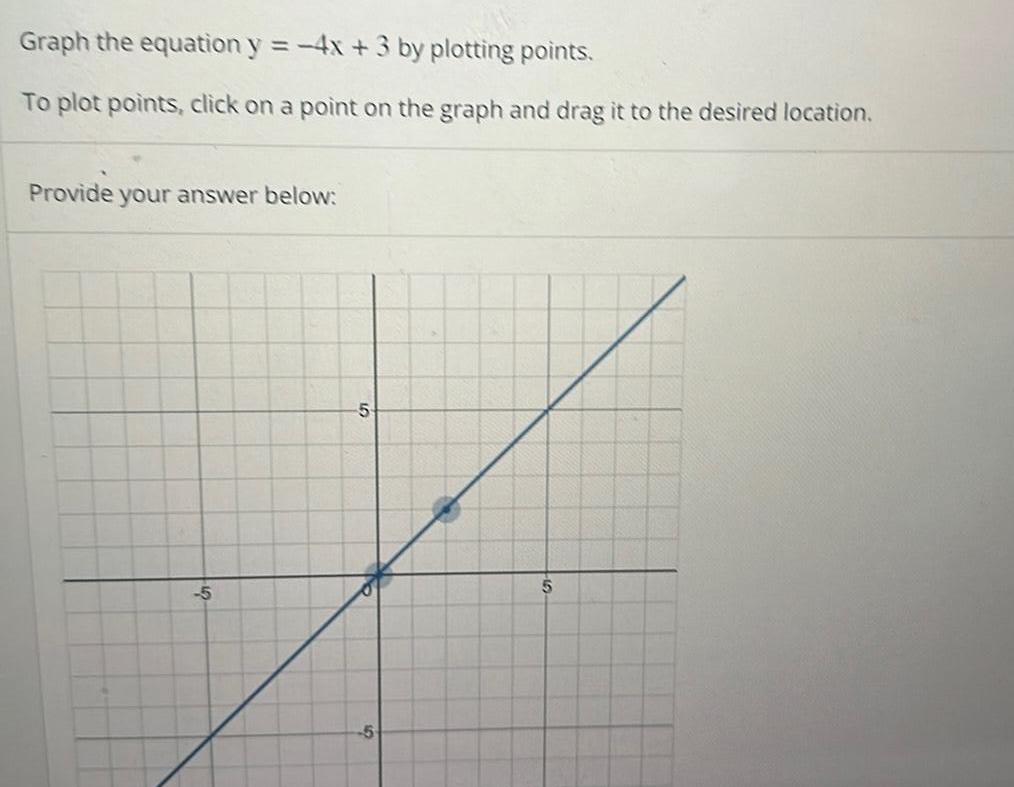
Differential equationsGraph the equation y 4x 3 by plotting points To plot points click on a point on the graph and drag it to the desired location Provide your answer below 5 5 IN 5 5

Calculus
Differential equationsthrough C below on was given to you by a student whom you are tutoring Complete parts A A The proposed solution is right B The proposed solution is wrong The student should have used integration by parts rather than the power rule C The proposed solution is wrong Only constant factors can be combined across the integral OD The proposed solution is wrong The integrating factor is incorrect C Show a correct solution if the solution is incorrect and check the result Select the correct answer below and if necessary fill in the answer box to complete your choice OA The proposed solution is correct OR The corrected solution is Equation Solution OA Take the derivative of the solution and determine whether it is equivalent to the original equation O B Determine y Then evaluate the expressions for y and y and the original equation for various values of x and determine whether true statements result c Determine y and substitute the expressions for y and y into the original equation Then simplify and determine whether a true statement results Use technology to compare the slope fields of the solution and the original equation B is the solution right or wrong If the solution is wrong explain what is wrong and how it can be corrected y y 5 x 8 x x 8 dx x 8 C y

Calculus
Differential equationsFactor by factoring out the greatest common factor GCF 7x 6 y 4 63x 4 y 3 42xy
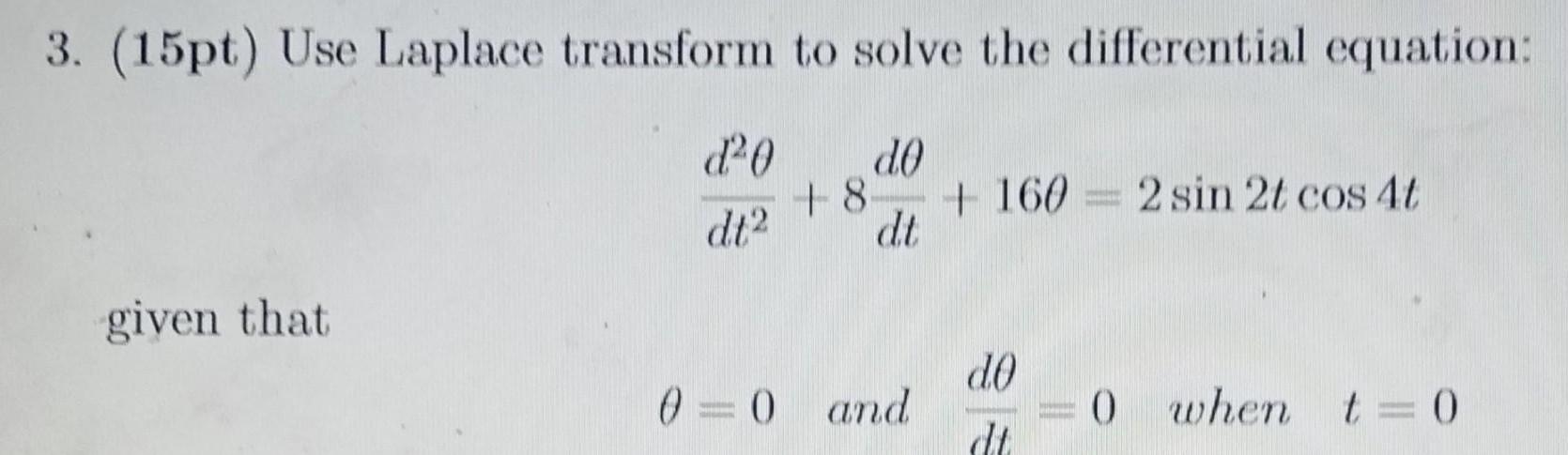
Calculus
Differential equations3 15pt Use Laplace transform to solve the differential equation d0 d t given that d 0 dt 8 0 0 and 1602 sin 2t cos 4t d0 dt PESEM 0 when t 0
Calculus
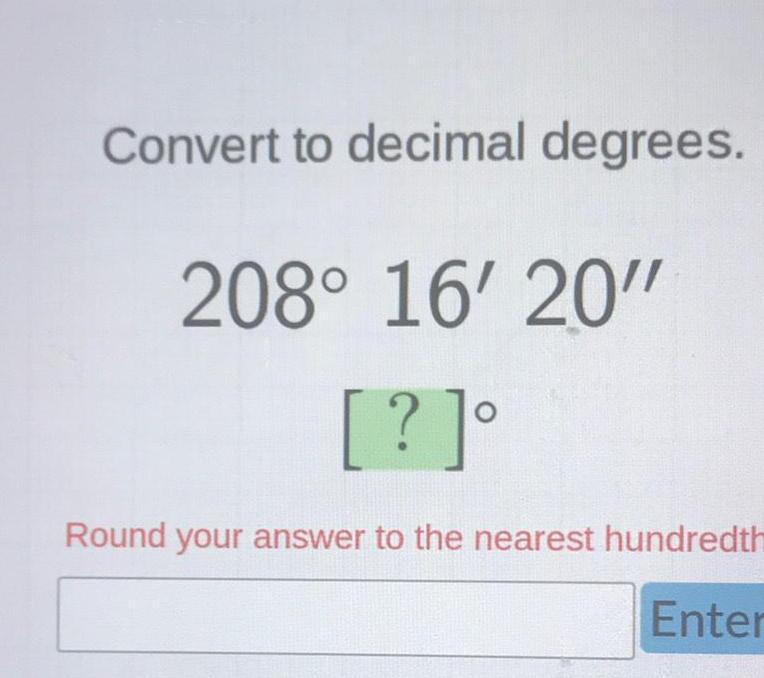
Differential equationsConvert to decimal degrees 208 16 20 Round your answer to the nearest hundredth Enter

Calculus
Differential equationsDetermine the following limits numerically and paste the table of values If pasting a link e g to a google sheet make sure it is shared with the teacher correctly a lim h 0 b lim h 0 c lim h 0 sin h h cos h 1 h b 1 h Note b is a constant 0 Pick any value for b 1 e g set b to be 2 3 4 etc
Calculus
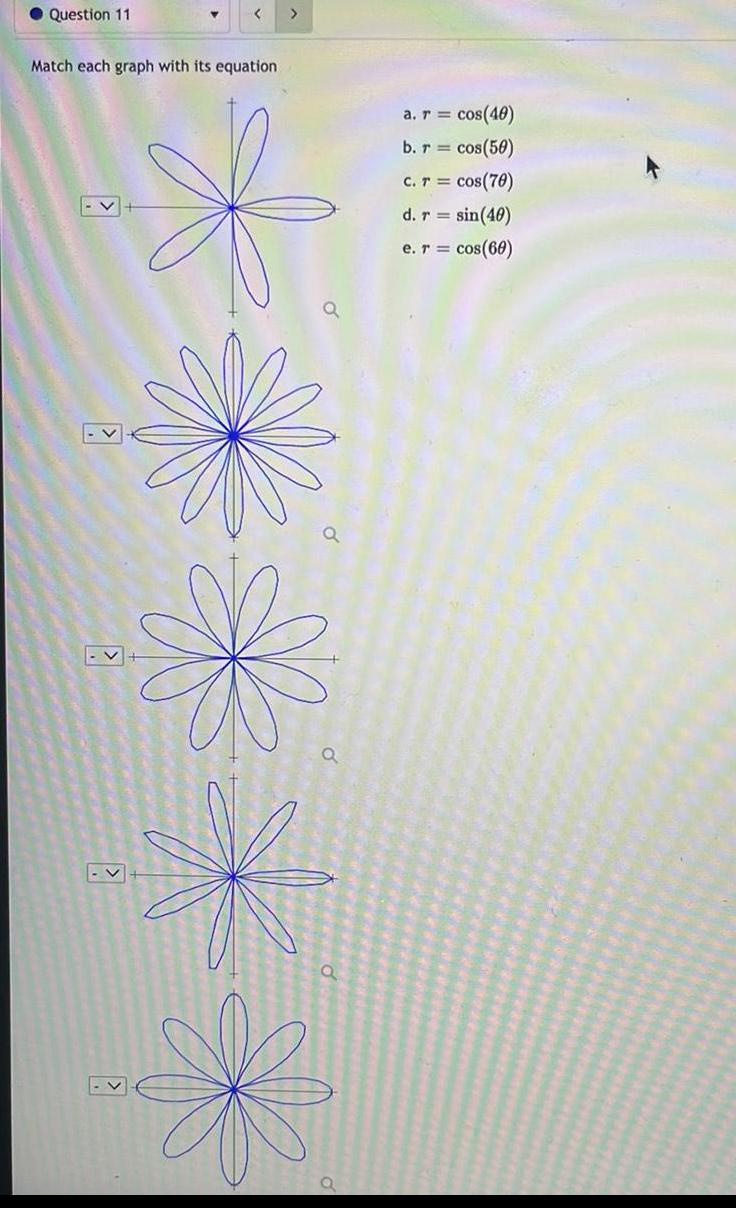
Differential equationsO Question 11 Match each graph with its equation a a a r cos 40 b r cos 50 c r cos 70 d r sin 40 e r cos 60
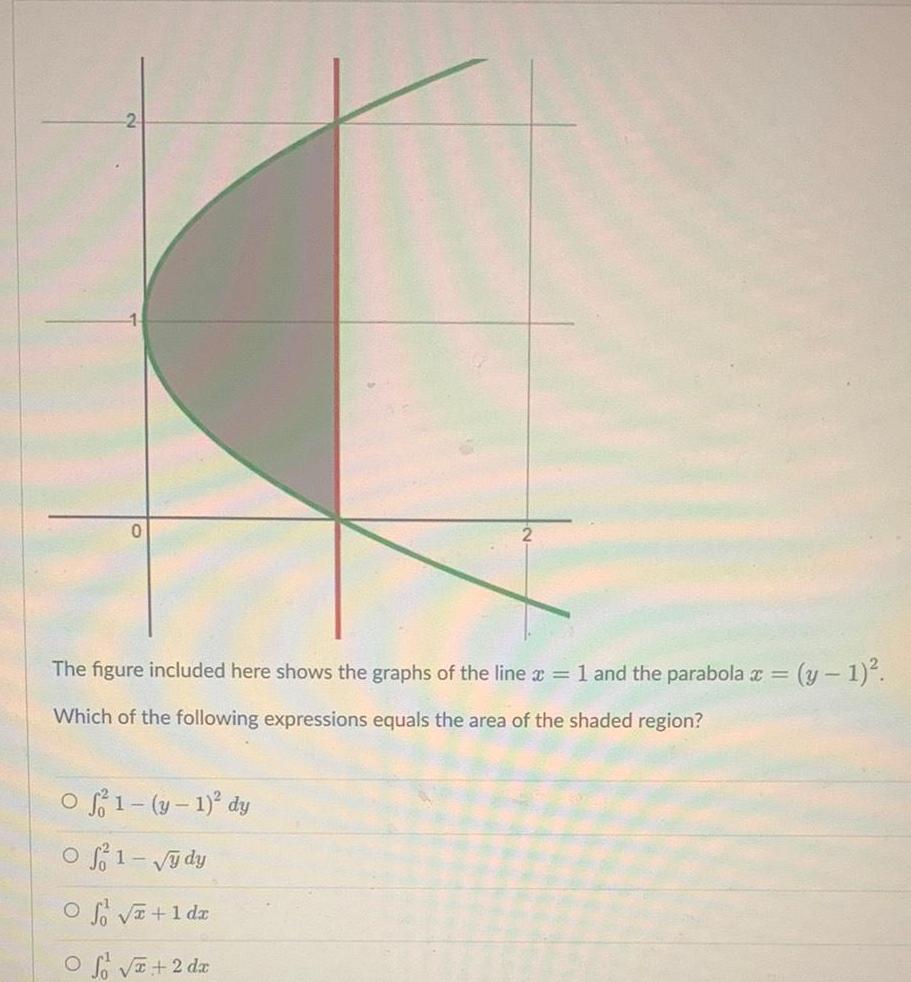
Calculus
Differential equationsThe figure included here shows the graphs of the line x 1 and the parabola x y 1 Which of the following expressions equals the area of the shaded region Of 1 y 1 dy 01 ydy 1 dx 2 dx O

Calculus
Differential equationsLet f x P 4 9 x 28 a f 1 11x 35 Compute each of the following values b f 4 c f 6 if x 4 if x 4 if x 4 100
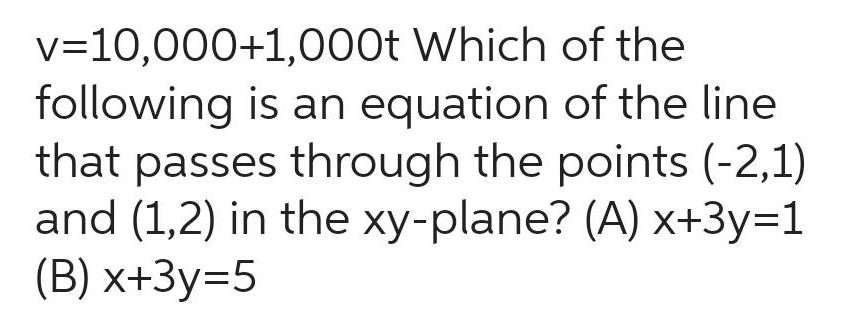
Calculus
Differential equationsv 10 000 1 000t Which of the following is an equation of the line that passes through the points 2 1 and 1 2 in the xy plane A x 3y 1 B x 3y 5
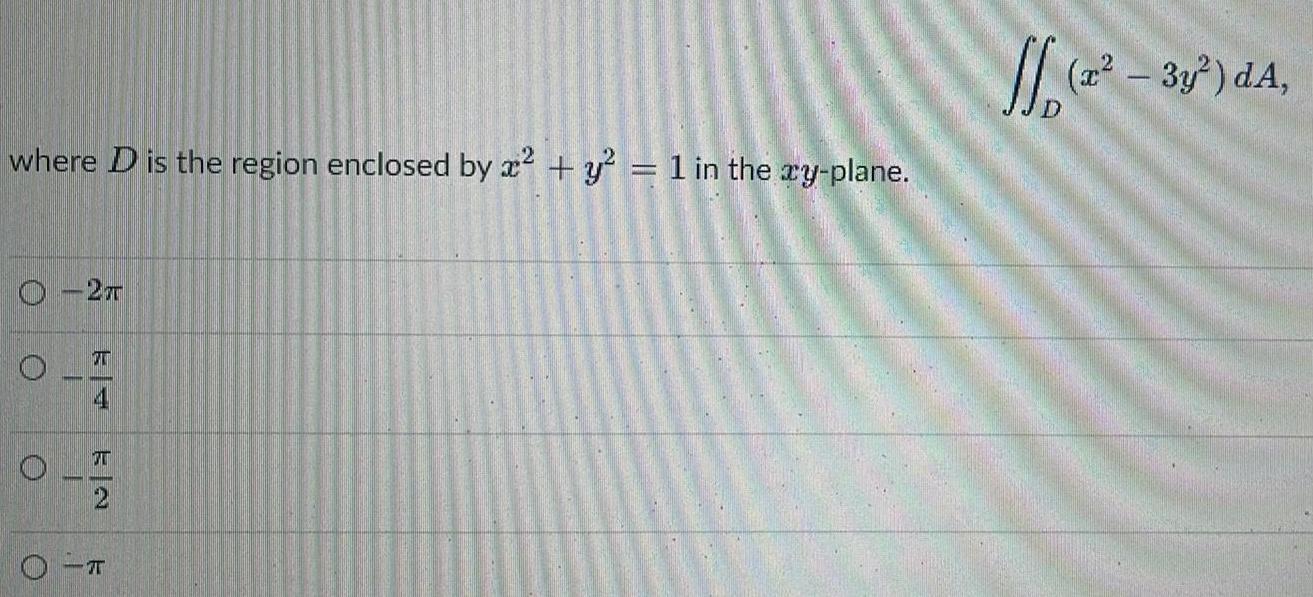
Calculus
Differential equationswhere D is the region enclosed by x y 1 in the xy plane O O 2T CL 31 2 T J1 2 3y dA
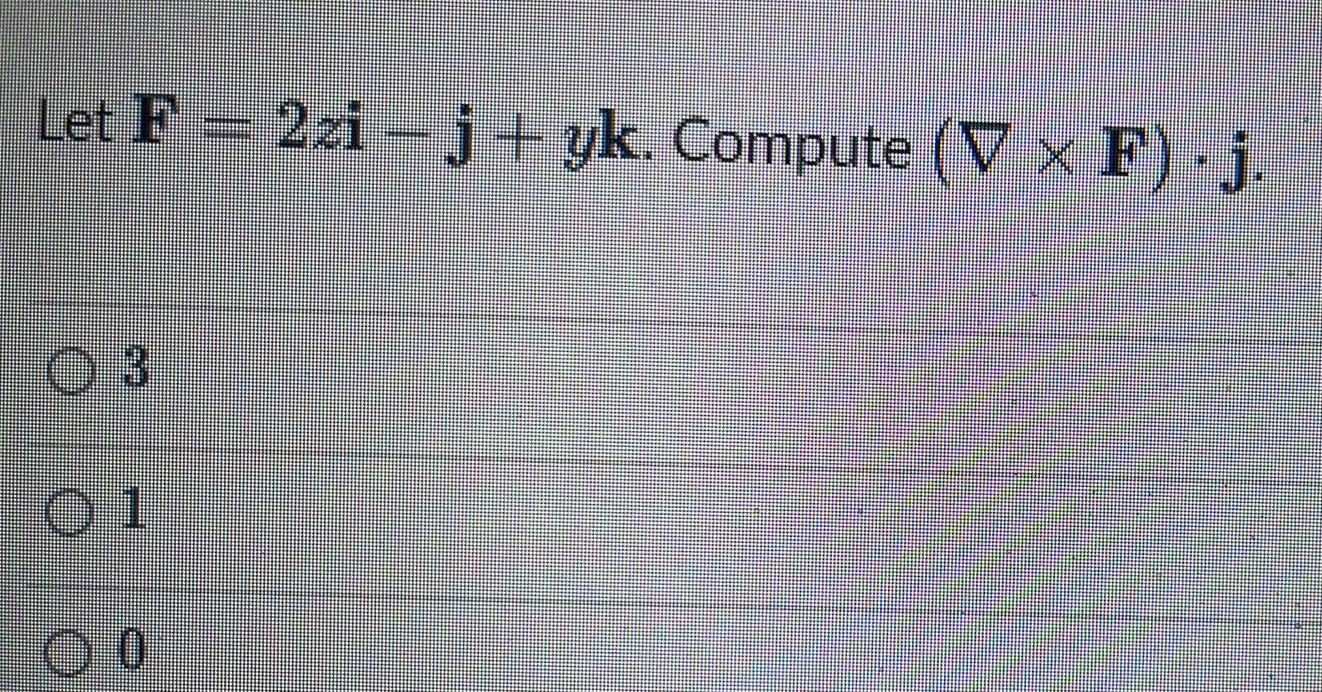
Calculus
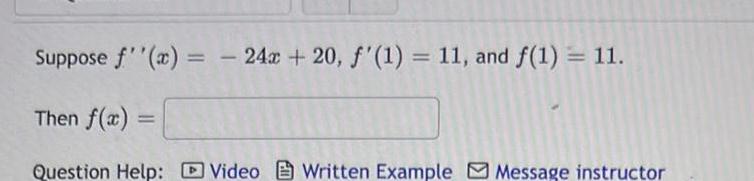
Differential equationsSuppose f x 24x 20 f 1 11 and f 1 11 Then f x Question Help Video Written Example Message instructor

Calculus
Differential equationsA company makes two types of biscuits Jumbo and Regular The oven can cook at most 300 biscuits per day Each jumbo biscuit requires 2 oz of flour each regular biscuit requires 1 oz of flour and there is 500 oz of flour available The income from each jumbo biscuit is 0 11 and from each regular biscuit is 0 13 How many of each size biscuit should be made to maximize income What is the maximum income The company should make jumbo and Type whole numbers regular biscuits

Calculus
Differential equationsSolve the following differential equation with given initial condition y 7ty 12t y 0 1

Calculus
Differential equationsA team of haymakers each of whom works at the same rate is assigned to harvest hay from two meadows One meadow is twice the area of the other The team worked on the larger meadow for half a day at which point the team split into two groups of equal size One of these teams continued to work on the larger meadow and they finished harvesting this meadow at the end of the day The other group spent the rest of the day harvesting the smaller meadow At the end of the day what portion of the smaller meadow remained to be harvested

Calculus
Differential equationsUsing the traces and contour lines draw the quadratic surface x 1 y 4 9 N 2 0
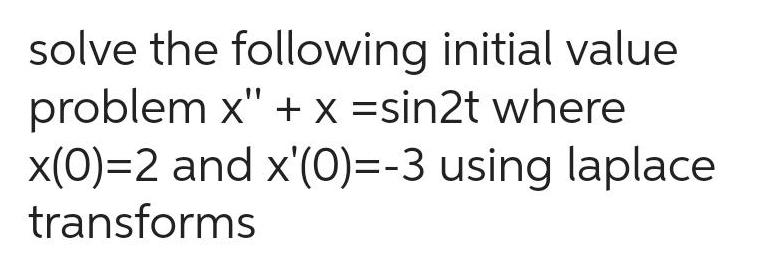
Calculus
Differential equationssolve the following initial value problem x x sin2t where x 0 2 and x 0 3 using laplace transforms

Calculus
Differential equationsFind the component form and magnitude of the indicated vector Given that P 5 11 and Q 6 4 find the component form and magnitude of the vector QP O 1 7 50 O 11 7 38 O 1 7 50 O 1 7 50


Calculus
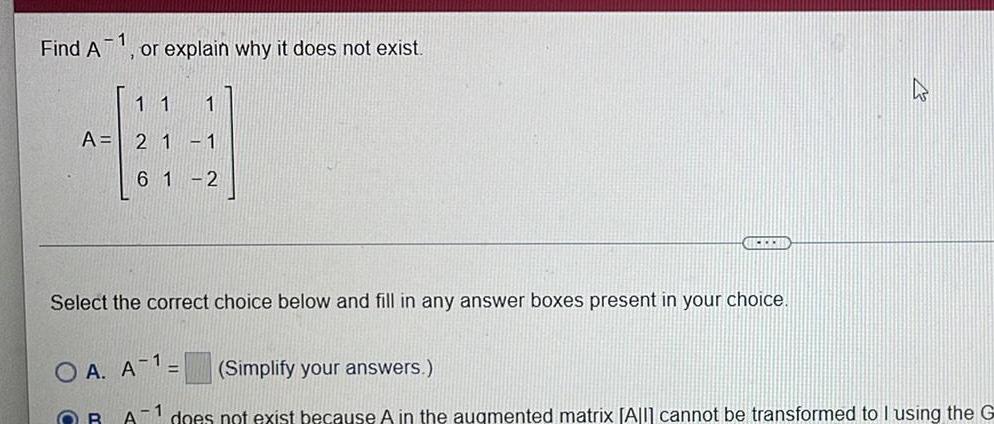
Differential equationsFind A 1 or explain why it does not exist 11 1 A 2 1 1 6 1 2 OCCHI Select the correct choice below and fill in any answer boxes present in your choice 2 OA A Simplify your answers OB A does not exist because A in the augmented matrix All cannot be transformed to I using the G

Calculus
Differential equationsx 6 selecting a type of graph then select the center then moving the cursor until the graph is correct 7 6 5 4 3 2 1 Sketch the graph of 7 6 5 4 3 2 1 1 2 3 4 5 6 7 Clear AlL Draw 3 5 1 Graph by 1 2 3 4 5 60 ta
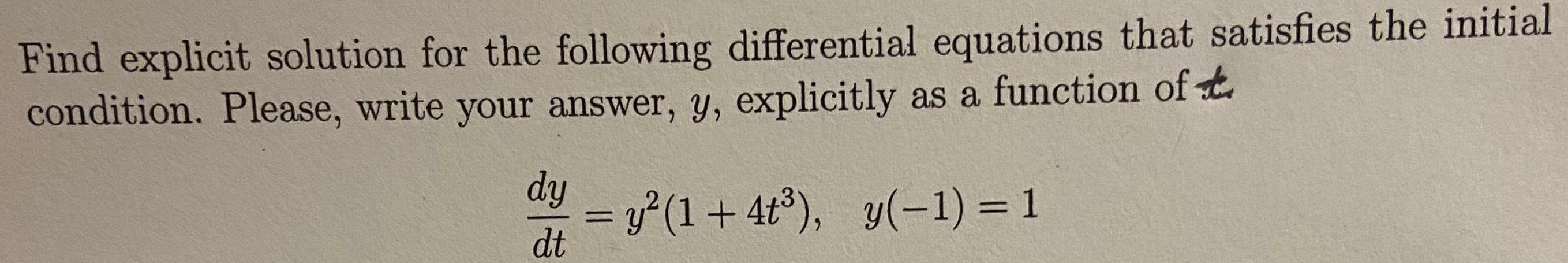
Calculus
Differential equationsFind explicit solution for the following differential equations that satisfies the initial condition Please write your answer y explicitly as a function of t dy dt y 1 4t y 1 1
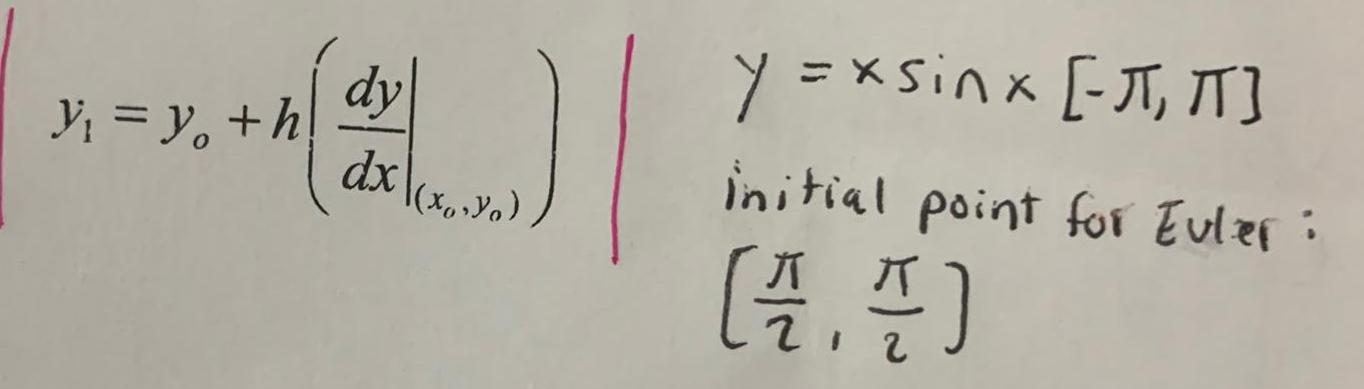
Calculus
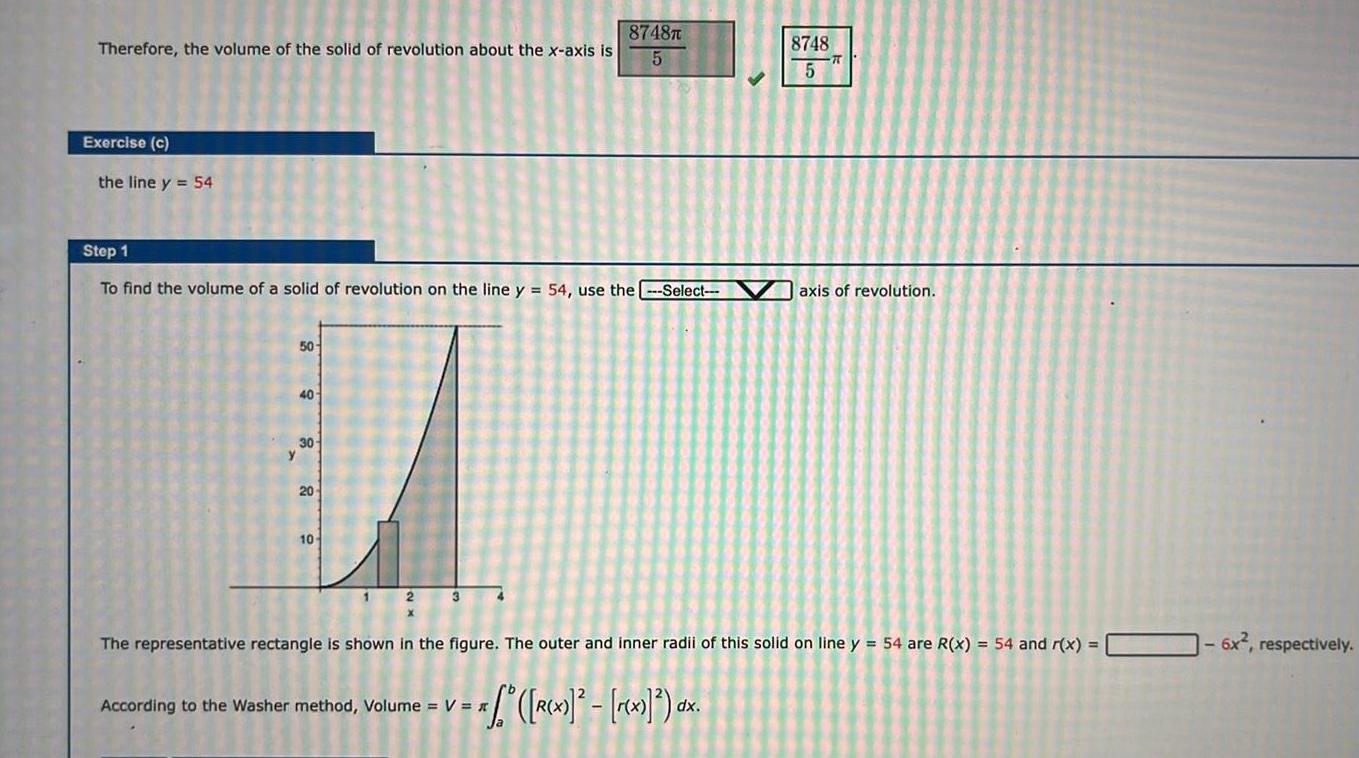
Differential equationsTherefore the volume of the solid of revolution about the x axis is Exercise c the line y 54 Step 1 To find the volume of a solid of revolution on the line y 54 use the Select 50 40 30 20 10 8748T 5 According to the Washer method Volume V 1 f R x r x dx 8748 5 The representative rectangle is shown in the figure The outer and inner radii of this solid on line y 54 are R x 54 and r x axis of revolution 6x respectively
Calculus
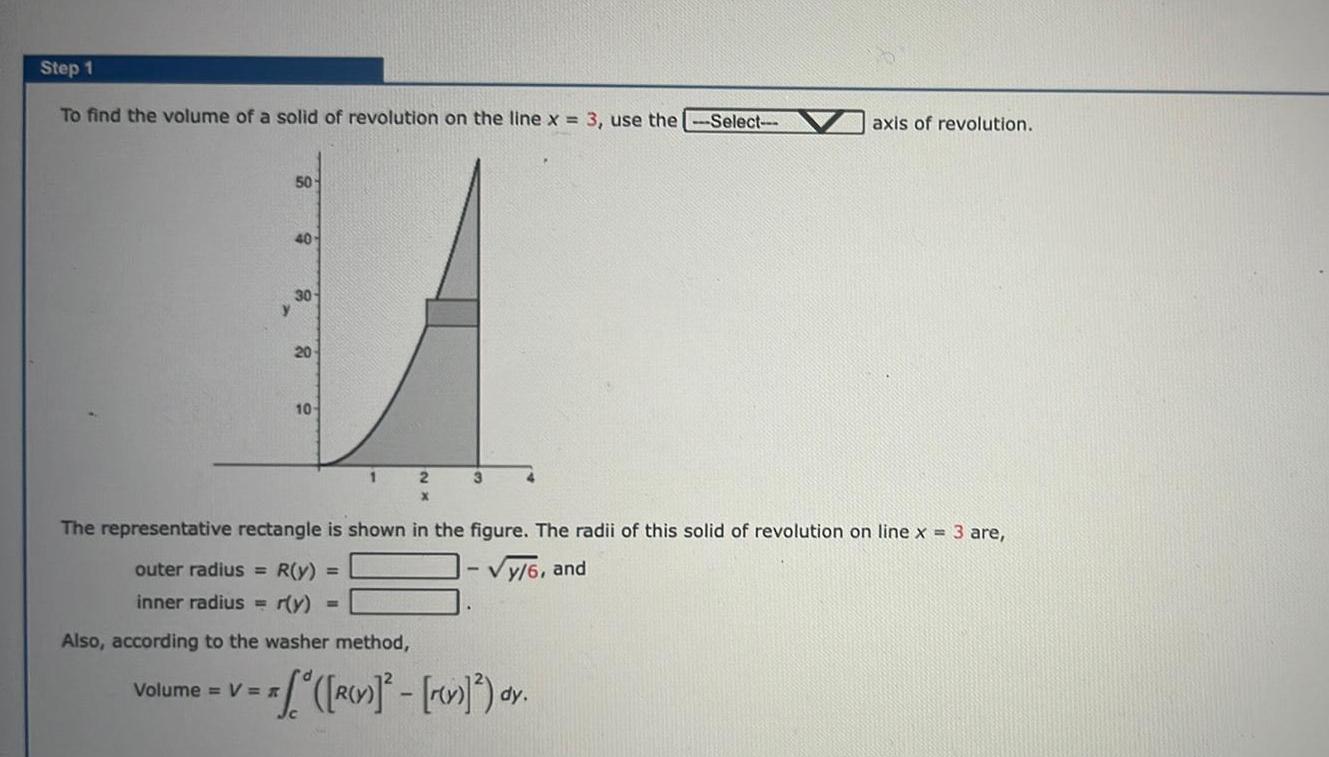
Differential equationsStep 1 To find the volume of a solid of revolution on the line x 3 use the Select 50 40 30 y Volume V 20 10 1 The representative rectangle is shown in the figure The radii of this solid of revolution on line x 3 are outer radius R y y 6 and inner radius r y Also according to the washer method 2 3 R v rev dy axis of revolution
Calculus
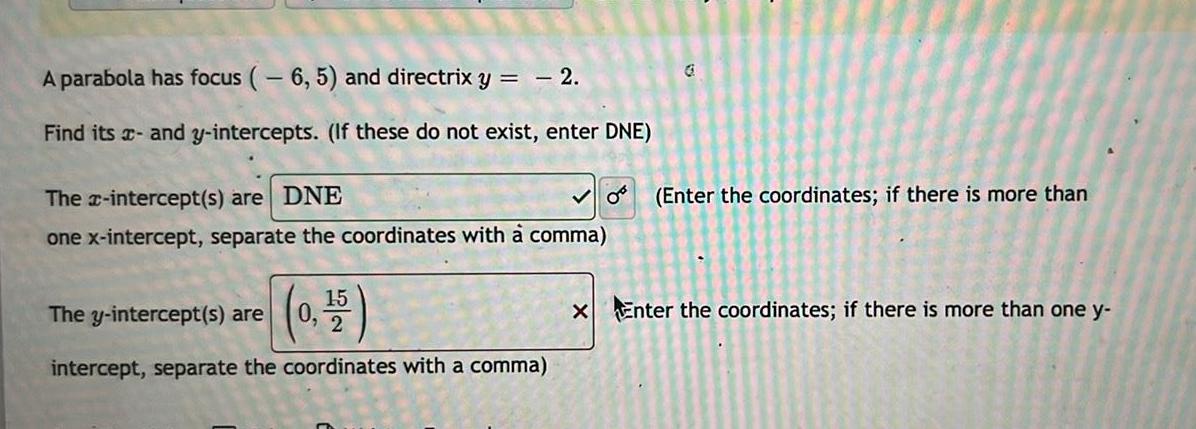
Differential equationsA parabola has focus 6 5 and directrix y 2 Find its and y intercepts If these do not exist enter DNE The x intercept s are DNE one x intercept separate the coordinates with a comma The y intercept s are 0 15 intercept separate the coordinates with a comma 0 G Enter the coordinates if there is more than x Enter the coordinates if there is more than one y
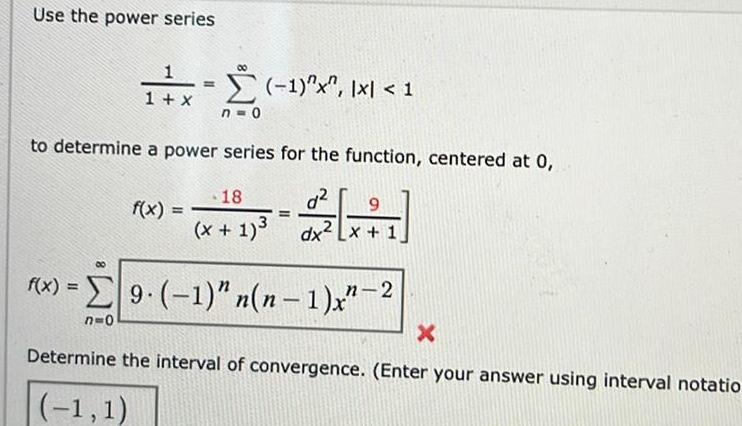
Calculus
Differential equationsUse the power series 1 x 80 f x n 0 1 x 1 to determine a power series for the function centered at 0 d 9 dx x 1 18 x 1 f x 9 1 n n 1 x 2 n 0 X Determine the interval of convergence Enter your answer using interval notatio 1 1
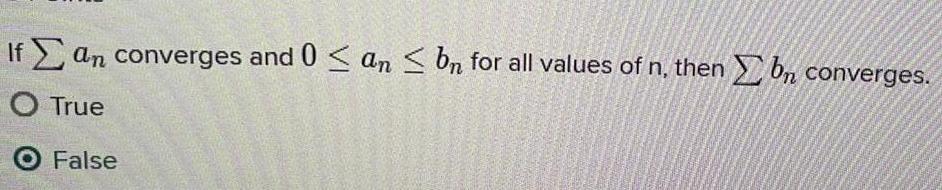
Calculus
Differential equationsIf an converges and 0 an b for all values of n then bn converges O True O False
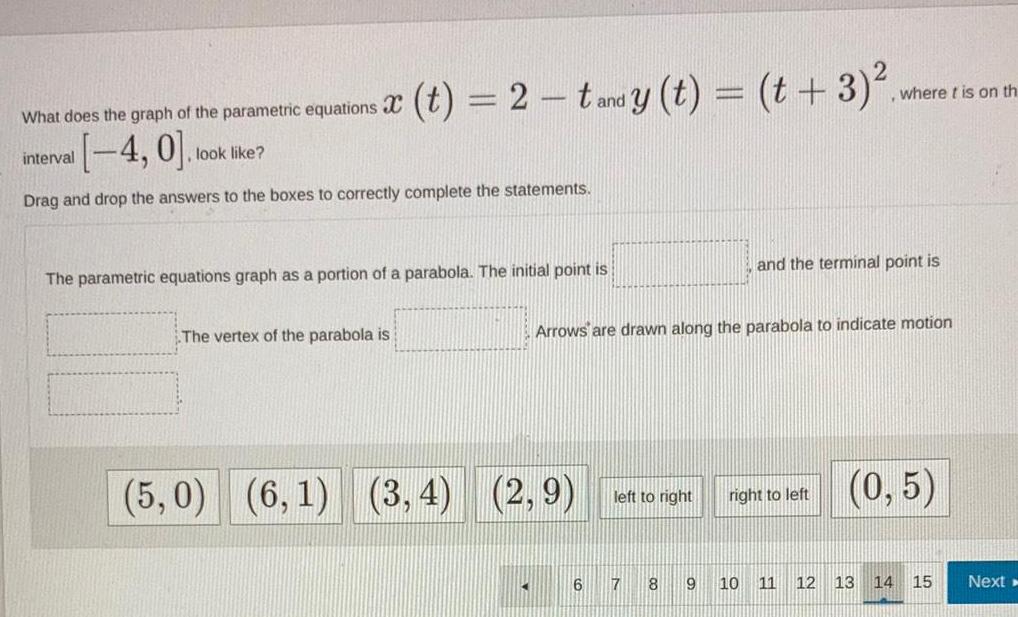
Calculus
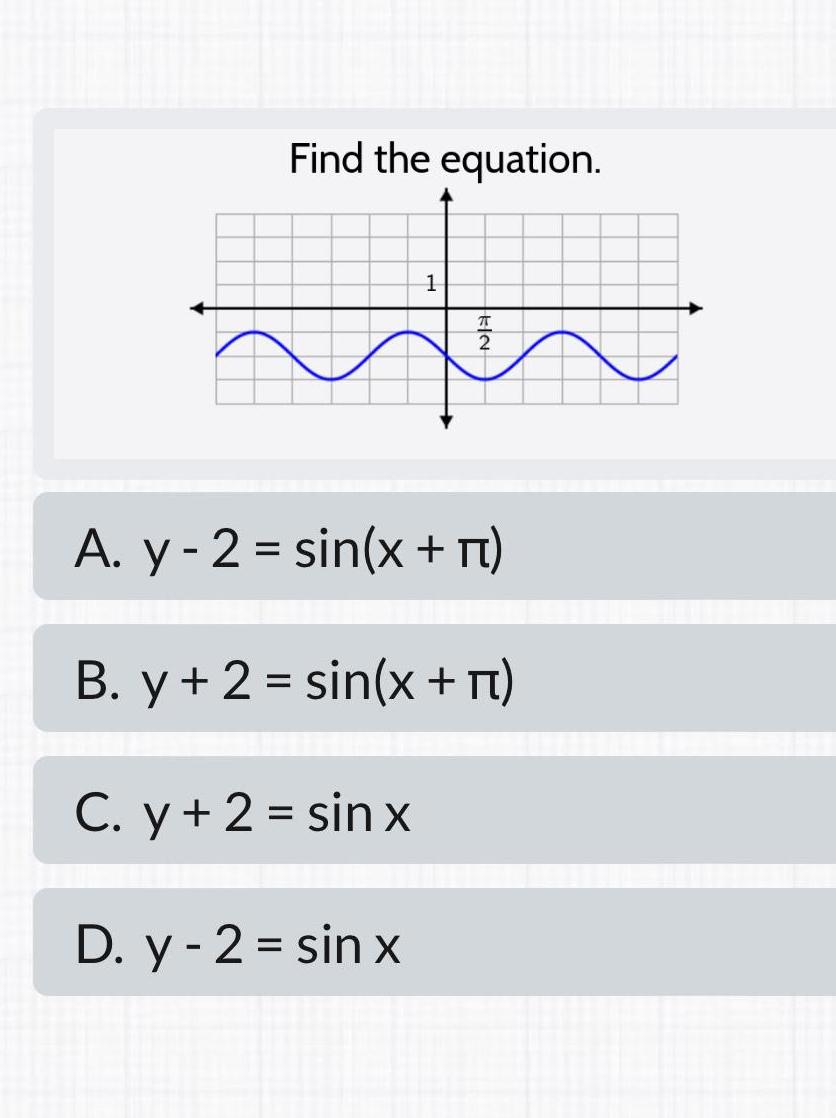
Differential equationsWhat does the graph of the parametric equations 4 0 Drag and drop the answers to the boxes to correctly complete the statements interval X t 2 t and y t t 3 look like The parametric equations graph as a portion of a parabola The initial point is The vertex of the parabola is 5 0 6 1 3 4 2 9 11 Arrows are drawn along the parabola to indicate motion 6 left to right 7 8 9 and the terminal point is right to left where t is on th 10 11 12 0 5 13 14 15 Next
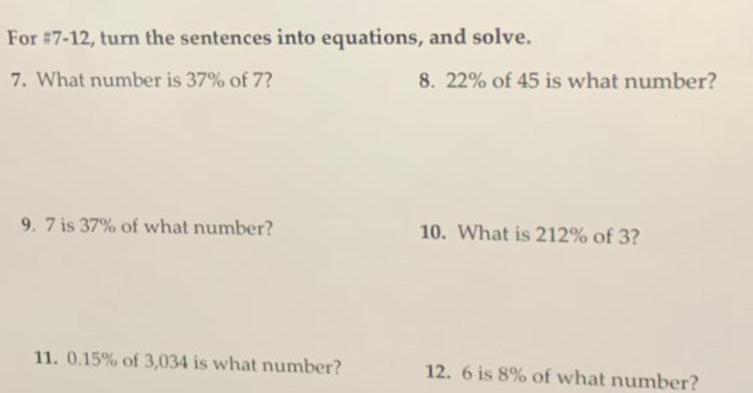
Calculus
Differential equationsFor 7 12 turn the sentences into equations and solve 7 What number is 37 of 7 9 7 is 37 of what number 11 0 15 of 3 034 is what number 8 22 of 45 is what number 10 What is 212 of 3 12 6 is 8 of what number
Calculus
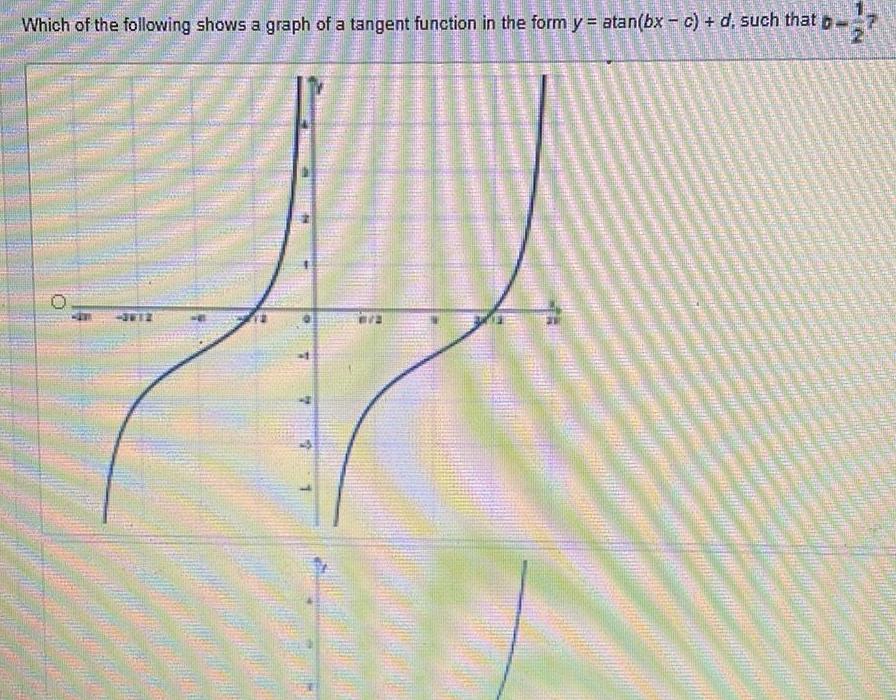
Differential equationsWhich of the following shows a graph of a tangent function in the form y atan bx c d such that b 2 H 3612 7 4 7

Calculus
Differential equations55 60 Product to Sum 55 sin 2x cos 3x 57 cos x sin 4x 59 3 cos 4x cos 7x Formulas Write the product as a sum 56 sin x sin 5x 58 cos 5x cos 3x I 60 11 sin cos K14 X

Calculus
Differential equationsSolve the initial value problem for y as a function of x x 4 dy dx 1 y 2 0
Calculus
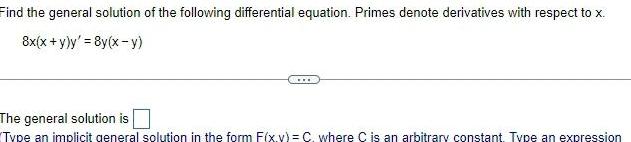
Differential equationsFind the general solution of the following differential equation Primes denote derivatives with respect to x 8x x y y 8y x y The general solution is Type an implicit general solution in the form F x y C where C is an arbitrary constant Type an expression
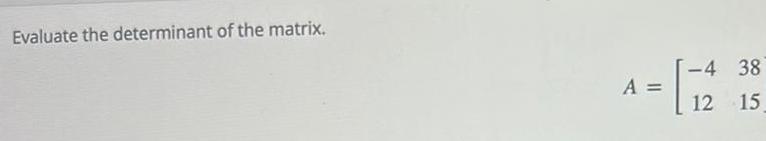

Calculus
Differential equationsConsider the following matrix 6 3 2 2 1 4 10 10 13 Step 2 of 3 Determine the value of d21 if possible If the element indicated is not in the matrix state None Answer Let D Selecting a radio button will replace the entered answer value s with the radio button value If the radio button is not selected the entered answer is use

Calculus
Differential equationsFind the 6th term of the geometric sequence with a2 45 16 and ag a6 98415 262144

Calculus
Differential equationsind the solution of the heat conduction problem Uxx 4 0 x 2 1 0 u 0 t 0 u 2 1 0 1 0 u x 0 2 sin x 2 sin rx 4 sin 27x

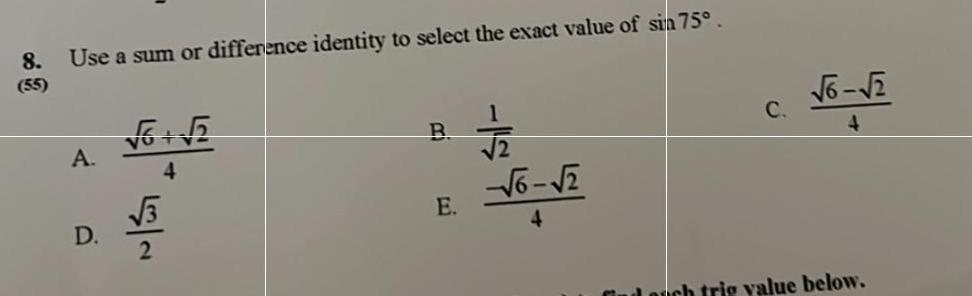
Calculus
Differential equations8 Use a sum or difference identity to select the exact value of sin 75 55 A D 6 5 4 3 2 B E 7 22 6 2 4 C 6 2 4 Gind auch tris value below

Calculus
Differential equations16 Find the volume of each solid obtained by rotating the bounded region around the given axis using the disk method Remember with disk method the general equation is fo b a f x x 1 x 1 x 4 and y 0 rotated about the r axis dy for a y axis rotation r dx for a x axis rotation and

Calculus
Differential equationsA rocket is launched from a tower The height of the rocket y in feet is related to the time after launch x in seconds by the given equation Using this equation find the maximum height reached by the rocket to the nearest tenth of a foot y 16x 2 201x 132