Differential equations Questions and Answers
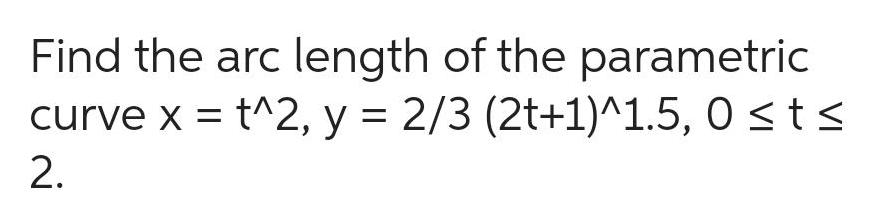
Calculus
Differential equationsFind the arc length of the parametric curve x t 2 y 2 3 2t 1 1 5 0 t 2
Calculus
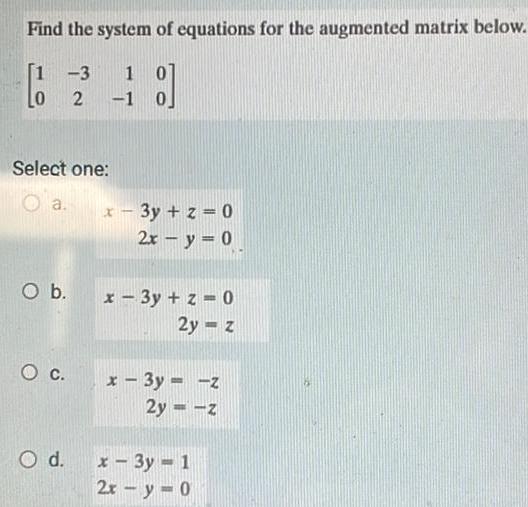
Differential equationsFind the system of equations for the augmented matrix below 3 1 LO Select one Oa O b O C 2 1 0 O d x 3y z 0 2x y 0 x 3y z 0 2y z x 3y z 2y z x 3y 1 2x y 0

Calculus
Differential equationsUse the discriminant to identify the graph of 2x 4xy 2y2 3x y 5 Select one O a The graph is a hyperbola O b The graph is an ellipse O c The graph is a circle O d The graph is a parabola

Calculus
Differential equationsLet z f x y be a second order differentiable function with x u v and y u v Evaluate the derivative zxy and express the result with respect to the variables u v
Calculus
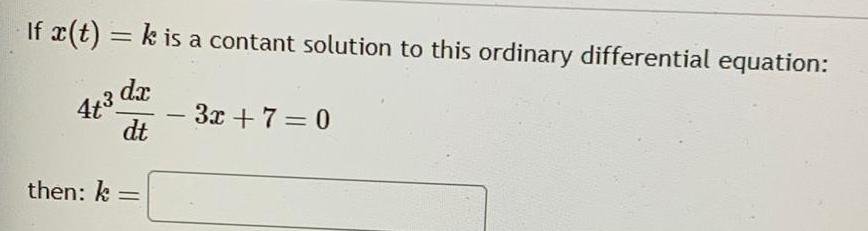
Differential equationsIf x t k is a contant solution to this ordinary differential equation dx dt then k 3x 7 0
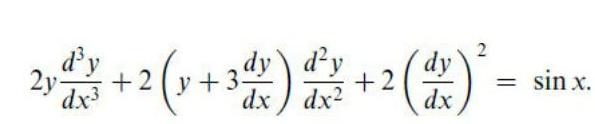
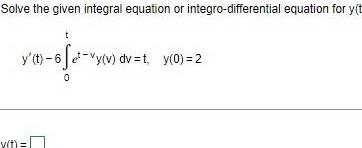
Calculus
Differential equationsSolve the given integral equation or integro differential equation for y t 80 02 y t 6fe vy v dv t y 0 2 0 v t
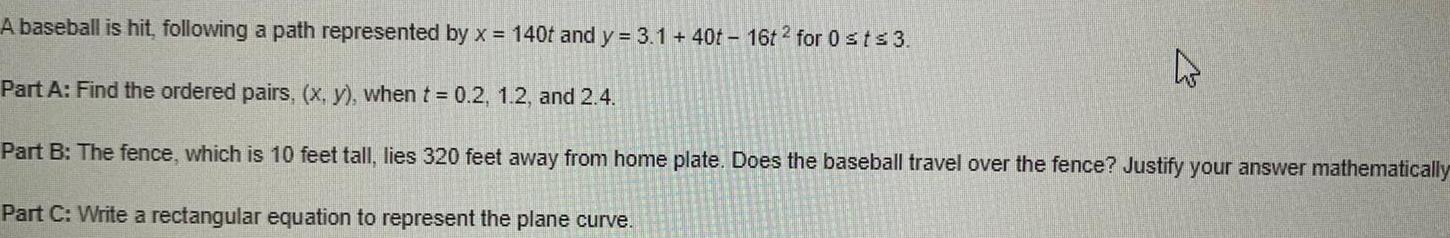
Calculus
Differential equationsA baseball is hit following a path represented by x 140t and y 3 1 40t 16t2 for 0 st 3 Part A Find the ordered pairs x y when t 0 2 1 2 and 2 4 Part B The fence which is 10 feet tall lies 320 feet away from home plate Does the baseball travel over the fence Justify your answer mathematically Part C Write a rectangular equation to represent the plane curve 4
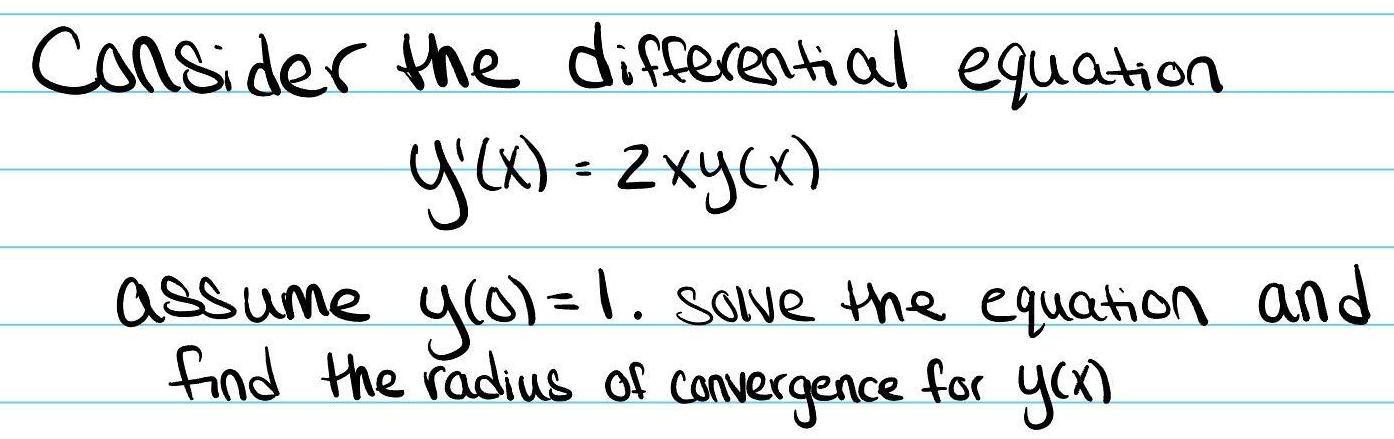
Calculus
Differential equationsConsider the differential equation Y x 2xy x assume y 0 1 solve the equation and find the radius of convergence for y x
Calculus
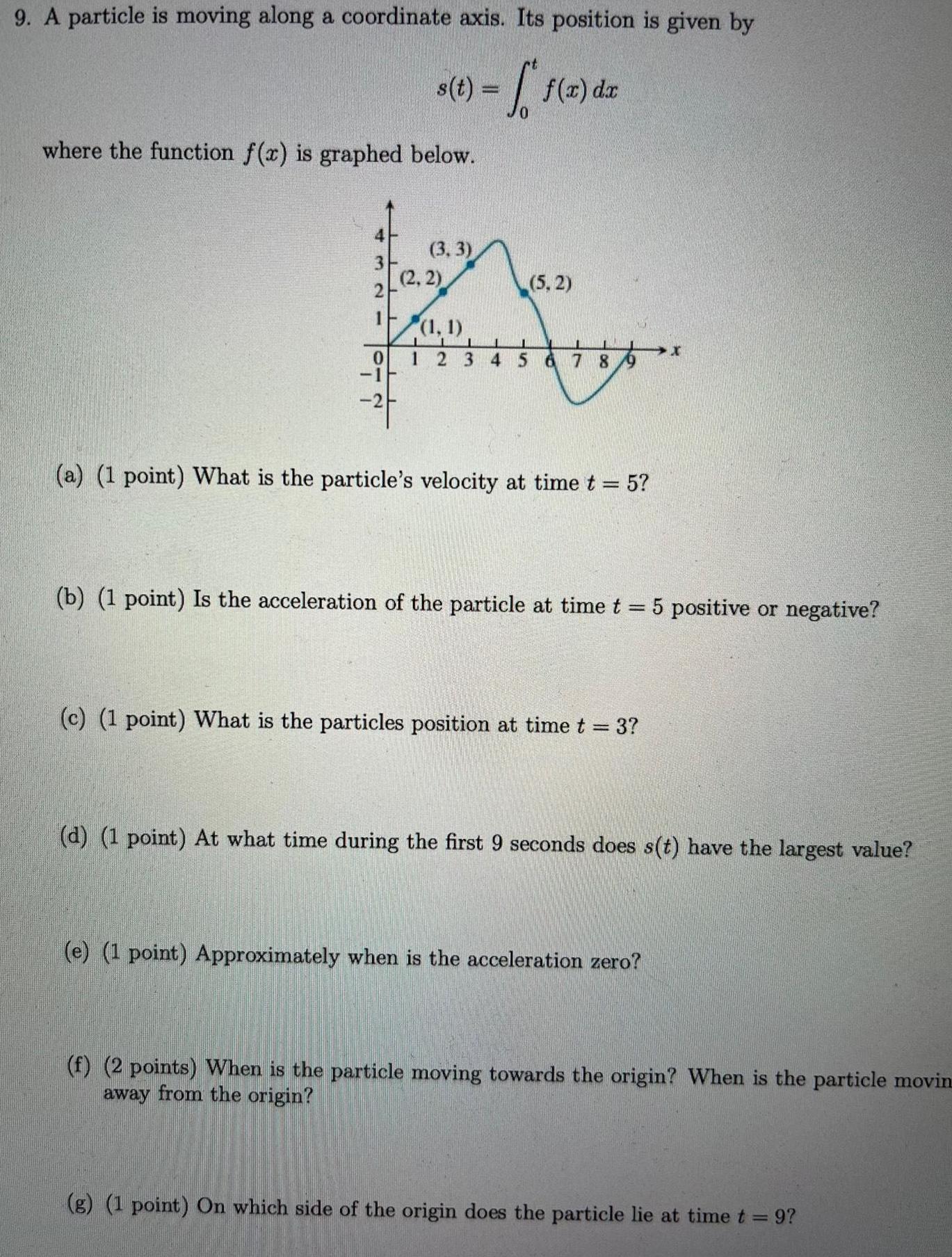
Differential equations9 A particle is moving along a coordinate axis Its position is given by s t f f x dx where the function f x is graphed below 4321 2 0 1F T 3 3 2 2 5 2 1 1 L I 1 n 1 2 3 4 5 6 7 8 9 a 1 point What is the particle s velocity at time t 5 b 1 point Is the acceleration of the particle at time t 5 positive or negative c 1 point What is the particles position at time t 3 x d 1 point At what time during the first 9 seconds does s t have the largest value e 1 point Approximately when is the acceleration zero f 2 points When is the particle moving towards the origin When is the particle movin away from the origin g 1 point On which side of the origin does the particle lie at time t 9

Calculus
Differential equations2 Consider the line integral F dr where the vector field C 2y e sin x y i 3 3 e cos y z 2 j F and C is the closed curve in the first quadrant consisting of the curve r y 1 and the coordinate axes a 0 and y 0 oriented anticlockwise a Use Green s theorem to express the line integral in terms of a double integral over the region R enclosed by C b Calculate the double integral using a repeated integral with respect to y first and second c Now reverse the order of integration and evaluate the double integral using a re peated integral with respect to a first and y second

Calculus
Differential equationsConsider the following function f x x a 5 points Approximate f by a Taylor polynomial T3 x with the center x 1 Your answer must be of the form co c x 1 c x 1 c x 1 b 5 points How good is the approximation on the small interval 0 9 x 1 1 Use the Taylor s Inequality to find an upper bound of the error R3 x f x T x c 5 points Find the Taylor series of f x with center at x 1 Use the summation notation whoch displays the n th term clearly Then determine the interval of convergence of this series d Extra Credit 3 points Show by using Taylor Ineqality that the absolute value of the n th remainder R x converges to 0 for every x in the interval 0 6 1 4 e Extra Credit 3 points Find a rational expression to which this series converges on its interval of convergence You must show your systematic procedure instead of simply making a wild guess Hint Try differentiation or integration

Calculus
Differential equationsdy dx 5 Find the equation of the solution to xy through the point x y 1 4 help equations If you round to find the constant please make sure your answers is correct to 3 decimal places
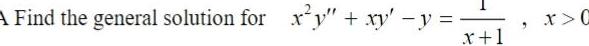

Calculus
Differential equationsProblem 3 10 points Find the solution of the following DE that satisfies the indicated conditions using the Laplace transform method Y 4Y 4Y te2t 25sin t Y 0 1 and Y 0 4

Calculus
Differential equationsFind the particular solution of the differential equation satisfying the initial condition y 3 ln 3 YF Your answer should be a function of x dy dx e 2y 3e 2y xe

Calculus
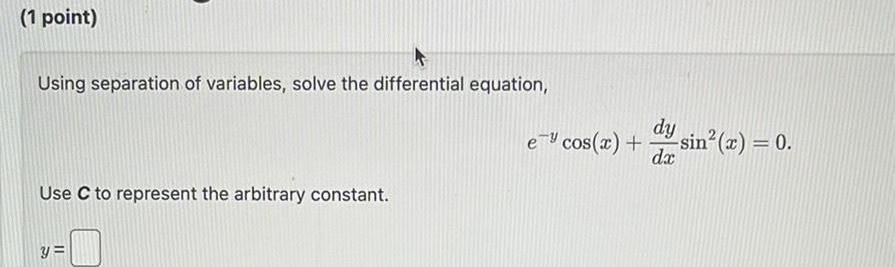
Differential equations1 point Using separation of variables solve the differential equation Use C to represent the arbitrary constant y e cos x dy da sin x 0

Calculus
Differential equations1 point dy Find the equation of the solution to da 16 help equations ay through the point x y 1 4

Calculus
Differential equations3 Bluegill Population There are 1100 bluegill in Lake Tawaga at present Year 0 Each year the population decreases by 25 from the combined effects of deaths and harvesting and at the end of each year 800 bluegill are added to the lake Let b be a sequence that represents the bluegill population n years into the future a Write a recursive formula for the sequence b b Graph the sequence b as a time plot that is as a function of time n Upload a picture of your graph

Calculus
Differential equations2 10Pts Find an equation of the plane tangent to the surface of the cone 3x y z 0 at the point P 0 2 2

Calculus
Differential equationsFor the following exercises use shells to find the volume generated by rotating the regions between the given curve and y 0 around the x axis 130 y 1 x x 0 x 1 and the x axis 131 y x x 0 x 2 and the x axis 2

Calculus
Differential equationsWilson Inc has budgeted unit sales of 204 000 units for March 2020 and 240 000 units for April 2020 The company has a policy of having an inventory of units on hand at the end of each month equal to 30 of next month s budgeted unit sales If there were 61 200 units of inventory on hand at the end of February how many units should be produced in March in order for the company to meet its goals

Calculus
Differential equationsThe time that a butterfly lives after emerging from its chrysalis can be modelled by a continuous random variable t in days whose probability density function is given by 72 f t 6 t 0 For these problems please ensure your answers are accurate to within 3 decimals Part a What is the probability that a butterfly will die within 4 days of emerging Part b If a large number of butterflies emerge on the same day after how many days would you expect only 4 to be alive Part c Calculate the mean lifetime of a butterfly after emerging from its chrysalis

Calculus
Differential equations2 Find the particular solution to the differential equation xy In x 0 with the

Calculus
Differential equations47 Express log 6 2log 3 log 316 as a single logarithm A log 6 32 316 B 6 32 109316 C log316 6 32 D log 6 3 2 316
Calculus
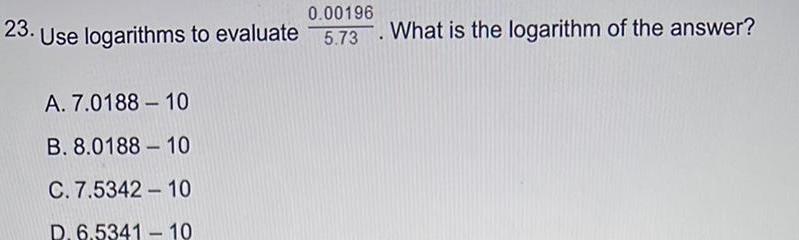
Differential equations0 00196 23 Use logarithms to evaluate 5 73 A 7 0188 10 B 8 0188 10 C 7 5342 10 D 6 5341 10 What is the logarithm of the answer
Calculus
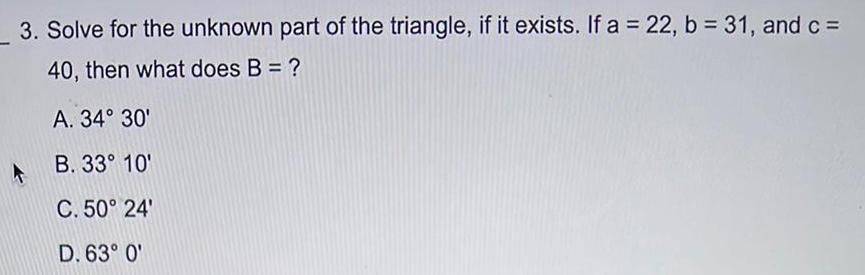
Differential equations3 Solve for the unknown part of the triangle if it exists If a 22 b 31 and c 40 then what does B A 34 30 B 33 10 C 50 24 D 63 0 4

Calculus
Differential equationsA gallon of chlorine is put into a swimming pool Each hour later for the following 6 hours the percent of chlorine that remains in the pool is measured The following information is obtained Use the data provided in the table to complete parts a through d Time Chlorine 3 4 1 2 5 6 78 3 73 2 65 148 7 31 4 21 4 remaining percent i Click the icon to view the correlation coefficient r for various values of n and a a Determine the correlation coefficient for time and percent of chlorine remaining 0 The correlation coefficient between time and percent of chlorine remaining is r Type an integer or decimal rounded to the nearest thousandth as needed
Calculus
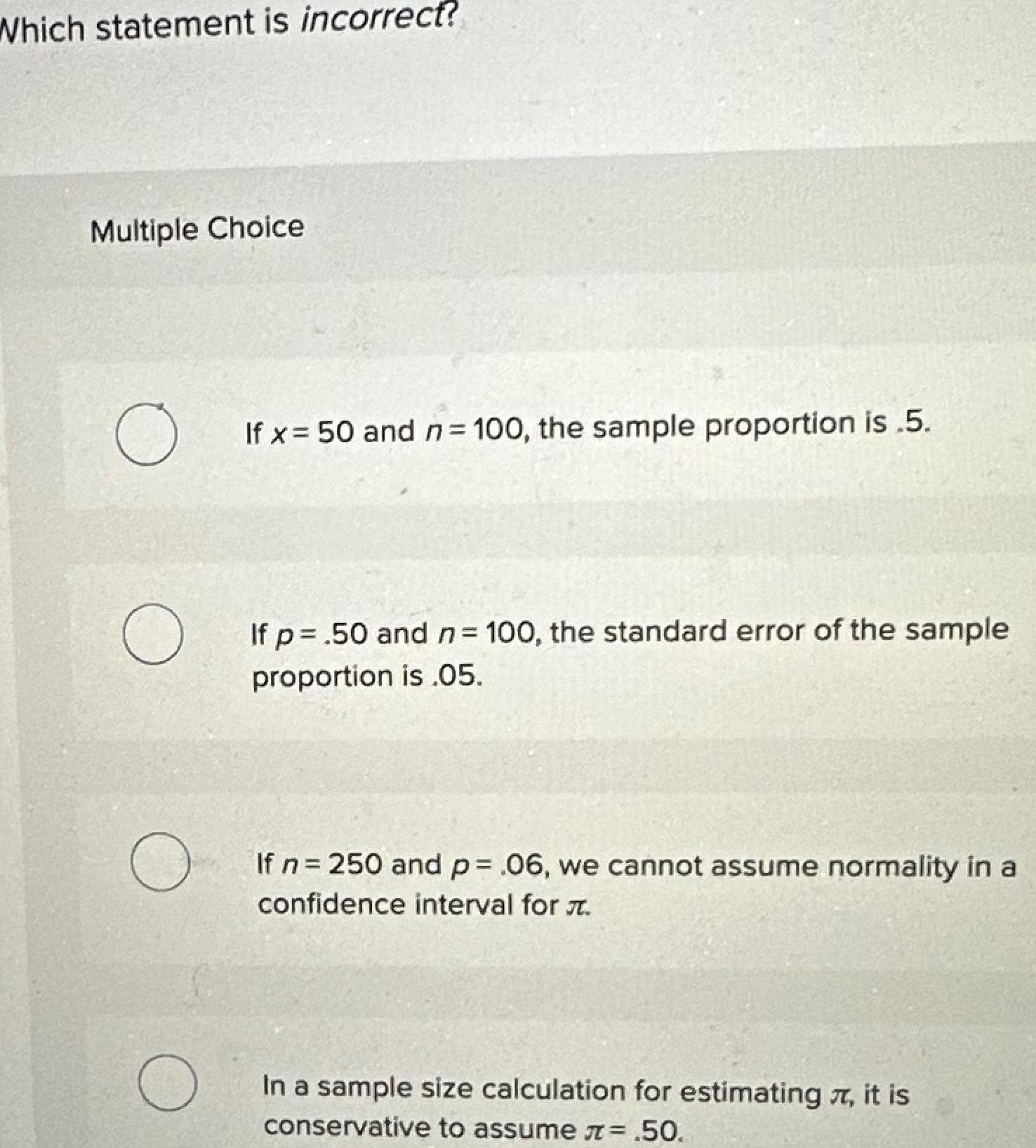
Differential equationsWhich statement is incorrect Multiple Choice O O O O If x 50 and n 100 the sample proportion is 5 If p 50 and n 100 the standard error of the sample proportion is 05 If n 250 and p 06 we cannot assume normality in a confidence interval for In a sample size calculation for estimating it is conservative to assume 50
Calculus
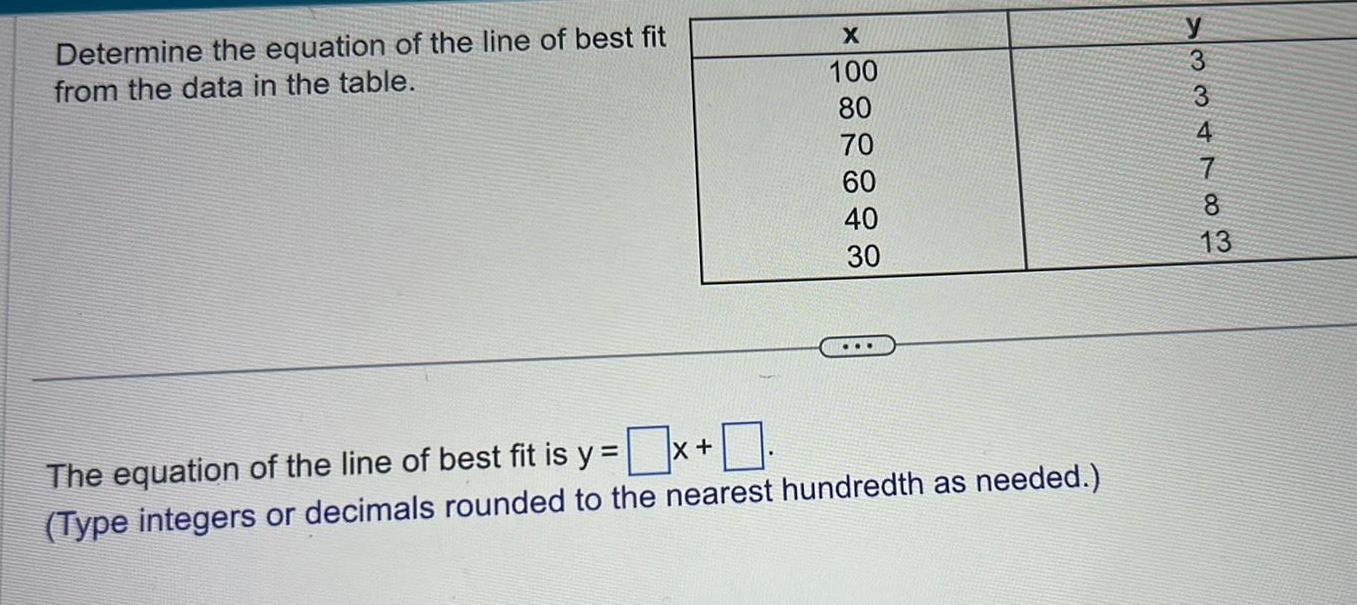
Differential equationsDetermine the equation of the line of best fit from the data in the table X 100 80 70 60 40 30 The equation of the line of best fit is y x Type integers or decimals rounded to the nearest hundredth as needed y 77433 wk 3 8 13

Calculus
Differential equationsAssume that the speed of automobiles on an expressway during rush hour is normally distributed with a mean of mph and a standard deviation of 5 mph What percent of cars are traveling faster than 72 mph Click the icon to view page 1 of the table of z scores Click the icon to view page 2 of the table of z scores The percentage of cars traveling faster than 72 mph is Type an integer or a decimal rounded to two decimal places as needed

Calculus
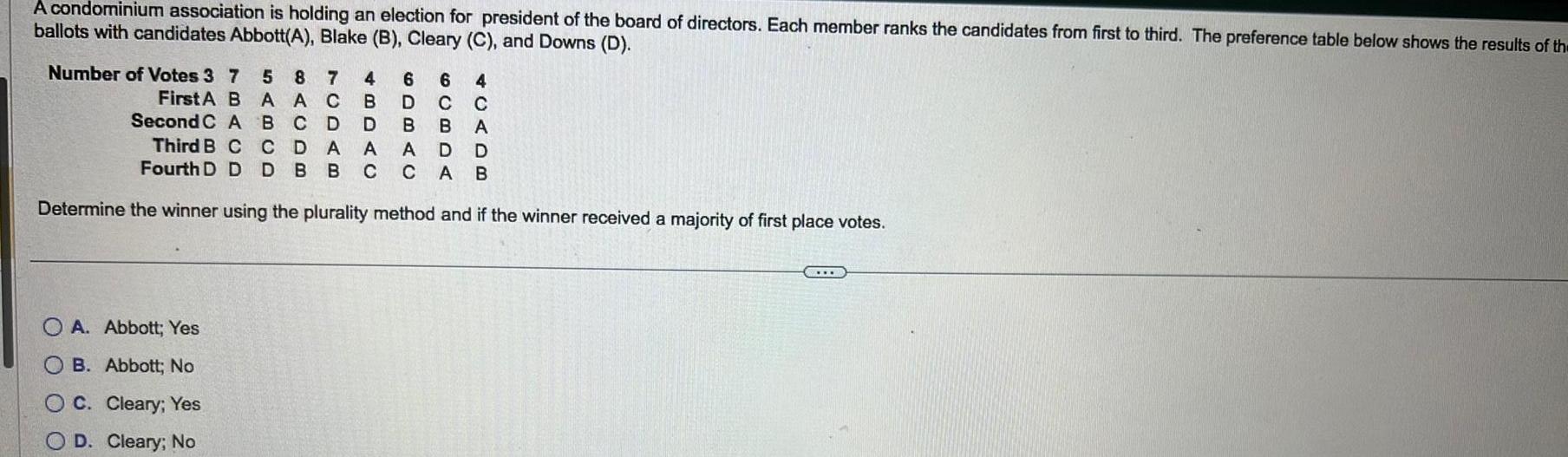
Differential equationsA condominium association is holding an election for president of the board of directors Each member ranks the candidates from first to third The preference table below shows the results of th ballots with candidates Abbott A Blake B Cleary C and Downs D Number of Votes 3 7 5 8 7 B A AC B C D CDA 4 6 6 4 B D C C D A A First A Second C A Third B C Fourth D D B B A D D D BB C C A B Determine the winner using the plurality method and if the winner received a majority of first place votes OA Abbott Yes OB Abbott No OC Cleary Yes D Cleary No

Calculus
Differential equations3 A plane heads in the direction 45 North of West at 535 mph It encounters a South wind of 55 mph What is the actual heading of the plane with respect to the ground


Calculus
Differential equationsFor 12 13 and 14 draw the area and find a the signed area bounded by y f x and the x axis from x a to x b b the absolute area bounded by y f x and the x axis from x a to x b 12 y cos x a 0 b 3 2

Calculus
Differential equationsA corn selling company determines that if it sets the price of its daypacks is set at p dollars then It can sell q 400 000 8 p 2 daypacks per year 1 Find the Revenue Function 2 What price should the daypacks be priced at to maximize revenue 3 What is that maximum Revenue
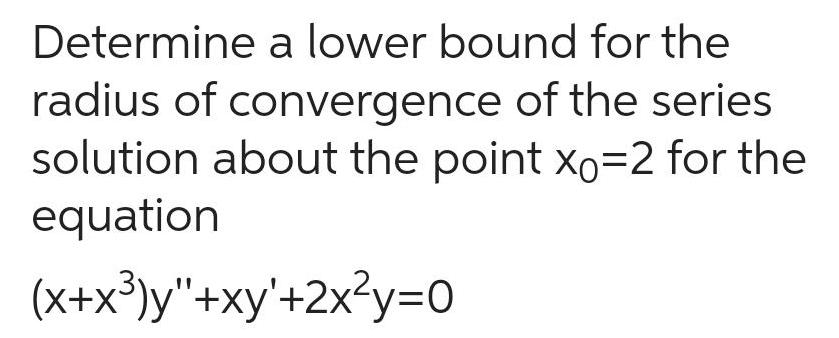
Calculus
Differential equationsDetermine a lower bound for the radius of convergence of the series solution about the point xo 2 for the equation x x y xy 2x y 0

Calculus
Differential equationsFind the derivative of f x O f x O f x O f x 3e7x 4x 3x 1 84x e7x 36x e7x 63xe 7x 30e 4x 3x 1 O f x 21e7x 12x 3 84x e7x 36x e7x 63xe7x 30e7x 4x 3x 1 84x e7x 36x e7x 63xe7x 12e7x
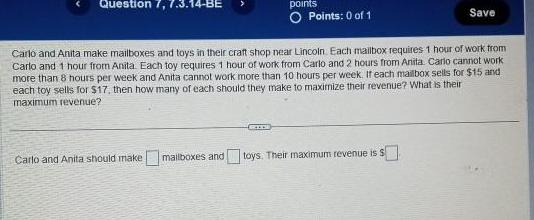
Calculus
Differential equationsQuestion 7 7 3 14 BE points O Points 0 of 1 RIDE Carlo and Anita make mailboxes and toys in their craft shop near Lincoln Each mailbox requires 1 hour of work from Carlo and 1 hour from Anita Each toy requires 1 hour of work from Carlo and 2 hours from Anita Carlo cannot work more than 8 hours per week and Anita cannot work more than 10 hours per week If each mailbox sells for 15 and each toy sells for 17 then how many of each should they make to maximize their revenue What is their maximum revenue Save Carlo and Anita should make mailboxes and toys Their maximum revenue is s
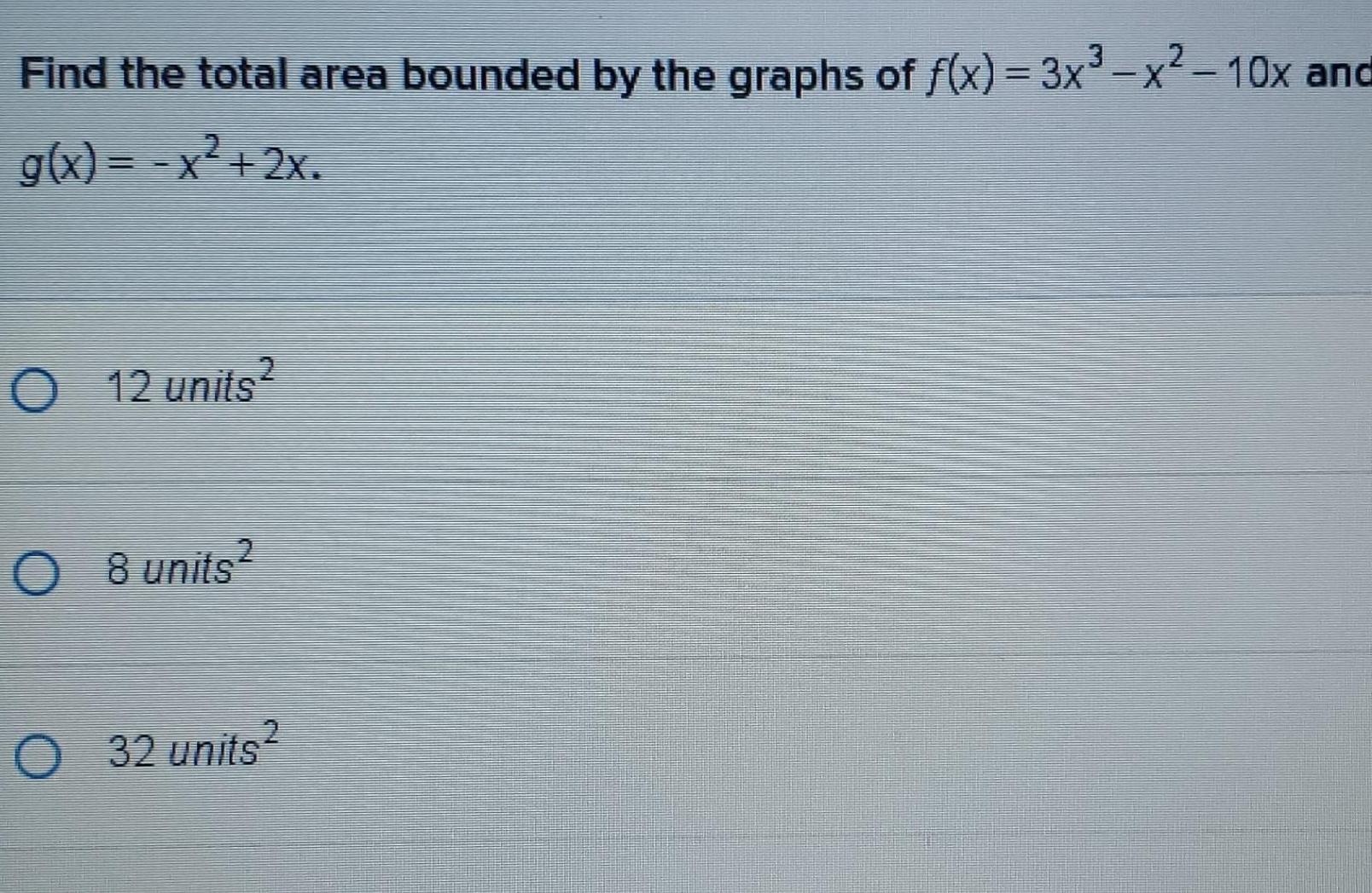
Calculus
Differential equationsFind the total area bounded by the graphs of f x 3x x 10x and g x x 2x O 12 units O 8 units2 O 32 units

Calculus
Differential equationsDeluxe coffee is to be mixed with regular coffee to make at least 52 pounds of a blended coffee The mixture must contain at least 9 pounds of deluxe coffee Deluxe coffee costs 4 per pound and regular coffee 3 per pound How many pounds of each kind of coffee should be used to minimize costs To attain the minimum cost use regular coffee pounds of deluxe coffee and pounds

Calculus
Differential equationsLet F 2xy z x yz 2xz fr d C dr using any method PE 4 and let C be the circle r t 6 cos t 5 cos t 3 sin t for 0 st 2x Evaluate 2
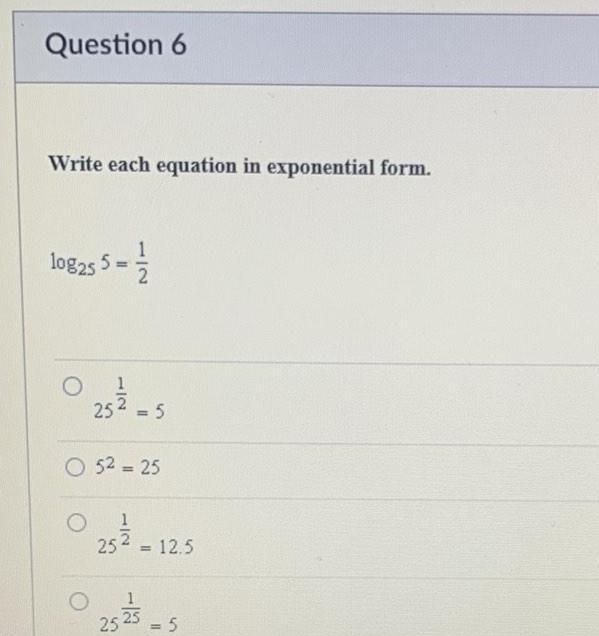
Calculus
Differential equationsQuestion 6 Write each equation in exponential form 108255 0 25 1 5 O 5 25 1 25 12 5 25 252 5

Calculus
Differential equationsFind the equation of an ellipse satisfying the given condition Foci 2 0 and 2 0 length of major axis 10 Select one 21 25 FF
Calculus
Differential equationsIdentify the conic 3x 8xy 6y Cx Dy E 0 where C D and E are constants Jelect one O a It is a hyperbola O b It is an ellipse Oc It cannot be determined Od It is a parabola
Calculus
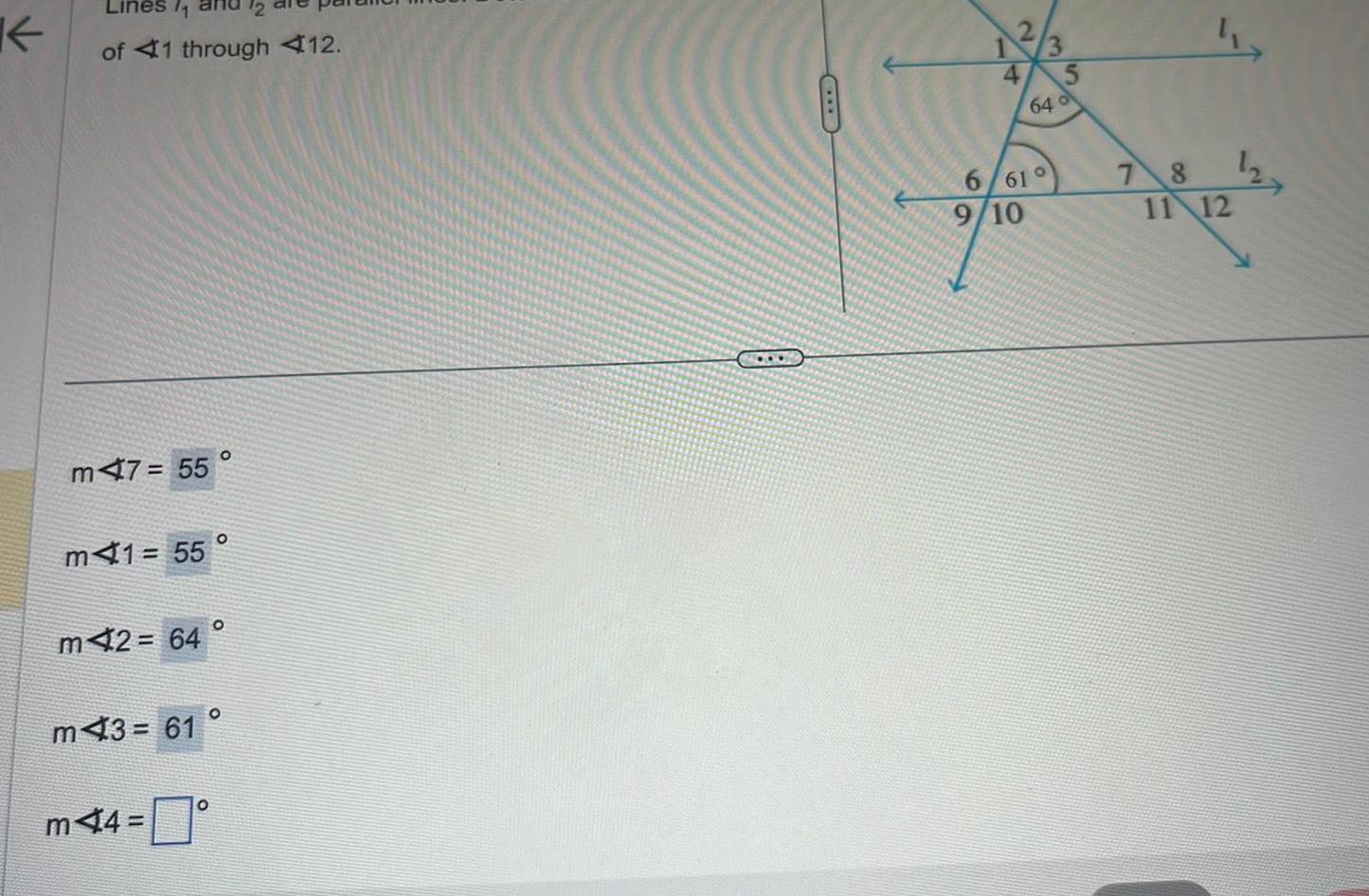
Differential equationsK 11 of 1 through 12 m47 55 m41 55 O m42 64 m44 O m43 61 O 4 64 o 6 610 9 10 78 2 11 12

Calculus
Differential equationsdealer buys a car for 19 500 00 His profit is 23 of the cost and his overhead is 6 of the cost What is his selling price