Differential equations Questions and Answers

Calculus
Differential equationsAshton has an offer to buy an item with a sticker price of 4900 by paying 140 a month for 48 months Which of these groups of values plugged into the TVM Solver of a graphing calculator will give him the correct answer for the interest rate being offered A N 4 1 PV 4900 PMT 0 FV 140 P Y 1 C Y 12 PMT END B N 4 1 PV 0 PMT 4900 FV 140 P Y 1 C Y 12 PMT END C N 4 1 PV 0 PMT 4900 FV 6720 P Y 1 C Y 12 PMT END OD N 4 1 PV 4900 PMT 0 FV 6720 P Y 1 C Y 12 PMT END

Calculus
Differential equationsFor the following exercises consider the function f x 1 x x 32 T Make a table showing the values of f for x 0 01 0 001 0 0001 0 00001 and for x 0 01 0 001 0 0001 0 00001 Round your solutions to five decimal places X 0 01 0 001 0 0001 0 00001 f x a b C d X 0 01 0 001 0 0001 0 00001 f x e f g h 33 What does the table of values in the preceding exercise indicate about the function f x 1 x x 34 To which mathematical constant does the limit in the preceding exercise appear to be getting closer

Calculus
Differential equationsA Lorenz curve is given by y L x where 0 x 1 represents the lowest fraction of the population of a society in terms of wealth and 0 sys1 represents the fraction of the total wealth that is owned by that fraction of the society Use this information to complete parts a through g Click the icon to view an example of a Lorenz curve Now show that 2A 1 2 L x dx First rewrite the expression 1 2 L x dx in terms of B 1 1 2 L x dx 1 2B Substitute the expression for B in terms of A found in a previous step for B and then simplify 1 2 0 D 1 2 24 1 1 A Therefore G 2A 1 2 L x dx by the O Substitute Simplify transitive property completing the proof e Compute the Gini index for the cases L x x and p 1 3 1 9 2 3 4 The Gini index for p 1 3 is 0 130 Type an integer or decimal rounded to three decimal places as needed The Gini index for p 19 Type an integer or decimal rounded

Calculus
Differential equationsPerform a first derivative test on the function f x x 5x 2 5 5 a Locate the critical points of the given function b Use the first derivative test to locate the local maximum and minimum values c Identify the absolute maximum and minimum values of the function on the given interval when they exist Simplify your answer Use a comma to separate answers as needed OB The function does not have a critical point b Locate the minimum value Select the correct choice below and if necessary fill in the answer box within your choice There is a local minimum at x TE 5 2 Simplify your answer OB There is no local minimum Locate the maximum value Select the correct choice below and if necessary fill in the answer box within your choice OA The absolute minimum value is Simplify your answer OA There is a local maximum at x Simplify your answer B There is no local maximum c Identify the absolute minimum value of the function Select the correct choice below and if necessary fill in the answer boxes to complete your


Calculus
Differential equationsGiven the function f x 3x 10 find the net signed area between f x and the x axis over the interval 6 2 Do not include any units in your answer

Calculus
Differential equationsDirections The following function f x has one relative maximum and one relative minimum point Find these points using the First Derivative Test and a sign chart f x x 27x Part 1 Critical Numbers 1 Find the derivative f x 2 List the z values where f x 0 separate by commas Part 2 Intervals of Increase and Decrease Since there are two critical numbers there should be three intervals to consider on our sign chart State the indicated interval below and whether the function is increasing or decreasing there Help with entering help intervals 1 The left most interval is and there the function is inc or dec 2 The middle interval is 3 The right most interval is and there the function is inc or dec and there the function is inc or dec

Calculus
Differential equationsPart 1 Intervals of Concavity 1 Find the open interval s on which f is concave up 2 Find the open interval s on which f is concave down f x x 8x 24x x 6 Part 2 Inflection Points 1 Find the x values s where f has an inflection point Answer 0 00 Answer Formats If necessary use INF and INF to denote and o If the function does not have any enter NONE If the function has more than one type your answer as a comma separated list For example a1 b a2 b Answer none Answer

Calculus
Differential equationsUse a calculator in radian mode to find approximations for coss and sins for the number s 3 86 These are NOT exact values they are only approximations Then determin the quadrant in which the point on the unit circle corresponding to s lies Finally find approximations for tan s cots secs and csc s sin 3 86 Round to three decimal places ACCED

Calculus
Differential equationsDirections Consider the following function f z at a 2 Part 1 Difference Quotient It h 0 then the difference quotient can be simplified into the form Ah B That is 2 h f 2 Ah B h where A and B are constants Find these constants A 0 and B2 Note It s possible for one or more of these constants to be 0 Part 2 Derivative Use the simplified expression from Part 1 to then calculate the derivative f 2 f 2 2 f x 2x 6 where A and B are constants Find these constants A 0 and B 2 Note It s possible for one or more of these constants to be 0 f 2 2 f 2 lim h f 2 h f 2 J 21 J 2 h Part 2 Derivative Use the simplified expression from Part 1 to then calculate the derivative f 2 f 2 lim 40 Part 3 Tangent Line Find the equation of the tangent line to the curve y f a at a 2 Tangent Line y Ah B f 2 h f 2 h



Calculus
Differential equationsUse the formula to find the value of the missing variable 0 radians t 9 sec radians per sec Simplify your answer Use integers or fractions for any numbers in the expression Type an exact answer as needed

Calculus
Differential equationsLet L be the line through points P and Q in the figure a Suppose P 4 2 and Q 8 5 Find the slope of L and the length of d b As the point Q moves towards P along the curve does the slope of L increase or decrease a The slope of Lis d

Calculus
Differential equationsConvert the following degree measure to radians 270 270 radians Simplify your answer Type an exact answer using as needed

Calculus
Differential equationsConvert the following angle to decimal degree notation 31 9 31 9 Round to two decimal places as needed

Calculus
Differential equationsFind the intervals on which f is increasing and the intervals on which it is decreasing f x cos x on Select the correct choice and if necessary fill in the answer box es within your choice A The function is increasing on the open interval s and decreasing on the open interval s Simplify your answers Type your answers in interval notation Type exact answers using as needed Use a comma to separate answers as need OB The function is increasing on the open interval s The function is never decreasing Simplify your answer Type your answer in interval notation Type exact answers using as needed Use a comma to separate answers as needed OC The function is decreasing on the open interval s The function is never increasing Simplify your answer Type your answer in interval notation Type exact answers using as needed Use a comma to separate answers as needed OD The function is never increasing or decreasing

Calculus
Differential equationsConsider an object moving along a line with the following velocity and initial position v t 16 1 on 0 5 s 0 3 Determine the position function for 120 using both the antiderivative method and the Fundamental Theorem of Calculus Check for agreement between the two methods To determine the position function for 120 using the antiderivative method first determine how the velocity function and the position function are related Choose the correct answer below OA The position function is the absolute value of the antiderivative of the velocity function OB The position function is the derivative of the velocity function OC The velocity function is the antiderivative of the absolute value of the position function D The position function is the antiderivative of the velocity function Which equation below will correctly give the position function according to the Fundamental Theorem of Calculus b OA s t s 0 v t d Sv t dt a t Sv x dx 0 CELLE OC s 0 s t b OB s t Sv tydt a t Sv x dx 0 D s t s 0 Determine the position function for t20 using both methods Select the correct choice below and fill in the answer box es to complete your choice OA The same function is obtained using each method The position function is s t OB Different functions are obtained using each method The position function obtained using the antiderivative method is s t and the position function obtained using the Fundamental Theo
Calculus
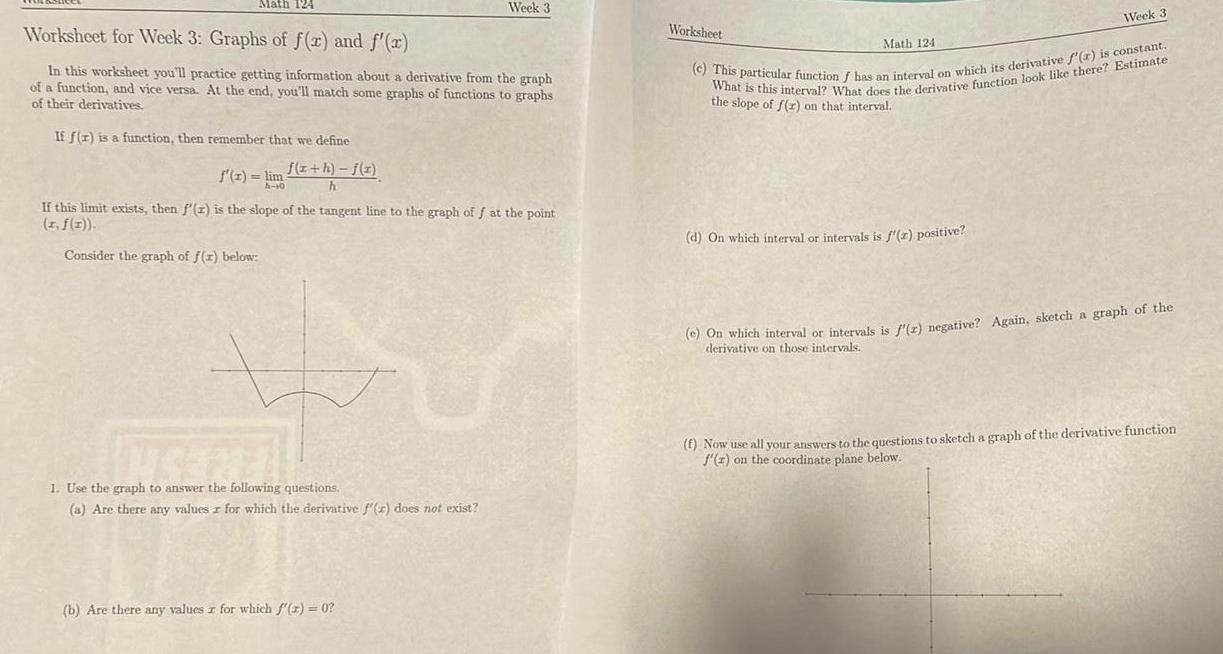
Differential equationsMath 124 Worksheet for Week 3 Graphs of f x and f x In this worksheet you ll practice getting information about a derivative from the graph of a function and vice versa At the end you ll match some graphs of functions to graphs of their derivatives If f r is a function then remember that we define f x h f x h f x lim A 10 Week 3 If this limit exists then f z is the slope of the tangent line to the graph off at the point I f x Consider the graph of f x below UNSERE 1 Use the graph to answer the following questions a Are there any values for which the derivative f x does not exist b Are there any values z for which f x 0 Worksheet Math 124 Week 3 c This particular function f has an interval on which its derivative f r is constant What is this interval What does the derivative function look like there Estimate the slope of f r on that interval d On which interval or intervals is f x positive e On which interval or intervals is f r negative Again sketch a graph of the derivative on those intervals f Now use all your answers to the questions to sketch a graph of the derivative function f z on the coordinate plane below

Calculus
Differential equationsDetermine whether the statement is true or false lim x x245 5x 6 X 1 True False x 45X6 lim x 1 x 4x 5 lim x 4x 5 X 1

Calculus
Differential equationsA simple model for the flow of air in and out of the lungs of a certain mammal is given by the following equation where V t measured in liters is the volume of air in the lungs at time 120 tis me in seconds and t 0 corresponds to a time at which the lungs are full and exhalation begins Only a fraction of the air in the lungs is exchanged with each breath The amount that is exchanged is the tidal volume Complete parts a through c below V t T sin a Find the volume function V assuming that V 0 14 L Notice that V changes over time at a known rate V Which equation below correctly gives the volume function A V t V 0 V x dx Sv x d 0 OC V t V 0 at V t 13 cos at 2 b a Find the volume function V assuming that V 0 14 L t dt Type an exact answer COLLE b What is the breathing rate in breaths minute The breathing rate is 15 breaths minute Type an integer or a simplified fraction c What is the tidal volume and what is the total capacity of the lungs Sv x dx 0 OB V 0 V t b OD V 0 V t V t di fv t dt a

Calculus
Differential equations5 Each angle measure is given in degrees Write the corresponding angle measure in radians a 0 60 b 0 72 c 0 200 d 0 450
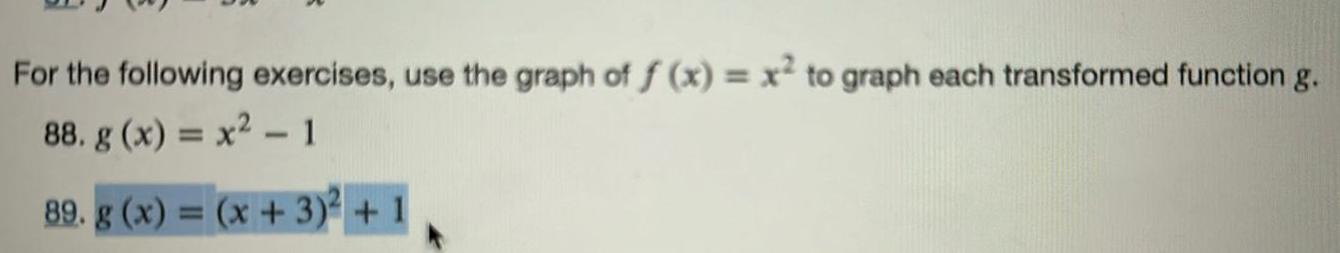
Calculus
Differential equationsFor the following exercises use the graph of f x x to graph each transformed function g 88 g x x 1 89 g x x 3 1
Calculus
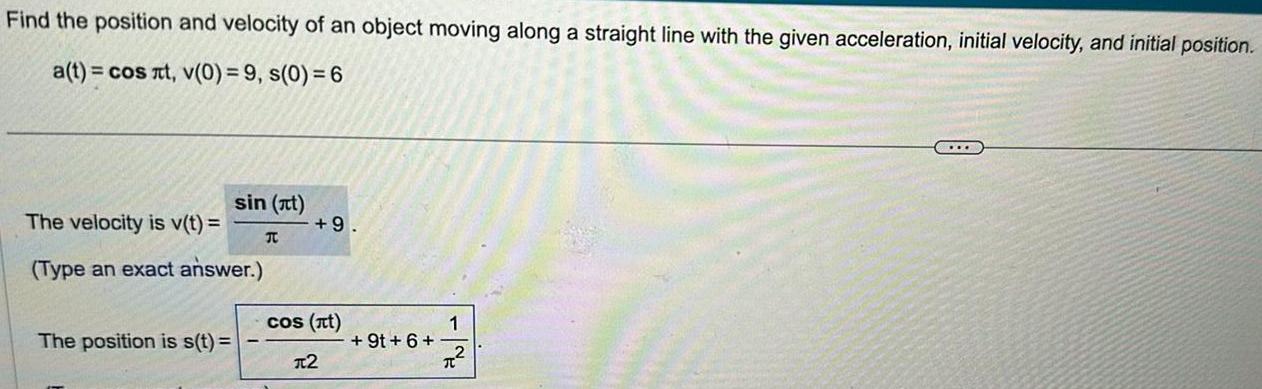
Differential equationsFind the position and velocity of an object moving along a straight line with the given acceleration initial velocity and initial position a t cos t v 0 9 s 0 6 sin it The velocity is v t Type an exact answer The position is s t T 9 cos t 2 9t 6 1 C

Calculus
Differential equationsA rancher raises goats and llamas on her 500 acre ranch Each goat needs 3 acres of land and requires 100 of veterinary care per year and each llama requires 5 acres of land and requires 120 of veterinary care per year The rancher can afford no more than 11 700 for veterinary care this year If the expected profit is 60 for each goat and 100 for each llama how many type of each animal should she raise to obtain the maximum profit SET UP BUT DO NOT SOLVE BE SURE TO PUT YOUR MAXIMIZE OR MINIMIZE EQUATION ALSO

Calculus
Differential equationsEstablish the identity 1 sin 0 sec 0 1 Which of the following shows the key steps in establishing the identity O A OB 1 sin 20 sec 0 csc 0 cos 0 1 sin 20 sec 0 tan 0 sec 0 1 sin 20 1 sin20 sec 0 cos 0sec 0 1 2 sec 0 cos 0 cos 0 cot 0 sec 0 tan 0 20 1 OC 1 sin20 sec 0 sec 0 sin 0 sec 0 sec 0 tan OD 1 sin e sec 0 cos 20 cos 20 1

Calculus
Differential equationsThe figure below shows a fixed circle C with equation x 1 2 y2 1 and another shrinking circle C centered at the origin with positive y intercept P 0 r Let Q be the point of intersection between the two circles pictured draw a line through P am Q and let R be the x intercept of that line b The line through P and Q has equation y a Find the coordinates of the point Q your answers will involve r Q c The point R lim R d 20 y X O C R

Calculus
Differential equationsA circle of radius r centered at the point 0 r in the plane will intersect the y axis at the origin and the point A 0 2r as pictured below A line passes through the point A and the point C 3 2 0 on the x axis In this problem we will investigate the coordinates of the intersection point B between the circle and the line as roo A 0 2r Y 0 0 B a The line through A and C has equation b The x coordinate of the point B is c The y coordinate of the point B is d The limit as roo of the x coordinate of B is e The limit as roo of the y coordinate of B is if your answer is oo write infinity if your answer is oo write infinity

Calculus
Differential equationsUse the given graph off to state the value of each quantity if it exists If an answer does not exist enter DNE a lim f x x 2 b lim f x c lim f x x 2 d f 2 e lim f x X 4 f f 4 2 0 2 4


Calculus
Differential equations3 x Find the intervals of increasing decreasing for the function f x x e Find the minimum value s of the function f x e 2x The position of a particle as it moves horizontally is described by the given equation S s sint cost 0 t 2 If s is the displacement in metres and t is the time in seconds find the maximum and minimum displacements

Calculus
Differential equations4 Points DETAILS The cup on the 9th hole of a golf course is located dead center in the middle of a circular green which is 40 feet in radius Your ball is located as in the picture below The ball follows a straight line path and exits the green at the right most edge Assume the ball travels 9 ft sec Introduce coordinates so that the cup is the origin of an xy coordinate system Provide numerical answers below with two decimal places of accuracy 50 feet green ball 40 feet 9 cup smallest x coordinate largest x coordinate ball pathi rough a The x coordinate of the position where the ball enters the green will be MY NOTES seconds after it is hit b The ball will exit the green exactly c Suppose that L is a line tangent to the boundary of the golf green and parallel to the path of the ball Let Q be the point where the line is tangent to the circle Notice that there are two possible positions for Q Find the possible x coordinates of Q



Calculus
Differential equationsB G R Match each equation with a graph above y 2 0 84 y 2 0 75 y 3 1 29 y 2 1 54 y 2 1 29 a blue B b green G C orange 0 d black K


Calculus
Differential equations1 Solve the Initial Value Problem by using the Laplace Transform Show all your calculations y t 2y t 8y t 0 y 0 m y 0 n where m and n are last two digits of your student ID number 2 Find the Fourier Series for the periodic function f x m 1 x n x TT where m and n are last two digits of your student ID number m 4 and n 0 50 points 50 points

Calculus
Differential equationsUnit 5 Question 2 of 8 This quiz 28 point s possible This question 2 point s poss Does the function satisfy the hypotheses of the mean value theorem on the given interval Give reasons for your answer 8 9 f x x 10 11 Choose the correct answer OA No f x is differentiable for every point in 0 1 but is not continuous for every point of 0 1 B Yes f x is continuous for every point of 0 1 and differentiable for every point in 0 1 OC No f x is continuous for every point of 0 1 but is not differentiable for every point in 0 1 OD Yes f x is continuous for every point of 0 1 and differentiable for every point in 0 1


Calculus
Differential equationsAn exponential function G has a known common ratio of and includes the input ouut pair 1 4 Which of the following could define G z B C 4 1 x 1 4 4

Calculus
Differential equations1 The table shows the total weight of shrimp a fisherman catches each week Time weeks Weight pounds 2 3 5 6 110 130 170 500 530 What is the average rate of change from Week 2 to 5 in pounds per week

Calculus
Differential equationsDetermine where the function f x is continuous f x 4 x The function is continuous on the interval Simplify your answer Type your answer in interval notation

Calculus
Differential equationsA Calculate the change in Fox from x 8 to x 13 8 Graph F x and use geometric formulas to calculate the area between the graph of F and the x axis from x 8 to x 13 C Verily that your answers from A and B are equal as quaranteed by the fundamental theorem of calculus A Calculate the change in F x from x 8 to x 13 The change is Simplify your answer B Graph F x and use geometric formulas to calculate the area between the graph of F x and the x axis from x 8 to x 13 Choose the graph of F x below OA 400 UND 5000 The area between the graph of F x and the x axis from x 8 to x 13 Simplify your answer 10 C Verity that your answers from A and 8 are equal as guaranteed by the fundamental theorem of calculus Are your answers in part A and part B equal Yes DR O 553

Calculus
Differential equationsAssuming that x 0 use differentiation to justify the formula dx In x C if Sdx In x C then The derivative of In x is and the derivative of a constant C is so dx In x C for x 0 dx In x C for x 0

Calculus
Differential equationsUse the given information to sketch the graph off Domain All real x except x 6 and x 6 9 4 1 0 0 1 9 4 f x 0 on 6 and 6 oo f x 0 on 6 6 f x 0 on 6 and 6 0 f x 0 on 0 6 and 6 co Vertical asymptotes x 6 and x 6 Horizontal asymptote y 0 Choose the correct graph below O A LV OB 12 Q Q 63 O C 1 16 Q Q

Calculus
Differential equationsSketch the graph given the following conditions f 3 0 f 9 0 f 2 0 f 3 0 f 9 20 f 2 1 f 3 8 f 9 6


Calculus
Differential equationsSuppose that you meet 20 new people each year but each year you forget 20 of all of the people that you know If y t is the total number of people who you remember after t years then y satisfies the differential equation y 200 2y Do you see why Solve this differential equation subject to the condition y 0 0 you knew no one at birth y

Calculus
Differential equationsA medical examiner called to the scene of a murder will usually take the temperature of the body A corpse cools at a rate proportional to the difference between its temperature and the temperature of the room If y t is the temperature in degrees Fahrenheit of the body t hours after the murder and if the room temperature is 60 then y satisfies y 0 32 y 60 y 0 98 6 body temperature initially 98 6 a Solve this differential equation and initial condition y b Use your answer to part a to estimate how long ago the murder took place if the temperature of the body when it was discovered was 80 Hint Find the value of t that makes your solution equal 80 Round your answer to two decimal places t hr
