Differential equations Questions and Answers

Calculus
Differential equations5 2 1 a 5 g x 9 7 C 7 b 145 y c 2 The continuous function g x is odd and increasing with selected values shown in the table above Find the values of a and b If the average rate of change of g x over the interval 1 5 is 2 find the value of c
Calculus
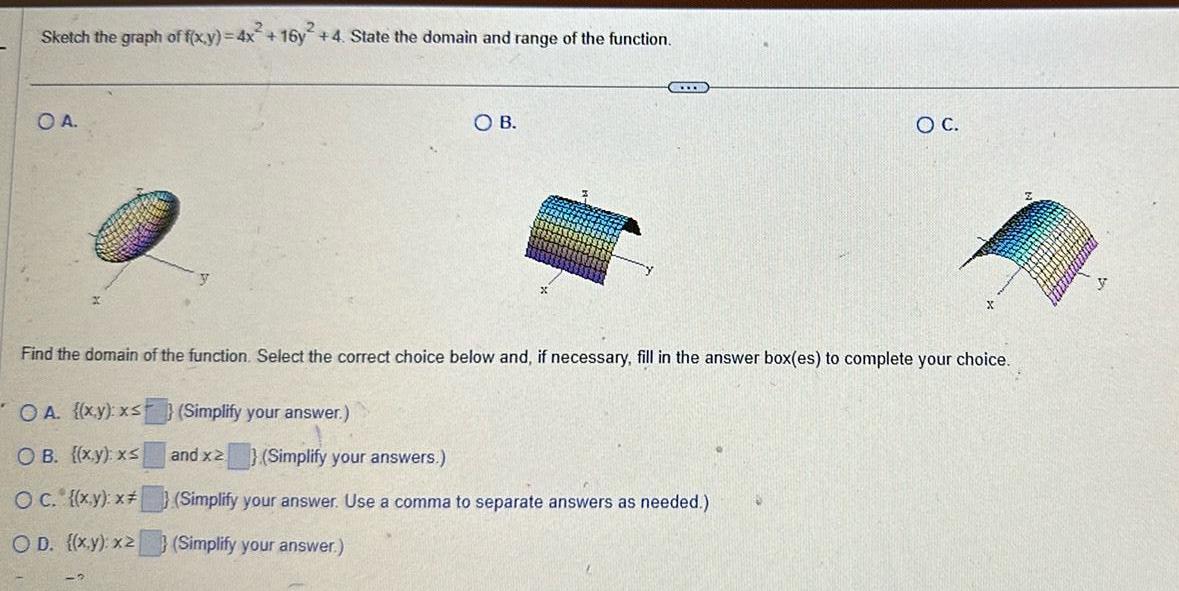
Differential equationsSketch the graph of f x y 4x 16y 4 State the domain and range of the function O A OA x y x Simplify your answer OB x y xs OC x y x OD x y x2 Simplify your answer SOB C Find the domain of the function Select the correct choice below and if necessary fill in the answer box es to complete your choice and x2 Simplify your answers Simplify your answer Use a comma to separate answers as needed O C 2 y

Calculus
Differential equationsConsider the function f t 1 2t 41 What is the smallest value of such that the relative rate of change is given by R 2 Give your answer as a decimal
Calculus
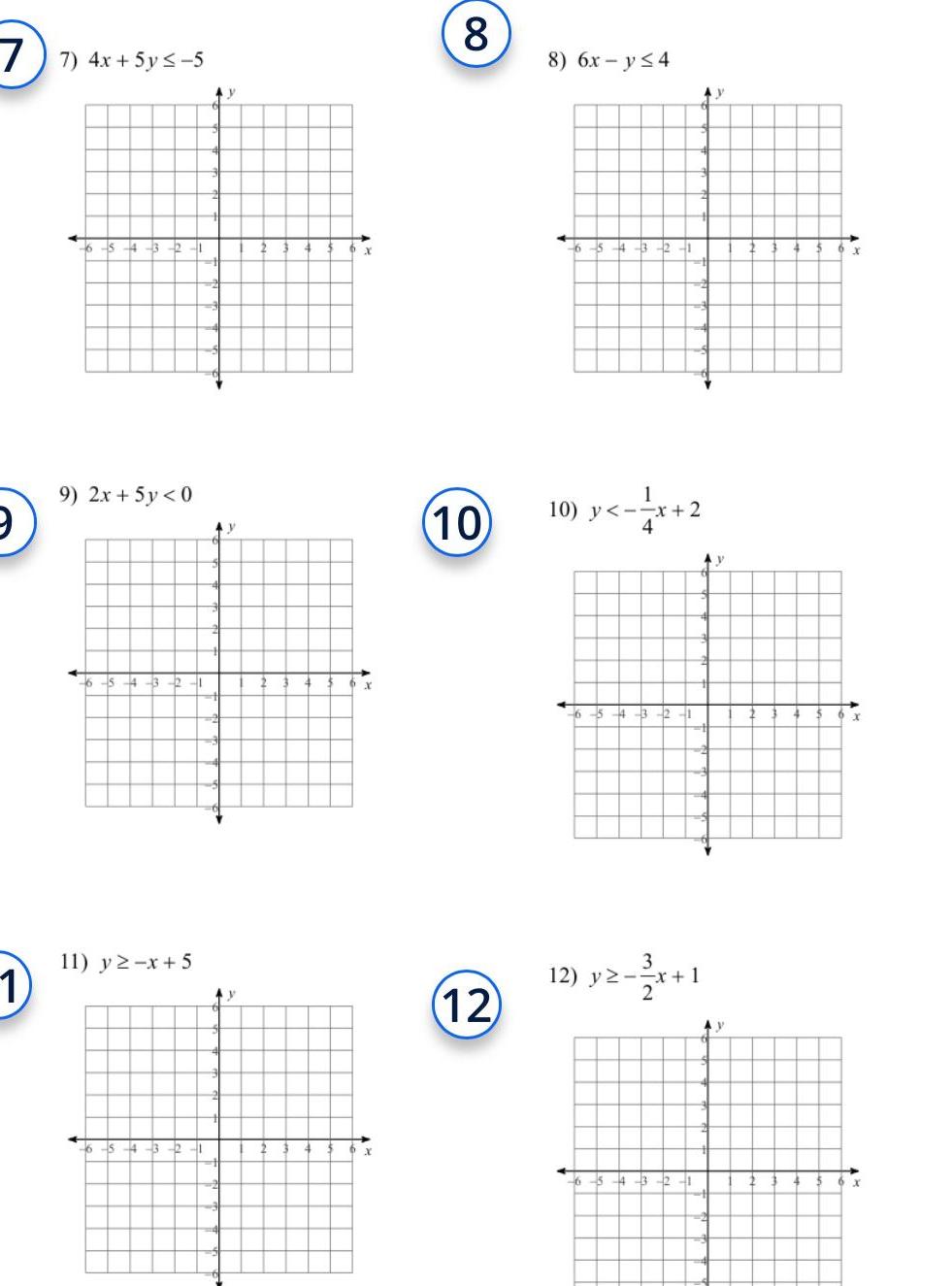
Differential equations77 4x 5y 5 9 1 54321 9 2x 5y 0 6 15 s 4 3 2 1 11 y x 5 54321 y Ay y 23 X 4 X x 8 10 12 8 6x y 4 6 5 4 3 2 1 10 y x 2 6 5 4 3 41 12 y2 3x 1 6543 2 AY Ay Ay 43 15 x 15 X

Calculus
Differential equationsx 5 MR 6 5 36 66 When Hence the required marginal revenue is 66 EXERCISE 6 1 1 Find the rate of change of the area of a circle with respect to its radius r when a r 3 cm b r 4 cm 2 The volume of a cube is increasing at the rate of 8 cm s How fast is the surface area increasing when the length of an edge is 12 cm 3 The radius of a circle is increasing uniformly at the rate of 3 cm s Find the rate at which the area of the circle is increasing when the radius is 10 cm 4 An edge of a variable cube is increasing at the rate of 3 cm s How fast is the volume of the cube increasing when the edge is 10 cm long 5 A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm s At the instant when the radius of the circular wave is 8 cm how fast is the enclosed area increasing Rationalised 2023 24 APPLICATION OF DERIVATIVES 151 6 The radius of a circle is increasing at the rate of 0 7 cm s What is the rate of increase of its circumference 7 The length x of a rectangle is decreasing at the rate of 5 cm minute and the width y is increasing at the rate of 4 cm minute When x 8cm and y 6cm find the rates of change of a the perimeter and b the area of the rectangle 8 A balloon which always remains spherical on inflation is being inflated by pumping in 900 cubic centimetres of gas per second Find the rate at which the radius of the balloon increases when the radius is 15 cm 9 A balloon which always remains spherical has a variable radius Find the rate at which its volume is increasing with the radius when the later is 10 cm 10 A ladder 5 m long is leaning against a wall The bottom of the ladder is pulled along the ground away from the wall at the rate of 2cm s How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall 11 A particle moves along the curve 6y x 2 Find the points on the curve at which the y coordinate is changing 8 times as fast as the x coordinate the 12 The radius of an air bubble is increasing at the rate of cm s At what rate is the volume of the bubble increasing when the radius is 1 cm 3 2 2x 1 13 A balloon which always remains spherical has a variable diameter Find the rate of change of its volume with respect to x 14 Sand is pouring from a pipe at the rate of 12 cm s The falling sand forms a cone on the ground in such a way that the height of the cone is always one sixth of the radius of the base How fast is the height of the sand cone increasing when the height is 4 cm 15 The total cost C x in Rupees associated with the production of x units of an item is given by C x 0 007x 0 003x 15x 4000 Find the marginal cost when 17 units are produced 16 The total revenue in Rupees received from the sale of x units of a product is given by

Calculus
Differential equationsdt Thus the enclosed area is increasing at the rate of 80 cm s when dy Note is positive if y increases as x ncreases and negative if y decreases dx as x increases Example 4 The length x of a rectangle is decreasing at the rate of 3 cm minute and the width y is increasing at the rate of 2cm minute When x 10cm and y 6cm find the rates of change of a the perimeter and b the area of the rectangle Solution Since the length x is decreasing and the width y is increasing with respect to time we have and a The perimeter P of a rectangle is given by P 2 x y dP dt b The area A of the rectangle is given by A x y 150 dx dt Therefore When not be MATHEMATICS 2 dA dt dx dy dt dt dy dt Marginal Revenue When dx dt 3 6 10 2 as x 10 cm and y 6 cm 2 cm min y x Rationalised 2023 24 cost MC 2 cm min dy dt Example 5 The total cost C x in Rupees associated with the production of x units of an item is given by 2 3 2 2 cm min C x 0 005x 3 0 02 x 30x 5000 Find the marginal cost when 3 units are produced where by marginal cost we mean the instantaneous rate of change of total cost at any level of output dC dx Solution Since marginal cost is the rate of change of total cost with respect to the output we have Marginal 10 cm 0 005 3x 0 02 2x 30 x 3 MC 0 015 3 0 04 3 30 0 135 0 12 30 30 015 Hence the required marginal cost is 30 02 nearly Example 6 The total revenue in Rupees received from the sale of x units of a product is given by R x 3x 36x 5 Find the marginal revenue when x 5 where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant p rd Solution Since marginal revenue is the rate of change of total revenue with respect to the number of units sold we have dR dx x 5 MR 6 5 36 66 MR 6x 36

Calculus
Differential equationswhich its volume is increasing with the radius when the later is 10 cm 10 A ladder 5 m long is leaning against a wall The bottom of the ladder is pulled along the ground away from the wall at the rate of 2cm s How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall 11 A particle moves along the curve 6y x 2 Find the points on the curve at which the y coordinate is changing 8 times as fast as the x coordinate 12 The radius of an air bubble is increasing at the rate of cm s At what rate is the volume of the bubble increasing when the radius is 1 cm 3 2x 1 13 A balloon which always remains spherical has a variable diameter 2x Find the rate of change of its volume with respect to x 14 Sand is pouring from a pipe at the rate of 12 cm s The falling sand forms a cone on the ground in such a way that the height of the cone is always one sixth of the radius of the base How fast is the height of the sand cone increasing when the height is 4 cm 15 The total cost C x in Rupees associated with the production of x units of an item is given by x in Rupe C x 0 007x 0 003x 15x 4000 Find the marginal cost when 17 units are produced 16 The total revenue in Rupees received from the sale of x units of a product is given by Find the marginal revenue when x 7 Choose the correct answer for questions 17 and 18 17 The rate of change of the area of a circle with respect to its radius r at r 6 cm is A 10T B 12 C 8T D 11T 152 MATHEMATICS 18 The total revenue in Rupees received from the sale of x units of a product is given by R x 3x 36x 5 The marginal revenue when x 15 is A 116 B 96 C 90 D 126 6 3 Increasing and Decreasing Functions In this section we will use differentiation to find out whether a function is increasing or decreasing or none Values left to origin f x x R x 13x 26x 15 Consider the function f given by f x x x R The graph of this function is a parabola as given in Fig 6 1 X 2 3 2 1 1 2 4 9 4 Rationalised 2023 24 1 1 4 X 0 0 as we move from left to right the height of the graph decreases f x height of graph at x EX 2 10 Values right to origin f x x X 0 10 132 0 1 4 1 9 4 2 4 as we move from left to right the height of the graph increases

Calculus
Differential equationsListen Find the degree measure that corresponds to the giv 5t 6 a 216 b 216 c 150 T d 150

Calculus
Differential equationsListen Which of the following angles is co terminal with an angle that measures Select all that apply a 120 b 960 c 60 d 360 240
Calculus
Differential equations4 A small oil refinery estimates that its daily profit P in dollars from refining barrels of oil is P 8x 0 02x2 How many barrels should be refined for maximum daily profit and what is the maximum profit Paragraph V BI U A DII OB EE
Calculus
Differential equationswide is being filled at the rate of 0 80 m min At one end it is 1 0 m deep and at the other end it is 2 5 m deep with a constant slope between ends How fast is the height of water rising when the depth of water at the deep end is 1 0 m Paragraph M B I U A EE PIL o v

Calculus
Differential equations4 is continuous at x g Proof We are investigating continuity of f g at x c Clearly it is defined at x c We have 114 lim f g x MATHEMATICS provided g c 0 lim f x g x X C lim f x lim g x X C X C f c g c f g c Hence f g is continuous at x c Proofs for the remaining parts are similar and left as an exercise to the reader Rationalised 2023 24 Remarks i As a special case of 3 above iffis a constant function i e f x for some real number 2 then the function 2 g defined by 2 g x 2 g x is also continuous In particular if 1 the continuity of fimplies continuity of f ii As a special case of 4 above if f is the constant function f x 2 then the 2 2 2 function defined by x is also continuous wherever g x 0 In g g x g particular the continuity of g implies continuity of g by definition of f g by the theorem on limits as fand g are continuous by definition of f g The above theorem can be exploited to generate many continuous functions They also aid in deciding if certain functions are continuous or not The following illustrate this examples Example 16 Prove that every rational function is continuous Solution Recall that every rational function fis given by q x 0 p x q x f x where p and q are polynomial functions The domain offis all real numbers except points at which qis zero Since polynomial functions are continuous Example 14 fis continuous by 4 of Theorem 1 Example 17 Discuss the continuity of sine function Solution to see this we use the following facts We have not proved it but is intuitively clear from the graph of sin x near 0 Now observe that f x sin x is defined for every real number Let c be a real xc we know that h 0 Therefore number Put x c h lim f x lim sin x X C X C oblishe lim sin c h h 0 lim sinc cos h cos c sin h h 0 lim Isin c cos hl lim cosc sin hl
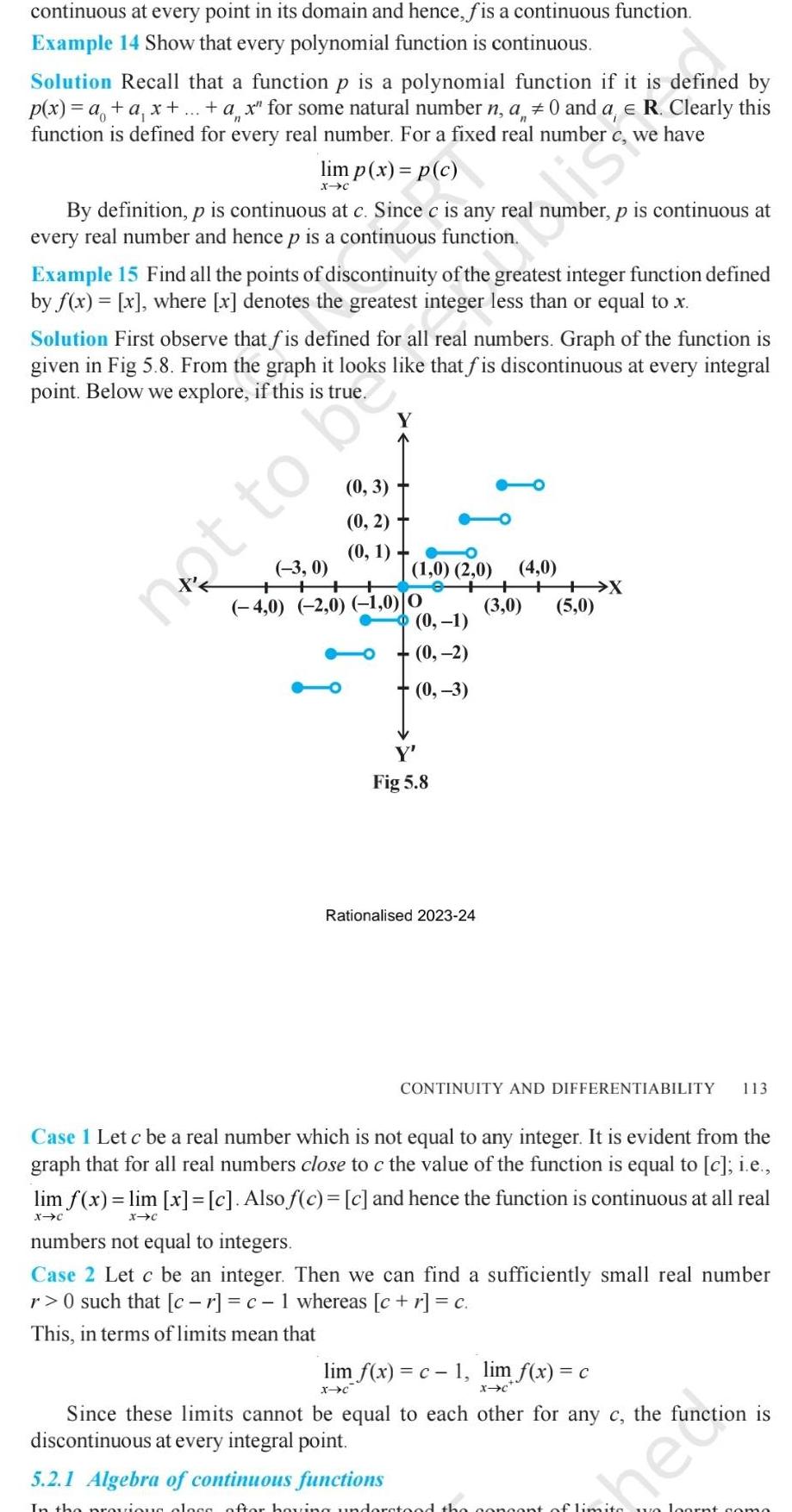
Calculus
Differential equationscontinuous at every point in its domain and hence f is a continuous function Example 14 Show that every polynomial function is continuous Solution Recall that a function p is a polynomial function if it is defined by p x a a x ax for some natural number n a 0 and a e R Clearly this function is defined for every real number For a fixed real number c we have lim p x p c X C By definition p is continuous at c Since c is any real number p is continuous at every real number and hence p is a continuous function Example 15 Find all the points of discontinuity of the greatest integer function defined by f x x where x denotes the greatest integer less than or equal to x Solution First observe that fis defined for all real numbers Graph of the function is given in Fig 5 8 From the graph it looks like that fis discontinuous at every integral point Below we explore if this is true Y 0 3 0 2 0 1 3 0 4 0 2 0 1 0 0 1 0 2 0 not to b 0 1 0 2 0 3 Y Fig 5 8 Rationalised 2023 24 4 0 3 0 X 5 0 CONTINUITY AND DIFFERENTIABILITY 113 Case I Let c be a real number which is not equal to any integer It is evident from the graph that for all real numbers close to c the value of the function is equal to c i e lim f x lim x c Also f c c and hence the function is continuous at all real X C X C numbers not equal to integers Case 2 Let c be an integer Then we can find a sufficiently small real number r 0 such that cr c 1 whereas c r c This in terms of limits mean that lim f x c 1 lim f x c X C X C Since these limits cannot be equal to each other for any c the function is discontinuous at every integral point 5 2 1 Algebra of continuous functions In the previous clogs after having understood the concept of limits we loont como he Anction

Calculus
Differential equationsBetween 2006 and 2016 the number of applications for patents N grew by about 4 2 per year That is N t 0 042N t Find the function that satisfies this equation Assume that t 0 corresponds to 2006 when approximately 456 000 patent applications were received Estimate the number of patent applications in 2021 Estimate the rate of change in the number of patent applications in 2021 a b c
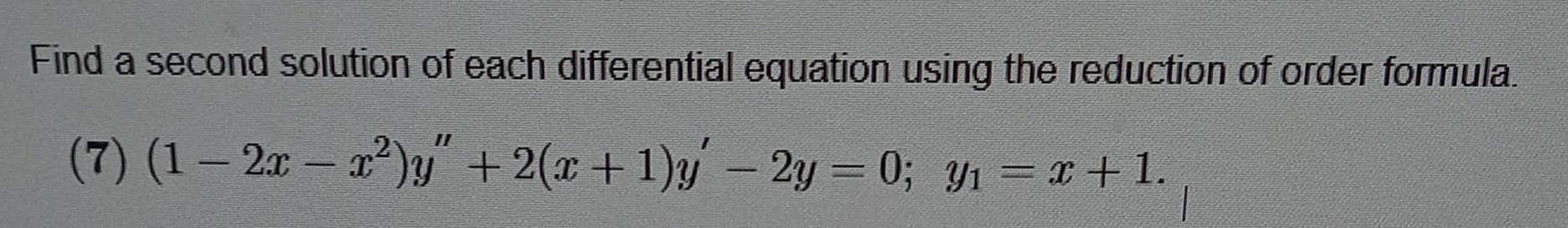
Calculus
Differential equationsFind a second solution of each differential equation using the reduction of order formula 7 1 2x x y 2 x 1 y 2y 0 Y x 1 1

Calculus
Differential equationsIf function g x is odd and g 3 2 lies on the graph of the function what are the coordinates of the point that will also lie on the graph of the function If function g x is even and g 3 4 lies on the graph of the function what are the coordinates of the point that will also lie on the graph of the function

Calculus
Differential equationsSolve the differential equation by the method of integrating factors dy dx y 2xy Use C to represent any constant of integration
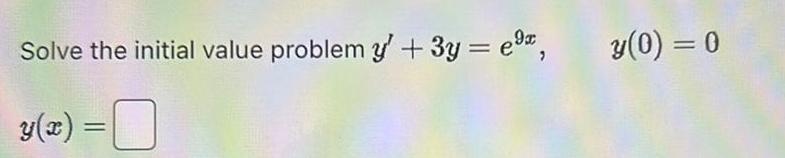

Calculus
Differential equationsSolve y 7x y x6 y 1 7 a Identify the integrating factor a z a x 0 b Find the general solution y x Note Use C for an arbitrary constant c Solve the initial value problem y 1 7 y x

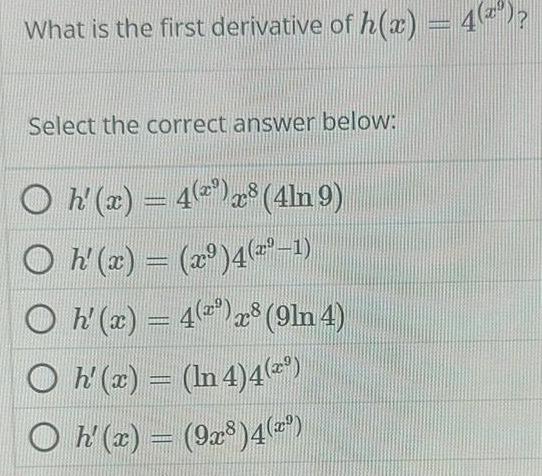
Calculus
Differential equationsWhat is the first derivative of h x 4 Select the correct answer below h x 4 x 4ln 9 h x x 4 1 Oh x 4 2 28 9ln 4 O h x ln 4 4 2 h x 9x 4 x
Calculus
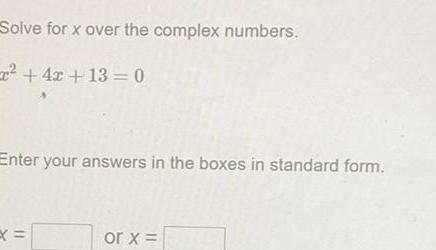
Differential equationsSolve for x over the complex numbers 4x 13 0 Enter your answers in the boxes in standard form or x
Calculus
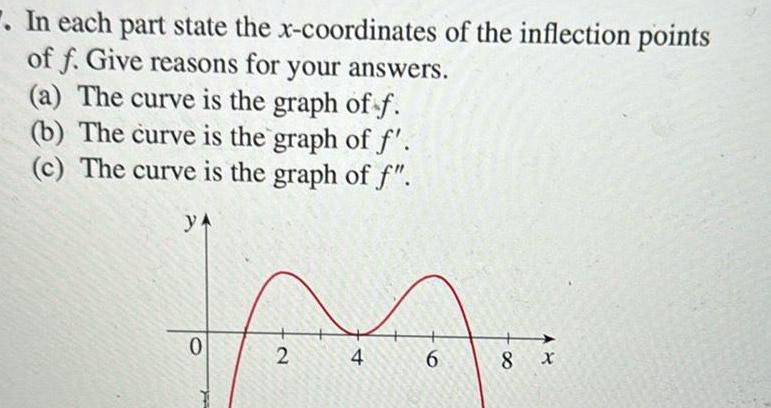
Differential equationsIn each part state the x coordinates of the inflection points of f Give reasons for your answers a The curve is the graph of f b The curve is the graph of f c The curve is the graph of f YA 0 2 4 6 8 X

Calculus
Differential equationsUse Euler s method with step size 0 25 to compute the approximate y values 31 32 33 and y4 of the solution of the initial value problem Y1 Y2 Y3 20 11 y 2 5x 2y y 1 5

Calculus
Differential equationsUsing separation of variables solve the differential equation dy 10 x dx Use C to represent the arbitrary constant 11 Y

Calculus
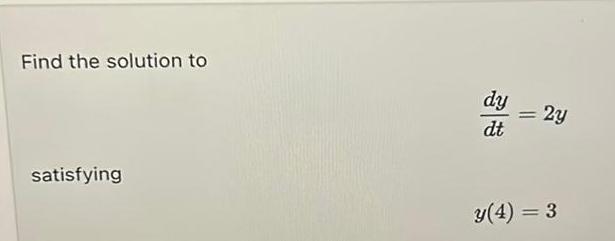
Differential equationsFind an equation of the form y f x for a curve with z intercept 0 whose tangent line at any point z y has slope ze

Calculus
Differential equationsMatch each differential equation to a function which is a solution FUNCTIONS A y 3x x B y e 8 C y sin x D y x E y 6 exp 2x DIFFERENTIAL EQUATIONS 1 2x2y 3xy y 2 y y 0 3 y 15y 56y 0 4 xy y x

Calculus
Differential equationsnsider the all equation dy y y 1 y 2 y 0 0 dt a 2 points Find the equilibria b 4 points Draw the phase line diagram and determine stability of equilibria c 7 points Find the general solution to the differential equation Notice that it is separable

Calculus
Differential equations5 2 points A type of ocean wave found near the equator called a Kelvin wave is described by the following equations du h g 0 t x du x h t H 0 Here h h x t is the height of water u and 9 and H are constants representing gravity and average water height u x t is the water s east west velocity 0 h a Eliminate u from the system of equations to find 32 gHh 0 Hint use Clairaut s Theorem b Solutions to equations involving waves typically look like Acos kx wt The coefficient w is a time frequency of the wave and k describes the wave s spatial frequency Treat A as a constant and substitute this solution into the equation you found in a What is the relationship between w and k c Assume k and w are positive We describe the velocity of waves in two ways The crest of a wave moves with phase speed A group of waves moves with group velocity Show that the phase speed and group velocity of a Kelvin wave are the same We call this type of wave nondispersive which means that it travels without changing shape Kelvin waves take about 2 months to go across the Pacific Ocean

Calculus
Differential equationsExpand the quotient by partial fractions 6 x 14x 48 2 x 6 2 x 14x 48 Simplify your answer 3 X 8 I 3 X 6
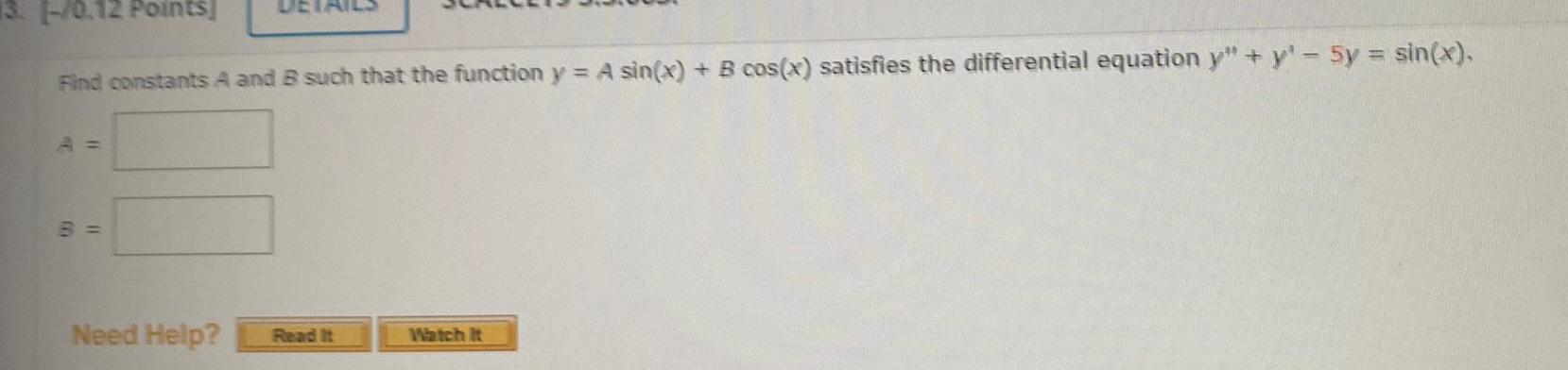
Calculus
Differential equations13 1 0 12 Points Find constants A and B such that the function y A sin x B cos x satisfies the differential equation y y 5y sin x A B Need Help Read It Watch It

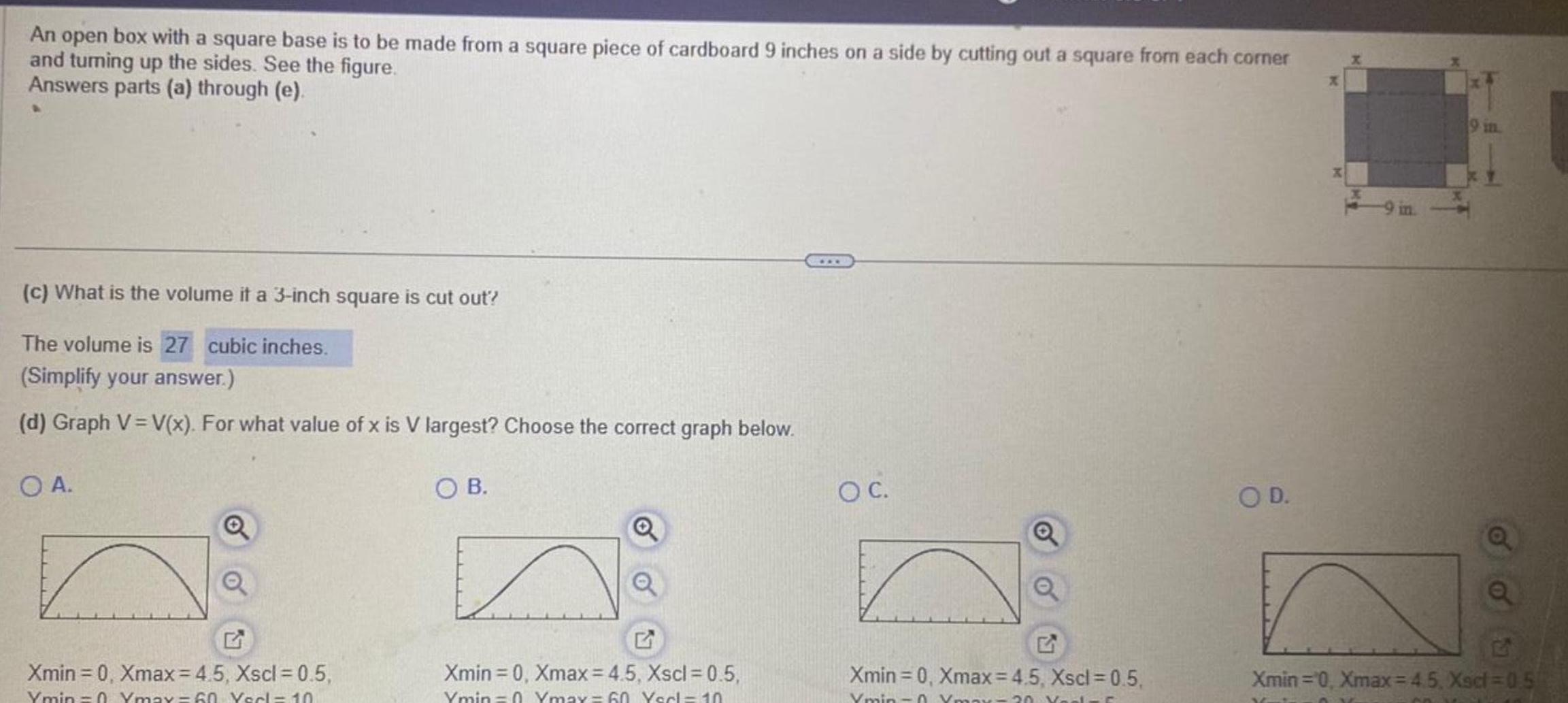
Calculus
Differential equationsAn open box with a square base is to be made from a square piece of cardboard 9 inches on a side by cutting out a square from each corner and turning up the sides See the figure Answers parts a through e c What is the volume it a 3 inch square is cut out The volume is 27 cubic inches Simplify your answer d Graph V V x For what value of x is V largest Choose the correct graph below OA Q Q Xmin 0 Xmax 4 5 Xscl 0 5 Ymin 0 Ymax 60 Yerl 10 OB Xmin 0 Xmax 4 5 Xscl 0 5 Ymin 0 Ymax 60 Yerl 10 O C Q Xmin 0 Xmax 4 5 Xscl 0 5 Ymin Ymax 20 Yaels C O D a Q 2 Xmin 0 Xmax 45 Xsd 0
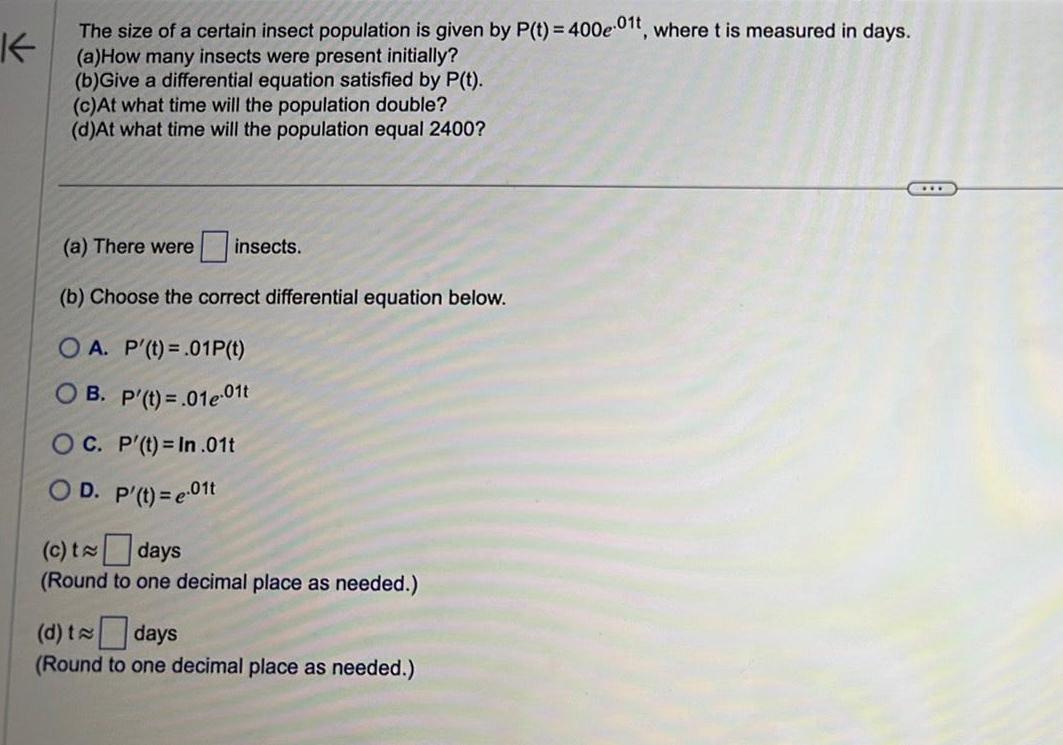
Calculus
Differential equationsK The size of a certain insect population is given by P t 400e01t where t is measured in days a How many insects were present initially b Give a differential equation satisfied by P t c At what time will the population double d At what time will the population equal 2400 a There were insects b Choose the correct differential equation below OA P t 01P t OB P t 01e 01t OC P t In 01t OD P t e 01t c t days Round to one decimal place as needed d t days Round to one decimal place as needed

Calculus
Differential equationsIn an animal hospital 14 units of a certain medicine were injected into a dog After 45 minutes only 7 units remained in the dog Let f t be the amount of the medicine present after t minutes At any time the rate of change of f t is proportional to the value of f t Find the formula for f t The formula is f t Use integers or decimals for any numbers in the equation Round to three decimal places as needed

Calculus
Differential equations8 A spotlight on the ground shines on a wall 12 m away If a man 2 m tall walks from the spotlight toward the building at a speed of 1 6 m s how fast is the length of his shadow on the building decreasing when he is 4 m from the building

Calculus
Differential equationsEvaluate the integrals that converge enter DNC if integral Does Not Converge S 0 8 x da
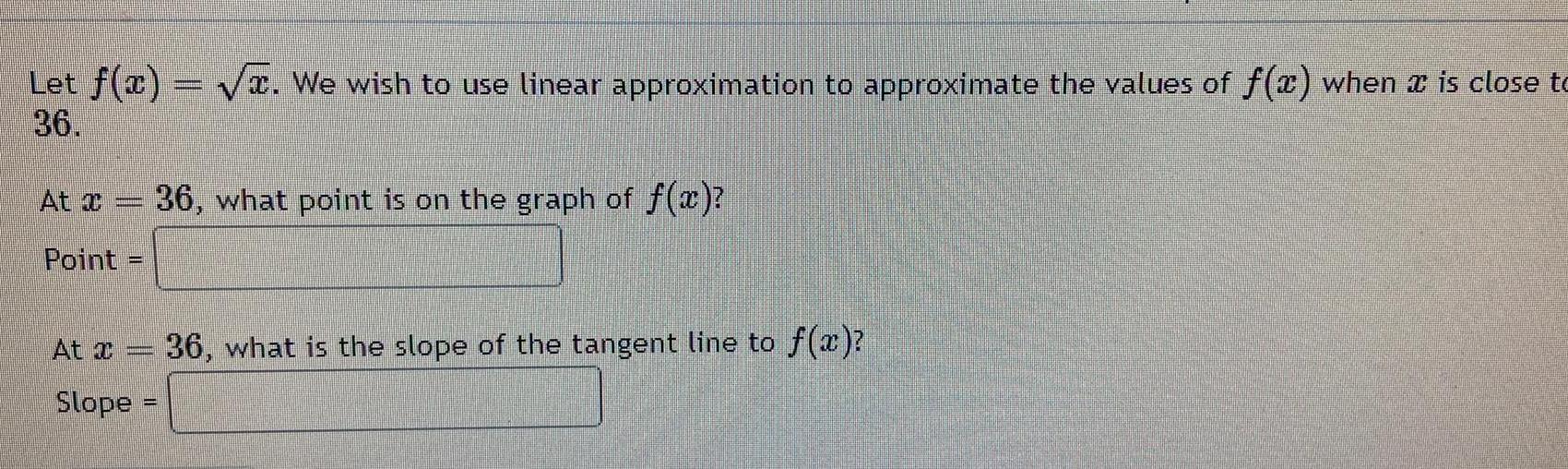
Calculus
Differential equationsLet f x We wish to use linear approximation to approximate the values of f x when is close to 36 At x 36 what point is on the graph of f x Point At Jumanni Comm Slope 36 what is the slope of the tangent line to f x
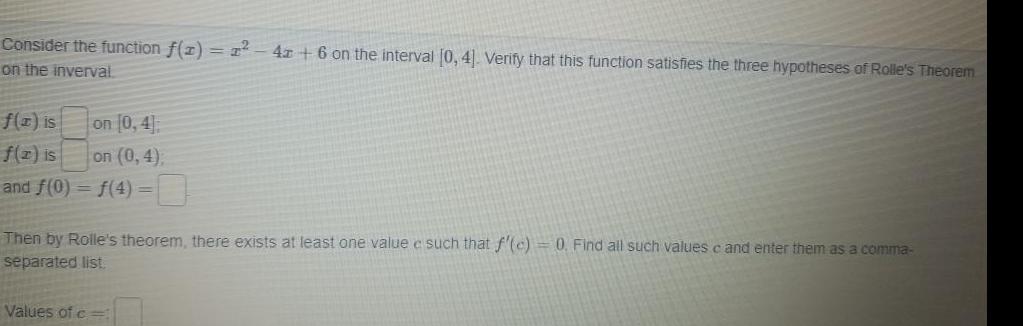
Calculus
Differential equationsConsider the function f 1 1 4z 6 on the interval 0 4 Verify that this function satisfies the three hypotheses of Rolle s Theorem on the inverval f x is on 0 4 f z is on 0 4 and f 0 f 4 Then by Rolle s theorem there exists at least one value e such that f c 0 Find all such values c and enter them as a comma separated list Values of c

Calculus
Differential equationsFind all angles between 0 and 180 satisfying the given equation Round your answer to one decimal place Enter your answers as a comma separated list Enter your answer in degrees sin 0 0 51 05 9

Calculus
Differential equationsblem 4 When a bacteria colony reaches 150 thousand it is treated with antibiotics Due to the antibiotics the bacteria population decreases by 10 each week a Find an exponential model B t that approximates the bacteria population in thousands after t weeks b Estimate the bacteria population to the nearest thousand after 3 5 weeks c Use limits to explain what will happen to the bacteria population as time continues to increase d Sketch the graph of B t Label and appropriately scale the axes to include the entire graph

Calculus
Differential equationsDetermining values of 6 from a graph The function f in the fig ure satisfies lim f x 5 Determine the largest value of 8 0 x 2 satisfying each statement a If 0 x2 8 then f x 5 2 b If 0 x2 8 then f x 5 1

Calculus
Differential equationsind an equation of the tangent line to the graph of y g x at x 6 if g 6 3 and g 6 5 Enter your answer as an equation in terms of y and x X Enhanced Feedback Please try again Remember the slope of g at x is the derivative function g x Use the point of intersection along with the slope to find an equation for the tangent line


Calculus
Differential equations41 48 Functions with roots Determine the interval s on which the following functions are continuous At which finite endpoints of the intervals of continuity is f continuous from the left or continuous from the right 41 f x 5 x 43 f x 2x 16 45 f x x 2x 3 47 f x 2x 3 2 3 42 f x 25 x 44 f x x 3x 2 46 f t t 1 3 2 48 f z z 1 3 4
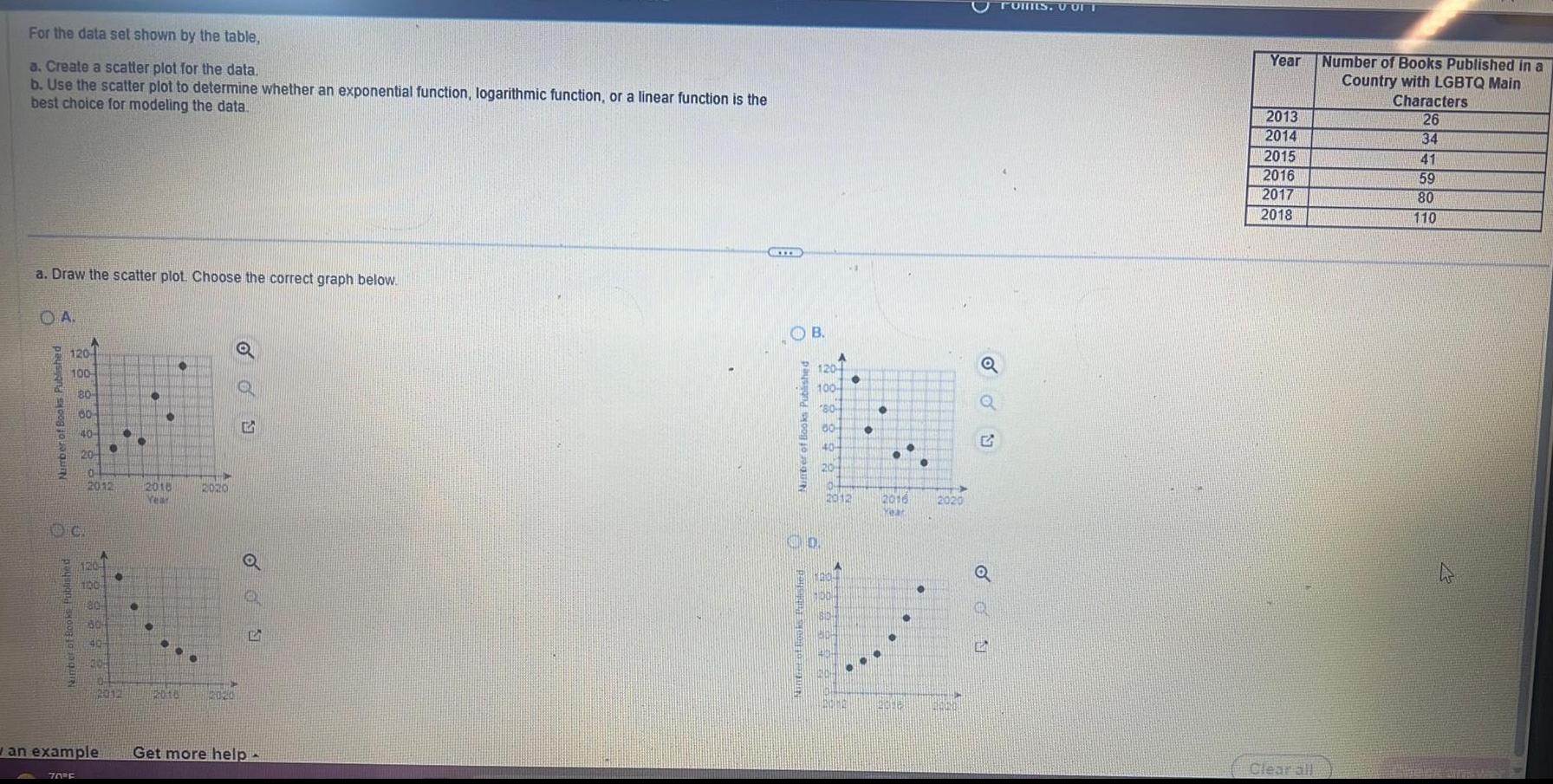
Calculus
Differential equationsFor the data set shown by the table a Create a scatter plot for the data b Use the scatter plot to determine whether an exponential function logarithmic function or a linear function is the best choice for modeling the data a Draw the scatter plot Choose the correct graph below A Number of Books Published 120 100 Nimber of Books Published A 70 F 80 60 40 20 0 2012 100 80 30 40 2012 2018 Year HIPP 2020 12016 2020 o wan example Get more help CYTE Nimber of Books Published B 1204 100 60 60 40 10 20 10 2012 2016 Year 2020 Q G G TOMES U OFT Year 2013 2014 2015 2016 2017 2018 Clear all Number of Books Published in a Country with LGBTQ Main Characters 26 34 41 59 80 110

Calculus
Differential equationsX 1 Solution We have y t 20 1 j 4 s ds 1 Thus x 1 2 2 1 3 0 2 3 ds 2 91 2 1 3 3ds 3 3r 3 3r 191 441 2 3 3 4 1 41 3 0 2 9s ds 4t 3 x 1 34 y 1 9t 3 2 0 3r 2 3 123 91 441 19 91 1 17 2 36 200 3 jx d 31 2 4 9 4 9 6 2 3 62 3 91 191 2 3 2 3 4 4s 35 ds 271 3 4 2 8 27 41 44 m 4 4 91
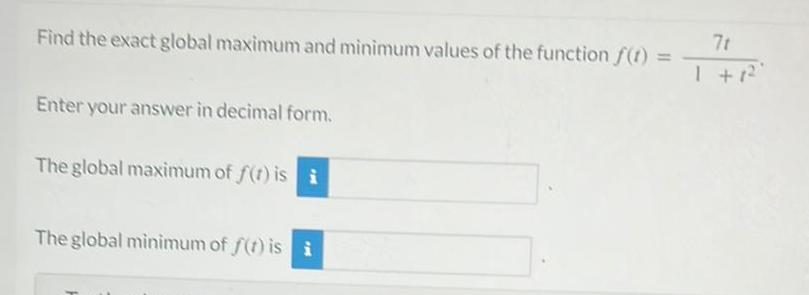
Calculus
Differential equationsFind the exact global maximum and minimum values of the function f 1 Enter your answer in decimal form The global maximum of f t is i The global minimum of f t is i 7t 1 1
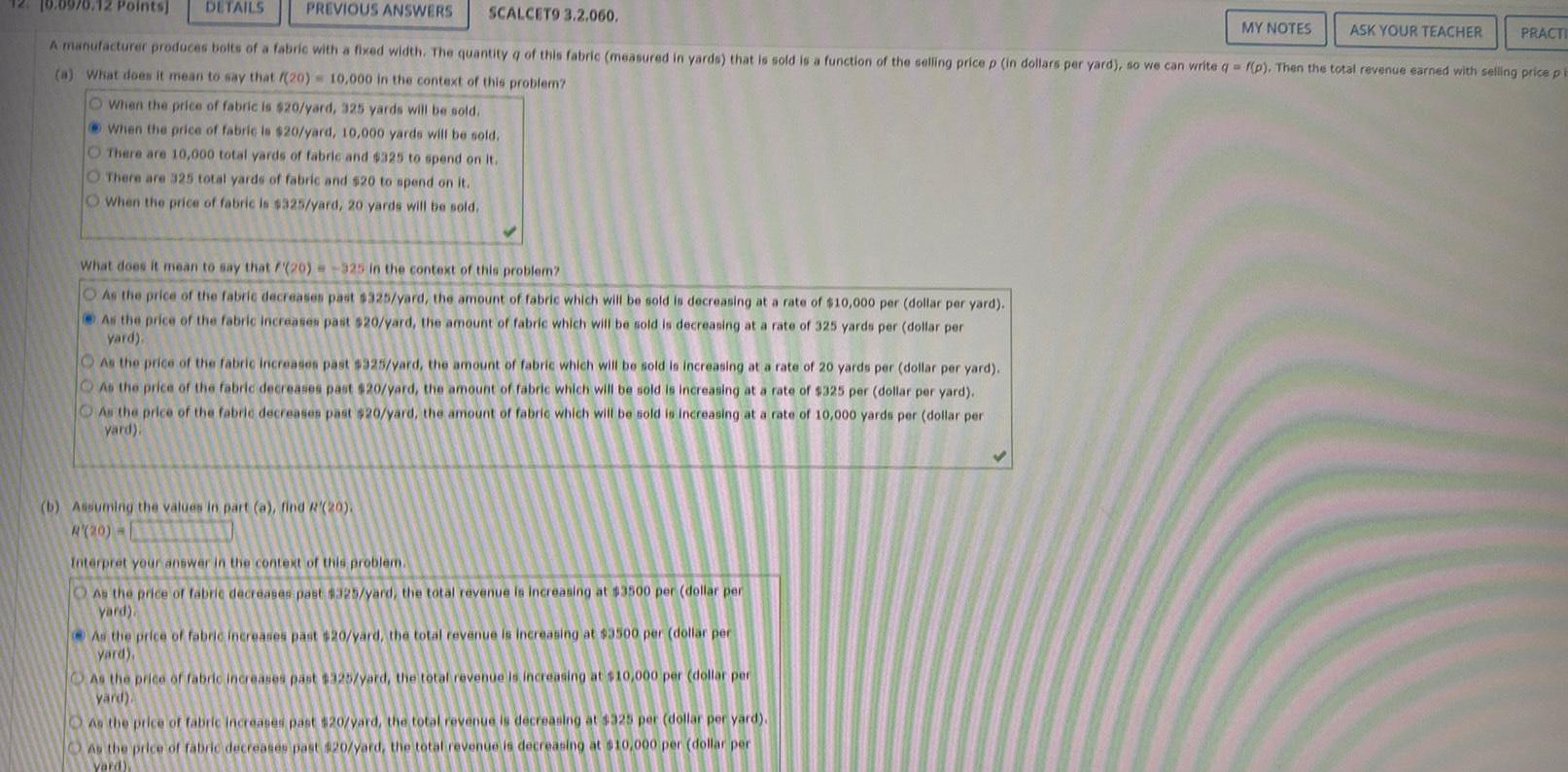
Calculus
Differential equationsPREVIOUS ANSWERS SCALCET9 3 2 060 A manufacturer produces bolts of a fabric with a fixed width The quantity q of this fabric measured in yards that is sold is a function of the selling price p in dollars per yard so we can write q f p Then the total revenue earned with selling price pi a What does it mean to say that 20 10 000 in the context of this problem O When the price of fabric is 20 yard 325 yards will be sold When the price of fabric is 20 yard 10 000 yards will be sold There are 10 000 total yards of fabric and 325 to spend on it 10 0970 12 Points DETAILS O There are 325 total yards of fabric and 20 to spend on it O When the price of fabric is 325 yard 20 yards will be sold What does it mean to say that 20 325 in the context of this problem As the price of the fabric decreases past 325 yard the amount of fabric which will be sold is decreasing at a rate of 10 000 per dollar per yard As the price of the fabric increases past 20 yard the amount of fabric which will be sold is decreasing at a rate of 325 yards per dollar per yard As the price of the fabric increases past 325 yard the amount of fabric which will be sold is increasing at a rate of 20 yards per dollar per yard As the price of the fabric decreases past 20 yard the amount of fabric which will be sold is increasing at a rate of 325 per dollar per yard As the price of the fabric decreases past 20 yard the amount of fabric which will be sold is increasing at a rate of 10 000 yards per dollar per yard b Assuming the values in part a find R 20 R 20 D Interpret your answer in the context of this problem As the price of fabric decreases past 325 yard the total revenue is increasing at 3500 per dollar per yard As the price of fabric increases past 20 yard the total revenue is increasing at 3500 per dollar per yard As the price of fabric increases past 325 yard the total revenue is increasing at 10 000 per dollar per yard As the price of fabric increases past 20 yard the total revenue is decreasing at 325 per dollar per yard As the price of fabric decreases past 20 yard the total revenue is decreasing at 10 000 per dollar per Yard MY NOTES ASK YOUR TEACHER PRACTI