Differentiation Questions and Answers

Calculus
DifferentiationGiven f (x) = 3(x-7)(x+3)², list the zeros and determine whether the graph crosses or touches the x-axis at each x-intercept. Determine the maximum number of turning points on the graph and the end behavior of the graph. What is the power function that resembles this end behavior?
Zeros: __________
Max Turning Pts: __________
End behavior: __________
Power Function: __________
![Compute the Fourier coefficients and write the Fourier series in the complex and real forms. f(x) = x² on [0,π], and extended to R by π-periodicity.](https://media.kunduz.com/media/sug-question/raw/78937939-1660222489.0350351.jpeg?w=256)
Calculus
DifferentiationCompute the Fourier coefficients and write the Fourier series in the complex and real forms. f(x) = x² on [0,π], and extended to R by π-periodicity.
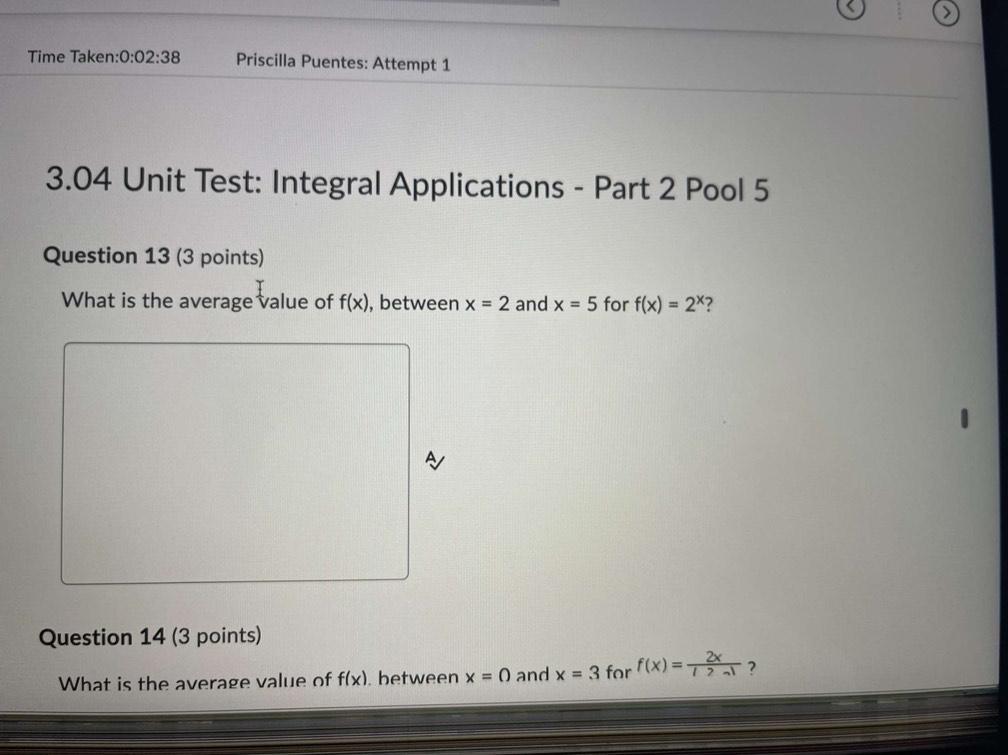
Calculus
DifferentiationWhat is the average value of f(x), between x = 2 and x = 5 for f(x) = 2ˣ?
What is the average value of flx), between x = 0 and x = 3 for f(x) = ?
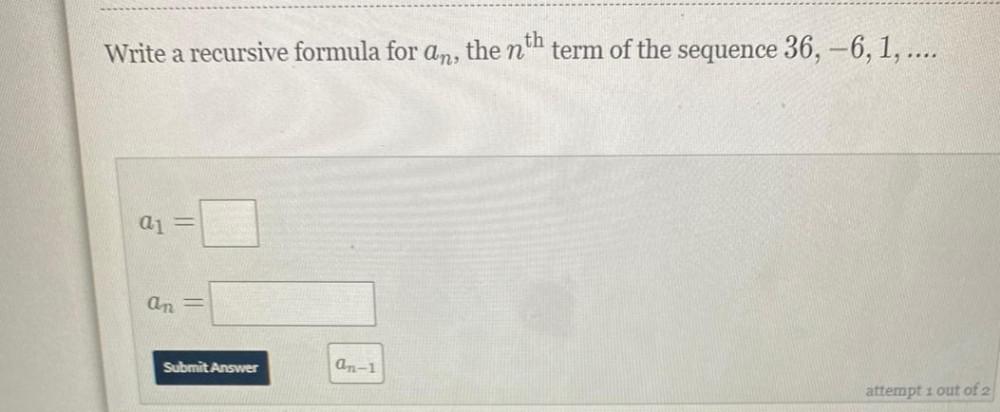
Calculus
DifferentiationWrite a recursive formula for an, the nth term of the sequence 36, -6,1, ....
a1 = ____.
an = _____.
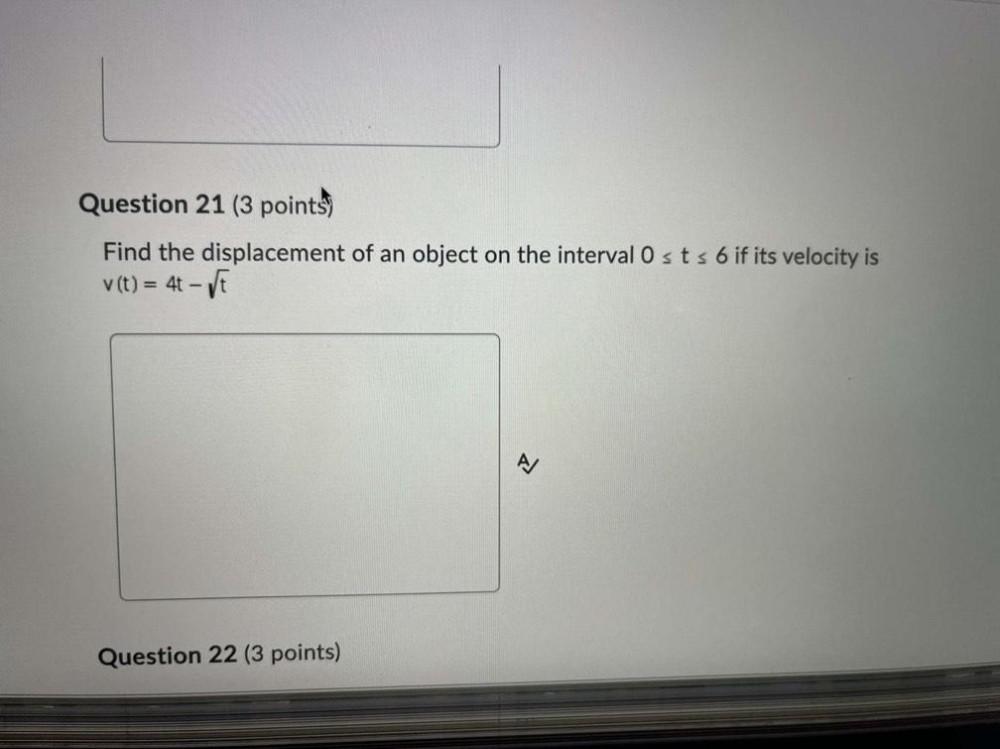
Calculus
DifferentiationFind the displacement of an object on the interval 0 ≤ t ≤ 6 if its velocity is
v(t) = 4t - √t
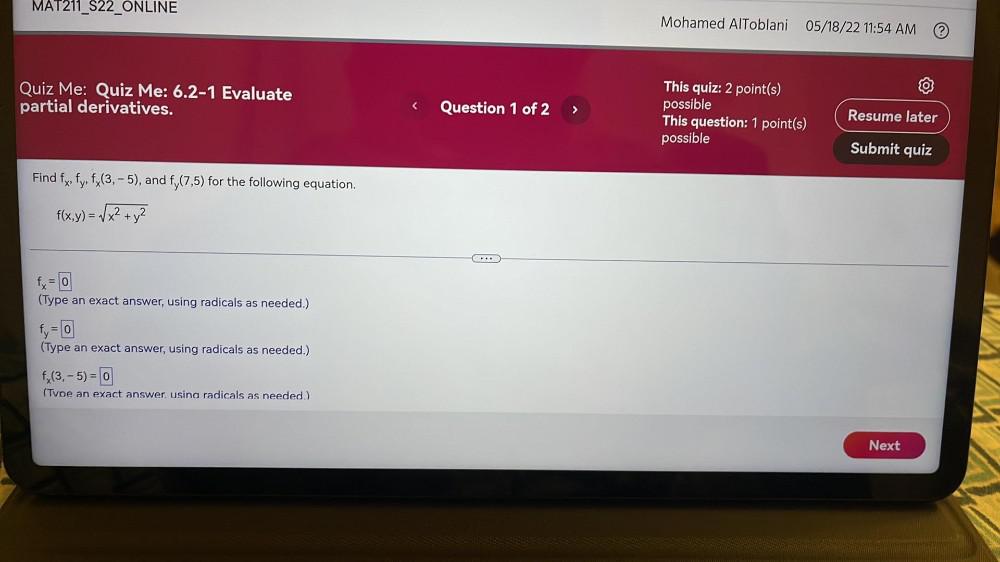
Calculus
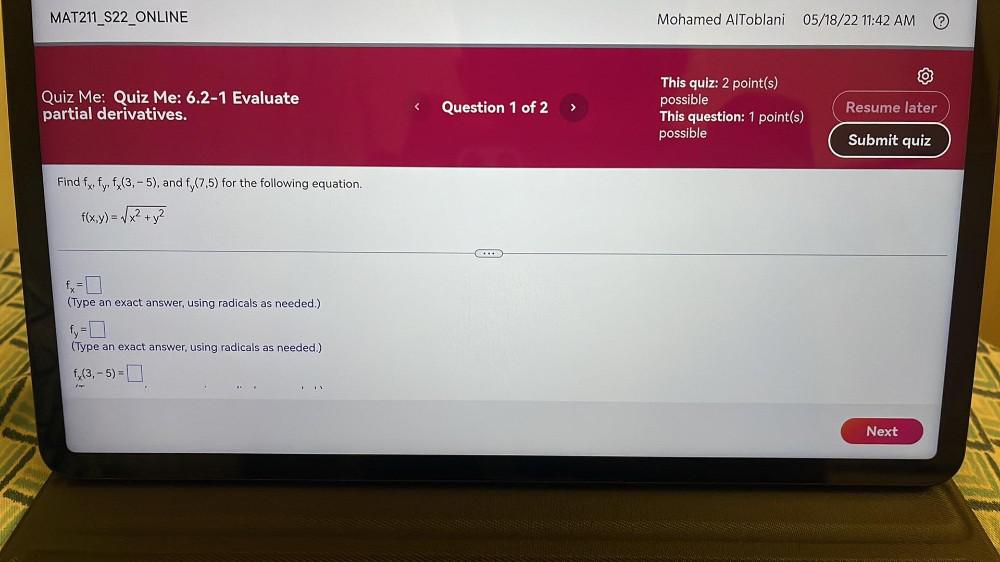
DifferentiationFind fx, fy, fx(3,-5), and fy(7,5) for the following equation.
f(x,y) = √(x² + y²)
fx = ____
(Type an exact answer, using radicals as needed.)
fy = ____
(Type an exact answer, using radicals as needed.)
f (3, 5) = ____
(Type an exact answer using radicals as needed.)
Calculus
DifferentiationFind fx, fy, fx(3, - 5), and fy(7,5) for the following equation.
f(x,y) = √(x² + y²)
fx=_______(Type an exact answer, using radicals as needed.)
fy=_______(Type an exact answer, using radicals as needed.)
fx(3 - 5) =________
Calculus
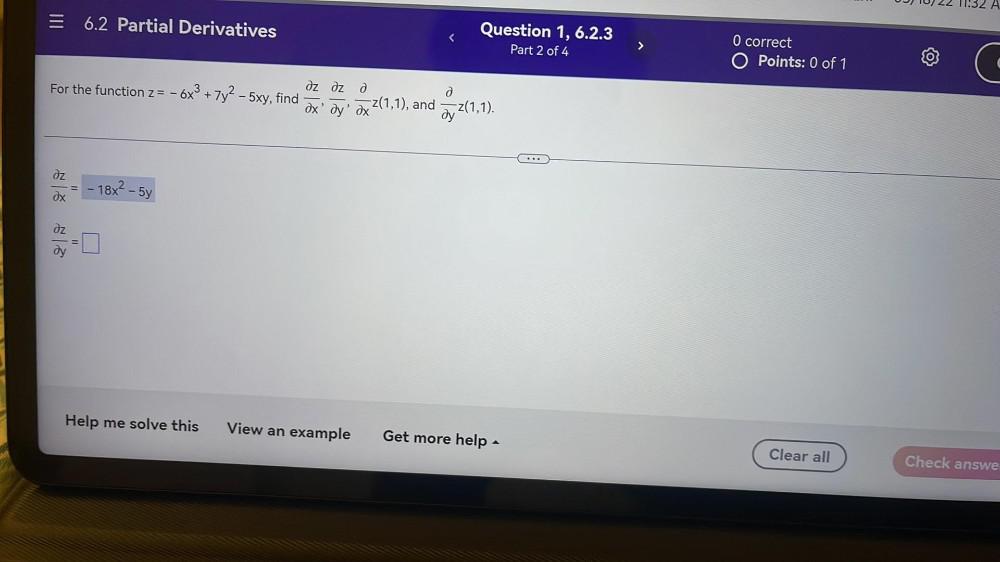
DifferentiationFor the function z= - 6x³ + 7y² - 5xy, find ∂z/∂x , ∂z/∂y , ∂z(1,1)/∂x ,
and ∂z(1,1)/∂y.
Calculus
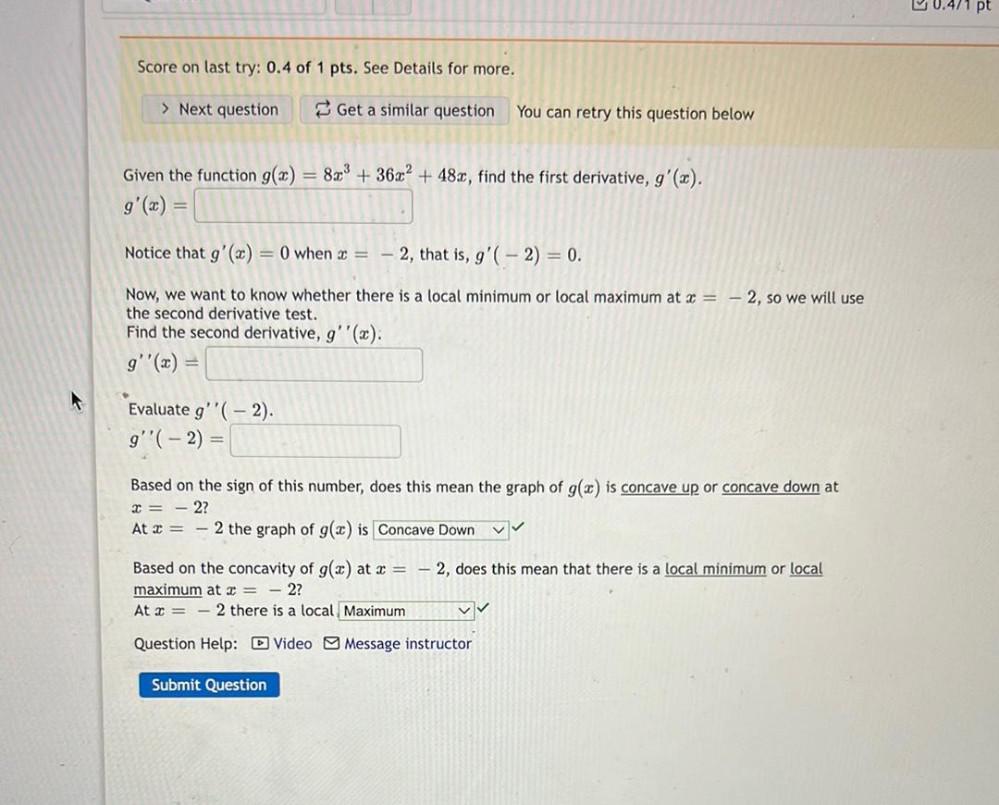
DifferentiationGiven the function g(x) = 8x^33 + 36x^2 + 48x, find the first derivative, g'(x)=______________
Notice that g'(x) = 0 when x = -2, that is, g'( - 2) = 0.
Now, we want to know whether there is a local minimum or local maximum at x = -2, so we will use the second derivative test.
Find the second derivative, g''(x).
g''(x)=____________
Evaluate g''(-2).
g''( - 2) =_______________
Based on the sign of this number, does this mean the graph of g(x) is concave up or concave down at x= - 2?
At x = – 2 the graph of g(x) is ____________
Based on the concavity of g(x) at x = – 2, does this mean that there is a local minimum or local maximum at x= - 2?
At x = - 2 there is a ____________
Calculus
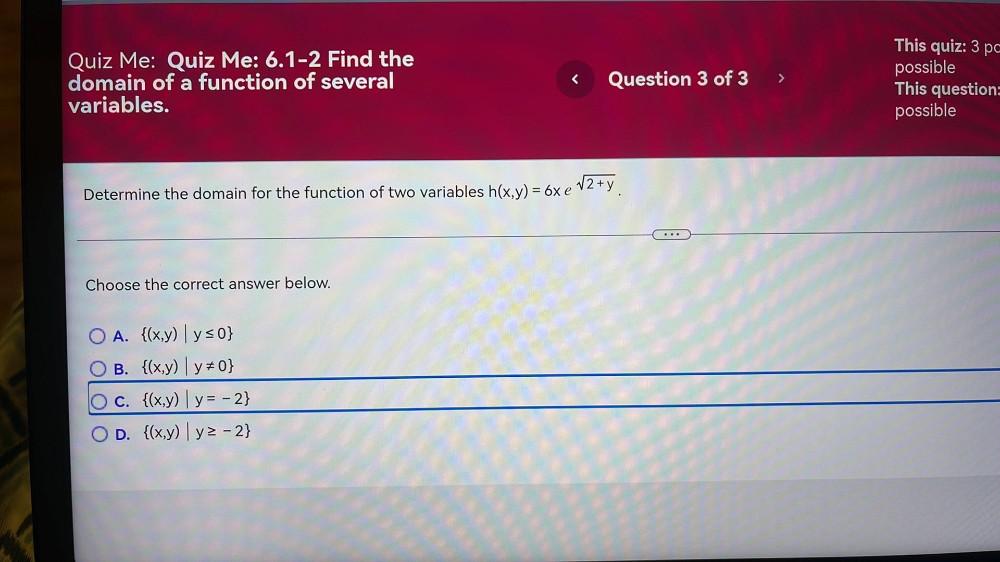
DifferentiationDetermine the domain for the function of two variables h(x, y) = 6xe^√(2+Y).
Choose the correct answer below.
O A. {(x, y) | y ≤ 0}
O B. {(x, y) | y ≠ 0}
O C. {(x, y) | y = -2}
O D. {(x, y) | y ≥ -2}
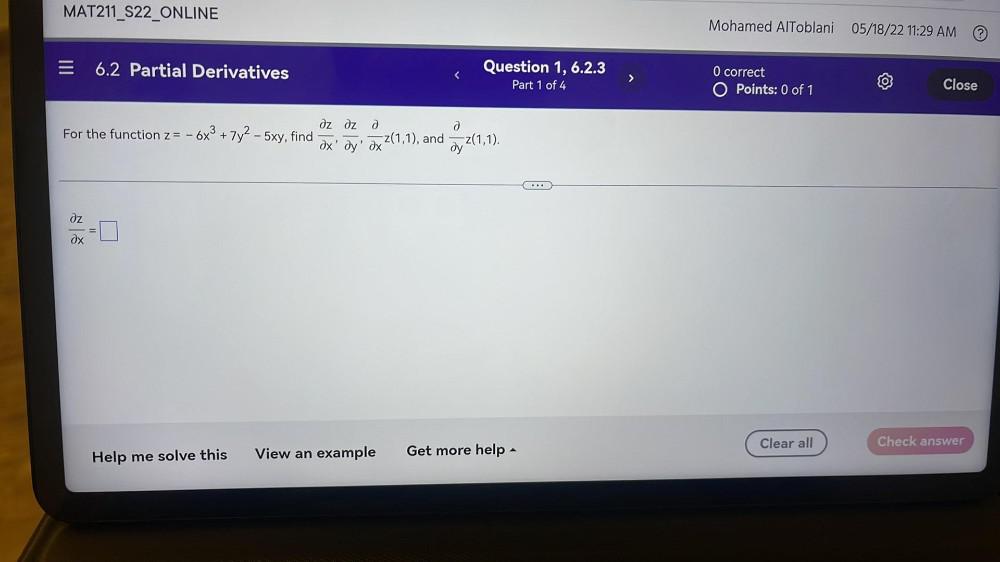
Calculus
DifferentiationFor the function z= -6x³ + 7y² - 5xy, find ∂z/∂x , ∂z/∂y , ∂z(1,1)/∂x , and ∂z(1,1)/∂y
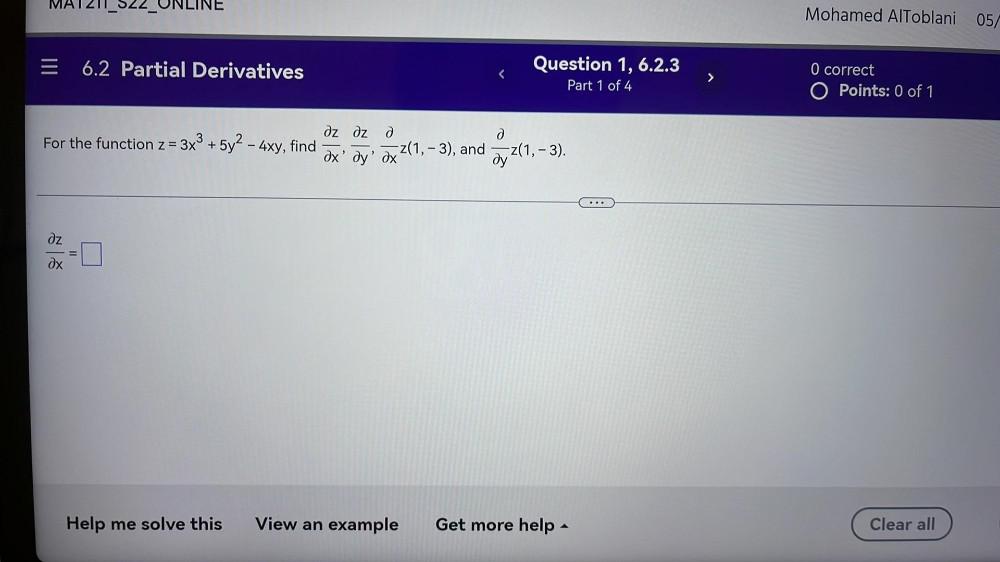
Calculus
DifferentiationFor the function z = 3x³ + 5y² - 4xy, find ∂z/∂x , ∂z/∂y , ∂z(1,-3)/∂x , and ∂z(1,-3)/∂y
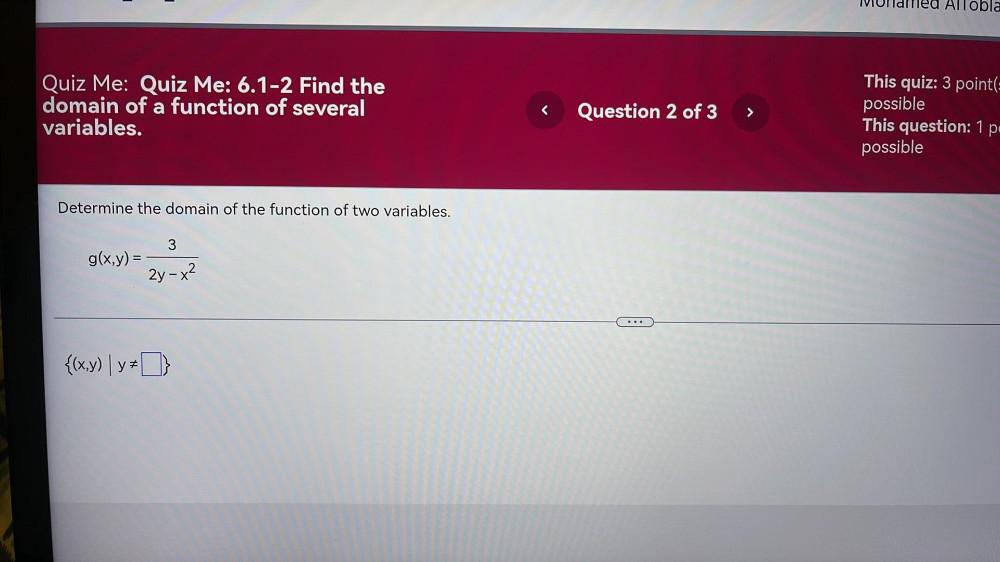
Calculus
DifferentiationDetermine the domain of the function of two variables.
g(x, y) = 3/(2y - x^2)
{(x, y) | y ≠ ___ }
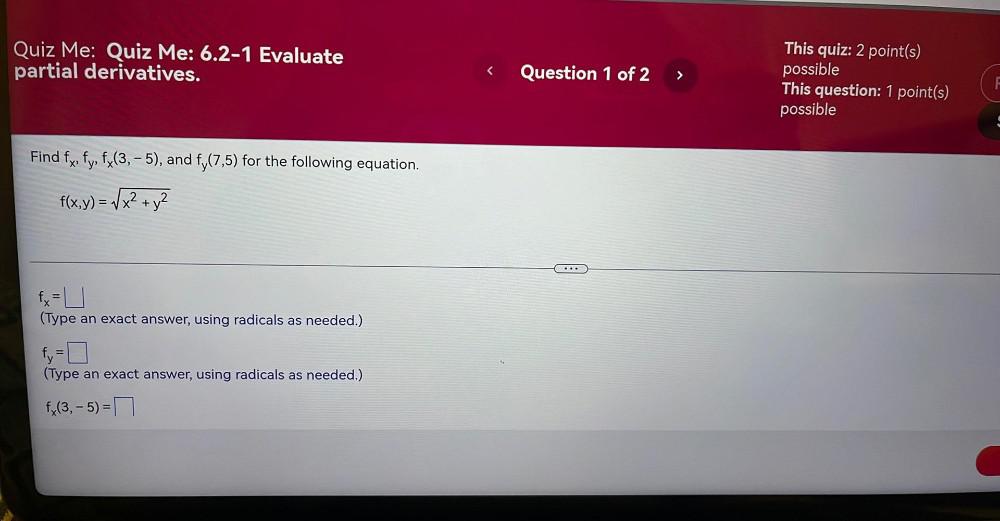
Calculus
DifferentiationFind fx, fy, fx(3, - 5), and fy(7, 5) for the following equation.
f(x,y) = √(x² + y²
fx = _______________(Type an exact answer, using radicals as needed.)
fy = ________________(Type an exact answer, using radicals as needed.)
fx(3,-5) = __________.
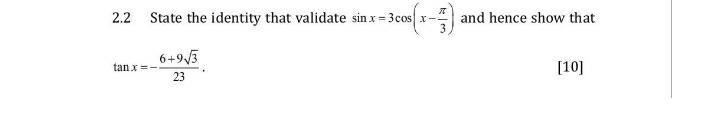
Calculus
DifferentiationState the identity that validate sin x=3cos ( x - ( π/3) ) and hence show that
tan x = -( 6 + 9 √3) / 23

Calculus
DifferentiationFind the derivative of
y=tan(4x² – 3x)
Find the derivative of
y=e²ˣ (x² + 5x –1)
Calculus
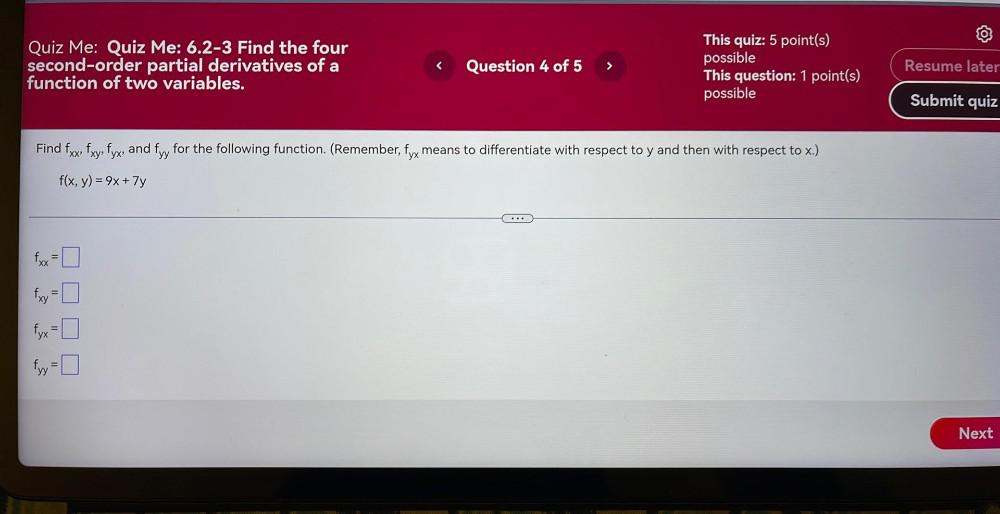
DifferentiationFind the four second-order partial derivatives of a
function of two variables.
Find fxx, fxy, fyx, and fyy for the following function. (Remember, fyx means to differentiate with respect to y and then with respect to x.)
f(x, y) = 9x + 7y
1. fxx
2. fxy =
3. fyx =
4. fyy=

Calculus
DifferentiationUsing the limit definition of the derivative (first principles), determine the derivative of f(x) = 2x / (3 - x)
Calculus
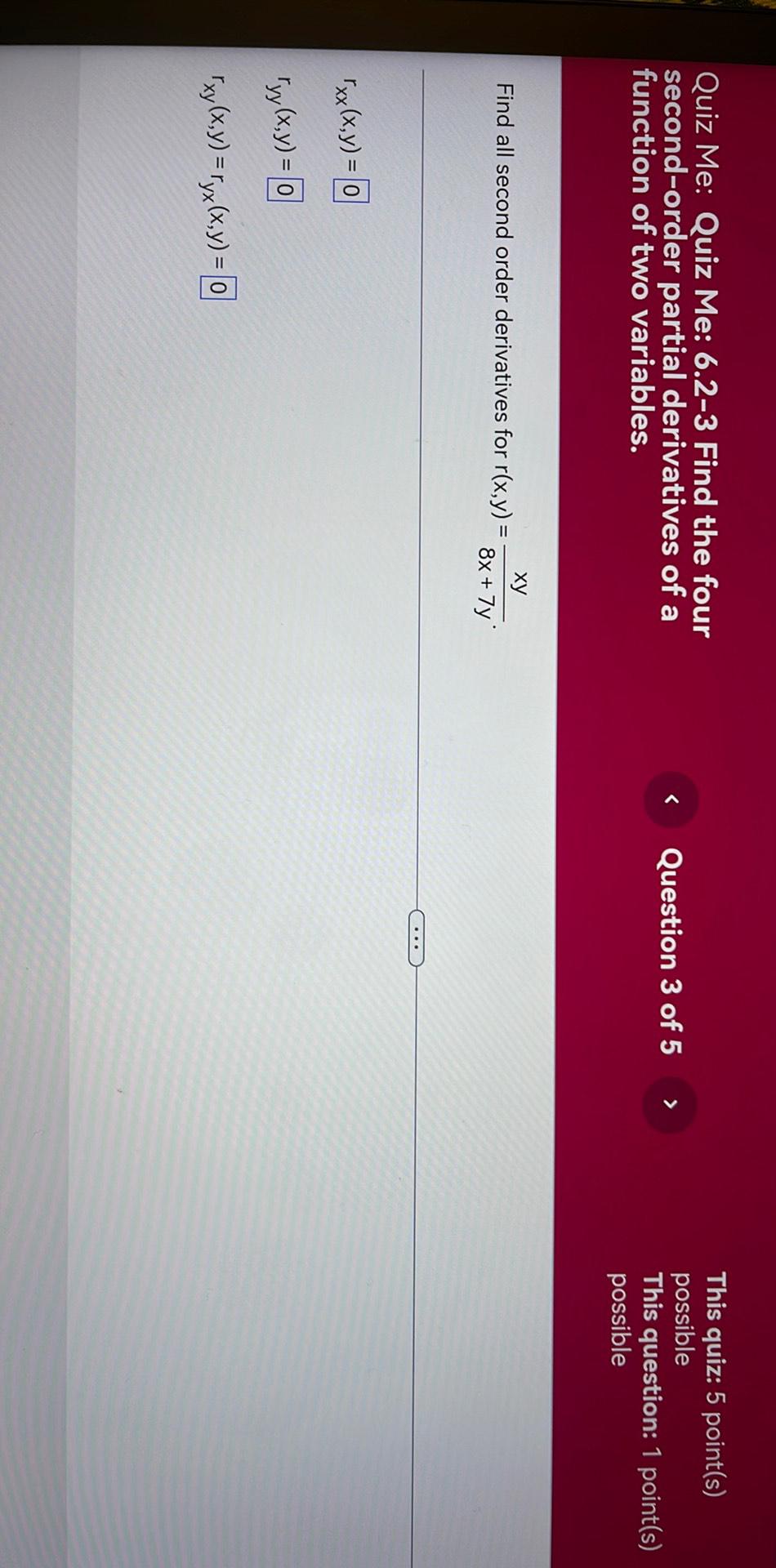
DifferentiationFind all second order derivatives for r(x,y) = xy / (8x + 7y).
rₓₓ(x, y) = ____
rᵧᵧ(x, y) = ____
rₓᵧ(x, y) = rᵧₓ(x, y) = ____

Calculus
DifferentiationThe length of the major axis of the ellipse with the equation ((x-2)^2)/16+((y+7)^2)/9=1
(A) 3
(B) 4
(C) 6
(D) 8
(E) 16
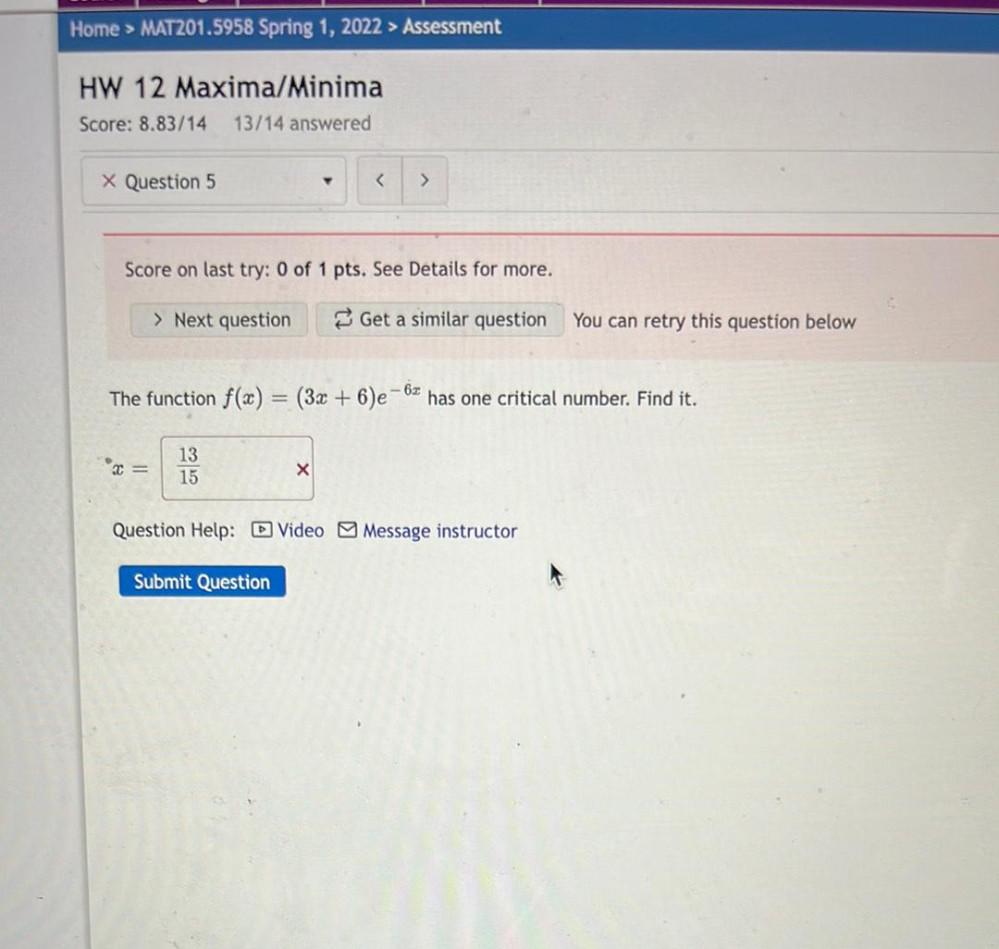
Calculus
DifferentiationThe function f(x) = (3x + 6)e^(- 6x) has one critical number. Find it.
x=_______
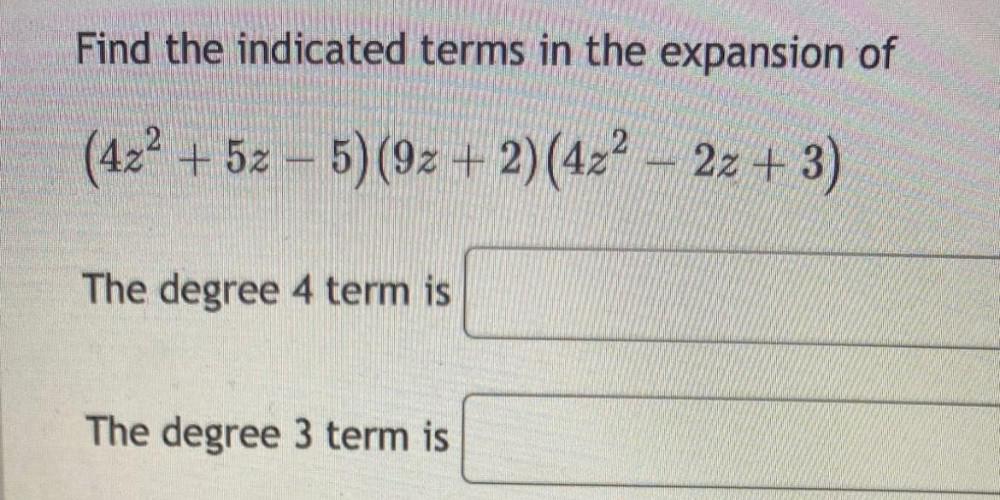
Calculus
DifferentiationFind the indicated terms in the expansion of
(4z^2 + 5z – 5) (9z + 2)(4z² – 2z + 3)
The degree 4 term is___________
The degree 3 term is__________
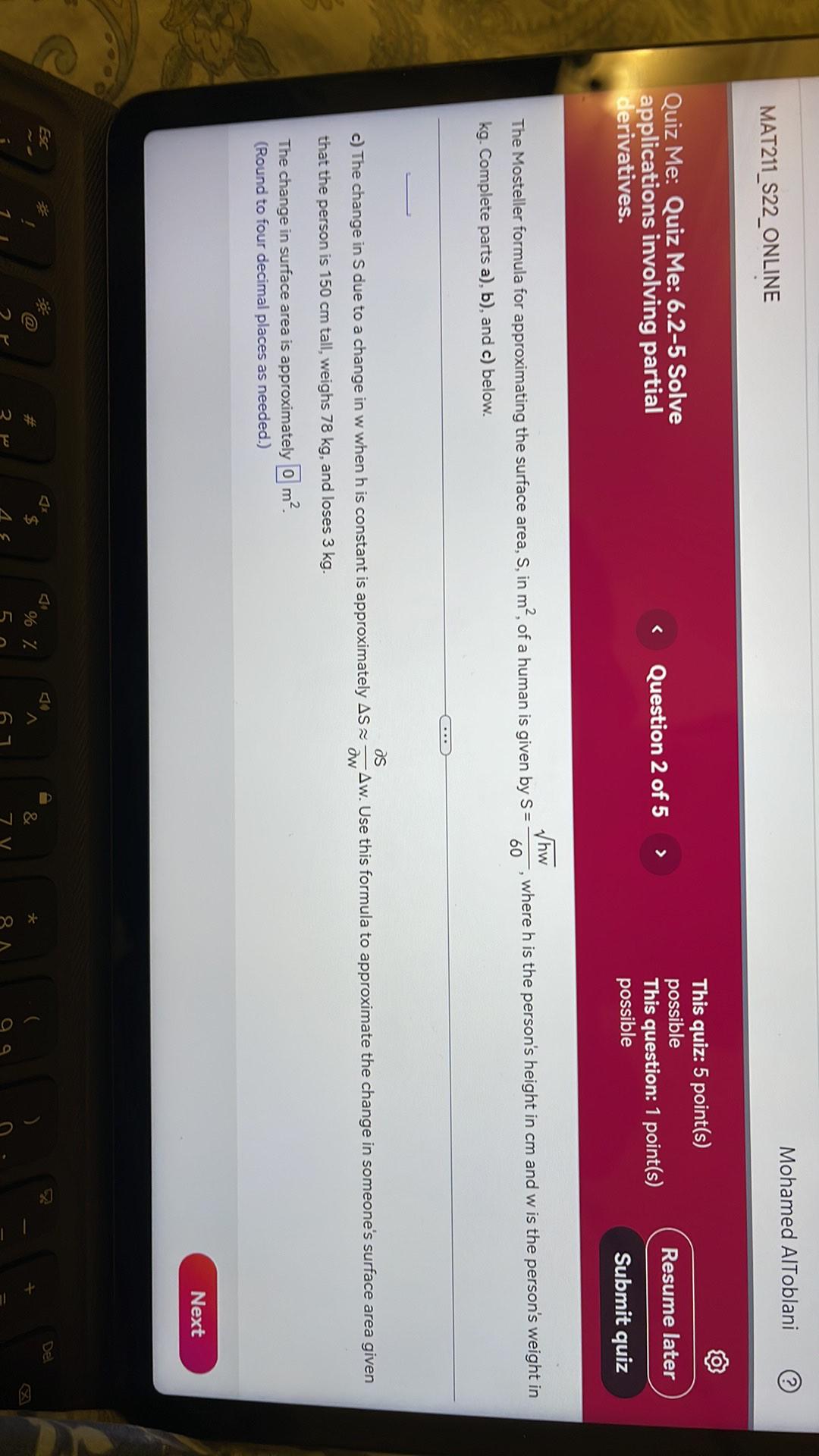
Calculus
DifferentiationThe Mosteller formula for approximating the surface area, S, in m^2, of a human is given by S = √hw/60, where h is the person's height in cm and w is the person's weight in kg. Complete parts a), b), and c) below.
c) The change in S due to a change in w when h is constant is approximately △S ≈ (∂s/∂w)△w. Use this formula to approximate the change in someone's surface area given that the person is 150 cm tall, weights 78 kg, and losses 3kg.
The change in surface area is approximately _______ m^2.
(Round to four decimal places as needed.)
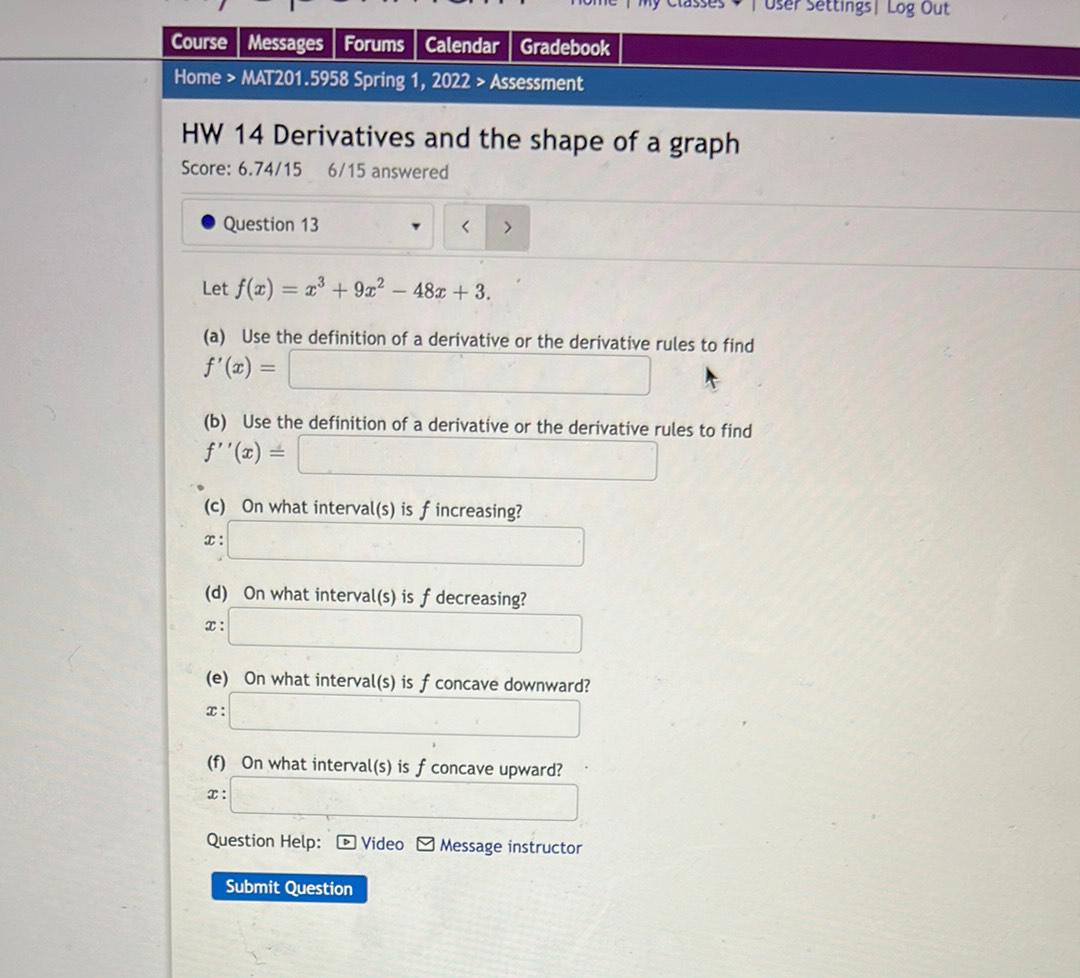
Calculus
DifferentiationLet f(x)= x^3 + 9x^2 – 48x + 3.
(a) Use the definition of a derivative or the derivative rules to find
f'(x)=_______________
(b) Use the definition of a derivative or the derivative rules to find
f''(x) =______________
(c) On what interval(s) is f increasing?
x:_______________
(d) On what interval(s) is f decreasing?
x:_______________
(e) On what interval(s) f is concave downward?
x:________________
(f) On what interval(s) is f concave upward?
x:_______________
![Consider the function f(1) = 3x^3 – 4x on the closed interval [1,6].
Find the exact value of the slope of the secant line connecting (1, f(1)) and (6, f(6)).
m =_____________
By the Mean Value Theorem, there exists c in (1,6) so that m = f'(c). Find all values of such c in (1,6).
Enter exact values. If there is more than one solution, separate them by a comma.
c=________________](https://media.kunduz.com/media/sug-question/raw/79081046-1660219629.3989472.jpeg?w=256)
Calculus
DifferentiationConsider the function f(1) = 3x^3 – 4x on the closed interval [1,6].
Find the exact value of the slope of the secant line connecting (1, f(1)) and (6, f(6)).
m =_____________
By the Mean Value Theorem, there exists c in (1,6) so that m = f'(c). Find all values of such c in (1,6).
Enter exact values. If there is more than one solution, separate them by a comma.
c=________________

Calculus
DifferentiationCompute the Instantaneous rate of change of the function f(x) = x³ + 12x²-3x - 8 at x = 2.
Calculus
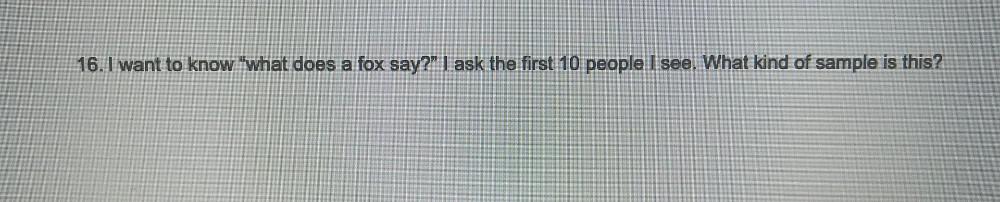
DifferentiationI want to know "what does a fox say?" I ask the first 10 people I see. What kind of sample is this?

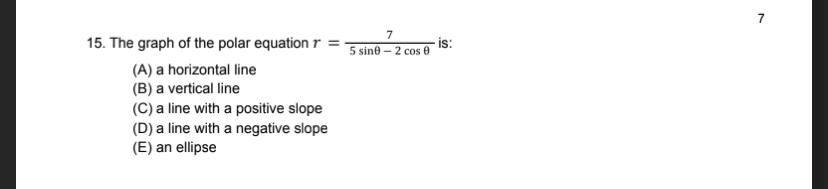
Calculus
DifferentiationThe graph of the polar equation r =
(A) a horizontal line
(B) a vertical line
(C) a line with a positive slope
(D) a line with a negative slope
(E) an ellipse
Calculus
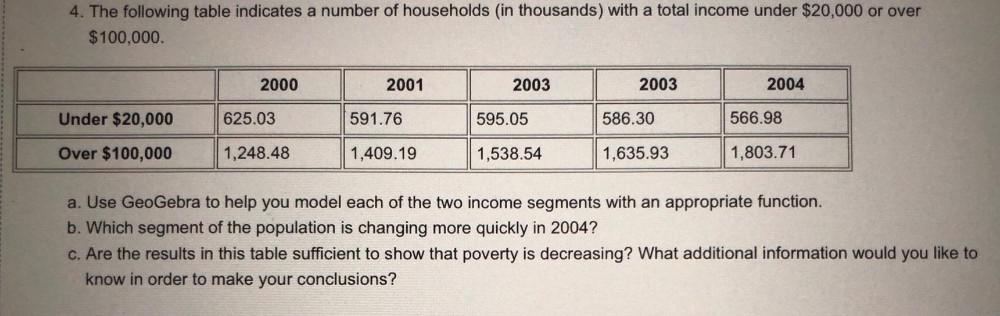
DifferentiationThe following table indicates a number of households (in thousands) with a total income under $20,000 or over
$100,000.
Under $20,000
625.03
591.76
595.05
586.30
566.98
Over $100,000
1,248.48
1,409.19
1,538.54
1,635.93
1,803.71
a. Use GeoGebra to help you model each of the two income segments with an appropriate function.
b. Which segment of the population is changing more quickly in 2004?
c. Are the results in this table sufficient to show that poverty is decreasing? What additional information would you like to know in order to make your conclusions?
Calculus
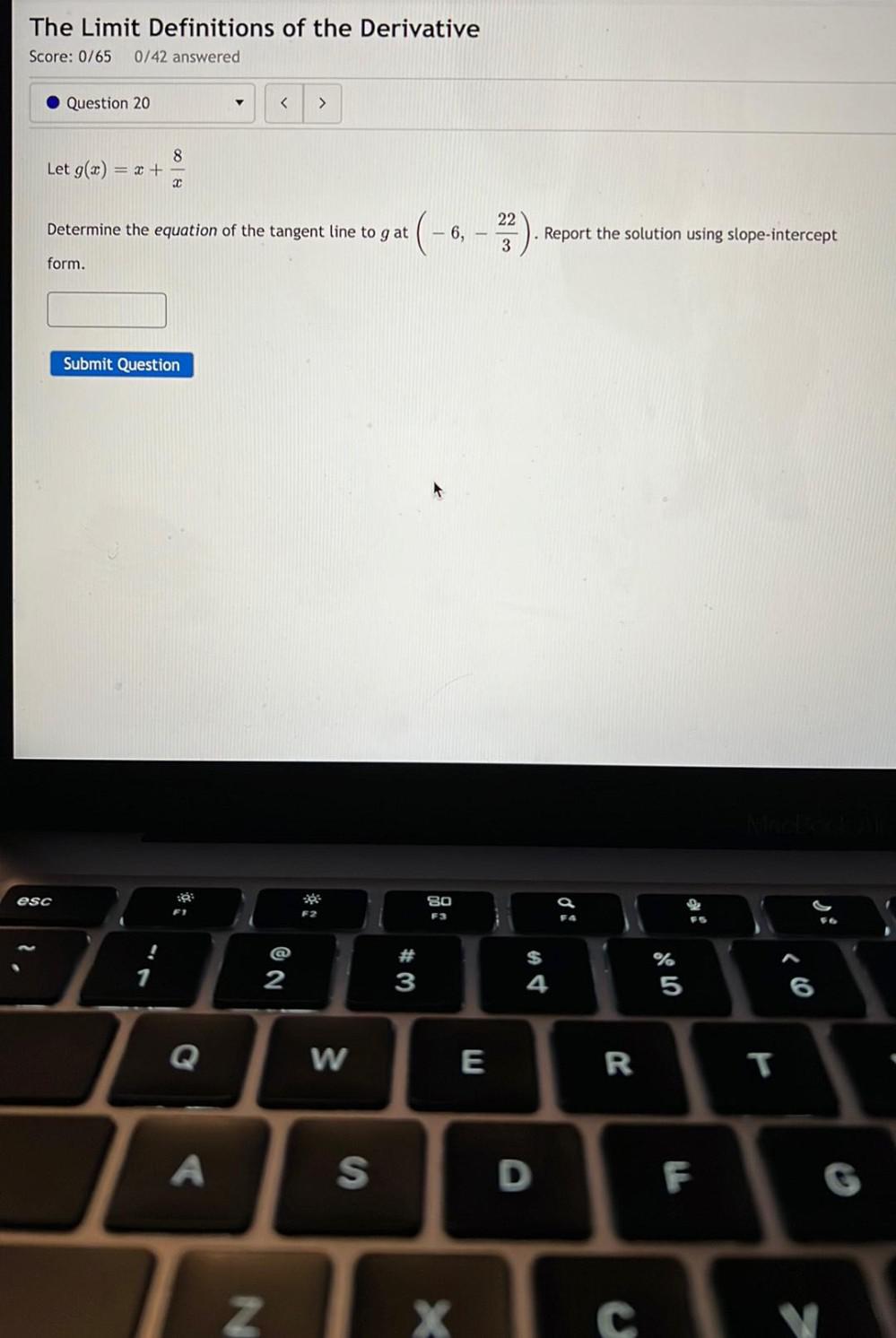
DifferentiationLet g(x) = x + (8/x)
Determine the equation of the tangent line to g at ( -6 , -22/3). Report the solution using slope-intercept form ?
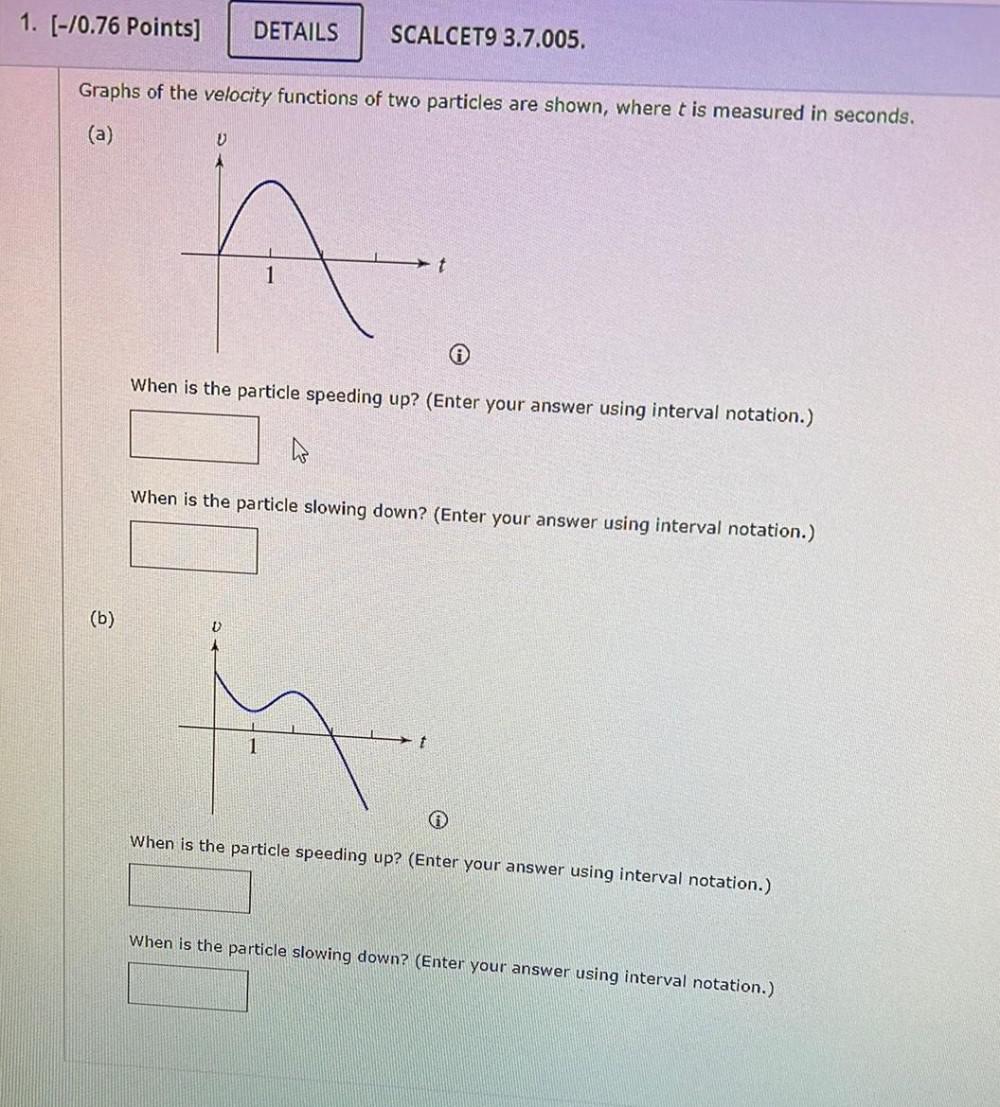
Calculus
DifferentiationGraphs of the velocity functions of two particles are shown, where t is measured in seconds.
(a) When is the particle speeding up? (Enter your answer using interval notation.)
(b) When is the particle slowing down? (Enter your answer using interval notation.)
(c) When is the particle speeding up? (Enter your answer using interval notation.)
(d) When is the particle slowing down? (Enter your answer using interval notation.)

Calculus
Differentiationmaximize(minimize) 3x² + y subject to the constraints: 4x - 3y = 9 and x² + z² = 9
a) Write down the Lagrangian function.
b) What are the first-order conditions?
c) Find the solutions for the given problem.

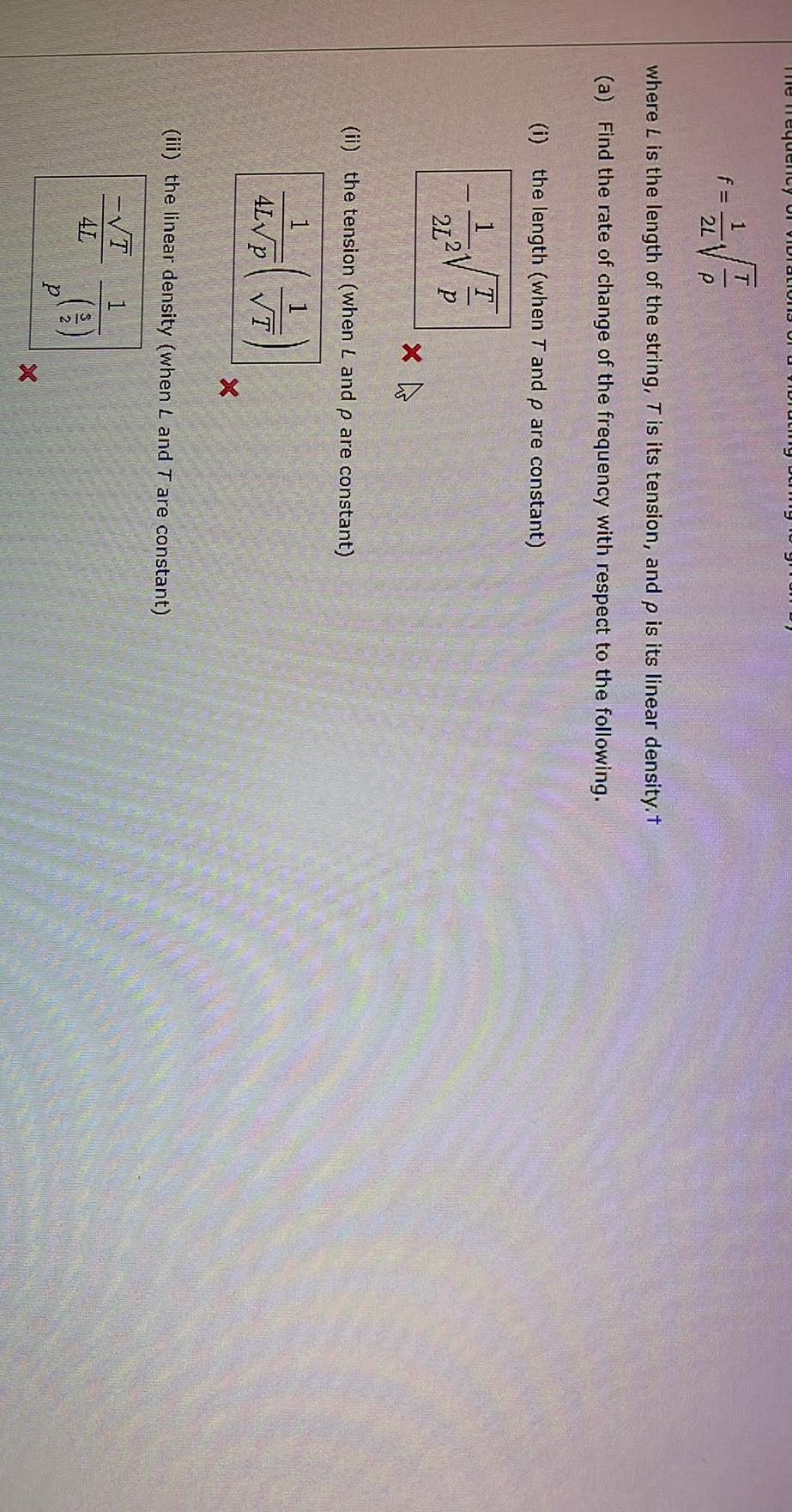
Calculus
Differentiationf = 1/2L √T/P
where L is the length of the string, T is its tension, and p is its linear density.
(a) Find the rate of change of the frequency with respect to the following.
(i) the length (when T and p are constant)
-1/2L² √T/P
(ii) the tension (when L and p are constant)
1/4L√p (1/√T)
(iii) the linear density (when L and T are constant)
-√T/4L 1/p(⁵/²)

Calculus
DifferentiationIn your own words, define the following.
(a)Secant line
(b)Tangent line
(c) Instantaneous rate of change
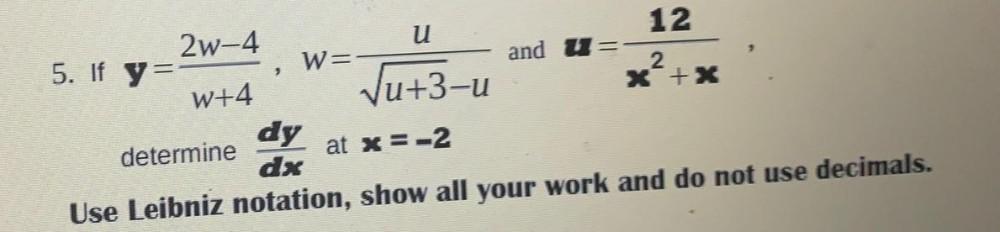
Calculus
DifferentiationIf y= (2w - 4)/(w+4) , w = u/ (√(u+3) - u) and u = 12/(x^2 + x)
determine dy/dx at x= -2
use leibniz notation, show all your work and do not use decimals.
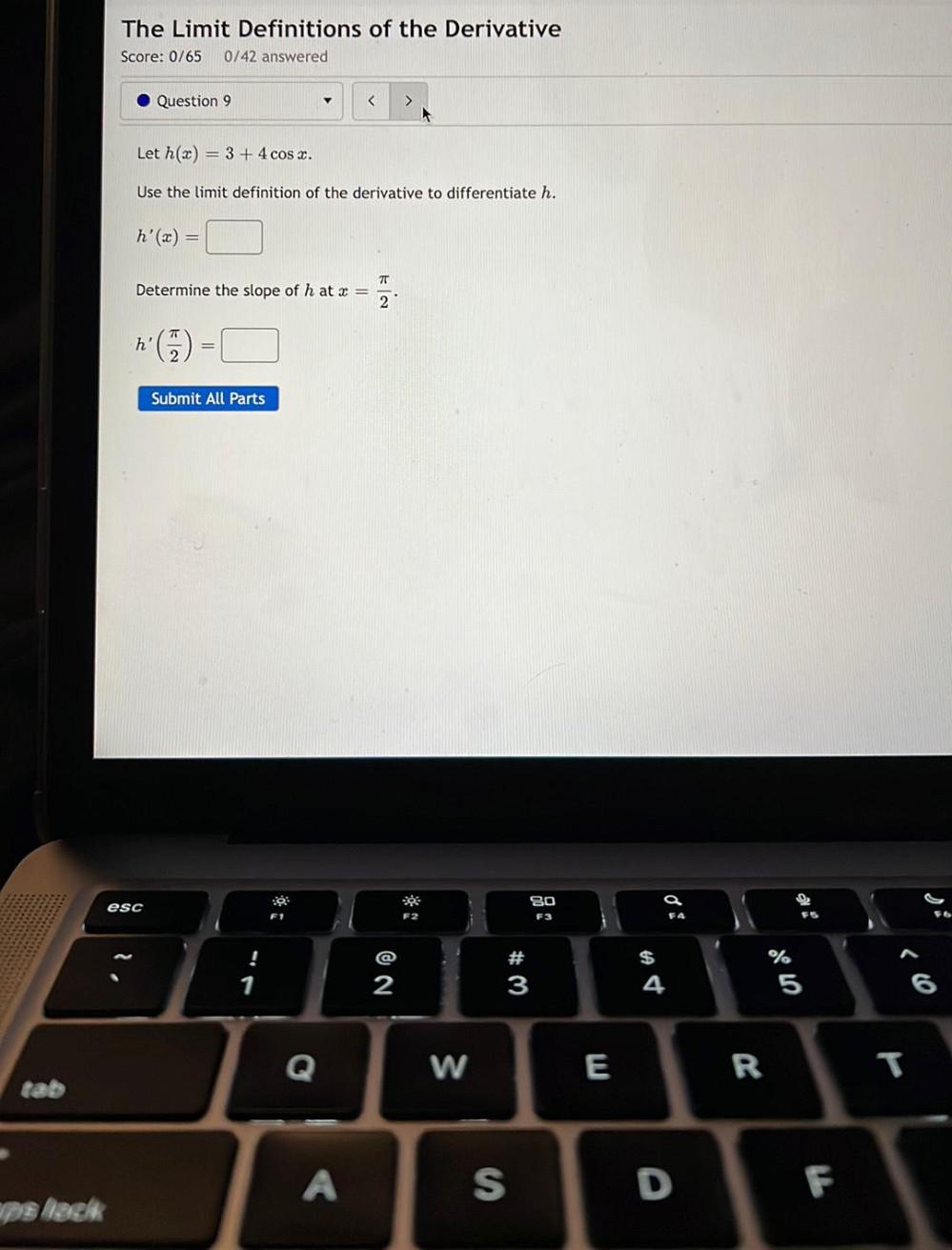
Calculus
DifferentiationLet h(x) = 3 + 4cos x.
Use the limit definition of the derivative to differentiate h.
h'(x) =________
Determine the slope of h at x =π /2
h'(π /2)=______
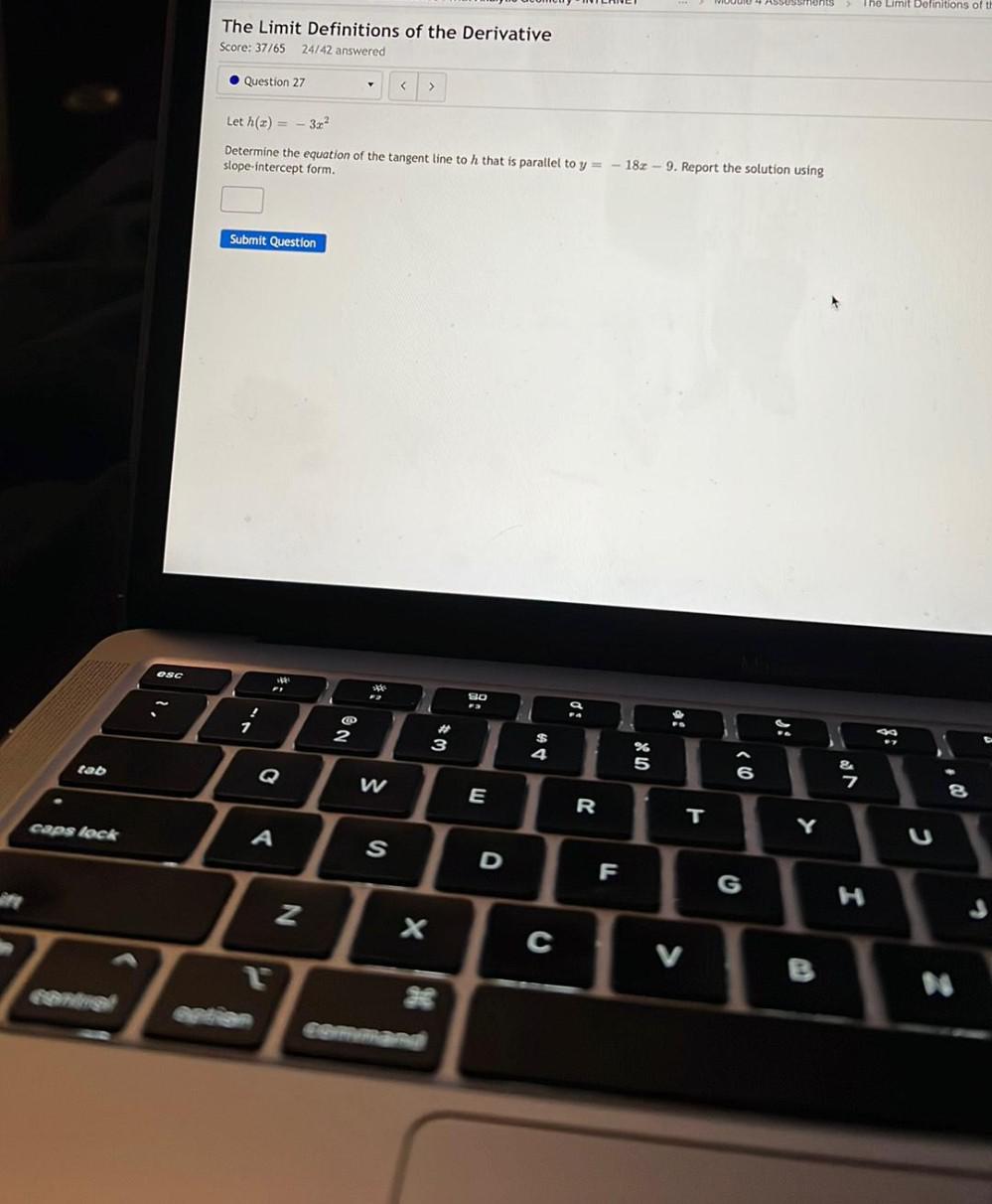
Calculus
DifferentiationLet h(x) = -3x²
Determine the equation of the tangent line to h that is parallel to
y = -18x - 9 . Report the solution using slope - intercept form.
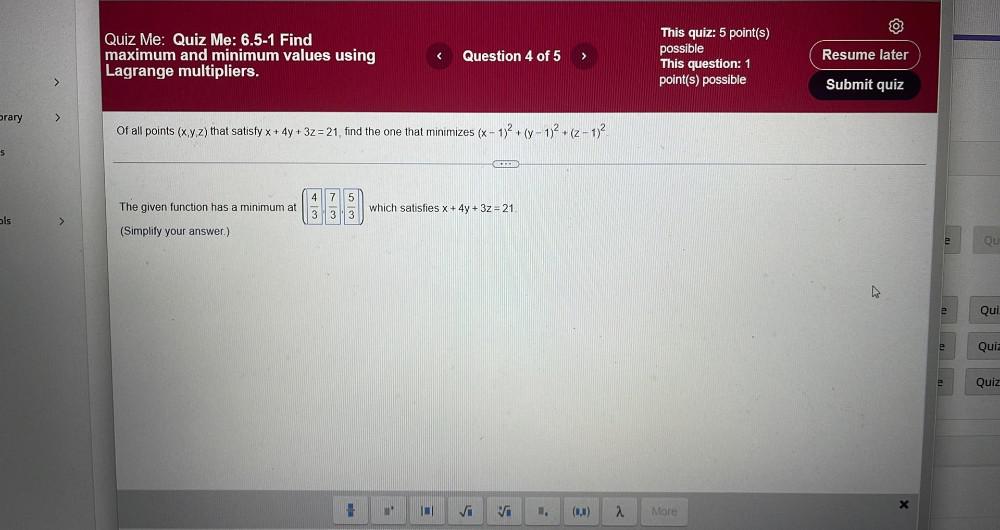
Calculus
DifferentiationOf all points (x, y, z) that satisfy x + 4y + 3z=21, find the one that minimizes
(x - 1)² + (y− 1)² + (z − 1)².
The given function has a minimum at __________which satisfies x + 4y + 3z = 21.

Calculus
DifferentiationA graphing software can quickly create a triangle with base, b (cm), and height, h (cm), represented by b= (t+3)² and h=t² +3, where t is time in seconds. Determine the rate of change of the area of the triangle at 3 seconds & explain your answer.

Calculus
DifferentiationLet f(x) = 2 _-e‾ˣ/x Does f(x) have any horizontal or vertical asymptotes? What are they?. Use limit calculations to justify your answer.
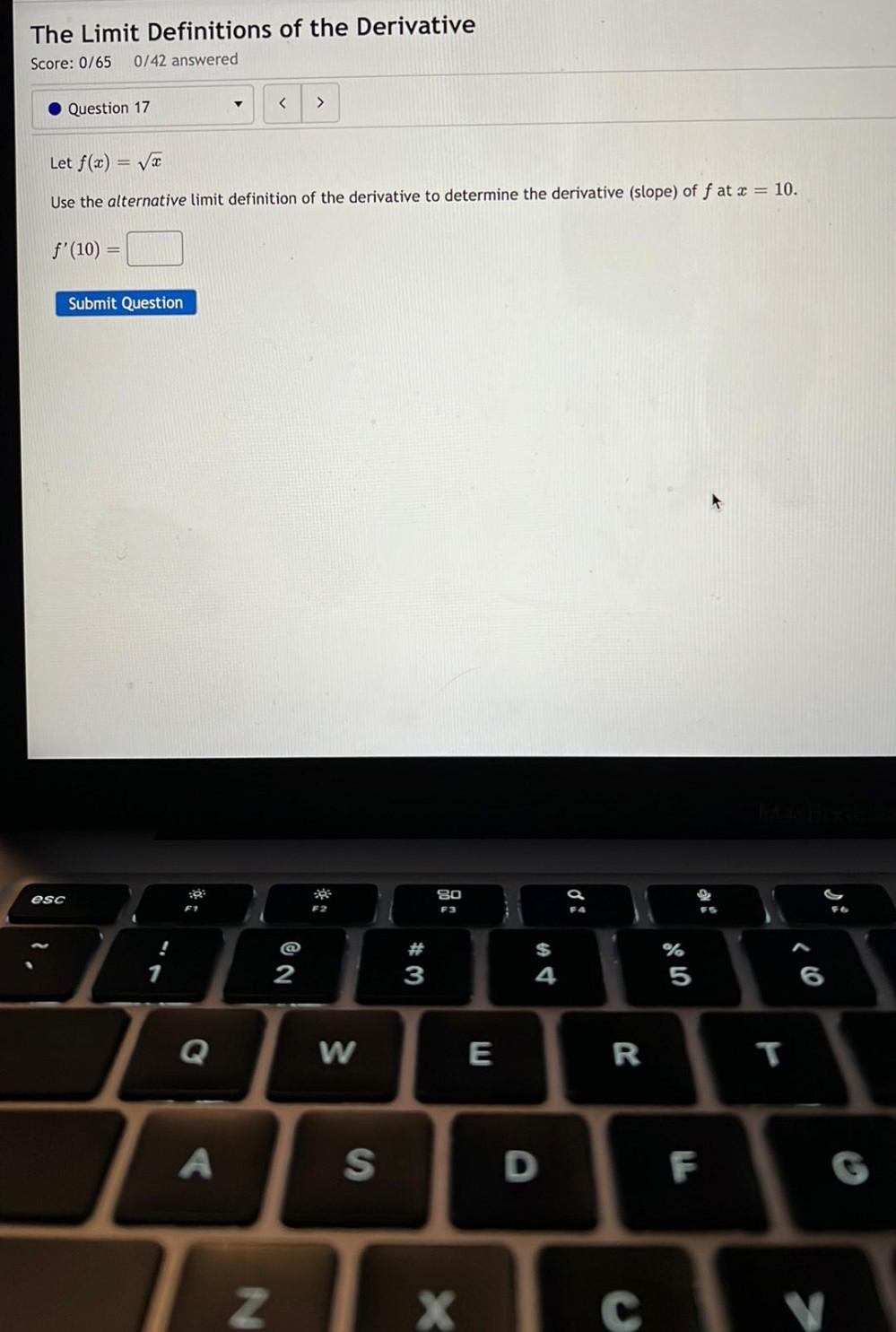
Calculus
DifferentiationLet f(x)=√x
Use the alternative limit definition of the derivative to determine the derivative (slope) of f at x = 10.
f'(10) = __________
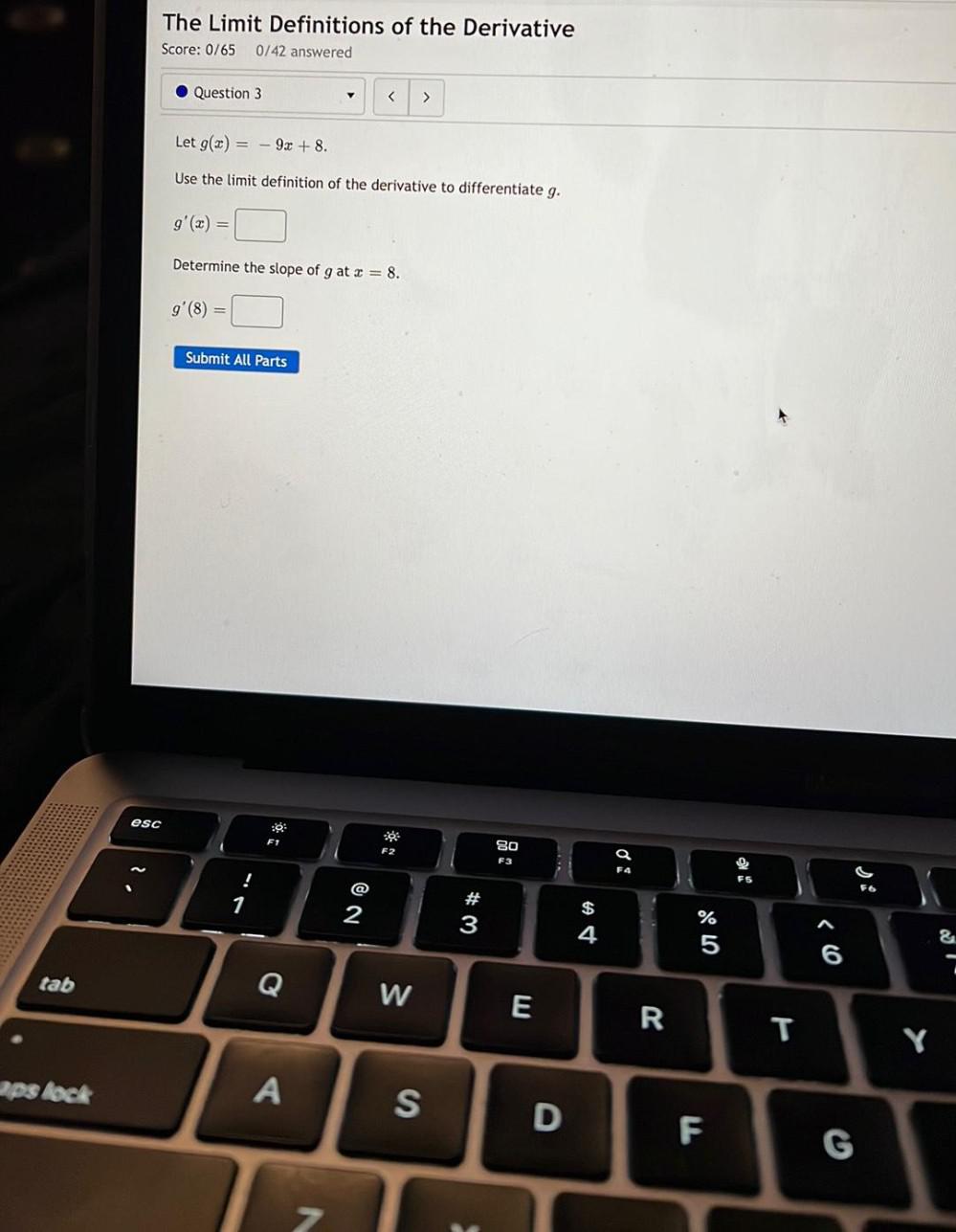
Calculus
DifferentiationLet g(x)= -9x + 8.
Use the limit definition of the derivative to differentiate g.
g'(x) = ________
Determine the slope of g at x = 8.
g'(8) = ______________
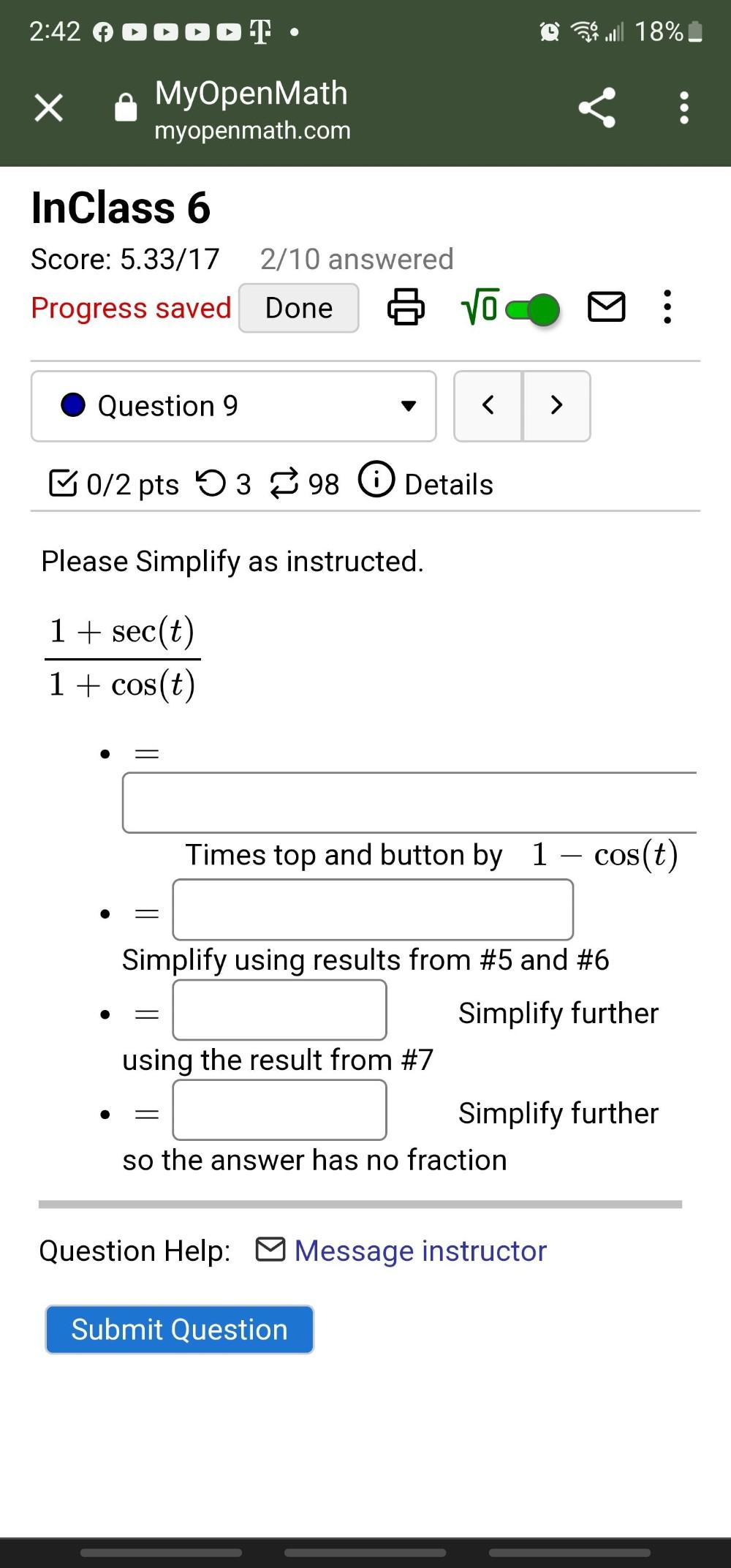
Calculus
DifferentiationPlease Simplify as instructed.
1 + sec(t)//1 + cos(t)
●=□Times top and button by 1 - cos(t)
●=□Simplify using results from #5 and #6
●=□Simplify further using the result from #7
●=□Simplify further so the answer has no fraction
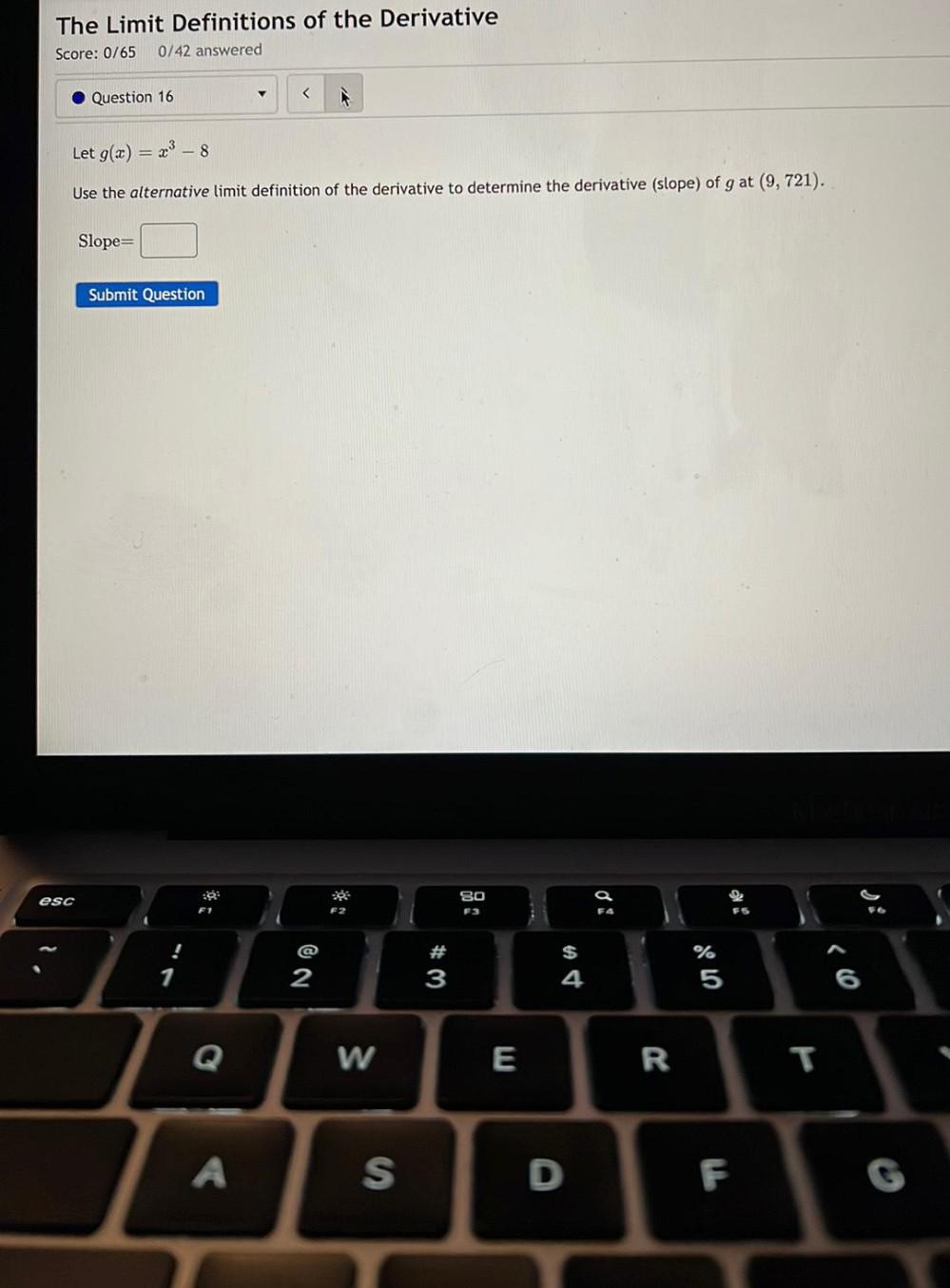
Calculus
DifferentiationLet g(x) = x³ - 8
Use the alternative limit definition of the derivative to determine the derivative (slope) of g at (9, 721).
Slope = __________
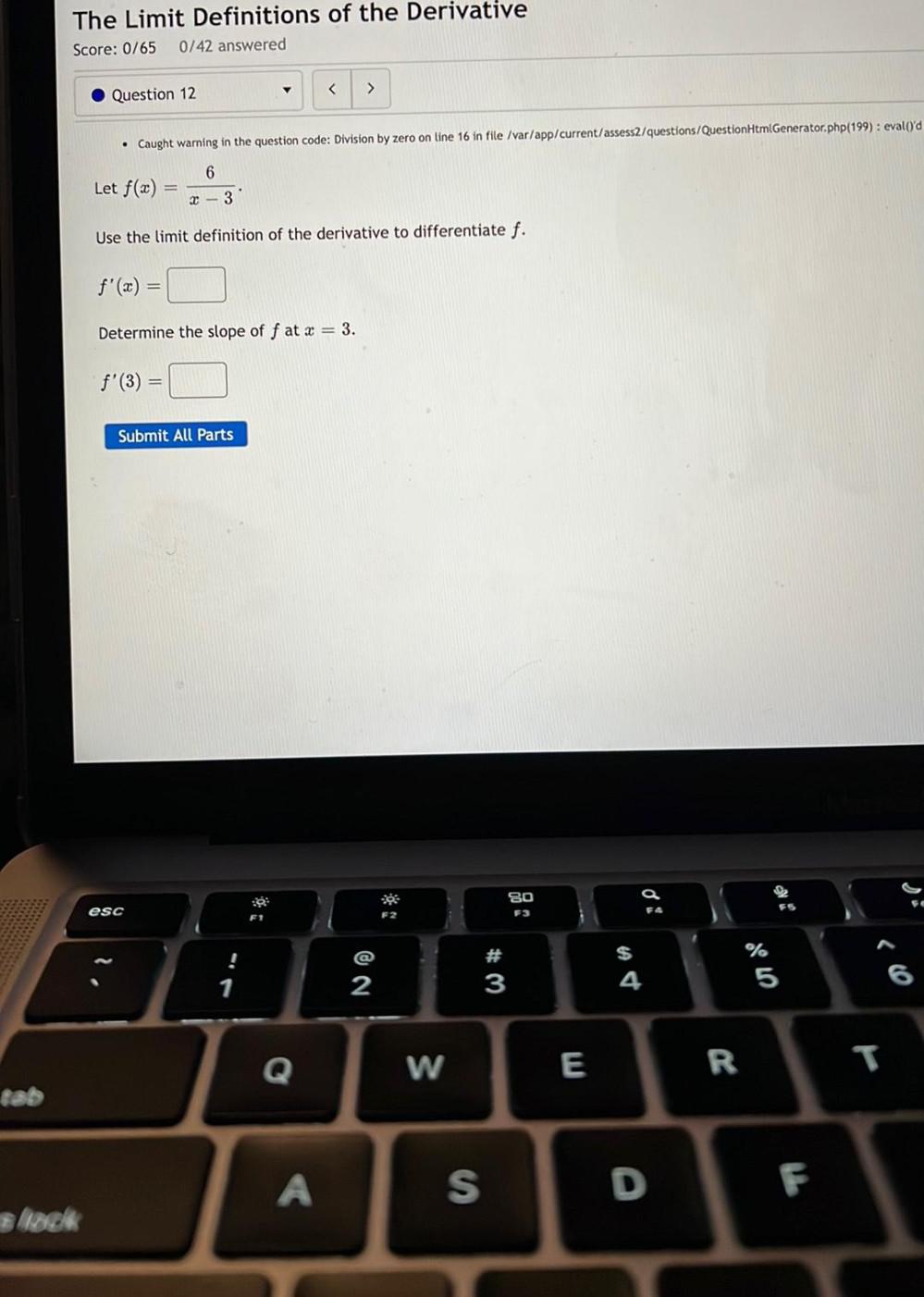
Calculus
DifferentiationLet f(x) = 6/x-3
Use the limit definition of the derivative to differentiate f.
f'(x) = □
Determine the slope of f at x = 3.
f'(3) = □
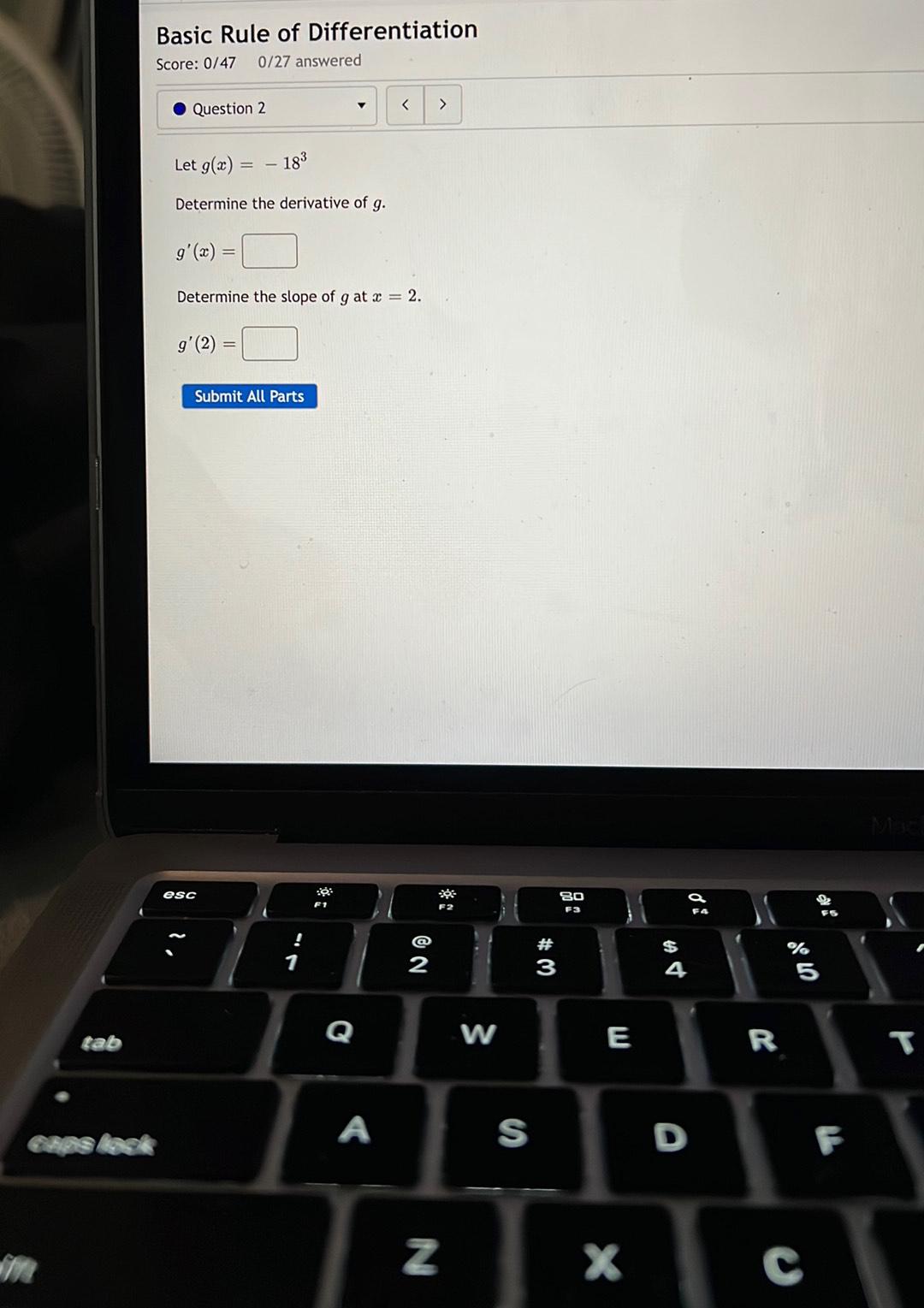
Calculus
DifferentiationLet g(x) = -18³
Determine the derivative of g.
g'(x) = ________
Determine the slope of g at x = 2.
g'(2) = _________
Calculus
DifferentiationLet f(x) = 5x² +9.
Use the limit definition of the derivative to differentiate f.
f'(x)= □
Determine the slope of f at x = 3.
f'(3)= □