Differentiation Questions and Answers

Calculus
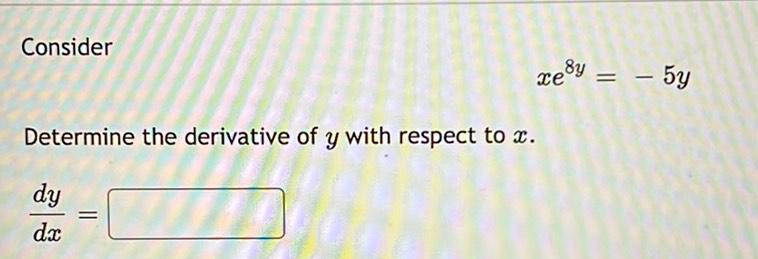
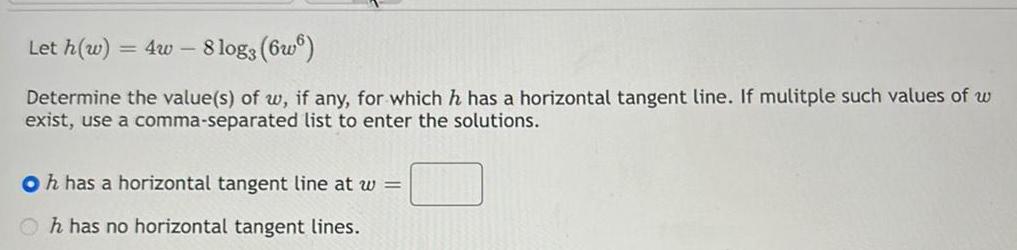
DifferentiationLet h(w) = 4w - 8 log3 (66)
Determine the value(s) of w, if any, for which h has a horizontal tangent line. If mulitple such values of w
exist, use a comma-separated list to enter the solutions.
Oh has a horizontal tangent line at w =
Oh has no horizontal tangent lines.
Calculus
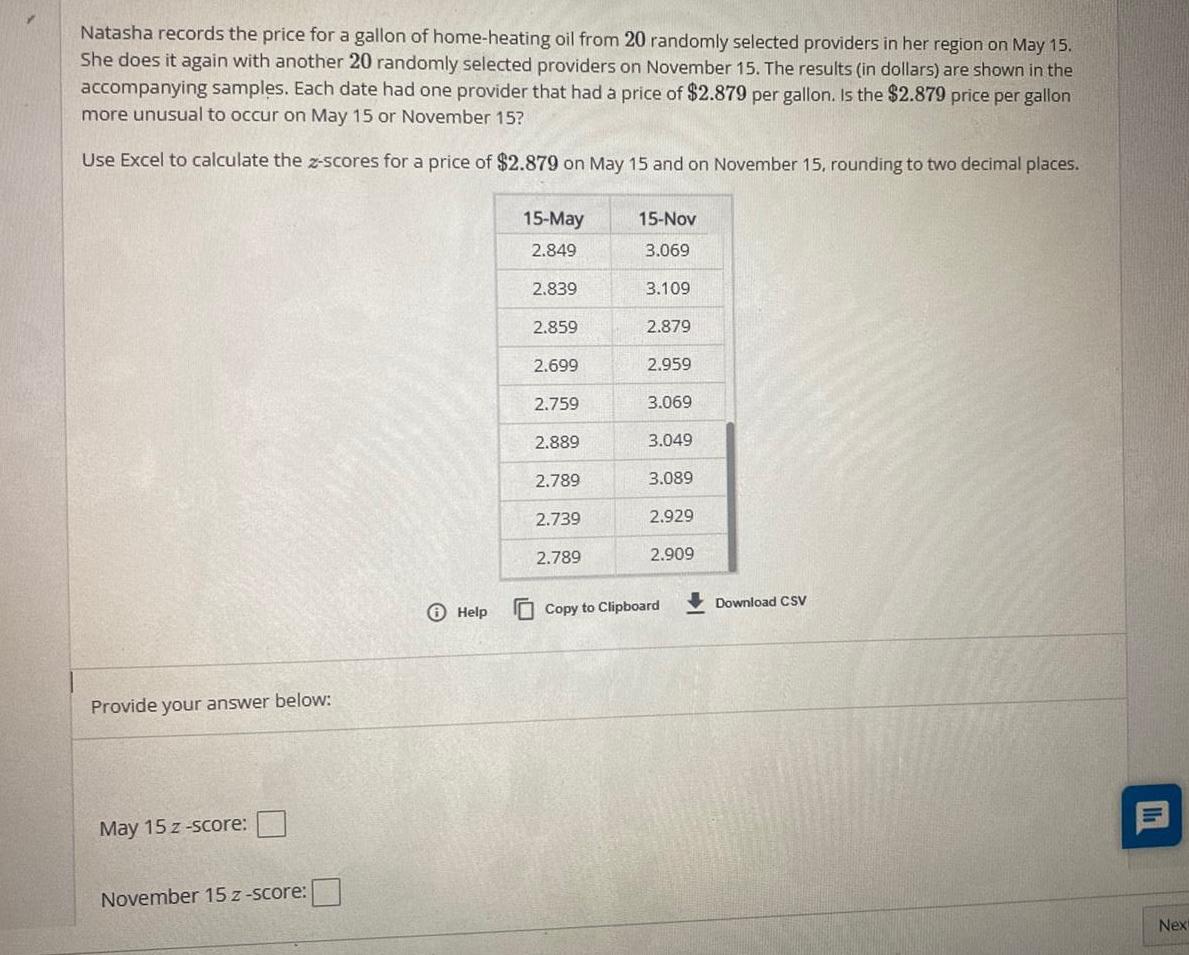
DifferentiationNatasha records the price for a gallon of home-heating oil from 20 randomly selected providers in her region on May 15.
She does it again with another 20 randomly selected providers on November 15. The results (in dollars) are shown in the
accompanying samples. Each date had one provider that had a price of $2.879 per gallon. Is the $2.879 price per gallon
more unusual to occur on May 15 or November 15?
Use Excel to calculate the z-scores for a price of $2.879 on May 15 and on November 15, rounding to two decimal places.
Provide your answer below:
May 15 z-score:
November 15 z-score:
✪ Help
15-May
2.849
2.839
2.859
2.699
2.759
2.889
2.789
2.739
2.789
15-Nov
3.069
3.109
2.879
2.959
3.069
3.049
3.089
2.929
2.909
Copy to Clipboard
Download CSV
Next

Calculus
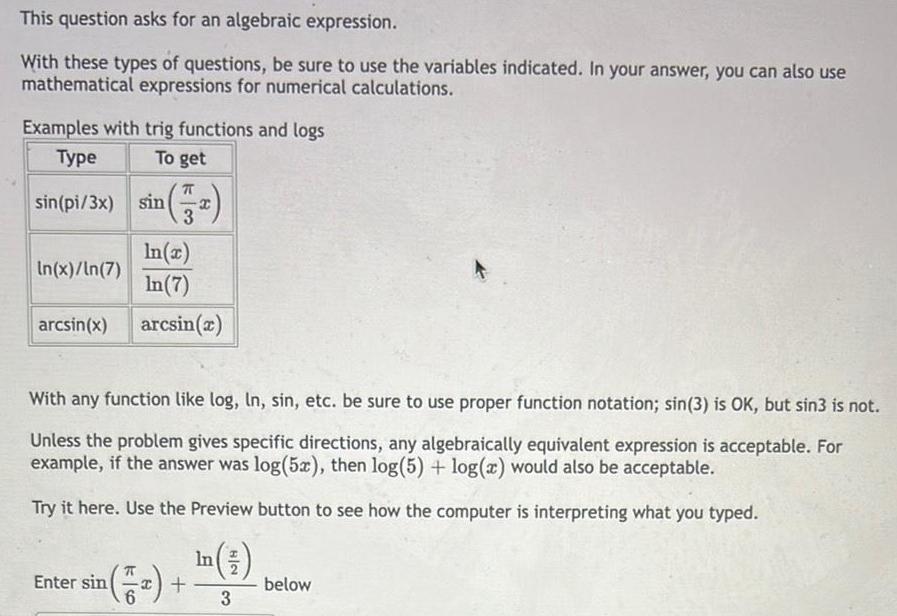
DifferentiationThis question asks for an algebraic expression.
With these types of questions, be sure to use the variables indicated. In your answer, you can also use
mathematical expressions for numerical calculations.
Examples with trig functions and logs
Type
To get
sin(pi/3x)
In(x)/Ln(7)
arcsin(x)
sin
Enter sin
(*)
In(x)
In (7)
arcsin(x)
With any function like log, In, sin, etc. be sure to use proper function notation; sin(3) is OK, but sin3 is not.
Unless the problem gives specific directions, any algebraically equivalent expression is acceptable. For
example, if the answer was log(5x), then log(5) + log(x) would also be acceptable.
Try it here. Use the Preview button to see how the computer is interpreting what you typed.
In (3)
3
(5₂) +
below

Calculus
DifferentiationA plant can manufacture 50 golf clubs per day at a total daily cost of $4883 and 60 golf clubs per day for a total cost of $5533.
(A) Assuming that daily cost and production are linearly related, find the total daily cost, C, of producing x golf clubs.
(B) Graph the total daily cost for 0≤x≤ 200.
(C) Interpret the slope and y intercept of the cost equation.

Calculus
DifferentiationPrecision Aviation had a profit margin of 6.25%, a total assets turnover of 1.5, and an equity multiplier of 1.8. What was the firm's ROE?
O a. 20.93%
O b. 16.88%
c. 13.84%
d. 14.34%
e. 17.72%
Calculus
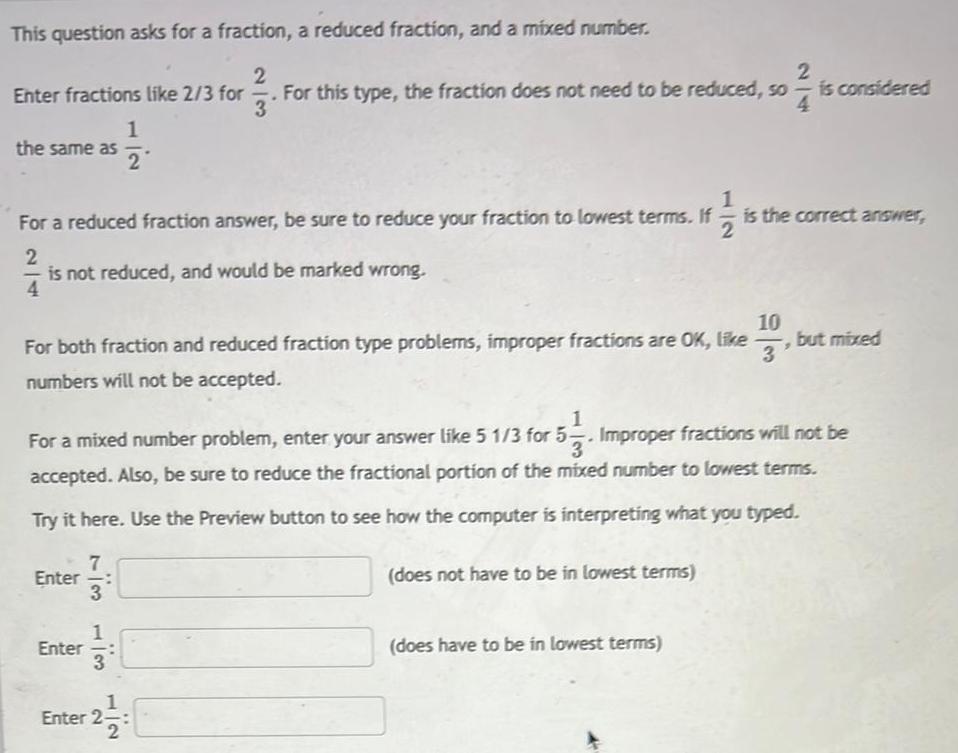
DifferentiationThis question asks for a fraction, a reduced fraction, and a mixed number.
2
Enter fractions like 2/3 for
the same as
if 1/1/1 15
For a reduced fraction answer, be sure to reduce your fraction to lowest terms. If
2
Enter
2
is not reduced, and would be marked wrong.
4
Enter
1
2
711 171
For both fraction and reduced fraction type problems, improper fractions are OK, like
numbers will not be accepted.
3
3
3
.
For this type, the fraction does not need to be reduced, so
2²/14
1
+2/7/20
Enter 2-
3
For a mixed number problem, enter your answer like 5 1/3 for 5. Improper fractions will not be
accepted. Also, be sure to reduce the fractional portion of the mixed number to lowest terms.
Try it here. Use the Preview button to see how the computer is interpreting what you typed.
(does not have to be in lowest terms)
is the correct answer,
(does have to be in lowest terms)
10
is considered
-, but mixed
3
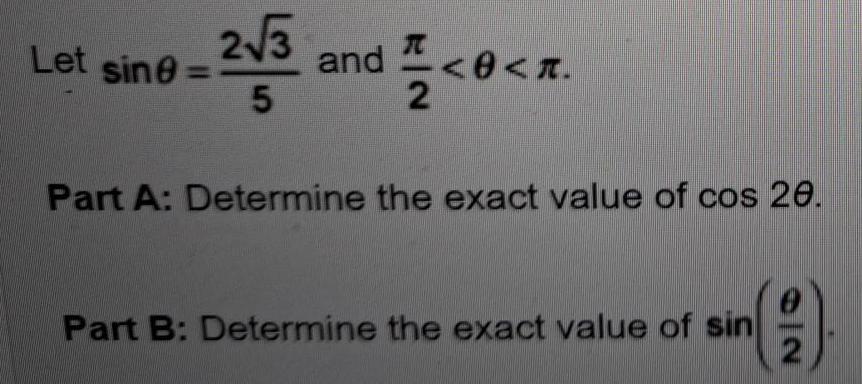
Calculus
DifferentiationLet sine=
2√3 and <0<x
5
2
Part A: Determine the exact value of cos 20.
Part B: Determine the exact value of sin
O|N

Calculus
Differentiation3
=
Given g(x)
find g' (1).
Round your answer to the nearest hundredths (two digits after the decimal).
800
x
-
6x
Calculus
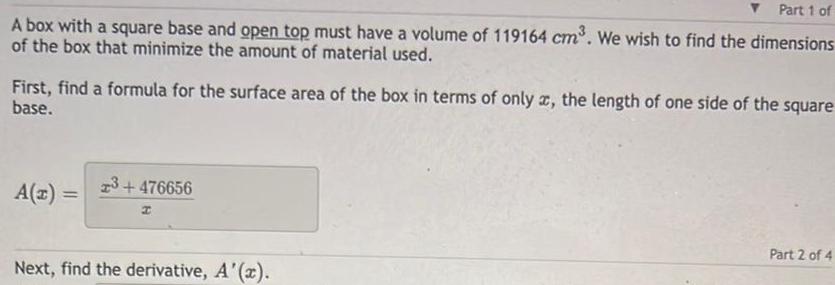
DifferentiationPart 1 of
A box with a square base and open top must have a volume of 119164 cm³. We wish to find the dimensions
of the box that minimize the amount of material used.
First, find a formula for the surface area of the box in terms of only x, the length of one side of the square
base.
A(z) =
=
3+476656
H
Next, find the derivative, A'(x).
Part 2 of 4

Calculus
Differentiation(1 point) Let F = xi + (x + y) j + (x − y + z) k. Let the line / be
(a) Find a point P = (xo, Yo, Zo) where F is parallel to 1.
P =
Find a point Q = (x₁, №₁, Z₁ ) at which I and I are perpendicular.
Q=
=
3-t, y = 5t-1, z = 1+ 3t.
Give an equation for the set of all points at which I and I are perpendicular.
equation:

Calculus
DifferentiationUse the x-cubed tool
to graph the x-cubed function. Update the function
to have a Vertical Stretch of 3, a Horizontal Stretch of 1, a Vertical Shift of 0, a
Horizontal Shift of 5, and a Reflection over the x-axis.


Calculus
DifferentiationUse logarithmic differentiation to determined at x =1 for the following function:
y=√x+1/(x+2)(x³+1)
-7√2/72
7/ 2√2
√2/6
7/12

Calculus
Differentiation=
. Let u(x, y) be the solution to the boundary value problem uxx + Uyy 0,
for all (x, y) such that x² + y² < 1, and u(x, y) = x², for all (x, y) such
that x² + y² = 1. Find u(0, 0).
![Determine, with motivation, whether the following function satisfies Dirichlet's
conditions on the given interval:
f(x) = cosec(x) with f(x) = f(x + π) on (-₁)
[2]](https://media.kunduz.com/media/sug-question/raw/82777895-1660233221.6287816.jpeg?w=256)
Calculus
DifferentiationDetermine, with motivation, whether the following function satisfies Dirichlet's
conditions on the given interval:
f(x) = cosec(x) with f(x) = f(x + π) on (-₁)
[2]

Calculus
DifferentiationWhat are the Cartesian coordinates of the point whose cylindrical coordinates are
(r, 0, z) = (4, 2.6, -6) ?
(x, y, z) = (
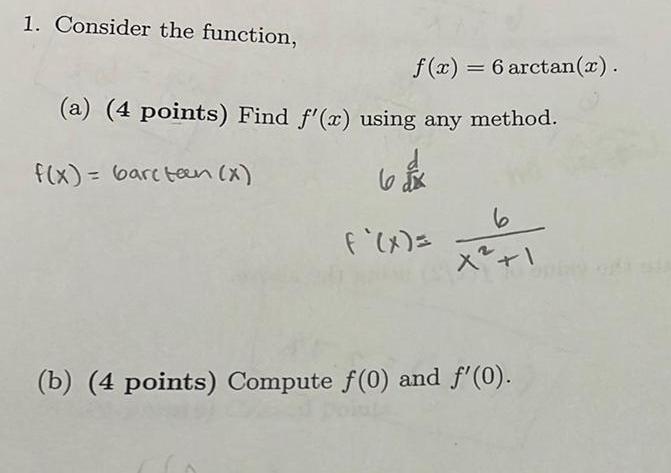
Calculus
Differentiation1. Consider the function,
f(x) = 6 arctan(x).
(a) (4 points) Find f'(x) using any method.
f(x)= barctan (x)
bask
6
x² +1
(b) (4 points) Compute f(0) and f'(0).
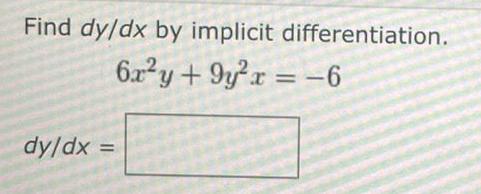

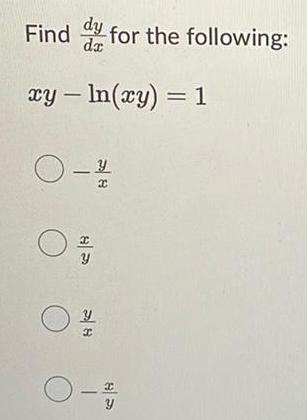

Calculus
DifferentiationConsider the following.
x² + y² = 9
(a) Find two explicit functions by solving the equation for y in terms of x.
(positive function)
Y1 =
Y2 =
(negative function)

Calculus
DifferentiationPerform the indicated operations
(2x^2-6x+11)+(-3x^2+7x-2)
(-4y^2 - 3y+8)-(2y2-6y - 2)
6x(-2x^2+5x+6)
(9k+q)(2k-q)
5. (2m+1)(4m^2-2m + 1)
All up arrows are to the 2nd power
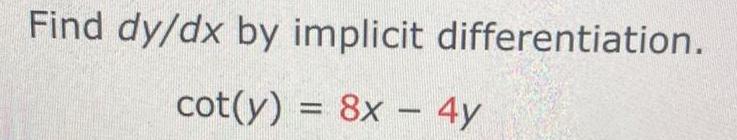

Calculus
DifferentiationThe
loudness L(x), measured in decibels, of a sound of intensity x, measured in watts per square meter, is defined as L(x) = 10 log
can detect. Determine the loudness, in decibels, of a sound with intensity of x = 10-10.8 watt per square meter.
where lo = 10
- 12
watt per square meter is the least intense sound that a human ear

Calculus
DifferentiationFind the vertices, foci, equation of the asymptotes, transverse and conjugate axis length for 9y² - 25x²= 225. Type the
equation in standard form and then state the five answers.
Checklist:
1) State equation in standard form
(2) State the vertices
3) State the foci
4) State the equation of the asymptotes
5) Give the length of the transverse axis
6) Give the length of the conjugate axis

Calculus
DifferentiationThe Louvre museum in Paris features an inverted square
pyramid with a height of 10 m. The side of the square is 13 m.
Super-villains decide to fill the pyramid with water, and do so at
a rate of 10 m³ per second. How quickly is the water level rising
when it reaches the top? (10 marks)

Calculus
DifferentiationIf you make $2500 in Gross Income every month, but 35% is taken out in taxes, what will your monthly Net Income paycheck be?
O $1500
$875
$2500
$1625
Calculus
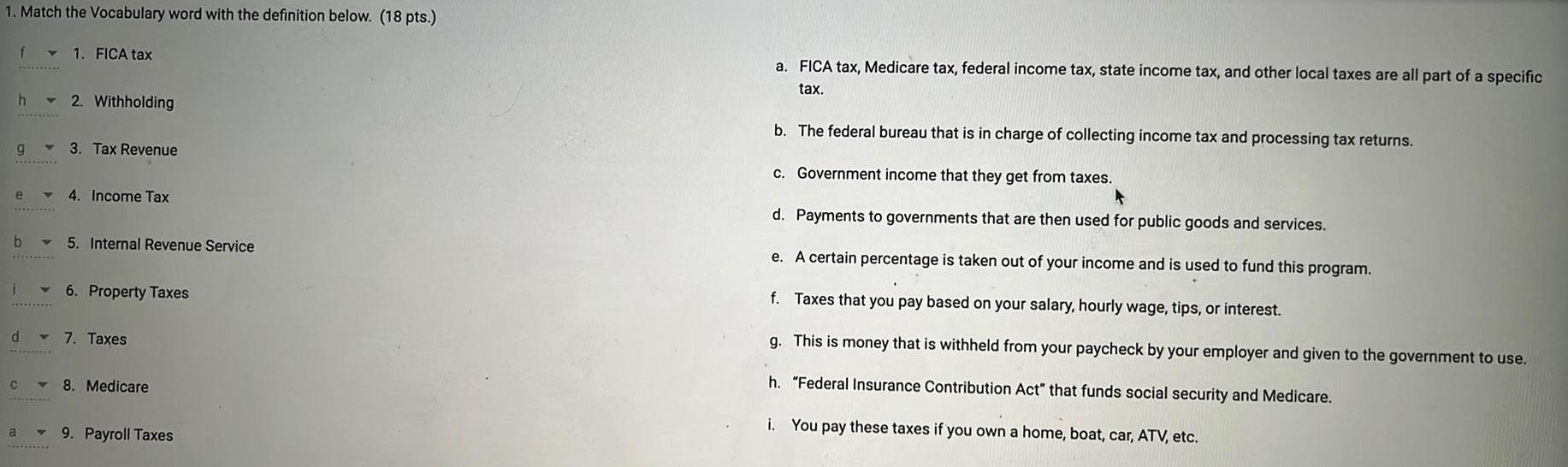
Differentiation1. Match the Vocabulary word with the definition below. (18 pts.)
f
h
9
e
b
d
C
a
Y 1. FICA tax
▾ 2. Withholding
V
3. Tax Revenue
4 4. Income Tax
V
5. Internal Revenue Service
6. Property Taxes
7. Taxes
8. Medicare
9. Payroll Taxes
a. FICA tax, Medicare tax, federal income tax, state income tax, and other local taxes are all part of a specific
tax.
b. The federal bureau that is in charge of collecting income tax and processing tax returns.
c. Government income that they get from taxes.
d. Payments to governments that are then used for public goods and services.
e. A certain percentage is taken out of your income and is used to fund this program.
f. Taxes that you pay based on your salary, hourly wage, tips, or interest.
g. This is money that is withheld from your paycheck by your employer and given to the government to use.
h. "Federal Insurance Contribution Act" that funds social security and Medicare.
i.
You pay these taxes if you own a home, boat, car, ATV, etc.

Calculus
Differentiation5. Enter your response into the blank field using one word only.
income is the total amount of what you earned. (2 pts.)
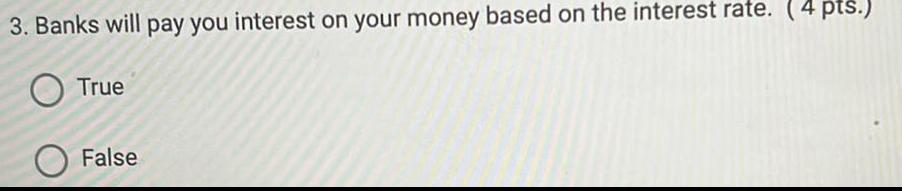
Calculus
Differentiation3. Banks will pay you interest on your money based on the interest rate. (4 pts.)
O True
False

Calculus
DifferentiationMatch the financial institution with its definition. (6 pts.)
V
▼
1. Credit Union
2. Bank
3. Brokerage Firm
a. A business where stocks, bonds or mutual funds are sold. The
can be found in your hometown or on the internet.
b. An organization chartered by either the state where it is
headquartered or by the federal government.
c. A non-profit company that is owned by its stockholders and
provides checking accounts and other financial services.

Calculus
DifferentiationComplete the table to find the derivative of the function.
Original Function
Rewrite
7
y =
Differentiate Simplify
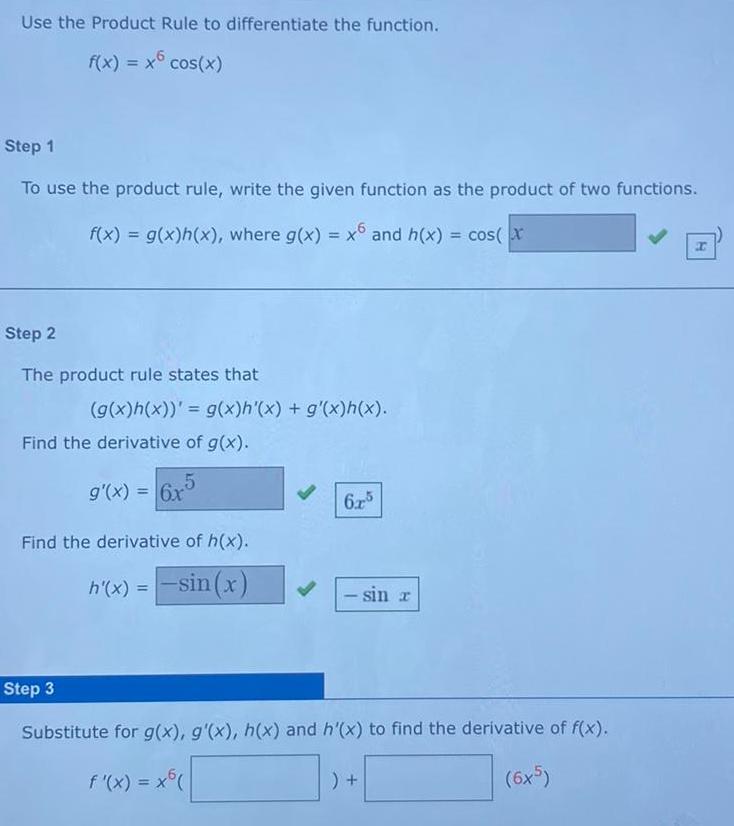
Calculus
DifferentiationUse the Product Rule to differentiate the function.
f(x) = x cos(x)
Step 1
To use the product rule, write the given function as the product of two functions.
f(x) = g(x)h(x), where g(x) = x and h(x)
Step 2
The product rule states that
(g(x)h(x))' = g(x)h'(x) + g'(x)h(x).
Find the derivative of g(x).
g'(x) = 6x5
Find the derivative of h(x).
h'(x) = sin(x)
6x5
- sin r
= = cos(x
Step 3
Substitute for g(x), g'(x), h(x) and h'(x) to find the derivative of f(x).
f'(x) = x(
(6x5)
) +
H
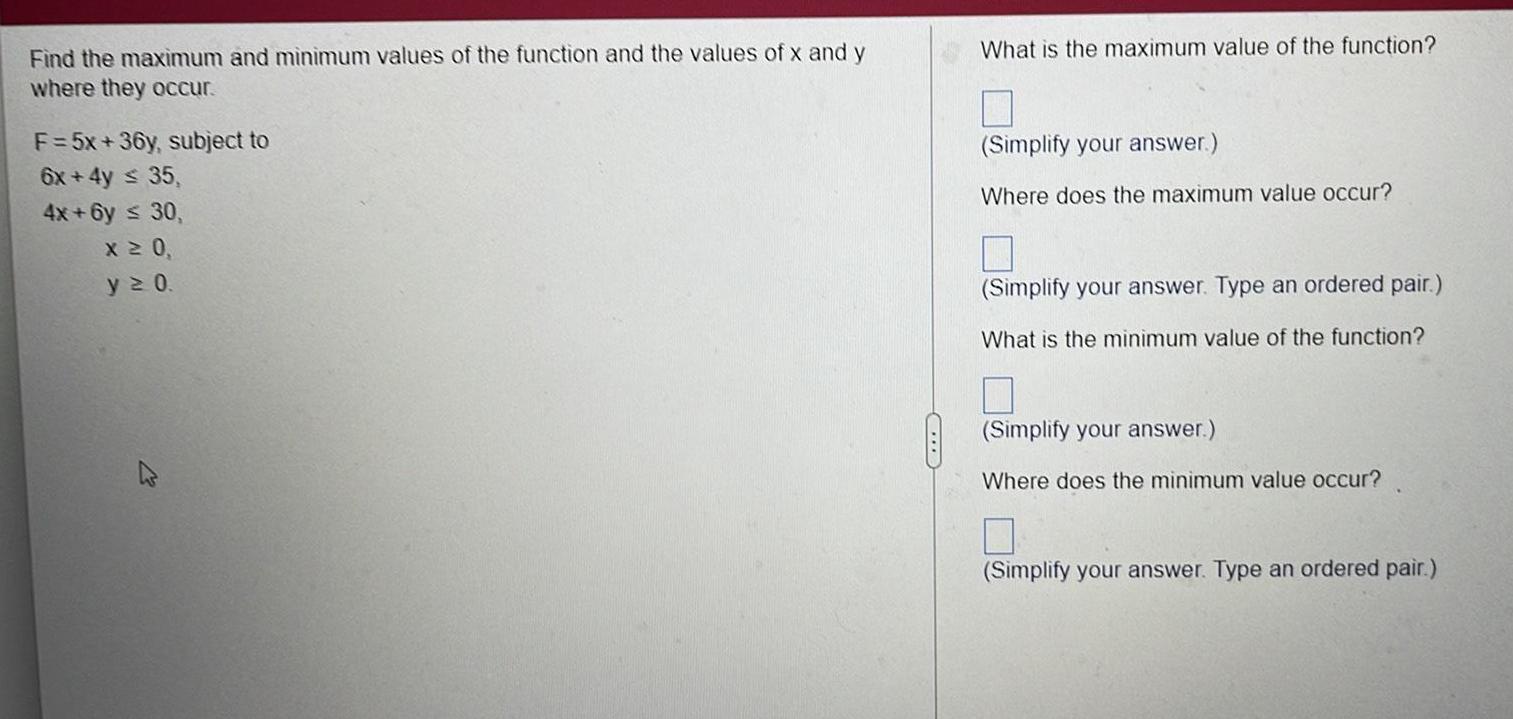
Calculus
DifferentiationFind the maximum and minimum values of the function and the values of x and y
where they occur.
F = 5x +36y, subject to
6x + 4y ≤ 35,
4x+6y ≤ 30,
x ≥ 0,
≥
0.
y
M
What is the maximum value
the function?
(Simplify your answer.)
Where does the maximum value occur?
7
(Simplify your answer. Type an ordered pair.)
What is the minimum value of the function?
(Simplify your answer.)
Where does the minimum value occur?
1
(Simplify your answer. Type an ordered pair.)
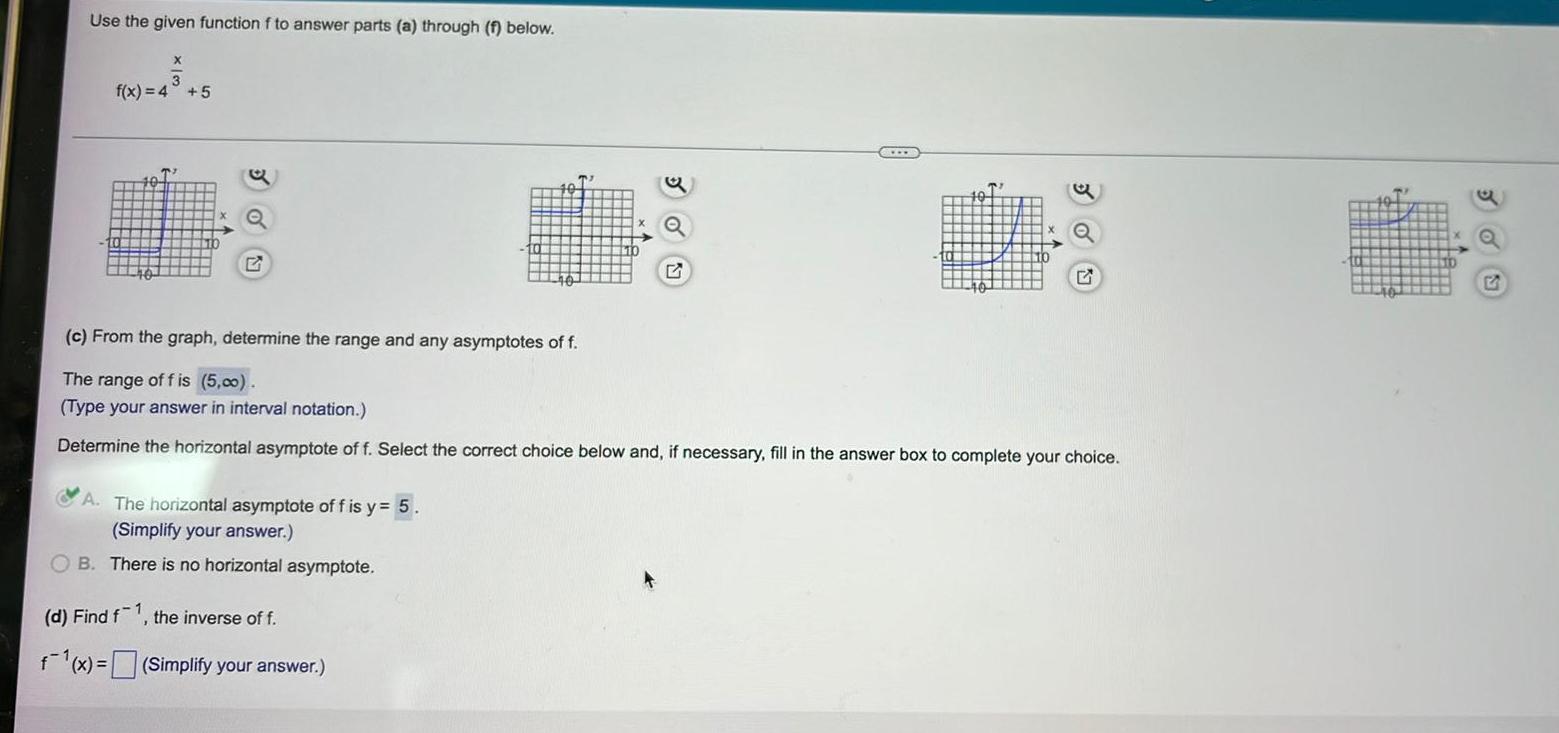
Calculus
DifferentiationUse the given function f to answer parts (a) through (f) below.
X
f(x) = 4 +5
T
A. The horizontal asymptote of f is y = 5.
(Simplify your answer.)
OB. There is no horizontal asymptote.
(d) Find f1, the inverse of f.
f(x)= (Simplify your answer.)
G
(c) From the graph, determine the range and any asymptotes of f.
The range of f is (5,00).
(Type your answer in interval notation.)
Determine the horizontal asymptote of f. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
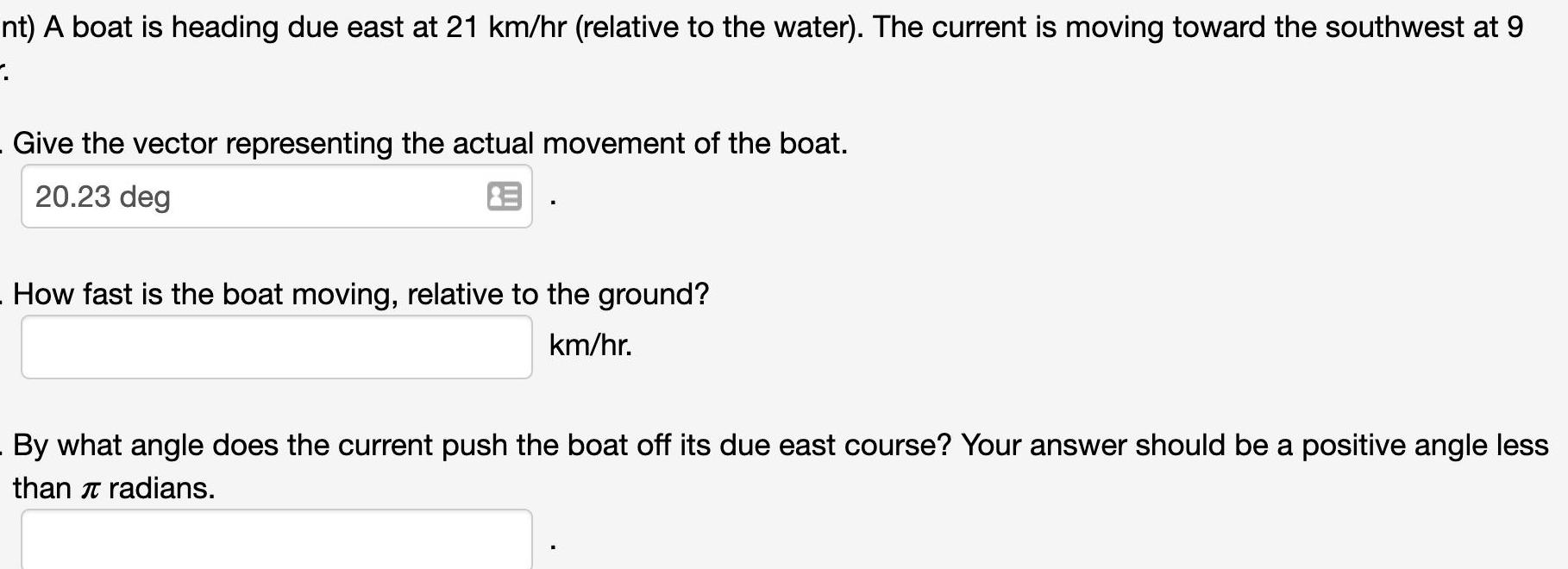
Calculus
Differentiationnt) A boat is heading due east at 21 km/hr (relative to the water). The current is moving toward the southwest at 9
7
. Give the vector representing the actual movement of the boat.
20.23 deg
How fast is the boat moving, relative to the ground?
km/hr.
By what angle does the current push the boat off its due east course? Your answer should be a positive angle less
than radians.
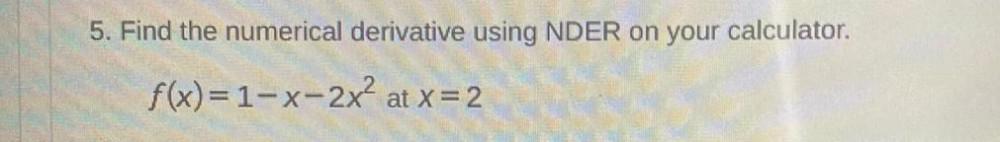
Calculus
DifferentiationFind the numerical derivative using NDER on your calculator.
f(x)=1-x-2x^2 at x = 2

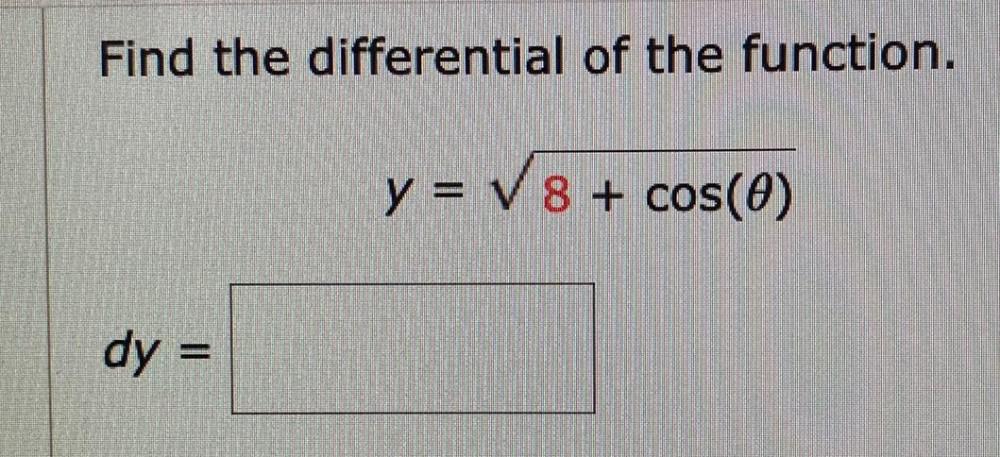

Calculus
DifferentiationUse the definition of a derivative, lim f(x+h)-f(x)/h to find the
h→0
derivative of the following function: f(x)=x²-3x

Calculus
DifferentiationA street light is mounted at the top of a 15-ft-tall pole. A man 6 feet tall walks away from the pole with a speed of 7 ft/s along a straight path. How fast (in ft/s) is the tip of his shadow moving when he is 40 feet from the pole?

Calculus
DifferentiationIf x^2 + y^2 + z^2 = 9,
(dx/dy) = 3, and (dy/dt)= 9, find (dt/dz) when (x, y, z) = (2, 2, 1).
dz/dt =
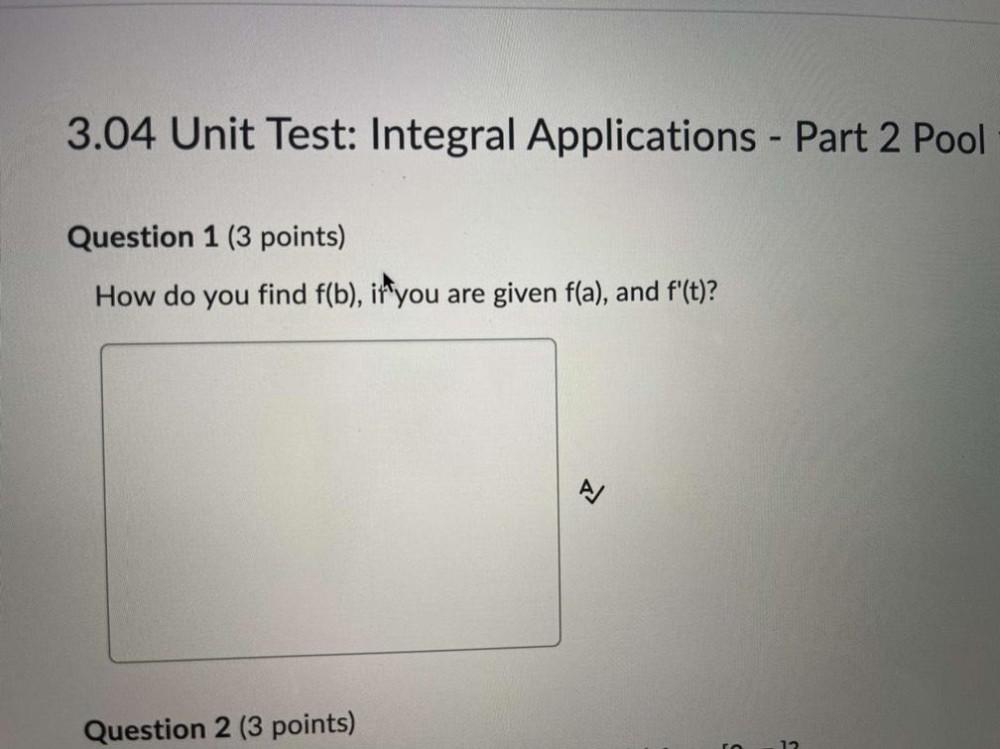
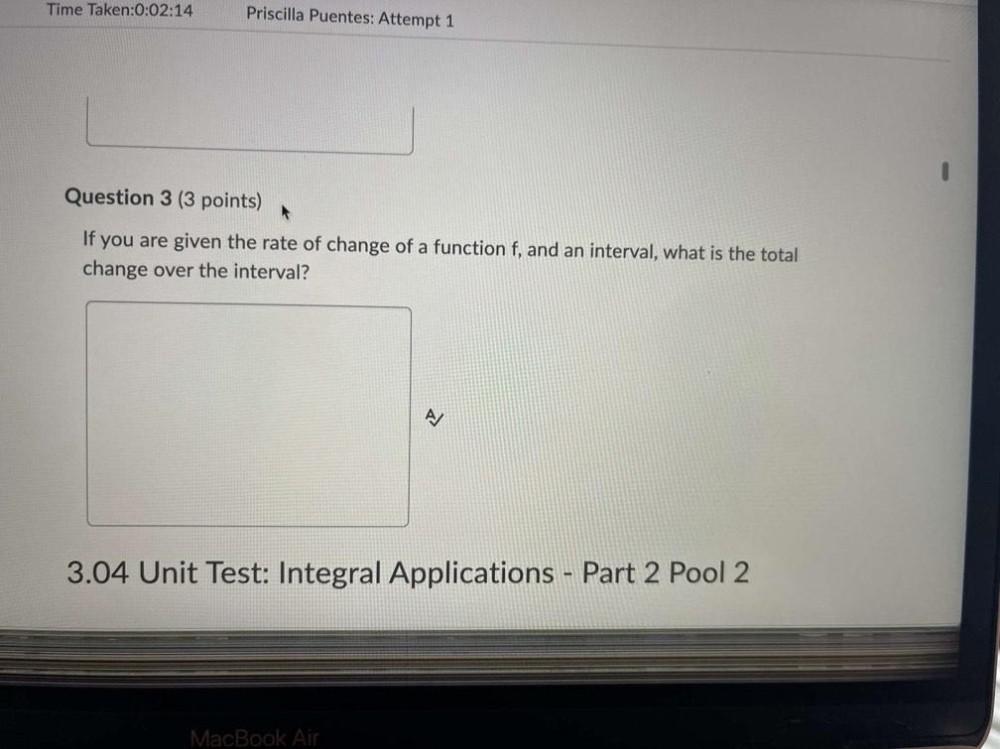
Calculus
DifferentiationIf you are given the rate of change of a function f, and an interval, what is the total change over the interval?
Calculus
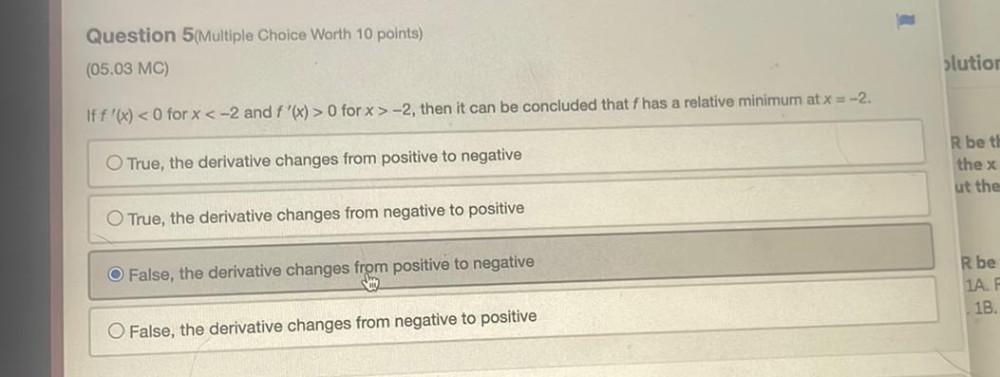
DifferentiationIf f'(x) < 0 for x < -2 and f'(x) > 0 for x > -2, then it can be concluded that f has a relative minimum at x = -2.
A) True, the derivative changes from positive to negative.
B) True, the derivative changes from negative to positive.
C) False, the derivative changes from positive to negative.
D) False, the derivative changes from negative to positive.