Differentiation Questions and Answers
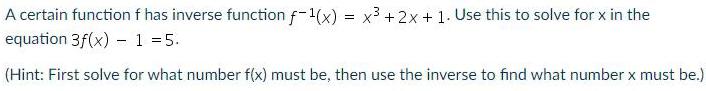
Calculus
DifferentiationA certain function f has inverse function f⁻¹(x) = x³ + 2x + 1. Use this to solve for x in the
equation 3f(x) - 1 = 5.
(Hint: First solve for what number f(x) must be, then use the inverse to find what number x must be.)
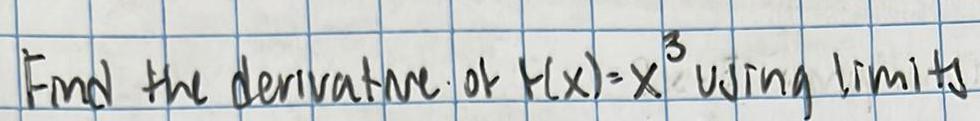

Calculus
DifferentiationSuppose f'(x) is continuous over an interval α ≤ x ≤ b, and a < c < d < b.
If f'(c) = 5, then (check all that apply)
f(x) is decreasing through x = c
f(c) = 5
f(c) exists
f does not have a minimum at x = c
f does not have a maximum at x = c
f(x) is increasing through x = c
If f'(d) = -5, then (check all that apply)
f(d) exists
f does not have a maximum at x = d
f does not have a minimum at x = d
f(d) = -5
f(x) is increasing through x = d
f(x) is decreasing through x = d
Based on this, we know that for some x between x = c and x = d:
f has a maximum
f has a minimum
f does not exist
f'(x) = 0
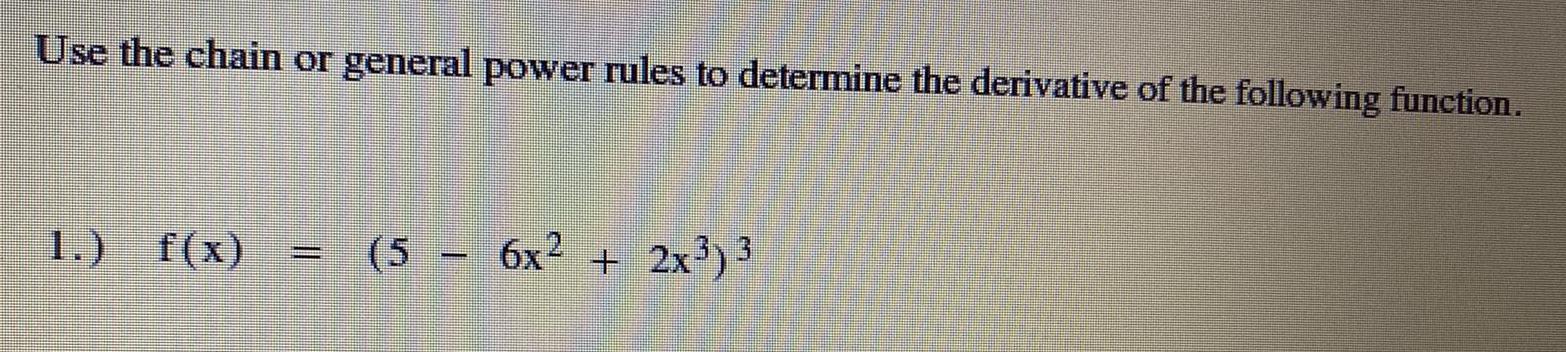
Calculus
DifferentiationUse the chain or general power rules to determine the derivative of the following function.
f(x)=(5-6x²+2x³)³

Calculus
DifferentiationLet a≠0 be a complex number, and define the αth branch of zª by f(z) := exp(aLogα(z)). Show that, for z € C \ Rα, we have ƒ'(z) = af(z)/z. This means d/dzzª= aza-1 where we pick the same branch on both sides of the identity.

Calculus
DifferentiationUse differentials to estimate the amount of paint needed (in m³) to apply a coat of paint 0.04 cm thick to a hemispherical dome with diameter 56 m. (Round your answer to two decimal places.)
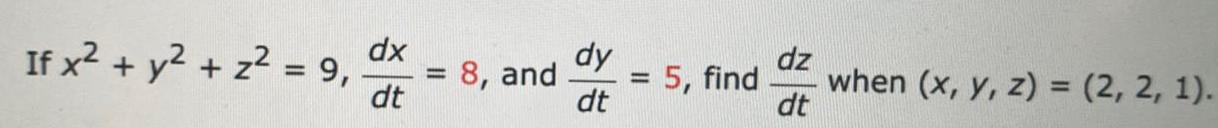
Calculus
DifferentiationIf x² + y² + z² = 9, dx/dt= 8, and dy/dt =5, find dz/dt when (x, y, z) = (2, 2, 1).
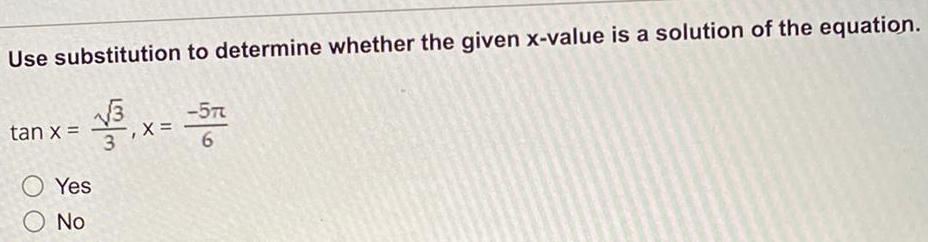
Calculus
DifferentiationUse substitution to determine whether the given x-value is a solution of the equation.
tan x =√3/3, x= -5π/6
Yes
No
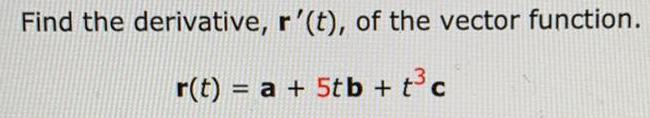
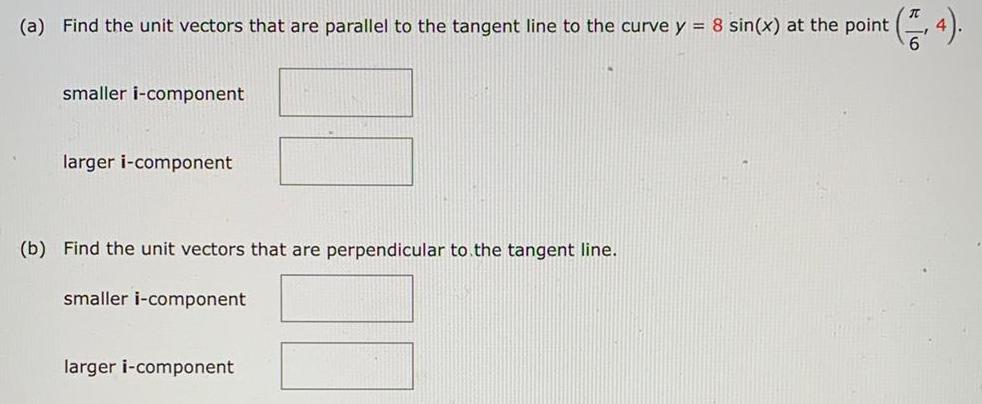
Calculus
Differentiation(a) Find the unit vectors that are parallel to the tangent line to the curve y = 8 sin(x) at the point (π/6 ,4).
smaller i-component
larger i-component
(b) Find the unit vectors that are perpendicular to the tangent line.
smaller i-component
larger i-component
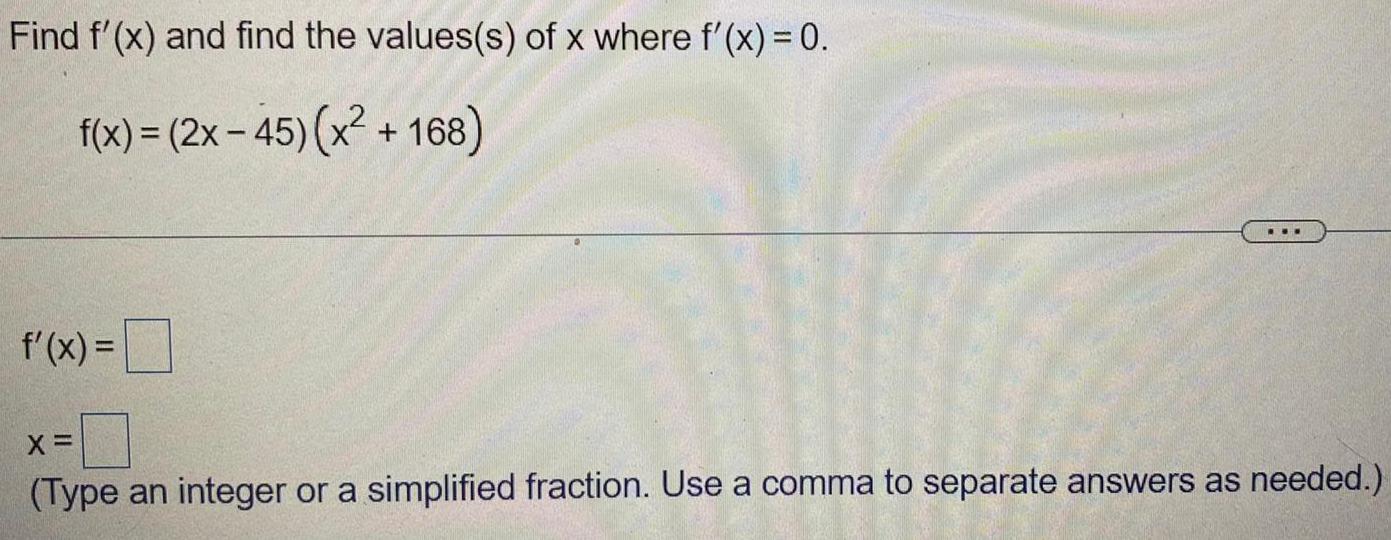
Calculus
DifferentiationFind f'(x) and find the values(s) of x where f'(x) = 0.
f(x) = (2x - 45) (x² +168)
f'(x) =
x=
(Type an integer or a simplified fraction. Use a comma to separate answers as needed.)

Calculus
DifferentiationAn investment of $9,000 earns interest at an annual rate of 8.5% compounded continuously. Complete parts (A) and (B) below.
(A) Find the instantaneous rate of change of the amount in the account after 2 year(s).
$ (Round to two decimal places as needed).
(B) Find the instantaneous rate of change of the amount in the account at the time the amount is equal to $13,500.
(Round to two decimal places as needed).
$
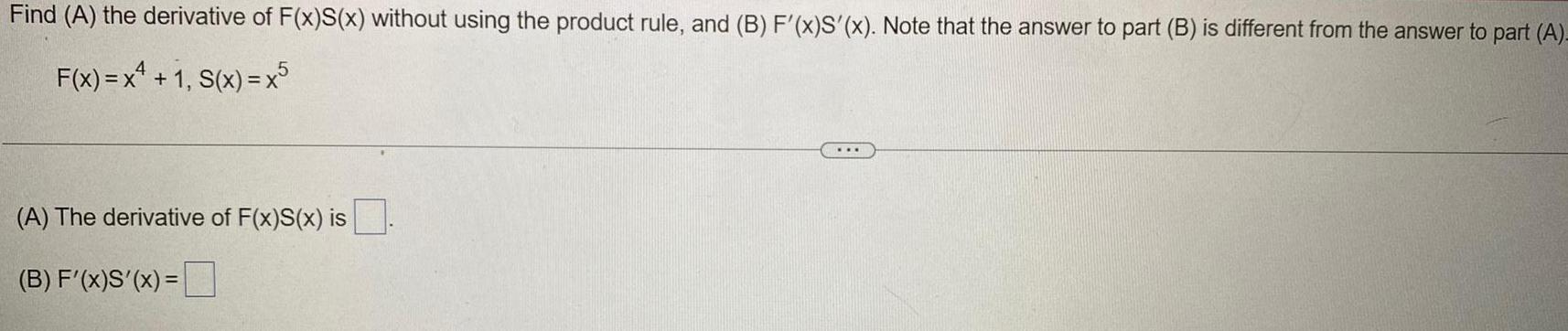
Calculus
DifferentiationFind (A) the derivative of F(x)S(x) without using the product rule, and (B) F'(x)S'(x). Note that the answer to part (B) is different from the answer to part (A)-
F(x) = x^4 + 1, S(x) = x^5
(A) The derivative of F(x)S(x) is.
(B) F'(x)S'(x) =
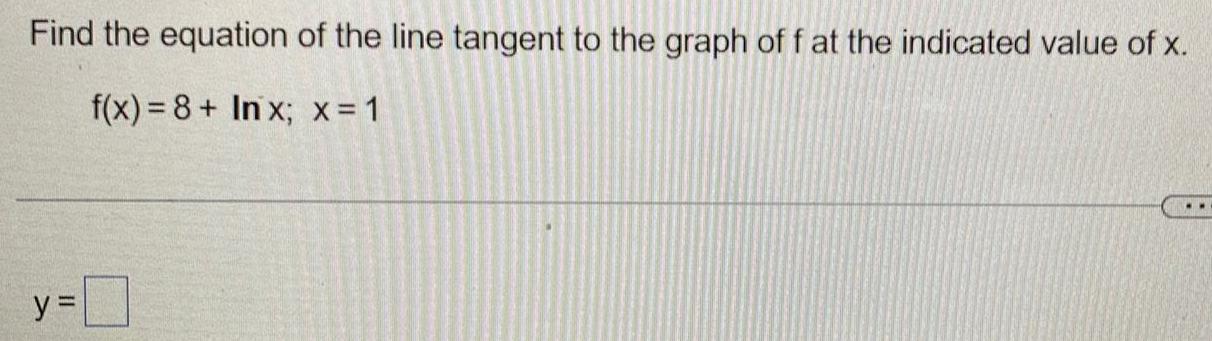
Calculus
DifferentiationFind the equation of the line tangent to the graph of f at the indicated value of x.
f(x)= 8+ Inx; x = 1

Calculus
DifferentiationCreamy Bugs Yogurt has found that the cost, in dollars per pound, of the yogurt it produces, is C'(x) = -0.003x + 450, for x ≤ 300, where x is the number of pounds of yogurt produced. Find the total cost of producing 260 pounds of yogurt.
A. $116,898.60
B. $449.22
C. $449.61
D. $233,797.20
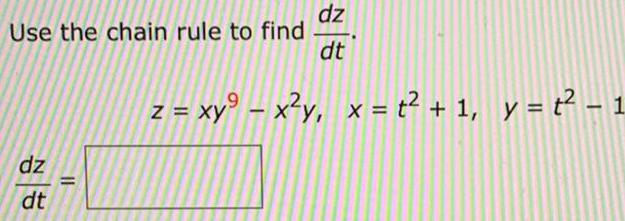
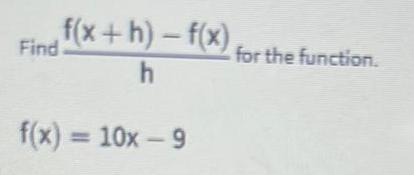

![Let (u, v) be the inner product on R² generated by A = [4 1] [-2 1]
and let u = (0, -2), v = (4,2). Find (u, v).
(u, v) =
Current Attempt in Progress
Compute the standard inner product on M22 of the given matrices.](https://media.kunduz.com/media/sug-question/raw/84322164-1657720374.355629.jpeg?w=256)
Calculus
DifferentiationLet (u, v) be the inner product on R² generated by A = [4 1] [-2 1]
and let u = (0, -2), v = (4,2). Find (u, v).
(u, v) =
Current Attempt in Progress
Compute the standard inner product on M22 of the given matrices.

Calculus
DifferentiationLet f(x) = |x|-2 Evaluate the function at the given values. Then select the appropriate graph that represents this function.
a. f(-2) = Type your answer here
b.f(-1) = Type your answer here
c. f(0) = Type your answer here
d. f(1) = Type your answer here
e. f(2)= Type your answer here
f. The graph that represents this function is graph Write your response here.

Calculus
DifferentiationConsider the following.
3/x - 1/y =7
(a) Find y' by implicit differentiation.
y' =
(b) Solve the equation explicitly for y and differentiate to get y' in terms of x.
y' =
(c) Check that your solutions to parts (a) and (b) are consistent by substituting the expression for y into your solution for part (a).
y' =



Calculus
DifferentiationFind an exponential function of the form P(t)= Pon^1/T that models the situation, and then find the equivalent exponential model of the form P(t)=Poe. Doubling time of 4 yr, initial population of 500.
Find an exponential function of the form P(t) = Pon^1/T that models the situation.
The exponential function is P(t) = 500(2)^1/4
(Use integers or fractions for any numbers in the expression.)
Find the equivalent exponential model of the form P(t) = Poe^rt.

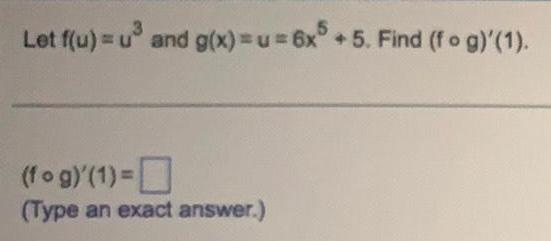
Calculus
DifferentiationLet f(u) = u³ and g(x)=u=6x^5 +5. Find (fog)'(1).
(fog)'(1) =
(Type an exact answer.)


Calculus
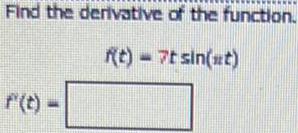
DifferentiationThe demand for a new computer game can be modeled by p(x) = 41-8 In x, for 0 ≤x≤ 800, where p(x) is the price consumers will pay, in dollars, and x is the number of games sold, in thousands. Recall that total revenue is given by R(x)=x p(x). Complete parts (a) through (c) below.
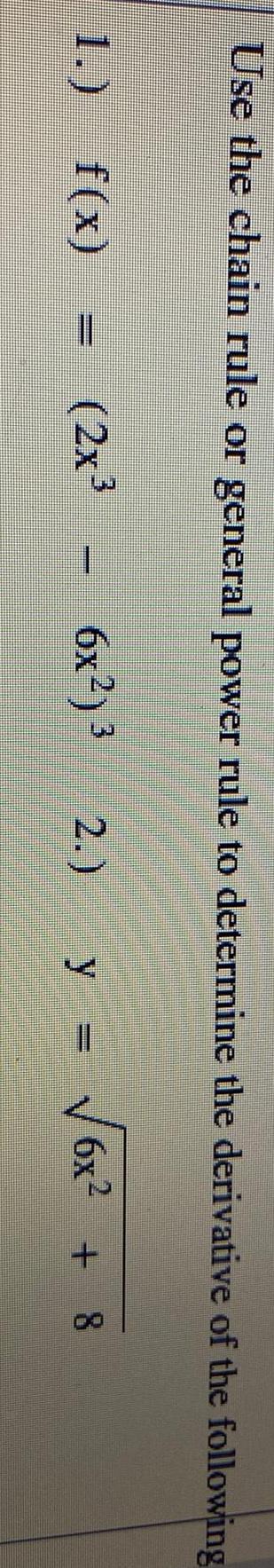
Calculus
DifferentiationUse the chain rule or general power rule to determine the derivative of the following
f(x)=(2x³-6x²)^ 3
2.) y=√6x² +8
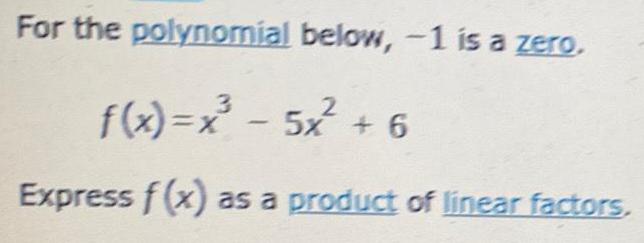
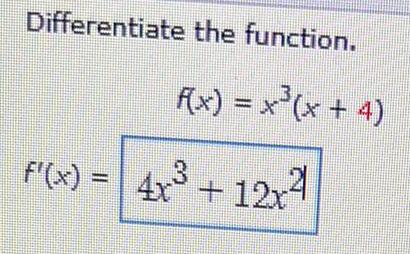
Calculus
DifferentiationFor the polynomial below, -1 is a zero.
f(x)=x²³ - 5x² + 6
Express f(x) as a product of linear factors.
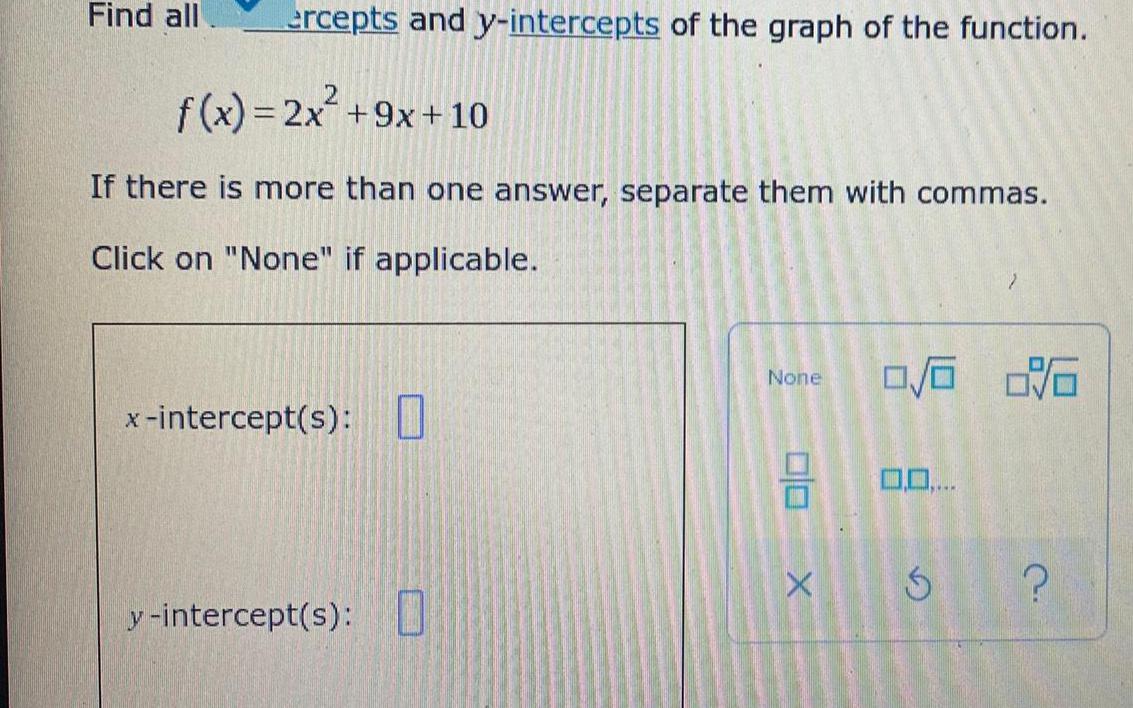
Calculus
DifferentiationFind all ercepts and y-intercepts of the graph of the function.
f(x) = 2x² +9x+10
If there is more than one answer, separate them with commas.
Click on "None" if applicable.
x-intercept(s): 0
y-intercept(s): 0
None
0/0
Xx
0/6
0,0....
S
0/6
?

Calculus
Differentiation- 23x² + 48
x²6
Determine the intervals on which f is decreasing.
Consider f(x)
Of is decreasing on:
Of is decreasing nowhere.
Determine the intervals on which f is increasing.
Of is increasing on:
Of is increasing nowhere.
Determine the value and location of any local minimum of f. Enter the solution in (x, f(x)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
of has a local minimum at:
Of has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (x, f(x)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
of has a local maximum at:
Of has no local maximum.
![Consider h(y) = -7 cos y +7√3 siny on [0, 2π].
Determine the intervals on which h is decreasing.
Oh is decreasing on:
Oh is decreasing nowhere.
Determine the intervals on which h is increasing.
Oh is increasing on:
h is increasing nowhere.
Determine the value and location of any local minimum of f. Enter the solution in (y, h(y)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
Oh has a local minimum at:
Oh has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (y, h(y)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
Oh has a local maximum at:
h has no local maximum.](https://media.kunduz.com/media/sug-question/raw/84288907-1657635417.2766936.jpeg?w=256)
Calculus
DifferentiationConsider h(y) = -7 cos y +7√3 siny on [0, 2π].
Determine the intervals on which h is decreasing.
Oh is decreasing on:
Oh is decreasing nowhere.
Determine the intervals on which h is increasing.
Oh is increasing on:
h is increasing nowhere.
Determine the value and location of any local minimum of f. Enter the solution in (y, h(y)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
Oh has a local minimum at:
Oh has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (y, h(y)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
Oh has a local maximum at:
h has no local maximum.
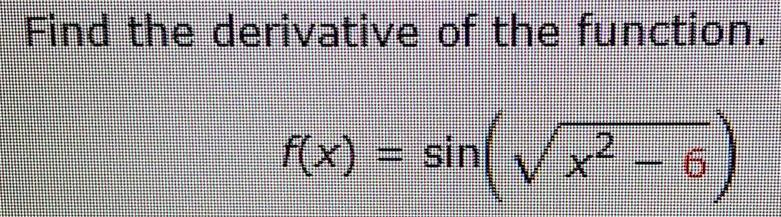
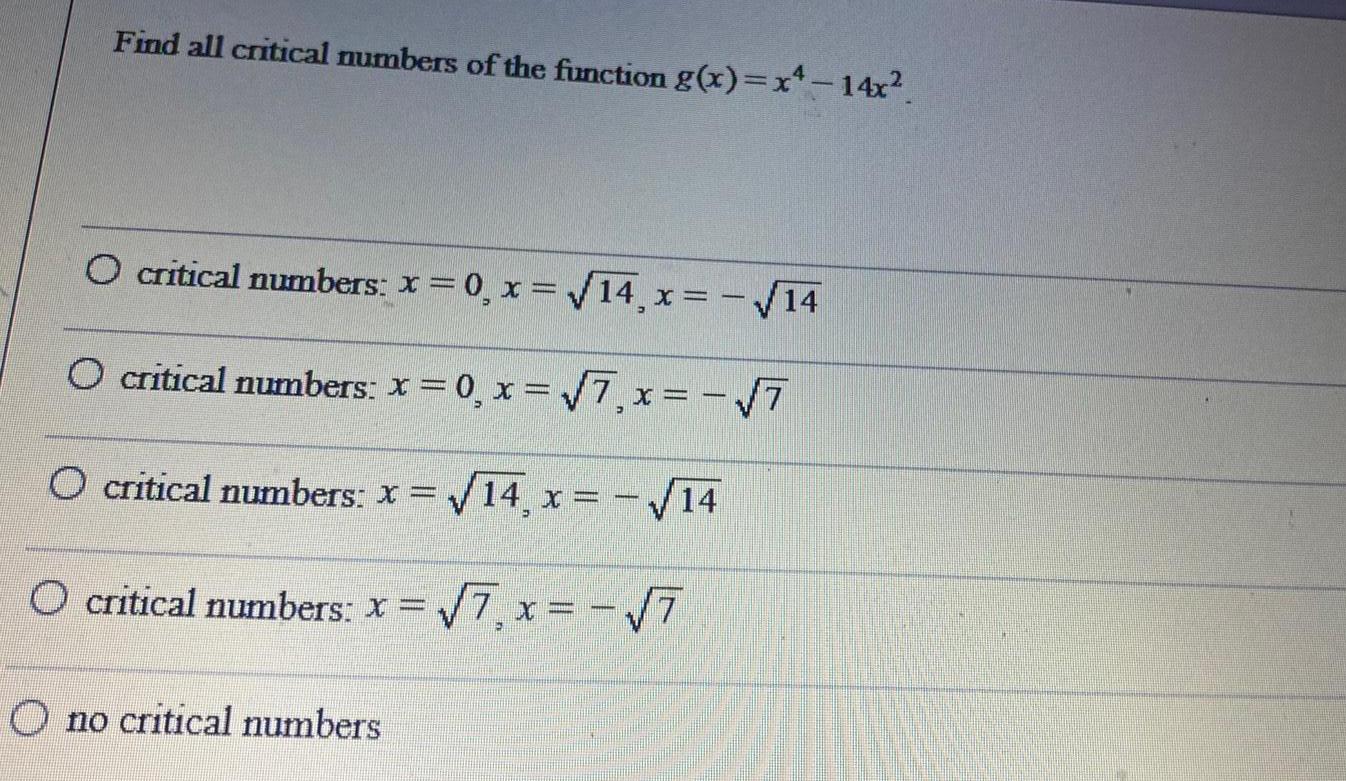
Calculus
DifferentiationFind all critical numbers of the function g(x)=x²-14x².
O critical numbers: x=0, x=√14, x= -√14
O critical numbers: x=0, x=√√7, x= -√7
O critical numbers: x = √14, x =
O critical numbers: x =
no critical numbers
= -√14
√7,x= -√7
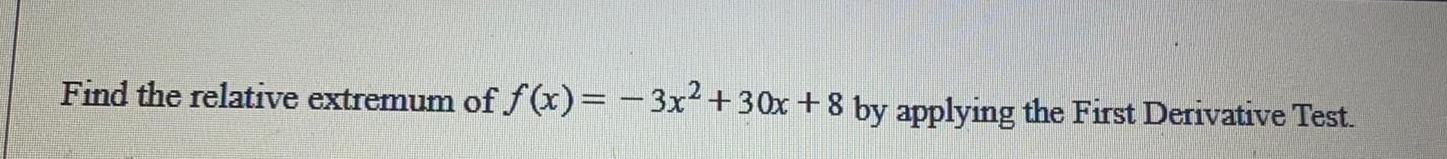
Calculus
DifferentiationFind the relative extremum of f(x)=-3x² +30x+8 by applying the First Derivative Test.

Calculus
DifferentiationComplete two iterations of Newton's Method for the function using the given initial guess.
f(x) = x² - 4₁ x₁ = 1.1


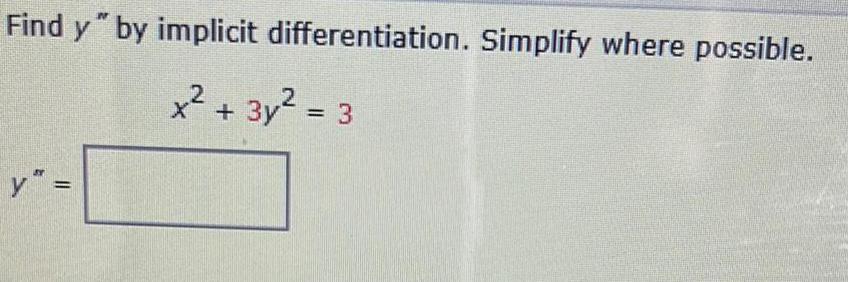
Calculus
DifferentiationFind y" by implicit differentiation. Simplify where possible.
x² + 3y² =3
y" =


Calculus
Differentiation1. Which of the following statement is false?
(a) d/dx In(2x) = d/dx In(x) for x > 0.
(b) d/dx csc(x) = cot(x) csc (x) for x = (0, π).
(c) d/dx sin(x)/ cos(x) - = 1 + tan² (x) for x = (-π /2, π/2).
(d) d/dx2* = ln(2) - 2^x for x € (-∞, ∞).
(e) d/dx (x³ + 2x + 1) = 3x² + 2 for x € (-∞0,00).


Calculus
Differentiationlet f(x) = sin x. Write an expression for f(x) using the definition of the derivative, but don't evaluate the limit.
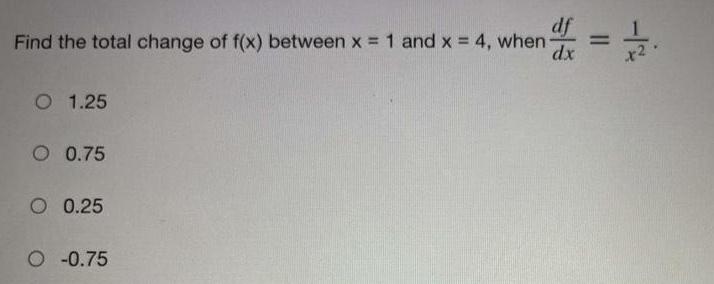
Calculus
DifferentiationFind the total change of f(x) between x = 1 and x = 4, when df/dx =1/x²
1.25
0.75
0.25
-0.75

Calculus
DifferentiationIf the number of fruit flies F increases at a rate that is proportional to the number of flies present, write the differential equation that describes the rate of change in the number of fruit flies at a given time, t. Do not solve.
dF/dt = k/F
dF/dt = -k/F
dF/dt = kF
dF/dt = tF
Calculus
DifferentiationThe interest on an account increases exponentially.
If an initial investment of $5000 earns $900 in two years, what is the rate of increase at the end of that second year?
A. $500.00
B. $488.52
C. $462.17
D. $450.00