Differentiation Questions and Answers


Calculus
DifferentiationFind the dimensions of a rectangle with an area of 225 square feet that has the minimum perimeter.
The dimensions of this rectangle are ft.

Calculus
DifferentiationTwo sides of a triangle have lengths 13 m and 17 m. The angle between them is increasing at a rate of 20/min. How fast (in m/min) is the length of the third side increasing when the angle between the sides of fixed length is 60°?

Calculus
DifferentiationAt age 35, Cynthia earns her MBA and accepts a position as a vice president of an asphalt company. Assume that she will retire at the age of 65, having received an annual salary of $105,000, and that the interest rate is 4%, compounded continuously.
a) What is the accumulated present value of her position?
b) What is the accumulated future value of her position?

Calculus
DifferentiationA price ceiling is given along with demand and supply functions, where D(x) is the price, in dollars per unit, that consumers will pay for x units, and S(x) is the price, in dollars per unit, at which producers will sell x units. Find (a) the equilibrium point, (b) the point (xc.Pc), (c) the new consumer surplus, (d) the new producer surplus, and (e) the deadweight loss. D(x)=91-x, S(x) = 35+0.75x, Pc = $47
a) Find the equilibrium point. (Type an ordered pair.)

Calculus
DifferentiationA point is moving on the graph of xy = 12. When the point is at (4,3), its x-coordinate is increasing by 4 units per second. How fast is the y-coordinate changing at that moment?
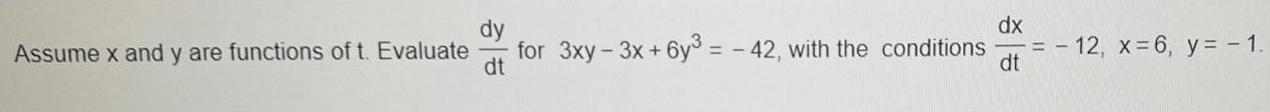
Calculus
DifferentiationAssume x and y are functions of t. Evaluate dy/dt for 3xy-3x+6y³ = -42, with the conditions dx/dt = 12, x=6, y = -1.
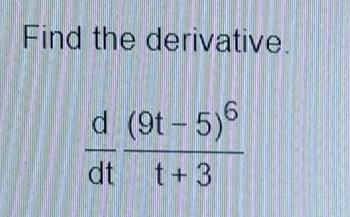
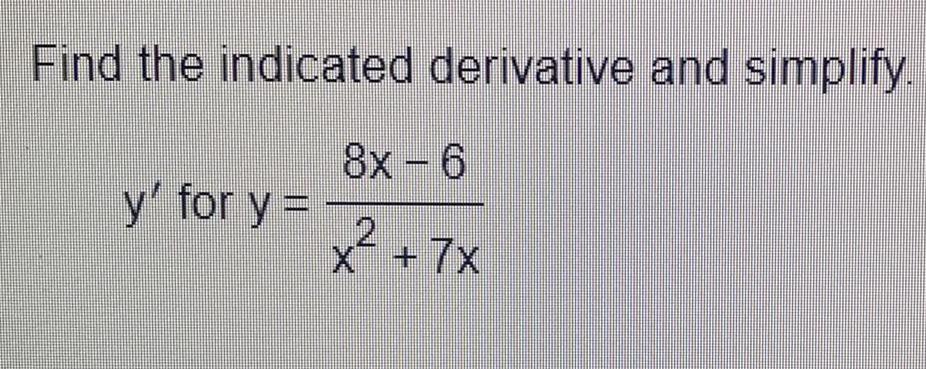
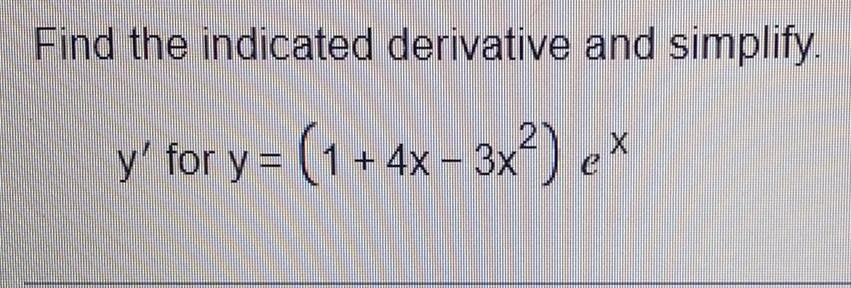
![Find the derivative.
d/dx [2x (x²-1)^4]](https://media.kunduz.com/media/sug-question/raw/84443641-1658076818.6870446.jpeg?w=256)

Calculus
DifferentiationUse one or more of the six sum and difference identities to find the exact value of the expression.
sin(45° +60°)
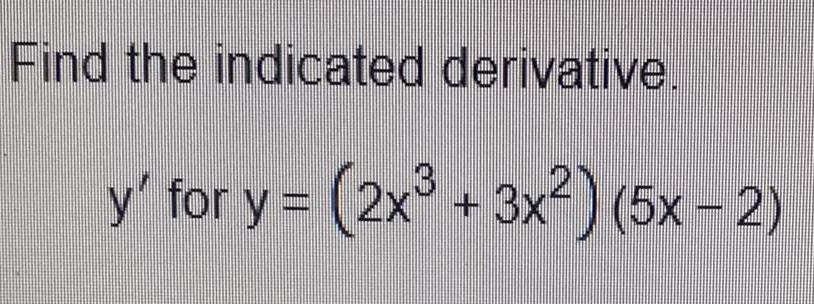
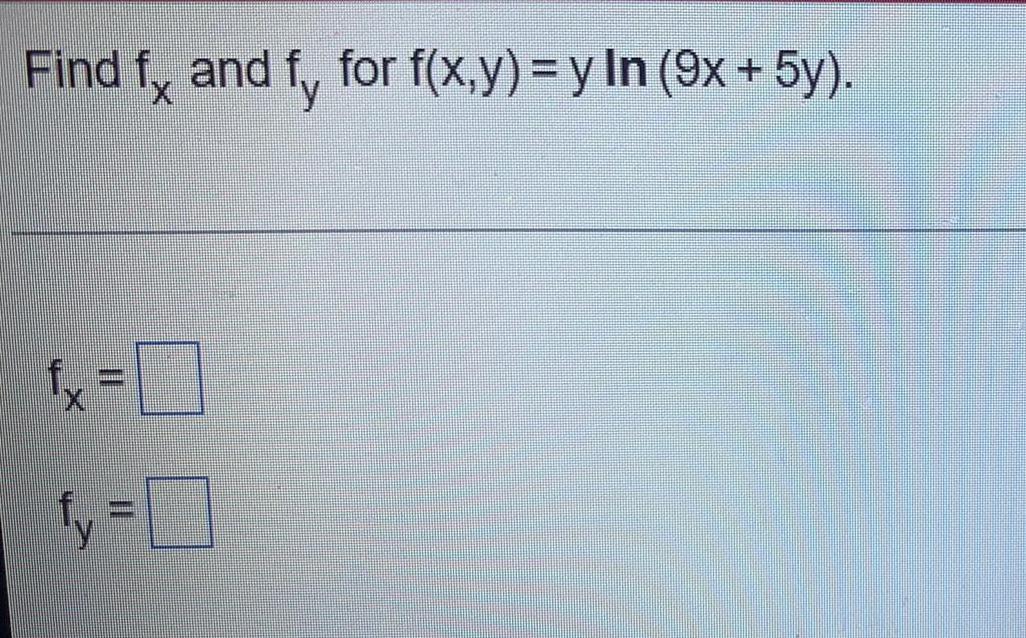

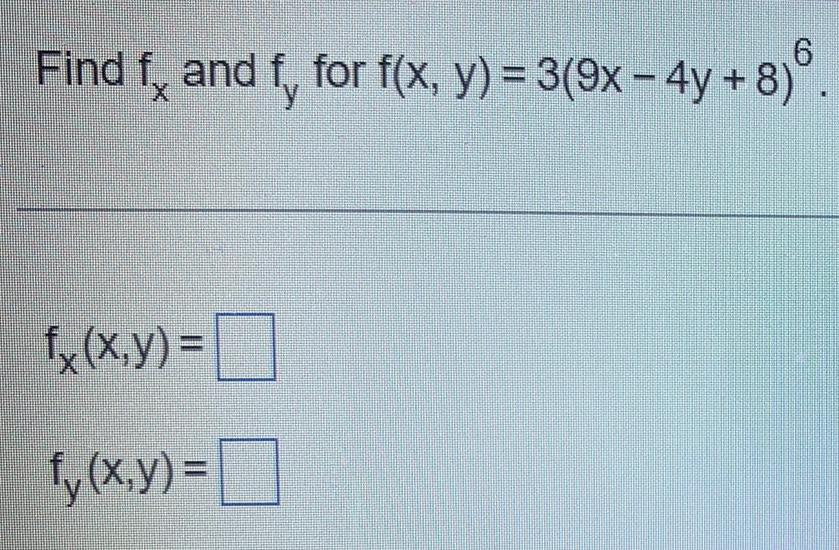
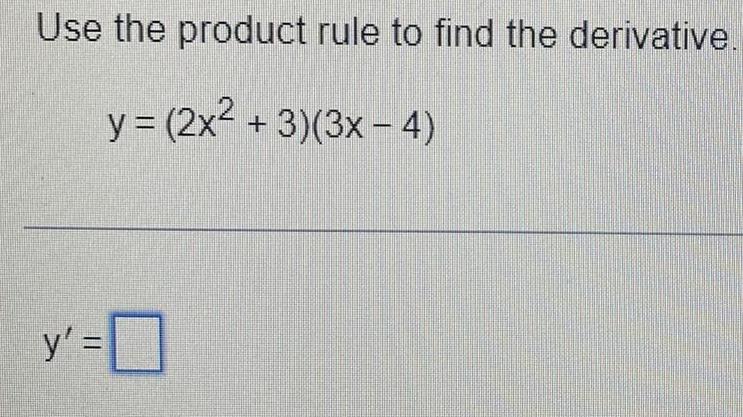
Calculus
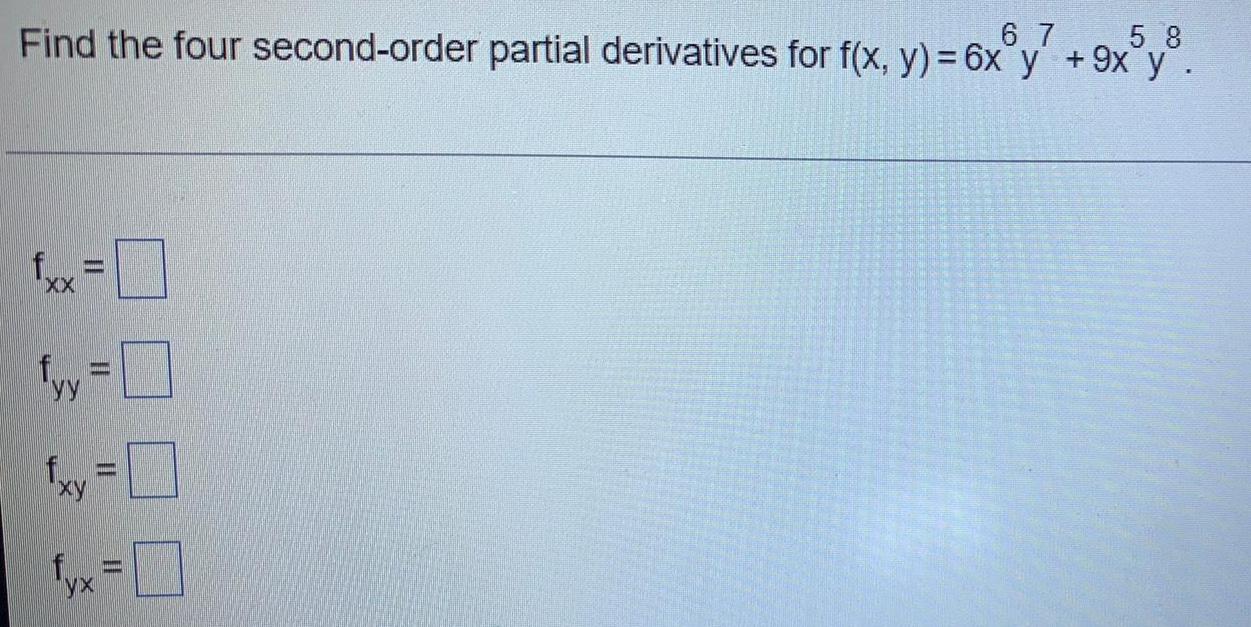
DifferentiationFind the four second-order partial derivatives for f(x, y) = 6x^6y^7 + 9x^5y^8.

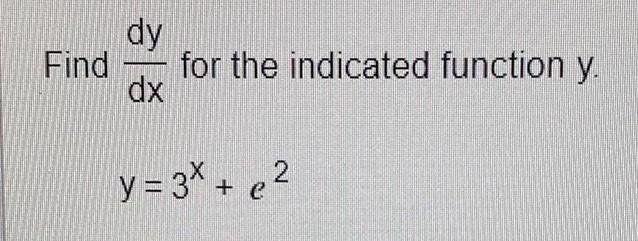

Calculus
DifferentiationPresent value. A promissory note will pay $40,000 at maturity 10 years from now. How much should you be willing to pay for the note now if money is worth 3.5% compounded continuously?

Calculus
DifferentiationA zoo supplier is building a glass-walled terrarium whose interior volume is to be 16 ft³. Material costs per square foot are estimated as shown below.
Walls: $1.00
Floor: $2.00
Ceiling: $2.00
What dimensions of the terrarium will minimize the total cost? What is the minimum cost?
x= ft
y= ft
z= ft
The minimum cost of the terrarium is $
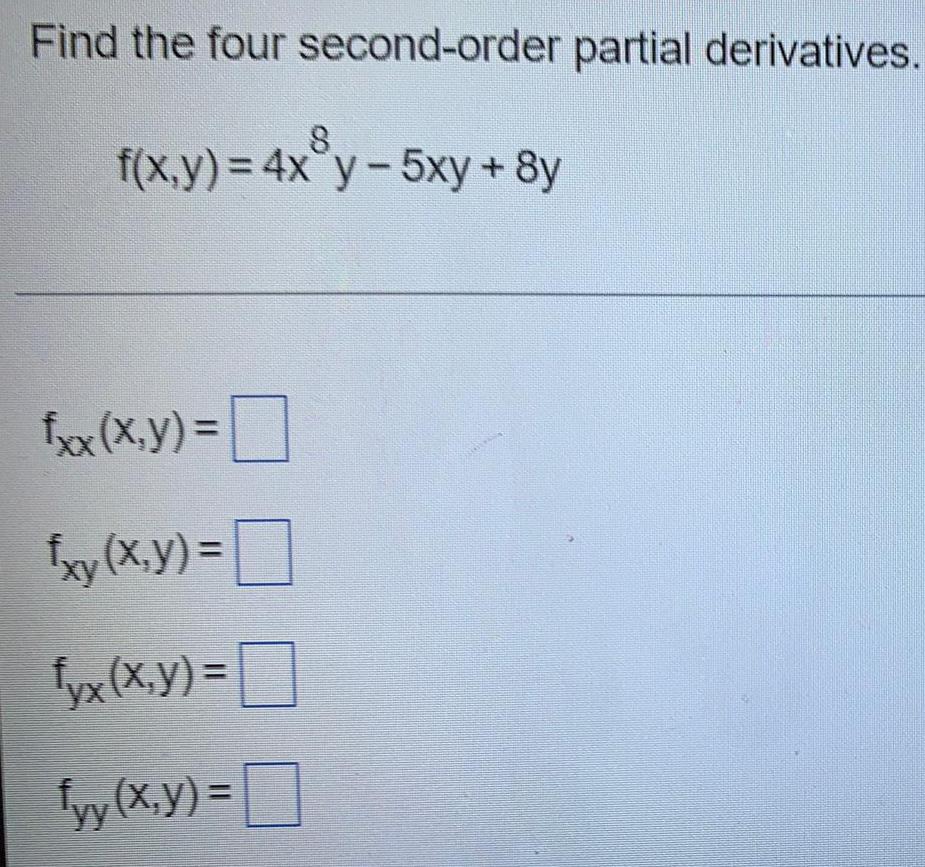
Calculus
DifferentiationFind the four second-order partial derivatives.
f(x,y) = 4x8y-5xy + 8y
fxx (x,y) =
fxy (x,y) =
fyx (x,y) =
fyy (x,y) =

Calculus
DifferentiationFind all second order derivatives for r(x,y)= xy / 8x + 5y
rxx(x,y) =
ryy(x,y) =
rxy (x,y)=ryx (x,y) =

Calculus
DifferentiationFind fxx fxy: fyx and fy for the following function. (Remember, fx means to differentiate with respect to y and then with respect to x.)
![Give the domain of f, the domain of g, and the domain of m, where m(x) = f[g(x)].
f(u) = In u; g(x) = 25-x²](https://media.kunduz.com/media/sug-question/raw/84443023-1658067327.8394024.jpeg?w=256)
Calculus
DifferentiationGive the domain of f, the domain of g, and the domain of m, where m(x) = f[g(x)].
f(u) = In u; g(x) = 25-x²
![Find the absolute extrema of the function f(x) = 12+x / 12-x on the interval [4,6].
The absolute maximum occurs at x =
The absolute minimum occurs at x =](https://media.kunduz.com/media/sug-question/raw/84443175-1658066984.5567389.jpeg?w=256)
Calculus
DifferentiationFind the absolute extrema of the function f(x) = 12+x / 12-x on the interval [4,6].
The absolute maximum occurs at x =
The absolute minimum occurs at x =
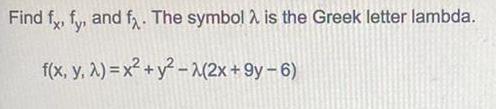
Calculus
DifferentiationFind fx, fy, and fλ. The symbol λ is the Greek letter lambda.
f(x, y, λ) = x² + y²-λ(2x +9y-6)
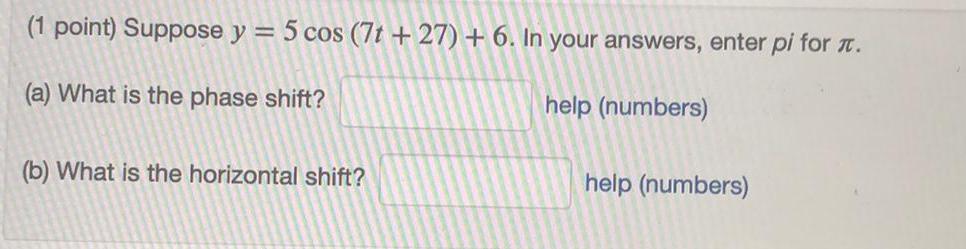
Calculus
DifferentiationSuppose y = 5 cos (7t +27) + 6. In your answers, enter pi for π.
(a) What is the phase shift?
(b) What is the horizontal shift?

Calculus
DifferentiationThe total sales, S. of a one-product firm are given by S(L,M) = ML-L2, where M is the cost of materials and L is the cost of labor. Find the maximum value of this function subject to the budget constraint shown below.
M+L=120
The maximum value of the sales is $
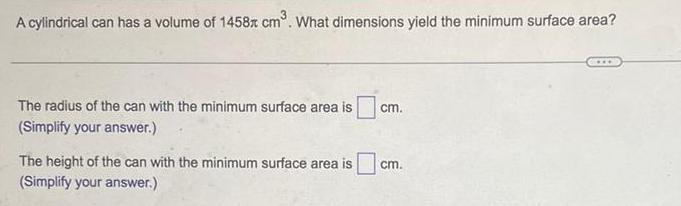
Calculus
DifferentiationA cylindrical can has a volume of 1458π cm³. What dimensions yield the minimum surface area?
The radius of the can with the minimum surface area is cm.
(Simplify your answer.)
The height of the can with the minimum surface area is cm.
(Simplify your answer.)

Calculus
DifferentiationFind the degree, leading term, leading coefficient, and the maximum number of real zeros of the given polynomial.
f(x) = -x²- 5x⁶ - 3x⁷ +6
Degree: 7, the leading term: 3x7, the leading coefficient: -3, the maximum number of
real zeros: 6
Degree: 7, the leading term: -3x7, the leading coefficient: -3, the maximum number of
real zeros: 7
Degree: 4, the leading term: -3x7, the leading coefficient: -3, the maximum number
of real zeros: 4
Degree: 4, the leading term: -x4, the leading coefficient: -1, the maximum number of
real zeros: 7

Calculus
DifferentiationEach side of a square is increasing at a rate of 7 cm/s. At what rate (in cm²/s) is the area of the square increasing when the area of the square is 81 cm²?
cm²/s
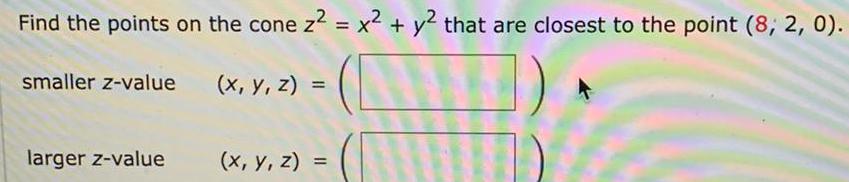
Calculus
DifferentiationFind the points on the cone z² = x² + y² that are closest to the point (8, 2, 0).
smaller z-value (x, y, z) =
larger z-value (x, y, z) =

Calculus
DifferentiationFind the derivative of the function.
f(x)=2x⁶-6e²
12x⁵ - 12e
12x⁵
12x⁵ - 12e²
12x⁵ - 6e²

Calculus
DifferentiationFind the derivative of the function.
y = (3x+1)⁴(x⁴ − 6)⁶
y' = (24x + 12) (3x + 1)⁴(x⁴ - 6)⁶
y' = 12(3x + 1)³ (x⁴ - 6)⁶ +24x (3x + 1)⁴ (x⁴ - 6)⁵
y' = 12(3x + 1)³ (x⁴ - 6)⁶ +24x³ (3x + 1)⁴ (x⁴ - 6)⁵
y' =(x + 1)³ (x⁴ − 6)⁶ +24x(3x + 1)⁴(x³ - 6)⁵

Calculus
DifferentiationFind the derivative of the function.
g(t)=tan(cos 2t)
sin 2t sec²(cos 2t)
2sin 2t sec²(cos 2t)
-sin 2t sec²(cos 2t)
-2sin 2t sec² (cos 2t)
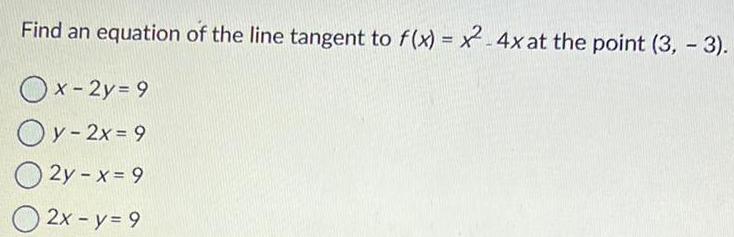
Calculus
DifferentiationFind an equation of the line tangent to f(x)=x^2-4x at the point (3, -3).
x-2y=9
y-2x = 9
2y-x=9
2x - y = 9

Calculus
Differentiation2(x - 5)² + (y-4)² + (z-7^)2 = 10, (6, 6, 9)
(a) Find an equation of the tangent plane to the given surface at the specified point.
(b) Find an equation of the normal line to the given surface at the specified point.
(x(t), y(t), z(t)) =

![Find f'(x) and simplify.
f(x) = x / x +39
Which of the following shows the correct application of the quotient rule?
A.(x +39)(1)-(x)(1)/[x+39]²
B. (x +39)(1)-(x)(1)/[x]²
C.(x)(1)-(x +39)(1)/[x+39]²
D. (x)(1)-(x +39)(1)/[x]²
f'(x) =](https://media.kunduz.com/media/sug-question/raw/84421867-1657987139.7808921.jpeg?w=256)
Calculus
DifferentiationFind f'(x) and simplify.
f(x) = x / x +39
Which of the following shows the correct application of the quotient rule?
A.(x +39)(1)-(x)(1)/[x+39]²
B. (x +39)(1)-(x)(1)/[x]²
C.(x)(1)-(x +39)(1)/[x+39]²
D. (x)(1)-(x +39)(1)/[x]²
f'(x) =
Calculus
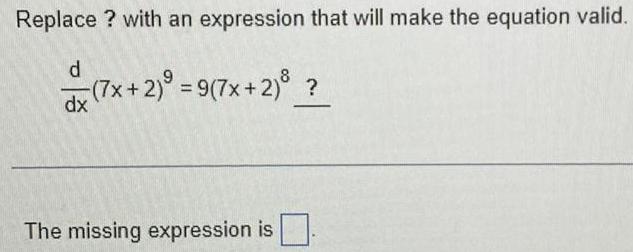
DifferentiationReplace ? with an expression that will make the equation valid.
d/dx (7x+2)⁹ = 9(7x+2)⁸ ?
The missing expression is

Calculus
DifferentiationUse implicit differentiation to find y' for the equation below and then evaluate y' at the indicated point.
y²+3y + 2x=0; (-2,1)
y' =
y'l(-2,1) = (Simplify your answer.)
Calculus
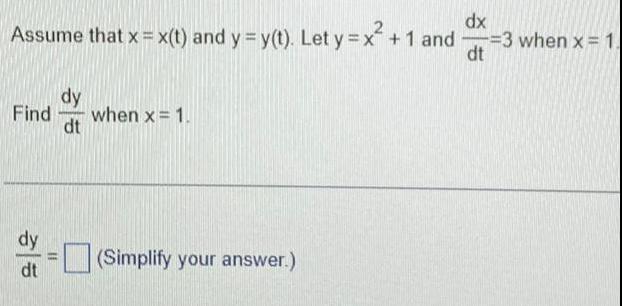
DifferentiationAssume that x = x(t) and y = y(t). Let y = x² +1 and dx/dt = 3 when x = 1.
Find dy/dt when x = 1.
dy/dt = (Simplify your answer.)

Calculus
DifferentiationWhen asked to simplify the following expressions, a student came up with the following plans. Unfortunately, they are incorrect. Point out what is wrong and give correct answers.
a) Simplify x/x+4 if possible.
The student: Split the expression into two fractions and then simplify each:
x/ x+4 = x/x + x/4 = 1 + x/4
b) Simplify t³-2t/ t
Divide the common factor t into t³:
t³-2t / t = t² - 2t
Calculus
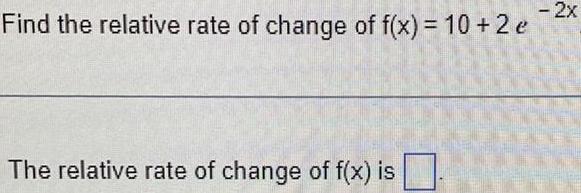
DifferentiationFind the relative rate of change of f(x) = 10 + 2e^-2x
The relative rate of change of f(x) is

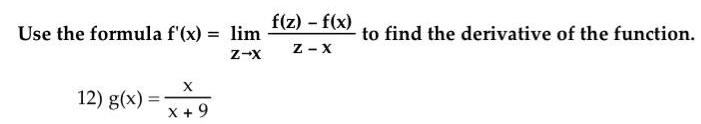
Calculus
DifferentiationUse the formula f'(x) = lim z→x f(z) - f(x) / (z-x) to find the derivative of the function.
g(x) = x/ (x+ 9)
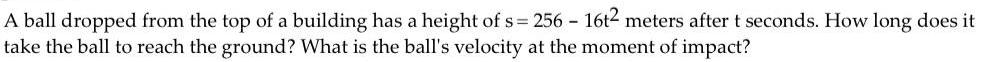
Calculus
DifferentiationA ball dropped from the top of a building has a height of s= 256 - 16t² meters after t seconds. How long does it take the ball to reach the ground? What is the ball's velocity at the moment of impact?