Limits & Continuity Questions and Answers
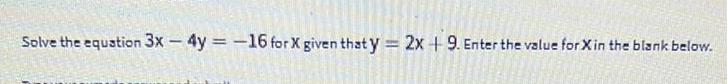
Calculus
Limits & ContinuitySolve the equation 3x - 4y = -16 for X given that y = 2x + 9. Enter the value for Xin the blank below.

Calculus
Limits & ContinuitySolve the equation 4x - y = 3 for y given that x = 3 - 2y. Enter the value of y below.

Calculus
Limits & ContinuityGiven the function g(x) = 3^0.25x - 7, identify the correct description of the graph's transformation from the graph of its parent function.
The graph of g(x) is a horizontal stretch of f(x)=3^x by a factor of 4 and a shift 7 units down.
The graph of g(x) is a horizontal stretch of f(x)=3^x by a factor of 1/4 and a shift 7 units up.
The graph of g(x) is a vertical stretch of f(x)=3^x by a factor of 4 and a shift 7 units down.
The graph of g(x) is a vertical stretch of f(x)=3^x by a factor of 1/4 and a shift 7 units down.

Calculus
Limits & ContinuityCheck all statements that are true.
In both Euclidean and spherical geometry, through any point not on a given line there is a line parallel to the given line.
In spherical geometry, some quadrilaterals are parallelograms.
In Euclidean geometry, the sum of the angle measures of a triangle is equal to 180°.
In Euclidean geometry, the shortest path between two points is a line.
In spherical geometry, a triangle can have two right angles.
None of these are true.

Calculus
Limits & ContinuitySuppose N = f(t) is the total number of inches of snow that fall in the first t days of January.
Which of the statements below best explains the meaning of the INVERSE function f^-1?
A. The number of inches of snow accumulated in t days
B. The number of inches of snow on the ground after t days
C. The days for which there are N inches of snow on the ground
D. The number of days it takes to accumulate N inches of snow
E. None of the above
Calculus
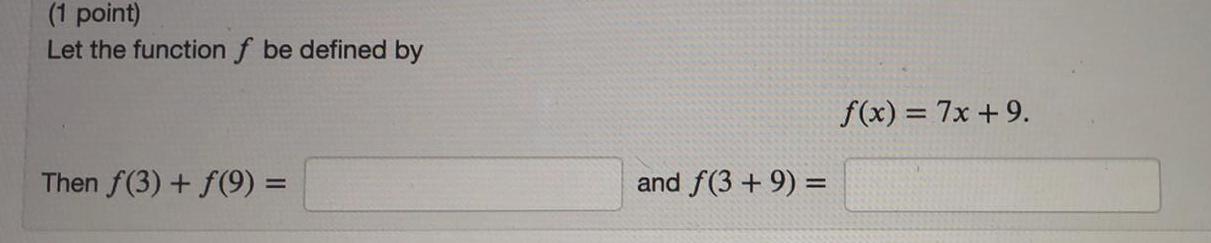
Limits & ContinuityLet the function f be defined by f(x) = 7x + 9.
Then f(3) + f(9) =
and f(3 + 9) =
Calculus
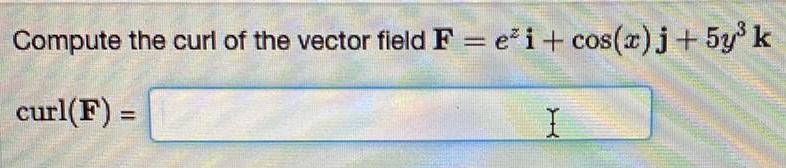
Limits & ContinuityCompute the curl of the vector field F = e^z(i) + cos(x)j + 5y³k
curl(F) =
![Let x be a continuous random variable over [a, b] with probability density function f. Then the median of the x-values is that number m for which ∫ f(x)dx=1/2 (a to m). Find the median.
f(x)=x/8, [0, 4]
A. 4
B. 2
C.3/2
D. 2√2](https://media.kunduz.com/media/sug-question/raw/84567290-1658663431.6102223.jpeg?w=256)
Calculus
Limits & ContinuityLet x be a continuous random variable over [a, b] with probability density function f. Then the median of the x-values is that number m for which ∫ f(x)dx=1/2 (a to m). Find the median.
f(x)=x/8, [0, 4]
A. 4
B. 2
C.3/2
D. 2√2
Calculus
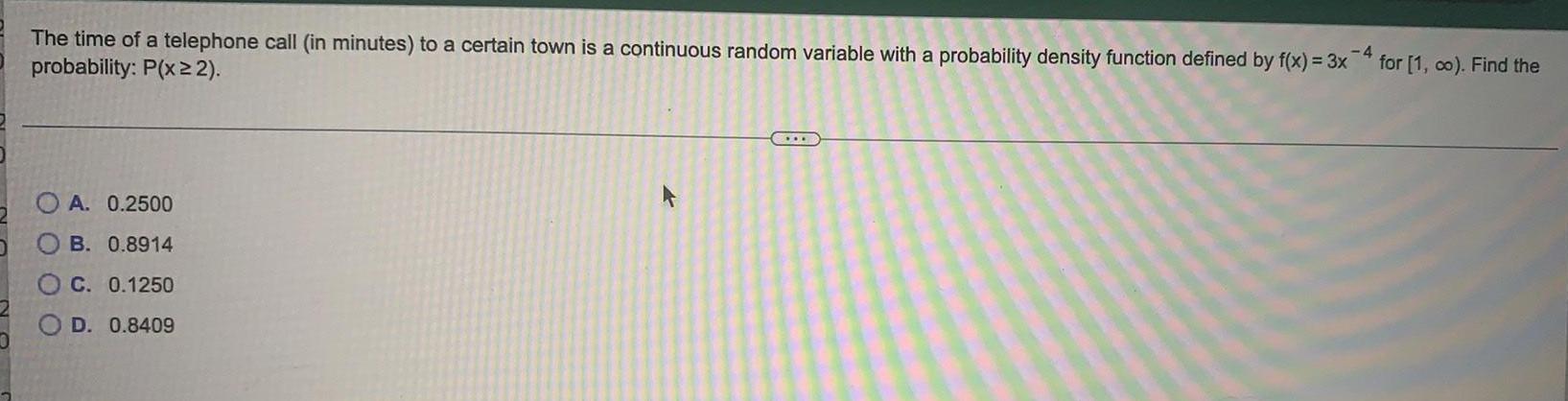
Limits & ContinuityThe time of a telephone call (in minutes) to a certain town is a continuous random variable with a probability density function defined by f(x) = 3x^-4 for [1,∞ ). Find the
probability: P(x≥2).
A. 0.2500
B. 0.8914
C. 0.1250
D. 0.8409

Calculus
Limits & ContinuitySolve the equation by expressing each side as a power of the same base. Enter the solution below.
5^(4x-1) = 125

Calculus
Limits & ContinuityIf a rock is thrown vertically upward from the surface of Mars with velocity of 15 m/s, its height (in meters) after t seconds is h = 15t-1.86t².
(a) What is the velocity (in m/s) of the rock after 1 s?
11.28 m/s
(b) What is the velocity (in m/s) of the rock when its height is 10 m on its way up? On its way down?
![Na Find k such that the function is a probability density function over the given interval. Then write the probability density function.
f(x) = k/x , [3,9]
What is the value of k?
What is the probability density function?
f(x) = (Type an exact answer.)](https://media.kunduz.com/media/sug-question/raw/84588591-1658662440.3562055.jpeg?w=256)
Calculus
Limits & ContinuityNa Find k such that the function is a probability density function over the given interval. Then write the probability density function.
f(x) = k/x , [3,9]
What is the value of k?
What is the probability density function?
f(x) = (Type an exact answer.)
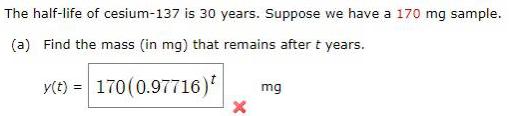
Calculus
Limits & ContinuityThe half-life of cesium-137 is 30 years. Suppose we have a 170 mg sample.
(a) Find the mass (in mg) that remains after t years.

Calculus
Limits & ContinuityUse the properties of logarithms to condense the expression to a single logarithm.
3 log10 (c) +log10 (a)/3+log10 (b)/3
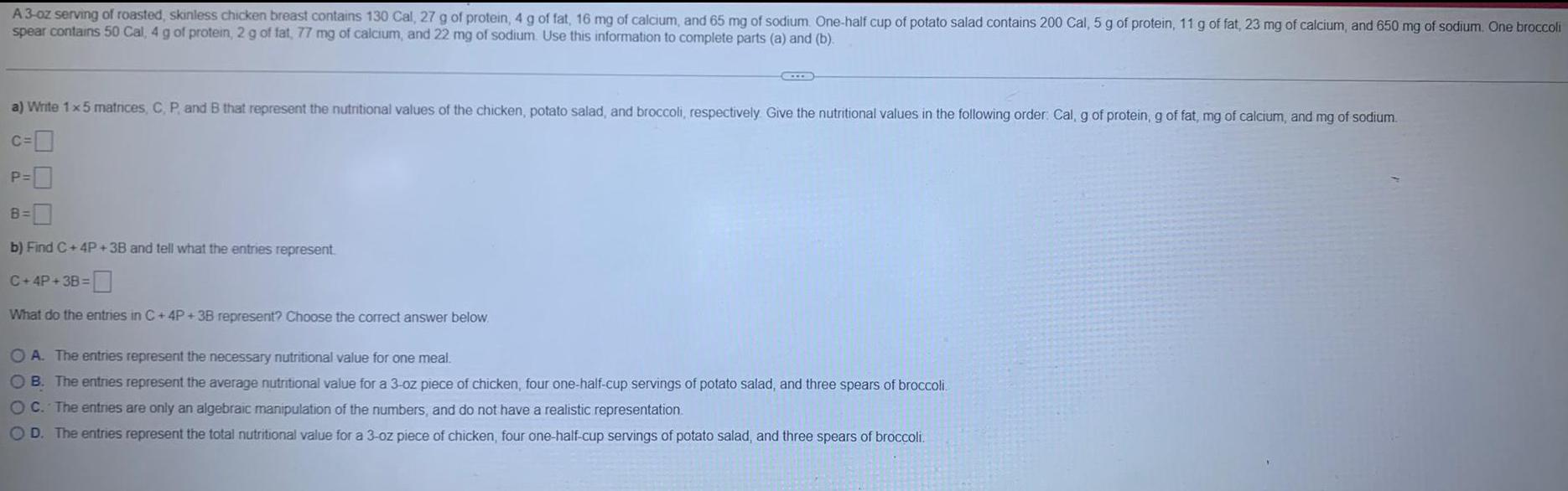
Calculus
Limits & ContinuityA 3-oz serving of roasted, skinless chicken breast contains 130 Cal, 27 g of protein, 4 g of fat, 16 mg of calcium, and 65 mg of sodium. One-half cup of potato salad contains 200 Cal, 5 g of protein, 11 g of fat, 23 mg of calcium, and 650 mg of sodium. One broccoli
spear contains 50 Cal, 4 g of protein, 2 g of fat, 77 mg of calcium, and 22 mg of sodium. Use this information to complete parts (a) and (b).
a) Write 1 x 5 matrices, C, P, and B that represent the nutritional values of the chicken, potato salad, and broccoli, respectively. Give the nutritional values in the following order: Cal, g of protein, g of fat, mg of calcium, and mg of sodium.
c=
P=
B=
b) Find C+4P+3B and tell what the entries represent.
C+4P+3B=
What do the entries in C+4P + 3B represent? Choose the correct answer below.
A. The entries represent the necessary nutritional value for one meal.
B. The entries represent the average nutritional value for a 3-oz piece of chicken, four one-half-cup servings of potato salad, and three spears of broccoli
C. The entries are only an algebraic manipulation of the numbers, and do not have a realistic representation.
D. The entries represent the total nutritional value for a 3-oz piece of chicken, four one-half-cup servings of potato salad, and three spears of broccoli.

Calculus
Limits & ContinuityThe enrollment at an elementary school is going to increase from 900 students to 3510 students. A parents' group is planning to increase the rectangular 200 ft by
900 ft playground area to a larger, similar rectangular area that is 800 ft by 3600 ft. Find the area of each playground.
The area of the smaller playground is t
(Simplify your answer.)

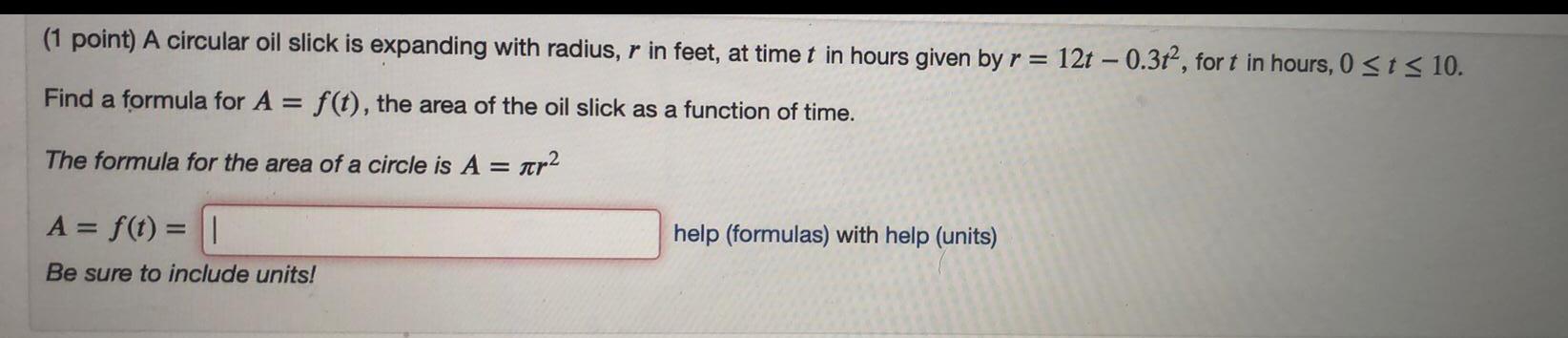
Calculus
Limits & ContinuityA circular oil slick is expanding with radius, r in feet, at time t in hours given by r = 12t - 0.3t^2, for t in hours, 0 ≤ t ≤ 10.
Find a formula for A = f(t), the area of the oil slick as a function of time.
The formula for the area of a circle is A = πr²
A = f(t) =
Be sure to include units!

Calculus
Limits & ContinuityWhat does the point (2 + 1 / 4.8 , 5) represent in x = 8 (y - 5)² + 2?
directrix
focus
axis of symmetry
vertex
![Graph the function f(x) over the given interval. Partition the interval into 4 subintervals of equal length. Then add to your sketch the rectangles associated with the Riemann sum Σf(ck) Δxk, using the indicated point in the kth subinterval for ck.
8) f(x)=x^2-2, [0, 8], left-hand endpoint](https://media.kunduz.com/media/sug-question/raw/84616835-1658657366.853593.jpeg?w=256)
Calculus
Limits & ContinuityGraph the function f(x) over the given interval. Partition the interval into 4 subintervals of equal length. Then add to your sketch the rectangles associated with the Riemann sum Σf(ck) Δxk, using the indicated point in the kth subinterval for ck.
8) f(x)=x^2-2, [0, 8], left-hand endpoint
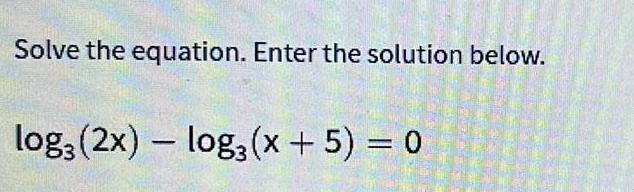
Calculus
Limits & ContinuitySolve the equation. Enter the solution below.
log3 (2x) - log3(x + 5) = 0
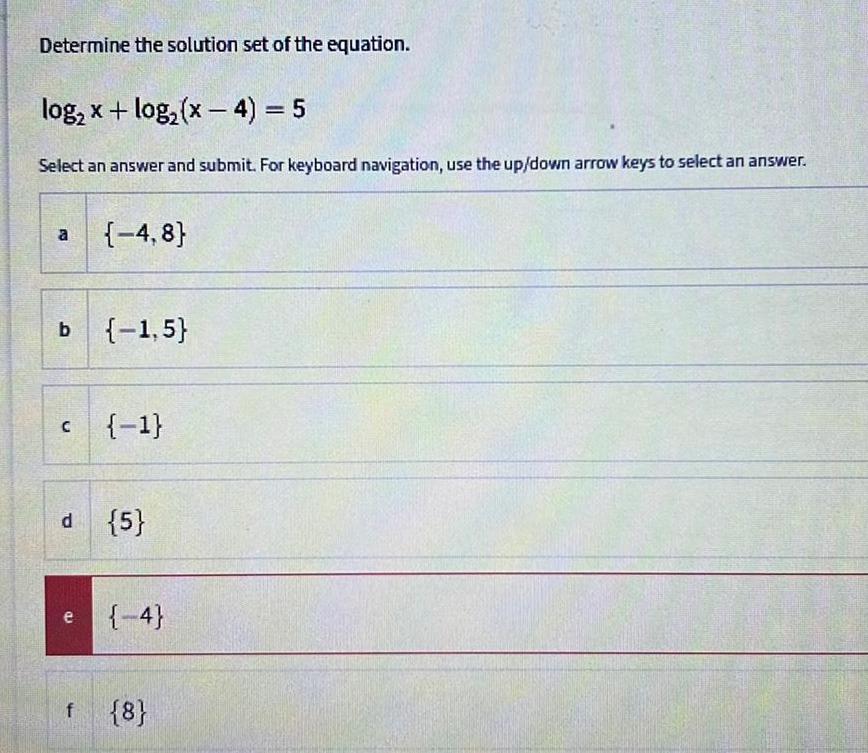
Calculus
Limits & ContinuityDetermine the solution set of the equation.
log₂x + log₂ (x-4) = 5
Select an answer and submit. For keyboard navigation, use the up/down arrow keys to select an answer.


Calculus
Limits & ContinuityEnter the simplified form of the expression. (When entering your answer, use symbol to denote an exponent. Do not enter any spaces in your answer.)
(-3x-²y4) (6x³y)

Calculus
Limits & ContinuitySolve the problem.
In a certain memory experiment, subject A is able to memorize words at a rate given by
dm/dt = -0.003t² + 0.4t (words per minute).
In the same memory experiment, subject B is able to memorize at the rate given by
dM/dt = -0.009t2 (words per minute).
How many more words does subject B memorize from t=0 to t = 19 (during the first 19 minutes)?
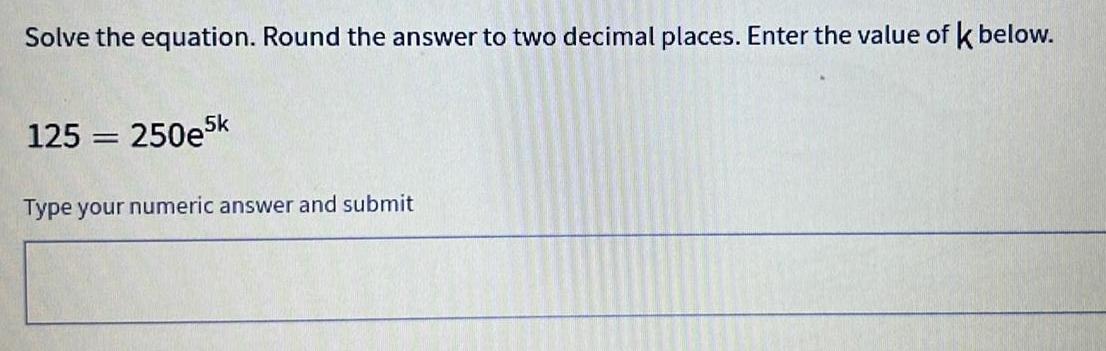
Calculus
Limits & ContinuitySolve the equation. Round the answer to two decimal places. Enter the value of k below.
125 = 250e5k
Type your numeric answer and submit

Calculus
Limits & ContinuityLet be an angle in quadrant III such that sinθ = -12/13
Find the exact values of secθ and cotθ.

Calculus
Limits & ContinuityAn initial investment doubled in value after 30
years. What annual interest rate, compounded
continuously, produced this return? Select the
equation that results when solving this problem.
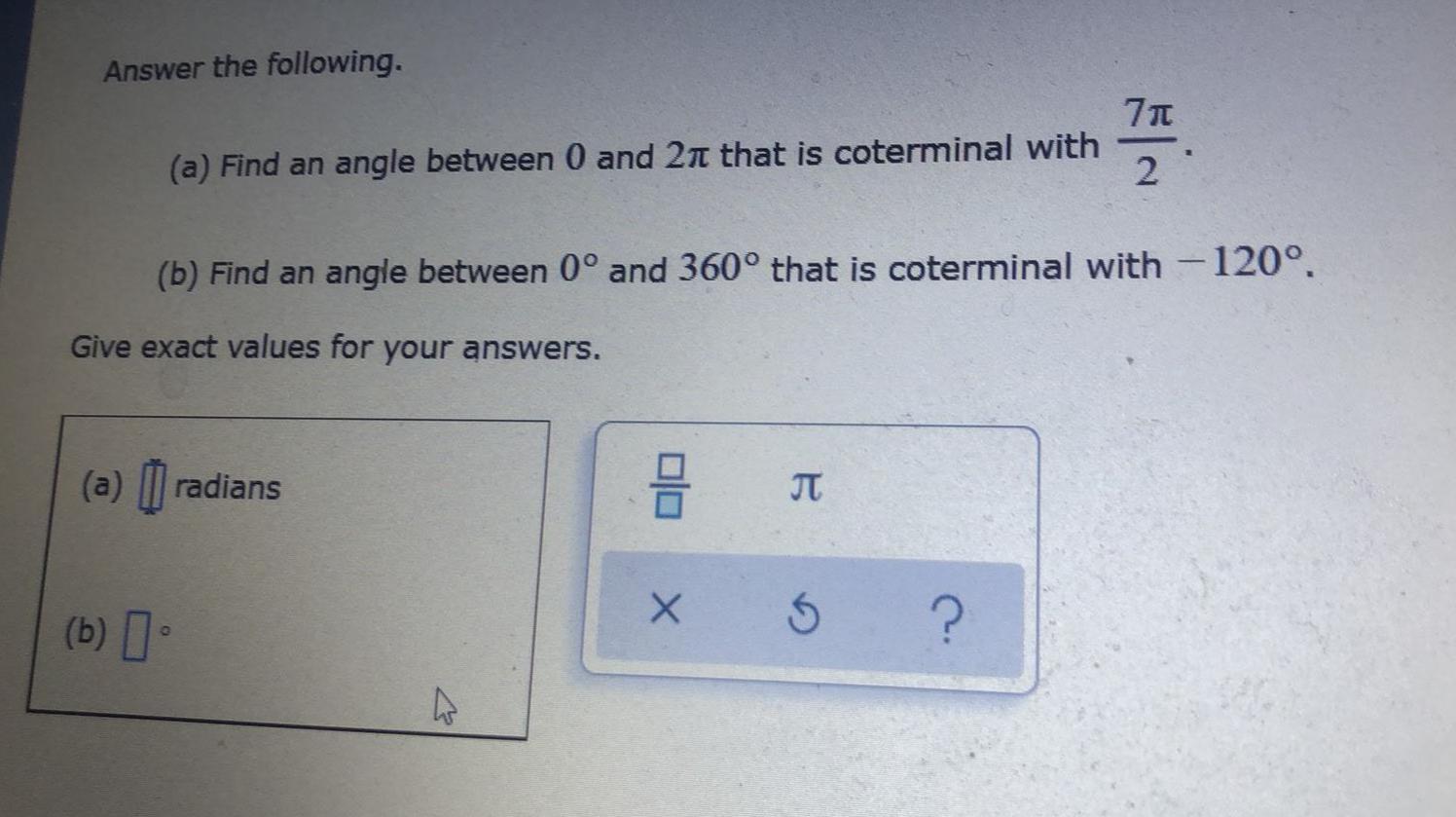
Calculus
Limits & ContinuityAnswer the following. (a) Find an angle between 0 and 2π that is coterminal with (b) Find an angle between 0° and 360° that is coterminal with - 120°. Give exact values for your answers.


Calculus
Limits & ContinuityFind the number of units that must be produced and sold in order to yield the maximum
profit, given the following equations for revenue and cost:
R(x) = 60x-0.5x²
C(x) = 5x + 3.

Calculus
Limits & ContinuityAt the end of 20 years, an initial investment of $10,000 grows to $51,551.70. Use the continuous compounding formula to determine the annual rate of return. Write your answer in decimal form rounded to three decimal places. Do NOT convert your
answer to a percentage.

Calculus
Limits & ContinuityA colony of bacteria grows exponentially according to the model P(t) = Poe^kt. If the number of bacteria doubles in three hours, what is the growth rate k? Express your answer as a decimal rounded to three places.
Type your numeric answer and submit
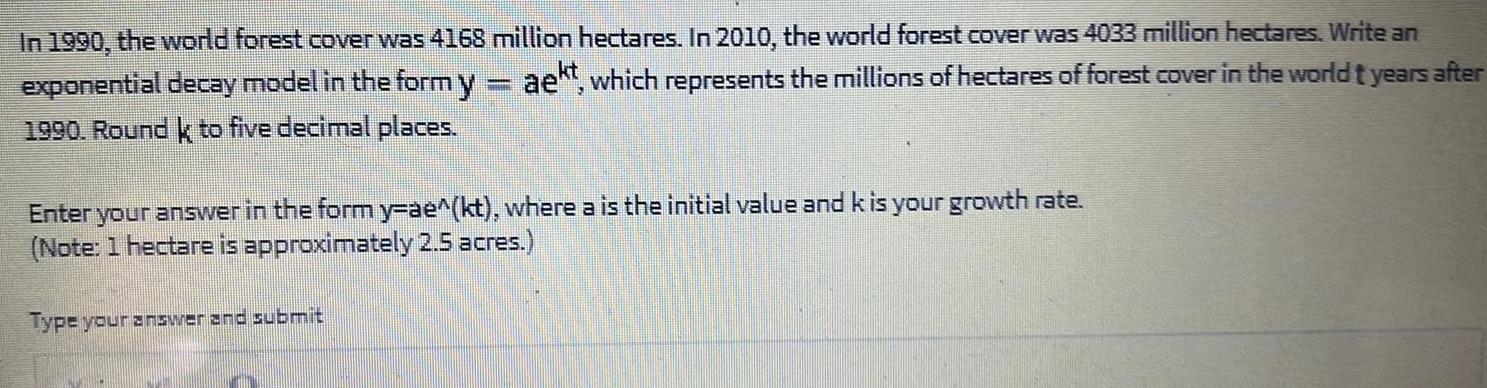
Calculus
Limits & ContinuityIn 1990, the world forest cover was 4168 million hectares. In 2010, the world forest cover was 4033 million hectares. Write an exponential decay model in the form y = ae^kt, which represents the millions of hectares of forest cover in the world t years after
1990. Round k to five decimal places.
Enter your answer in the form y-ae^(kt), where a is the initial value and k is your growth rate. (Note: 1 hectare is approximately 2.5 acres.)
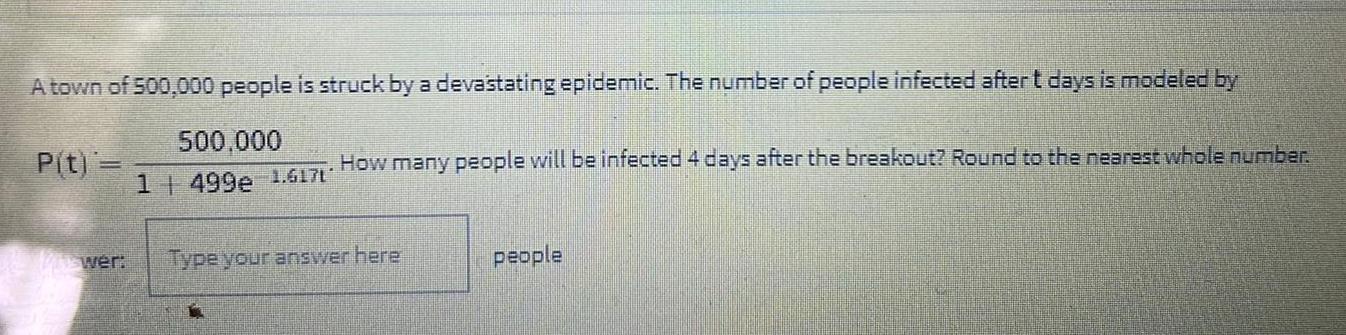
Calculus
Limits & ContinuityA town of 500,000 people is struck by a devastating epidemic. The number of people infected after t days is modeled by P(t)=500,000/1+499e^-1.617t. How many people will be infected 4 days after the breakout? Round to the nearest whole number.

Calculus
Limits & ContinuityA ball is thrown straight up with an initial velocity of 64 feet per second from the top of a building that is 80 ft tall. The height of the ball t seconds after it is thrown is given by the function s(t) = -16t² +64t + 80.
a. After how many seconds will the ball reach its maximum height?
b. What is the maximum height the ball reaches?
c. When will the ball reach the ground? In seconds.
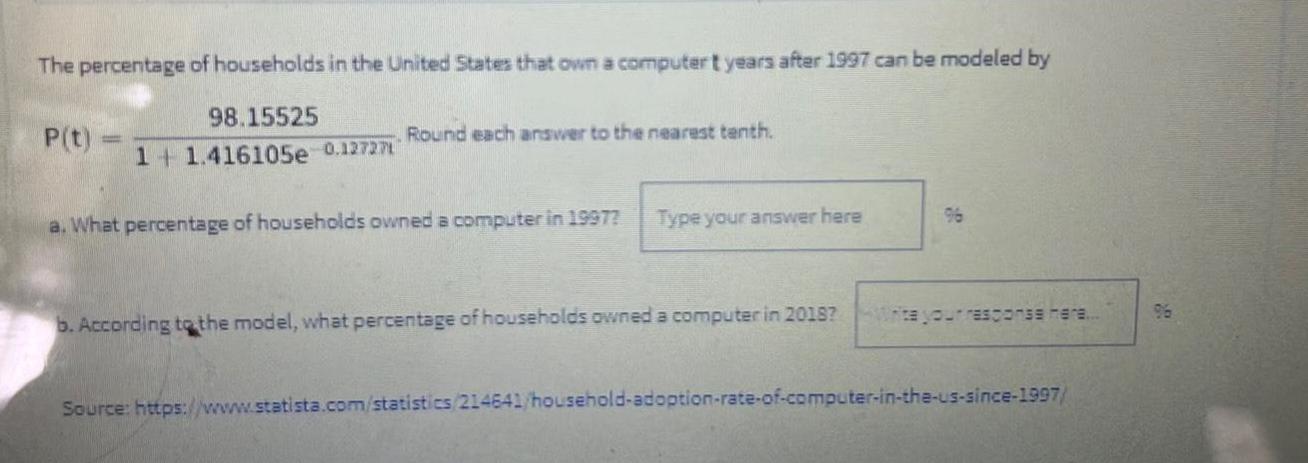
Calculus
Limits & ContinuityThe percentage of households in the United States that own a computer t years after 1997 can be modeled by
P(t)=98.15525/(1+ 1.416105e^-0,1272t) . Round each answer to the nearest tenth.
a. What percentage of households owned a computer in 1997?
b. According to the model, what percentage of households owned a computer in 2018?
![What is the center of (12.8, 5.7, 7.9, 1.3, 3.2, 2.8]? 5.62 4.45 11.55 4.22](https://media.kunduz.com/media/sug-question/raw/84616522-1658520560.755187.jpeg?w=256)
Calculus
Limits & ContinuityWhat is the center of (12.8, 5.7, 7.9, 1.3, 3.2, 2.8]? 5.62 4.45 11.55 4.22
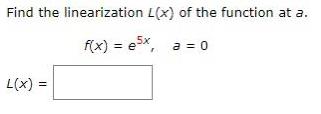
Calculus
Limits & ContinuityFind the linearization L(x) of the function at a. f(x) = e5x, a = 0 L(x) =
![The area A of the region S that lies under the graph of the continuous function is the limit of the sum of the areas of approximating rectangles.
A = lim n→∞ Rn=lim n→∞ [f(x₁)Ax + f(x₂)Ax+ ... + f(x)Ax]
Use this definition to find an expression for the area under the graph of f as a limit. Do not evaluate the limit.
f(x) = 3x cos(3x), 0≤x≤π/2
A = lim Σ i=1 to n
n→∞](https://media.kunduz.com/media/sug-question/raw/84605846-1658519745.7968724.jpeg?w=256)
Calculus
Limits & ContinuityThe area A of the region S that lies under the graph of the continuous function is the limit of the sum of the areas of approximating rectangles.
A = lim n→∞ Rn=lim n→∞ [f(x₁)Ax + f(x₂)Ax+ ... + f(x)Ax]
Use this definition to find an expression for the area under the graph of f as a limit. Do not evaluate the limit.
f(x) = 3x cos(3x), 0≤x≤π/2
A = lim Σ i=1 to n
n→∞


Calculus
Limits & ContinuityDetermine the domain for the function of two variables h(x,y) = 4x e√(4+y)
Choose the correct answer below.
A. {(x,y) | y≠0}
B. {(x,y) | y≤0}
C. {(x,y) | y≥-4}
D. ((x,y) | y=-4}
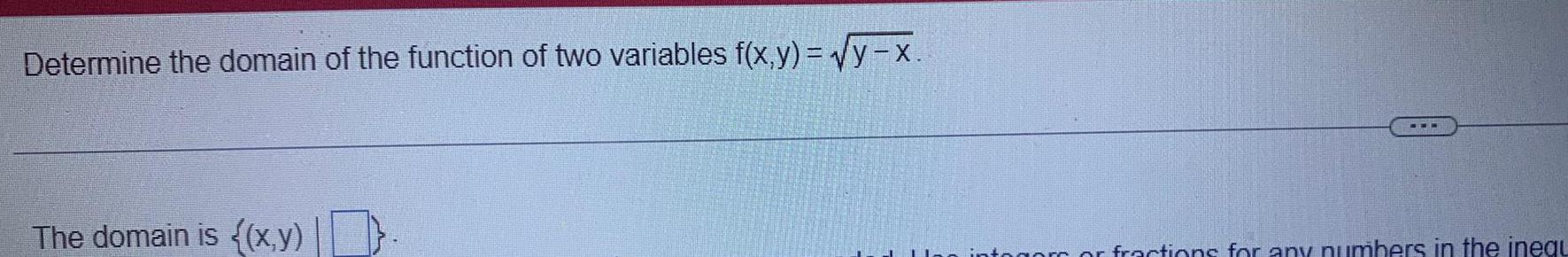
Calculus
Limits & ContinuityDetermine the domain of the function of two variables f(x,y)=√√y-x.
The domain is ((x,y)
Calculus
Limits & ContinuityIn a recent year, companies spent a total of $87.6 billion on newspaper, television, and radio ads. The total amount spent on television and radio ads was only $2.8 billion more than the amount spent on newspaper ads alone. The amount spent on newspaper ads was $5.5 billion more than what was spent on television ads. How much was spent on each form of advertising? (Hint: Let the variables represent numbers of billions of dollars.)
How much was spent on newspaper ads?
How much was spent on television ads?
How much was spent on radio ads?

Calculus
Limits & ContinuityIt takes Fena Tailoring 2 hr of cutting and 4 hr of sewing to make a tiered silk organza bridal dress. It takes 4 hr of cutting and 2 hr of sewing to make a lace sheath bridal dress. The shop has at most 22 hr per week available for cutting and at most 14 hr per week for sewing. The profit is $313 on an organza dress and $227 on a lace dress. How many of each kind of bridal dress should be made each week in order to maximize profit? What is the maximum profit?

Calculus
Limits & ContinuityThe price-earnings ratio of a stock is given by
R(P,E) = P/E where P is the price of the stock and E is the earnings per share. Recently, the price per share of a certain company was $33.59 and the earnings per share were $1.07. Find the price-earnings ratio.

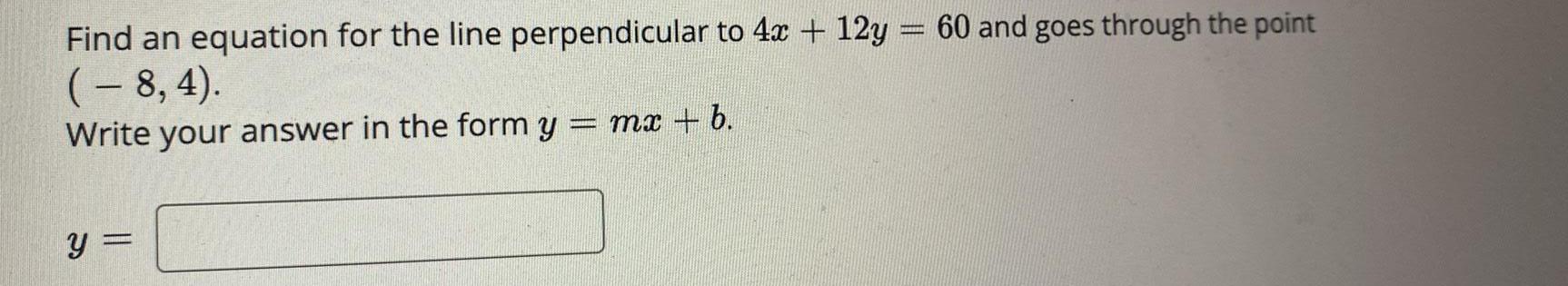
Calculus
Limits & ContinuityFind an equation for the line perpendicular to 4x + 12y=60 and goes through the point (– 8, 4).
Write your answer in the form y = mx + b.
y =

Calculus
Limits & ContinuityA trash company is designing an open-top, rectangular container that will have a volume of 1080 ft3. The cost of making the bottom of the container is $5 per square foot, and the cost of the sides is $4 per square foot. Find the dimensions of the container that will minimize total cost.

Calculus
Limits & ContinuityThe Ebbinghaus's Law of Forgetting states that if a task is learned at a performance level P0, then after a time interval t, the performance level P satisfies the relationship log P = log P0 - c log(t+1), where C is a constant that depends on the type of task and t is measured in months. Use the law to determine a student's expected score on a math test six months after the student scores an 80 on the test covering the same material. Assume C = 0.2. Round the intermediate steps to five decimal places. Round the final answer to the nearest whole number.