Limits & Continuity Questions and Answers
Calculus
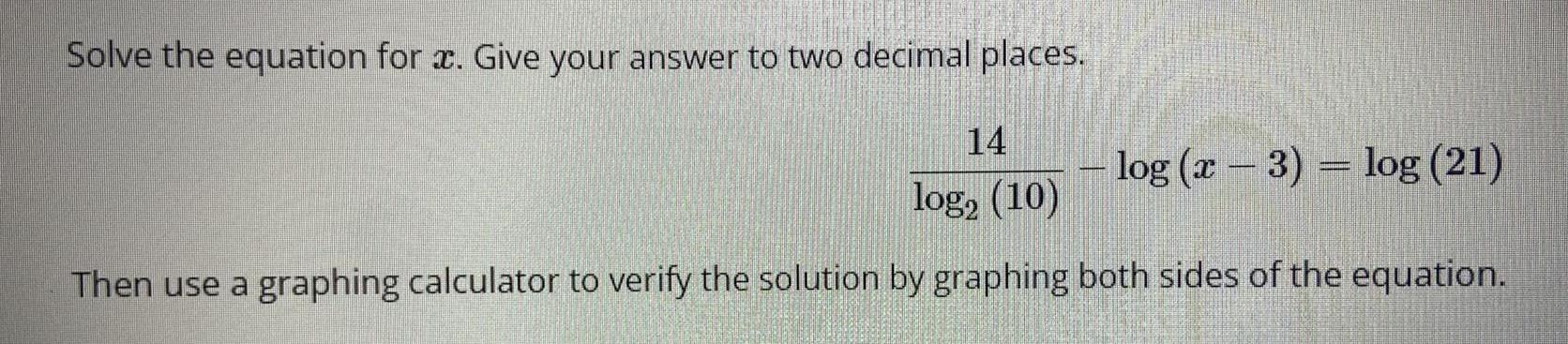
Limits & ContinuitySolve the equation for x. Give your answer to two decimal places.
Then use a graphing calculator to verify the solution by graphing both sides of the equation.
14/log₂ (10)-log (x-3) = log (21)

Calculus
Limits & ContinuityUse a graphing calculator to graph both sides of the equation.
-6 log6 (4-x) = -5
Based on the graph, what is the solution? Give your answer to two decimal places.
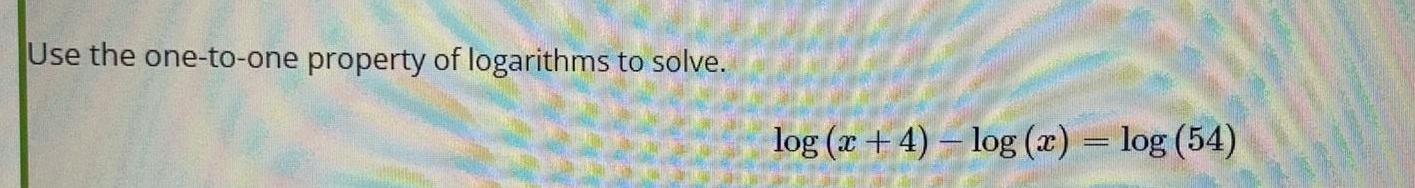
Calculus
Limits & ContinuityUse the one-to-one property of logarithms to solve.
log (x + 4) - log(x) = log (54)
Calculus
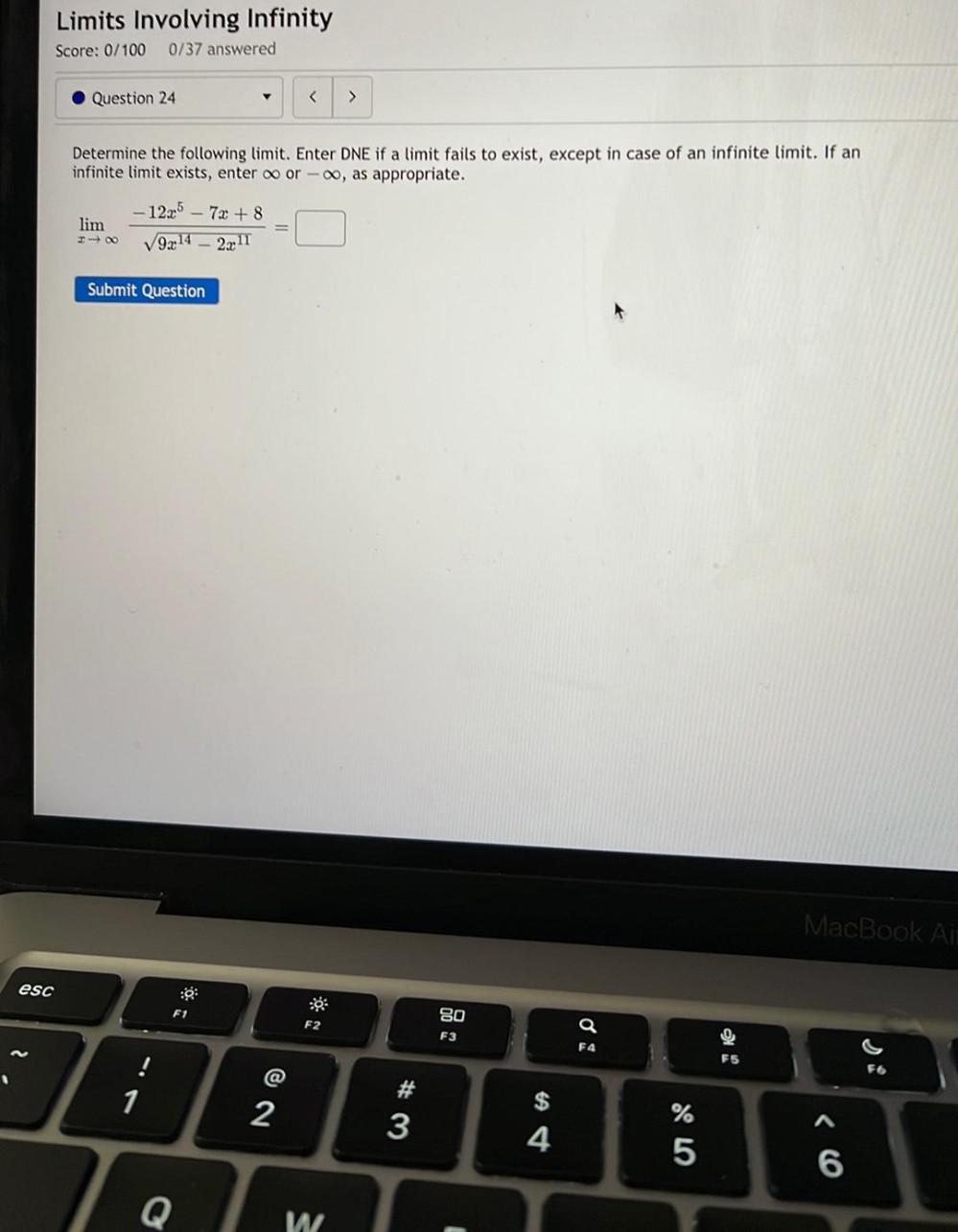
Limits & ContinuityDetermine the following limit. Enter DNE if a limit fails to exist, except in case of an infinite limit. If an infinite limit exists, enter ∞ or -∞, as appropriate.
lim -12x^5 - 7x + 8 / √9x^14 - 2x^11 =
z→∞

Calculus
Limits & ContinuityGiven the function P(x) = -7(x − 7)6(x + 4)7(x − 5),
its roots are
and their multipicities are

Calculus
Limits & ContinuityThe first term and a recursive formula for a geometric sequence are given. Find a10.
a₁ = 6, an = -2an-1
a10=




Calculus
Limits & ContinuityFind the first five terms of the geometric sequence given the first term and common ratio.
a₁ = 6, r= 0.3
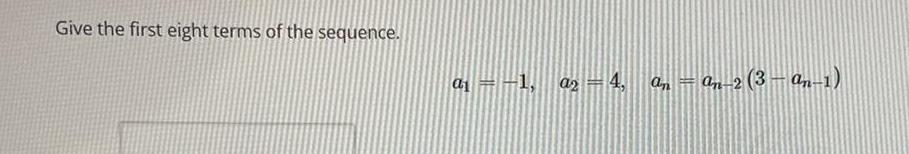
Calculus
Limits & ContinuityGive the first eight terms of the sequence.
a₁ = -1, a₂ = 4, an = an-2 (3-an-1)

Calculus
Limits & ContinuityGive the first eight terms of the piecewise sequence.
an = (-2)n - 4 if n is even
4n-1 if n is odd

Calculus
Limits & ContinuityTwo terms of an arithmetic sequence are given. Find the first five terms.
a1 = 10, a7 = -44

Calculus
Limits & ContinuityFind the common ratio for the geometric sequence.
2, 10, 50, 250, 1250,...

Calculus
Limits & ContinuityIs the sequence geometric?
4, 4.4, 4.8, 5.2, 5.6,...
If so, enter the common ratio. If not, enter "No".

Calculus
Limits & ContinuityIs the sequence geometric?
5, 9, 13, 17, 21,...
If so, enter the common ratio. If not, enter "No".
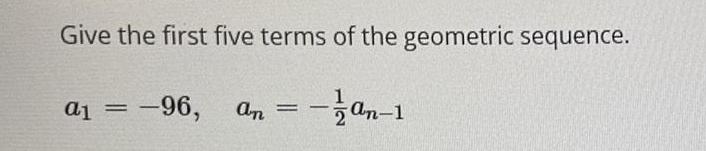
Calculus
Limits & ContinuityGive the first five terms of the geometric sequence.
a1 = -96, an = -1 2an-1


Calculus
Limits & ContinuityIs the sequence arithmetic?
{42, 38.7, 35.4, 32.1, 28.8,...}
If so, enter the common difference. If not, enter "No".

Calculus
Limits & ContinuityUse the explicit formula to find the first five terms of the arithmetic sequence.
an =1 5n - 1 5
for n = 1, 2, 3,...

Calculus
Limits & ContinuityFind the intercepts and the vertical asymptote of
f(x) = x2-3x-4
x-5
Enter the intercepts as points, (a, b).
![Sketch the graph of a function f that is continuous on [1, 8] and has the given properties.
absolute maximum at 3, absolute minimum at 8, 7 is a critical number but there is no local maximum or minimum there](https://media.kunduz.com/media/sug-question/raw/84675311-1659015991.717127.jpeg?w=256)
Calculus
Limits & ContinuitySketch the graph of a function f that is continuous on [1, 8] and has the given properties.
absolute maximum at 3, absolute minimum at 8, 7 is a critical number but there is no local maximum or minimum there
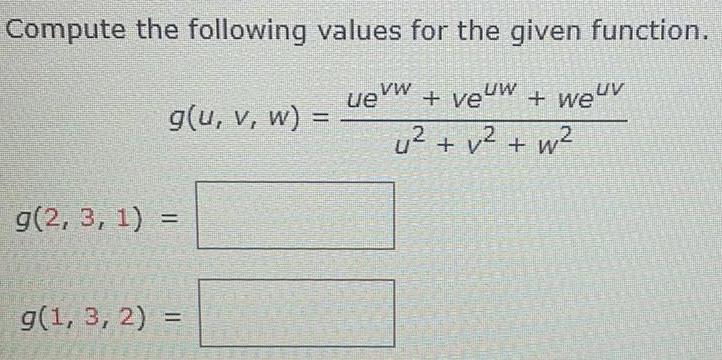
Calculus
Limits & ContinuityCompute the following values for the given function.
g(u, v, w) = uevw + veuw + weuv
u²+ v² + w²
g(2, 3, 1) =
g(1, 3, 2) =

Calculus
Limits & ContinuityThe system of equations of y = 2x 2y = 4x represents what kind of system?
(What could it be classified as?)
Inconsistent System
Consistent Dependent System
Consistent Independent System
Inconsistent and Independent System
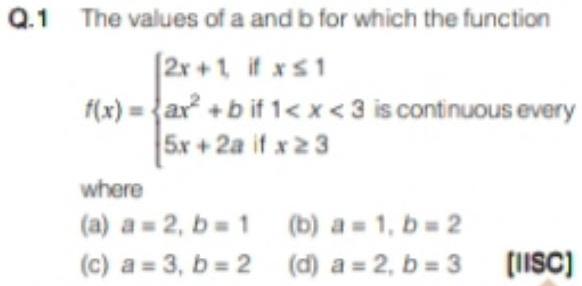
Calculus
Limits & ContinuityThe values of a and b for which the function
2x+1, if x≤1
f(x) = ax +b if 1<x<3 is continuous every
5x + 2a if x ≥ 3
where
(a) a= 2, b=1 (b) a = 1, b = 2
(c) a=3, b= 2 (d) a= 2, b=3

Calculus
Limits & ContinuityFind h(x, y) = g(f(x, y)).
g(t) = t + In(t), f(x, y) = 5-xy 2 + x²y²
h(x, y) =
Find the set of points at which h is continuous.
D = {(x, y) | xy > 5}
h is continuous on R²
D = {(x, y) | xy ≤ 5}
D = {(x, y) | xy < 5}
D = {(x, y) | xy ≥ 5}

Calculus
Limits & ContinuityIf f'(x) = 1 3-x² and f(0) = 1 then the lower bound and upper bound of f(1) estimated by mean value theorem are
(a) 1, 1.2 (b) 1.33, 1.5
(c) 1.5, 1.75 (d) None

Calculus
Limits & ContinuitySolve the equation for x. (Round your answer to three decimal places.)
arctan(4x - 6) = -1
x =
![Write the expression in algebraic form. [Hint: Sketch a right triangle, as demonstrated in Example 3.]
cos(arcsin 3x)](https://media.kunduz.com/media/sug-question/raw/84656149-1658958687.790814.jpeg?w=256)
Calculus
Limits & ContinuityWrite the expression in algebraic form. [Hint: Sketch a right triangle, as demonstrated in Example 3.]
cos(arcsin 3x)
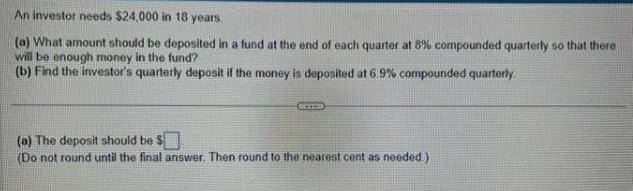
Calculus
Limits & ContinuityAn investor needs $24,000 in 18 years.
(a) What amount should be deposited in a fund at the end of each quarter at 8% compounded quarterly so that there will be enough money in the fund?
(b) Find the investor's quarterly deposit if the money is deposited at 6.9% compounded quarterly
(a) The deposit should be $
(Do not round until the final answer. Then round to the nearest cent as needed)
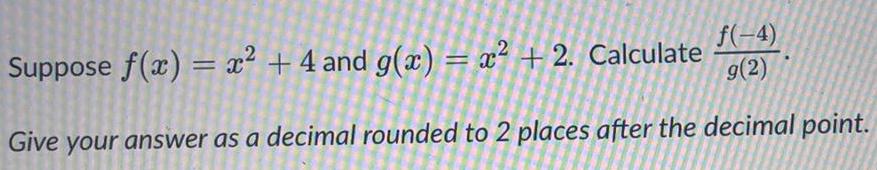
Calculus
Limits & ContinuitySuppose f(x) = x² + 4 and g(x) = x² + 2. Calculate f(-4) g(2)
Give your answer as a decimal rounded to 2 places after the decimal point.
![Solve the equation for x.
arctan (7x- 9) = -1
Step 1
The original equation arctan (7x - 9) = -1 specifies the arctan of an expression. To solve it, take the tangent of each side and rewrite the equation.
tan tan [arctan(7x- 9)]= tan ✔ tan(-1)
Step 2
Simplify the above equation. (Round your answers to three decimal places.)
7x - =tan( )
X =1(tan(-1)+9)/
x=1(-(tan(1)) + 9)/
x=](https://media.kunduz.com/media/sug-question/raw/84654029-1658824036.1014524.jpeg?w=256)
Calculus
Limits & ContinuitySolve the equation for x.
arctan (7x- 9) = -1
Step 1
The original equation arctan (7x - 9) = -1 specifies the arctan of an expression. To solve it, take the tangent of each side and rewrite the equation.
tan tan [arctan(7x- 9)]= tan ✔ tan(-1)
Step 2
Simplify the above equation. (Round your answers to three decimal places.)
7x - =tan( )
X =1(tan(-1)+9)/
x=1(-(tan(1)) + 9)/
x=

Calculus
Limits & Continuity3. In each of the following, use the Gauss-Jordan method as described in the online tutorial system.
Note Successive steps in the process will only become visible as you progress,
(a) Consider the system
-4z-2y+3z=0
-16z-6y + 12z = 1
82 +6y=-1.
The augmented matrix of the system is
(b) Consider the system
18z+2y-13: 11
-92-2y+7z = -5
12z+2y-92-7.
The augmented matrix of the system is

Calculus
Limits & Continuity(a) Trivially parametrize the function f(x) = x² +2.
(b) Construct a table of t, x, and y values with t ranging from -2 to 2.
(c) Draw the graph of this function with indicated range of motion.

Calculus
Limits & ContinuityFind the Maclaurin series for the following functions.
(a) f(x) = sin(x)/x
Hint: Just multiply the Maclaurin series for sin(x) by 1/x.
(b) f(x) = ex³
(c) f(x) = cos(x²)/x²

Calculus
Limits & Continuity4. Determine the vertical asymptotes of the graph of the function f(x) = sec π x. At each vertical asymptote, find the one-sided limits.
5. Determine the vertical asymptotes of the graph of the function .f(x) = ln x. At
the vertical asymptote, find the one-sided limit.
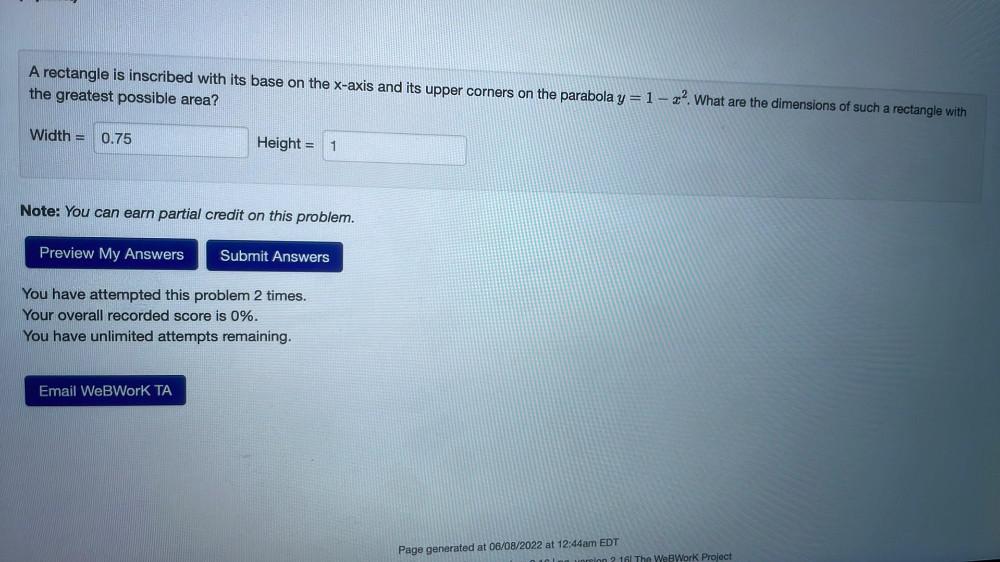
Calculus
Limits & ContinuityA rectangle is inscribed with its base on the x-axis and its upper corners on the parabola y = 1- x². What are the dimensions of such a rectangle with
the greatest possible area?
Width = 0.75
Height = 1
Note: You can earn partial credit on this problem.
Preview My Answers Submit Answers You have attempted this problem 2 times. Your overall recorded score is 0%. You have unlimited attempts remaining.
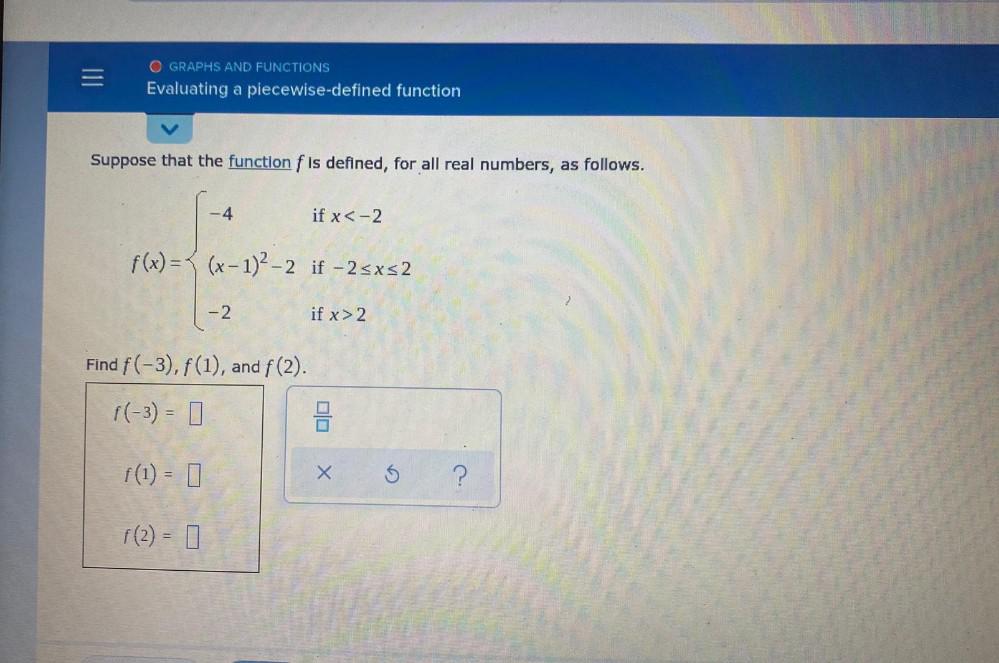
Calculus
Limits & ContinuityEvaluating a piecewise-defined function
Suppose that the function f is defined, for all real numbers, as follows.
f(x)= -4, if x < -2
(x-1)²-2. if -2≤x≤2
-2, if x > 2
Find f(-3), f(1), and f(2).
f(-3) = 0
f(1) = 0
f(2)=
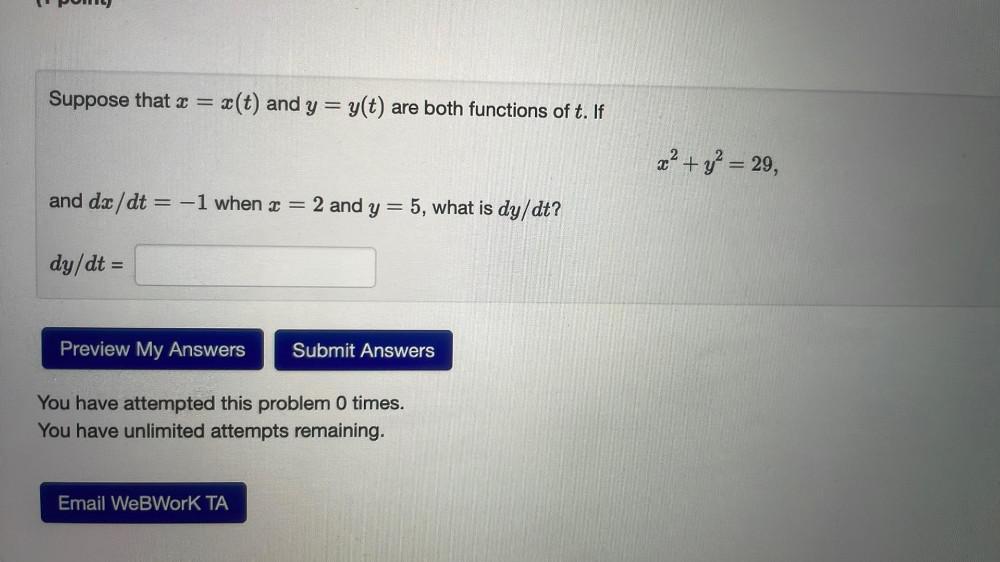
Calculus
Limits & ContinuitySuppose that x = x(t) and y = y(t) are both functions of t. If x² + y² = 29,
and dx/dt = -1 when x = 2 and y = 5, what is dy/dt?
dy/dt =
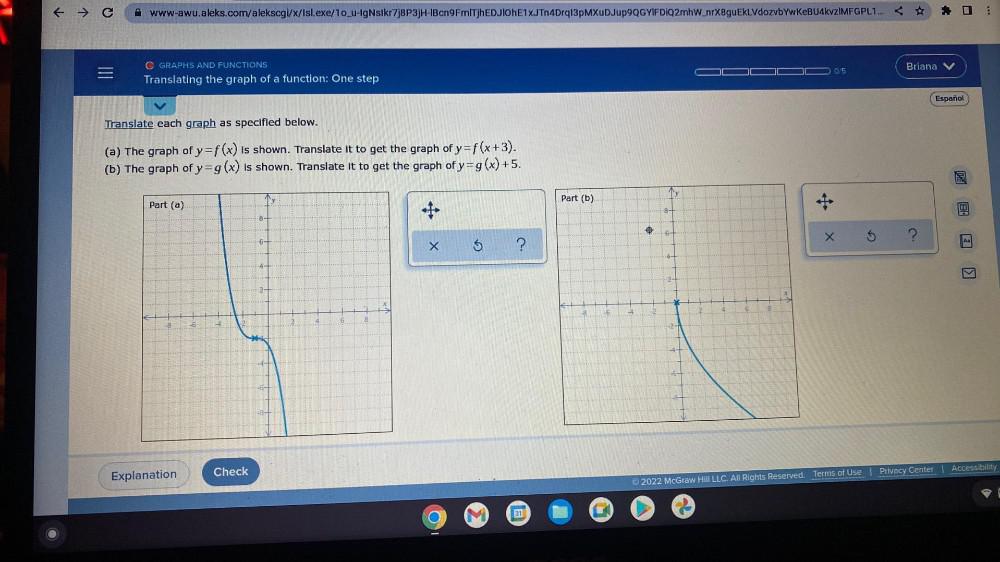
Calculus
Limits & ContinuityTranslate each graph as specified below.
(a) The graph of y = f(x) is shown. Translate it to get the graph of y = f(x+3).
(b) The graph of y = g(x) is shown. Translate it to get the graph of y = g(x) +5.

Calculus
Limits & ContinuityDiscuss algebraically the continuity of the function f(x)=(x-1)/(x²-4x+3). How many discontinuities does it have? Which one is removable or nonremovable and why?
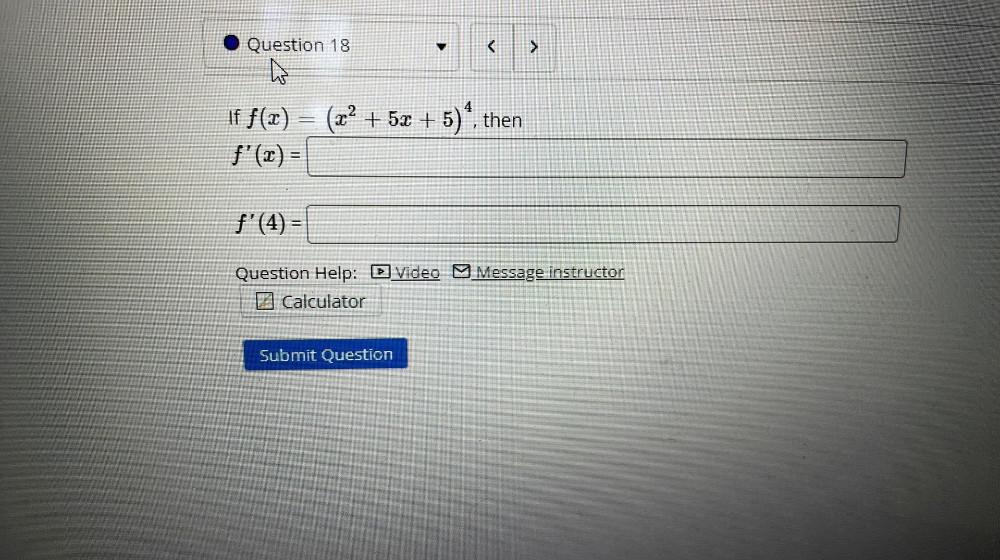

Calculus
Limits & ContinuityThe formal definition for the derivative of f(x) at x = a is
f'(a) = lim f(a+h) — f(a)/h
h→0
(1) Find the Taylor polynomial of order 5 about = 2 which approximates f(x) = eˣ.
(ii) Using this approximation, show, from the formal definition of a derivative, that f'(2) = e².

Calculus
Limits & ContinuityWhich of the following is the simplified expression of 1-1/csc² x?
cos²x
-cos²x
tan²x
-tan²x
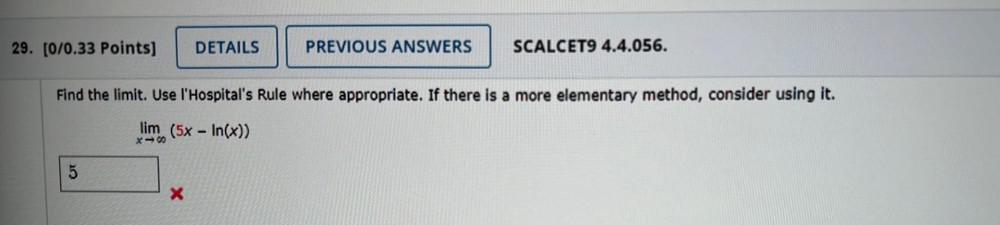
Calculus
Limits & ContinuityFind the limit. Use l' Hospital's Rule where appropriate. If there is a more elementary method, consider using it.
lim (5x-In(x))
x→∞
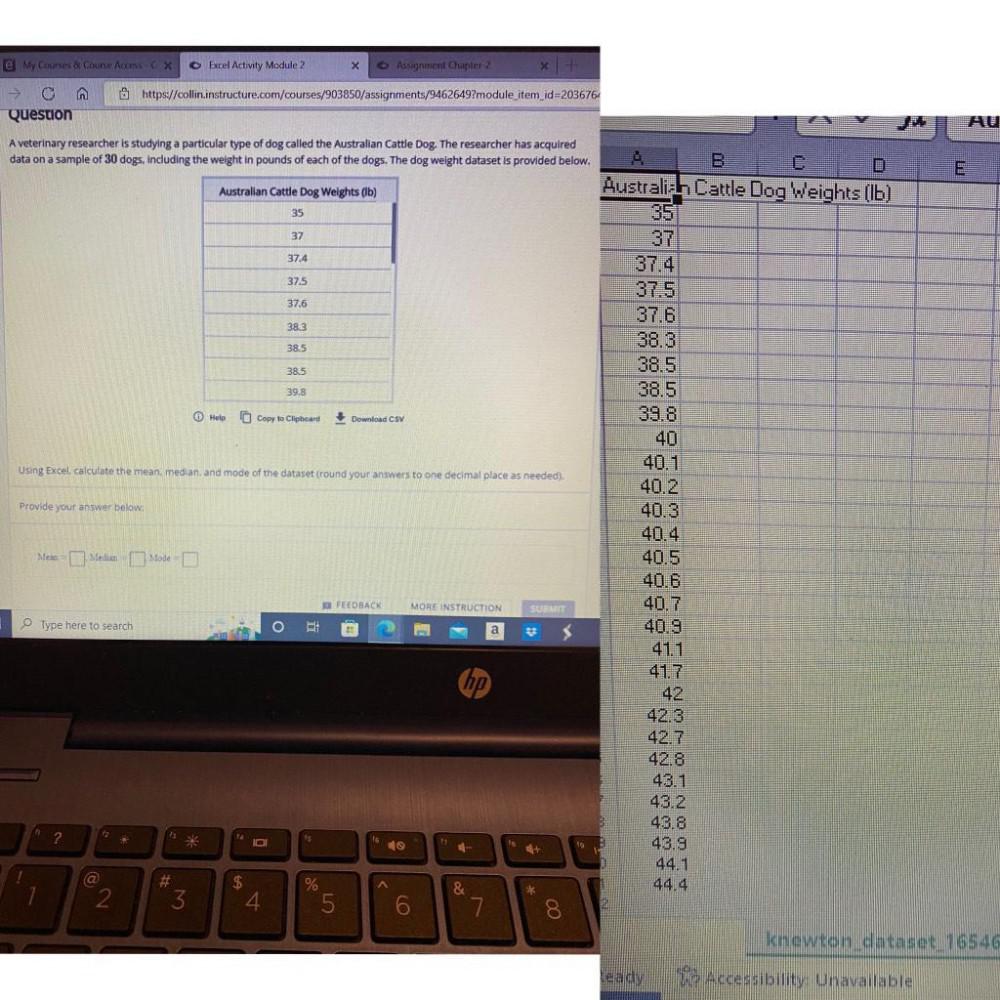
Calculus
Limits & ContinuityA veterinary researcher is studying a particular type of dog called the Australian Cattle Dog. The researcher has acquired data on a sample of 30 dogs, including the weight in pounds of each of the dogs. The dog weight dataset is provided below.
Australian Cattle Dog Weights (lb)
35
37
37.4
37.5
37.6
38.3
38.5
38.5
39.8
Calculus
Limits & ContinuityFind the difference quotient f(x+ h)-f(x)/(h), where h ≠ 0, for the function below.
f(x)=-x²-2x+5
Simplify your answer as much as possible. f(x +h)-f(x)/(h)=

Calculus
Limits & ContinuityWhich restriction on the domain of y=sin x results in a function whose inverse is also a function? Check the three that apply.
y = sin x, 0≤x≤π
y = sin x, 0≤x≤π/2
y = sin x, -π/2≤x≤π/2
y = sin x, 0≤x≤ 2π
y = sin x, π/2≤x≤3π/2

Calculus
Limits & ContinuityIf a family had three children,
Find the probability that at least two of the three children is a girl.
3/8
4/8
7/8
None of these
Find the probability that at least one of the three children is a girl.
3/8
4/8
7/8
None of these
