Limits & Continuity Questions and Answers
Calculus
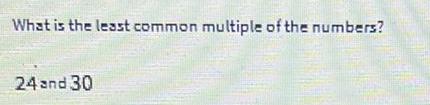
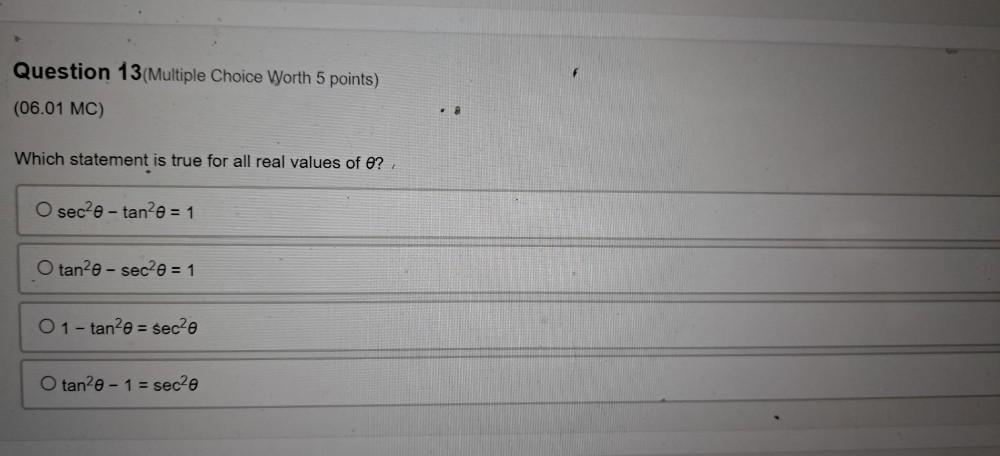
Limits & ContinuityWhich statement is true for all real values of θ?
sec²θ- tan²θ = 1
tan²θ-sec²θ = 1
1 - tan²θ = sec²θ
tan²θ - 1 = sec²θ
Calculus
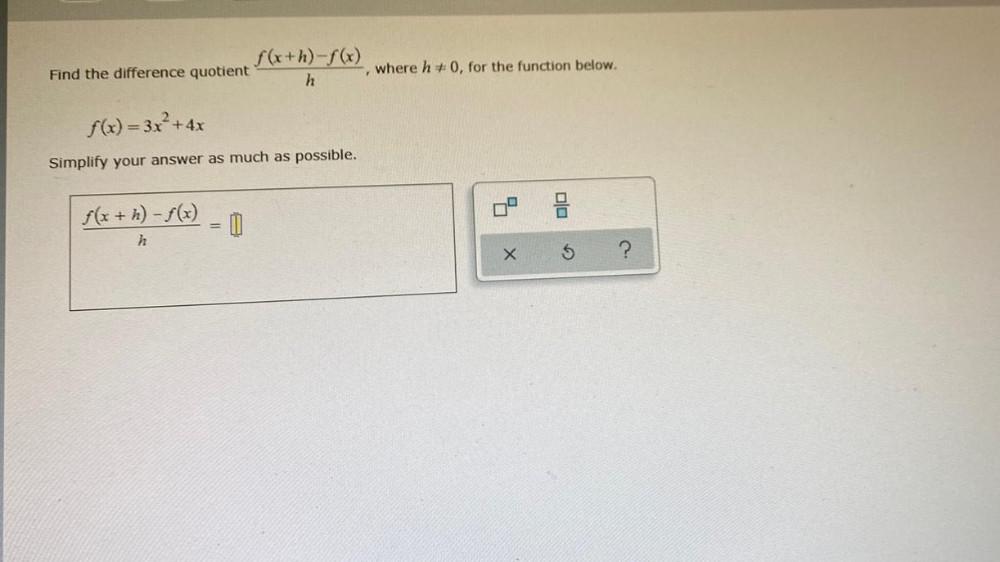
Limits & ContinuityFind the difference quotient f(x+ h)-f(x)/(h),where h≠0, for the function below.
f(x) = 3x² + 4x
Simplify your answer as much as possible.
f(x +h)-f(x)/(h)=
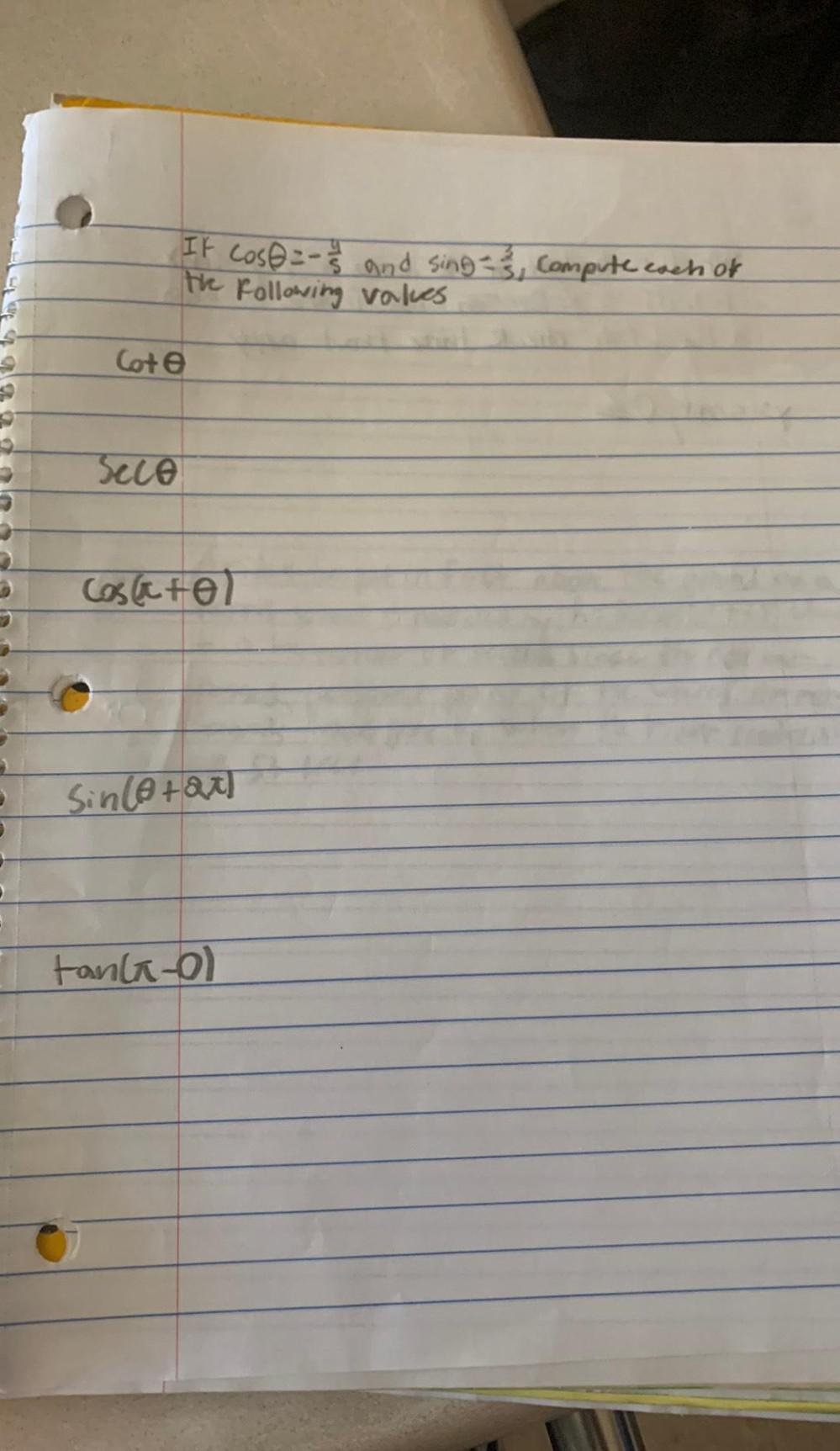
Calculus
Limits & ContinuityIt Cosθ=-4/5 and sinθ=3/5, compute each of the following values
cotθ=
secθ=
cos(π+θ)=
sin(θ+2π)=
tan(π-θ)=
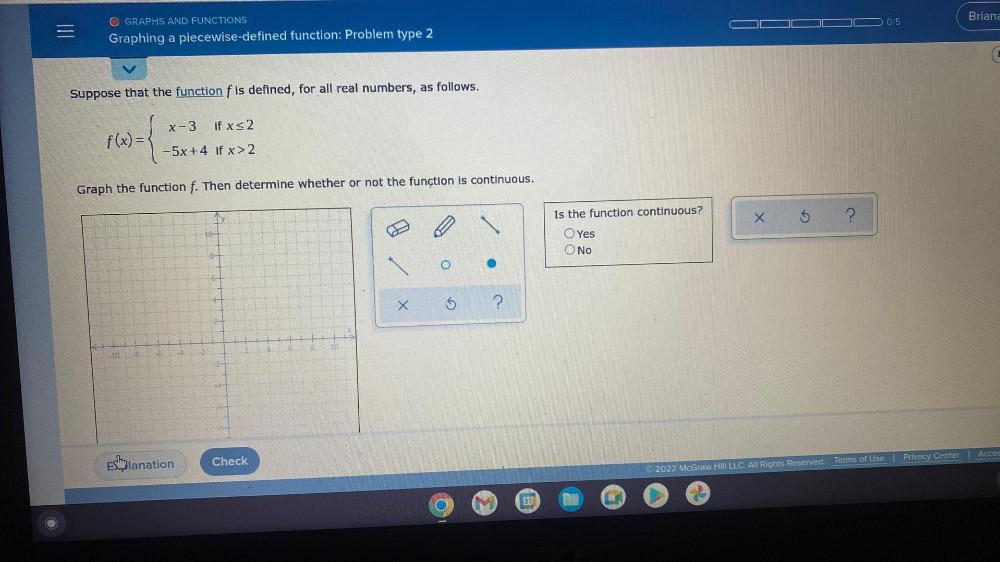
Calculus
Limits & ContinuitySuppose that the function f is defined, for all real numbers, as follows.
f(x)= x-3 if x≤2
-5x+4 if x > 2
Graph the function f. Then determine whether or not the function is continuous.
Is the function continuous?
Yes
No
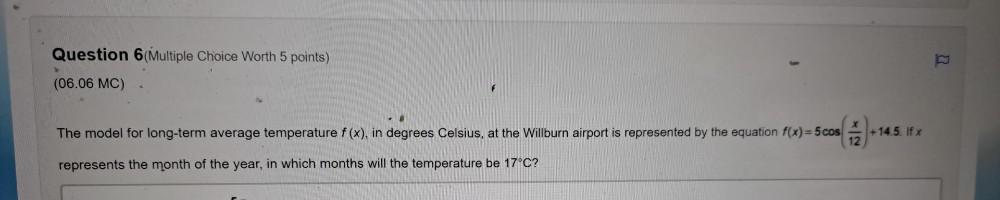
Calculus
Limits & ContinuityThe model for long-term average temperature f (x), in degrees Celsius, at the Willburn airport is represented by the equation f(x) = 5 cos(x/12)+14.5 represents the month of the year, in which months will the temperature be 17°C?
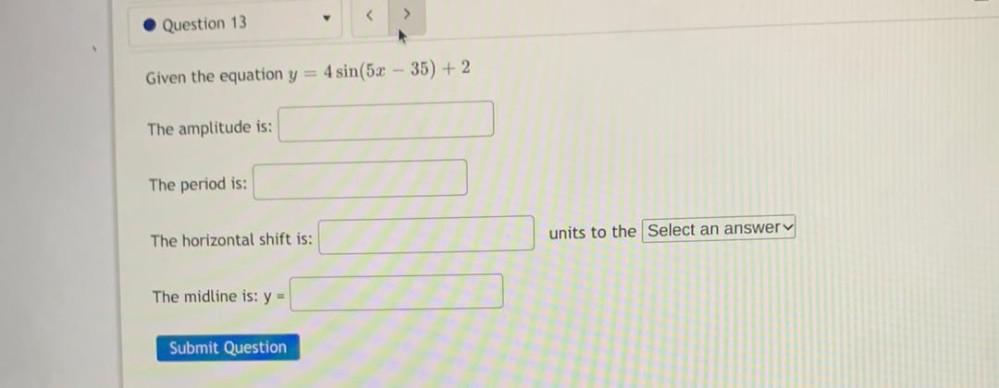
Calculus
Limits & ContinuityGiven the equation y = 4 sin(5x - 35) + 2
The amplitude is:
The period is:
The horizontal shift is:
The midline is: y =
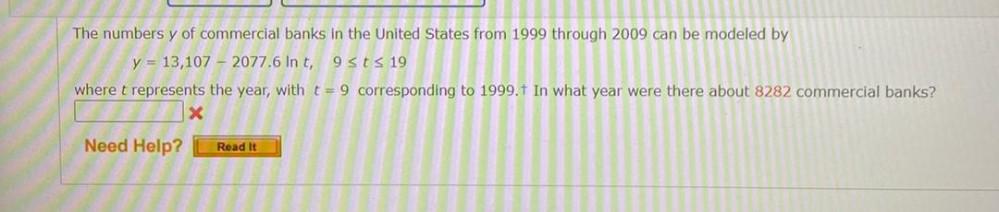
Calculus
Limits & ContinuityThe numbers y of commercial banks in the United States from 1999 through 2009 can be modeled by
y = 13,107 2077.6 In t, 9 ≤ t ≤ 19.
where t represents the year, with t = 9 corresponding to 1999.In what year were there about 8282 commercial banks?

Calculus
Limits & ContinuityWhat is the degree of the given polynomial?
a) f(x)=3x-5
b) f(x) = 5x⁶ -3x² +7
c) f(x)=(2x-5)(x-2)(x+1)
d) f(x) = 4(x-3)²(x+1)^5(x-11)
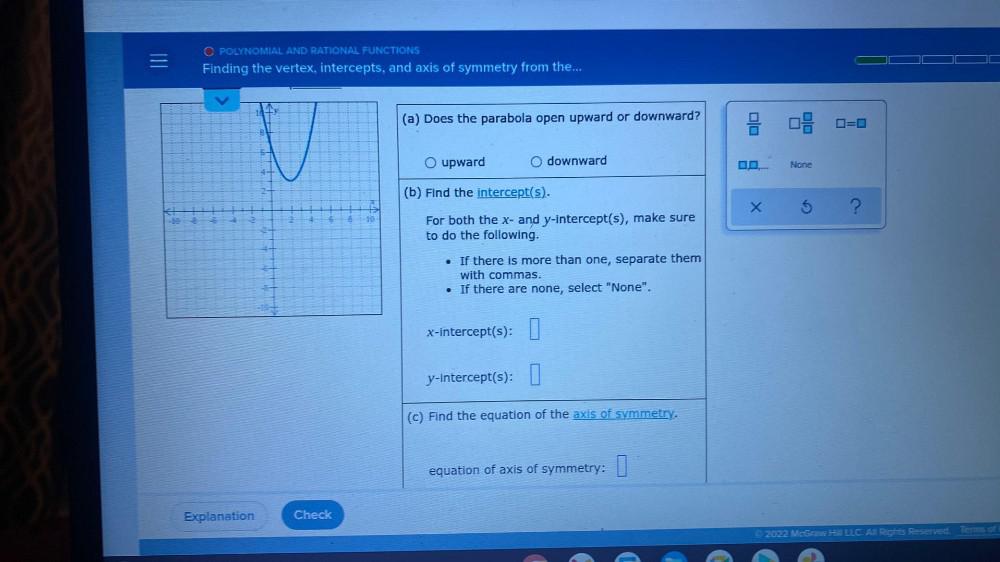
Calculus
Limits & Continuity(a) Does the parabola open upward or downward?
upward
(b) Find the intercept(s).
For both the x- and y-intercept(s), make sure
to do the following.
If there is more than one, separate them with commas.
If there are none, select "None". x-intercept(s)
(c) Find the equation of the axis of symmetry.
equation of axis of symmetry
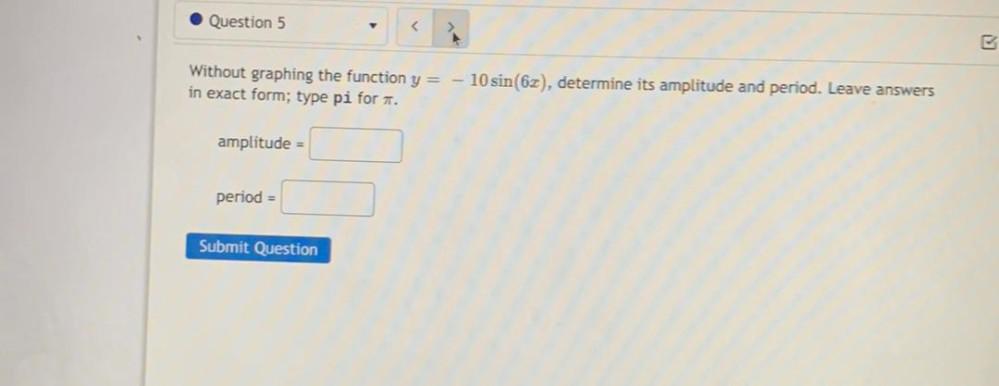
Calculus
Limits & ContinuityWithout graphing the function y = - 10 sin(6x), determine its amplitude and period. Leave answers in exact form; type pi for π .
amplitude =
period =
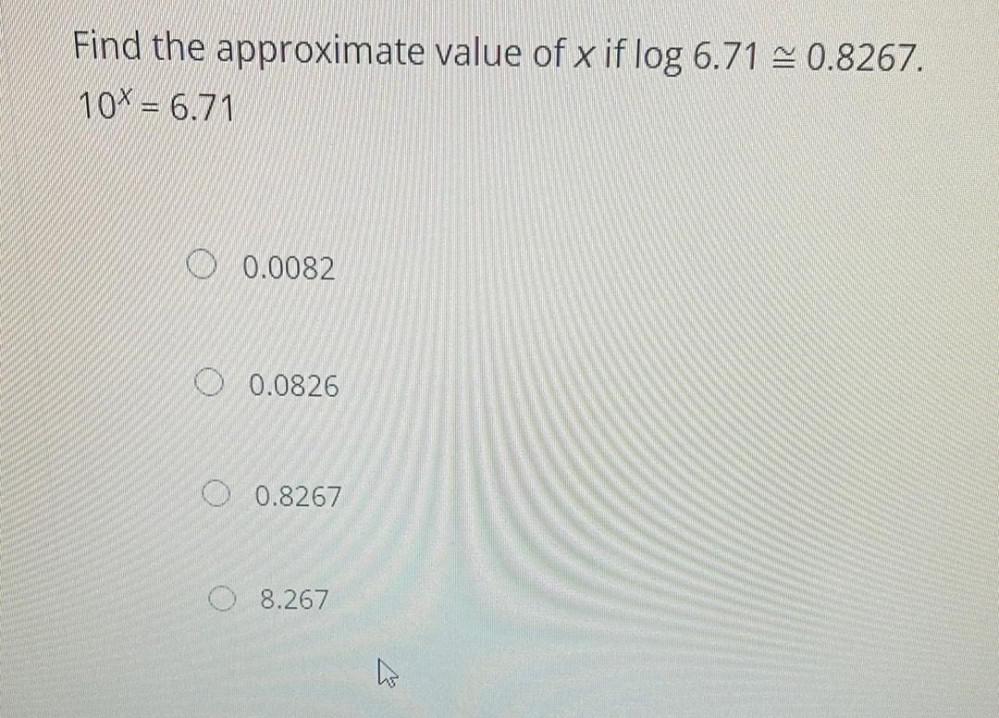
Calculus
Limits & ContinuityFind the approximate value of x if log 6.71 ≅ 0.8267.
10ˣ = 6.71
0.0082
0.0826
0.8267
8.267
![The distance between (7-4i) and [(4- i) - (2 + 3i)] is_
5
1
7
3](https://media.kunduz.com/media/sug-question/raw/83539980-1658666179.1636448.jpeg?w=256)
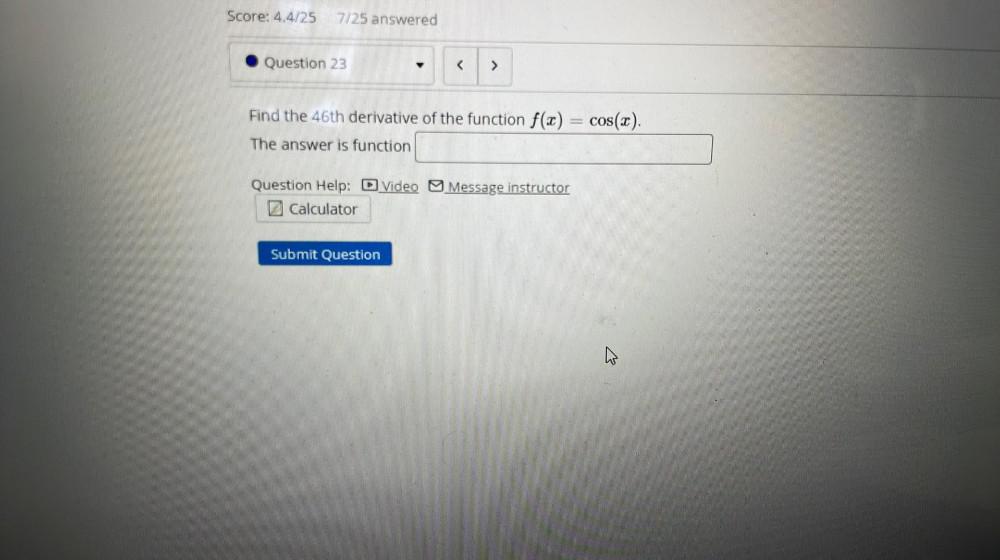
Calculus
Limits & ContinuityFind the 46th derivative of the function f(x) = cos(x).
The answer is function

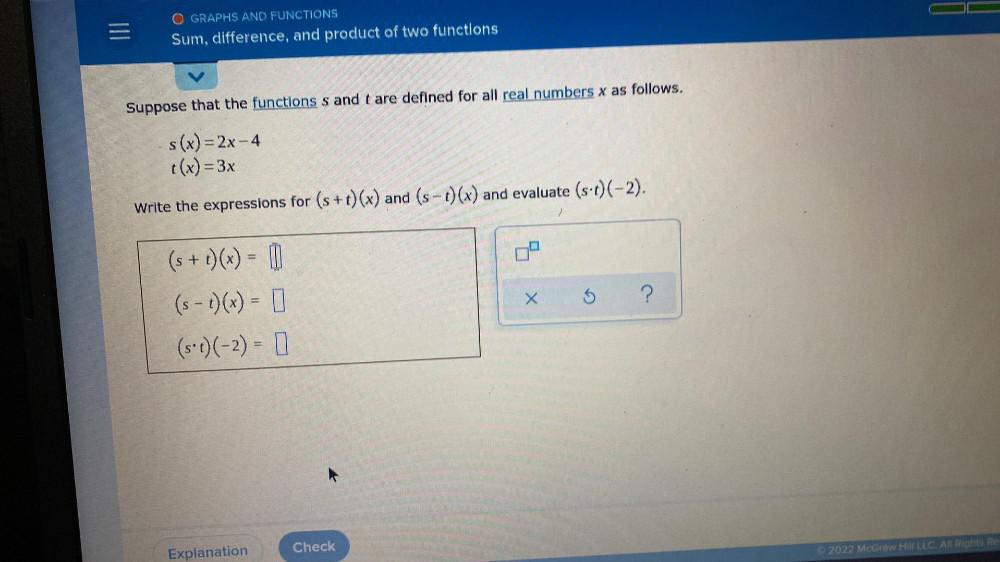
Calculus
Limits & ContinuitySuppose that the functions s and t are defined for all real numbers x as follows.
s(x)=2x-4
t(x) = 3x
Write the expressions for (s+t) (x) and (s-t) (x) and evaluate (s.t) (-2).
(s+ t)(x) =
(s - t)(x) =
(s.t) (-2) =
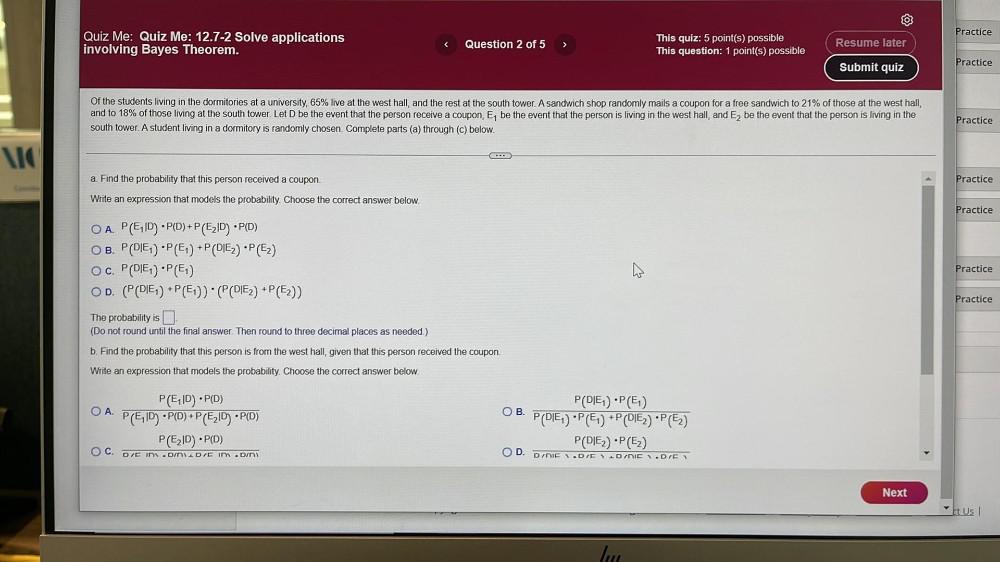
Calculus
Limits & ContinuityOf the students living in the dormitories at a university, 65% live at the west hall, and the rest at the south tower. A sandwich shop randomly mails a coupon for a free sandwich to 21% of those at the west hall, and to 18% of those living at the south tower. Let D be the event that the person receive a coupon, E₁ be the event that the person is living in the west hall, and E₂ be the event that the person is living in the south tower. A student living in a dormitory is randomly chosen. Complete parts (a) through (c) below.
a. Find the probability that this person received a coupon.
Write an expression that models the probability. Choose the correct answer below.
A. P(E₁ID).P(D) + P(E₂ID).P(D)
B. P (DIE₁).P(E₁) + P(DIE₂),P(E₂)
C. P (DIE₁).P(E₁)
D. (P(DIE₁) + P(E₁)) (P (DIE₂) + P(E₂))
The probability is
(Do not round until the final answer. Then round to three decimal places as needed.)
b. Find the probability that this person is from the west hall, given that this person received the coupon.
Write an expression that models the probability. Choose the correct answer below.
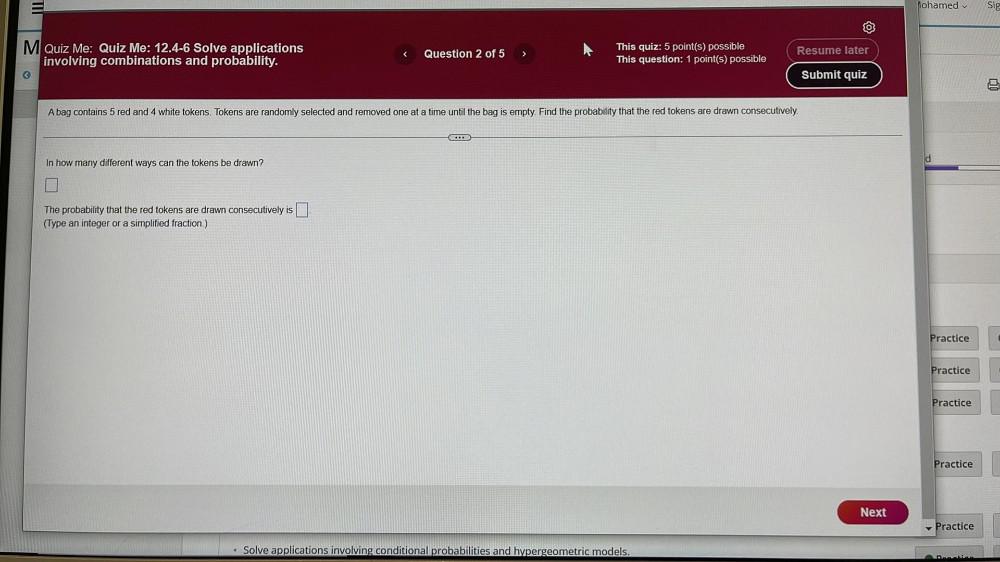
Calculus
Limits & ContinuityA bag contains 5 red and 4 white tokens. Tokens are randomly selected and removed one at a time until the bag is empty. Find the probability that the red tokens are drawn consecutively.
In how many different ways can the tokens be drawn?
The probability that the red tokens are drawn consecutively is
(Type an integer or a simplified fraction.)
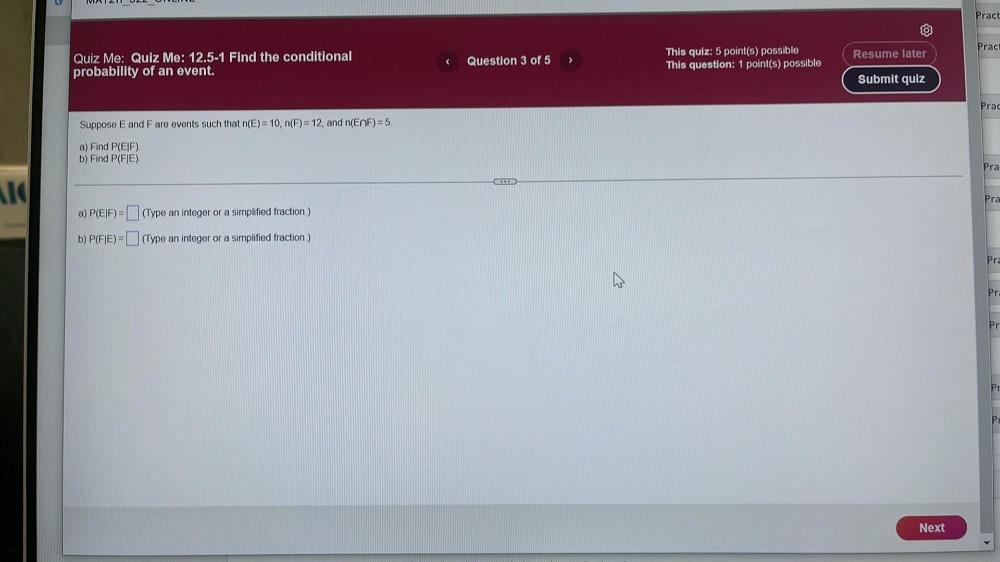
Calculus
Limits & ContinuitySuppose E and F are events such that n(E)= 10, n(F) = 12, and n(E⋂F) = 5.
a) Find P(EIF).
b) Find P(FIE).
a) P(EIF)=
(Type an integer or a simplified fraction.)
b) P(FIE)=
(Type an integer or a simplified fraction.)
![At a certain gas station, one of every 10 customers purchases premium gasoline, and the decision of each customer has no effect on the decisions of the others. What is the probability that of the next 5 customers, 4 purchase premium gasoline?
What expression can be used to calculate the probability?
A. [9 5] (1/10)⁵ (9/10)⁵
B. [5 4] (1/10)⁴ (9/10)¹
C. [5 4] (1/10 + 9/10)⁴
D. [5] 4 (1/10)⁵ (9/10)¹
The probability that of the next 5 customers, 4 purchase premium gasoline is 0
(Round to four decimal places as needed.)](https://media.kunduz.com/media/sug-question/raw/83655073-1658665704.5610785.jpeg?w=256)
Calculus
Limits & ContinuityAt a certain gas station, one of every 10 customers purchases premium gasoline, and the decision of each customer has no effect on the decisions of the others. What is the probability that of the next 5 customers, 4 purchase premium gasoline?
What expression can be used to calculate the probability?
A. [9 5] (1/10)⁵ (9/10)⁵
B. [5 4] (1/10)⁴ (9/10)¹
C. [5 4] (1/10 + 9/10)⁴
D. [5] 4 (1/10)⁵ (9/10)¹
The probability that of the next 5 customers, 4 purchase premium gasoline is 0
(Round to four decimal places as needed.)
![What is the distance between [(3 + 4i) + (2 - 3i)] and (9 - 2i)?](https://media.kunduz.com/media/sug-question/raw/83539885-1658665614.575956.jpeg?w=256)
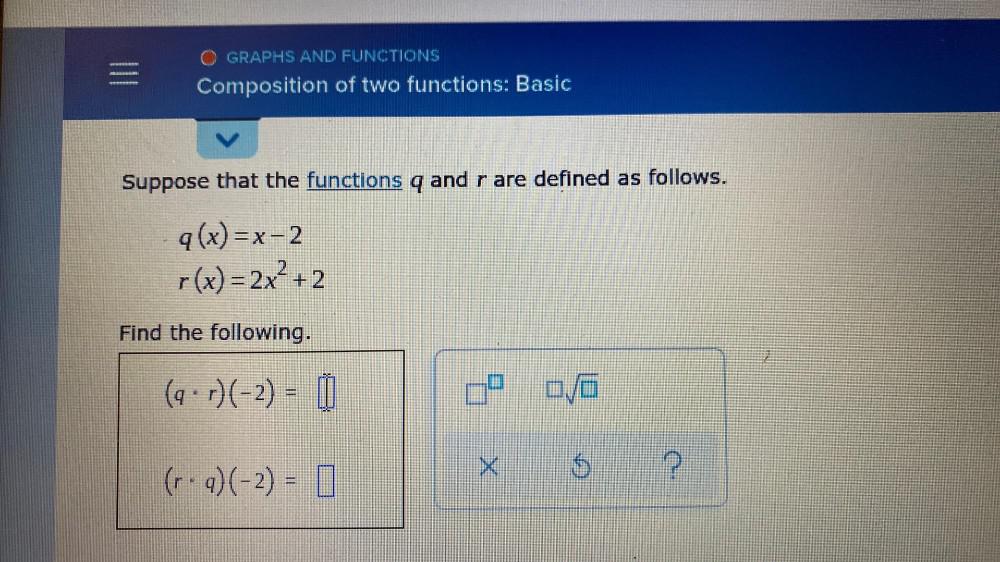
Calculus
Limits & ContinuitySuppose that the functions q and r are defined as follows.
q(x) = x-2
r(x) = 2x² +2
Find the following.
(q.r) (-2) =
(r.q) (-2) =
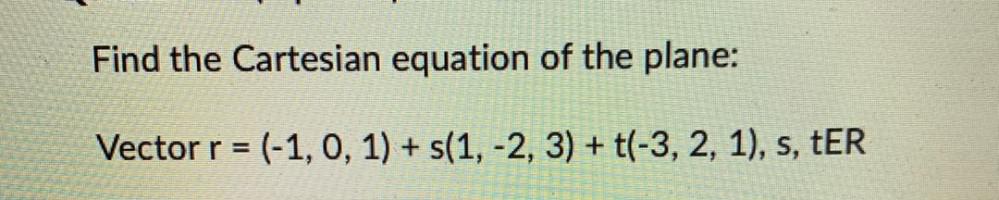
Calculus
Limits & ContinuityFind the Cartesian equation of the plane:
Vector r= (-1, 0, 1) + s(1, -2, 3) + t(-3, 2, 1), s, tER

Calculus
Limits & ContinuityCalculate the distance from point P(2, 4, 1) to the line:
Vector r = (1, 2, -1) + t(5, 1, -1), tER
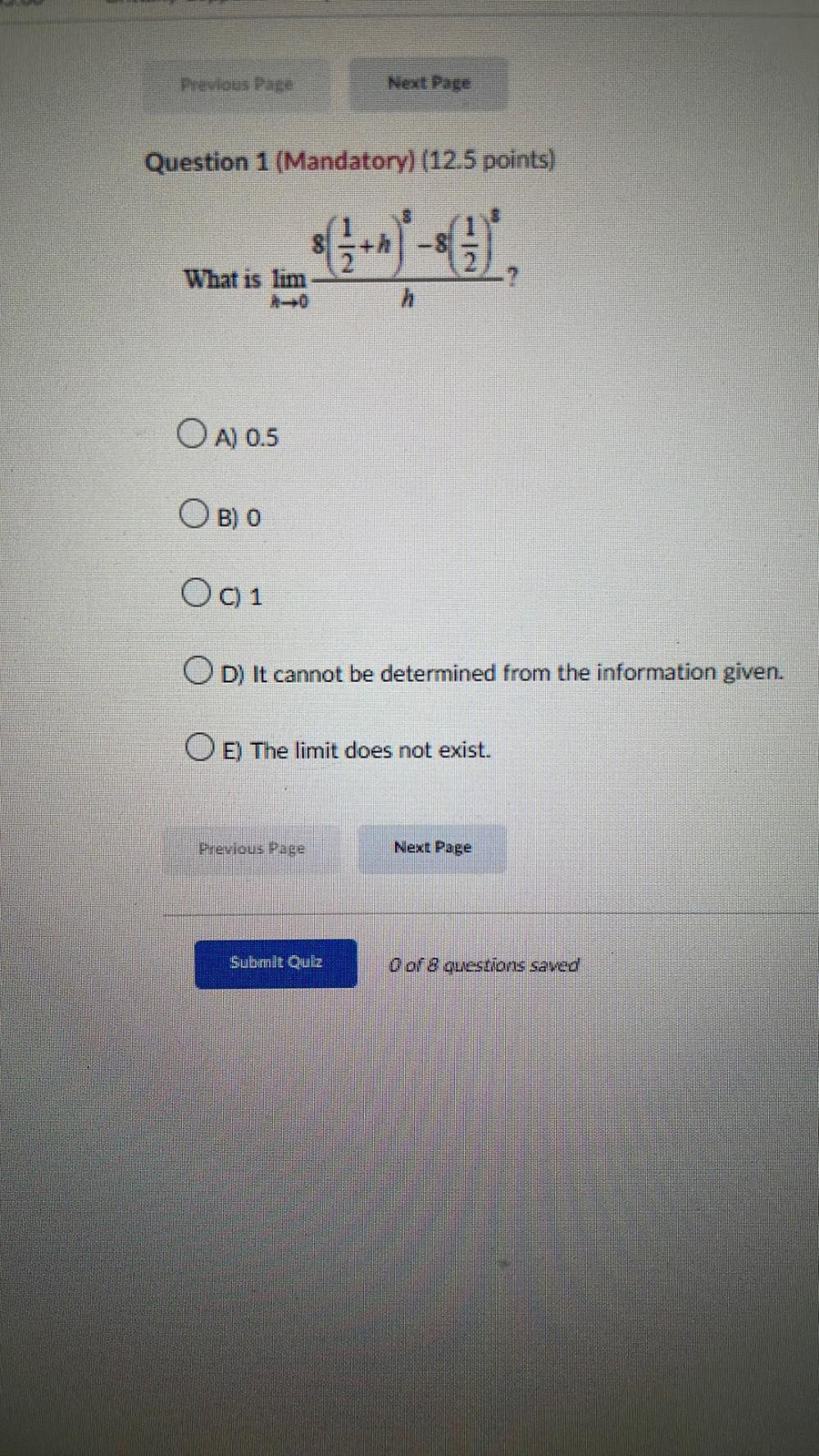
Calculus
Limits & ContinuityWhat is lim h→0 8(1/2+h)⁸ - 8(1/2)⁸ / h
A) 0.5
B) 0
C)1
D) It cannot be determined from the information given.
E) The limit does not exist.

Calculus
Limits & ContinuityUse the definition of the derivative to show f'(x) = 2x + 2 if f(x) = x² + 2x This means the "long way" by substituting into the limit: f'(x) = lim h→0 f(x+h)-f(x) / h

Calculus
Limits & ContinuityShow that f(x) =
{x²-2, x≤1
{2x-3, x>1
is continuous (5 pts) and differentiable (5 pts) at x = 1.
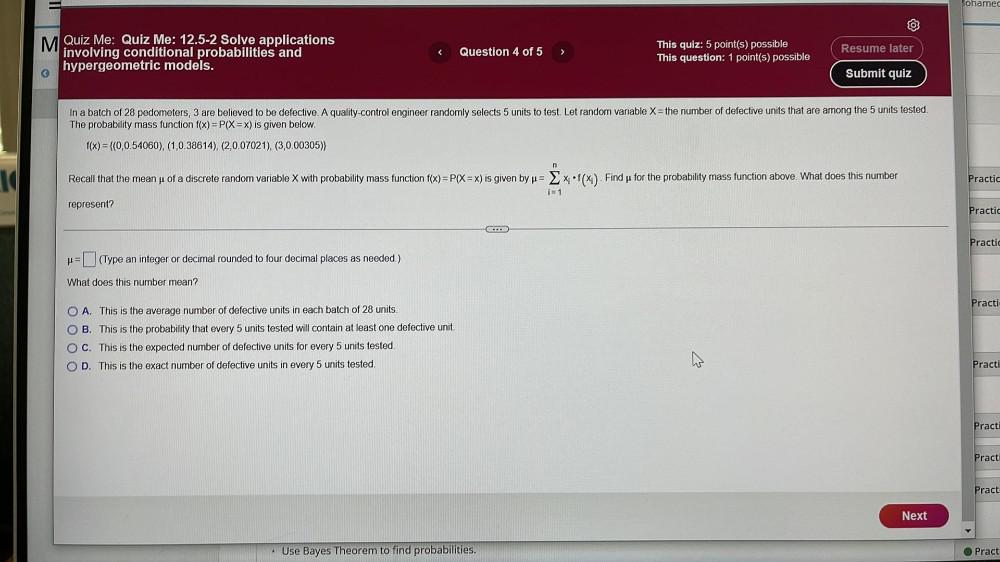
Calculus
Limits & ContinuityIn a batch of 28 pedometers, 3 are believed to be defective. A quality-control engineer randomly selects 5 units to test. Let random variable X= the number of defective units that are among the 5 units tested.
The probability mass function f(x) = P(X=x) is given below.
f(x) = {(0,0.54060), (1,0.38614), (2,0.07021), (3,0.00305)}
Recall that the mean μ of a discrete random variable X with probability mass function f(x)=P(X=x) is given by μ= ΣXi.f(x₁). Find μ for the probability mass function above. What does this number represent?
μ= (Type an integer or decimal rounded to four decimal places as needed.)
What does this number mean?
Practice
A. This is the average number of defective units in each batch of 28 units.
B. This is the probability that every 5 units tested will contain at least one defective unit.
C. This is the expected number of defective units for every 5 units tested.
D. This is the exact number of defective units in every 5 units tested.
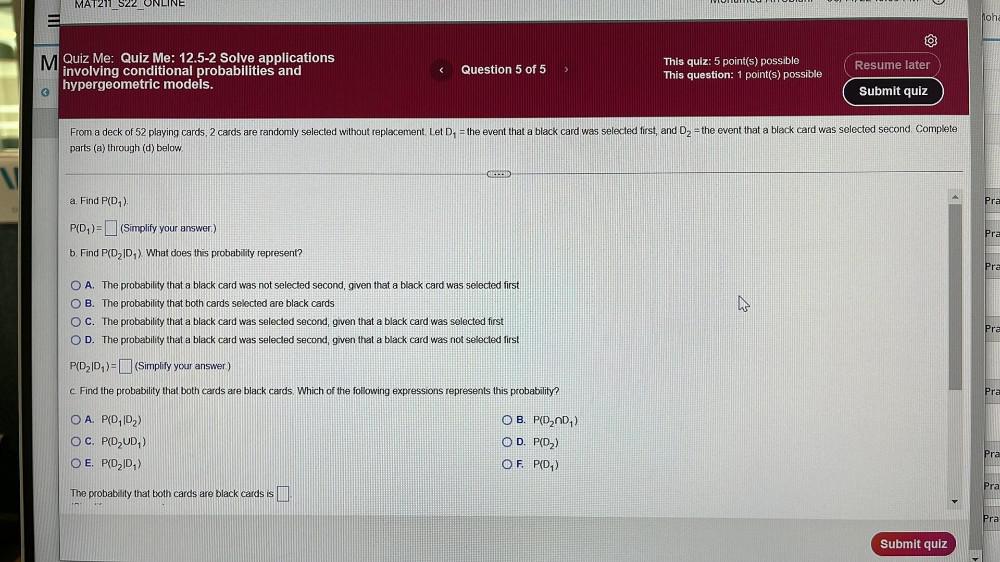
Calculus
Limits & ContinuityFrom a deck of 52 playing cards, 2 cards are randomly selected without replacement. Let D₁ = the event that a black card was selected first, and D₂ = the event that a black card was selected second. Complete parts (a) through (d) below.
a. Find P(D₁).
P(D₁)= (Simplify your answer.)
b. Find P(D₂|D₁). What does this probability represent?
A. The probability that a black card was not selected second, given that a black card was selected first
B. The probability that both cards selected are black cards
C. The probability that a black was selected second, given that a black card was selected first
D. The probability that a black card was selected second, given that a black card was not selected first
P(D₂ID₁)=(Simplify your answer.)
c. Find the probability that both cards are black cards. Which of the following expressions represents this probability?
A. P(D|D2)
B. P(D₂⋂D₁)
C. P(D₂UD₁)
D. P(D₂)
E. P(D₂D₁)
F. P(D₁)
The probability that both cards are black cards is
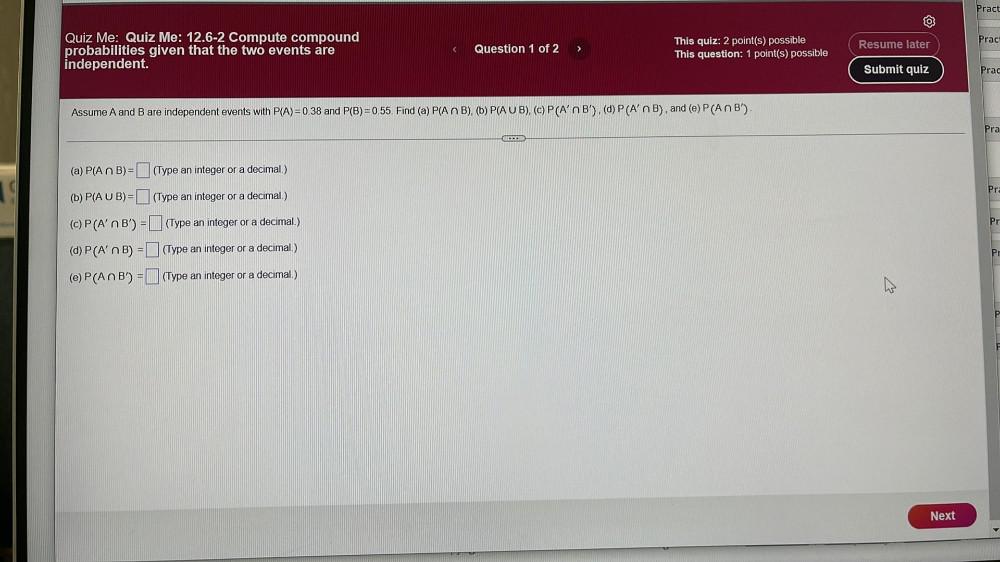
Calculus
Limits & ContinuityAssume A and B are independent events with P(A) = 0.38 and P(B) = 0.55. Find (a) P(An B), (b) P(A U B), (c) P (A' ⋂ B'), (d) P (A' ⋂ B), and (e) P (A ⋂ B').
(Type an integer or a decimal.)
(a) P(A ⋂ B) = (Type an integer or a decimal.)
(b) P(A U B) = (Type an integer or a decimal.)
(c) P (A' ⋂ B') = (Type an integer or a decimal.)
(d) P (A' ⋂ B) = (Type an integer or a decimal.)
(e) P (An B') = (Type an integer or a decimal.)
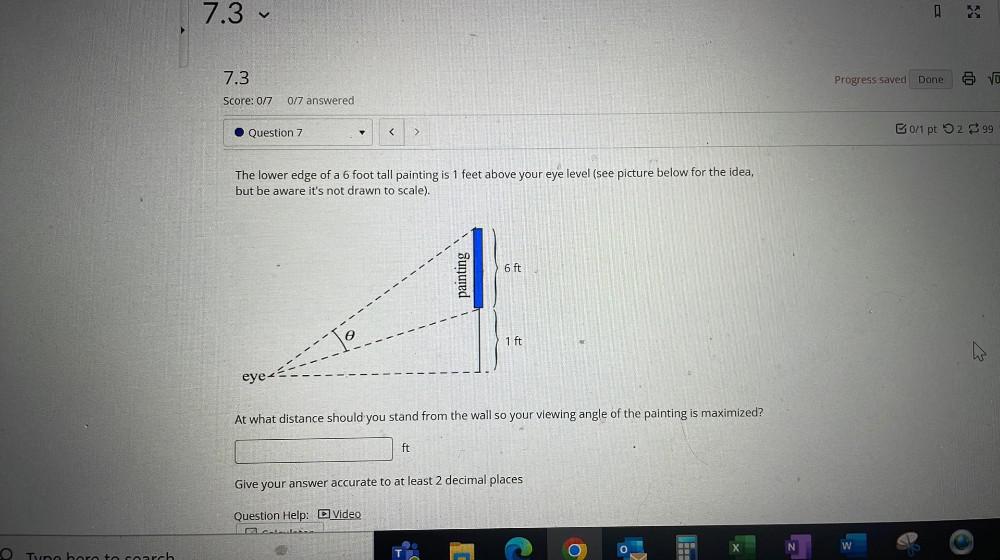
Calculus
Limits & ContinuityThe lower edge of a 6 foot tall painting is 1 feet above your eye level (see picture below for the idea, but be aware it's not drawn to scale).
At what distance should you stand from the wall so your viewing angle of the painting is maximized?
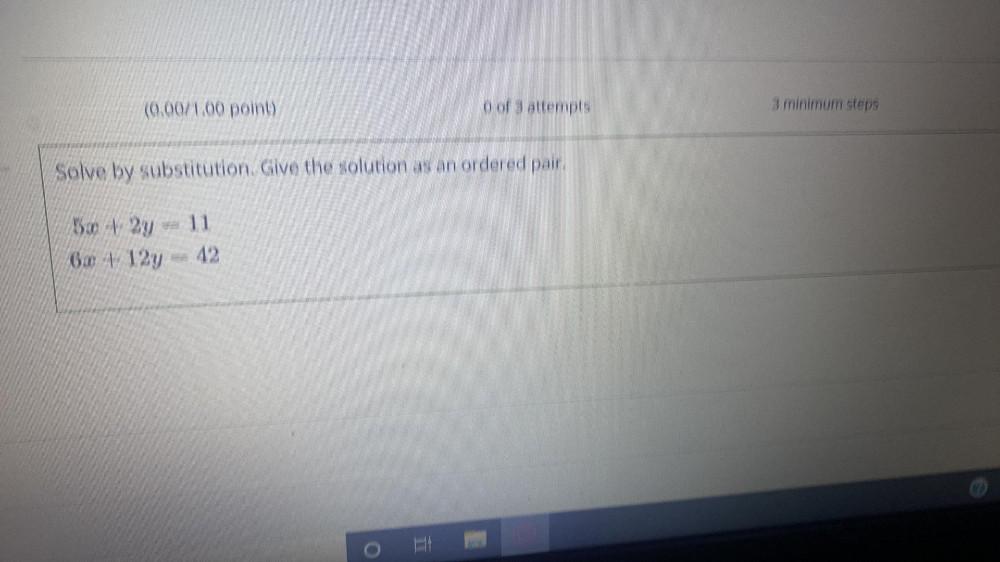
Calculus
Limits & ContinuitySolve by substitution. Give the solution as an ordered pair.
5x + 2y = 11
6x +12y = 42
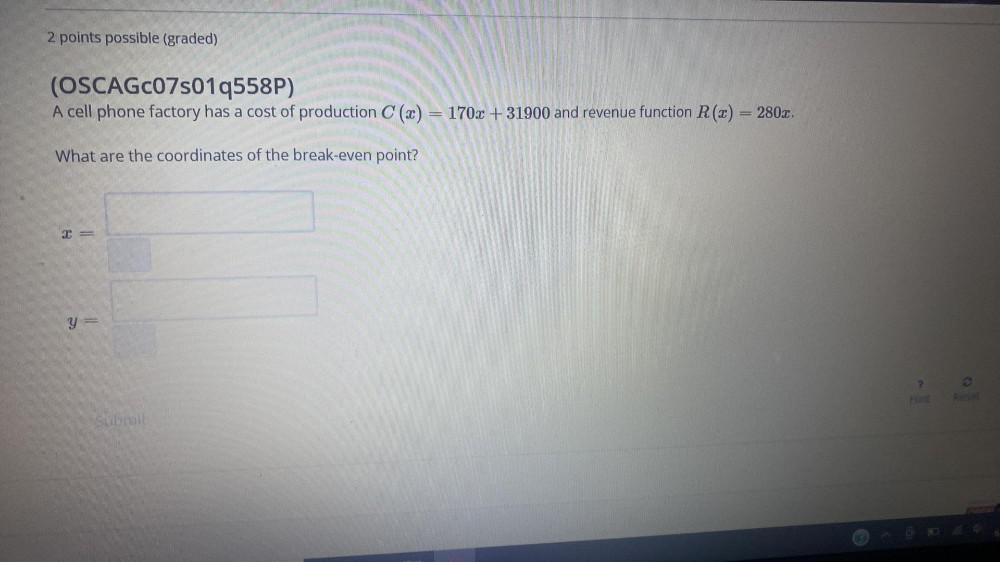
Calculus
Limits & ContinuityA cell phone factory has a cost of production C (x) = 170x + 31900 and revenue function R(x) = 280x.
What are the coordinates of the break-even point?
x=
Y =
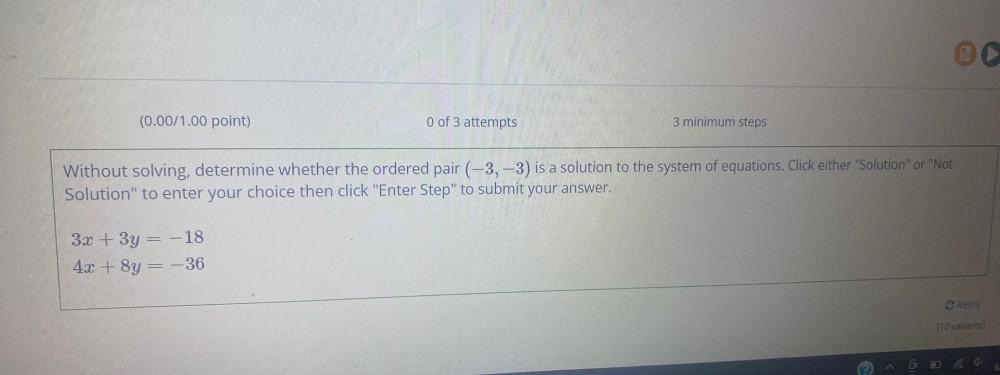
Calculus
Limits & ContinuityWithout solving, determine whether the ordered pair (-3,-3) is a solution to the system of equations. Click either "Solution" or "Not Solution" to enter your choice then click "Enter Step" to submit your answer.
3x + 3y = -18
4x + 8y = -36
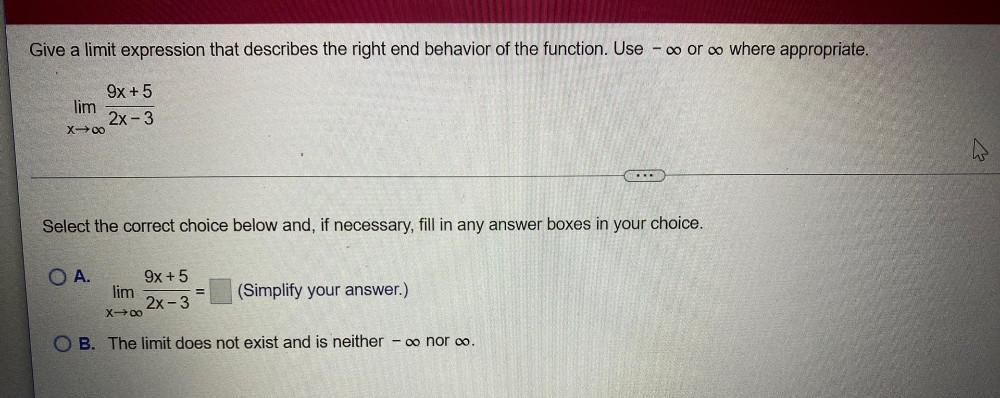
Calculus
Limits & ContinuityGive a limit expression that describes the right end behavior of the function. Use - ∞ or ∞ where appropriate.
lim x→∞ 9x+5/2x - 3
Select the correct choice below and, if necessary, fill in any answer boxes in your choice.
A. lim X→∞ 9x+5/2x - 3 = (Simplify your answer.)
B. The limit does not exist and is neither - ∞ nor ∞.
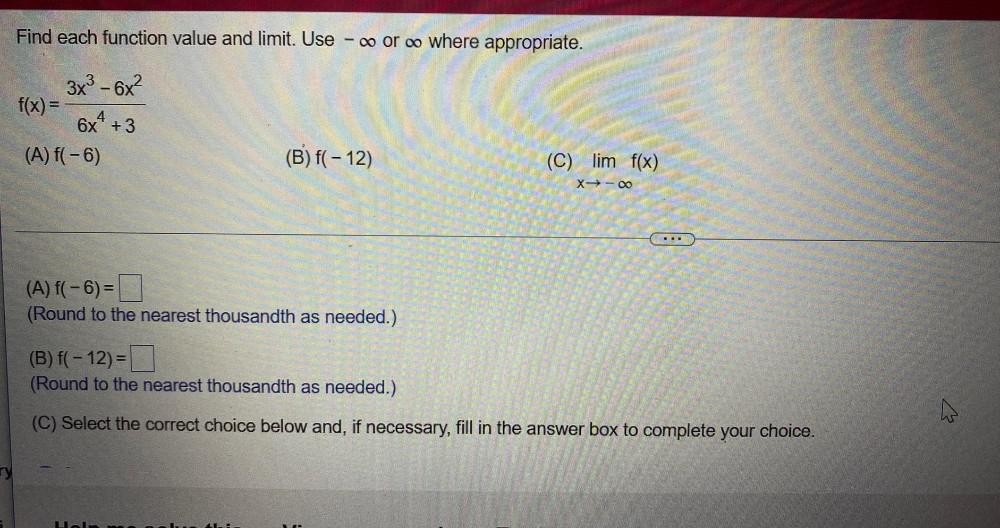
Calculus
Limits & ContinuityFind each function value and limit. Use - ∞ or ∞o where appropriate.
f(x) = 3x³-6x²/6x⁴+3
(A) f(-6)
(B) f(- 12)
(C) lim x→∞ f(x)
(A) f(-6)=
(Round to the nearest thousandth as needed.)
(B) f(-12) =
(Round to the nearest thousandth as needed.)
(C) Select the correct choice below and, if necessary, fill in the answer box to complete your choice.

Calculus
Limits & Continuity2. (20 points) Given the vector field F(x, y) = (ye^sinx cos x, e^sinx) and the curve C with equation y² -√ysin x = 0
a)Show that is conservative and find a potential f(x, y) of F
b)Compute the work done by force F along C from (π/2,1) to (π,0)
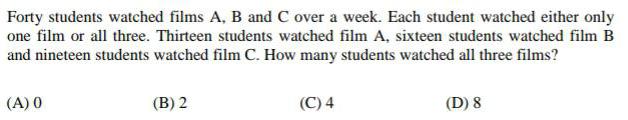
Calculus
Limits & ContinuityForty students watched films A, B and C over a week. Each student watched either only one film or all three. Thirteen students watched film A, sixteen students watched film B and nineteen students watched film C. How many students watched all three films?
(A) 0
(B) 2
(C) 4
(D) 8
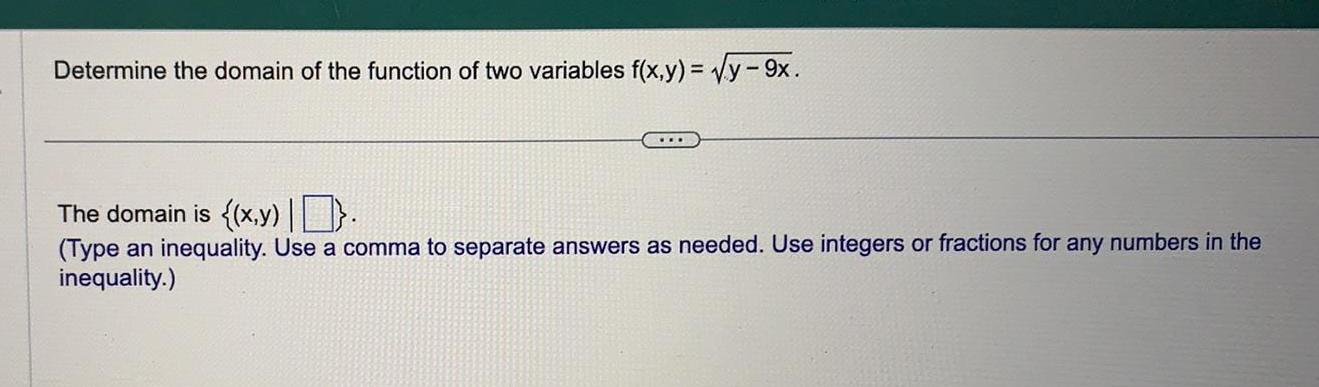
Calculus
Limits & ContinuityDetermine the domain of the function of two variables f(x,y) = √y - 9x. The domain is {(x,y)}. (Type an inequality. Use a comma to separate answers as needed. Use integers or fractions for any numbers in the inequality.)
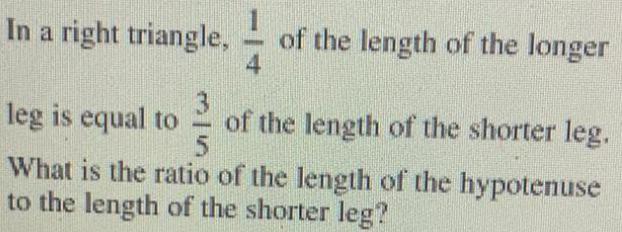
Calculus
Limits & ContinuityIn a right triangle,1/4 of the length of the longer leg is equal to 3/5 of the length of the shorter leg. What is the ratio of the length of the hypotenuse to the length of the shorter leg?

Calculus
Limits & ContinuityA car is purchased for $48,000. Each year it loses 20% of its value. After how many years will the car be worth $13,100 or less? (Use the calculator provided if necessary.)
Write the smallest possible whole number answer

Calculus
Limits & ContinuityWhat is the range of the secant function?
all real numbers
all real numbers, except odd multiples of (90)⁹
all real numbers greater than or equal to 1 or less than or equal to -1
all real numbers from -1 to 1, inclusive

Calculus
Limits & Continuitycot (θ) Suppose π ≤ ≤ 3π/2.
If tan (θ)=, what are sin (θ), cos (θ), sec(θ), csc (θ), and cot (θ)?
Give exact answers for each trigonometric function.

Calculus
Limits & ContinuityFind the exact value of the expression: sin(285°)
The final solution needs to be simplified for full credit.

Calculus
Limits & ContinuityIt is estimated that years from now the population of a city will be P(t)=10(60+3t)² - 1600t.
Step 2 of 2: Find the rate of change in population in 6 years.
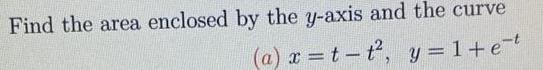
Calculus
Limits & ContinuityFind the area enclosed by the y-axis and the curve
(a) x = t-t², y = 1 + e^-t
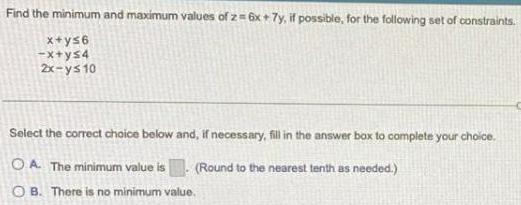
Calculus
Limits & ContinuityFind the minimum and maximum values of z= 6x + 7y, if possible, for the following set of constraints.
x+y≤6
-x+y≤4
2x-y≤10
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
(Round to the nearest tenth as needed.)
A. The minimum value is
B. There is no minimum value.
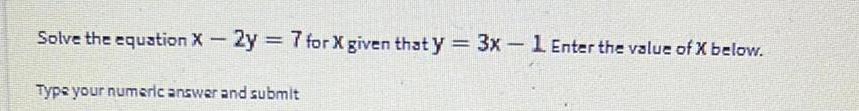
Calculus
Limits & ContinuitySolve the equation x - 2y = 7 for X given that y = 3x - 1 Enter the value of x below.