Matrices & Determinants Questions and Answers

Algebra
Matrices & DeterminantsSuppose you make a 4-minute local call using a calling card and are charged 7.6 cents. The cost of a local call
varies directly with the length of the call. How much more will it cost to make a 30-minute local call?
Select one:
O a.
More than $0.50.
Ob.
$0.50
O c. Not enough information is given.
O d. Less than $0.50

Algebra
Matrices & DeterminantsA personal account earmarked as a retirement supplement contains $342,400. Suppose $300,000 is used to establish an annuity that earns 4%, compounded quarterly, and pays $6500 at the end of each quarter. How long will it be until the account balance is $0? (Round your answer UP to the nearest quarter.) __ quarters
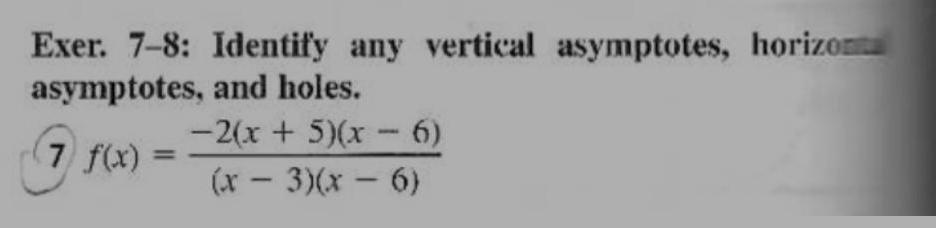
Algebra
Matrices & DeterminantsExer. 7-8: Identify any vertical asymptotes, horizo
asymptotes,
and holes.
-2(x + 5)(x-6)
(x - 3)(x - 6)
(7 f(x) =
=

Algebra
Matrices & DeterminantsSOLVE, GRAPH AND WRITE IN INTERVAL NOTATION
-3 ≤2x+1≤7
-10<2(3x+5) <16
13> 3x+4>-2
-2<-x-5<1

Algebra
Matrices & DeterminantsUse matrices to solve the system of linear equatio
W
of the parameter a.)
(2x
(x, y, z)
www
www
www
2y -
Sy
3z
318,408,144
X
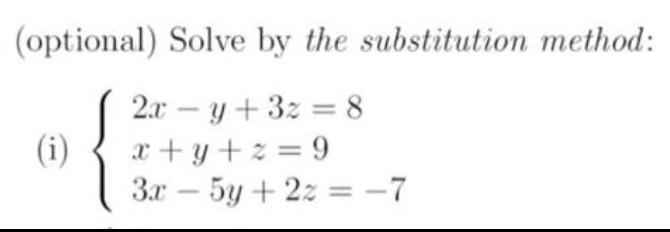
Algebra
Matrices & Determinants(optional) Solve by the substitution method:
2xy +32 = 8
x+y+z=9
3x - 5y + 2z = -7
(i)

Algebra
Matrices & DeterminantsFind the characteristic equation, the eigenvalues,
and bases for the eigenspaces of the following matrix:
6 4 -9
A 0-3 0
1
0 -4
The characteristic equation is
NOTE: Enter the eigenvalues in increasing order.
Eigenvalues
A =
Bases for the eigenspaces
Choose one
Choose one
= 0

Algebra
Matrices & DeterminantsSolve the system of equations by any method.
-4x+8y = 36
x-2y=-9
Enter the exact answer as an ordered pair, (x, y).
If there is no solution, enter NS. If there is an infinite number of solutions, enter the general solution as
an ordered pair in terms of x.
Include a multiplication sign between symbols. For example, a * x.

Algebra
Matrices & DeterminantsThe
following is a conic section with a focus
at the origin. Please classify the conic
section and provide the polar and
rectangular equations.
1) eccentricity: 0.5, vertices: (0, 4/7), (0, -4)
0.7, vertices: (14/19, 0),
2) eccentricity:
(-14/5, 0)

Algebra
Matrices & Determinantssolve the linear system
X, X, +5X, - X =0
x₁ + x₂ -2x, +3x₁ = 0
3x, x₂ +8x₂ + x₁ = 0
x, +3x₂ -9x, +7x₁ = 0

Algebra
Matrices & DeterminantsGiven the linear system:
-x+y+2z = a
2x-1y+Bz = 3
1x-ly+2z=3
Find the values of a and ß, if any, such that the system:
a) has one single solution, and give the solution.
b) has infinite solutions, and give the solutions.
c) has no solutions.

Algebra
Matrices & DeterminantsUse the backward substitution method to solve the system of equations. If the system is inconsistent, explain. If the system is consistent but has infinite solutions, write correct parametric equations. Make sure you label each step by showing the corresponding correct row operations in symbolic form as shown in class. 20x-10y- 5z = 25 -8x+4y+2z=10 -x+3y+4z=-3

Algebra
Matrices & DeterminantsLet L : R² → R³ be the function defined by L. ([*2)) =
1) Show that L is a linear transformation
2) Find ker(L)
3) Find range (L)
4) If S = span{e₁,e₂} find L(S)
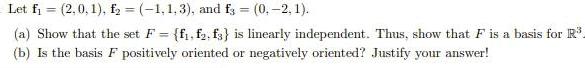
Algebra
Matrices & DeterminantsLet f₁ = (2,0,1), f₂ = (-1,1,3), and f = (0, -2, 1).
(a) Show that the set F= {f₁.f₂. fs} is linearly independent. Thus, show that F is a basis for R³.
(b) Is the basis F positively oriented or negatively oriented? Justify your answer!
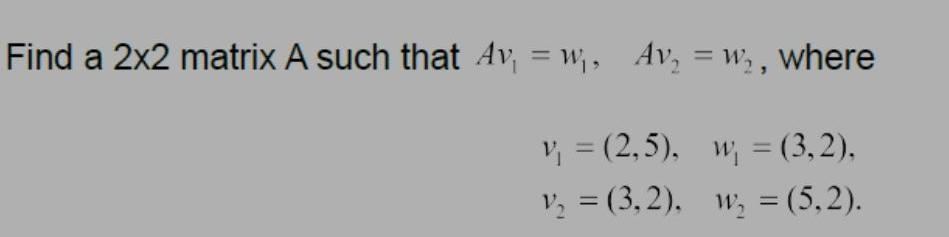
Algebra
Matrices & DeterminantsFind a 2x2 matrix A such that Av₁ = w₁, Av₁ = W₂, where
v₁ = (2,5), w₁ = (3,2).
v₂ =(3,2),
W₂ = (5,2).

Algebra
Matrices & DeterminantsIf one of the eigenvalues of an n x n matrix A is 0, then which of the following statements must be true?
A is not diagonalisable.
The determinant of A is 0.
The column space of A is n-dimensional.
The solution to Ax=b is unique for all bR".
![The goal of this problem is to fit a quadratic function of the form f(x) = c₁x² + ₂x to the data points
(-3,-82), (0, -1), (1, -2), (3, -82), using least squares.
(a) The problem is equivalent to finding the least squares solution to the system Xc = y where
X =
C2
||
3
(b) Find the coefficients of the best fit by finding the least squares solution to the system in part (a)
C1
||
y =
and c = [C₁, C₂]](https://media.kunduz.com/media/sug-question/raw/84081834-1660462614.5845098.jpeg?w=256)
Algebra
Matrices & DeterminantsThe goal of this problem is to fit a quadratic function of the form f(x) = c₁x² + ₂x to the data points
(-3,-82), (0, -1), (1, -2), (3, -82), using least squares.
(a) The problem is equivalent to finding the least squares solution to the system Xc = y where
X =
C2
||
3
(b) Find the coefficients of the best fit by finding the least squares solution to the system in part (a)
C1
||
y =
and c = [C₁, C₂]

Algebra
Matrices & DeterminantsComplete the analytic proof for the following.
2. The line segments that join the midpoints of the opposite sides of a quadrilateral bisect each
other.

Algebra
Matrices & DeterminantsCase Study - Math in Animal Science
5. Cattle feeds are specifically formulated to meet the nutritional needs of the cattle. A rancher wants to formulate
2,400 pounds of feed containing 14% crude protein using corn (8.8% crude protein) and a protein supplement (38%
crude protein). How many pounds of each should the rancher use to make the feed mix? Setup a system of equations
and solve. Round your answers to one decimal place and label them.

Algebra
Matrices & Determinantsdescribe each dilation and reflection as it
relates to the parent function y=-6x

Algebra
Matrices & Determinantsf
First find f+g, f-g, fg and Then determine the domain for each function.
g
f(x) = 4x² - 15x -54, g(x)=x-6
(f+g)(x) = (Simplify your answer.)

Algebra
Matrices & DeterminantsFifteen years after investing $20,000, a retired couple notices that their investment is worth $28,250 (including simple interest). Find the annual interest rate their money earned during that time. Round to the nearest tenth of a percent.

Algebra
Matrices & DeterminantsSolve the following system of linear equations.
x1 + x2 + 2x3 = 1
x1 + 2x2 - x3 = -2
x1+ 3x2 + x3 = 5.

Algebra
Matrices & DeterminantsUse Solver to solve this problem
Consider the linear programming problem.
Maximize : 6x + 5y + 4z
Subject to:
2x +y +z ≤180
x+3y+2z ≤ 300
2x+y+2z ≤ 240
x ≥ 0, y 20, z 20
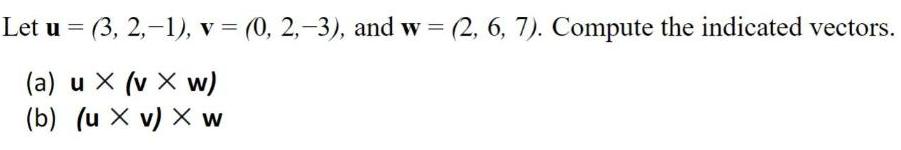
Algebra
Matrices & DeterminantsLet u =(3, 2,-1), v = (0, 2,-3), and w=(2, 6, 7). Compute the indicated vectors.
(a) u x (v Xw)
(b) (u X v) X w

Algebra
Matrices & DeterminantsFind a unit vector orthogonal to both u and v.
u = -3i+2j+ 5k
v = 1/2i - 3/4j +1/10k

Algebra
Matrices & DeterminantsGiven A={{11,3,4},{-9,1,-5},{-12,-2,-5}} Observe that the first column plus twice the second column equal the third column. Find a nontrivial solution Ax=0

Algebra
Matrices & DeterminantsFor questions 8 through 10, consider the function f(x) = 4x³-7x-3.
Lasitsmit pidus ort robizu
voiled 20 slo dergelus?
8. Use the Rational Zeroes Theorem to list all the possible rational zeroes. 02
9. a. Use synthetic division to evaluate f(5). Show your work below.
b. 1. Is 5 an upper bound on the real zeroes of f(x)?
2. How do you know?
c. 1. Is 5 a lower bound on the real zeroes of f(x)?
2. How do you know?
mol bono
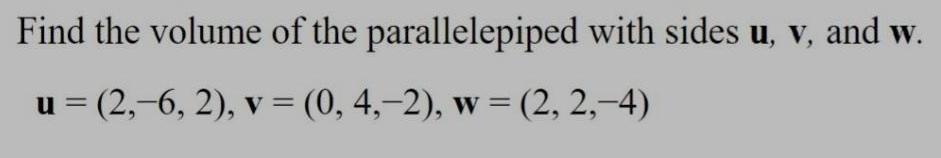
Algebra
Matrices & DeterminantsFind the volume of the parallelepiped with sides u, v, and w.
u = (2,−6, 2), v = (0, 4,−2), w = (2, 2,-4)
Algebra
Matrices & DeterminantsSolve the system of linear equations by graphing.
y = - 4x
2x+y = -2
Use the graphing tool to graph the system.
Click to
enlarge
graph
C
Points: 0 of 1
Q
Q
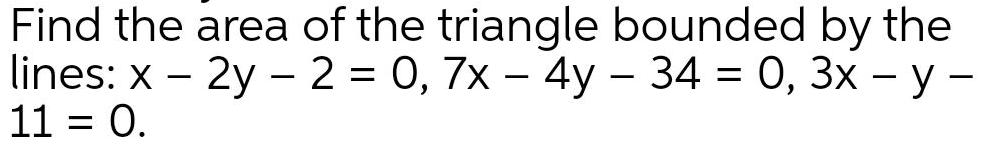
Algebra
Matrices & DeterminantsFind the area of the triangle bounded by the
lines: x - 2y - 2 = 0, 7x - 4y - 34 = 0, 3x-y-
11 = 0.
![Which of the following statement(s) is (are) true?
●
1.
B)
A) I and II
C) 1
The set of all 2x2 matrices of the form [] with the standard operations is a vector
space
The set of all 2x2 matrices of the form with the standard operations is a vector
II and III
D) III
space
The set of all 2x2 matrices of the form with
space
E) II
with the standard operations is a vector](https://media.kunduz.com/media/sug-question/raw/83991048-1660408291.332651.jpeg?w=256)
Algebra
Matrices & DeterminantsWhich of the following statement(s) is (are) true?
●
1.
B)
A) I and II
C) 1
The set of all 2x2 matrices of the form [] with the standard operations is a vector
space
The set of all 2x2 matrices of the form with the standard operations is a vector
II and III
D) III
space
The set of all 2x2 matrices of the form with
space
E) II
with the standard operations is a vector
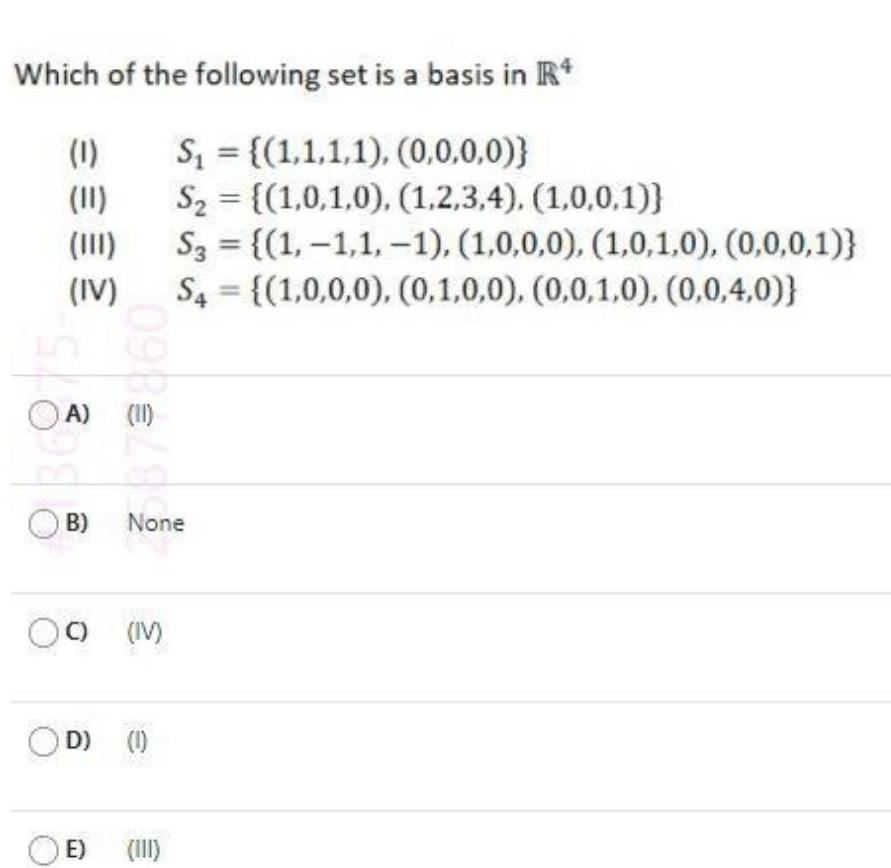
Algebra
Matrices & DeterminantsWhich of the following set is a basis in R*
(1)
S₁ = {(1,1,1,1), (0,0,0,0)}
S₂ = {(1,0,1,0), (1,2,3,4), (1,0,0,1))
S3 = {(1,-1,1, -1), (1,0,0,0), (1,0,1,0), (0,0,0,1))
S4= {(1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,4,0))
(IV)
OA) (II)
B) None
O) (M)
OD) (1)
E) (III)
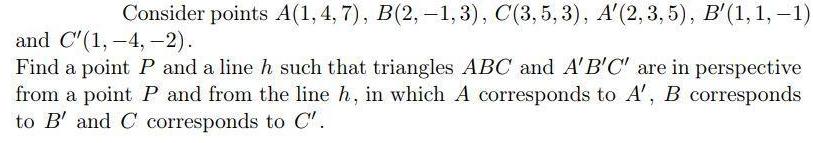
Algebra
Matrices & DeterminantsConsider points A(1,4,7), B(2, -1,3), C(3, 5, 3), A'(2,3,5), B'(1, 1, −1)
and C'(1, -4,-2).
Find a point P and a line h such that triangles ABC and A'B'C' are in perspective
from a point P and from the line h, in which A corresponds to A', B corresponds
to B' and C corresponds to C'.

Algebra
Matrices & DeterminantsOn the graph of f(x) = sinr and the domain 0 < x < 2, for which of the following intervals is f(z) strictly decreasing?
Choose all correct answers.
Select all that apply:
□ (0,5)
(1)
□ (1,4)
(3, 2)

Algebra
Matrices & Determinants(1 point) Find the matrix A of the linear transformation T from R2 to R² that rotates any vector through an angle of 135° in the counterclockwise
direction.
E
![The number of hours of daylight in Boston is given by
[365 (x-79)] + 12,
h(x) = 3 sin
where x is the number of days after January 1. (1 point for each part) (You can use a calculator)
a) What is the period of this function?
b) How many days after January 1 is the longest day of the year?
c) How many hours of daylight are there on the longest day of the year?
d) How many days after January 1 is the shortest day of the year?
e) How many hours of daylight are there on the shortest day of the year?](https://media.kunduz.com/media/sug-question/raw/83883497-1660396502.9085052.jpeg?w=256)
Algebra
Matrices & DeterminantsThe number of hours of daylight in Boston is given by
[365 (x-79)] + 12,
h(x) = 3 sin
where x is the number of days after January 1. (1 point for each part) (You can use a calculator)
a) What is the period of this function?
b) How many days after January 1 is the longest day of the year?
c) How many hours of daylight are there on the longest day of the year?
d) How many days after January 1 is the shortest day of the year?
e) How many hours of daylight are there on the shortest day of the year?

Algebra
Matrices & Determinants5. You are given three vectors below. It is known that these vectors are on the same plane. Determine the value of t=? (15 pts)
183
A) t = -4 B) t=0 C) t =4 D) any value of t satisfies E) More than one answers are correct F) None of them.

Algebra
Matrices & DeterminantsIs q=
0.5
0.6
a steady-state vector for A=
0.4 0.5
0.6 0.5
? Justify your answer.
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
OA. The vector q is a steady state vector because the sum of its entries is 1 and Aq=q.
OB. The vector q is not a steady state vector because Aq=
(Type an integer or decimal for each matrix element.)
OC. The vector q is not a steady state vector because the sum of its entries is
(Type an integer or a decimal.)

Algebra
Matrices & DeterminantsIn class, we discussed how a point and a nonzero vector emanating from it
completely determine a line. Explain how this affine representation (point plus
vector) is equivalent to those of symmetric equations in space: (x-a)/b = (y-
c)/d = (ze)/f. Provide a concrete example to illustrate your explanation.
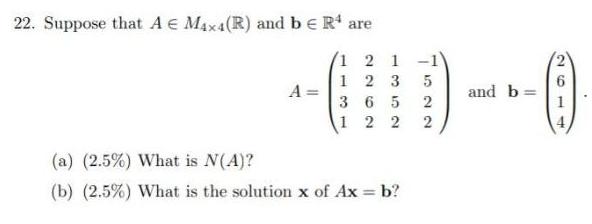
Algebra
Matrices & Determinants22. Suppose that A € M4x4(R) and b € R¹ are
A=
1 2 1 -1
123 5
365 2
122
2
(a) (2.5%) What is N(A)?
(b) (2.5%) What is the solution x of Ax = b?
and b=
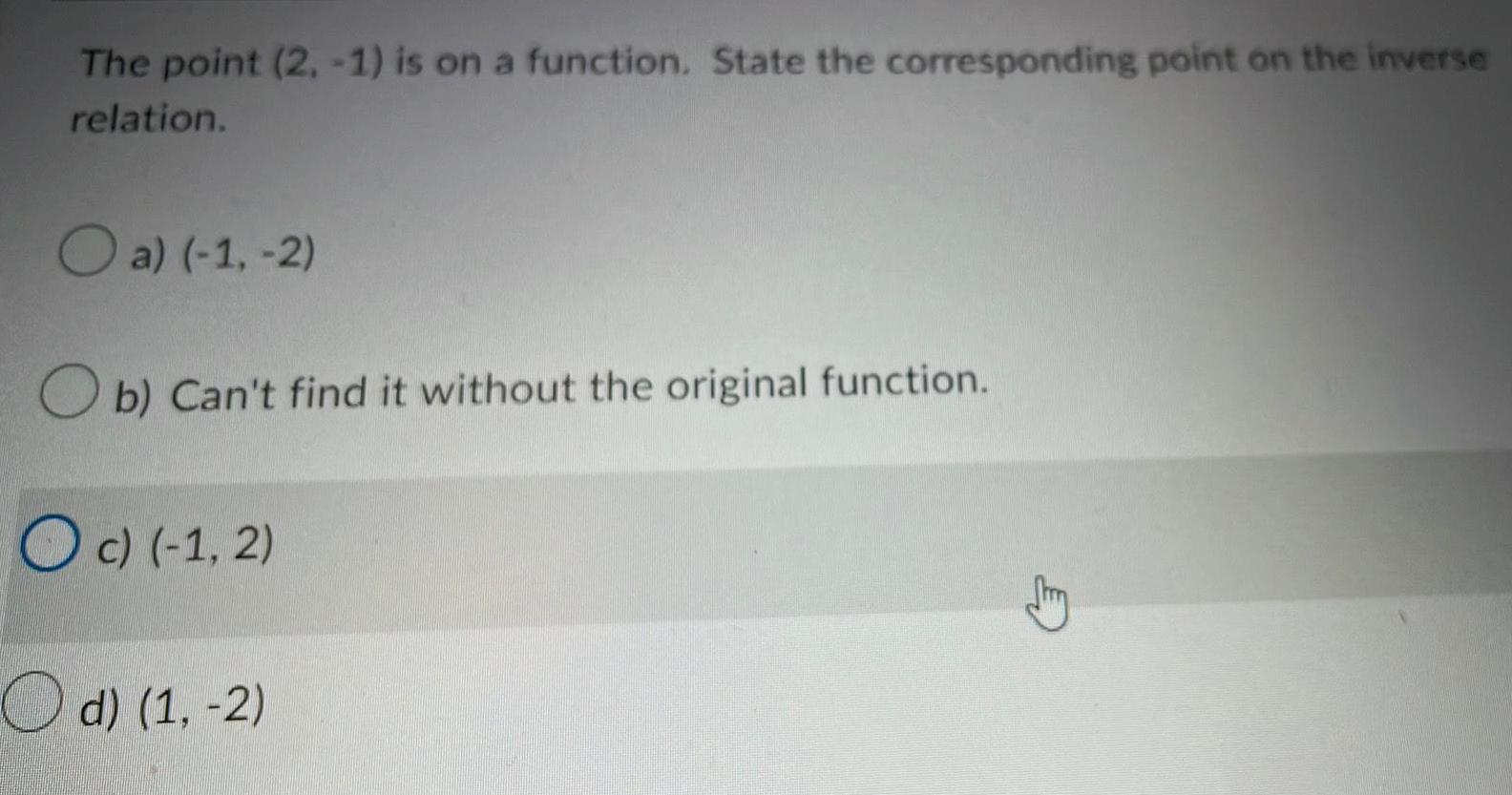
Algebra
Matrices & DeterminantsThe point (2, -1) is on a function. State the corresponding point on the inverse
relation.
a) (-1, -2)
Ob) Can't find it without the original function.
Oc) (-1,2)
d) (1, -2)

Algebra
Matrices & DeterminantsSimplify. Write the answer using positive exponents.
X
What is raising a quotient to a power?
OA. For any numbers a and any integers m and n, (am)" = amn
B. For any numbers a and any integers m and n,
am
an
-5
C. For any numbers a and b, and any integer n,
Use
(8)" =
OD. For any numbers a and b, and any integer n, (ab)" = a^b^.
bn
X
an
b b"
-4)-5
to start simplifying the expression.
=
X
-4-
=am-n
4.0
(3)^=
an
b#0.

Algebra
Matrices & DeterminantsFind the intersection of the following planes by letting z = t.
5x - 4y + z-1 = 0
X-Z+3=0
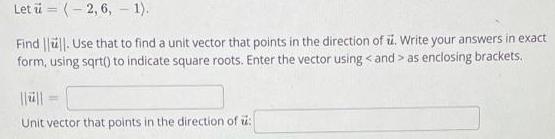
Algebra
Matrices & DeterminantsLet u= (-2, 6, 1).
Find ||u||. Use that to find a unit vector that points in the direction of u. Write your answers in exact
form, using sqrt() to indicate square roots. Enter the vector using <and > as enclosing brackets.
||u||
Unit vector that points in the direction of u

Algebra
Matrices & DeterminantsSolve the system of equations using Gauss-Jordan elimination.
x+2y-z = 0
2x + z = -1
x - y = 1
a. Write the system of linear equations as a matrix equation Ax = b.
b. Determine A-¹ using the Gauss-Jordan method.
c. Solve for x using A-1 and b from above.

Algebra
Matrices & DeterminantsClassify the quadratic form below. Then make a change of variable, x = Py, that transforms the quadratic form into one with no cross-product term. Write the new quadratic form.
-9x1² - 6x₁x2-x₂²
What is the most precise classification for the quadratic form?
A. Indefinite
B. Positive semidefinite
C. Negative definite
D. Positive definite
E. Negative semidefinite
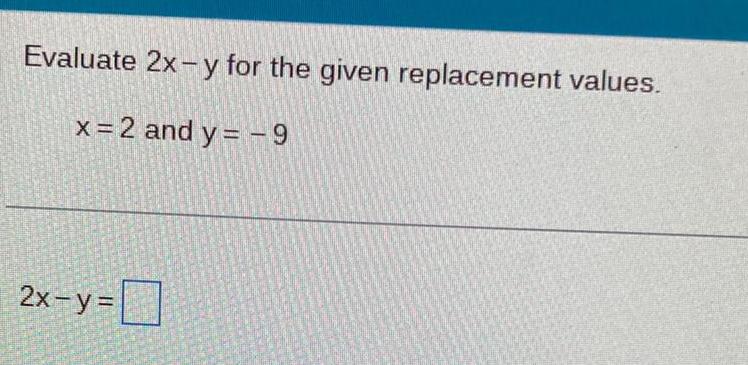
Algebra
Matrices & DeterminantsEvaluate 2x -y for the given replacement values.
x = 2 and y = -9
2x-y=

Algebra
Matrices & Determinantsproducts may differ. Describe qualitatively the solutions to the matrix equation X² - X = O
where X is a (2 x 2) matrix and is the zero matrix. Hint. Set a system of equations.