Matrices & Determinants Questions and Answers

Algebra
Matrices & Determinants1. A student took 60 minutes to answer a combination of 20 multiple-choice and extended-response questions. She took 2 minutes to answer each multiple-choice question and 6 minutes to answer each extended-response question.
a. Write a system of equations in two variables to model the relationship between the number of multiple-choice questions (m) and the
number of extended-response questions (r).
b. How many of each type of question was on the test? Show your work to solve the system.

Algebra
Matrices & DeterminantsShow that AX = XA where is a diagonal matrix whose diagonal entities are eigenvalues A =
And also show that X-¹AX = A
A= λ1 0
λ2
.
.
0 λn
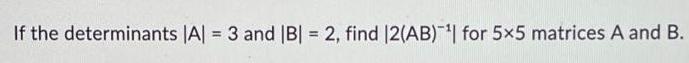
Algebra
Matrices & DeterminantsIf the determinants |A| = 3 and |B| = 2, find |2(AB)¹ for 5x5 matrices A and B.
Algebra
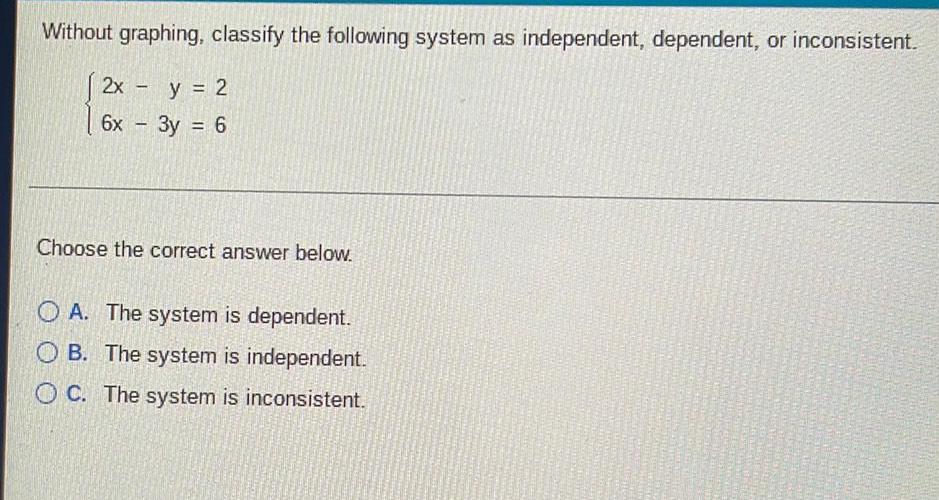
Matrices & DeterminantsWithout graphing, classify the following system as independent, dependent, or inconsistent.
2x - y = 2
6x - 3y = 6
Choose the correct answer below.
A. The system is dependent.
B. The system is independent.
C. The system is inconsistent.
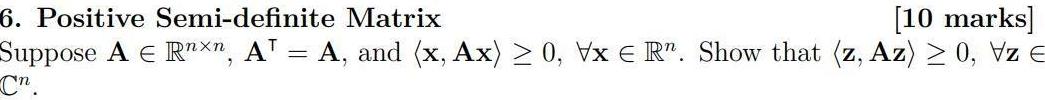
Algebra
Matrices & DeterminantsSuppose A E Rnxn, AT = A, and (x, Ax) ≥ 0, Vx ER". Show that (z, Az) ≥ 0, VzE Cn

Algebra
Matrices & DeterminantsIf the determinants |A| = 3 and |B| = 2, find |2(AB)-¹| for 5x5 matrices A and B.
Algebra
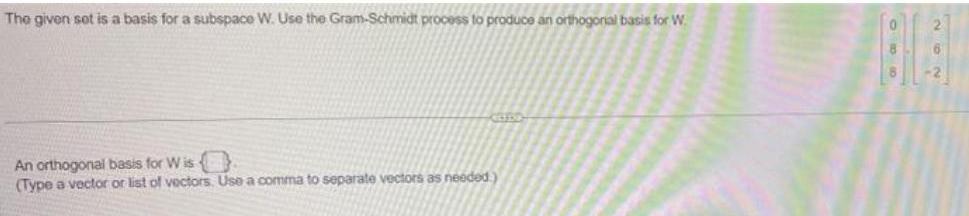
Matrices & DeterminantsThe given sot is a basis for a subspace W. Use the Gram-Schmidt process to produce an orthogonal basis for W An orthogonal basis for Wis
(Type a vector or list of vectors. Use a comma to separate vectors as needed)

Algebra
Matrices & DeterminantsLet V = R³ and let W be a the subspace of all (a, 0, b, 2a + b, -3b). Find a basis for W. Select the correct answer form the options below. W does not have a basis.
S = {(1,0,0,0,0), (0, 1, 0, 0, 0), (0, 0, 1, 0, 0), (0, 0, 0, 0, 1, 0), (0, 0, 0, 0, 1)}
S = {(0,0,1,1,-3), (1,0, 2, 0, -3))
S={(1,0,0,2,0), (0, 0, 1, 1, -3)}
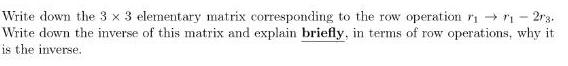
Algebra
Matrices & DeterminantsWrite down the 3 x 3 elementary matrix corresponding to the row operation ₁ → 1-2r3.
Write down the inverse of this matrix and explain briefly, in terms of row operations, why it is the inverse.

Algebra
Matrices & DeterminantsThe x-intercepts of the function f(x) = x^4 + 1 are:
a) 1
b) 1, -1
c) 0
d) there are no x-intercepts for the function

Algebra
Matrices & DeterminantsThe set B=(1-12, 2t+t², 1+t-1²} is a basis for P₂. Find the coordinate vector of p(t) = 1 + 12t+6t² relative to B.

Algebra
Matrices & DeterminantsThe set B=(1-t², 2t+t². 1+t-t2) is a basis for P₂. Find the coordinate vector of p(t) = 1 + 12t+ 6t² relative to B.
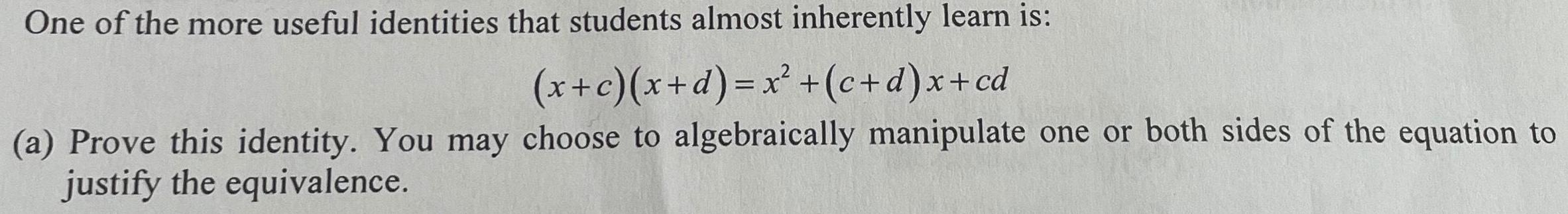
Algebra
Matrices & DeterminantsOne of the more useful identities that students almost inherently learn is:
(x+c)(x+d)=x+(c+d)x+cd
(a) Prove this identity. You may choose to algebraically manipulate one or both sides of the equation to
justify the equivalence.

Algebra
Matrices & DeterminantsFind formulas for the entries of M", where n is a positive integer. (Your formulas should not contain complex numbers.)
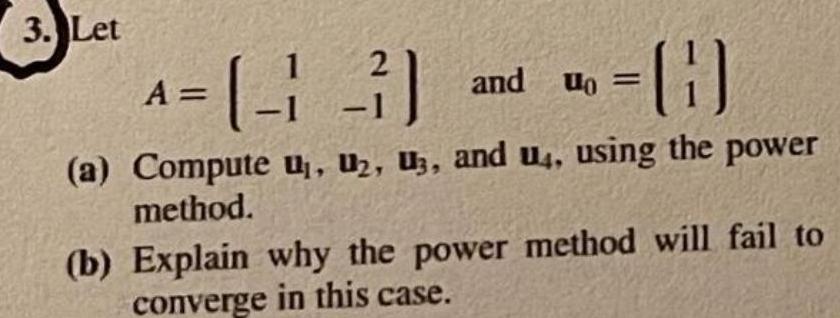
Algebra
Matrices & DeterminantsLet A=| 1 2 and u0= 1
-1-1 1
(a) Compute u₁, U₂, U3, and u, using the power method.
(b) Explain why the power method will fail to converge in this case.

Algebra
Matrices & DeterminantsUse Cramer's rule to solve the system of equations. If D = 0, use another method to determine the solution set.
9x -y + 2z = -25
3x +9y-z = 58
x + 2y +9z = 58

Algebra
Matrices & DeterminantsJed's online music club allows him to download 25 songs per month for $14.99. Additional songs cost $1.29 each. Which inequality represents this situation? Lett be his monthly spending limit and m represent the
total number of songs downloaded.
a. 1.29m St + 10.01
b. 1.29m ≤t + 17.26
c 1.29t m+ 10.01
d. 1.29t≤ m + 17.26

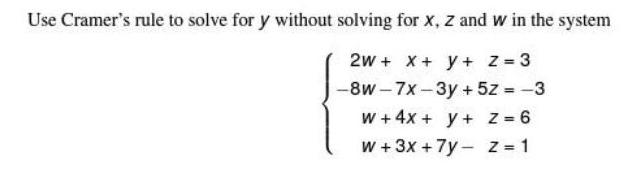
Algebra
Matrices & DeterminantsUse Cramer's rule to solve for y without solving for X, Z and w in the system
2W + x + y + z = 3
-8w-7x-3y + 5z = -3
W + 4x + y +
z = 6
W + 3x + 7y -
Z=1
Algebra
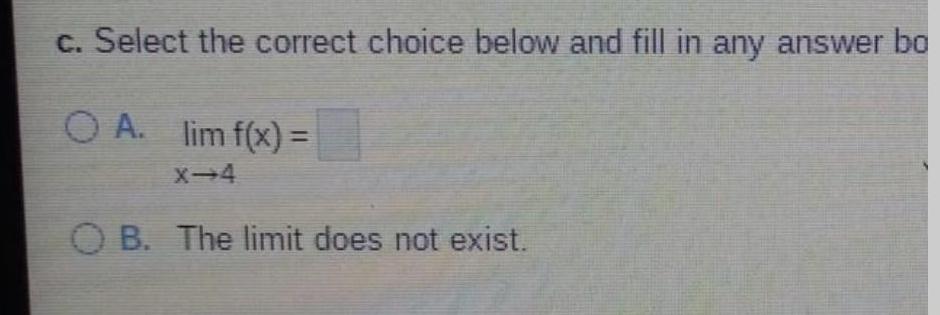
Matrices & Determinantsc. Select the correct choice below and fill in any answer bo
A. lim f(x) =
X-4
B. The limit does not exist.
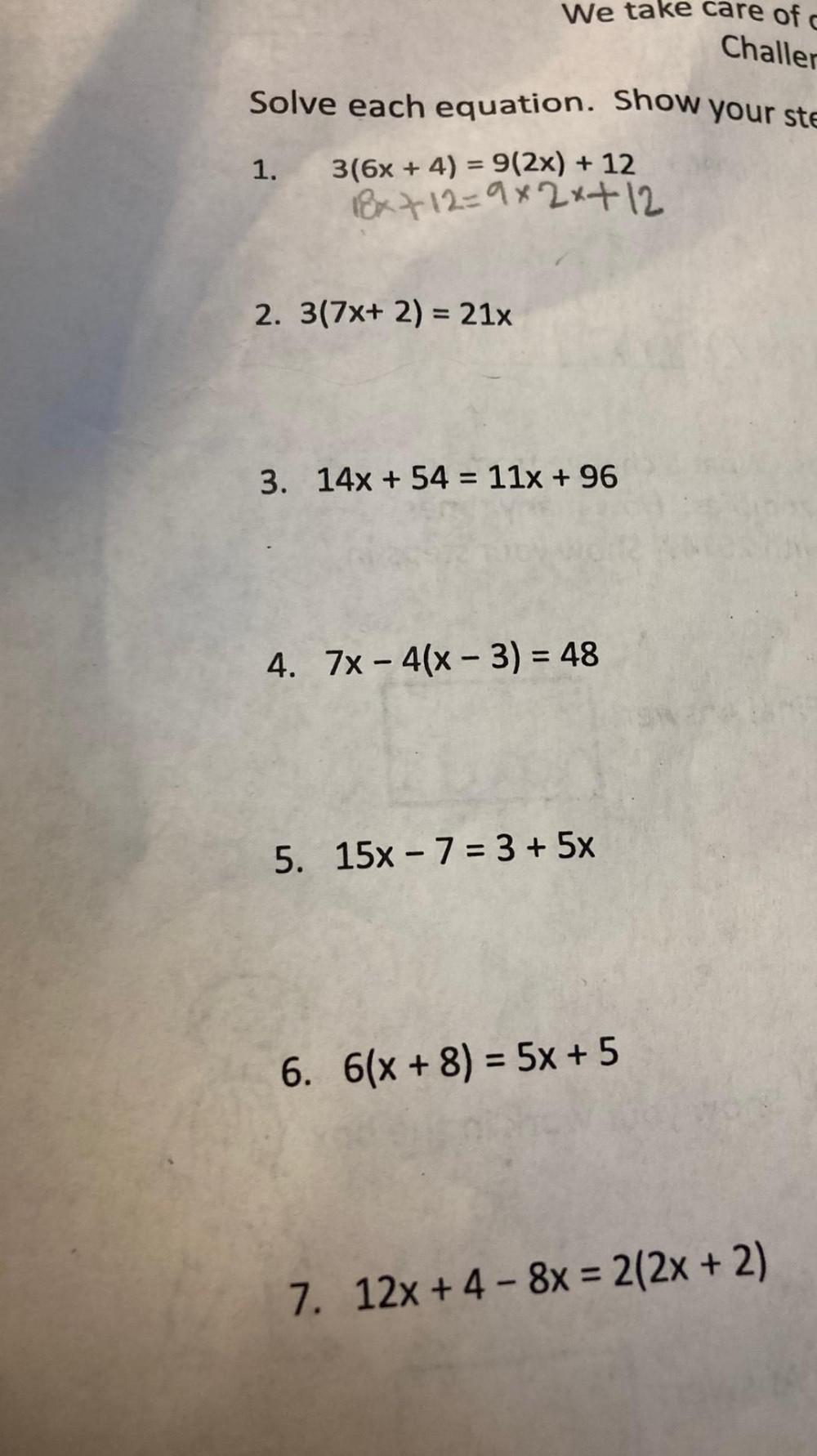
Algebra
Matrices & DeterminantsSolve each equation.
(1) 3(6x + 4) = 9(2x) + 12
(2) 3(7x+ 2) = 21x
(3) 14x + 54 = 11x + 96
(4) 7x - 4(x - 3) = 48
(5) 15x - 7 = 3 + 5x
(6) 6(x + 8) = 5x + 5
(7) 12x + 4 - 8x = 2(2x + 2)

Algebra
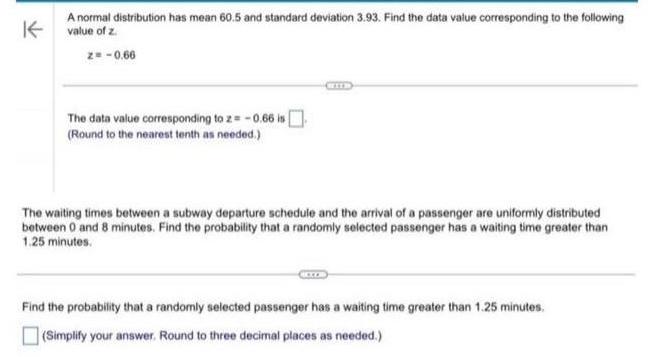
Matrices & DeterminantsA normal distribution has mean 60.5 and standard deviation 3.93. Find the data value corresponding to the following value of z
z= -0.66
The data value corresponding to z=-0.66 is
(Round to the nearest tenth as needed.)
The waiting times between a subway departure schedule and the arrival of a passenger are uniformly distributed between 0 and 8 minutes. Find the probability that a randomly selected passenger has a waiting time greater than 1.25 minutes.
Find the probability that a randomly selected passenger has a waiting time greater than 1.25 minutes.
(Simplify your answer. Round to three decimal places as needed.)
![Write the replacements for y = 1/4 √[6(x-3)] +4 E.G) y -> y - 4 for more information, [6(x-3)] is under the square root. This is for the transformations unit.](https://media.kunduz.com/media/sug-question/raw/84961597-1660123578.117458.jpeg?w=256)
Algebra
Matrices & DeterminantsWrite the replacements for y = 1/4 √[6(x-3)] +4 E.G) y -> y - 4 for more information, [6(x-3)] is under the square root. This is for the transformations unit.
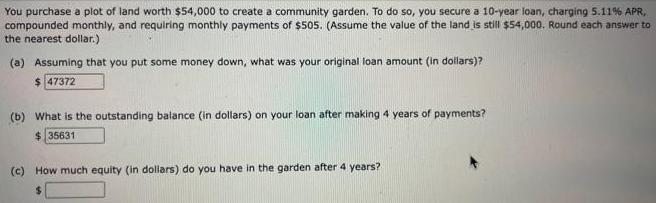
Algebra
Matrices & DeterminantsYou purchase a plot of land worth $54,000 to create a community garden. To do so, you secure a 10-year loan, charging 5.11% APR, compounded monthly, and requiring monthly payments of $505. (Assume the value of the land is still $54,000. Round each answer to the nearest dollar.)
(a) Assuming that you put some money down, what was your original loan amount (in dollars)?
(b) What is the outstanding balance (in dollars) on your loan after making 4 years of payments?
(c) How much equity (in dollars) do you have in the garden after 4 years?
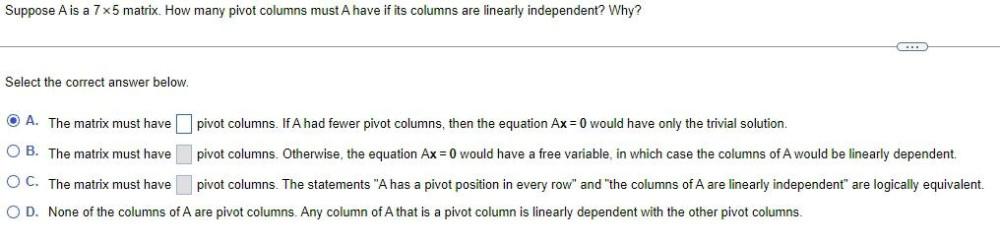
Algebra
Matrices & DeterminantsSuppose A is a 7x5 matrix. How many pivot columns must A have if its columns are linearly independent? Why?
Select the correct answer below.
A) The matrix must have ___ pivot columns. If A had fewer pivot columns, then the equation Ax = 0 would have only the trivial solution.
B) The matrix must have ___ pivot columns. Otherwise, the equation Ax = 0 would have a free variable, in which case the columns of A would be linearly dependent.
C) The matrix must have ____ pivot columns. The statements "A has a pivot position in every row" and "the columns of A are linearly independent" are logically equivalent.
D) None of the columns of A are pivot columns. Any column of A that is a pivot column is linearly dependent with the other pivot columns.
![Algebra
I = a(t)^2 [dx^2 + dy^2 + dz^2] - c^2 dt^2
For this metric, compute the Christoffel coefficients.](https://media.kunduz.com/media/sug-question/raw/78320231-1660071069.4596398.jpeg?w=256)
Algebra
Matrices & DeterminantsAlgebra
I = a(t)^2 [dx^2 + dy^2 + dz^2] - c^2 dt^2
For this metric, compute the Christoffel coefficients.

Algebra
Matrices & Determinants→ →
If { v1, v2 } is a basis for a vector space V, then the dimension of V is:
Select one:
A) 0.
B) 2.
C) 3.
D) 1.
![In the following, is the subset H a subgroup of the given group G?
(a) G = Z6, H = {[0], [2], [4]}
(b) G = S4, H = {e, (1 2 3), (2 4)(1 3), (1 3 2 4), (1 3)}
(c) G = Gl₂ (R),
Remember that Gl₂ (R) is the group of invertible matrices (non-zero determinant)
with the group operation being matrix multiplication.](https://media.kunduz.com/media/sug-question/raw/84950948-1660069538.2294753.jpeg?w=256)
Algebra
Matrices & DeterminantsIn the following, is the subset H a subgroup of the given group G?
(a) G = Z6, H = {[0], [2], [4]}
(b) G = S4, H = {e, (1 2 3), (2 4)(1 3), (1 3 2 4), (1 3)}
(c) G = Gl₂ (R),
Remember that Gl₂ (R) is the group of invertible matrices (non-zero determinant)
with the group operation being matrix multiplication.

Algebra
Matrices & Determinants4. FOOTBALL In a recent NFL season, the Miami Dolphins won 4 games and the Oakland Raiders won 5 games. What is the ratio of wins for the Dolphins to wins for the Raiders?
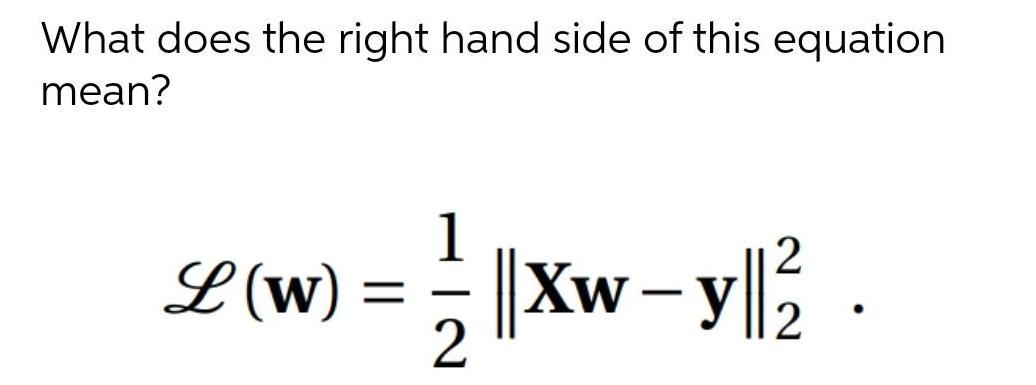
Algebra
Matrices & DeterminantsWhat does the right hand side of this equation
mean?
L (W) ==||Xw-y||²2
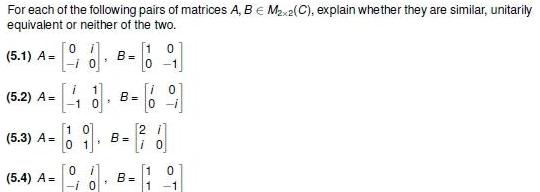
Algebra
Matrices & DeterminantsFor each of the following pairs of matrices A, B € M₂x2(C), explain whether they are similar, unitarily equivalent or neither of the two.
![Simplify the matrices. Remember the order of
operations.
[-1-1 + [-5 -1 . [3 6
-6 3] -4 2] 1 6]](https://media.kunduz.com/media/sug-question/raw/78697346-1660052899.7033503.jpeg?w=256)
Algebra
Matrices & DeterminantsSimplify the matrices. Remember the order of
operations.
[-1-1 + [-5 -1 . [3 6
-6 3] -4 2] 1 6]

Algebra
Matrices & DeterminantsSuppose that v1 = (2, 1,0, 3), v2 = (3,-1, 5, 2), and V3 = (1, 0, 2, 1). Which of the following vectors are in span { v1, v2, v3}? It means write the given vectors as a linear combination of v1, V2, v3 if it's possible.
a) (2, 3, -7,3)
b) (0,0,0,0)
c) (1, 1, 1, 1)
d) (-4, 6, -13, 4)
![Given the matrices A and B shown below, find -1/3A - 6B.
A = [0 -18 B= [4 3
3 6] 0 0]](https://media.kunduz.com/media/sug-question/raw/78697192-1660052830.85328.jpeg?w=256)
Algebra
Matrices & DeterminantsGiven the matrices A and B shown below, find -1/3A - 6B.
A = [0 -18 B= [4 3
3 6] 0 0]
![Given the matrices A and B shown below, find 4(A - B).
A = [-5 3 5]
B = [1 -2 -2]](https://media.kunduz.com/media/sug-question/raw/78697150-1660052785.2641253.jpeg?w=256)
Algebra
Matrices & DeterminantsGiven the matrices A and B shown below, find 4(A - B).
A = [-5 3 5]
B = [1 -2 -2]
![Find the product of the following two matrices
[-2 -1 3 0 [1 3
4 2 - 5 -1] -3 -1
0 1
1 2]](https://media.kunduz.com/media/sug-question/raw/78697298-1660052688.7409027.jpeg?w=256)
Algebra
Matrices & DeterminantsFind the product of the following two matrices
[-2 -1 3 0 [1 3
4 2 - 5 -1] -3 -1
0 1
1 2]
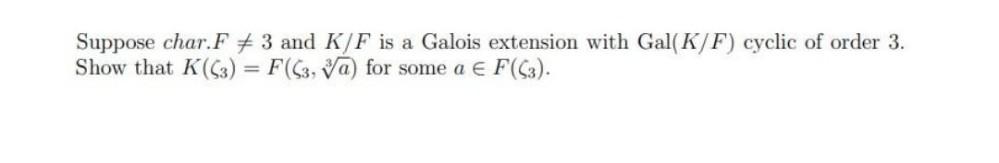
Algebra
Matrices & DeterminantsSuppose char. F + 3 and K/F is a Galois extension with Gal(K/F) cyclic of order 3.
Show that K(C3) = F(C3, ya) for some a E F(C3).

Algebra
Matrices & DeterminantsLet A be an m x n matrix and be R”. Suppose that the column vectors of A form an orthonormal set in RM. Show that the solution of the least squares problem Ax = b is
x = Alb. Also, prove that the orthogonal projection of b onto the column space of A is
AATb.
![Given that A = [-5 8] and B = [-2 10], determine the following.
9 -3 4 2
1) A - B.
2) 3B - 2A.
3) 2A + B.](https://media.kunduz.com/media/sug-question/raw/78865626-1660050973.7676969.jpeg?w=256)
Algebra
Matrices & DeterminantsGiven that A = [-5 8] and B = [-2 10], determine the following.
9 -3 4 2
1) A - B.
2) 3B - 2A.
3) 2A + B.
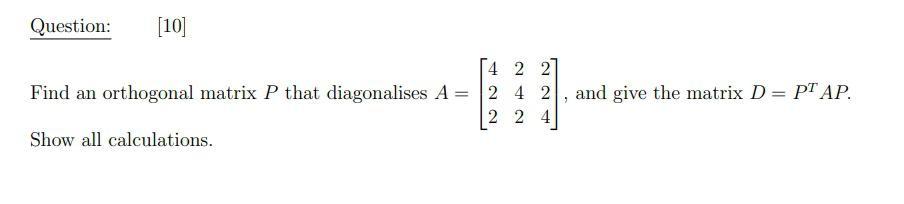
Algebra
Matrices & DeterminantsFind an orthogonal matrix P that diagonalises A= and give the matrix D= PT AP.
Show all calculations.
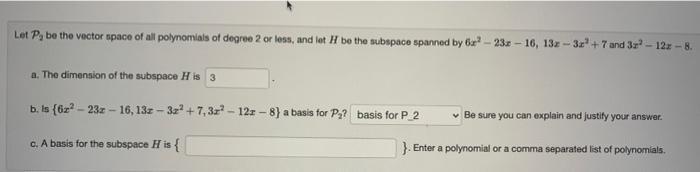
Algebra
Matrices & DeterminantsLet P, be the vector space of all polynomials of degree 2 or less, and let H be the subspace spanned by 6x² - 23² - 16, 13x - 3x² + 7 and 3x² - 12x -8.
a. The dimension of the subspace H is
b. Is {6x² - 23x - 16,13² - 3x²+7, 3x² - 12x-8} a basis for P2 basis for P 2. Be sure you can explain and justify your answer.
c. A basis for the subspace H is {Enter a polynomial or a comma-separated list of polynomials}

Algebra
Matrices & DeterminantsConsider the space V₂(R) of 2-tuple over R, then show that mapping f :V₂, V₂ defined as
f(x,y)=(x cos ϕ – ysin ϕ , xsin ϕ+ y cos ϕ) is an isomorphism
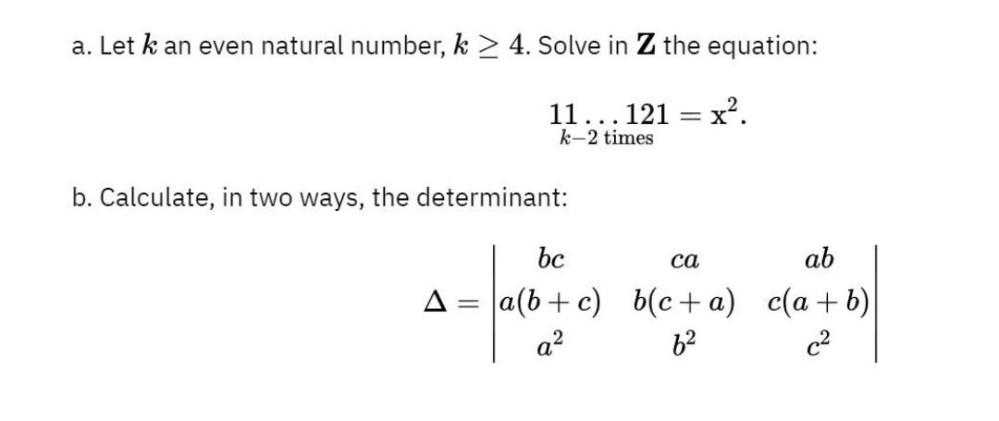
Algebra
Matrices & DeterminantsLet k an even natural number, k > 4. Solve in Z the equation:
11 ... 121 = x².
k-2 times
b. Calculate, in two ways, the determinant:
ca
bc
ab
A= a(b+c) b(c+a) c(a+b)
a
62 c2
=
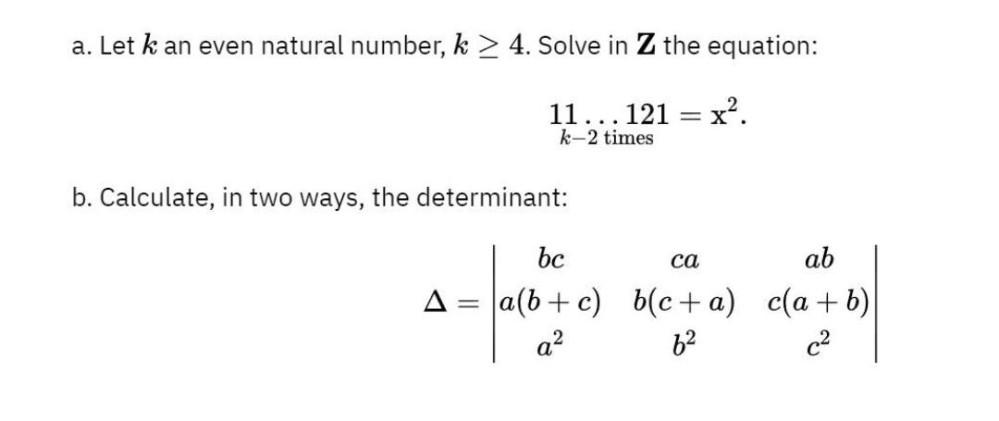
Algebra
Matrices & DeterminantsLet k an even natural number, k ≥ 4. Solve in Z the equation:
11 ......... 121 = x^2.
k-2 times
b. Calculate, in two ways, the determinant:
bc ca ab
△ = a(b +c) b(c + a) c(a+ b)
a^2 b^2 c^2
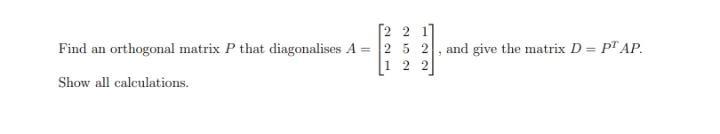
Algebra
Matrices & DeterminantsFind an orthogonal matrix P that diagonalises A = 2 2 1 2 5 2 1 2 2
and give the matrix D=P^TAP. Show all calculations.
![Algebra
If
R= [4 2
2 4]
R is the matrix of a linear transformation consisting of a rotation with angle and a scaling. Determine θ and r](https://media.kunduz.com/media/sug-question/raw/78774507-1660048338.3937757.jpeg?w=256)
Algebra
Matrices & DeterminantsAlgebra
If
R= [4 2
2 4]
R is the matrix of a linear transformation consisting of a rotation with angle and a scaling. Determine θ and r

Algebra
Matrices & DeterminantsFor the following matrix A, Do 3 QR steps to find the approximate values of the eigenvalues of
A=7 2 3
2 10 6
3 6 7