Matrices & Determinants Questions and Answers

Algebra
Matrices & DeterminantsIf u and are linearly independent, then u +, u are also linearly independent.
True
False
Justification:

Algebra
Matrices & DeterminantsA doctor's prescription calls for a daily intake containing 40 mg of vitamin C and 10 mg of vitamin D. Your pharmacy stocks two compounds that can be used: one contains 60% vitamin C and 10% vitamin D, the other 40% vitamin C and 20% vitamin D. How many milligrams of each compound should be mixed to fill the prescription?
To fill the prescription, mix _ mg of the first compound with _ mg of the second compound.

Algebra
Matrices & DeterminantsConsider the following 2*2 system:
2x₁ - x₂ = 1
-x₂ + 2x₂ = 0
a) Rewrite the linear system in the matrix format Ax=b .
b) Solve Ax=b with inner product, and show the row picture for this system.
c) Solve Ax=b with linear combination of columns in matrix A, and show the
column picture for this system.

Algebra
Matrices & Determinantswhy is a system with 50 equations and 51 variables is guaranteed to contain atleast one varable?

Algebra
Matrices & DeterminantsLet a= (1, 2, 5) and b = (3, 3, k).
Find k so that a and b will be orthogonal.

Algebra
Matrices & Determinants(a) The zero vector is orthogonal to all subspaces.
(b) If one of the eigenvalues is zero, the matrix is singular.
(c) Suppose the eigenvalues are 1, 2, 3, the matrix is NOT invertible.
(d) Cramer's rule can be applied to solve Ax=b when A is singular.
(e) If two eigenvalues are the same, the matrix is NOT be diagonalizable.
true or false?

Algebra
Matrices & DeterminantsConsider the set W of all 2 x 2 matrices A such that both (1, 2) and (2, -1) are eigenvectors of A. Prove that W is a subspace of the space of all 2 x 2 matrices and find the dimension of W.

Algebra
Matrices & DeterminantsA real quadratic form in three variables is equivalent to the diagonal form 6y + 3y+ Oy. Then the quadratic form is
Positive semi-definite
Positive definite
Indefinite
Negative definite

Algebra
Matrices & DeterminantsFactor completely, or state that the polynomial is prime.
x² +81
Select the correct choice below and fill in any answer boxes within your choice.
A. x² +81 =
B. The polynomial is prime.


Algebra
Matrices & DeterminantsConstruct a triangle of sides 68, 58 and 42 mm long respectively. Bisect the angles to
find the centre of a circle that will touch the three sides of the triangle. Draw the circle and state its radius.

Algebra
Matrices & DeterminantsTake A= 3, B=1, C=4
Find the orthogonal projection matrix P onto the plane ax + by - cz = 0 (a, b, c are defined in the instructions)

Algebra
Matrices & Determinants1 3 0
0 2 4
1 5 4
1 1-1
a) (7 points) What is the basis for the Row(B)?
3. Let B=
b) (7 points) What is the basis for the left null space of B

Algebra
Matrices & DeterminantsFind an orthogonal basis for the column space of the matrix to the right.
-1 5 5
1 -7 4
1 -1 7
1 -3 -4
An orthogonal basis for the column space of the given matrix is
(Type a vector or list of vectors. Use a comma to separate vectors as needed.)

Algebra
Matrices & DeterminantsSolve the initial va problem xi-Axt) for 120, with x0) (2.1) Classify the nature of the origin as an attractor, repeller, or saddin point of the dynamical system desobed by Find the actions of
greatest attraction and/or repulsion
Solve the initial value problem
Classify the nature of the origin as an attractor, repeller, or saddle point Choose the correct answer below

Algebra
Matrices & DeterminantsSuppose that S={(-1,1,0), (2,2,0), (0,0,3)} is orthogonal basis for a subspace W of R³.
Find the orthogonal projection of u in W where linear combination of the basis vector is
u =(2,1,3).

Algebra
Matrices & DeterminantsConsider the two points A = (-1,2) and B = (1,8) to be points on the curve.
a) Give a possible formula for the function of the form y = a(b) that passes through these two points.
b) Find the domain for the function you have found in part a)
c) Find the asymptote for the function you found in part a)
d) Find the x- and y-intercepts if any.
e) Graph the function you have found in part a).
![Using the matrix U = [U₁U₂U3], determine whether or not the columns of U span R³. Explain your approach.
Solution:
%code](https://media.kunduz.com/media/sug-question/raw/85006843-1660299905.002354.jpeg?w=256)
Algebra
Matrices & DeterminantsUsing the matrix U = [U₁U₂U3], determine whether or not the columns of U span R³. Explain your approach.
Solution:
%code

Algebra
Matrices & DeterminantsWrite the decomposition of a vector
X(-5; 4; 0), (0; 1; 2), (1; 0; 1), F(-1; 1; 0).
Solve the task and fill in the required fields.
Ansver:
A=
A₁=
X₂=
in terms of vectors P. 9,7 if:
X =0

Algebra
Matrices & DeterminantsWrite the decomposition of a vector
X(-5; 4; 0). p(0; 1; 2). ā (1; 0; 1), 7 (-1; 1; 0).
Solve the task and fill in the required fields.
Answer:
4₁=
x₁=
in terms of vectors P. 9, F if:
X =(

Algebra
Matrices & DeterminantsWhat is the solution of the system of linear equations
[a₂x+₂y=b₂
[a₂₁²x + a₂₂y = 6₂
a. The solution of SLE is a set of the ordered pairs of numbers (y; x).
b. The solution of SLE is a set of the ordered pairs of numbers (x, y).

Algebra
Matrices & DeterminantsSolve the following system
{3x + 5y - 7z = 8 (mod 83)
9y + 13z = 13 (mod 83)
8x-9Y+13z=13 (mod83)
7x + 4y + 5z = 15 (mod 83) }

![Let V=R² and B be the ordered basis,
B =[ 1 [-1
1 ] 1]
Find the coordinates of the vector, V = 1
5
relative to B.](https://media.kunduz.com/media/sug-question/raw/83253860-1660247305.9668806.jpeg?w=256)
Algebra
Matrices & DeterminantsLet V=R² and B be the ordered basis,
B =[ 1 [-1
1 ] 1]
Find the coordinates of the vector, V = 1
5
relative to B.

Algebra
Matrices & DeterminantsSelect the inequality that is equivalent to the given inequality.
-7x ≤14
Select an answer and submit. For keyboard navigation, use the up/down arrow keys to select an answer.
a x ≥ -2
b x ≥ 2
c x ≤ -2
d x ≤ 2


Algebra
Matrices & DeterminantsWe have a matrix a find a, b, c such that the matrix is a quadratic form

Algebra
Matrices & DeterminantsDetermine the values of k such that the
system of linear equations does not have a
unique solution. (Enter your answers as a
comma-separated list.)
x + y + kz = 6
x + ky + z = 4
kx + y + z = 3
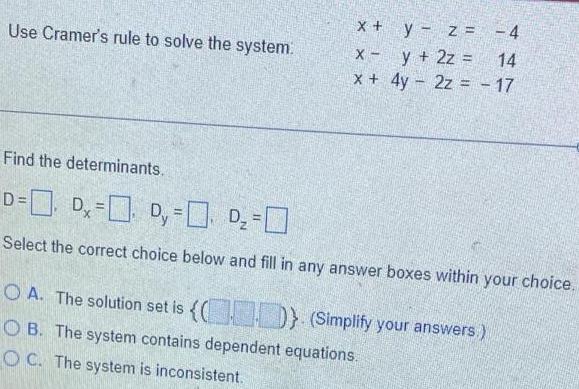
Algebra
Matrices & DeterminantsUse Cramer's rule to solve the system.
X +y-z = -4
x - y + 2z = 14
x + 4y 2z = -17
Find the determinants.
D =
Dx=
Dy=
Dz=
Select the correct choice below and fill in any answer boxes within your choice.
A. The solution set is {} (Simplify your answers.)
B. The system contains dependent equations.
C. The system is inconsistent.

Algebra
Matrices & DeterminantsDescribe how to transform the parent function y = x² to the graph of the function below. Choose all that apply.
y = -2(x + 3)² + 1
Select one or more:
a. reflected across the x-axis
b. compressed by a factor of 2
c. translated 3 units up
d. translated 3 units right
e. translated 1 unit up
f. translated 1 unit right
![Consider the following observation model
where [by 1 b₂ = 5 b3 = 3 b4 =4)= 4)
(a) x2.04, 4.52,-0.24]
(b) x-2.04
(c) x 6.45
(d) x [6.45, 4.52. -0.85]
b₁ = I₁ +23+7²₁
b₂r2-2r3+ n₂
b3=11-423+ng
b₁2r1 +223 +14
What
What is the least square estimate of x= [1,2,3]?](https://media.kunduz.com/media/sug-question/raw/83048359-1660212631.491801.jpeg?w=256)
Algebra
Matrices & DeterminantsConsider the following observation model
where [by 1 b₂ = 5 b3 = 3 b4 =4)= 4)
(a) x2.04, 4.52,-0.24]
(b) x-2.04
(c) x 6.45
(d) x [6.45, 4.52. -0.85]
b₁ = I₁ +23+7²₁
b₂r2-2r3+ n₂
b3=11-423+ng
b₁2r1 +223 +14
What
What is the least square estimate of x= [1,2,3]?

Algebra
Matrices & DeterminantsThis set of questions pertains to reference angles.
a. Name 3 different angles which could have a reference angle of 20 degrees. How did you
arrive at this answer? 2-3 sentences.
b. What are the characteristics of a reference angle? 2-3 sentences.
c. How is it possible that angles can have different measurements, but still have the exact same reference angle? 2-3 sentences.
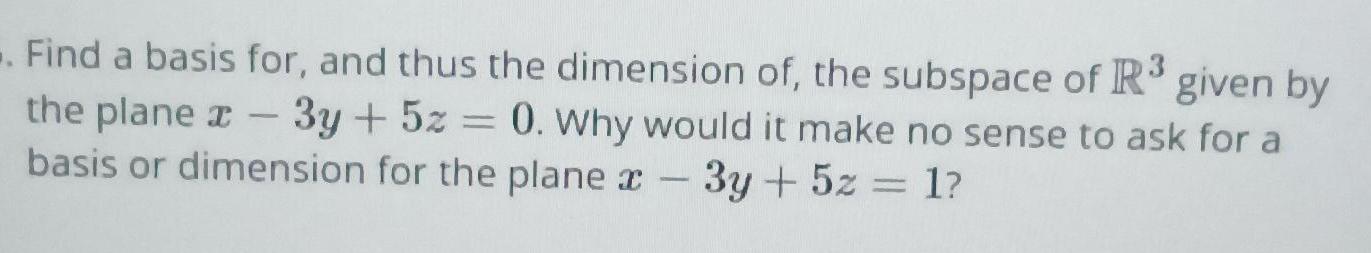
Algebra
Matrices & DeterminantsFind a basis for, and thus the dimension of, the subspace of R³ given by the plane * - 3y + 5z = 0. Why would it make no sense to ask for a basis or dimension for the plane 3y + 5z = 1?

Algebra
Matrices & DeterminantsEvaluate (without use of a calculator).
(a) log4 2 + log4 128 =
(b) log4 112- log4 7

Algebra
Matrices & Determinants(a) Let A be an invertible n x n and suppose that A-1 = A. Prove that det(A) = -1 or det(A) = 1.
(b) Let A be a square matrix such that A² -7A+8I = 0 [where I and 0 are the identity matrix and the zero matrix, respectively). Show that det(A) # 0.

Algebra
Matrices & Determinants(a) Suppose that A is a 3 x 3 diagonalizable matrix with a basis of eigenvectors of R³ given by {u₁, U₂, U3} with corresponding eigenvalues A1, A2, A3. Suppose that the matrix B is also a 3 x 3 diagonalizable matrix with the same eigenvectors although with possibly different eigenvalues 11, 12, 13. Prove that A + B is also a diagonalizable matrix.
(b) Suppose that the square matrices A and B are similar. Prove that the matrices A2+ A+ I and B2 +B+ I are also similar.
(c) Suppose that the square matrices A and B both have their characteristic polynomial equal to -³ + X. Prove that A is similar to B.

Algebra
Matrices & Determinants0.0116 0.0046 0.0023
0.0023 0.0046 0.0116
Let D= 0.0046 0.0093 0.0046 be a flexibility matrix, with flexibility measured in inches per pound. Suppose that forces of 40, 10, and 20 lb are applied to a beam at points 1,
0.0023 0.0046 0.0116 and 3, respectively. Find the corresponding deflections y₁, y2, and y3.
#1
#2

Algebra
Matrices & DeterminantsCalculate the inverse A^-1 of the matrix
A = ( -1 2 2)
(2 -1 2)
(2 2 -1)

Algebra
Matrices & DeterminantsFind the matrix P that orthogonally diagonalizes A. Compute P-¹AP.
A = 3 2 4
2 0 2
4 2 3
![Find 2A + 3B.
a=[4 8] b=[-5 9]
[1 7] [5 -8]](https://media.kunduz.com/media/sug-question/raw/80217977-1660160872.666108.jpeg?w=256)

Algebra
Matrices & DeterminantsMatrix A represents the number of points scored in each quarter for the first 4 games of football played by WCHS. Matrix B represents the number of points scored in each quarter for the first 4 games of football played by WJHS.
Matrix A Matrix B
Q1 Q2 Q3 Q4 Q1 Q2 Q3 Q4
Game1 6 0 13 3 Game1 0 3 9 0
Game2 21 18 0 7 Game2 7 14 7 6
Game3 14 28 6 0 Game3 3 9 12 17
Game4 0 0 35 17 Game4 23 0 9 7
(a) What does the number 28 represent? Be specific.
(b) Suppose WCHS was playing WJHS in game 3. Who won?
(C) What is the AVERAGE point scored by WJHS in the first quarter?

Algebra
Matrices & DeterminantsSolve each system of equations using elementary operations.
a. (i) x + y + z = 0
(ii) x - y = 1
(iii) y - z = -5
d.(i) x/3+y/4+z/5=14
(ii) x/4+y/5+z/3=-21
(iii)x/5+y/3+z/4=7

Algebra
Matrices & DeterminantsFor each, determine the amplitude, the axis of the curve, the range, the period, the phase shift
and the zero(s) within one period. Keep your solutions neat and organized. (7 marks each)
a. y 4 sin(18x) =- 5
=
b. y = -6 sin(x-40") - 3
c. y=-25 cos(60a) - 21

Algebra
Matrices & DeterminantsA n x n Hermitian matrix contains exactly k real entries. Show that k + n must be even.

Algebra
Matrices & DeterminantsSolve using Cramer's Rule.
- 5x + 2y + 3z = 27
6x + 6y + 5z = - 32
-5x + 3y + 3z = 25
The solution of the system is
(Type integers or simplified fractions.)

Algebra
Matrices & DeterminantsSolve using Cramer's Rule.
3x-y = 7
x-3y=9
What is the solution of the system?
(Simplify your answer. Type an ordered pair, using integers or fractions.)

Algebra
Matrices & DeterminantsSolve the following system of equations using Gaussian or Gauss-Jordan elimination.
- 10x-3y = - 17
4x + y = 7
Select the correct choice below and fill in any answer boxes in your choice.
(A). The solution to the system of equations is
(Simplify your answer. Type an ordered pair.)
(B).There are infinitely many solutions.
(C). There is no solution.
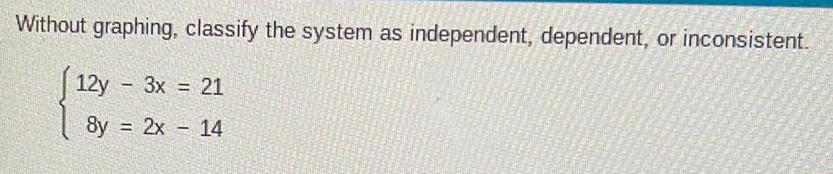
Algebra
Matrices & DeterminantsWithout graphing, classify the system as independent, dependent, or inconsistent.
12y - 3x = 21
8y = 2x 14

Algebra
Matrices & Determinantsrite the equations for f(x) and g(x). Then identify the reflection that transforms the graph of f(x) to the graph of g(x).

Algebra
Matrices & DeterminantsWrite an exponential function to model the following situation. A population of 120,000 grows 5% per year for 14 years. How much will the popluation be after 14 years? Write an exponential function in terms of x. y=*