Matrices & Determinants Questions and Answers
![the following sum is a right riemann sum for a certain definite integral using a partition of the interval [1,b] into n subintervals of equal length then the upper limit of integration must be :b = and the integrand must be the function f(x)=](https://media.kunduz.com/media/sug-question/raw/84821527-1659520275.0164595.jpeg?w=256)
Algebra
Matrices & Determinantsthe following sum is a right riemann sum for a certain definite integral using a partition of the interval [1,b] into n subintervals of equal length then the upper limit of integration must be :b = and the integrand must be the function f(x)=
![For what values of k the following matrix is
a reduced row echeleon form?
[12 k²2 - 4k-3]
[O O k 0]
options:
a) k = 0, 1 only
b) k = 0, 1, 4 only
no values of k
d) k = 1, 3 only
e) k = 0 only](https://media.kunduz.com/media/sug-question/raw/84821505-1659520179.9431677.jpeg?w=256)
Algebra
Matrices & DeterminantsFor what values of k the following matrix is
a reduced row echeleon form?
[12 k²2 - 4k-3]
[O O k 0]
options:
a) k = 0, 1 only
b) k = 0, 1, 4 only
no values of k
d) k = 1, 3 only
e) k = 0 only

Algebra
Matrices & DeterminantsFor each of the following, determine if the given operation defines an inner product on the given vector space V. If it does, show that it does by verifying that axioms (i), (ii), (iii), (iv) of an inner product holds. If it does not, give a counterexample to show that one of the axioms (i), (ii), (iii), (iv) fails.
(a) V = M₂ (R), (A, B) = det(AB)
(b) V = M₂ (R), (A, B) = Tr(ATB)
(c) V = F, (f, g) = f(1)g(0) + f(0)g(1)
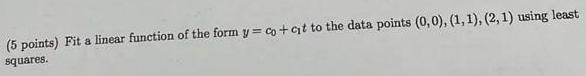
Algebra
Matrices & DeterminantsFit a linear function of the form y = co + cit to the data points (0,0), (1, 1), (2, 1) using least squares.
![Let T: P₂ P₂ be the linear operator defined as T (p(x)) = p(3x), and let B = (1, x, x²] be the standard basis for P₂-
Find [T]g, the matrix for T relative to B.
Let p(x) = 1-x+4x². Determine [p(x)]g, then find 7(p(x)) using [7], from part a.
Check your answer to part b by evaluating 7(1-x + 4x²) directly.](https://media.kunduz.com/media/sug-question/raw/84820330-1659517397.7914426.jpeg?w=256)
Algebra
Matrices & DeterminantsLet T: P₂ P₂ be the linear operator defined as T (p(x)) = p(3x), and let B = (1, x, x²] be the standard basis for P₂-
Find [T]g, the matrix for T relative to B.
Let p(x) = 1-x+4x². Determine [p(x)]g, then find 7(p(x)) using [7], from part a.
Check your answer to part b by evaluating 7(1-x + 4x²) directly.

Algebra
Matrices & DeterminantsLet A, B be (n x n)-matrices. Suppose AB = BA = In.
(a) Let X, C be n × m matrices.
Show that AX = C if and only if X = BC.
(b) Let b be a column vector of size n.
Suppose u is a solution of LS(A, b) (which is the linear system with coefficient matrix A and vector of constant b). Express u in terms of B and b.
(c) Let 1 0 1 -5 1 1 3
a= 5 1 3 B= 7 -1 -2 b= 2
1 -1 2 6 -1 -1 1
I). Verify that AB = BA= I₃ .
ii). Hence, or otherwise, find a solution of LS(A, b).
"
=

Algebra
Matrices & Determinants(ii) For n ≥ 3, does there exist three vectors u, v, w ∈ R" such that {u, v, w} is linearly dependent, and each pair {u, v}, {u, w} and {v, w} is linearly independent? Justify your answer.
![Given
[ 1 4 5 6 9]
[ 3 -2 1 4 -1 ]
[-1 0 -1 -2 -1]
[ 2 3 5 7 8]
a) Find bases for the null space, row space and column space of A.
b) Find the dimensions of the row space and null space of A.](https://media.kunduz.com/media/sug-question/raw/81772692-1659464839.685246.jpeg?w=256)
Algebra
Matrices & DeterminantsGiven
[ 1 4 5 6 9]
[ 3 -2 1 4 -1 ]
[-1 0 -1 -2 -1]
[ 2 3 5 7 8]
a) Find bases for the null space, row space and column space of A.
b) Find the dimensions of the row space and null space of A.

Algebra
Matrices & Determinants2. Let G be the group defined by the following Cayley's table
* 1 2 3 4 5 6
1 1 2 3 4 5 6
2 2 1 5 6 3 4
3 3 4 1 2 6 5
4 4 3 6 5 1 2
5 5 6 2 1 4 3
6 6 5 4 3 2 1
(i)Find the order of each element of G.
(ii)Determine the inverse of elements 1, 3, 4 and 6.

Algebra
Matrices & DeterminantsEvaluate det(det(det(det(A) A²) A) A‾¹), where A is a square matrix of order 3 with det(A) = 3.
Algebra
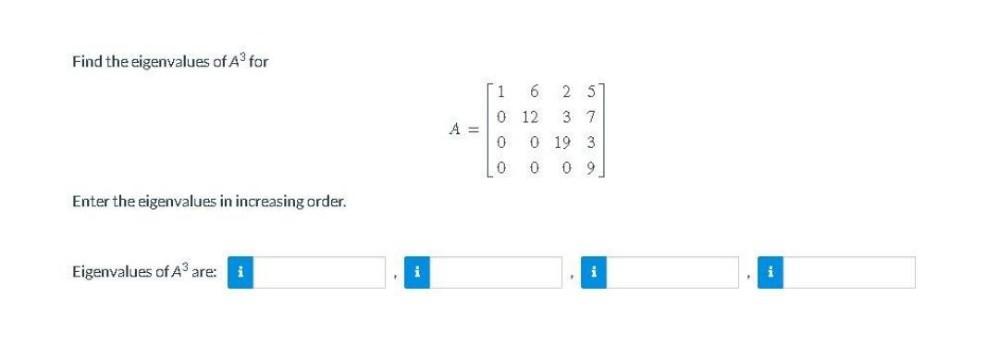
Matrices & DeterminantsFind the eigenvalues of A³ for
1 6 2 5
A=0 12 3 7
0 0 19 3
0 0 0 9
Enter the eigenvalues in increasing order.
Eigenvalues of A³ are:
Algebra
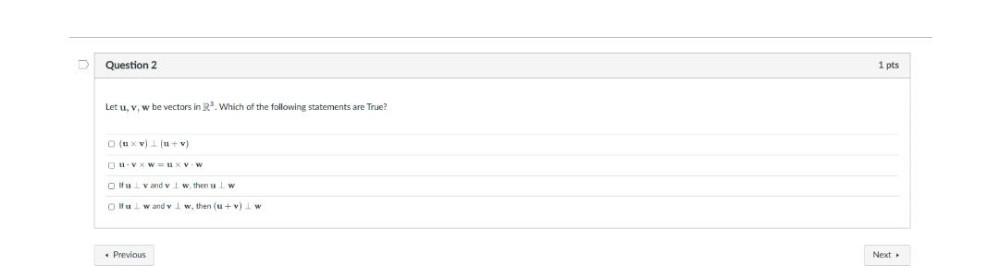
Matrices & DeterminantsLet u, v, w be vectors in R³. Which of the following statements are True?
(u x v) ⟂ (u+v)
u.v x w = u x v . w
lf u⟂v and v⟂w, then u⟂w
If u⟂w and v⟂w, then (u+v)⟂w
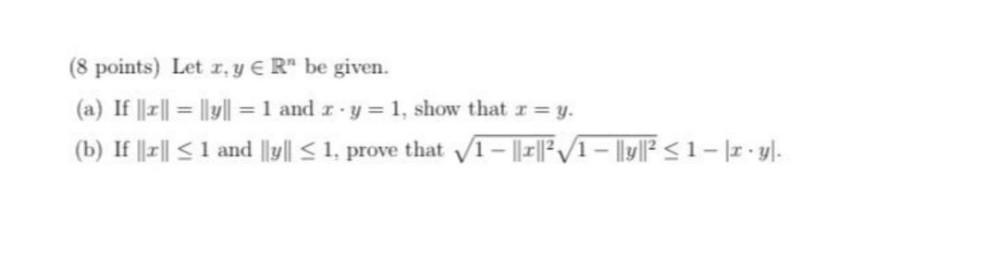
Algebra
Matrices & DeterminantsLet x, y € R" be given.
(a) If ||x|| = ||y|| = 1 and x * y = 1, show that x = y.
(b) If ||x|| ≤ 1 and ||y|| ≤ 1, prove that √(1 - ||x||²) √(1 - ||y||²) ≤ 1 − |x · y|.

Algebra
Matrices & DeterminantsGiven that a matrix
1 2 3
A = 2 3 4
1 1 5
and B=A-¹, find the entry in row 2 and column 3 of B.
-1/2
1/4
1/2
-1/4
1
![Find the eigenvalues & the eigenvectors of:
A = [1 2 1
0 3 1
0 5 -1]](https://media.kunduz.com/media/sug-question/raw/81869891-1659440202.6310227.jpeg?w=256)
![Compute the following product of powers of matrices:
You can resize a matrix (when appropriate) by clicking and dragging the bottom-right corner of the matrix.
[0 1 0 0
1 0 0 0
0 0 1 0
0 0 0 1]](https://media.kunduz.com/media/sug-question/raw/81870040-1659439956.1780415.jpeg?w=256)
Algebra
Matrices & DeterminantsCompute the following product of powers of matrices:
You can resize a matrix (when appropriate) by clicking and dragging the bottom-right corner of the matrix.
[0 1 0 0
1 0 0 0
0 0 1 0
0 0 0 1]

Algebra
Matrices & DeterminantsOlga buys 54 stickers. The stickers are arranged on 6 sheets, with the same number of stickers on each sheet. Which equation and answer show how many stickers are on each sheet?
54 - 6 ?
There are 48 stickers on each sheet.
54 ÷ 6 = ?
There are 9 stickers on each sheet.
6 x 6 = ?
There are 36 stickers on each sheet.
6 + ? = 54
There are 48 stickers on each sheet.
![If E, F, G are the following elementary matrices, compute the given matrix expression.
E=[1 0 0 0] F=[1 0 0 -4] G=[0 1 0 0]
[0 -4 0 0] [0 1 0 0] [1 0 0 0]
[0 0 1 0] [0 0 1 0] [0 0 1 0]
[0 0 0 1] [0 0 0 1] [0 0 0 1]
(F⁻¹GE⁻¹G⁻¹)⁻¹=[0 0 0]
[0 0 0]
[0 0 0]](https://media.kunduz.com/media/sug-question/raw/81870729-1659439068.4502044.jpeg?w=256)
Algebra
Matrices & DeterminantsIf E, F, G are the following elementary matrices, compute the given matrix expression.
E=[1 0 0 0] F=[1 0 0 -4] G=[0 1 0 0]
[0 -4 0 0] [0 1 0 0] [1 0 0 0]
[0 0 1 0] [0 0 1 0] [0 0 1 0]
[0 0 0 1] [0 0 0 1] [0 0 0 1]
(F⁻¹GE⁻¹G⁻¹)⁻¹=[0 0 0]
[0 0 0]
[0 0 0]

Algebra
Matrices & Determinants16. Let R⁴ have the Euclidean inner product. Find two unit vectors that are orthogonal to all three of the vectors u = (2, 1, -4,0), v = (-1,-1,2, 2), and w = = (3, 2, 5, 4).

Algebra
Matrices & DeterminantsIf A is an Antisymmetric A^2 is a Symmetric and Semi define positive matrix. (Matrix B is semi define positive for each vector z matrix. Prove that -

Algebra
Matrices & DeterminantsA spherical hot air balloon is about 55 feet in diameter. If air is let out at a rate of 800 feet cubed per minute, how long will it take to deflate the balloon?
![Consider the linear transformation T: R³ → R³ defined by T(x, y, z) = (y, y + 2z, 3x + y − 2z).
Part(a)[3 points] Find the standard matrix of T.
Part(b)[12 points] Show that I is invertible and then find the vector T-¹(x, y, z).
Part(c) [3 points] Find the pre-image of (3, 4, -1) under T.](https://media.kunduz.com/media/sug-question/raw/84802952-1659435548.4775271.jpeg?w=256)
Algebra
Matrices & DeterminantsConsider the linear transformation T: R³ → R³ defined by T(x, y, z) = (y, y + 2z, 3x + y − 2z).
Part(a)[3 points] Find the standard matrix of T.
Part(b)[12 points] Show that I is invertible and then find the vector T-¹(x, y, z).
Part(c) [3 points] Find the pre-image of (3, 4, -1) under T.
![A Math 110 student decides to make quarterly payments of $2,500 into a retirement account paying 5% interest per year compounded continuously. If the student continues to make these payments for 30 years, compute each of the following values.
Account balance after 30 years (exact value) =
Account balance after 30 years (rounded to the nearest cent) =
Total of all deposits (exact value] =
Total of all interest payments (rounded to the nearest cent) =](https://media.kunduz.com/media/sug-question/raw/84798183-1659434458.11195.jpeg?w=256)
Algebra
Matrices & DeterminantsA Math 110 student decides to make quarterly payments of $2,500 into a retirement account paying 5% interest per year compounded continuously. If the student continues to make these payments for 30 years, compute each of the following values.
Account balance after 30 years (exact value) =
Account balance after 30 years (rounded to the nearest cent) =
Total of all deposits (exact value] =
Total of all interest payments (rounded to the nearest cent) =

Algebra
Matrices & DeterminantsSuppose A is the augmented matrix of a linear system of 4 equations in 4 variables.
(a) What are the dimensions of A? A is __X___
(b) If the system has no solutions, what are the possible values for rank(A)? rank(A) = ____
(c) If the system has exactly one solution, what are the possible values for rank(A)? rank(A) = ____
(d) If the system has infinitely many solutions, what are the possible values for rank(A)? rank(A) = ____.

Algebra
Matrices & DeterminantsLet A be an nxn matrix and consider the linear homogeneous system Ar= 0. If the linear system has only the trivial solution state whether the following statements are true or false.
(a) 0 is an eigenvalue of A
(b) All columns of A are basic columns.
(c) Rank of A is n.
![Solve the system of equations by the addition method.
-4x+y = -2
16x-4y = 8
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A). The solution is
B). There are infinitely many solutions; {(x,y)] -4x+y=-2) or ((x,y)| 16x-4y=8}.
C). There is no solution;{} or Ø.](https://media.kunduz.com/media/sug-question/raw/81992464-1659353201.7724977.jpeg?w=256)
Algebra
Matrices & DeterminantsSolve the system of equations by the addition method.
-4x+y = -2
16x-4y = 8
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A). The solution is
B). There are infinitely many solutions; {(x,y)] -4x+y=-2) or ((x,y)| 16x-4y=8}.
C). There is no solution;{} or Ø.

Algebra
Matrices & DeterminantsLet A be an n x n square matrix with entries in C. Suppose A is normal, show that if λ ∈ C is an eigenvalue of A, then |λ| is a singular value of A.

Algebra
Matrices & Determinants(a) Determine whether the set of vectors in P₁ are linearly independent or linearly dependent.
S=(4t-t²,5+1,3t+5, 2t³-31²}
(b) is the set Sa basis for P₁? Why or why not?

Algebra
Matrices & DeterminantsLet A be the matrix below and define a transformation T:R³ ---> R³ by T(u) = Au. For each of the vectors b below, find a vector u such that I maps u to b, if possible. Otherwise state that there is no such u
1 2 2
A= -2 -4 1
-2 -3 -2
(a) b= 11
-2
-12
(b) b= 1
-2
-1

Algebra
Matrices & DeterminantsConsider the system of equations
x+2y+3z=0
2x-y=0
2+kz=0.
a) Calculate the determinant of the coefficient matrix using row operations.
b) For which value(s) of k (if any) does the system have no solution?
e) For which value(s) of k (if any) does the system have exactly one solution?
d) For which value(s) of k (if any) does the system have infinitely many solutions?
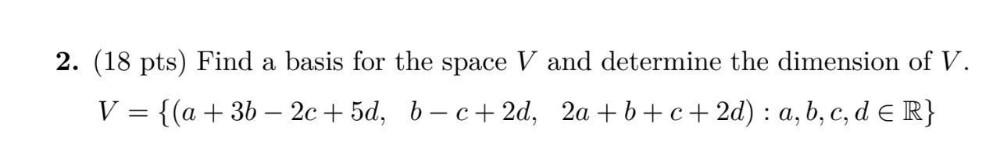
Algebra
Matrices & DeterminantsFind a basis for the space V and determine the dimension of V.
V = {(a + 3b - 2c+5d, b-c+2d, 2a+b+c+2d) : a, b, c, d ∈ R}

Algebra
Matrices & DeterminantsFind the elementary matrix E such that EC = A where
2 4 1 2 4 1
A = 4 -2 -2 and c= 4 -2 -2
6 -7 3 -2 -23 -1

Algebra
Matrices & DeterminantsSolve the following system by Gauss-Jordan elimination.
2x₁ + 9x₂ + 17x₃= 27
6x₁+28X₂ +53x₃ = 83
x₁ =
x₂ =
x₃= t

Algebra
Matrices & DeterminantsWrite an explicit formula for the nᵗʰ term of the arithmetic sequence where the fourth term is 28 and the thirteenth term is 55.
![The characteristic polynomial of the matrix
A=[5 -2 -4
-2 8 -2
-4 -2 5] is λ(λ-9)². The vector
[2
1
2] is an eigenvector of A. Find an orthogonal matrix P that diagonalizes A. and verify that P-¹AP is diagonal.](https://media.kunduz.com/media/sug-question/raw/82077457-1659309093.335851.jpeg?w=256)
Algebra
Matrices & DeterminantsThe characteristic polynomial of the matrix
A=[5 -2 -4
-2 8 -2
-4 -2 5] is λ(λ-9)². The vector
[2
1
2] is an eigenvector of A. Find an orthogonal matrix P that diagonalizes A. and verify that P-¹AP is diagonal.

Algebra
Matrices & Determinants(a) If Matrix A and B are orthogonal, determine whether the following are orthogonal or not. Give full justifications for your answer.
(i) A^T, (ii) B-¹, (iii) B-¹ AB.
(b) Consider the transformation f: R² R³ given by
f(x,y) = (x+2y,x-y,-2x+3y).
Show that f is a linear transformation. Find a matrix form of this transformation.

Algebra
Matrices & DeterminantsWhite cards are negative and graycards are positive. Find the value of the cards.9 5 3 1 7 2
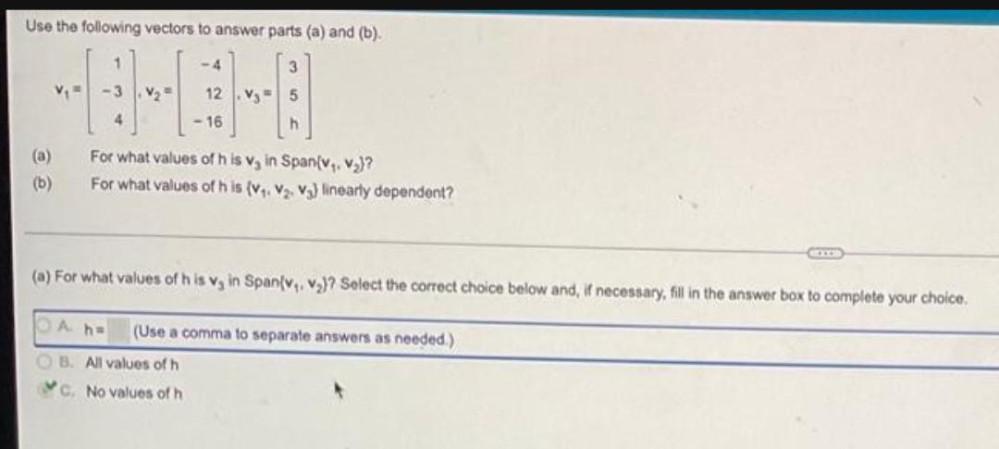
Algebra
Matrices & DeterminantsUse the following vectors to answer parts (a) and (b).
1 -4 3
v₁ = -3, v₂ = 12, v₃ = 5
4 -16 h
(a) For what values of his v₂ in Span(v₁. v₂)?
(b) For what values of h is (v₁. v₂. v₃) linearly dependent?
(a) For what values of h is v₃ in Span(v₁, v₂)? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
i) h=
(Use a comma to separate answers as needed.)
ii) All values of h
iii) No values of h

Algebra
Matrices & DeterminantsThe vector y has magnitude 6 and direction angle 0°. The vector z has magnitude 4 and direction angle 75°.
Find the magnitude and direction angle θ of the sum y + z.
Round your answers to the nearest thousandth.
ly + zl =?
θ = ___°
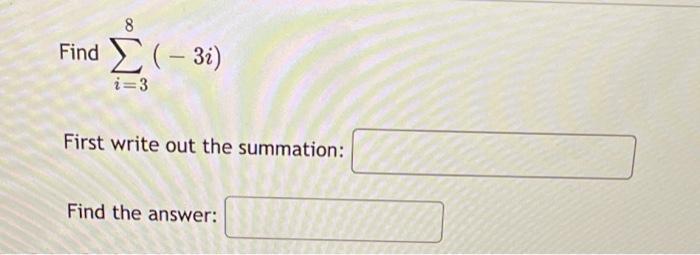
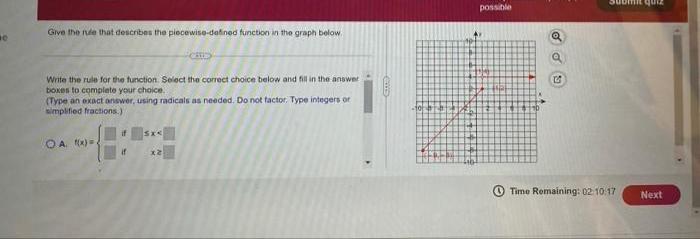
Algebra
Matrices & DeterminantsGive the nude that describes the piecewise-defined function in the graph below.
Write the rule for the function. Select the correct choice below and fill in the answer boxes to complete your choice. (Type an exact answer, using radicals as needed. Do not factor. Type integers or simplified fractions.)
(A) f(x) = { __ if __ ≤ x < __
{ __ if x ≥ __

Algebra
Matrices & DeterminantsFind the answer of the following determinant.
| 1 logₓ y logₓ z
logᵧ x 1 logᵧ z
logz x logz y 1 |
Note: you need to review the properties of log. What is the inverse of the above matrix?

Algebra
Matrices & DeterminantsConstruct an orthogonal basis for the columns space of the matrix
3 5 1
1 1 0
-1 0 -2
3 7 8

Algebra
Matrices & DeterminantsEvaluate the limit using L'Hospital's rule if necessary
lim (1 + 10/x)⁷/¹⁴.
x→∞

Algebra
Matrices & DeterminantsLet V be a vectors space with S = {(1, -2, 3), (2, 0, 1), (3, 0, 1), (1, 1, -1)}. Find the ff:
a. Basis of RS
b. dim(RS)
c. Nullity (RS)
![Determine if the vector [5 3 0] is a linear combination of the vectors:
2 1 8 -4
0, 4, 1, and 6
1 3 1 1
A) is not a linear combination of the other vectors.
B) is a linear combination of the other vectors.](https://media.kunduz.com/media/sug-question/raw/82230821-1659307683.4869497.jpeg?w=256)
Algebra
Matrices & DeterminantsDetermine if the vector [5 3 0] is a linear combination of the vectors:
2 1 8 -4
0, 4, 1, and 6
1 3 1 1
A) is not a linear combination of the other vectors.
B) is a linear combination of the other vectors.
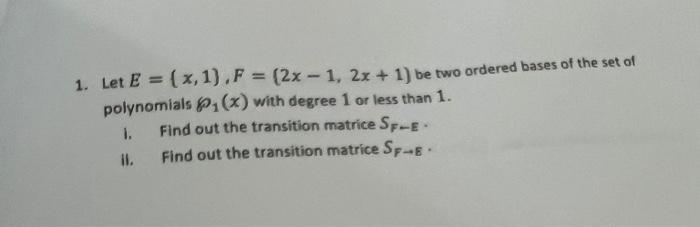
Algebra
Matrices & DeterminantsLet E = {x, 1}, F = {2x - 1, 2x + 1} be two ordered bases of the set of polynomials P1(x) with degree 1 or less than 1.
(a) Find out the transition matrice SF←E.
(b) Find out the transition matrice SF→E.
![Let G = (Z₁₈, +₁₈) and A ≤ G such that A = {0, 6, 12}.
1. Find all generators of G
2. Find number of subgroups of G
3. List all subgroups of G
4. Find [G: A]
5. List all elements of Z₁₈/A](https://media.kunduz.com/media/sug-question/raw/82248466-1659307437.9545324.jpeg?w=256)
Algebra
Matrices & DeterminantsLet G = (Z₁₈, +₁₈) and A ≤ G such that A = {0, 6, 12}.
1. Find all generators of G
2. Find number of subgroups of G
3. List all subgroups of G
4. Find [G: A]
5. List all elements of Z₁₈/A
![Let A=
[1 2 -2 11
3 6 -5 4
1 2 0 3]
(a) Find a basis for the column space of A, and determine its dimension.
(b) (Rank(A) = ? Justify your answer.](https://media.kunduz.com/media/sug-question/raw/82200669-1659307342.348621.jpeg?w=256)
Algebra
Matrices & DeterminantsLet A=
[1 2 -2 11
3 6 -5 4
1 2 0 3]
(a) Find a basis for the column space of A, and determine its dimension.
(b) (Rank(A) = ? Justify your answer.

Algebra
Matrices & DeterminantsWrite an equation for a function whose graph fits the given description
b) The graph of f(x)=|x| is reflected through the x-axis, then shifted upwards by 4 units.