Application of derivatives Questions and Answers

Calculus
Application of derivativesConsider g(t) = 2t(7 - t) ^1/3
Determine the intervals on which g is concave down.
g is concave down on:
g is concave down nowhere.
Determine the intervals on which g is concave up.
g is concave up on:
g is concave up nowhere.
Determine the value and location of any inflection point of g. Enter the solution in (t, g(t)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
g has an inflection point at:
g has no inflection point.

Calculus
Application of derivativesConsider h(u) = 6u²+2u^4 +4u-7-6u³
Determine the intervals on which is concave down.
h is concave down on:
h is concave down nowhere.
Determine the intervals on which is concave up.
h is concave up on:
h is concave up nowhere.
Determine the value and location of any inflection point of f. Enter the solution in (u, (u)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has an inflection point at:
h has no inflection point.

Calculus
Application of derivativesConsider f(x) =-7x²-20/x²-18
Determine the intervals on which f is concave down.
Consider f(x) =
f is concave down on:
f is concave down nowhere.
Determine the intervals on which f is concave up.
f is concave up on:
f is concave up nowhere.
Determine the value and location of any inflection point of f. Enter the solution in (x, f(x)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
f has an inflection point at:
f has no inflection point.

Calculus
Application of derivativesConsider h(y) = 2y√162 - y² and use the Second Derivative Test to address the following prompts.
Determine the value and location of any local minimum of f. Enter the solution in (y, h(y)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local minimum at:
h has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (y, h(y)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local maximum at:
h has no local maximum.

Calculus
Application of derivativesConsider g(w) =- 6w/w² + 11
Determine the intervals on which g is concave down.
g is concave down on:
g is concave down nowhere.
Determine the intervals on which g is concave up.
g is concave up on:
g is concave up nowhere.
Determine the value and location of any inflection point of g. Enter the solution in (w, g(w)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
g has an inflection point at:
g has no inflection point.

Calculus
Application of derivativesConsider f(x) = 40x + 17x² - 14 - 162³ and use the Second Derivative Test to address the following prompts.
Determine the value and location of any local minimum of f. Enter the solution in (x, f(x)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
f has a local minimum at:
f has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (x, f(x)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
f has a local maximum at:
f has no local maximum.

Calculus
Application of derivativesConsider h(t) = 10t (11^t) and use the Second Derivative Test to address the following prompts.
Determine the value and location of any local minimum of f. Enter the solution in (t, h(t)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local minimum at:
h has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (t, h(t)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local maximum at:
h has no local maximum.

Calculus
Application of derivativesConsider h (v)=- 5+5v + 3v² and use the Second Derivative Test to address the following prompts.
Determine the value and location of any local minimum of f. Enter the solution in (v, h(v)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local minimum at:
h has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (v, h(v)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local maximum at:
h has no local maximum.

Calculus
Application of derivativesConsider f(t) = 1/10 t^5 - 16/3 t^3
Determine the intervals on which f is concave down.
f is concave up on:
f is concave down on:
f is concave down nowhere.
Determine the intervals on which f is concave up.
f is concave up nowhere.
Determine the value and location of any inflection point of f. Enter the solution in (t, f(t)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
f has an inflection point at:
f has no inflection point.

Calculus
Application of derivativesConsider g(w) = w + 1 / w+6
Determine the intervals on which g is concave down.
g is concave down on:
g is concave down nowhere.
Determine the intervals on which g is concave up.
g is concave up on:
g is concave up nowhere.
Determine the value and location of any inflection point of g. Enter the solution in (w, g(w)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
g has an inflection point at:
g has no inflection point.
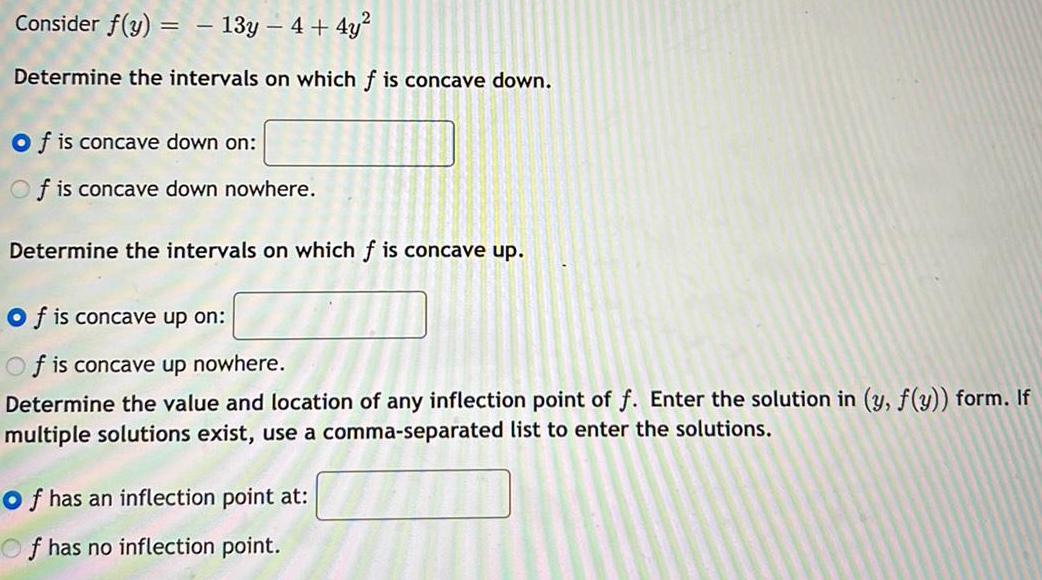
Calculus
Application of derivativesConsider f(y) = - 13y - 4 + 4y²
Determine the intervals on which f is concave down.
f is concave down on:
f is concave down nowhere.
Determine the intervals on which f is concave up.
f is concave up on:
f is concave up nowhere.
Determine the value and location of any inflection point of f. Enter the solution in (y, f(y)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
f has an inflection point at:
f has no inflection point.

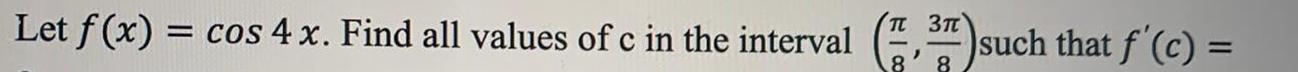
Calculus
Application of derivativesLet f(x) = cos 4 x. Find all values of c in the interval( π/8 ,3π/8) such that f'(c) =
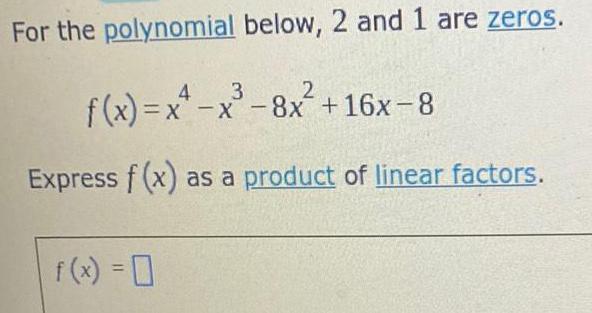
Calculus
Application of derivativesFor the polynomial below, 2 and 1 are zeros.
2
f(x)=x-x-8x + 16x-8
Express f(x) as a product of linear factors.
=
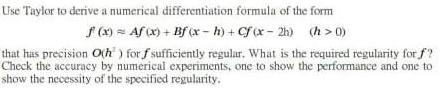
Calculus
Application of derivativesUse Taylor to derive a numerical differentiation formula of the form
f (x) = Af(x) + Bf (x-h) + Cf (x-2h) (h>0)
that has precision O(h) for f sufficiently regular. What is the required regularity for f?
Check the accuracy by numerical experiments, one to show the performance and one to
show the necessity of the specified regularity.

Calculus
Application of derivativesConsider f(z) = - 8z5e3z
Determine the intervals on which f is decreasing.
Of is decreasing on:
Of is decreasing nowhere.
Determine the intervals on which f is increasing.
Of is increasing on:
Of is increasing nowhere.
Determine the value and location of any local minimum of f. Enter the solution in (z, f(z)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
of has a local minimum at:
Of has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (z, f(z)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
of has a local maximum at:
Of has no local maximum.

Calculus
Application of derivativesConsider h(y) = 24y - 12 tan(y) on
-
7 TT
2' 2
Determine the intervals on which h is decreasing.
Oh is decreasing on:
Oh is decreasing nowhere.
Determine the intervals on which h is increasing.
Oh is increasing on:
Oh is increasing nowhere.
Determine the value and location of any local minimum of f. Enter the solution in (y, h(y)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
Oh has a local maximum at:
Oh has no local maximum.
Oh has a local minimum at:
h has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (y, h(y)) form. If
multiple solutions exist, use a comma-separated list to enter the solutions.
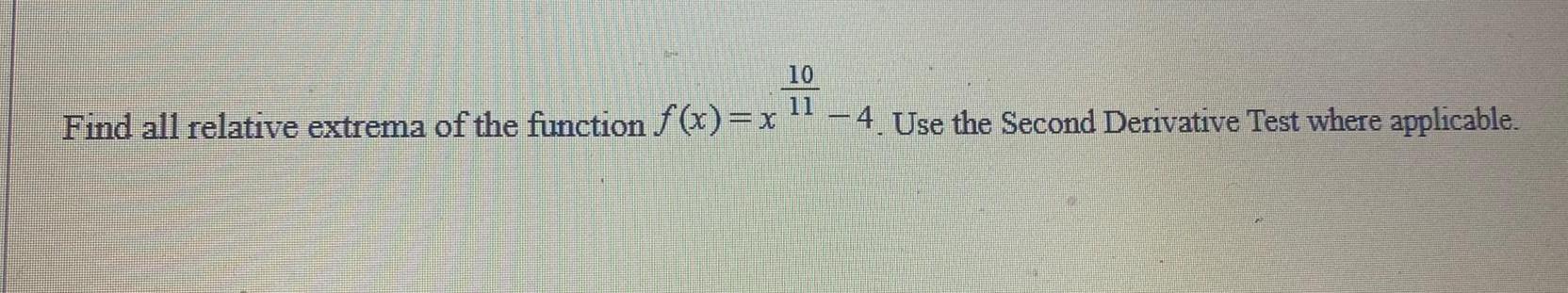
Calculus
Application of derivatives10
11
Find all relative extrema of the function f(x) = x
-4. Use the Second Derivative Test where applicable.

Calculus
Application of derivativesFind all points of inflection on the graph of the function f(x)= = = = x² + 6x³
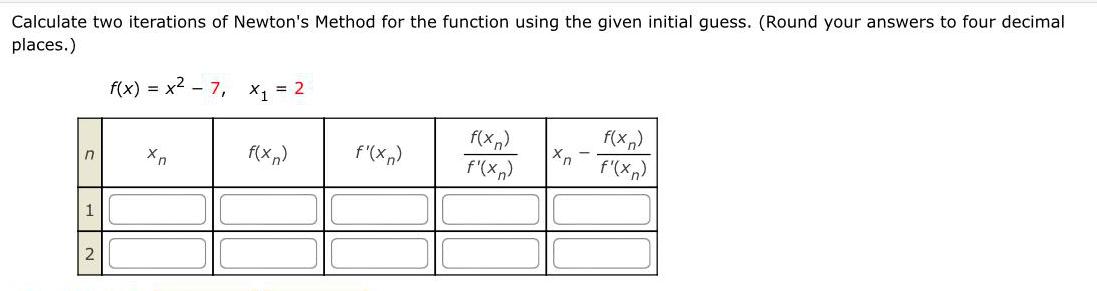
Calculus
Application of derivativesCalculate two iterations of Newton's Method for the function using the given initial guess. (Round your answers to four decimal
places.)
n
1
NH
2
f(x) = x² - 7₁ x₁ = 2
Xn
f(x)
f'(xn)
f(x)
f'(xn)
Xn
f(xn)
f'(xn)
![Estimate the area under f(x) = x² on [0,2] using right endpoint approximation given n = 4.
A.
B.
C.
D.
8
3
SIN 4](https://media.kunduz.com/media/sug-question/raw/84264382-1657634826.519333.jpeg?w=256)
Calculus
Application of derivativesEstimate the area under f(x) = x² on [0,2] using right endpoint approximation given n = 4.
A.
B.
C.
D.
8
3
SIN 4

Calculus
Application of derivativesIf f(x) > 0 on an interval, then f(x) is:
concave up on the interval
concave down on the interval
a straight line
cannot be determined
A.
B.
C.
D.

Calculus
Application of derivativesAn interior designer wants to decorate a newly constructed house. The function f(x) = 36x²-150 represents the amount of money he ears per room decorated
where x represents the number of rooms he designs. The function g(x)=x represents the number of rooms the Interior designer decorates, where x is the
number of hours he works.
Part A: Determine the amount of money the interior designer will make decorating the house as a function of hours he works (5 points)
Part B: If the newly constructed house requires 45 hours of work, how much will the interior designer earn? Show all necessary calculations (5 points)
Part C. Determine an expression to represent the difference quotient for the function found in Part A Show all necessary work. (5 points)

Calculus
Application of derivativesA rectangular poster is to contain 128 square inches of print. The margins at the top and bottom of the poster are to be 2 inches,
and the margins on the left and right are to be 1 inch. What should the dimensions of the poster be so that the least amount of
poster is used?
in (smaller value)
in (larger value)

Calculus
Application of derivativesFind the points on the graph of the function that are closest to the given point.
f(x) = x², (0, 3)
(x, y) =
(x, y) =
(smaller x-value)
(larger x-value)

Calculus
Application of derivativesFind the length and width of a rectangle that has the given perimeter and a maximum area.
Perimeter: 136 meters
length
width
m
m
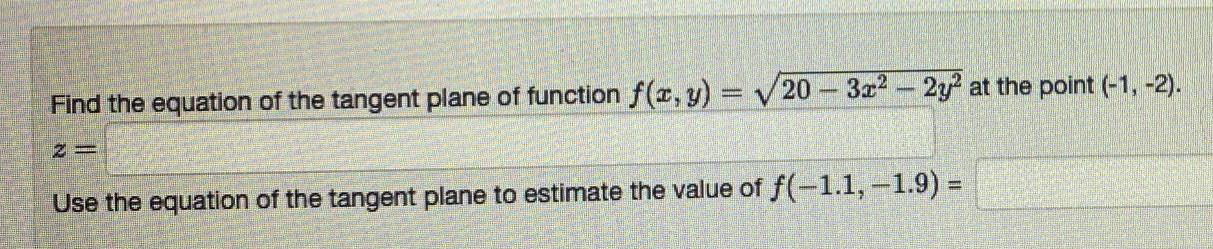
Calculus
Application of derivativesFind the equation of the tangent plane of function f(x, y) = √20-3x² - 2y² at the point (-1, -2).
z=
Use the equation of the tangent plane to estimate the value of f(-1.1, -1.9) =

Calculus
Application of derivativesFind the marginal cost function.
C(x) = 175 +0.9x
The marginal cost function is C'(x) =
![If f(x)=
= tan x, which of the equations below describes the average value of f(x) over the interval [0, 2]?
(tan (2))+ (tan (0))
2-0
o (tan (2)) + (tan (0))
tan x dx
02-0²
O
2
² tan 1/x dx
O](https://media.kunduz.com/media/sug-question/raw/84170723-1657400326.4614968.jpeg?w=256)
Calculus
Application of derivativesIf f(x)=
= tan x, which of the equations below describes the average value of f(x) over the interval [0, 2]?
(tan (2))+ (tan (0))
2-0
o (tan (2)) + (tan (0))
tan x dx
02-0²
O
2
² tan 1/x dx
O
![Assume v(t) = 4t - 16 on the interval [0, 6].
What is the total distance that the object traveled on [0, 6]?
O 50
O 40
O 30
O 24](https://media.kunduz.com/media/sug-question/raw/84170808-1657400273.513038.jpeg?w=256)
Calculus
Application of derivativesAssume v(t) = 4t - 16 on the interval [0, 6].
What is the total distance that the object traveled on [0, 6]?
O 50
O 40
O 30
O 24

Calculus
Application of derivativesFind the equation of the curve that passes through the point (0, 2) and has a slope of 3x-²/y at any point (x, y).
y = x³ + 2
y = x³ - 2
y = 2x³ - 4
y = 2x³ + 4

Calculus
Application of derivativesThe rate of change in the number of deer, D, within a town is inversely proportional to the number of people, p, living within the town.
Write the differential equation to solve for D(t).
Do not solve.
dD/dp = k/D
dD/dp =Dk
dD/dp = pk
dD/dp = k/p

Calculus
Application of derivativesAssume that the distance, D, a baseball is thrown is proportional to the force exerted, F.
Does it make sense to use differential equations to model the distance thrown?
If so, write the differential equation. If not, explain why.
A. No, D = k/F is a simple relationship and there is no rate of change so no need to use differential equations.
B. No, D = KF is a simple relationship and there is no rate of change so no need to use differential equations.
C. Yes, dD/dt = k/F is a differential equation with a rate of change.
D. dD/dt = kF is a differential equation with a rate of change.
![The absolute maximum of f(x) = 2x²-3x² +3 on [-1,1] is
A) 2
B) 1
C) 3
D) O
E) 7](https://media.kunduz.com/media/sug-question/raw/84171736-1657372378.5443358.jpeg?w=256)
Calculus
Application of derivativesThe absolute maximum of f(x) = 2x²-3x² +3 on [-1,1] is
A) 2
B) 1
C) 3
D) O
E) 7

Calculus
Application of derivativesLet h(v) = -15v/v² +4
Determine the critical values of h. If multiple such values exist, enter the solutions using a comma-separated list.

Calculus
Application of derivativesIf a population of endangered salmon, S(t), starts out with 80 fish and decreases at a rate proportional to 0.02 times the number of fish present each year, write the particular solution to the differential equation which describes the number of fish over time.
Lett be measured in years.
A. S(t) = 80e^-0.02t
B. S(t) = 80e^0.02t
C. S(t) = 100e^0.02t
D. S(t) = 100e^-0.2t

Calculus
Application of derivativesIf the rate of change of Q is directly proportional to Q, and if Q(0) = 100 and Q(4) = 440, find k, the proportionality constant.
A. k = 0.370
B. k = 1.482
C. k = 4.605
D. k=6.087

Calculus
Application of derivativesAssume that a population P of cheetah on the Savannah of Africa is proportional to the size of an elephant herd, E. Does it make sense to use differential equations to model the population size? If so, write the differential equation. If not, explain why.
A. Yes, dP/dt = k/E is a differential equation with a rate of change.
B. P = k/E is a simple relationship and there is no rate of change so no need to use differential equations.
C. No, P = kE is a simple relationship and there is no rate of change so no need to use differential equations.
D. Yes, dP/dt = kE is a differential equation with a rate of change.

Calculus
Application of derivativesA lighthouse is located 560 feet from the nearest point P on a straight shoreline. The revolving beacon in the lighthouse makes one revolution every 6 seconds. Find the rate at which a ray from the light moves along the shore at a point 235 feet from P.

Calculus
Application of derivativesLet f(x) = - 8x² - 14/x
Determine the critical values of f. If multiple such values exist, enter the solutions using a comma-separated list.

Calculus
Application of derivativesLet g(z) = 8z ln(-4z)
Determine the critical values of g. If multiple such values exist, enter the solutions using a comma-separated list.
![The function f(x) = In x satisfies the Mean Value Theorem on the interval [1, e²] at c =
A) 2
B) e
C) 1/e
D) e-1/e
E) e²-1/2](https://media.kunduz.com/media/sug-question/raw/84171744-1657368083.9568417.jpeg?w=256)
Calculus
Application of derivativesThe function f(x) = In x satisfies the Mean Value Theorem on the interval [1, e²] at c =
A) 2
B) e
C) 1/e
D) e-1/e
E) e²-1/2

Calculus
Application of derivativesLet g(u) = u-5/u+19
Determine the critical values of g. If multiple such values exist, enter the solutions using a comma-separated list.
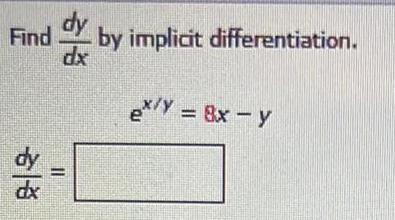
Calculus
Application of derivativesA model for a company's revenue from selling a software package is R = -2.5p² +500p, where p is the price in dollars of the software. What price will maximize revenue? Find the maximum revenue.

Calculus
Application of derivativesSuppose that for a company manufacturing calculators, the cost, revenue, and profit equations are given by C = 80,000+ 20x, R=300x-x²/20,P=R-C
where the production output in 1 week is x calculators. If production is increasing at a rate of 500 calculators per week when production output is 6,000 calculators. Find the rate of increase (decrease) in cost,
A) Costs are ___ at the rate of $_____ per week at this production level.
(Simplify your answer.)
B) Revenue is _______ at the rate of $ _______ per week at this production level.
(Simplify your answer.)
C) Profits are ___ at the rate of $ ___ per week at this production level.

Calculus
Application of derivativesFind the critical point and classify it as a local maximum, local minimum, saddle point, or none of these.
f(x, y) = x² - 2xy +9y² - 80y

Calculus
Application of derivativesFind the critical points and classify them as local maxima, local minima, saddle points, or none of these.
f(x, y) = (x+y)(xy + 9)
(x, y)=________ (smaller x-value)
(x, y) =_______ (larger x-value)

Calculus
Application of derivativesThe revenue from sales of x units of a product is given by R(x) = 200x-0.01x², and the cost of producing and selling the product is C(x) = 38x+0.01x² + 16,000.
Producing and selling how many units will result in a profit?
Producing and selling between________ and______-units of the products will result in a profit.

Calculus
Application of derivatives(a) If A is the area of a circle with radius r and the circle expands as time passes, find dA/dt in terms of
(b) Suppose oil spills from a ruptured tanker and spreads in a circular pattern. If the radius of the oil spill increases at a constant rate of 1 m/s, how fast is the area of the spill increasing when the radius is 38 m?