Application of derivatives Questions and Answers

Calculus
Application of derivativesLet h' (u)=6/u
Find the particular solution to the above differential equation that satisfies the following initial condition.
h(e^8) =-2
h(u) =

Calculus
Application of derivativesLet h''(v) = 0
Find the particular solution to the above differential equation that satisfies the following initial conditions.
h'(8) = - 4
h(9) = -6
h(v)=
Calculus
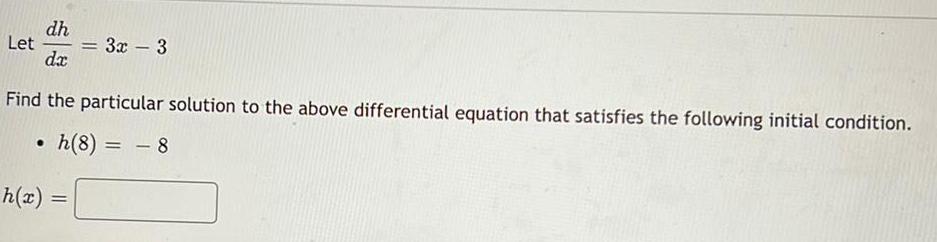
Application of derivativesLet dh/dx = 3x - 3
Find the particular solution to the above differential equation that satisfies the following initial condition.
• h(8) = -8
h(x)=

Calculus
Application of derivativesConsider the following function.
f(x) = x³ - 3x2 + 3x
Find the derivative of the function.
f'(x) =
Use the derivative to determine whether the function is strictly monotonic on its entire domain and therefore has an inverse function.
This function is strictly monotonic and therefore has an inverse.
This function is not strictly monotonic and therefore does not have an inverse.
It can not be determined whether or not this function is strictly monotonic.
Calculus
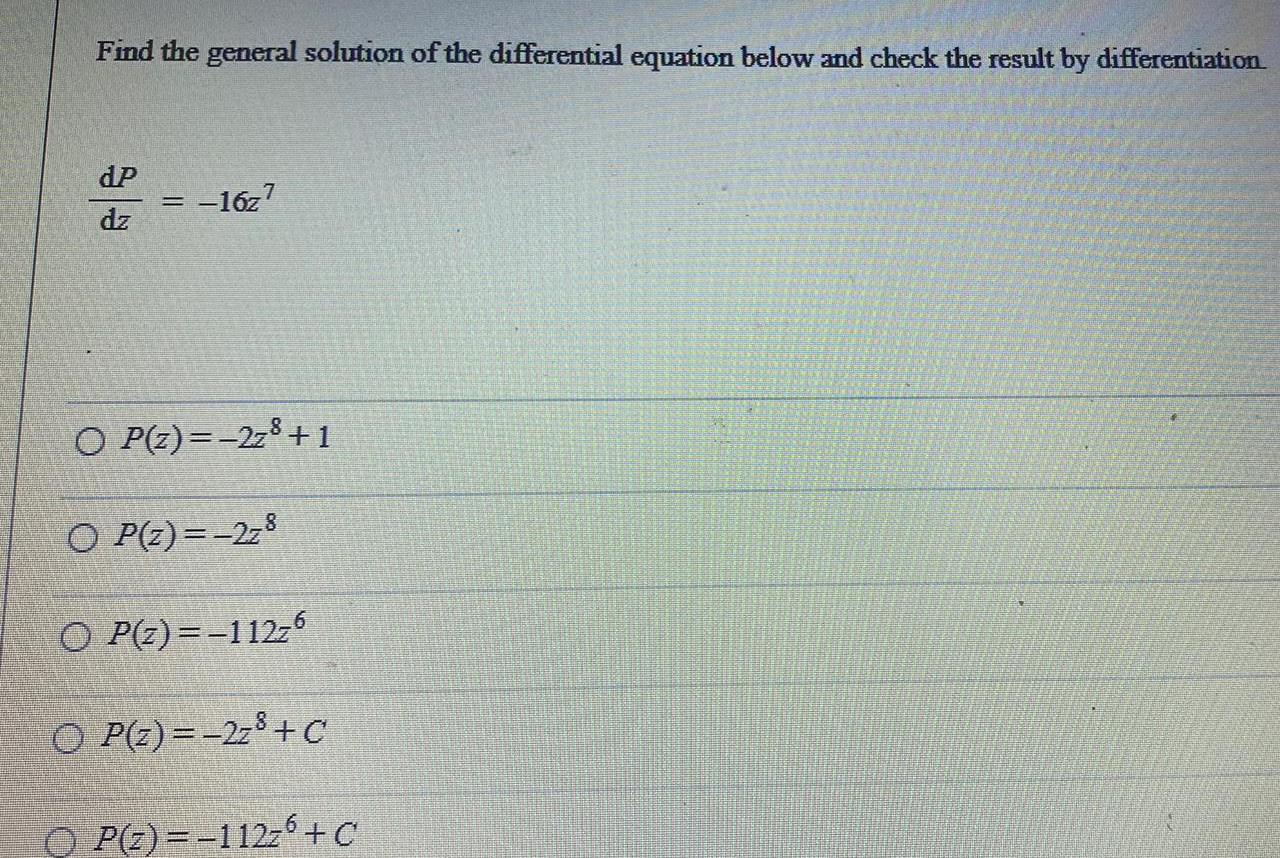
Application of derivativesFind the general solution of the differential equation below and check the result by differentiation
dp/dz=-16z^7
P(z)=-2z^8+1
P(z)=-2z^8
P(z)=-112z^6
P(z) = -2z^8+ C
P(z)=-112z^6 +C


Calculus
Application of derivativesFind the vertex of the graph of the function. Do not enter any spaces in the answer.
f(x) = (x+80)² - 21
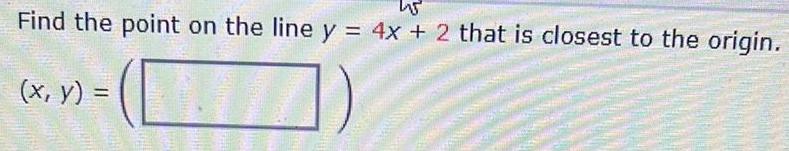
Calculus
Application of derivativesFind the point on the line y = 4x + 2 that is closest to the origin.
(x, y) =

Calculus
Application of derivativesA Norman window has the shape of a rectangle surmounted by a semicircle. (Thus the diameter of the semicircle is equal to the width of the rectangle, labeled x.)
If the perimeter of the window is 8 feet, find the exact value of x (in ft) so that the greatest possible amount of light is admitted.

Calculus
Application of derivativesFind the (a) period, (b) phase shift (if any), and (c) range of the following function.
y=-3-tan (x + π 2)
Calculus
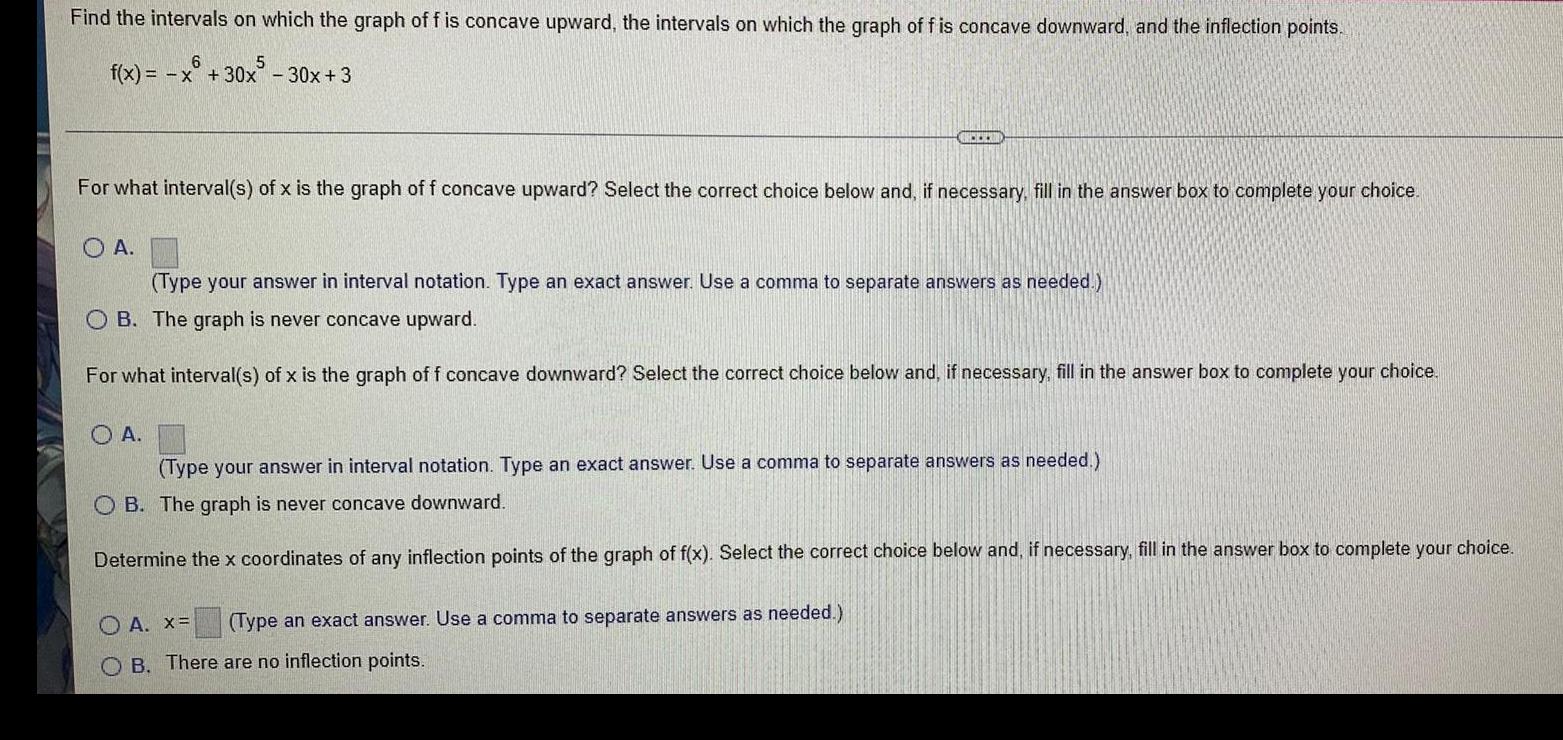
Application of derivativesFind the intervals on which the graph of f is concave upward, the intervals on which the graph of f is concave downward, and the inflection points.
f(x) = -x6 + 30x5 - 30x +3
For what interval(s) of x is the graph of f concave upward? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A.
(Type your answer in interval notation. Type an exact answer. Use a comma to separate answers as needed.)
B. The graph is never concave upward.
For what interval(s) of x is the graph of f concave downward? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A.
(Type an exact answer. Use a comma to separate answers as needed.)
B. There are no inflection points.
(Type your answer in interval notation. Type an exact answer. Use
Determine the x coordinates of any inflection points of the graph of f(x). Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
separate answers needed.)
A. x=
B. The graph is never concave downward.
![Let
g(x) = 6x²-18x+8, f₁(x) = |g(x)|, f₂(x) = |f₁(x) - P₁|,
f3(x) = |f₂(x) - P₂|
and if
P₁ = 7
then the range of
P₂
such that
f3(x)
has exactly 10 points of non-
differentiability is,
(A).
(1,5,7)
(B).
[2,5,8]
(C).
[2,9]
(D).
(1,8)](https://media.kunduz.com/media/sug-question/raw/84508726-1658277109.3638122.jpeg?w=256)
Calculus
Application of derivativesLet
g(x) = 6x²-18x+8, f₁(x) = |g(x)|, f₂(x) = |f₁(x) - P₁|,
f3(x) = |f₂(x) - P₂|
and if
P₁ = 7
then the range of
P₂
such that
f3(x)
has exactly 10 points of non-
differentiability is,
(A).
(1,5,7)
(B).
[2,5,8]
(C).
[2,9]
(D).
(1,8)

Calculus
Application of derivativesFind two positive numbers whose product is 22 and whose sum is a minimum.
The two numbers are
(Type an exact answer, using radicals as needed. Use a comma to separate answers as needed.)
Calculus
Application of derivativesFind two numbers whose sum is 24 and whose product is a maximum.
The two numbers are
(Simplify your answer. Use a comma to separate answers as needed.)
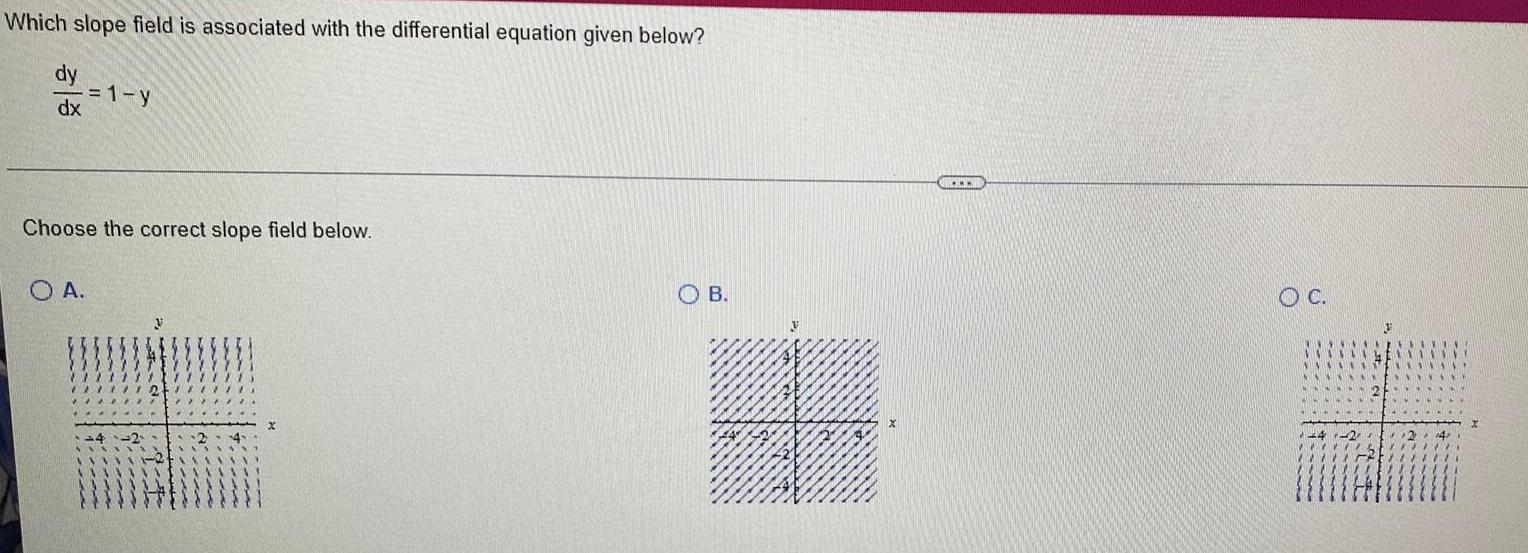
Calculus
Application of derivativesWhich slope field is associated with the differential equation given below?
dy/dx= 1-y
Calculus
Application of derivativesGonzalez Manufacturing borrowed $33000. Part of the money was borrowed at 10%, part at 12%, and part at 14%. The annual interest was $3980, and the total amount borrowed at 10% and 12% was twice the amount borrowed at 14%. Use Gaussian elimination or Gauss-Jordan elimination to find the amount borrowed at each rate.
How much money was borrowed at 10%?
How much money was borrowed at 12%?
How much money was borrowed at 14%?
Calculus
Application of derivativesFind the x and y coordinates of all inflection points.
f(x) = x³ +27x²
What is/are the inflection point(s)? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The inflection point(s) is/are
(Type an ordered pair. Use a comma to separate answers as needed.)
B. There are no inflection points.
Calculus
Application of derivativesFind the x and y coordinates of all inflection points.
f(x)=x³ +21x²
What is/are the inflection point(s)? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The inflection point(s) is/are
(Type an ordered pair. Use a comma to separate answers as needed.)
B. There are no inflection points.
Calculus
Application of derivativesOf all numbers whose difference is 12, find the two that have the minimum product.
What are the two numbers?
(Use a comma to separate answers as needed.)
Calculus
Application of derivativesFind two positive numbers whose product is 91 and whose sum is a minimum.
The two numbers are
(Type an exact answer, using radicals as needed. Use a comma to separate answers as needed.)
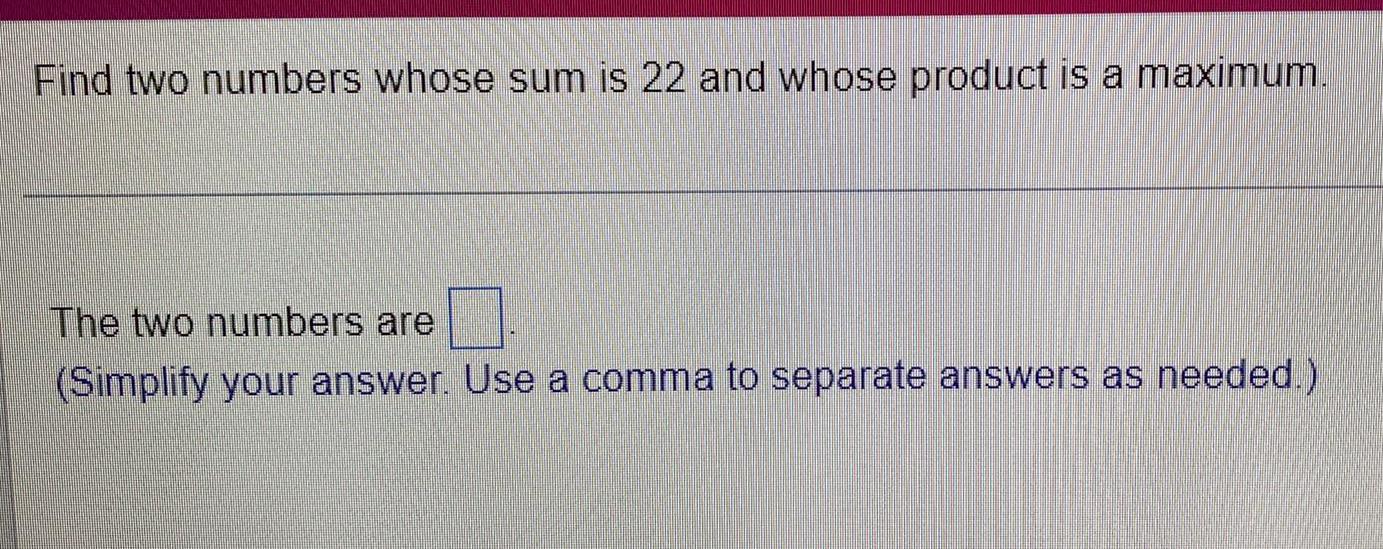
Calculus
Application of derivativesFind two numbers whose sum is 22 and whose product is a maximum.
The two numbers are
(Simplify your answer. Use a comma to separate answers as needed.)
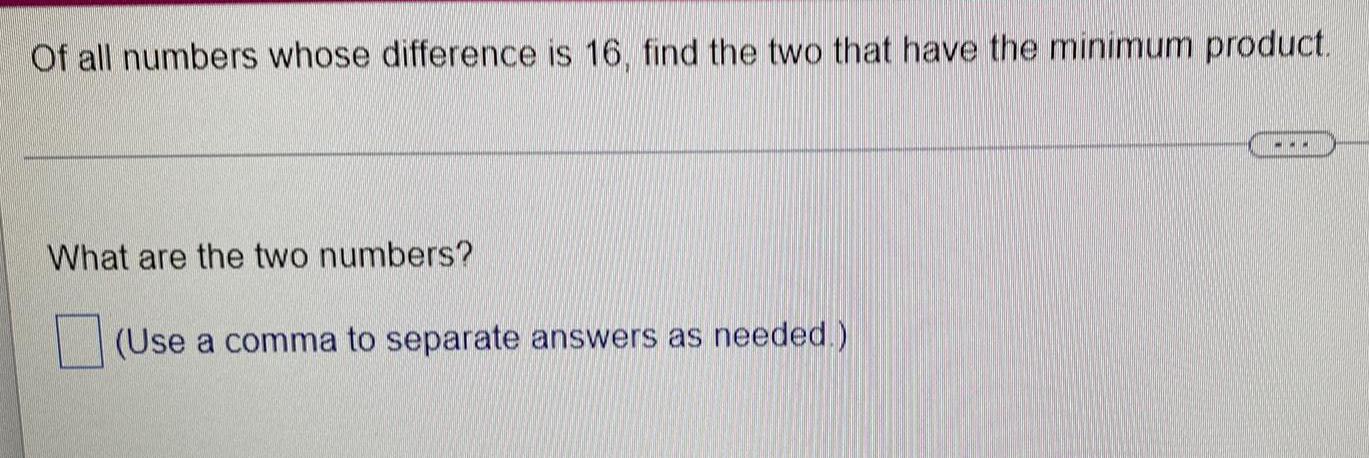
Calculus
Application of derivativesOf all numbers whose difference is 16, find the two that have the minimum product.
What are the two numbers?
(Use a comma to separate answers as needed.)
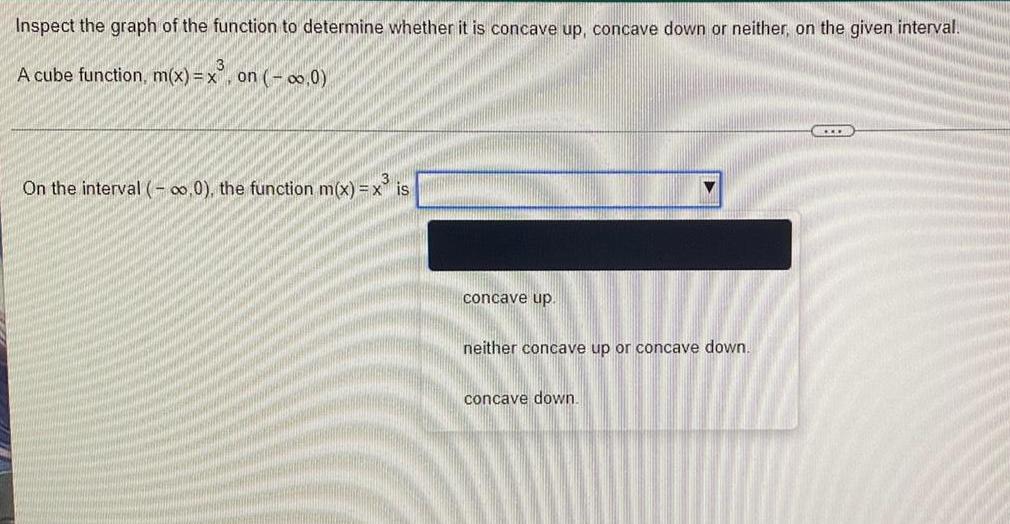
Calculus
Application of derivativesInspect the graph of the function to determine whether it is concave up, concave down or neither, on the given interval.
A cube function, m(x)=x^3, on (-∞,0)
On the interval (-∞o,0), the function m(x) = x is
concave up.
neither concave up or concave down.
concave down.
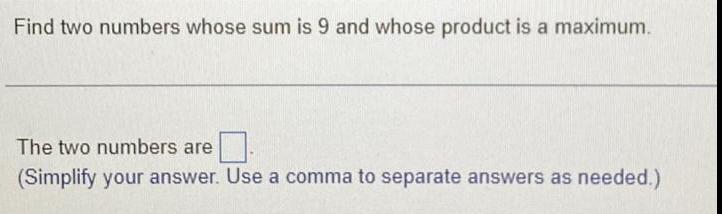
Calculus
Application of derivativesFind two numbers whose sum is 9 and whose product is a maximum.
The two numbers are
(Simplify your answer. Use a comma to separate answers as needed.)
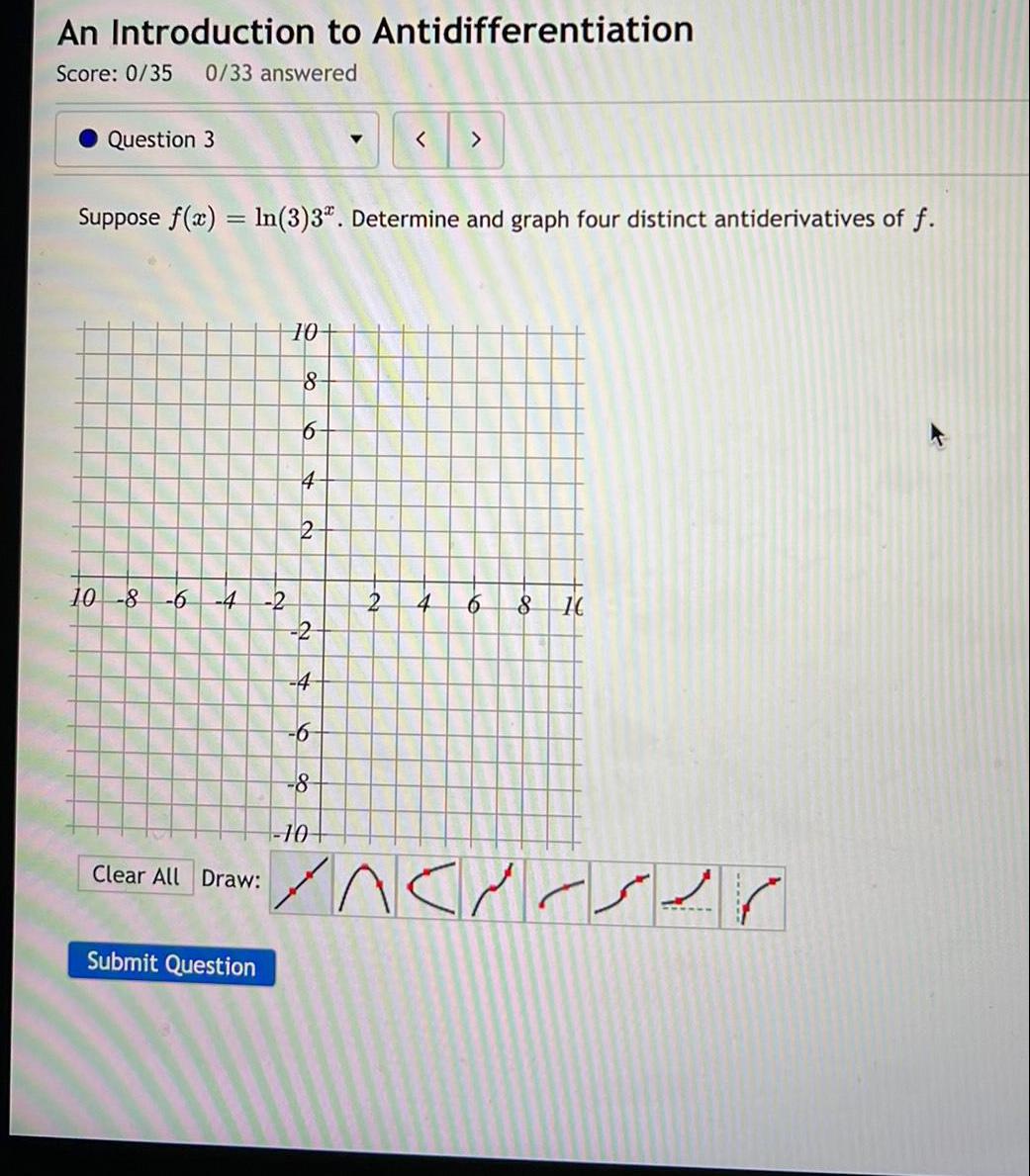
Calculus
Application of derivativesSuppose f(x) = ln (3)3x. Determine and graph four distinct antiderivatives of f.

Calculus
Application of derivativesNumber 2.) 8, 21, 46, 89, 156, ...
General Rule = ?
23rd term = ?
32nd term = ?

Calculus
Application of derivativesFirst use appropriate properties of logarithms to rewrite f(x), and then find f'(x).
f(x) = 4 In(2/x)

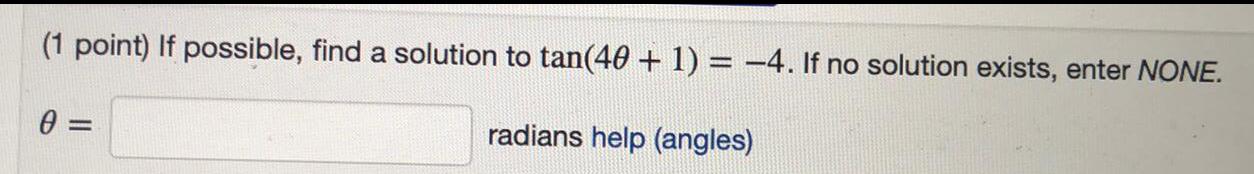
Calculus
Application of derivativesIf possible, find a solution to tan(4θ + 1) = -4. If no solution exists, enter NONE.
radians help (angles)
θ

Calculus
Application of derivativesConsider the following curve.
y =X+3/X-4
Find the slope m of the tangent line at the point (3, -6).
m =
y =
Find an equation of the tangent line to the curve at the point (3, -6).
Calculus
Application of derivativesHow many years will it take $9,000 to grow to $14,200 if it is invested at 3.50% compounded continuously?

Calculus
Application of derivativesConsider h(v) = 13v / (v²+18)
Determine the intervals on which h is decreasing.
h is decreasing on:
h is decreasing nowhere.
Determine the intervals on which h is increasing.
h is increasing on:
h is increasing nowhere.
Determine the value and location of any local minimum of h. Enter the solution in (v, h(v)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local minimum at:
h has no local minimum.
Determine the value and location of any local maximum of h. Enter the solution in (v, h(v)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local maximum at:
h has no local maximum.
![Let g(x) = x³ +24x
Determine the absolute extrema of g on [1, 5]. If multiple such values exist, enter the solutions using a comma-separated list.
The absolute minimum of g is and it occurs at x =
The absolute maximum of g is and it occurs at x =](https://media.kunduz.com/media/sug-question/raw/84463941-1658180153.1813545.jpeg?w=256)
Calculus
Application of derivativesLet g(x) = x³ +24x
Determine the absolute extrema of g on [1, 5]. If multiple such values exist, enter the solutions using a comma-separated list.
The absolute minimum of g is and it occurs at x =
The absolute maximum of g is and it occurs at x =
![At 2:00 p.m. a car's speedometer reads 30 mi/h. At 2:10 p.m. it reads 50 mi/h. Show that at some time between 2:00 and 2:10 the acceleration is exactly 120 mi/h².
Let v(t) be the velocity of the car t hours after 2:00 p.m. Then [v(1/6) - v(0)] / (1/6 - 0) = By the Mean Value Theorem, there is a number c such that 0 < c < with v'(c) = Since v'(t) is the acceleration at time t, the acceleration c hours after 2:00 p.m. is exactly 120 mi/h².](https://media.kunduz.com/media/sug-question/raw/84456591-1658179317.0492742.jpeg?w=256)
Calculus
Application of derivativesAt 2:00 p.m. a car's speedometer reads 30 mi/h. At 2:10 p.m. it reads 50 mi/h. Show that at some time between 2:00 and 2:10 the acceleration is exactly 120 mi/h².
Let v(t) be the velocity of the car t hours after 2:00 p.m. Then [v(1/6) - v(0)] / (1/6 - 0) = By the Mean Value Theorem, there is a number c such that 0 < c < with v'(c) = Since v'(t) is the acceleration at time t, the acceleration c hours after 2:00 p.m. is exactly 120 mi/h².
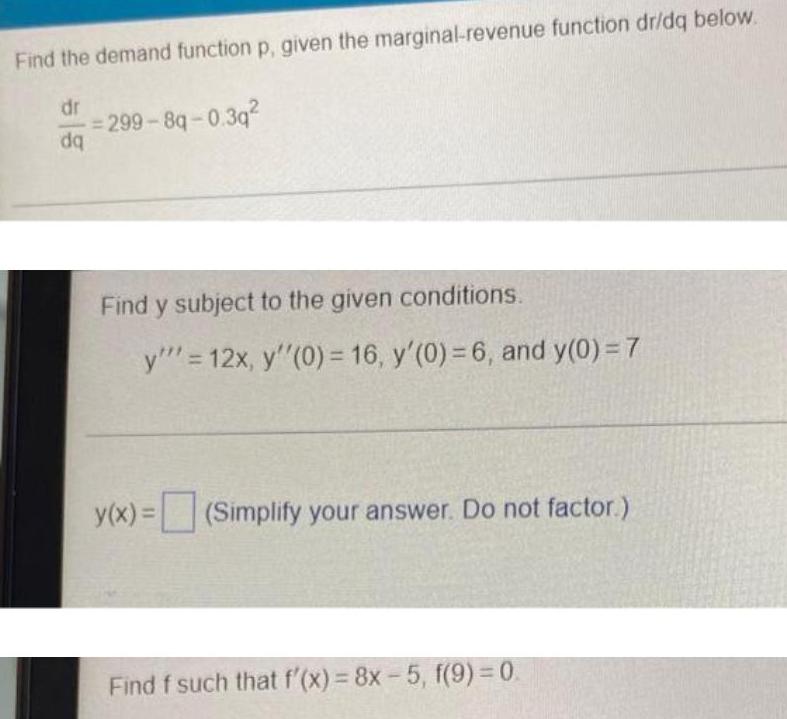
Calculus
Application of derivativesFind the demand function p, given the marginal-revenue function dr/dq below.
dr/dq=299-8q-0.3q²
Find y subject to the given conditions.
y''' = 12x, y''(0) = 16, y'(0) = 6, and y(0) = 7
y(x) = (Simplify your answer. Do not factor.)

Calculus
Application of derivativesFirst use the appropriate properties of logarithms to rewrite f(x), and then find f'(x).
f(x) = 13x + In 13x
Rewrite f(x) using properties of logarithms.
f(x) = (Do not simplify.)
Find f'(x).
f'(x) =
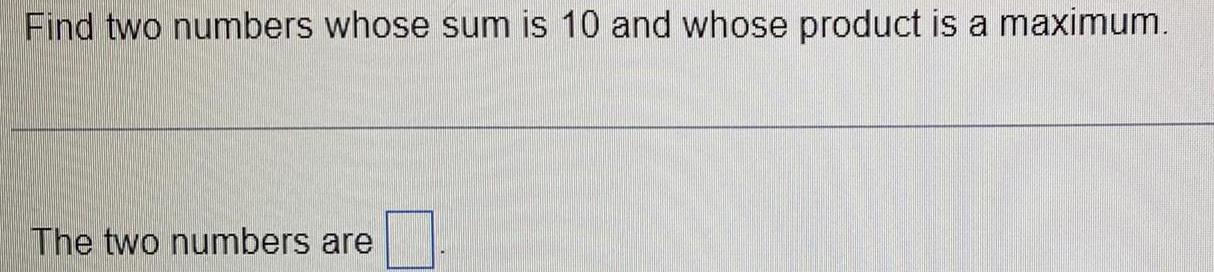
Calculus
Application of derivativesFind two numbers whose sum is 10 and whose product is a maximum.
The two numbers are

Calculus
Application of derivativesA couple who borrow $80,000 for 30 years at 6%, compounded monthly, must make monthly payments of $479.64.
(a) Find their unpaid balance after 1 year. (Round your answers to the nearest cent.)
(b) During that first year, how much do they pay towards the principle? (Round your answer to the nearest cent.)
During that first year, what are their total payments? (Round your answer to the nearest cent.)
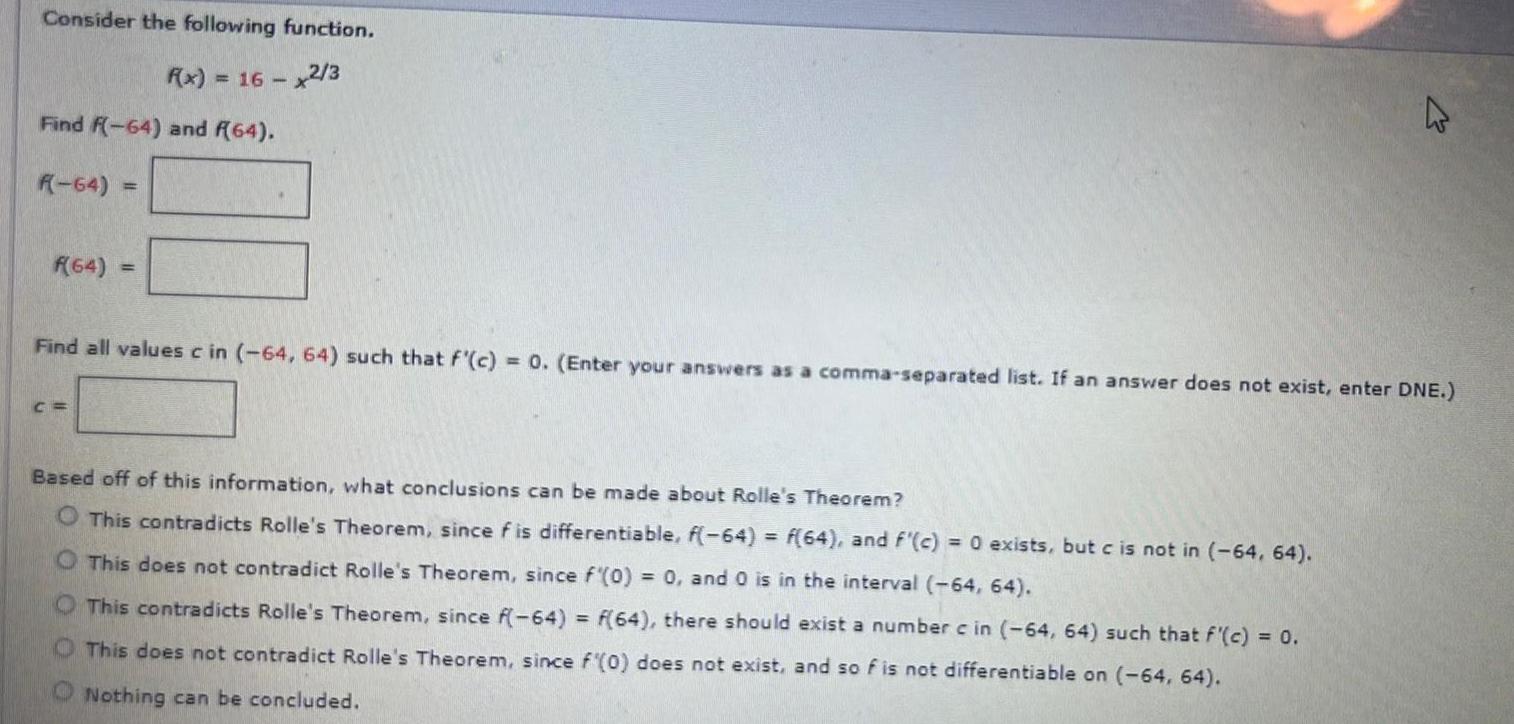
Calculus
Application of derivativesConsider the following function.
f(x) = 16 - x^(2/3)
Find f(-64) and f(64).
Find all values c in (-64, 64) such that f'(c) = 0. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.)
Based off of this information, what conclusions can be made about Rolle's Theorem?
This contradicts Rolle's Theorem, since f is differentiable, f(-64) = f(64), and f'(c) = 0 exists, but c is not in (-64, 64).
This does not contradict Rolle's Theorem, since f(0) = 0, and 0 is in the interval (-64, 64).
This contradicts Rolle's Theorem, since f(-64) = f(64), there should exist a number c in (-64, 64) such that f'(c) = 0.
This does not contradict Rolle's Theorem, since f'(0) does not exist, and so f is not differentiable on (-64, 64).
Nothing can be concluded.
![Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval?
f(x) = 3x² - 4x + 2, [0, 2]
Yes, it does not matter if f is continuous or differentiable, every function satisfies the Mean Value Theorem.
Yes, f is continuous on [0, 2] and differentiable on (0, 2) since polynomials are continuous and differentiable on R.
No, F is not continuous on [0, 2].
No, f is continuous on [0, 2] but not differentiable on (0, 2).
There is not enough information to verify if this function satisfies the Mean Value Theorem.
If it satisfies the hypotheses, find all numbers c that satisfy the conclusion of the Mean Value Theorem. (Enter your answers as a comma-separated list. If it does not satisfy the hypotheses, enter DNE).](https://media.kunduz.com/media/sug-question/raw/84449011-1658082394.4035122.jpeg?w=256)
Calculus
Application of derivativesDoes the function satisfy the hypotheses of the Mean Value Theorem on the given interval?
f(x) = 3x² - 4x + 2, [0, 2]
Yes, it does not matter if f is continuous or differentiable, every function satisfies the Mean Value Theorem.
Yes, f is continuous on [0, 2] and differentiable on (0, 2) since polynomials are continuous and differentiable on R.
No, F is not continuous on [0, 2].
No, f is continuous on [0, 2] but not differentiable on (0, 2).
There is not enough information to verify if this function satisfies the Mean Value Theorem.
If it satisfies the hypotheses, find all numbers c that satisfy the conclusion of the Mean Value Theorem. (Enter your answers as a comma-separated list. If it does not satisfy the hypotheses, enter DNE).

Calculus
Application of derivativesThe altitude of a triangle is increasing at a rate of 1 cm/min while the area of the triangle is increasing at a rate of 2 cm2/min. At what rate is the base of the triangle changing when the altitude is 10 cm and the area is 190 cm²?

Calculus
Application of derivativesD(x) is the price, in dollars per unit, that consumers are willing to pay for x units of an item, and S(x) is the price, in dollars per unit, that producers are willing to accept for x units. Find (a) the equilibrium point, (b) the consumer surplus at the equilibrium point, and (c) the producer surplus at the equilibrium point
D(x)=-3x/10+15, S(x) = x/5+5
(a) Find the equilibrium point.

Calculus
Application of derivativesA Company operates 12 oil wells in a designated area, Each pump, on average, extracts 156 barrels of oil daily. Company can but well reducep every added output of each of the wells by 6 barrels. How many wells should the Company add in order to maximize daily production ?

Calculus
Application of derivativesSolve for the variable P to two decimal places.
63,300 Pe ^0.072(9)
P = (Round to two decimal places as needed.)

Calculus
Application of derivativesAn investor bought stock for $20,000. Eight years later, the stock was sold for $40,000. If interest is compounded continuously, what annual nominal rate of interest did the original $20,000 investment earn?
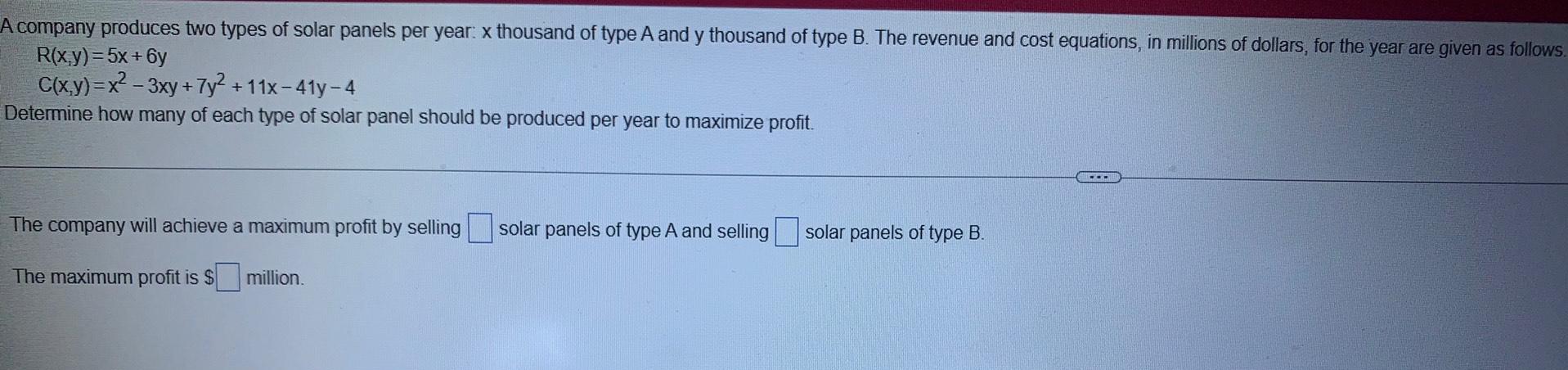
Calculus
Application of derivativesA company produces two types of solar panels per year: x thousand of type A and y thousand of type B. The revenue and cost equations, in millions of dollars, for the year are given as follows.
R(x,y) = 5x + 6y
C(x,y)=x²-3xy + 7y² +11x-41y-4
Determine how many of each type of solar panel should be produced per year to maximize profit.
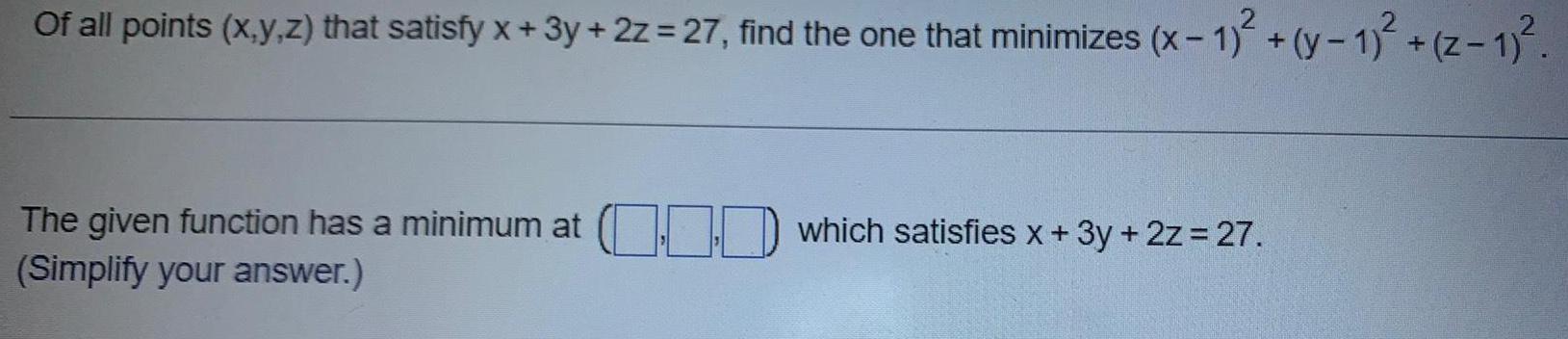
Calculus
Application of derivativesOf all points (x,y,z) that satisfy x + 3y + 2z = 27, find the one that minimizes (x-1)² + (y-1)²+(z-1)².
The given function has a minimum at which satisfies x + 3y + 2z = 27.
(Simplify your answer.)
Calculus
Application of derivativesMari needs to design an open-top box with a square base. Due to the nature of the project, the box must have a volume of 48,668 cubic inches. Determine the dimensions of the box that requires the least amount of materials to construct.
Each side of the base of the box has of length ____ inches.
The box has a height of ____ inches.

Calculus
Application of derivativesA cylindrical container must hold 92 cubic centimeters of fluid. Determine the radius the cylinder such that the construction materials necessary are as least as possible.