Application of derivatives Questions and Answers

Calculus
Application of derivativesDetermine two positive values such that the sum of the first number and four times the second number is 546 and whose product is a maximum.
Enter the solutions using a comma-separated list.
Determine the maximum value.
Calculus
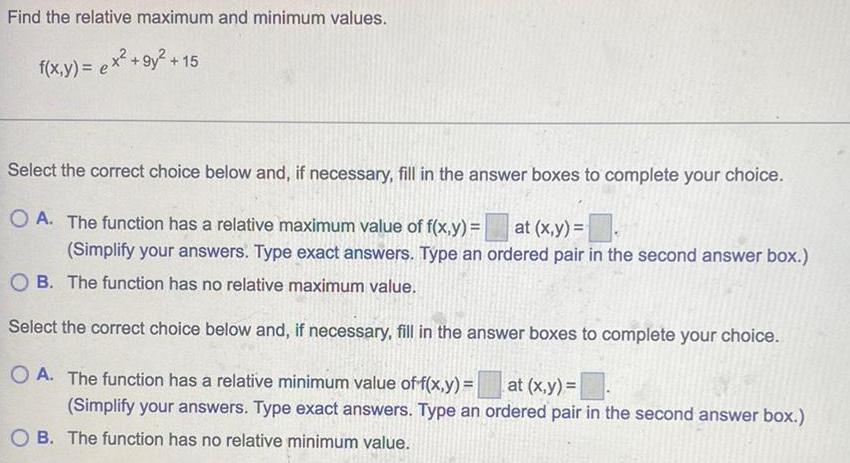
Application of derivativesFind the relative maximum and minimum values.
f(x,y) = e^x² +9y² +15
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative maximum value of f(x,y) = at (x,y)=
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative maximum value.
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative minimum value of f(x,y)= at (x,y)=
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative minimum value.

Calculus
Application of derivativesSuppose that a problem grows according to a logistical model with a carrying capacity 6200 and k=0.0015 use Euler's method with a step size h=1 to estimate the population after 50 years in the initial population is 1000
Calculus
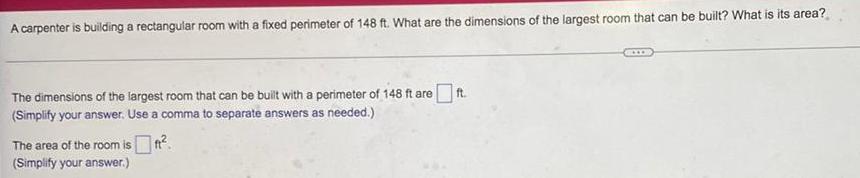
Application of derivativesA carpenter is building a rectangular room with a fixed perimeter of 148 ft. What are the dimensions of the largest room that can be built? What is its area?
The dimensions of the largest room that can be built with a perimeter of 148 ft are ft.
(Simplify your answer. Use a comma to separate answers as needed.)
The area of the room is ft2.
(Simplify your answer.)
Calculus
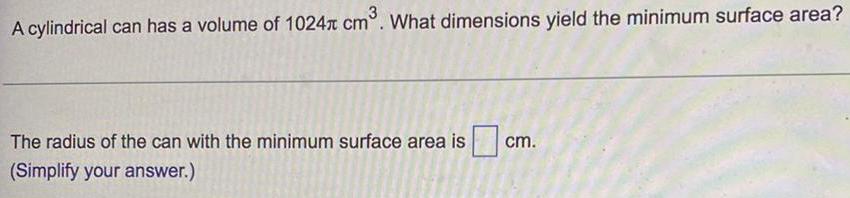
Application of derivativesA cylindrical can has a volume of 1024π cm³. What dimensions yield the minimum surface area?
The radius of the can with the minimum surface area is cm.
(Simplify your answer.)
Calculus
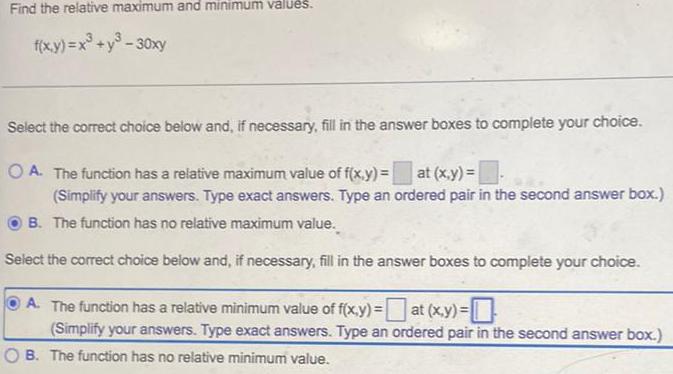
Application of derivativesFind the relative maximum and minimum values.
f(x,y)=x³+y³-30xy
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative maximum value of f(x,y)= at (x,y)=
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative maximum value.
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative minimum value of f(x,y) = at (x,y)=
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative minimum value.

Calculus
Application of derivativesTwo variable quantities A and B are found to be related by the equation given below. What is the rate of change dA/ dt at the moment when A=3 and dB/dt = 1?
A5 +B5 = = 275
dA/dt= when A=3 and dB / dt = 1.

Calculus
Application of derivativesA one-product company finds that its profit, P, in millions of dollars, is given by the following equation where a is the amount spent on advertising, in millions of dollars, and p is the price charged per item of the product, in dollars.
P(a.p) = 4ap+120p-20p²-(1/10)a²p-120
Find the maximum value of P and the values of a and p at which it is attained.
The maximum value of P is attained when a is $ million and p is $
The maximum value of P is $ million.
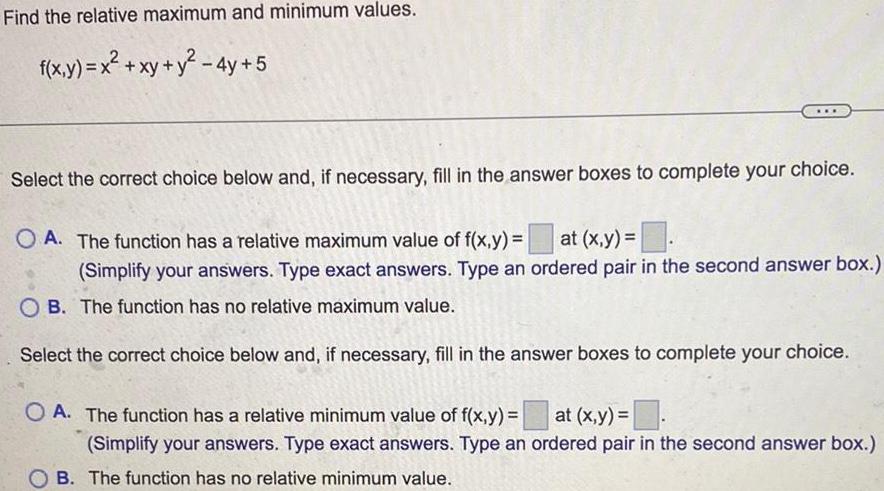
Calculus
Application of derivativesFind the relative maximum and minimum values.
f(x,y) = x² + xy + y² - 4y +5
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative maximum value of f(x,y) = at (x,y) =
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative maximum value.
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative minimum value of f(x,y) = at (x,y) =
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative minimum value.
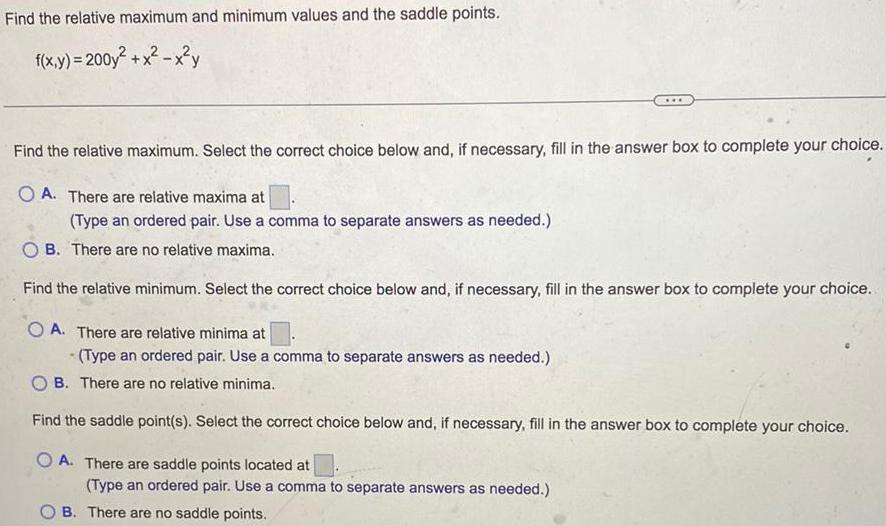
Calculus
Application of derivativesFind the relative maximum and minimum values and the saddle points.
f(x,y) = 200y² + x²-x²y
Find the relative maximum. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. There are relative maxima at
(Type an ordered pair. Use a comma to separate answers as needed.)
B. There are no relative maxima.
Find the relative minimum. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. There are relative minima at
(Type an ordered pair. Use a comma to separate answers as needed.)
B. There are no relative minima.
Find the saddle point(s). Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. There are saddle points located at
(Type an ordered pair. Use a comma to separate answers as needed.)
B. There are no saddle points.
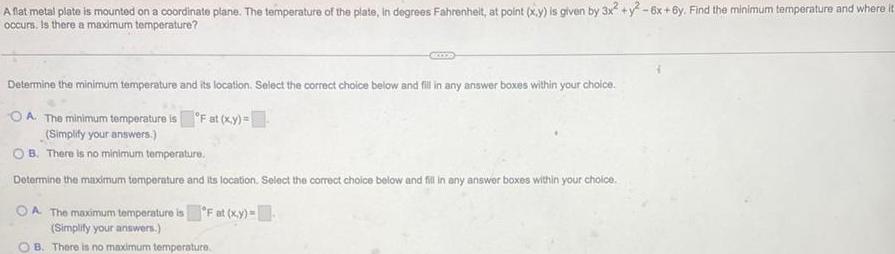
Calculus
Application of derivativesA flat metal plate is mounted on a coordinate plane. The temperature of the plate, in degrees Fahrenheit, at point (x,y) is given by 3x2 + y²-6x+6y. Find the minimum temperature and where it occurs. Is there a maximum temperature?
Determine the minimum temperature and its location. Select the correct choice below and fill in any answer boxes within your choice.
A. The minimum temperature is °F at (x,y)=
(Simplify your answers.)
B. There is no minimum temperature.
Determine the maximum temperature and its location. Select the correct choice below and fill in any answer boxes within your choice.
A The maximum temperature is °F at (x,y)=
(Simplify your answers.)
B. There is no maximum temperature.

Calculus
Application of derivativesA ball is thrown upward from the top of a building. The ball's height above ground at t seconds can be modeled by the equation
H(t) = -8t² + 40t + 60
A. When does the ball reach the maximum height?
The ball will reach the maximum height at seconds.
B. What is the maximum height of the ball?
The maximum height of the ball is
![Find the absolute maximum and absolute minimum values off on the given interval.
f(x) = 19 + 2x - x², [0,5]
absolute minimum value
absolute maximum value](https://media.kunduz.com/media/sug-question/raw/84433051-1657990186.2113678.jpeg?w=256)
Calculus
Application of derivativesFind the absolute maximum and absolute minimum values off on the given interval.
f(x) = 19 + 2x - x², [0,5]
absolute minimum value
absolute maximum value

Calculus
Application of derivativesThis extreme value problem has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint.
f(x, y) = x² - y², x² + y² = 16
maximum value
minimum value

Calculus
Application of derivativesUse Lagrange multipliers to find three positive numbers whose sum is 15 and the sum of whose squares is as small as possible. (Enter your answers as a comma-separated list.)

Calculus
Application of derivativesUse a graph or level curves or both to find the local maximum and minimum values and saddle point(s) of the function. Then use calculus to find these values precisely. (Enter your answers as comma-separated lists. If an answer does not exist, enter DNE.)
f(x, y) = x² + y² + x⁻²y⁻² + 3
local maximum value(s)
local minimum value(s)
saddle point(s) (x, y) =
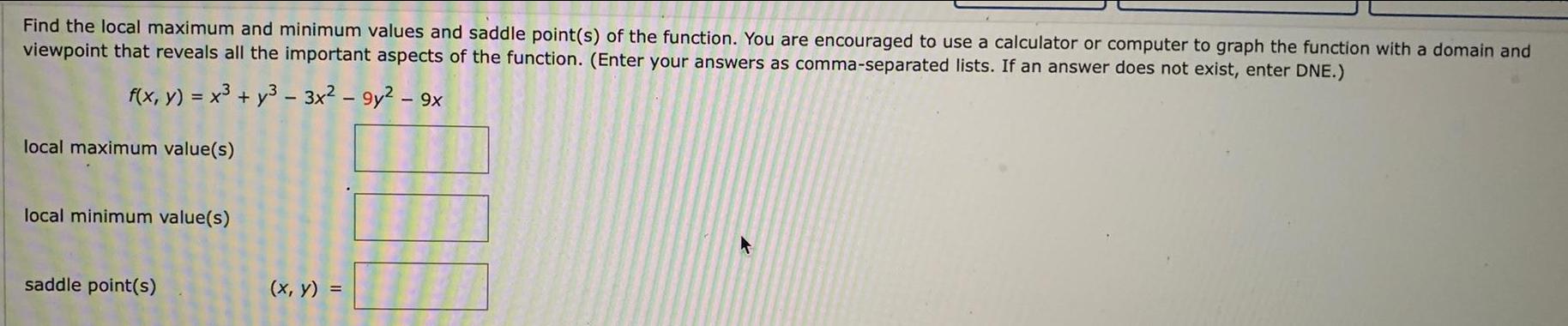
Calculus
Application of derivativesFind the local maximum and minimum values and saddle point(s) of the function. You are encouraged to use a calculator or computer to graph the function with a domain and viewpoint that reveals all the important aspects of the function. (Enter your answers as comma-separated lists. If an answer does not exist, enter DNE.)
f(x, y) = x³ + y³ - 3x² - 9y² - 9x
local maximum value(s)
local minimum value(s)
saddle point(s) (x, y) =

Calculus
Application of derivativesThe temperature at a point (x, y, z) is given by
T(x, y, z) = 400e^(-x²-5y²-9z²)
where T is measured in °C and x, y, z in meters.
(a) Find the rate of change of temperature (in °C/m) at the point P(2, -1, 4) in the direction toward the point (3, -5, 6).
(b) In which direction does the temperature increase fastest at P?
(c) Find the maximum rate of increase at P.

Calculus
Application of derivativesUse the Quotient Rule to find the derivative of the function.
y = x⁶ / (1 - x⁵)
x⁵ (6 - x⁵) / (1- x⁵)²
6x⁵ / 1-5x⁴
(x⁵ - 1)² / (x⁵(x⁶ - 5)
-x⁵(x⁵-1) / (x⁵ -6)²
![Suppose the distance s (in feet) covered by a car moving along a straight road after t seconds is given by the function s = f(t) = 3t² + 13t.
a. Find the average velocity of the object over the time period [1,2]. Round your answer to nearest 1 decimal place.
b. Find the instantaneous velocity when t-35 second. Round your answer to nearest 1 decimal place.](https://media.kunduz.com/media/sug-question/raw/84420406-1657987815.671786.jpeg?w=256)
Calculus
Application of derivativesSuppose the distance s (in feet) covered by a car moving along a straight road after t seconds is given by the function s = f(t) = 3t² + 13t.
a. Find the average velocity of the object over the time period [1,2]. Round your answer to nearest 1 decimal place.
b. Find the instantaneous velocity when t-35 second. Round your answer to nearest 1 decimal place.
Calculus
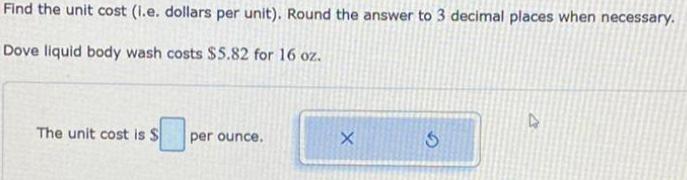
Application of derivativesFind the unit cost (l.e. dollars per unit). Round the answer to 3 decimal places when necessary.
Dove liquid body wash costs $5.82 for 16 oz.
The unit cost is $ per ounce.
Calculus
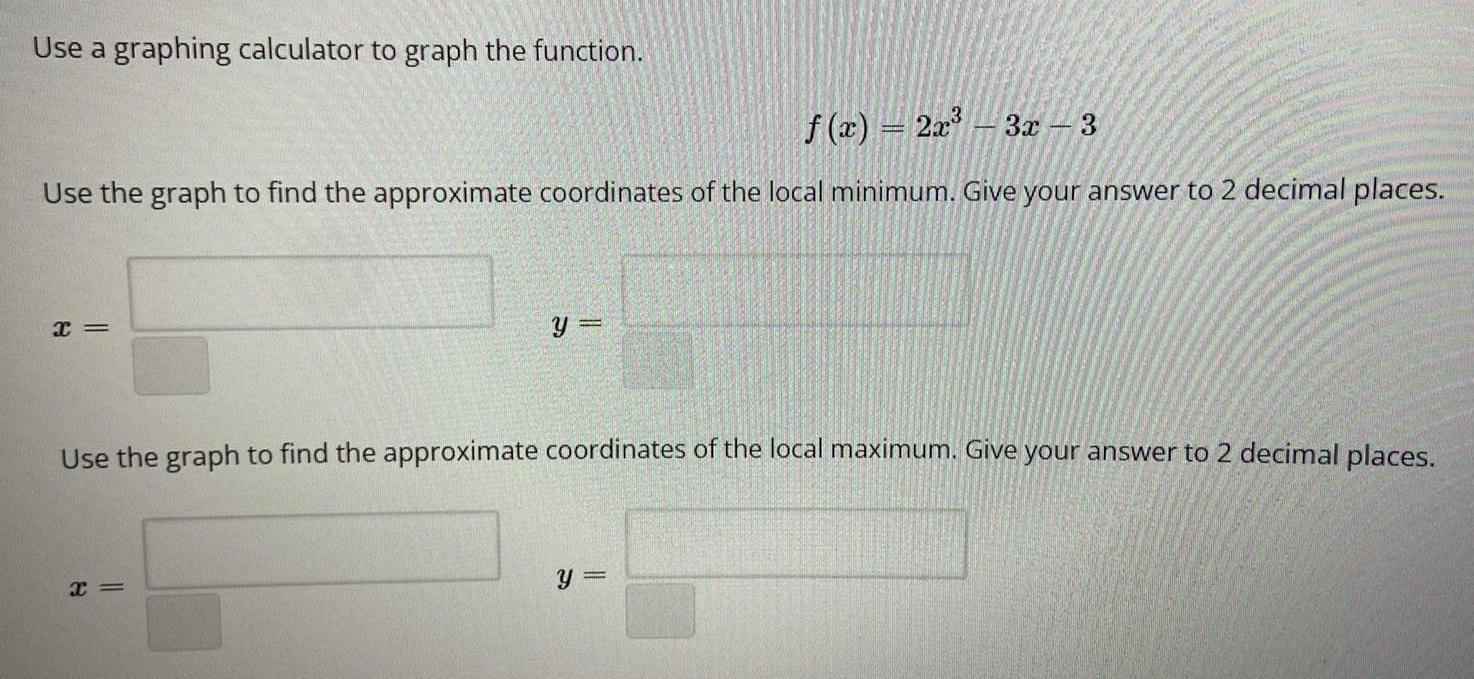
Application of derivativesUse a graphing calculator to graph the function.
f(x)=2x³- 3x-3
Use the graph to find the approximate coordinates of the local minimum. Give your answer to 2 decimal places.
x=
y =
Use the graph to find the approximate coordinates of the local maximum. Give your answer to 2 decimal places.
x=
y =
Calculus
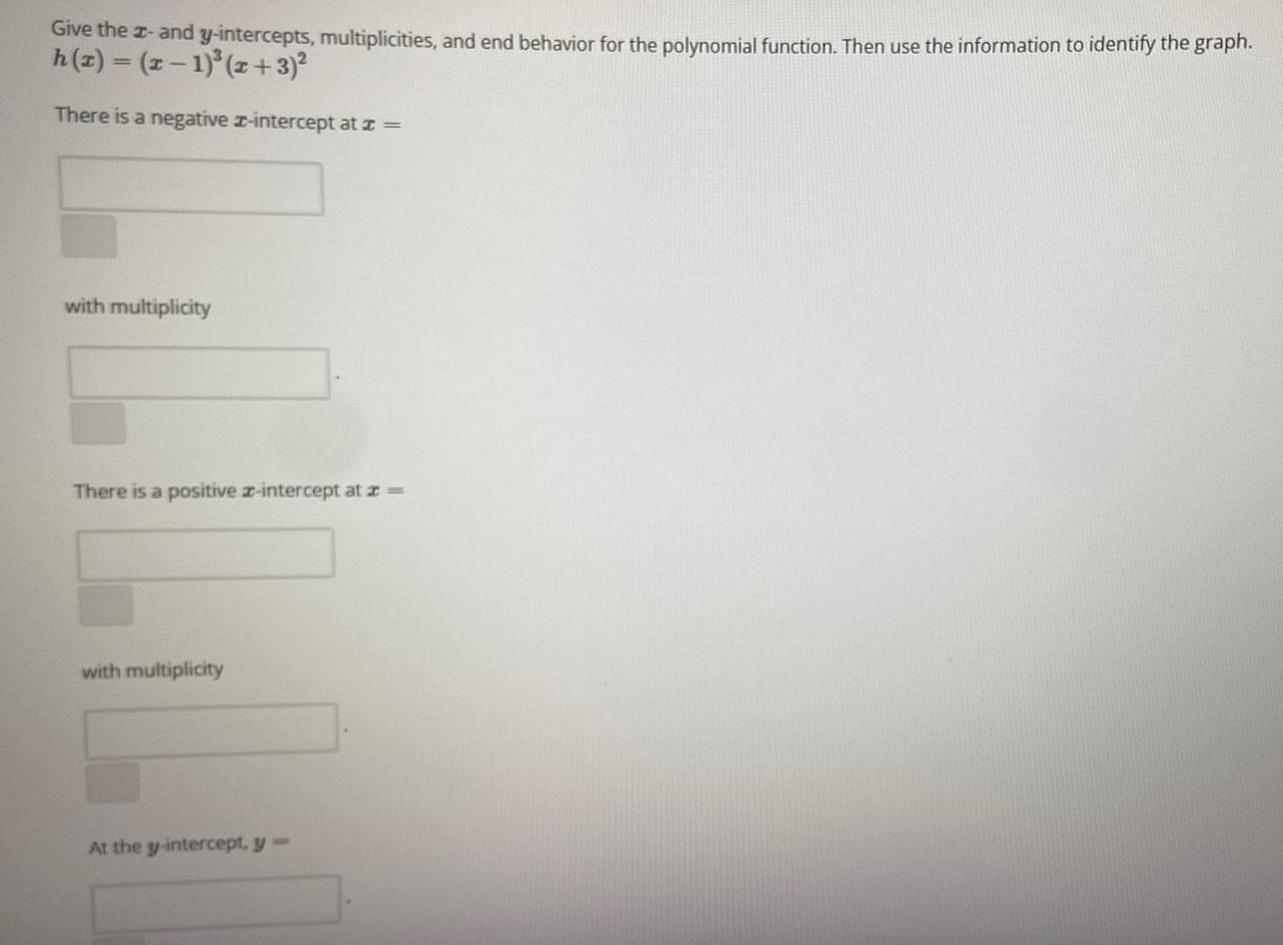
Application of derivativesGive the x- and y-intercepts, multiplicities, and end behavior for the polynomial function. Then use the information to identify the graph.
h(x) = (x-1)³ (x+3)²
There is a negative x-intercept at x =
with multiplicity
There is a positive x-intercept at x =
with multiplicity
At the y-intercept, y=

Calculus
Application of derivativesA man 6 ft tall walks at a rate of 5 ft/sec away from a lamppost that is 14 ft high. At what rate is the length of his shadow changing when he is 65 ft away from the lamppost? (Do not round your answer)
Calculus
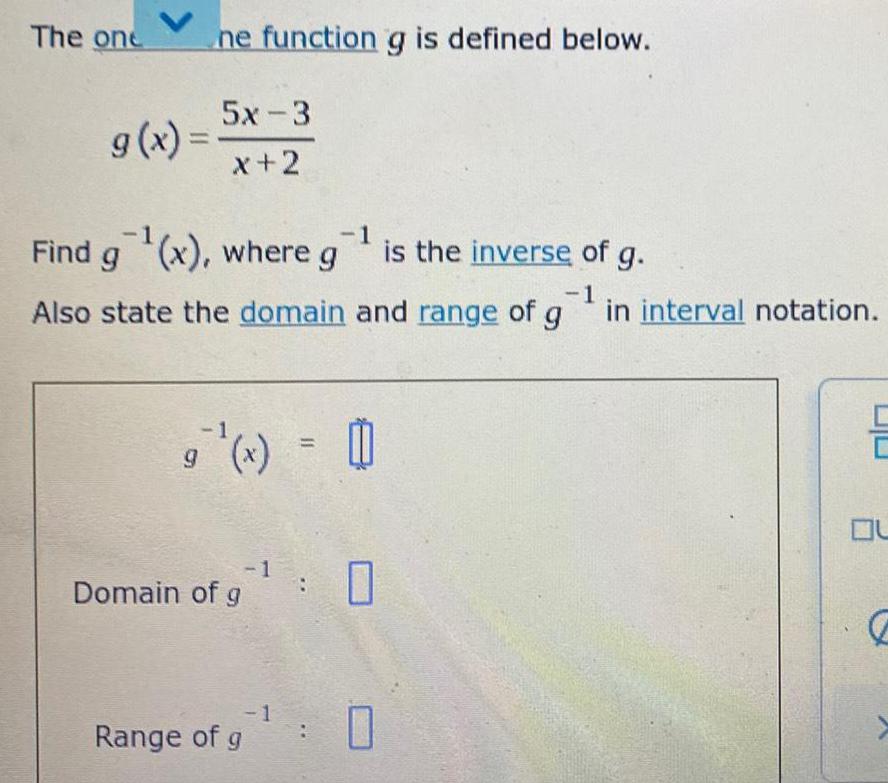
Application of derivativesThe one of the function g is defined below.
g(x) =5x-3/x+2
Find g⁻¹(x), where g⁻¹ is the inverse of g.
Also state the domain and range of g⁻¹ in interval notation.
g⁻¹(x) =
Domain of g⁻¹ :
Range of g⁻¹ :

Calculus
Application of derivativesThe one-to-one function f is defined below.
f(x)=x³ - 2
Find f⁻¹(x), where f⁻¹ is the inverse of f.
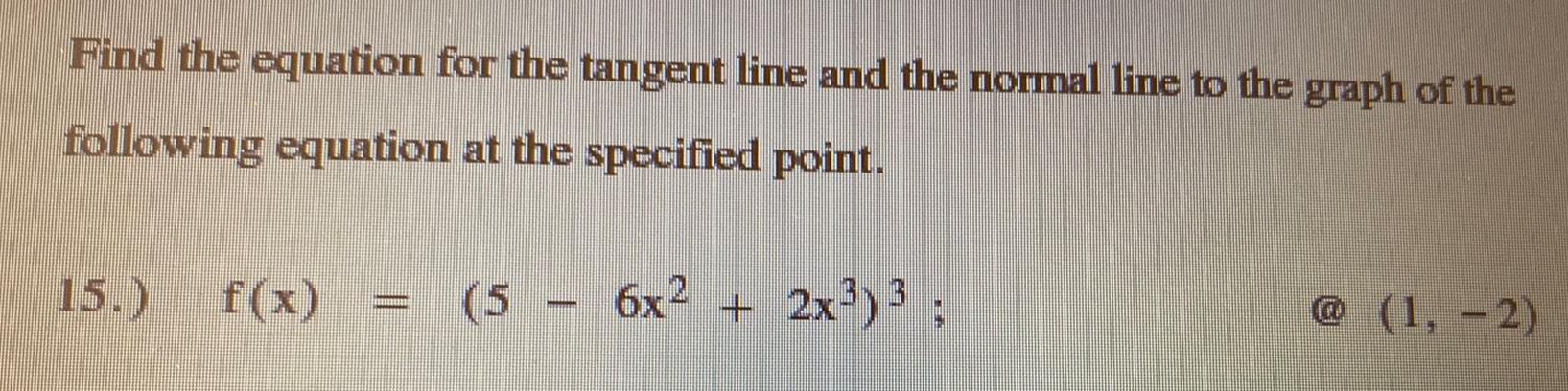
Calculus
Application of derivativesFind the equation for the tangent line and the normal line to the graph of the following equation at the specified point.
f(x) = (5- 6x² + 2x³)³ ; @ (1, -2)

Calculus
Application of derivativesA population of a particular yeast cell develops with a constant relative growth rate of 0.4285 per hour. The initial population consists of 3.5 million cells. Find the population size (in millions of cells) after 6 hours. (Round your answer to one decimal place.) I looking for this problem in textbook, or some where to learn how to resolve it. Does anybody know where it is?
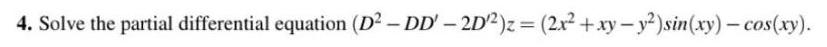
Calculus
Application of derivativesSolve the partial differential equation (D² - DD' - 2D'²)z = (2x²+xy-y²) sin(xy) - cos(xy).
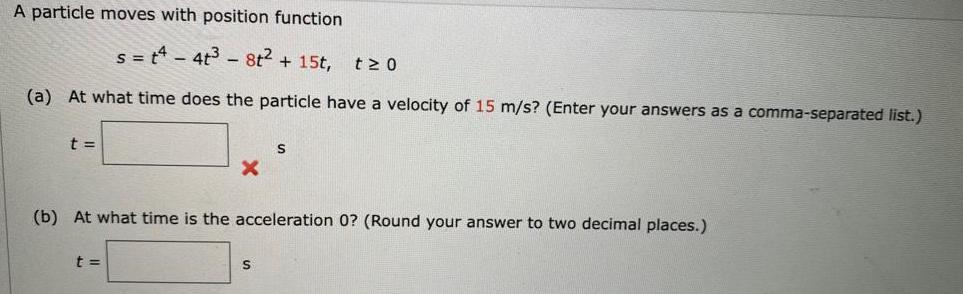
Calculus
Application of derivativesA particle moves with position function
s=t^4-4t³ - 8t² + 15t, t≥ 0
(a) At what time does the particle have a velocity of 15 m/s? (Enter your answers as a comma-separated list.)
t =
(b) At what time is the acceleration 0? (Round your answer to two decimal places.)
t =
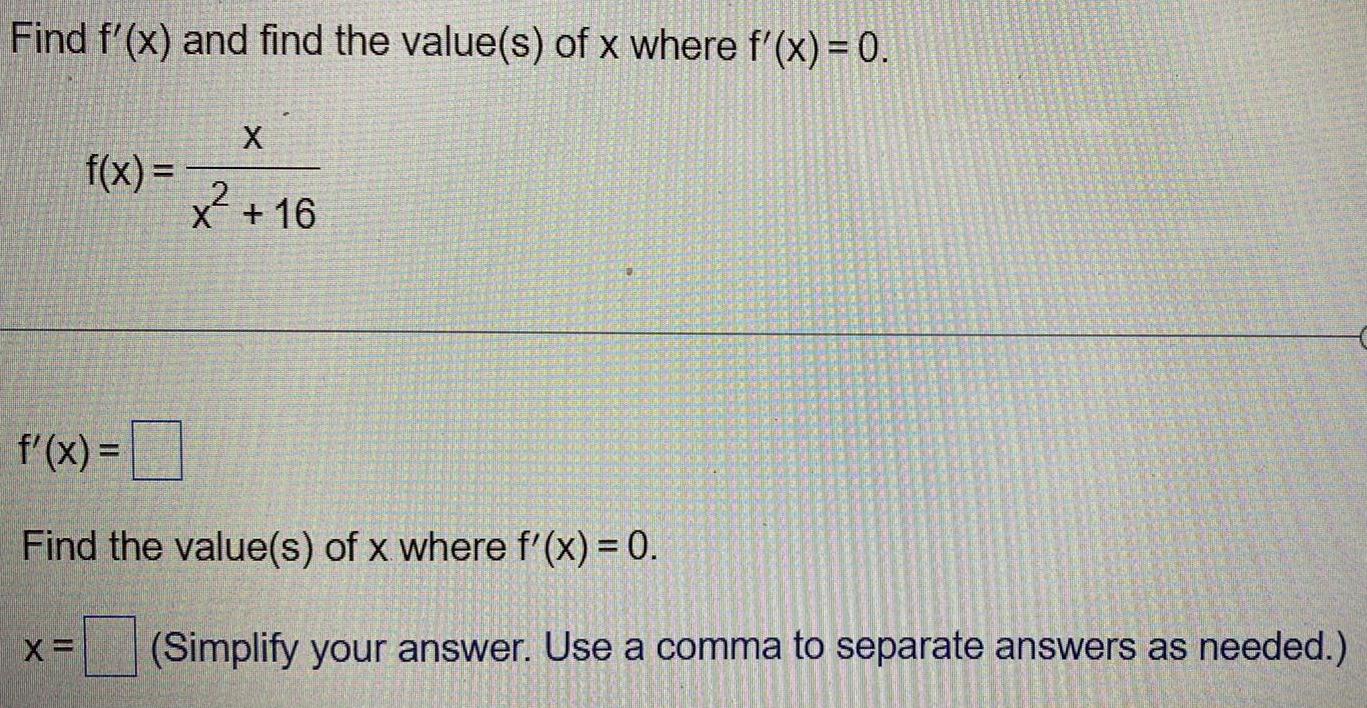
Calculus
Application of derivativesFind f'(x) and find the value(s) of x where f'(x) = 0.
f(x) = x/ x^2 +16
f'(x) =
Find the value(s) of x where f'(x) = 0.
x=
(Simplify your answer. Use a comma to separate answers as needed.)
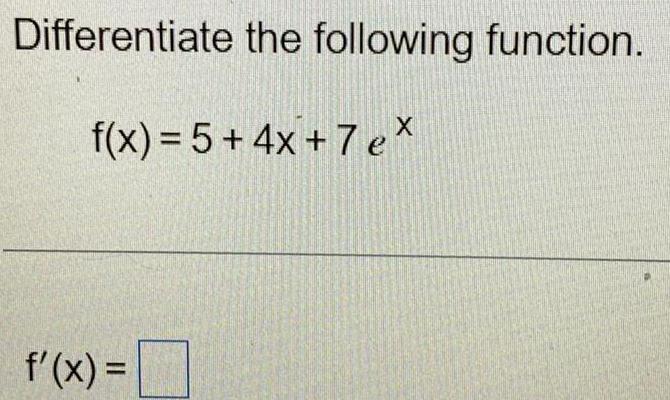

Calculus
Application of derivativesWhich of the following functions passes through the point (0, 10) and satisfies f'(x)=8?
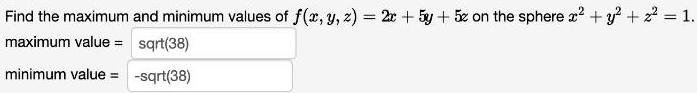
Calculus
Application of derivativesFind the maximum and minimum values of f(x, y, z) = 2x + 5y + 5x on the sphere x² + y² + z² = 1.
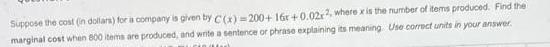
Calculus
Application of derivativesSuppose the cost (in dollars) for a company is given by C(x)=200+ 16x +0.02x^2, where x is the number of items produced. Find the marginal cost when 800 items are produced, and write a sentence or phrase explaining its meaning Use correct units in your answer.


Calculus
Application of derivativesGiven that (x, y) = (x+2y)/k if x = -2,1 and y = 3,4, is a joint probability distribution function for the random variables X and Y. Find:
a. The value of K
b. The marginal function of x
c. The marginal function of y.
d. (f(xly = 4)

Calculus
Application of derivativesFind the equation of the line tangent to the graph of f(x) = (In x)^4 at x = 6.

Calculus
Application of derivativesIn 2012, 34.1% of all glass containers were recycled. A beverage company used 400,000 lb of glass containers per year. After recycling, the amount of glass, in
pounds, still in use after t years is given by N(t) = 400,000(0.332)¹.
a) Find N(5), and explain its meaning.
b) Find N'(5), and explain its meaning.
c) When will 2% of the original amount of glass still be in use?

Calculus
Application of derivativesAt what point does the curve have maximum curvature?
y = 5e^x
(x, y) =
What happens to the curvature as x → ∞?
k(x) approaches as x → ∞o.

Calculus
Application of derivativesConsider g(w) = - 2e^-2/w
Determine the intervals on which g is concave down.
g is concave down on:
g is concave down nowhere.
Determine the intervals on which g is concave up.
g is concave up on:
g is concave up nowhere.
Determine the value and location of any inflection point of g. Enter the solution in (w, g(w)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
g has an inflection point at:
g has no inflection point.

Calculus
Application of derivativesConsider g(y) = 6y(ln( – 5y))³
Determine the intervals on which g is concave down.
g is concave down on:
g is concave down nowhere.
Determine the intervals on which g is concave up.
g is concave up on:
g is concave up nowhere.
Determine the value and location of any inflection point of g. Enter the solution in (y, g(y)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
g has an inflection point at:
g has no inflection point.

Calculus
Application of derivativesConsider h(t):=14t^4 + 28/5t² and use the Second Derivative Test to address the following prompts.
Determine the value and location of any local minimum of f. Enter the solution in (t, h(t)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local minimum at:
h has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (t, h(t)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local maximum at:
h has no local maximum.
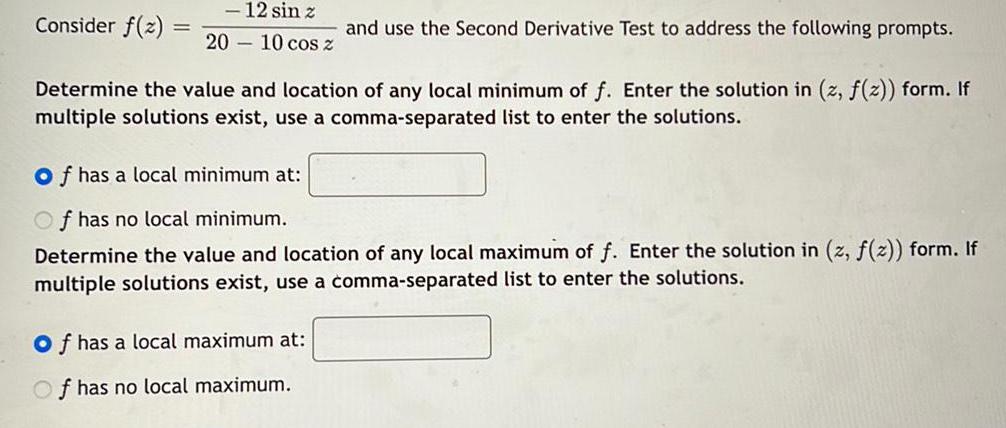
Calculus
Application of derivativesConsider f(z)=-12 sin z/20-10 cos z
and use the Second Derivative Test to address the following prompts.
Determine the value and location of any local minimum of f. Enter the solution in (z, f(z)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
f has a local minimum at:
f has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (z, f(z)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
f has a local maximum at:
f has no local maximum.

Calculus
Application of derivativesConsider h(t) = t3(-4+ 5t) + 5 and use the Second Derivative Test to address the following prompts.
Determine the value and location of any local minimum of f. Enter the solution in (t, h(t)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local minimum at:
h has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (t, h(t)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has a local maximum at:
h has no local maximum.
![Consider g(x) = 6 sin x + 13x on [-π/2 , 3π/2]
Determine the intervals on which g is concave down.
g is concave down on:
g is concave down nowhere.
Determine the intervals on which g is concave up.
g is concave up on:
g is concave up nowhere.
Determine the value and location of any inflection point of g. Enter the solution in (x, g(x)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
g has an inflection point at:
g has no inflection point.](https://media.kunduz.com/media/sug-question/raw/84304673-1657696170.2962596.jpeg?w=256)
Calculus
Application of derivativesConsider g(x) = 6 sin x + 13x on [-π/2 , 3π/2]
Determine the intervals on which g is concave down.
g is concave down on:
g is concave down nowhere.
Determine the intervals on which g is concave up.
g is concave up on:
g is concave up nowhere.
Determine the value and location of any inflection point of g. Enter the solution in (x, g(x)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
g has an inflection point at:
g has no inflection point.
![Consider f(x) = - 8 sin² x - 16 cos x on [0, 2π].
Determine the intervals on which f is concave down.
f is concave down on:
f is concave down nowhere.
Determine the intervals on which f is concave up.
f is concave up on:
f is concave up nowhere.
Determine the value and location of any inflection point of f. Enter the solution in (x, f(x)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
f has an inflection point at:
f has no inflection point.](https://media.kunduz.com/media/sug-question/raw/84304680-1657696100.0682094.jpeg?w=256)
Calculus
Application of derivativesConsider f(x) = - 8 sin² x - 16 cos x on [0, 2π].
Determine the intervals on which f is concave down.
f is concave down on:
f is concave down nowhere.
Determine the intervals on which f is concave up.
f is concave up on:
f is concave up nowhere.
Determine the value and location of any inflection point of f. Enter the solution in (x, f(x)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
f has an inflection point at:
f has no inflection point.

Calculus
Application of derivativesConsider h(x) = 16 (x² - 64)^2/3
Determine the intervals on which h is concave down.
h is concave down on:
h is concave down nowhere.
Determine the intervals on which h is concave up.
h is concave up on:
h is concave up nowhere.
Determine the value and location of any inflection point of h. Enter the solution in (x, h(x)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has an inflection point at:
h has no inflection point.

Calculus
Application of derivativesConsider g(w) = 11(w - 9)^4 - 2 - 22(w - 9)^2 and use the Second Derivative Test to address the following prompts.
Determine the value and location of any local minimum of f. Enter the solution in (w, g(w)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
g has a local minimum at:
g has no local minimum.
Determine the value and location of any local maximum of f. Enter the solution in (w, g(w)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
g has a local maximum at:
g has no local maximum.

Calculus
Application of derivativesConsider h(y)= -1/5 y + 1/2 y^2 -3/7+7/6y^3
h is concave up on:
Determine the intervals on which h is concave down.
h is concave down on:
h is concave down nowhere.
Determine the intervals on which h is concave up.
h is concave up on:
h is concave up nowhere.
Determine the value and location of any inflection point of h. Enter the solution in (y, h(y)) form. If multiple solutions exist, use a comma-separated list to enter the solutions.
h has an inflection point at:
h has no inflection point.