Application of derivatives Questions and Answers
Calculus
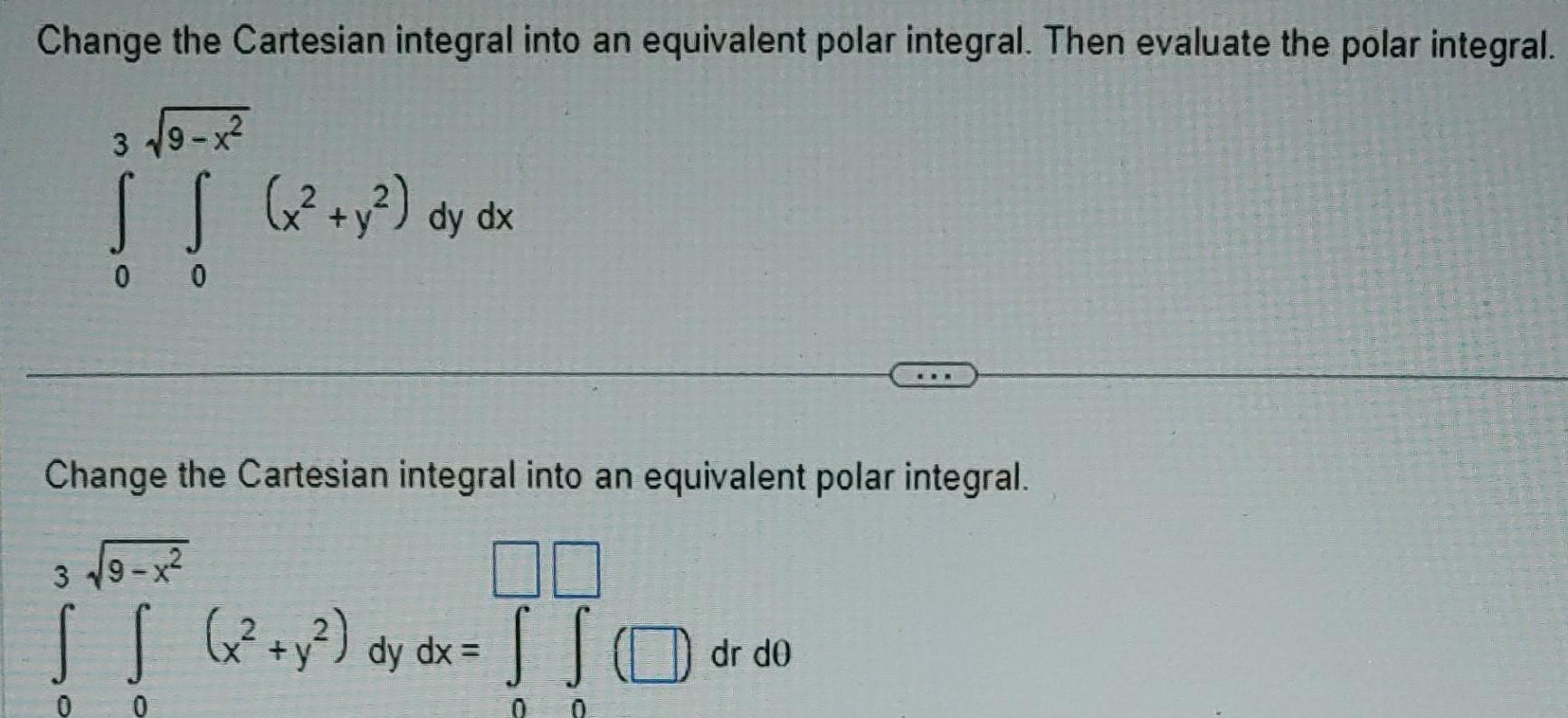
Application of derivativesChange the Cartesian integral into an equivalent polar integral Then evaluate the polar integral 3 9 x S S x y dy dx 0 0 Change the Cartesian integral into an equivalent polar integral 3 9 x IT TIC S S x y dy dx 0 dr de
Calculus
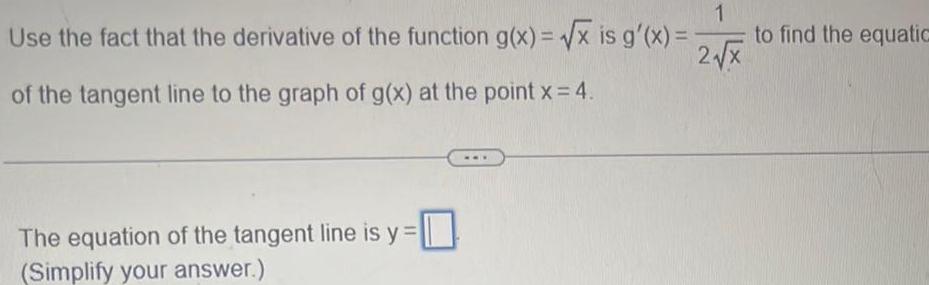
Application of derivativesUse the fact that the derivative of the function g x x is g x 1 2 x of the tangent line to the graph of g x at the point x 4 The equation of the tangent line is y Simplify your answer to find the equatic

Calculus
Application of derivativesx 1 Thus y 1 1 91 441 6 2 3 1 91 17 2 6 3 31 8 2 6 HIGHER ORDER ODE 41 271 41 4 16 As mentioned earlier we associate a first order ODE with a order k ODE and try to get information about the solutions of the higher order ODE in terms of those of the associated first order ODE In particular we are interested in a condition on the function f f t X which will di di ensure existence and uniqueness of the initial value problem for the higher order ODE In this article we explain the theory To begin with we consider the ODE dx dx f 1 x dt 4 Together with the initial condition dx MATHEMATICS di We introduce a new variable y 2 where y ranges in 2 and y y ranging in R Next we define F 1x2xRx R R by putting F t y F t Y Y3 f t y Now the given initial value problem for the order k ODE give rise to the following initial value problem in the first order ODE to W 1 dr F t y 5 the initial condition for it being y t x W W Clearly the above first order ODE is actually the following system of first order ODE 27
Calculus
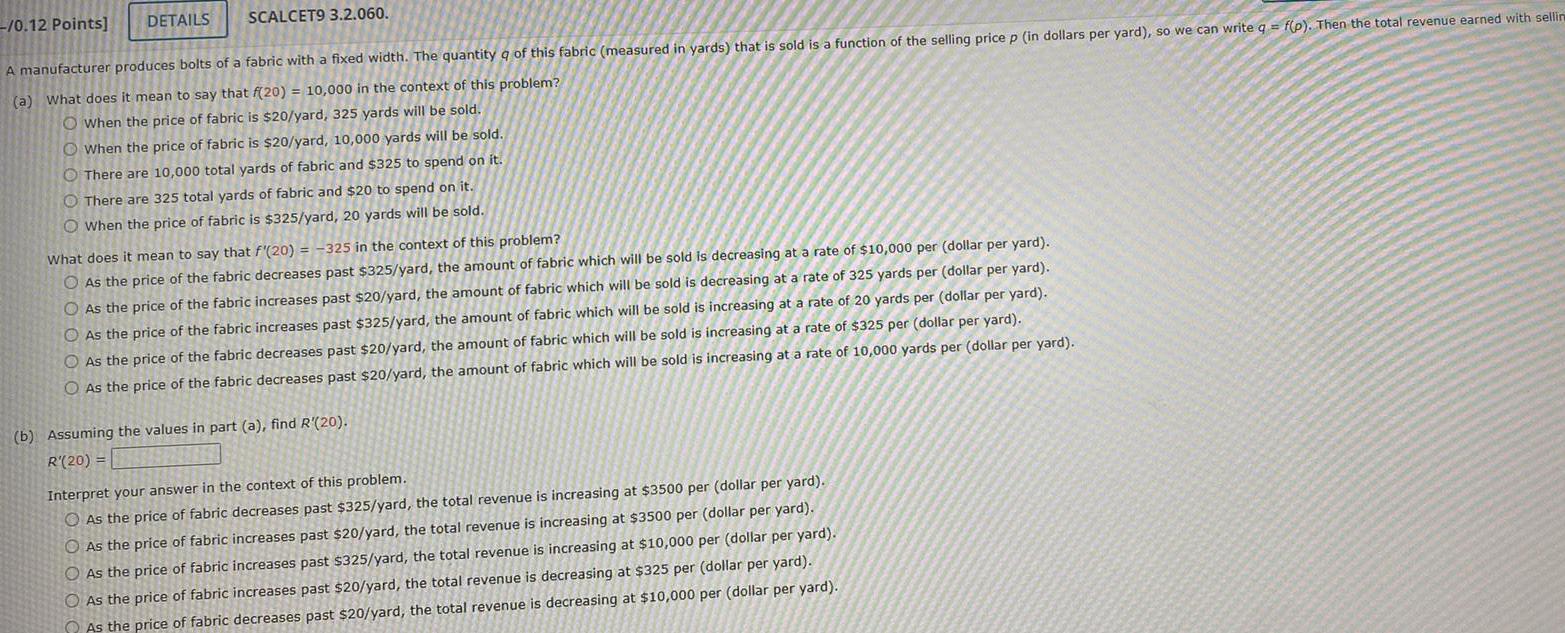
Application of derivatives0 12 Points DETAILS SCALCET9 3 2 060 A manufacturer produces bolts of a fabric with a fixed width The quantity of this fabric measured in yards that is sold is a function of the selling price p in dollars per yard so we can write q f p Then the total revenue earned with sellin a What does it mean to say that f 20 10 000 in the context of this problem O When the price of fabric is 20 yard 325 yards will be sold When the price of fabric is 20 yard 10 000 yards will be sold There are 10 000 total yards of fabric and 325 to spend on it O There are 325 total yards of fabric and 20 to spend on it When the price of fabric is 325 yard 20 yards will be sold What does it mean to say that f 20 325 in the context of this problem O As the price of the fabric decreases past 325 yard the amount of fabric which will be sold is decreasing at a rate of 10 000 per dollar per yard O As the price of the fabric increases past 20 yard the amount of fabric which will be sold is decreasing at a rate of 325 yards per dollar per yard As the price of the fabric increases past 325 yard the amount of fabric which will be sold is increasing at a rate of 20 yards per dollar per yard O As the price of the fabric decreases past 20 yard the amount of fabric which will be sold is increasing at a rate of 325 per dollar per yard O As the price of the fabric decreases past 20 yard the amount of fabric which will be sold is increasing at a rate of 10 000 yards per dollar per yard b Assuming the values in part a find R 20 R 20 Interpret your answer in the context of this problem As the price of fabric decreases past 325 yard the total revenue is increasing at 3500 per dollar per yard As the price of fabric increases past 20 yard the total revenue is increasing at 3500 per dollar per yard O As the price of fabric increases past 325 yard the total revenue is increasing at 10 000 per dollar per yard O As the price of fabric increases past 20 yard the total revenue is decreasing at 325 per dollar per yard As the price of fabric decreases past 20 yard the total revenue is decreasing at 10 000 per dollar per yard

Calculus
Application of derivativeswith components 8 828 18 x dx 8 2010 x dx Equivalently form we have 18 x dx 18 x dx 182 x dx 1 j de Thus We will use these notations in this article Example 1 Obtain approximate solutions upto of the following initial value problem 2x 3y x 0 1 dx di dy dt Solution t y y 0 2 Thus We have x t 1 y t 2 x 1 1 2 x 8 3y s ds 1 8ds X 1 2 2 s y s ds x 1 0 2 2 2 2 y 1 2 s 8r 1 Next x 1 2x 0 35 404 ds 1 1 8 2 2x 2 s x 1 LY C 11 8 1 2 s y s d 2 3 2 31 2 1 35 2 d 2 3 6 2 21 11 8 1 21 2 6 1 8ds 8t 1 then 3 2 24 written in the columnal and so on 18 x dx Chapter 2 Systmes of First Order ODE Example 2 Obtain approximate solution upto dx tx 1 y x 0 1 dt
Calculus
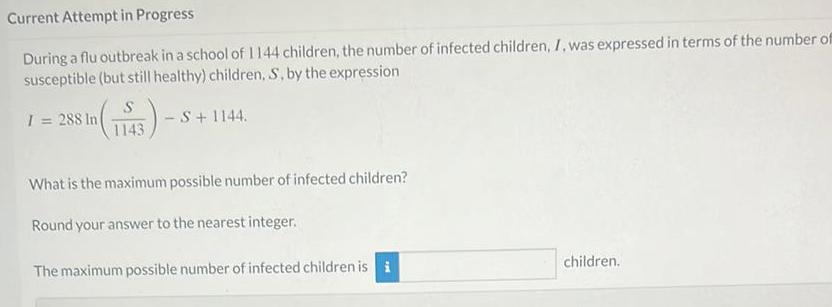
Application of derivativesCurrent Attempt in Progress During a flu outbreak in a school of 1144 children the number of infected children I was expressed in terms of the number of susceptible but still healthy children S by the expression 153 S S 1144 1143 I 288 In What is the maximum possible number of infected children Round your answer to the nearest integer The maximum possible number of infected children is i children
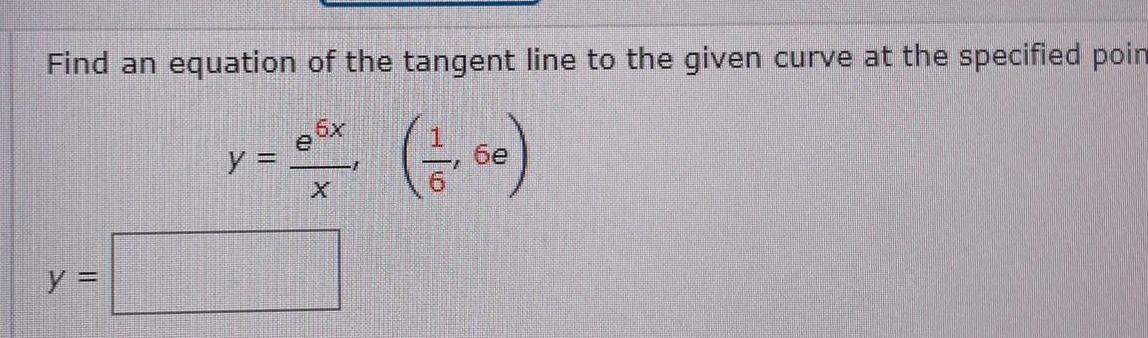
Calculus
Application of derivativesFind an equation of the tangent line to the given curve at the specified poin y ath 1 00 X y
Calculus
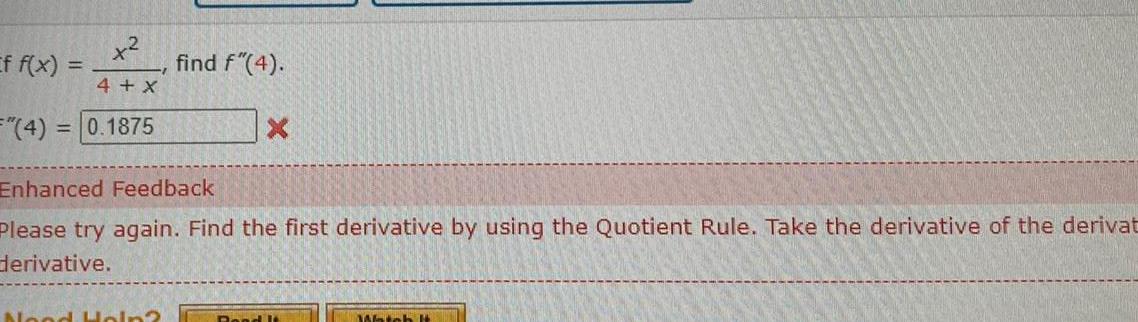
Application of derivativesx 4 X 0 1875 Ef f x 4 find f 4 Enhanced Feedback Please try again Find the first derivative by using the Quotient Rule Take the derivative of the derivat derivative Nood Hain Rond I Watch It
Calculus
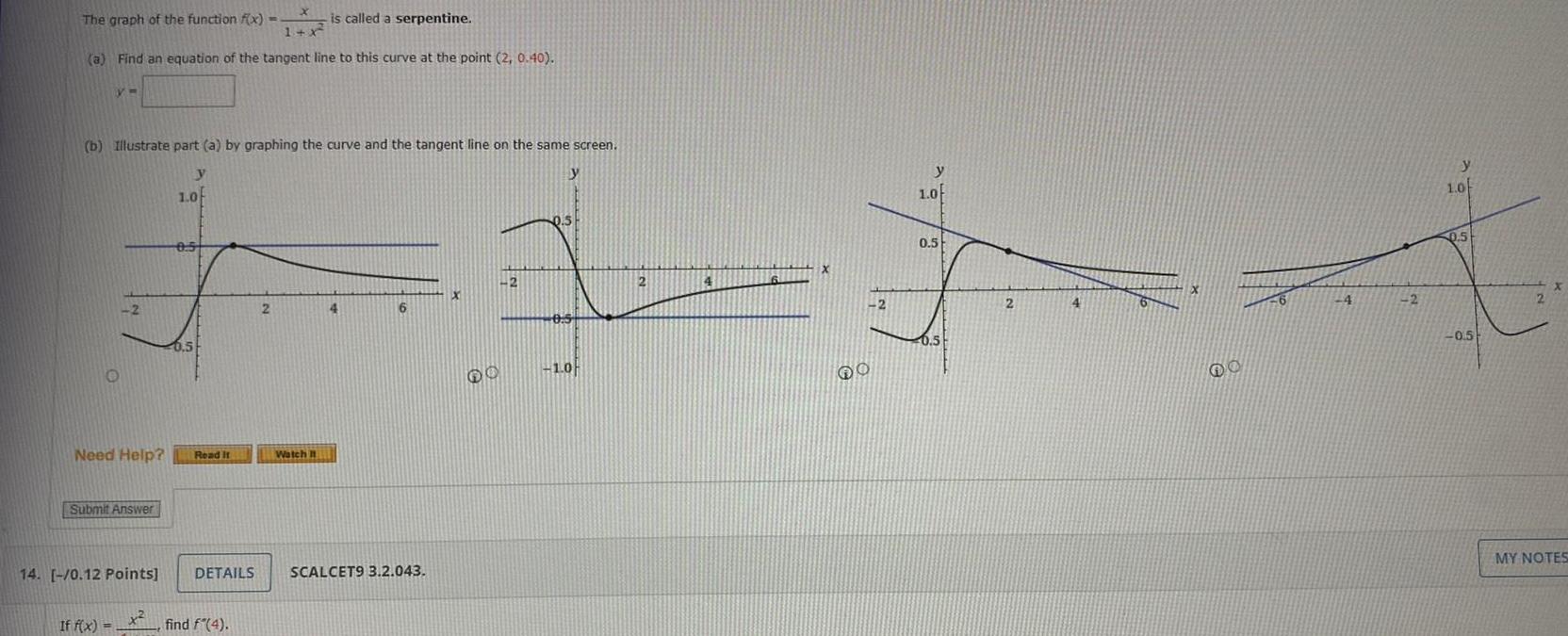
Application of derivativesX is called a serpentine 1 x 2 a Find an equation of the tangent line to this curve at the point 2 0 40 The graph of the function f x VW b Illustrate part a by graphing the curve and the tangent line on the same screen y O 2 Need Help Submit Answer If f x 14 0 12 Points 1 0 05 0 5 Read It DETAILS find f 4 2 Watch It 4 6 SCALCET9 3 2 043 60 2 y 0 5 0 5 1 0 2 4 X 60 2 y 1 0 0 5 0 5 2 4 6 x 4 2 y 1 0 0 5 0 5 2 MY NOTES
Calculus
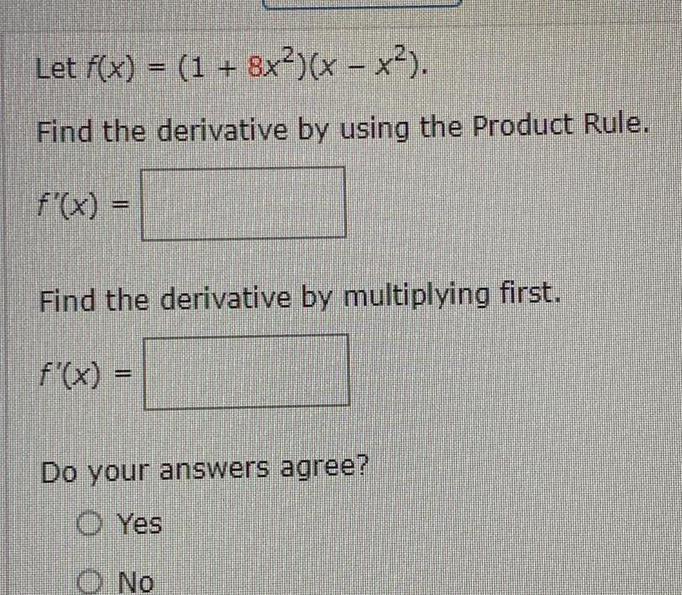
Application of derivativesLet f x 1 8x x x Find the derivative by using the Product Rule f x Find the derivative by multiplying first f x Do your answers agree Yes O No
Calculus
Application of derivativesSuppose that f 5 1 f 5 4 g 5 3 and g 5 5 Find the following values a fg 5 b c 5 7 5

Calculus
Application of derivativesCurrent Attempt in Progress Find all critical points and then use the first derivative test to determine local maxima and minima Check your answers by graphin f x 3x 4x 6 Enter the critical points in increasing order If there is no local maximum or local minimum enter NA X The local maximum is at x The local minimum is at x
Calculus
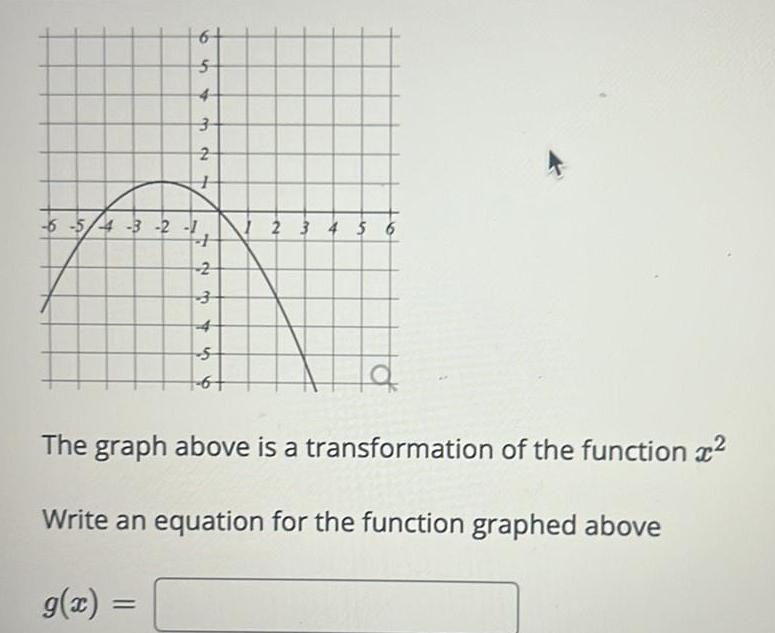
Application of derivatives5 3 2 6 5 4 3 2 1 1234 S 1 2 3 4 5 6 The graph above is a transformation of the function Write an equation for the function graphed above g x
Calculus
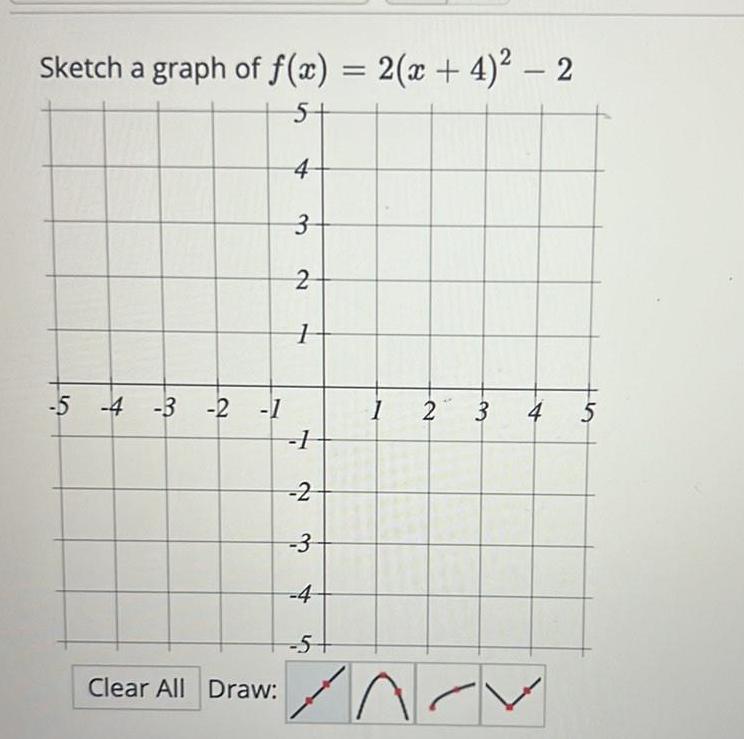
Application of derivativesSketch a graph of f x 2 x 4 2 5 4 5 4 3 2 1 Clear All Draw 3 2 1 1 2 3 4 5 1 2 3 INOV er 4 5
Calculus
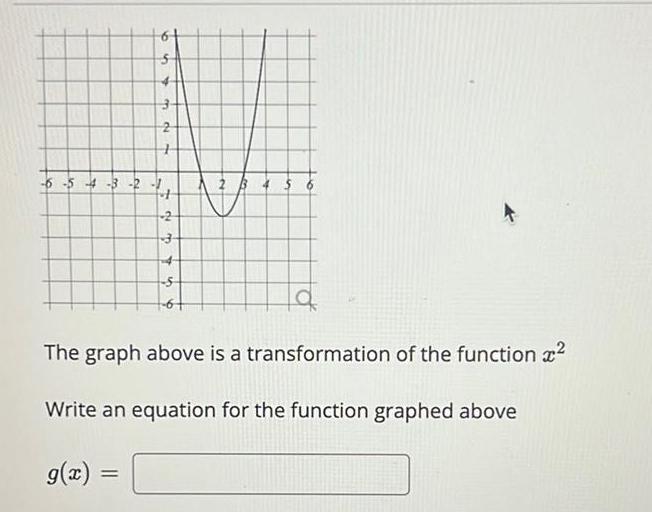
Application of derivatives6 54 3 9 4 2 4 q The graph above is a transformation of the function x Write an equation for the function graphed above g x
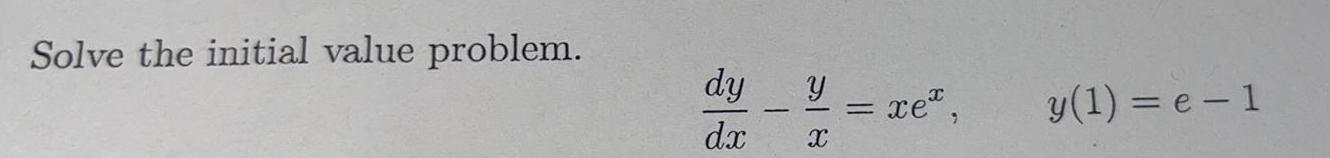

Calculus
Application of derivativesLogistic functions such as N t 500 1 50e 0 13t are often used to model population growth Suppose a population is modeled by this function with time t measured in years Logistic population growth always has a limiting value known as the environmental carrying capacity It is the largest population that the environment can suppor Plot the graph of the population and the line that corresponds to the value of the environmental carrying capacity for this population over the first 80 years Enter expressions in terms of t to graph Separate multiple expressions with commas
Calculus
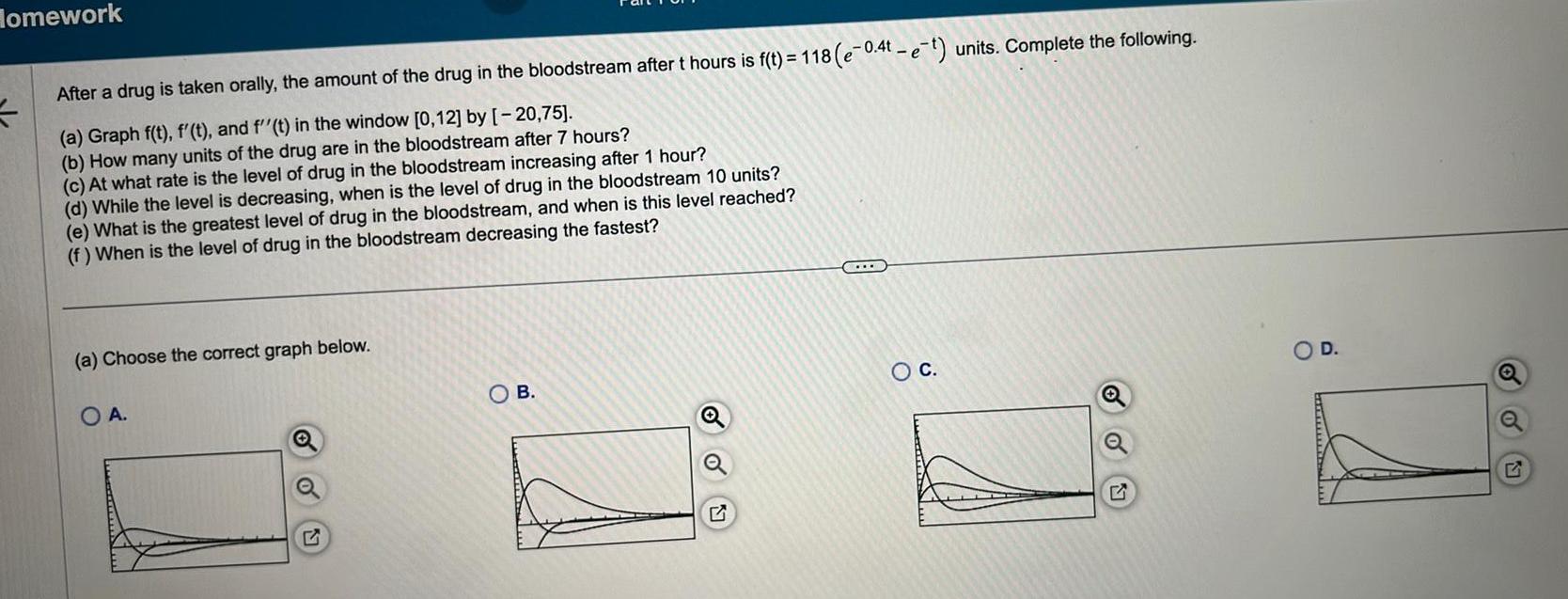
Application of derivativesHomework After a drug is taken orally the amount of the drug in the bloodstream after t hours is f t 118 e 0 4t e t units Complete the following a Graph f t f t and f t in the window 0 12 by 20 75 b How many units of the drug are in the bloodstream after 7 hours c At what rate is the level of drug in the bloodstream increasing after 1 hour d While the level is decreasing when is the level of drug in the bloodstream 10 units e What is the greatest level of drug in the bloodstream and when is this level reached f When is the level of drug in the bloodstream decreasing the fastest a Choose the correct graph below OA Q OB O C D

Calculus
Application of derivativest Suppose that the annual sales S in dollars of a company may be approximated empirically by the formula S 30 000 e logarithmic derivative to determine the percentage rate of growth of sales at t 16 The percentage rate of growth is Round to one decimal place as needed C where t is the number of years beyond some fixed reference date Use a
Calculus
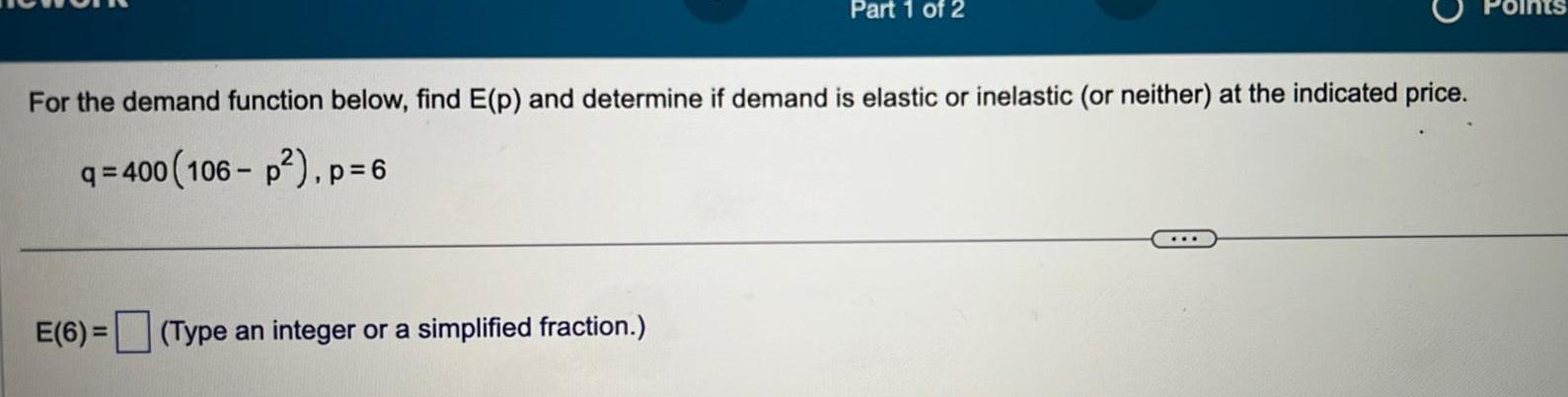
Application of derivativesPart 1 of 2 For the demand function below find E p and determine if demand is elastic or inelastic or neither at the indicated price q 400 106 p p 6 E 6 Type an integer or a simplified fraction
Calculus
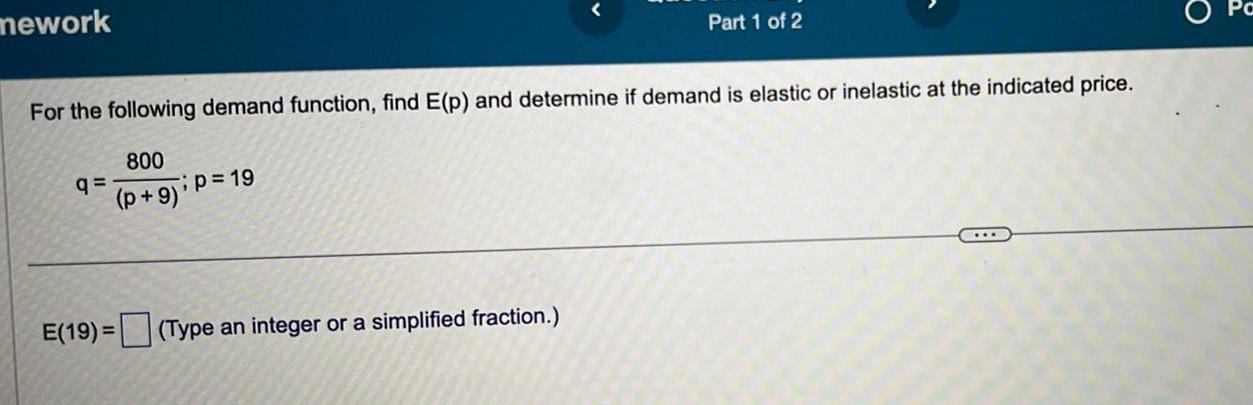
Application of derivativesmework For the following demand function find E p and determine if demand is elastic or inelastic at the indicated price 800 p 9 q p 19 Part 1 of 2 E 19 Type an integer or a simplified fraction O

Calculus
Application of derivativesFind the present value of 8000 payable at the end of 3 years if money may be invested at 7 with interest compounded continuously The present value of 8000 is Round to the nearest cent as needed
Calculus
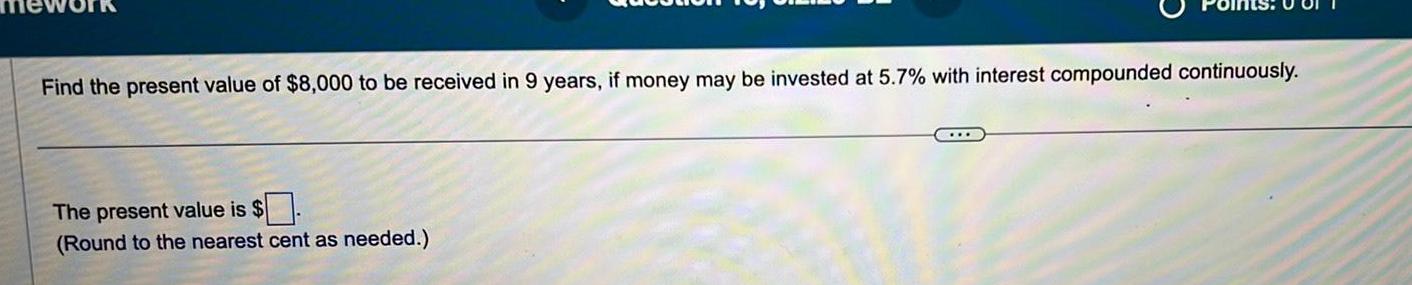
Application of derivativesFind the present value of 8 000 to be received in 9 years if money may be invested at 5 7 with interest compounded continuously The present value is Round to the nearest cent as needed
Calculus
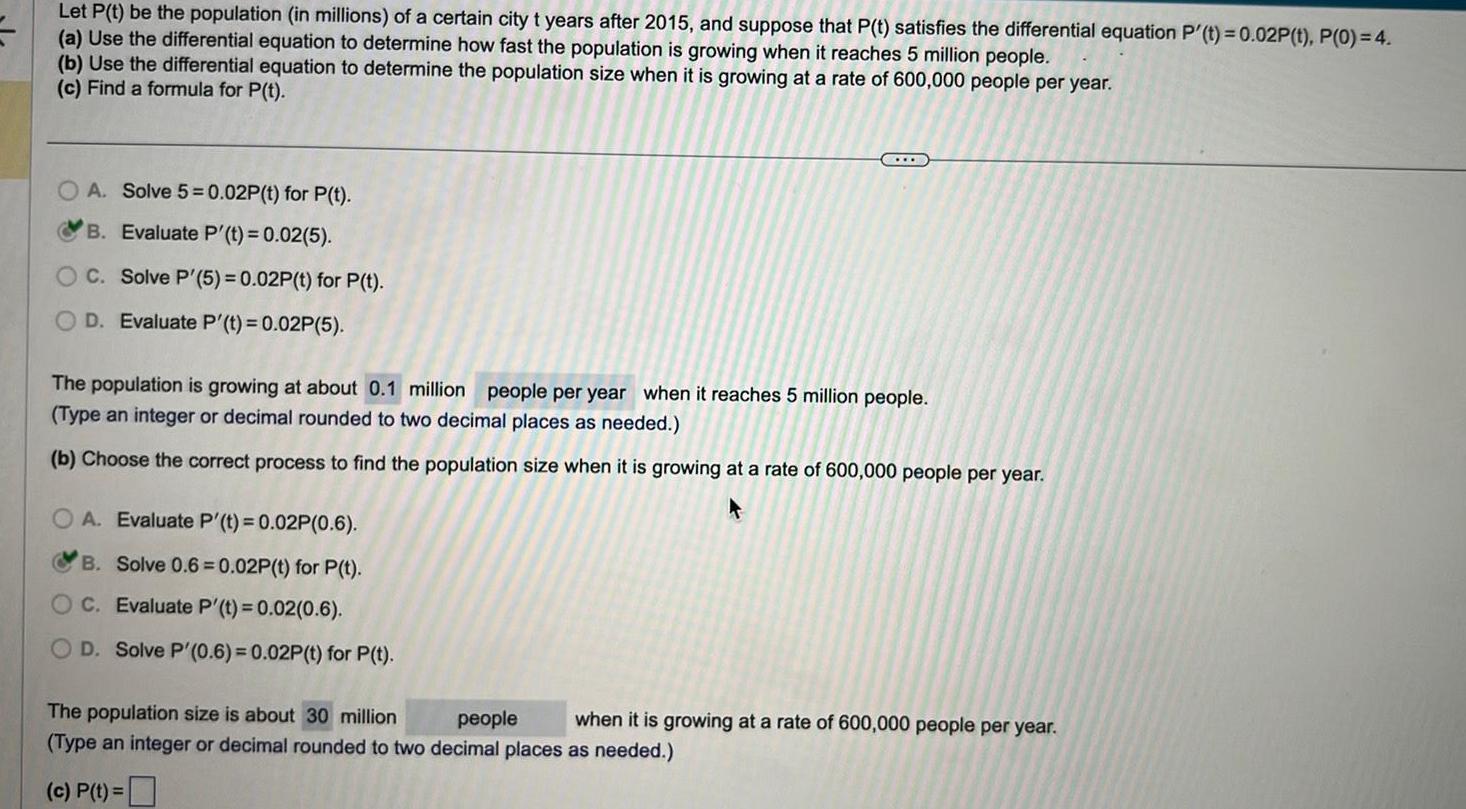
Application of derivativesLet P t be the population in millions of a certain city t years after 2015 and suppose that P t satisfies the differential equation P t 0 02P t P 0 4 a Use the differential equation to determine how fast the population is growing when it reaches 5 million people b Use the differential equation to determine the population size when it is growing at a rate of 600 000 people per year c Find a formula for P t A Solve 5 0 02P t for P t B Evaluate P t 0 02 5 OC Solve P 5 0 02P t for P t D Evaluate P t 0 02P 5 The population is growing at about 0 1 million people per year when it reaches 5 million people Type an integer or decimal rounded to two decimal places as needed b Choose the correct process to find the population size when it is growing at a rate of 600 000 people per year OA Evaluate P t 0 02P 0 6 B Solve 0 6 0 02P t for P t C Evaluate P t 0 02 0 6 OD Solve P 0 6 0 02P t for P t The population size is about 30 million people when it is growing at a rate of 600 000 people per year Type an integer or decimal rounded to two decimal places as needed c P t
Calculus
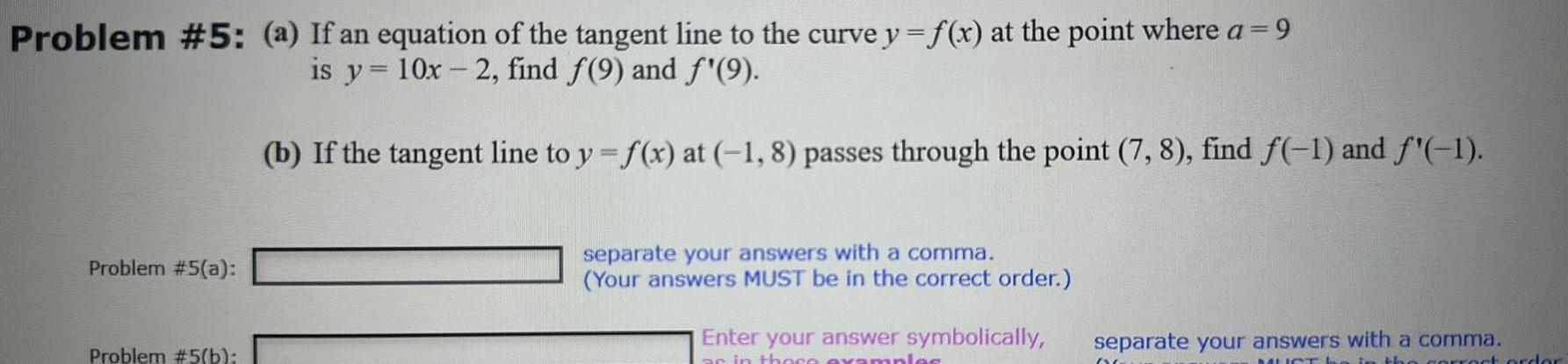
Application of derivativesProblem 5 a If an equation of the tangent line to the curve y f x at the point where a 9 is y 10x 2 find 9 and f 9 Problem 5 a Problem 5 b b If the tangent line to y f x at 1 8 passes through the point 7 8 find f 1 and f 1 separate your answers with a comma Your answers MUST be in the correct order Enter your answer symbolically as in these examples separate your answers with a comma MUST the correct order

Calculus
Application of derivativesProblem 4 Suppose that f is continuous on 0 6 and that the only solutions of the equation f x 3 are x 1 and x 5 If f 4 5 then which of the following statements must be true 1 2 3 11 f 0 3 iii f 6 3 A i and iii B ii and iii C iii only D all of them E i only F none of them G i and ii HDG only

Calculus
Application of derivatives2 a Find the horizontal and vertical asymptotes of the graph of the function f x 5x 7 2x 3 h Find the values of a and h for a rational function

Calculus
Application of derivatives17 Distance between Two Ships Two ships leave a port at the same time The first ship sails on a bearing of 40 at 18 knots nautical miles per hour and the second on a bearing of 130 at 26 knots How far apart are they after 1 5 hr

Calculus
Application of derivatives15 Distance Flown by a Plane A plane flies 1 3 hr at 110 mph on a bearing of 38 It then turns and flies 1 5 hr at the same speed on a bearing of 128 How far is the plane from its starting point N 38 N 128
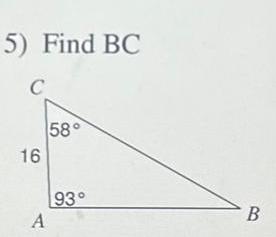

Calculus
Application of derivatives304 EXEMPLAR PROBLEMS MATHEMATICS 39 C 41 B 45 1 43 C 46 n B 47 AB 48 9 1 2 1 2 49 0 1 2 3 4 5 6 8 50 6 1 5 9 10 ii 1 2 3 5 6 7 9 10 31 AUB 53 True 57 True 38 C 42 B 2 3 2 3 EXERCISE 1 1 1 1 3 2 1 2 3 3 1 3 3 1 1 1 2 1 3 3 1 3 2 3 3 52 1 b ii c ii a iv f v d vi e 55 False 54 False 56 True 58 False 1 1 1 3 3 1 3 3 iv 1 1 1 2 1 3 2 1 2 2 2 3 3 1 i 40 A 44 1 2 0 1 0 2 1 1 1 2 2 1 2 2 i 0 3 1 3 ii 0 2 0 3 0 4 0 5 1 2 1 3 1 4 1 5 11 and h i a 0 and b 2 3 4 5 b 1 4 2 3 3 2 4 1 1 1 1 2 1 3 2 1 2 2 3 1 i 4 5 5 4 5 5 6 Domain of R 0 3 4 5 Range of R 7 Domain of R 1 5 51 and Range of R 1 3 17 8 R 0 8 8 0 0 8 8 0 9 Domain of RR and range of R R U 0 b 10 1 is not a function ii f is a function g is a function iv is a function v is a constant function 11 a 6 1364 4 12 a x 4 b x 4 13 8 x x 2x 2 3 2 3 3 c 13 d 4 e 5 ii f g x 2x alished

Calculus
Application of derivatives8 The value of stock in Chelsea s Chocolate Company increased between 2017 and 2019 then decreased until June of 2020 then started increasing again Which of the following conclusions is true A The value of the stock was at its absolute highest in 2019 B The value of the stock reached a relative maximum in 2019 C The value of the stock reached a relative minimum in 2017 D The value of the stock was at its absolute lowest in June of 2020
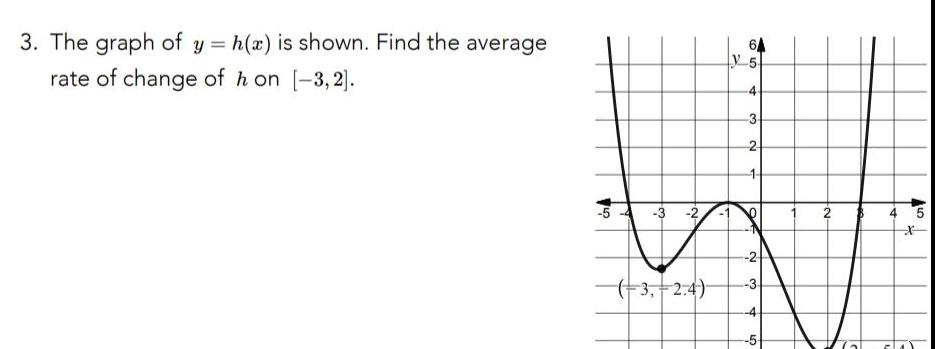
Calculus
Application of derivatives3 The graph of y h x is shown Find the average rate of change of h on 3 2 3 2 3 2 4 64 5 4 3 2 1 9 N 3 4 5 2

Calculus
Application of derivatives2 2 2 Find the maximum and the minimum values of f x y z 5x 2y 9z on the sphere x y z 110 The maximum value is Simplify your answer
Calculus
Application of derivatives2 Find the points on the surface z xy 9 closest to the origin The points on the surface closest to the origin are Type an ordered triple Use a comma to separate answers as needed
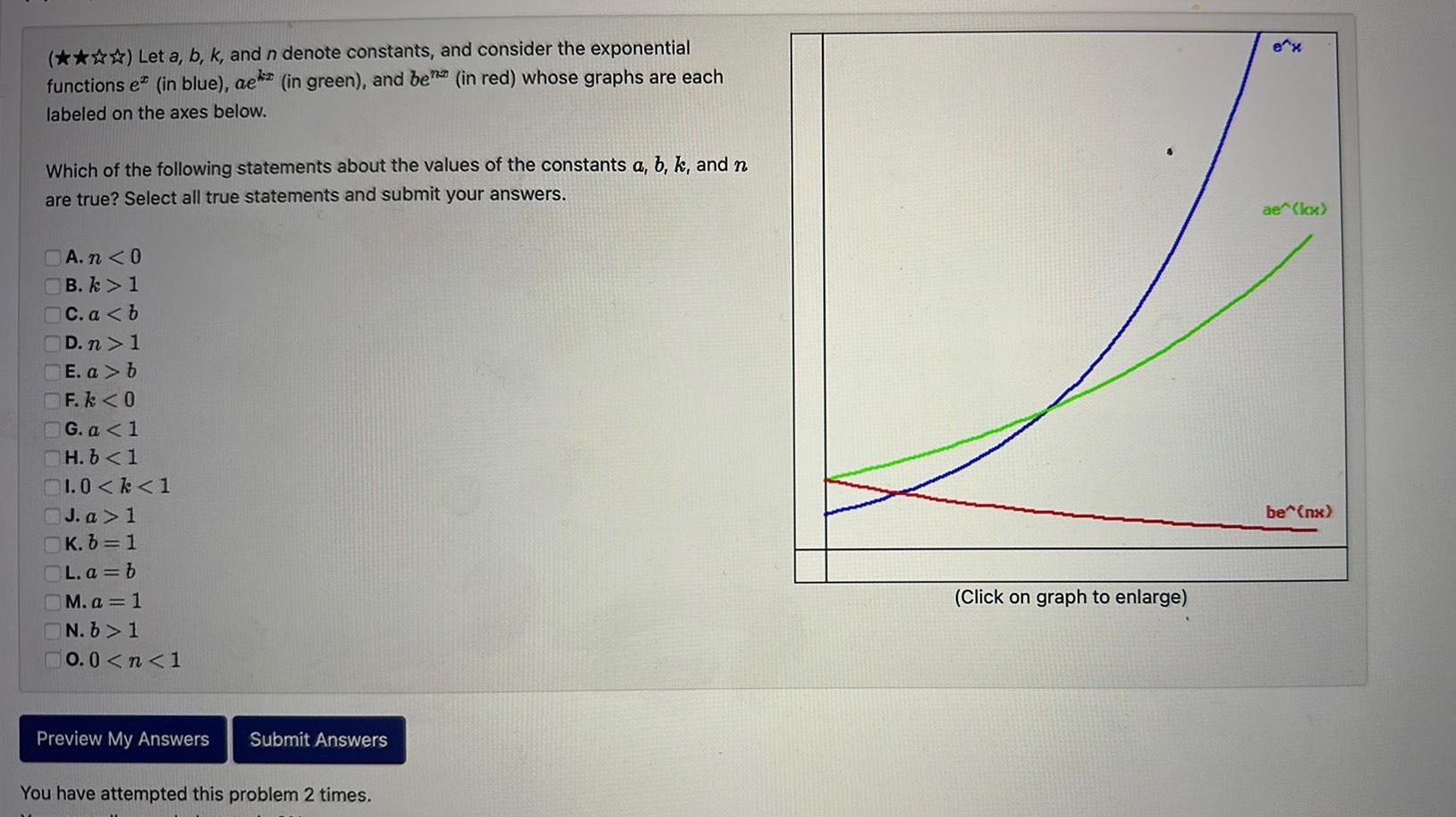
Calculus
Application of derivativesLet a b k and n denote constants and consider the exponential functions e in blue ae in green and ben in red whose graphs are each labeled on the axes below Which of the following statements about the values of the constants a b k and n are true Select all true statements and submit your answers A n 0 B k 1 C a b D n 1 E a b F k 0 G a 1 H b 1 1 0 k 1 J a 1 K b 1 L a b M a 1 N b 1 0 0 n 1 Preview My Answers Submit Answers You have attempted this problem 2 times Click on graph to enlarge ae kx be nx
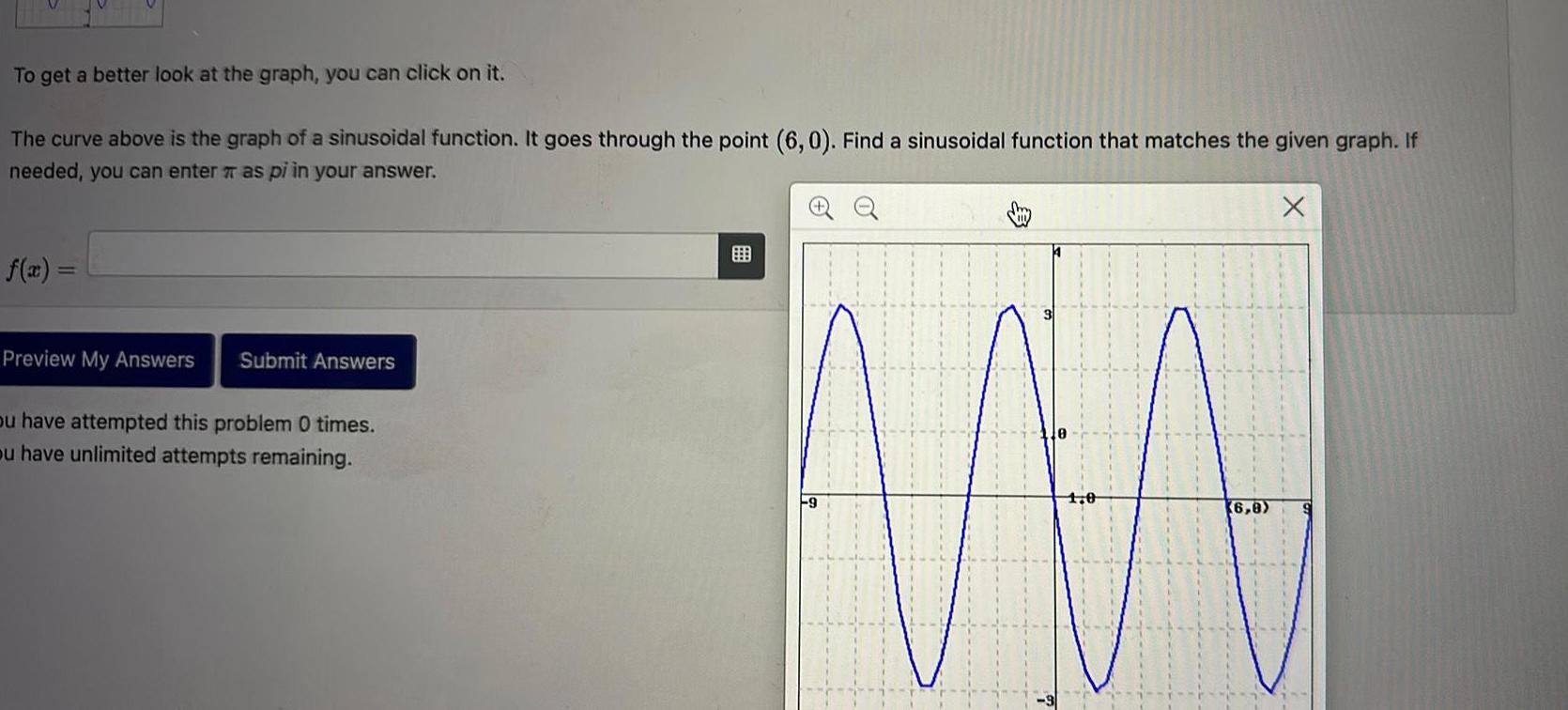
Calculus
Application of derivativesTo get a better look at the graph you can click on it The curve above is the graph of a sinusoidal function It goes through the point 6 0 Find a sinusoidal function that matches the given graph If needed you can enter as pi in your answer f x Preview My Answers Submit Answers ou have attempted this problem 0 times ou have unlimited attempts remaining 9 6 8 X
Calculus
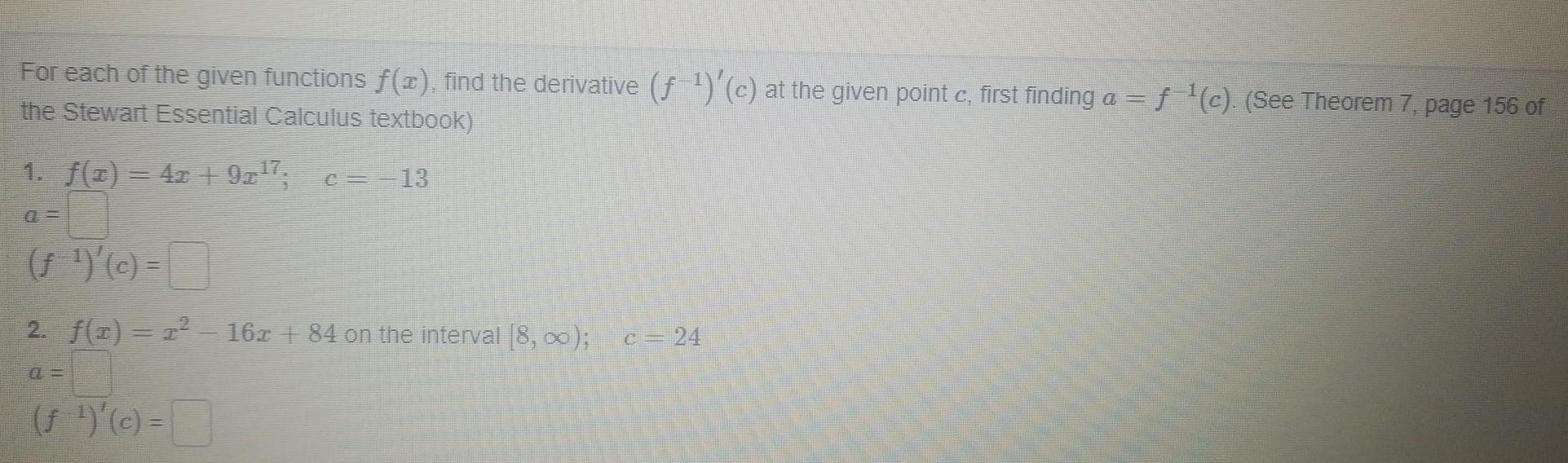
Application of derivativesFor each of the given functions f x find the derivative f c at the given point c first finding a f c See Theorem 7 page 156 of the Stewart Essential Calculus textbook 1 x 4x 9x 7 c 13 c 2 f 1 1 16x 84 on the interval 8 f c c 24
Calculus
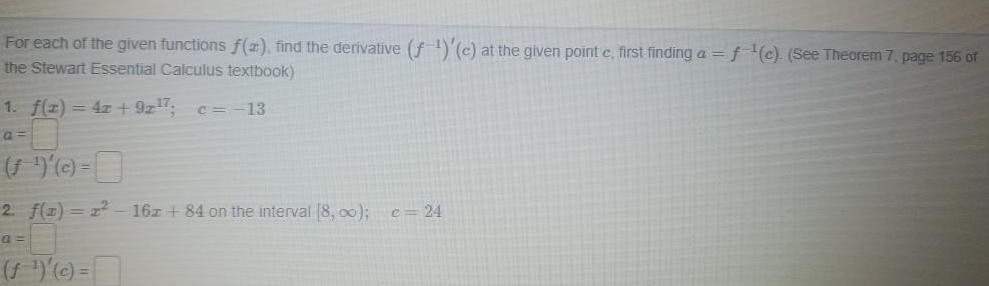
Application of derivativesFor each of the given functions f 2 find the derivative f c at the given point c first finding a f c See Theorem 7 page 156 of the Stewart Essential Calculus textbook 1 f x 4z 9x 7 c 13 a f c 2 f 2 x 16z 84 on the interval 8 00 c 24 a f c

Calculus
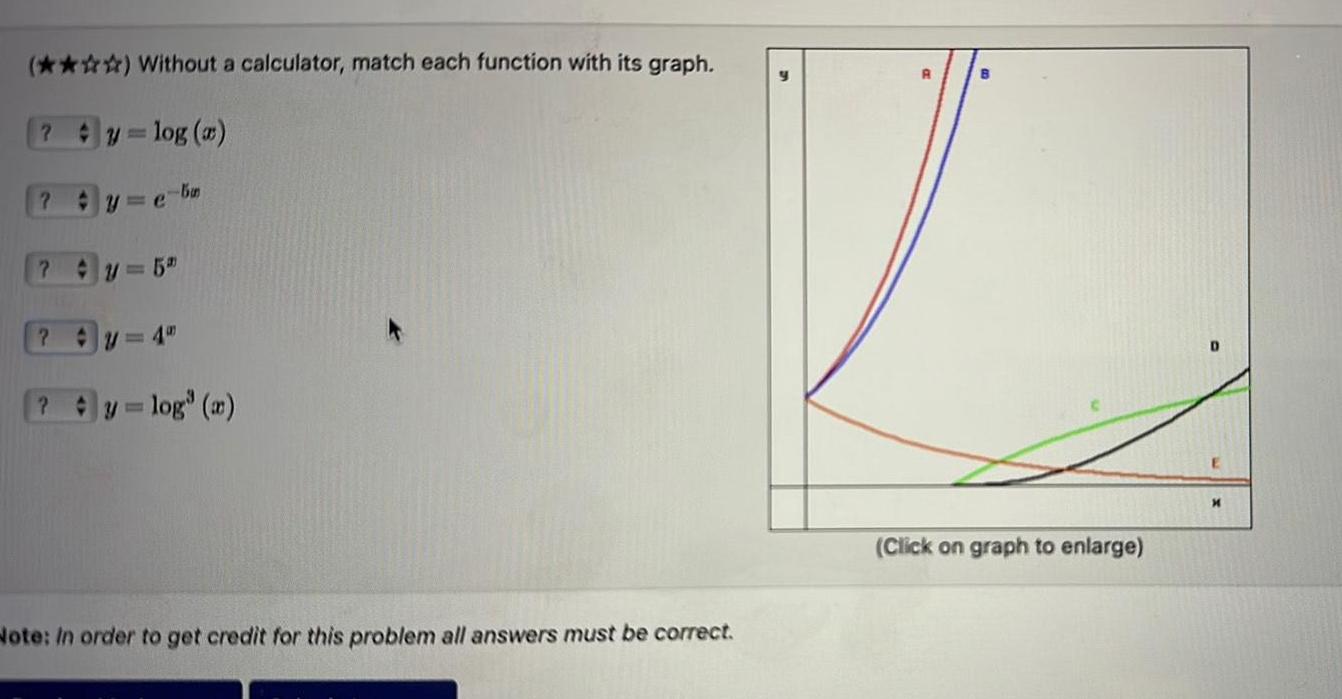
Application of derivativesWithout a calculator match each function with its graph y log x e ba y e 97 5 4 y log a Note In order to get credit for this problem all answers must be correct y Click on graph to enlarge D X
Calculus
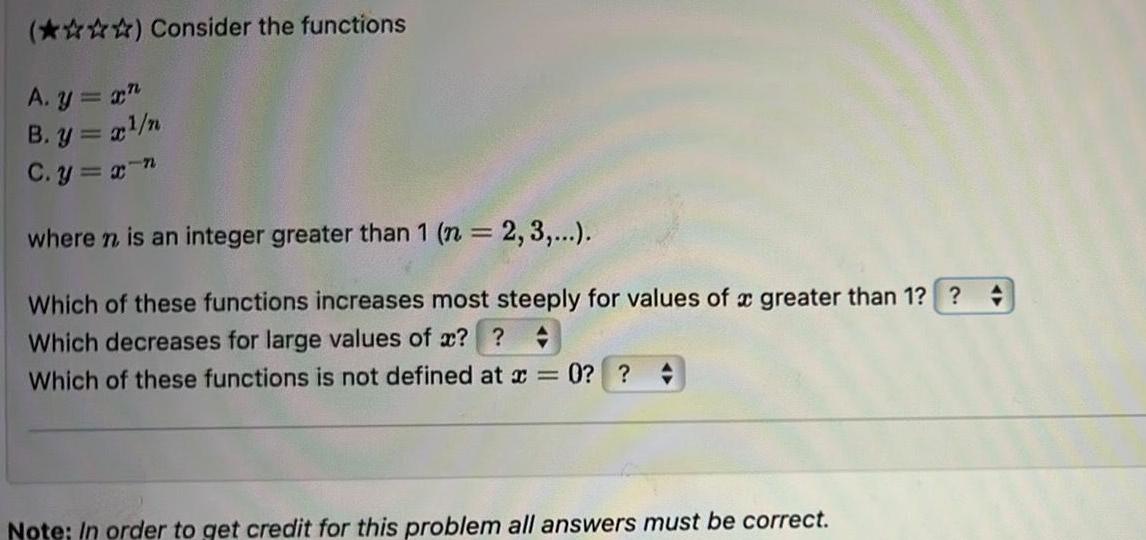
Application of derivativesConsider the functions A y x B y x n C y x n where n is an integer greater than 1 n 2 3 4 Which of these functions increases most steeply for values of a greater than 1 Which decreases for large values of x Which of these functions is not defined at x 0 Note In order to get credit for this problem all answers must be correct

Calculus
Application of derivativesTo say that where A is and B is 5 5 2 is the same as saying is in the closed interval A B

Calculus
Application of derivativesA particle is moving along the curve y 3 4x 1 As the particle passes through the point 2 9 its z coordinate increases at a rate of 3 units per second Find the rate of change of the distance from the particle to the origin at this instant 6
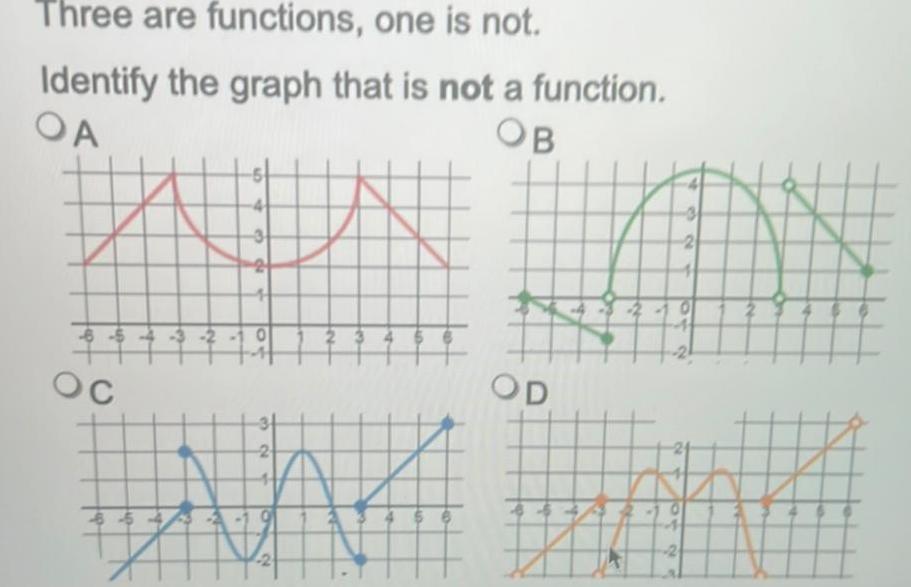
Calculus
Application of derivativesThree are functions one is not Identify the graph that is not a function OB OA OC 654 3 di N 3 2 2 OD N O


Calculus
Application of derivativesomework A cave with beautiful prehistoric wall paintings was discovered Some charcoal found in the cave contained 15 of the constant for 14C is 00012 The cave paintings are years old Round to the nearest year as needed Points 0 OT 14 C expected in living trees How old are the cave paintings The decay
Calculus
Application of derivativesa Find the formula for P t P t 12e 0 027t Type an expression using t as the variable b What is P 0 P 0 12 c What is the decay constant Part 3 of 9 A sample of 12 grams of radioactive material is placed in a vault Let P t be the amount remaining after t years and let P t satisfy the differential equation P t 0 027P t Answer parts through g C Points 0 of 1
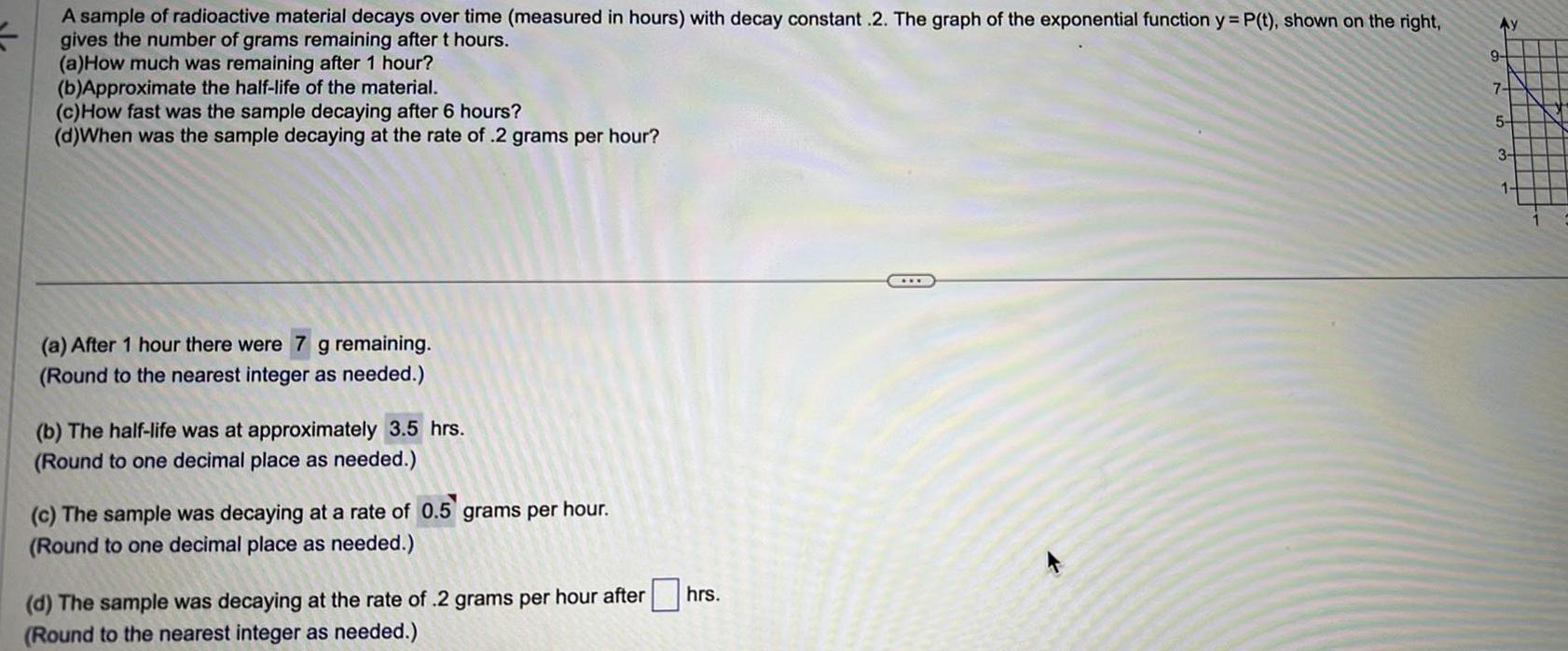
Calculus
Application of derivativesA sample of radioactive material decays over time measured in hours with decay constant 2 The graph of the exponential function y P t shown on the right 5 gives the number of grams remaining after t hours a How much was remaining after 1 hour b Approximate the half life of the material c How fast was the sample decaying after 6 hours d When was the sample decaying at the rate of 2 grams per hour a After 1 hour there were 7 g remaining Round to the nearest integer as needed b The half life at approximately 3 5 hrs Round to one decimal place as needed c The sample was decaying at a rate of 0 5 grams per hour Round to one decimal place as needed d The sample was decaying at the rate of 2 grams per hour after Round to the nearest integer as needed hrs Ay 9 7 5 3 1

Calculus
Application of derivativesPoints 0 of 1 At the beginning of 1990 22 3 million people lived in the metropolitan area of a particular city and the population was growing exponentially The 1994 population was 27 million If this trend continues how large will the population be in the year 2009 The population will be million people Round to the nearest integer as needed