Application of derivatives Questions and Answers
Calculus
Application of derivativesPart 2 of 3 a Find the formula for P t P t 4e0 04t Type an expression using t as the variable b What was the initial population that is the population in 1990 The initial population was million Points 0 of 1 Let P t be the population in millions of a certain city t years after 1990 and suppose that P t satisfies the differential equation P 04P t P 0 4
Calculus
Application of derivativesHomework A sample of radioactive material disintegrates from 4 to 3 grams in 50 days After how many days will just 2 grams remain days 2 grams will remain after Round up to the nearest day
Calculus
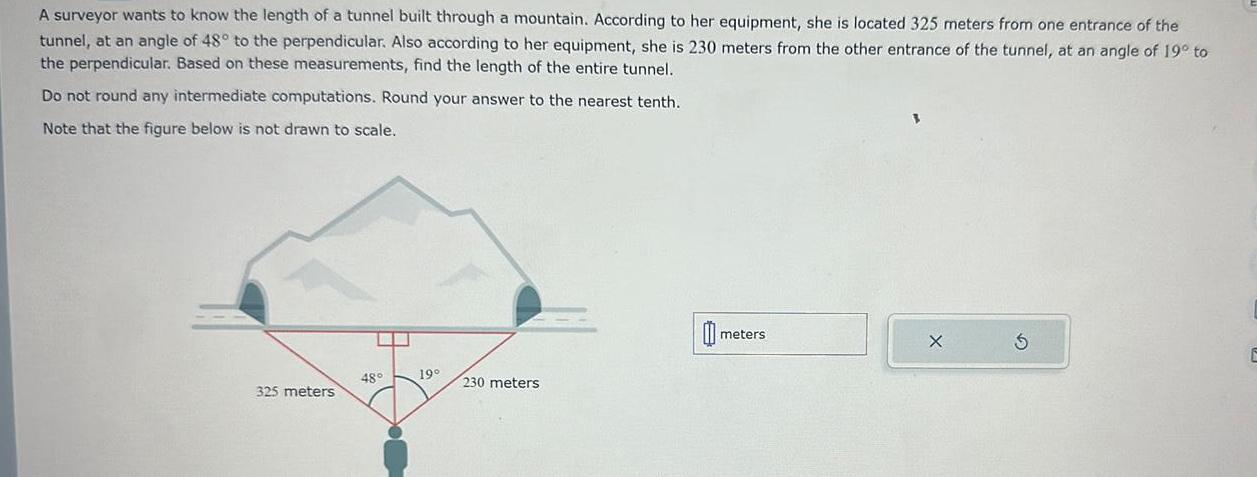
Application of derivativesA surveyor wants to know the length of a tunnel built through a mountain According to her equipment she is located 325 meters from one entrance of the tunnel at an angle of 48 to the perpendicular Also according to her equipment she is 230 meters from the other entrance of the tunnel at an angle of 19 to the perpendicular Based on these measurements find the length of the entire tunnel Do not round any intermediate computations Round your answer to the nearest tenth Note that the figure below is not drawn to scale 325 meters 48 19 230 meters 0 meters E
Calculus
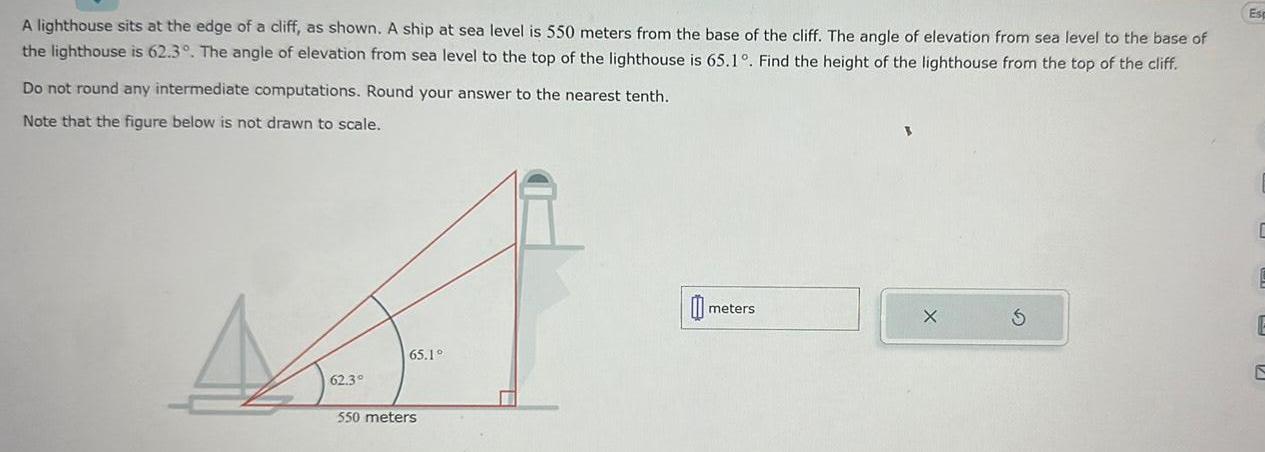
Application of derivativesA lighthouse sits at the edge of a cliff as shown A ship at sea level is 550 meters from the base of the cliff The angle of elevation from sea level to the base of the lighthouse is 62 3 The angle of elevation from sea level to the top of the lighthouse is 65 1 Find the height of the lighthouse from the top of the cliff Do not round any intermediate computations Round your answer to the nearest tenth Note that the figure below is not drawn to scale 62 3 65 1 550 meters 0 meters Es C E E

Calculus
Application of derivativesRewrite the following expression in terms of exponentials and simplify the result as much as you can 5 sinh 5 In x 5 sinh 5 Inx Simplify your answer Use integers or fractions for any numbers in the expression Do not factor

Calculus
Application of derivatives3 sinh 2 In x Simplify your answer Use integers or fractions for any numbers in the expression D
Calculus
Application of derivativesFind the derivative of y with respect to x F 5 y 3 sinh The derivative of y with respect to x is
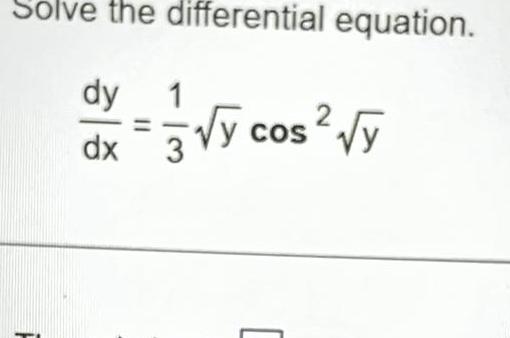
Calculus
Application of derivativesFind the equation for a the tangent plane and b the normal line at the point Po 1 1 e on the surface 2x ln y y ln z X Z a Using a coefficient of 3 for y the equation for the tangent plane is x 3y b Find the equations for the normal line Let x 1 t 0 y 0 z 0 Type expressions using t as the variable X 3 0

Calculus
Application of derivativesSuppose that the bacteria in a colony grow unchecked according to the Law of Exponential Change The colony starts with 1 bacterium and triples in number every 30 minutes How many bacteria will the colony contain at the end of 24 hours At the end of 24 hours the colony will contain bacteria Use scientific notation Use the multiplication symbol in the math palette as needed Round to one decimal place as needed
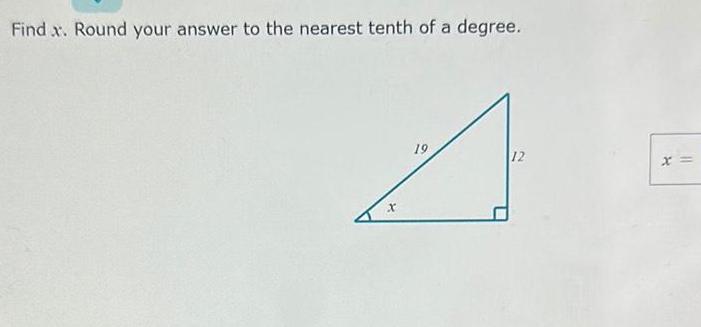

Calculus
Application of derivativesFind an equation for the plane that is tangent to the surface z In x y at the point P 0 1 0 Using a coefficient of 1 for z the equation of the plane is 0

Calculus
Application of derivatives1 Evaluate the limit if it exists otherwise give the reason why the limit does not exist a lim cos 2 N 1 b lim 4x x 2x
Calculus
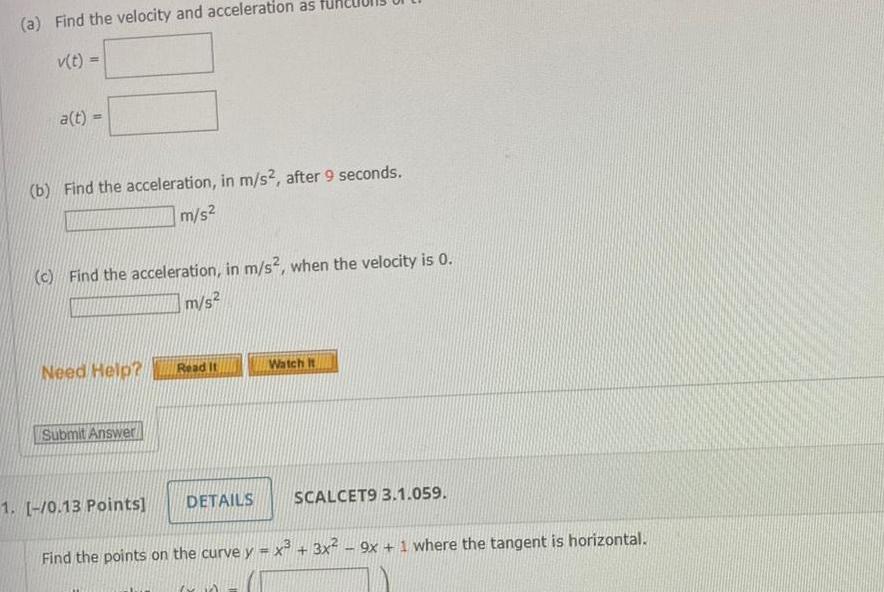
Application of derivativesa Find the velocity and acceleration as v t a t b Find the acceleration in m s2 after 9 seconds m s c Find the acceleration in m s2 when the velocity is 0 m s Need Help Submit Answer 1 0 13 Points Read It DETAILS Watch It ww SCALCET9 3 1 059 Find the points on the curve y x 3x 9x 1 where the tangent is horizontal
Calculus
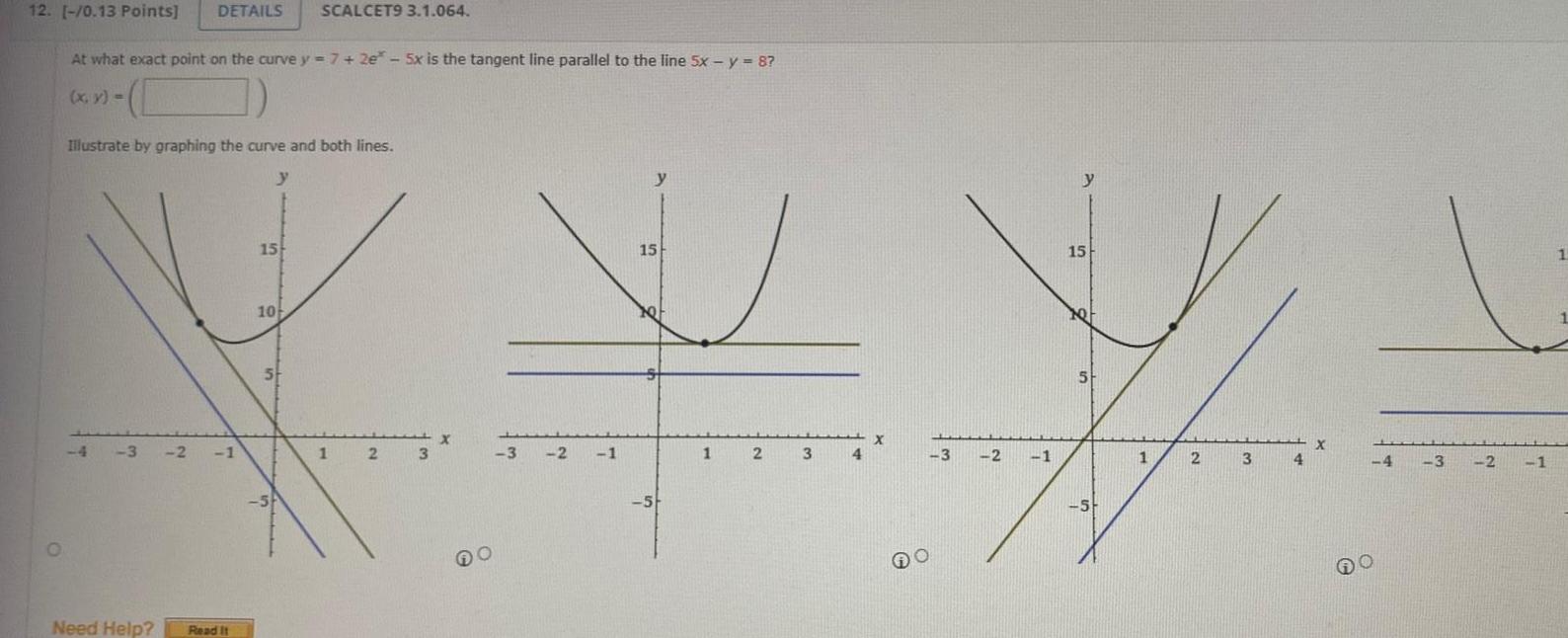
Application of derivatives12 0 13 Points DETAILS SCALCET9 3 1 064 O At what exact point on the curve y 7 2e 5x is the tangent line parallel to the line 5x y 8 x y Illustrate by graphing the curve and both lines y 4 3 2 1 Need Help Read It 15 10 5 SA 1 2 3 X O 3 2 1 15 x S 5 1 2 3 4 X 3 2 1 15 5 5 1 2 3 4 X 4 3 2 1 1

Calculus
Application of derivativesFind the domain of the function I 4x 3x 1 X g x 0 0 00 1 4 U 1 4 O 1 U 4 00 O 0 1 4 U 1 4 00 0 4 U 4 00
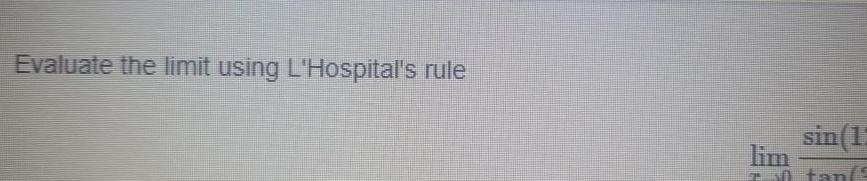
Calculus
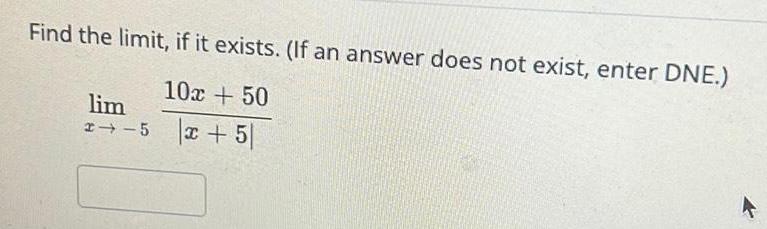
Application of derivativesFind the limit if it exists If an answer does not exist enter DNE 10x 50 x 5 lim 2 5
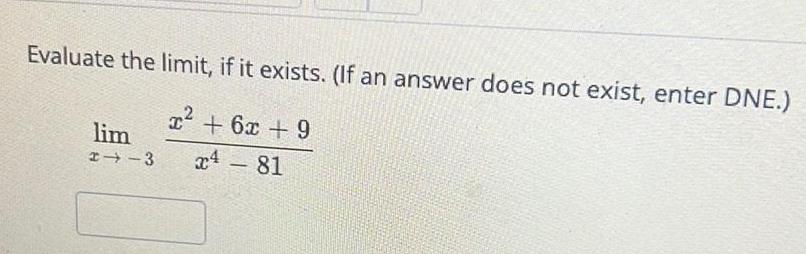
Calculus
Application of derivativesEvaluate the limit if it exists If an answer does not exist enter DNE x 6x 9 24 81 lim 24 3

Calculus
Application of derivativesName Instructions Use algebraic techniques to solve problems unless otherwise instructed Show the calculations leading to your answers except basic algebra arithmetic when there is work to show Simplify and circle your final answers 1 18 pts In the vicinity of a bonfire the temperature T in C at a distance x meters from the center of the fire is described by T x 500 000 x 400 a What is the average rate of change of T between 0 and 10 meters Also what is the interpretation of this average rate of change Use correct units in your interpretation b What is the average rate of change of T between 10 and 20 meters Also what is the interpretation of this average rate of change Use correct units in your interpretation c What is the equation of the secant line through 10 T 10 and 20 T 20 Write the answer in slope

Calculus
Application of derivativesis that it costs 3 000 to produce 100 chairs in one day and it costa 5 200 to produce 300 chairs in one day a Express the daily cost as a function of x where x is the number of chairs produced Assume that is a linear function of x b What is the C intercept of the line and what is its interpretation e What is the slope of this line and what is its interpretation d Use the function to predict the daily cost of producing 470 chairs e If the daily cost of producing chairs is 5 064 use the function to find the number of chairs produced

Calculus
Application of derivativesClassification of phy srics of fat stoffaszeg Physics Classical physics PRIN A Kma 3 modem physic A

Calculus
Application of derivativesin calculus than the other lo functions y logb x 2 26 Differentiate the function 2 g t In 3 1

Calculus
Application of derivatives126 Homework 7 Sect 2 6 ts A function g is given In parts a and b start with a standard function f and show the ic steps for transforming the graph of f into the graph of g Also describe each transformation s In parts c and d just describe the transformation steps in words x 2 x 0 5 x 2 1 g x 4 f 3x

Calculus
Application of derivativesFind equations for the tangent plane and the normal line at point Po XoYo Zo 2 5 0 on the surfa 6 cos xx 6x y 2x yz 116 Using a coefficient of 40 for x the equation for the tangent plane is
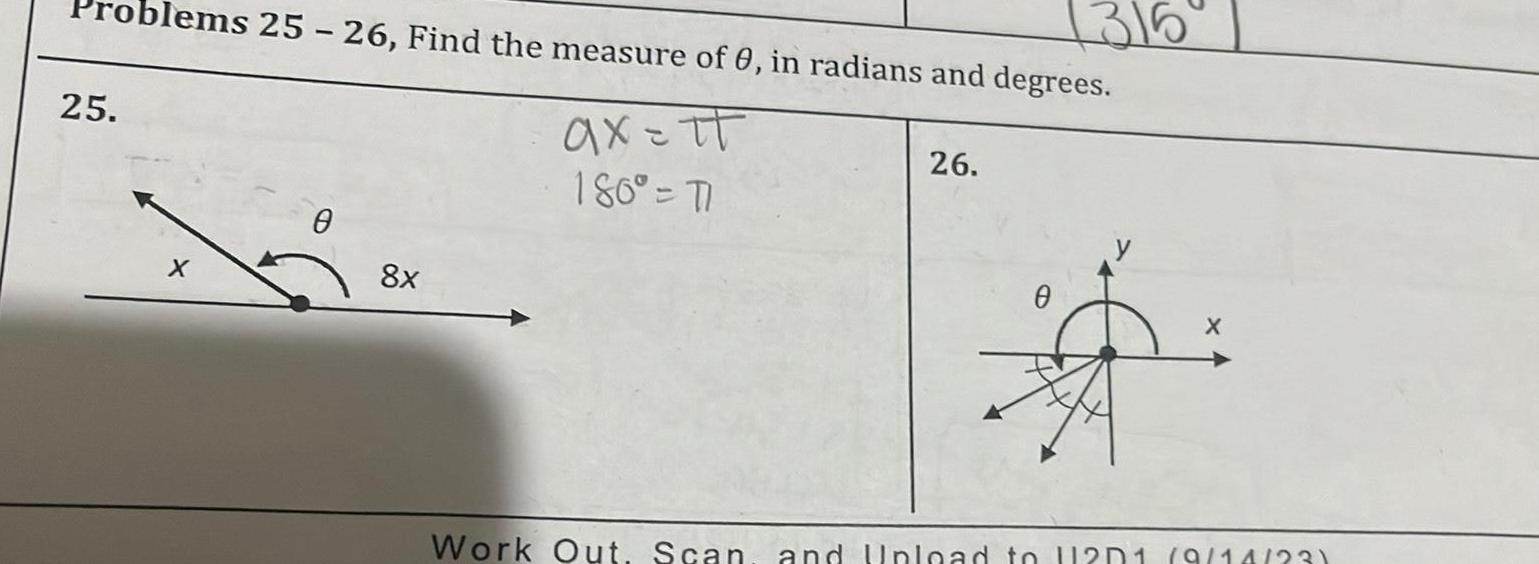
Calculus
Application of derivatives25 blems 25 26 Find the measure of 0 in radians and degrees ax tt 180 TI X 8x 26 0 X Work Out Scan and Upload to 12D1 9 14 23
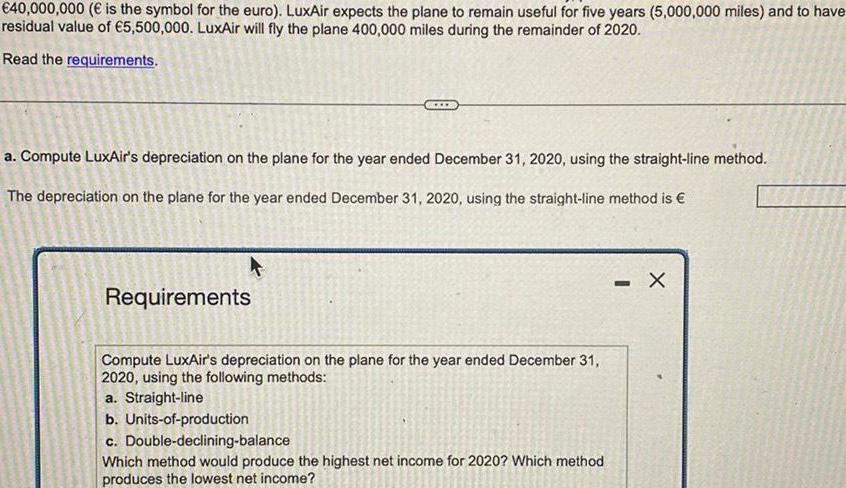
Calculus
Application of derivatives40 000 000 is the symbol for the euro LuxAir expects the plane to remain useful for five years 5 000 000 miles and to have residual value of 5 500 000 LuxAir will fly the plane 400 000 miles during the remainder of 2020 Read the requirements a Compute LuxAir s depreciation on the plane for the year ended December 31 2020 using the straight line method The depreciation on the plane for the year ended December 31 2020 using the straight line method is Requirements Compute LuxAir s depreciation on the plane for the year ended December 31 2020 using the following methods a Straight line b Units of production c Double declining balance Which method would produce the highest net income for 2020 Which method produces the lowest net income X

Calculus
Application of derivativesRewrite the expression as an algebraic expresion in 1 tan sin 2 Note by algebraic we mean that the answer is not allowed to use trig functions or inverse trig functions It is allowed to involve poly quotients and roots
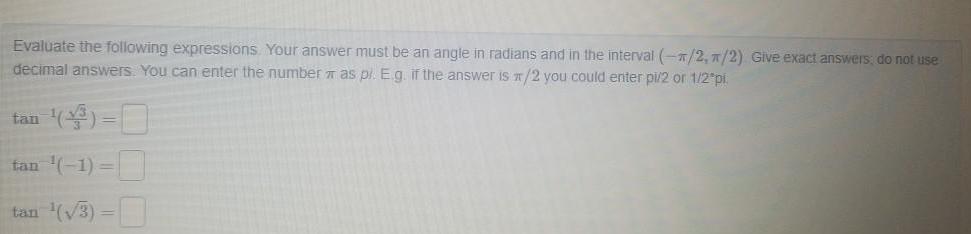
Calculus
Application of derivativesEvaluate the following expressions Your answer must be an angle in radians and in the interval 1 2 1 2 Give exact answers do not use decimal answers You can enter the number as pi E g if the answer is x 2 you could enter pi 2 or 1 2 pi 3 tan 1 tan 3 tan 0
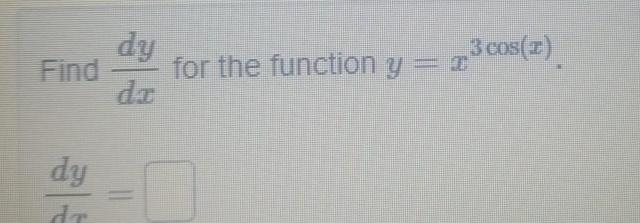
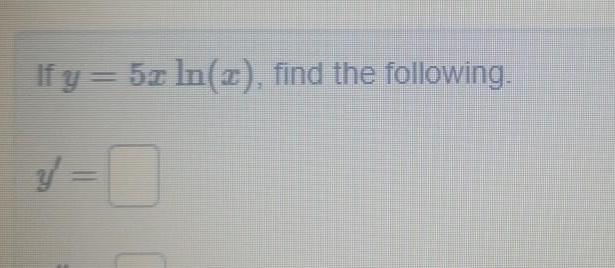

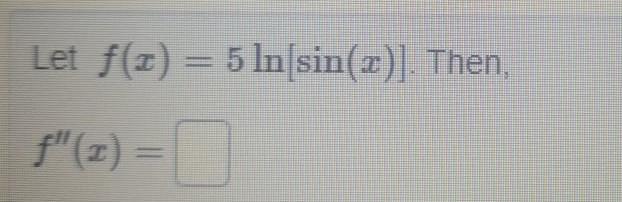
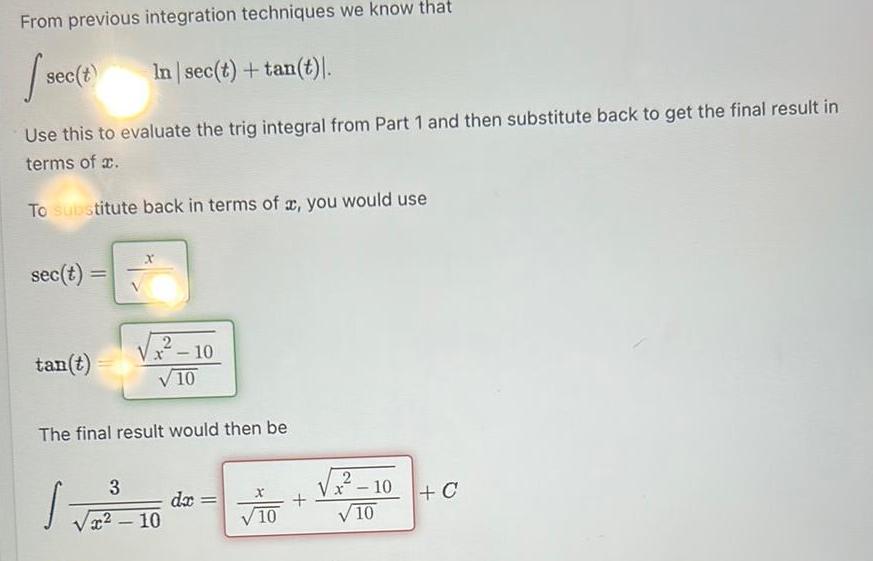
Calculus
Application of derivativesFrom previous integration techniques we know that sec t In sec t tan t Use this to evaluate the trig integral from Part 1 and then substitute back to get the final result in terms of To substitute back in terms of x you would use sec t tan t 2 x 10 10 The final result would then be 3 10 dx 10 2 Vx 10 10 C

Calculus
Application of derivativesFrom previous integration techniques we know that sec t dt In sec t tan t Use this to evaluate the trig integral from Part 1 and then substitute back to get the final result in terms of To substitute back in terms of x you would use tan t sec t The final result of the integration would then be 2 2 16 d 15 dx C
Calculus
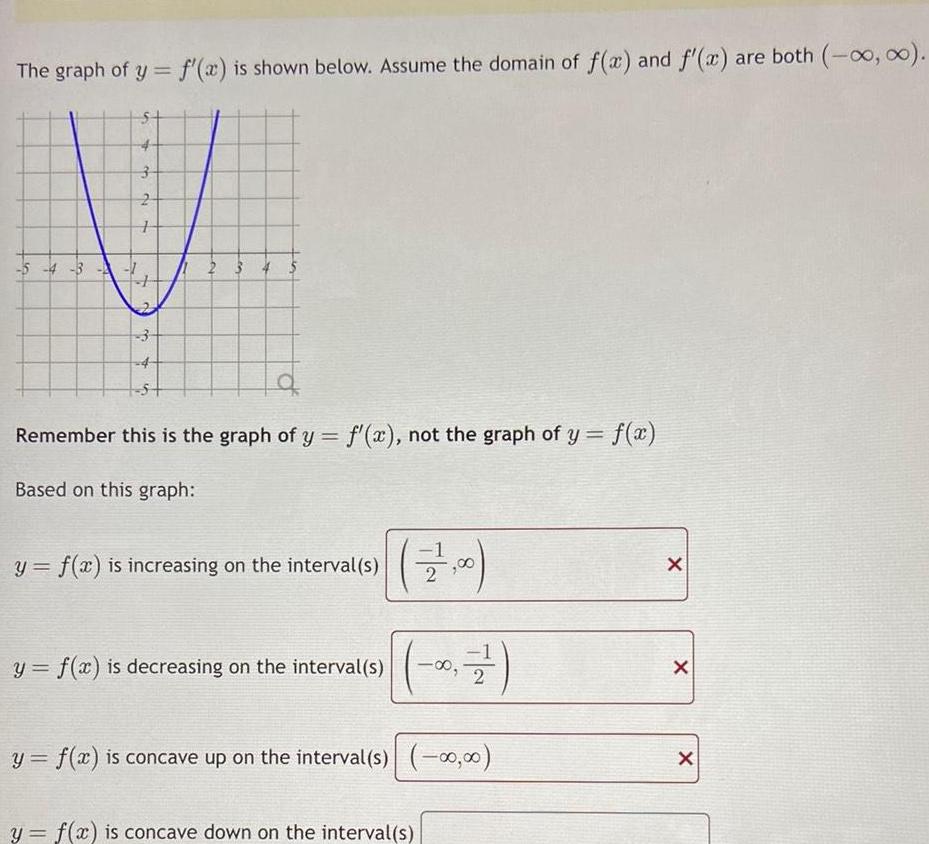
Application of derivativesThe graph of y f x is shown below Assume the domain of f x and f x are both 5 4 3 3 2 1 3 23 Remember this is the graph of y f x not the graph of y f x Based on this graph y f x is increasing on the interval s y f x is decreasing on the interval s y f x is concave up on the interval s 00 y f x is concave down on the interval s 2 2 7 00 00 X X X
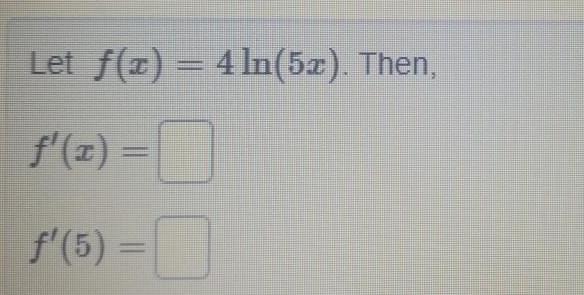
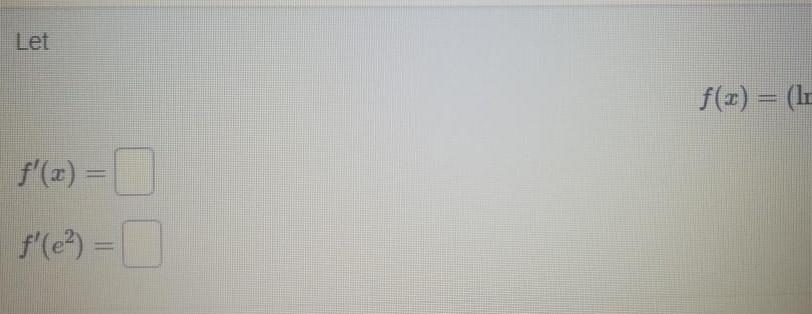
Calculus
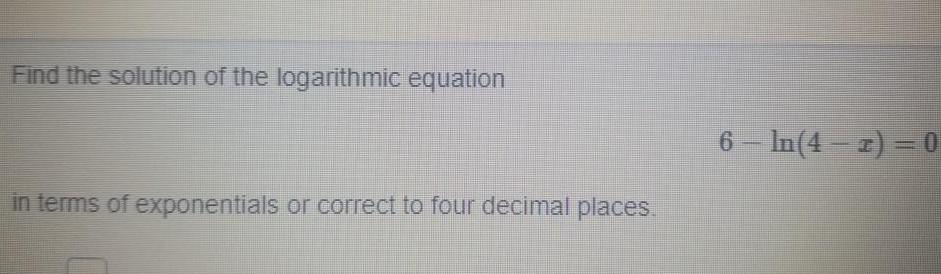
Application of derivativesFind the solution of the logarithmic equation in terms of exponentials or correct to four decimal places 6 In 4 2 0
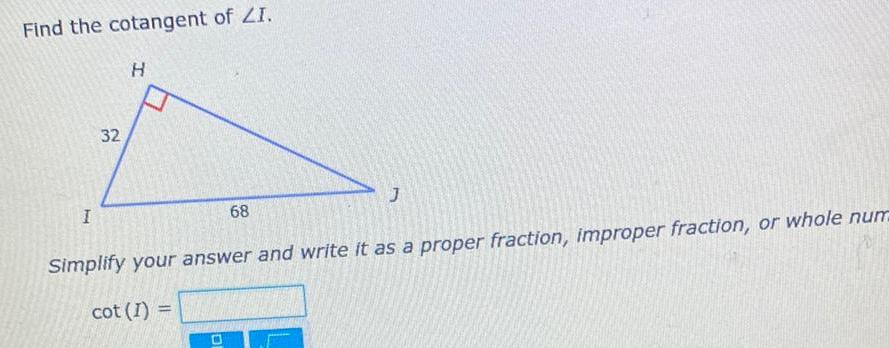
Calculus
Application of derivativesFind the cotangent of ZI I 32 H 68 Simplify your answer and write it as a proper fraction improper fraction or whole num cot 1 0 J

Calculus
Application of derivativesoblem 3 Consider the following equations In each case suppose that we apply the Intermediate Value Theorem using the interval 0 1 i e we take a 0 b 1 in the Intermediate Value Theorem x x 1 0 ii 2e x 4 iii ln x 1 1 2x For which equations does the Intermediate Value Theorem conclude that there must be a root of the equation in the interval 0 1 A i and iii B ii and iii C none of them D iii only E i only F ii only G all of them H i and ii

Calculus
Application of derivativesLet h a 5 x and let f be the inverse function of h Notice that h 1 7 f 7
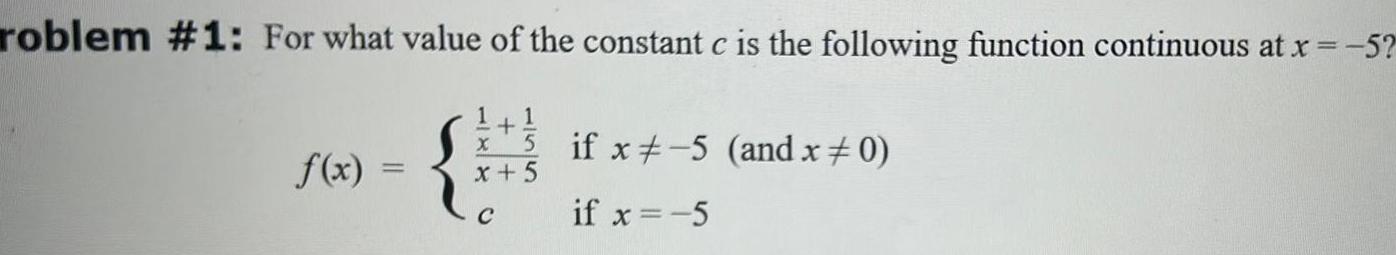
Calculus
Application of derivativesroblem 1 For what value of the constant c is the following function continuous at x 5 f x 1 5 if x 5 and x 0 if x 5 x 5 C
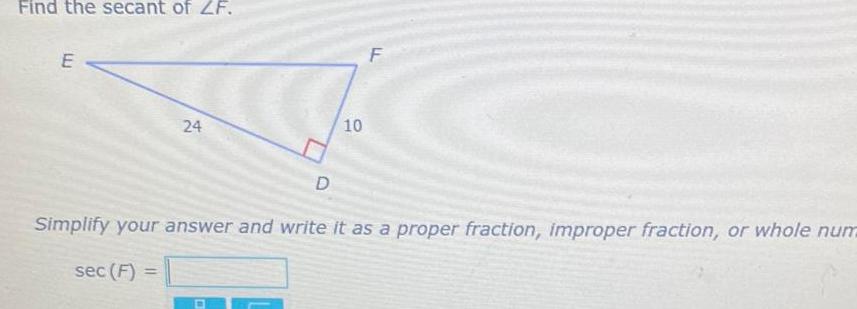
Calculus
Application of derivativesFind the secant of ZF E 24 D 10 F Simplify your answer and write it as a proper fraction improper fraction or whole num sec F

Calculus
Application of derivativesStep 2 The second integration by parts Step 1 has shown that Jeta s sin 5x dx The integral on the right is not much different than the one you started with Let s try using integration by parts again on the integral on the right u el cos 52 e cos 52 dr 4z 5 Fill in the table below with the appropriate terms for setting up the integration by parts for the integral du e cos 5x da dx V dv dx Now substitute all of this into the Integration by Parts formula giving e cos 5x dx 0 0 da


Calculus
Application of derivativesAll fractions are to be written in lowest terms NO DECIMAL NUMBERS ALLOWED Answers need to be submitted as ONE file 1 Expand and Simplify the following a 3x x 6 5x 2x 4 3x 18x10x 20 1 4x 2x 6 Marks b 3xy 5x 2y 1 2xy 3y 2 7x 15x y Gxyt 3xy Gry axy 14x y x y 12vy 7xy

Calculus
Application of derivatives2 Solve the following equations a 9x 13 103 9x 103 15 9x 90 X 10 3 11 16A 32 29 15n 3 25 07 14 31 12 multiply borth vides by 12
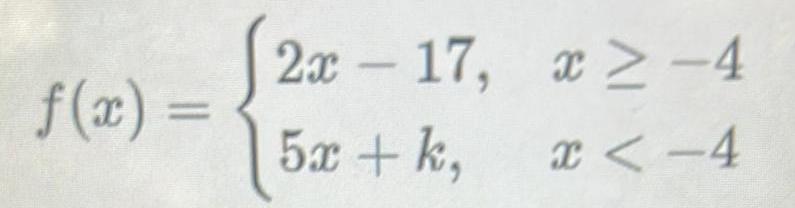

Calculus
Application of derivativesHence f x is continuous on R Institute of Lifelong Learning University of Delhi I Q 2 I Q 3 Theorem 1 Statement Only A function f X R is said to be continuous at a point X EX if and only if for given any E neighborhood V f x of f x there exist a 8 neighborhood V x of xo such that if x is any point of XV x then f x belongs to V f x is f xV x V f x Continuity of Functions 5 Discontinuity of a Function at a Point Let X be a non empty subset of R let f X R and let X Then the function f x is said to be discontinuous at if and only if it is not continuous at 5 1 Types of Discontinuity Let f be a function defined as f X R and let x eX and let left hand limit right hand limit limit of the function and the value of the function at xare denoted by lim f x lim f x lim f x and f x 195 respectively Then I Removable Discontinuity at x let at s The function f X R is said to have the removable discontinuity at X EX if the limit of the function exist at x but not equal to the value of the function at x i e lim f x f x X pg 8 efa II Discontinuity of the First Kind at x The function f X R is said to have a discontinuity of first kind at x if both the left hand limit and right hand limit exist at x but are not equal to each other i e lim f x lim f x 294 Institute of Lifelong Learning University of Delhi Continuity of Functions III Discontinuity of the First Kind from the left pg 9 9