Application of derivatives Questions and Answers

Calculus
Application of derivativesIf F x f xf xf x where f 1 3 f 3 6 f 1 4 f 3 5 and f 6 6 Find F F 1



Calculus
Application of derivativesAlgebraically find the inverse function of f x 6 5e Graph f f and the line y x on the same screen and check whether the graphs of f and fare reflections about the li

Calculus
Application of derivatives1 0 101 and find the equation of the tangent line in slope intercept form to f z at a nice point near 0 101 1 0 101 Use linear approximation i e the tangent line to approximate Let f z Then use this to approximate 1 as follows

Calculus
Application of derivatives1 5 20 A4 1 Place each of the following numbers in the most appropriate box above 510 28 20 08 3 6 12 2 Check each box that is correct to classify the number given Natural Whole Integers 1 20 7 35 Natural Numbers 3 A 44 H B Rational V Irrational Real 3 Place each on a number line Label it with the capital letter DRAW A NUMBER LINE A 67 5 c 13 D 5 E 75 411 10 9 8 7 6 5 3 2 1 0 4 Place each on a number line Label with the capital letter DRAW A NUMBER LINE 4 B 64 c 21 12 C D 3 6 E 23 E 2 3 4 56 1 7 8 1111 11 10 9 8 7 6 54 3 2 1 0 1 2 3 4 5 6 9 10 7 8 9 10
Calculus
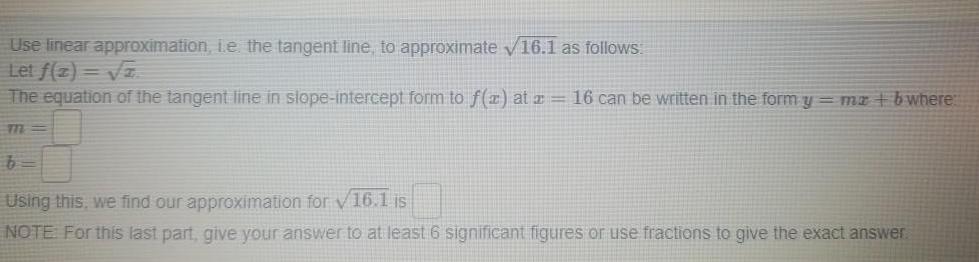
Application of derivativesUse linear approximation i e the tangent line to approximate 16 1 as follows Let f 2 2 The equation of the tangent line in slope intercept form to f x at 16 can be written in the form y mx bwhere m b Using this we find our approximation for 16 1 is NOTE For this last part give your answer to at least 6 significant figures or use fractions to give the exact answer

Calculus
Application of derivativesIndicate the answer choice that best completes the statement or answers the question Which function is an odd function Oa f x 2x b f x x 4 Oc f x x 9 Od f x x 4x

Calculus
Application of derivatives1 Suppose that the height of a skydiver t seconds after jumping from an airplane is given by s t 4500 20t 16t2 feet neglecting air resistance The skydiver pulls the ripcord after 10 seconds of free fall to deploy the parachute after he has fallen Write a velocity function for the skydiver t How fast is the skydiver falling the instant before he pulls the ripcord ft sec miles per hour Calculate the skydiver s average velocity over the time interval from 5 seconds to 10 seconds What is the skydiver s acceleration function 2 A car moves along the x axis so that at any time t t 0 the position is given by s t 4t 18t 15t 1 Write a velocity function for the car Write an acceleration function for the car What is the velocity of the car at t 2 What is the velocity of the car at t 4 What is the average velocity of the car on the time interval from 4 to 6 When is the car at rest circle

Calculus
Application of derivativesHelium is pumped into a spherical balloon at a rate of 3 cubic feet per second How fast is the radius increasing after 2 minutes Note The volume of a sphere is given by V 4 3 TT Rate of change of radius in feet per second

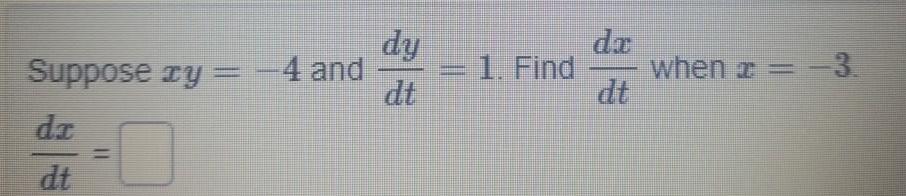
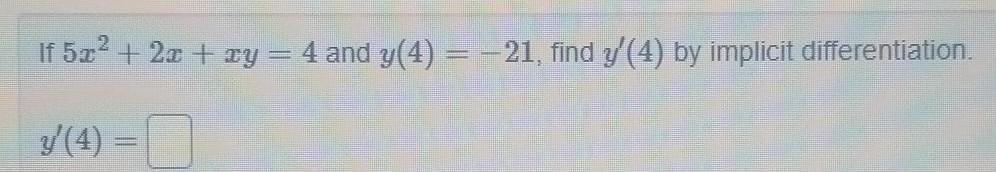
Calculus
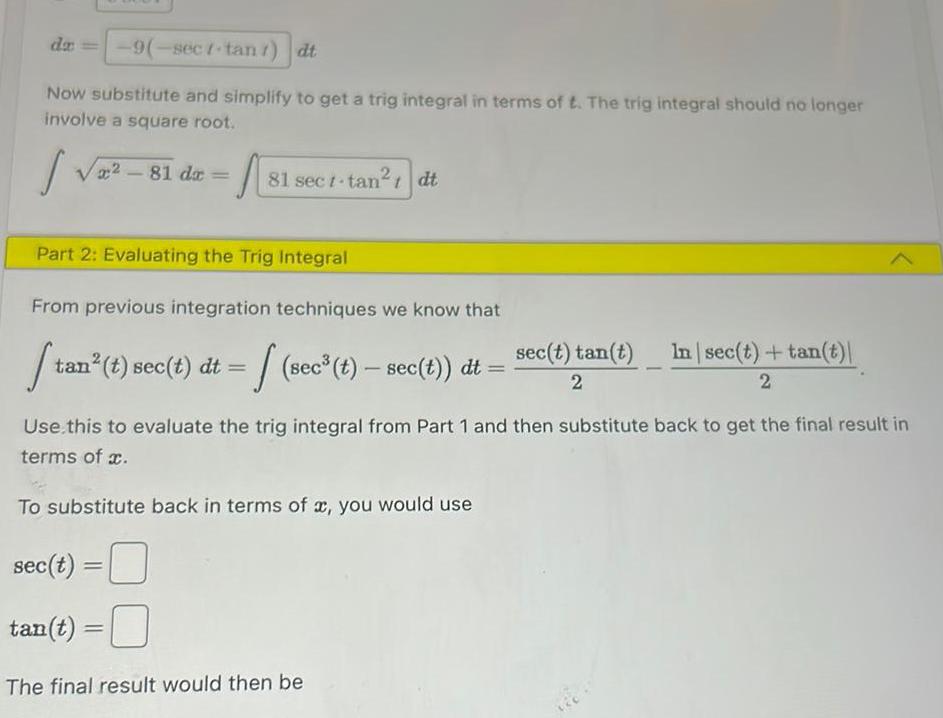
Application of derivativesda 9 sect tan dt Now substitute and simplify to get a trig integral in terms of t The trig integral should no longer involve a square root 81 da A 81 sect tan dt t Part 2 Evaluating the Trig Integral From previous integration techniques we know that St tan t sec t dt sec t sec t dt sec t tan t 2 The final result would then be In sec t tan t 2 Use this to evaluate the trig integral from Part 1 and then substitute back to get the final result in terms of x To substitute back in terms of x you would use sec t tan t

Calculus
Application of derivatives1 Assume that f x is a function on the interval 0 1 that has a Fourier sine series on 0 given by 00 give the value of ba 1 12 f x sin nx 71 1 Use a Fourier sine series to find a solution to This solution will have the form 3v x f x 0 x n v 0 v n 0 v x b sin nx n 1
Calculus
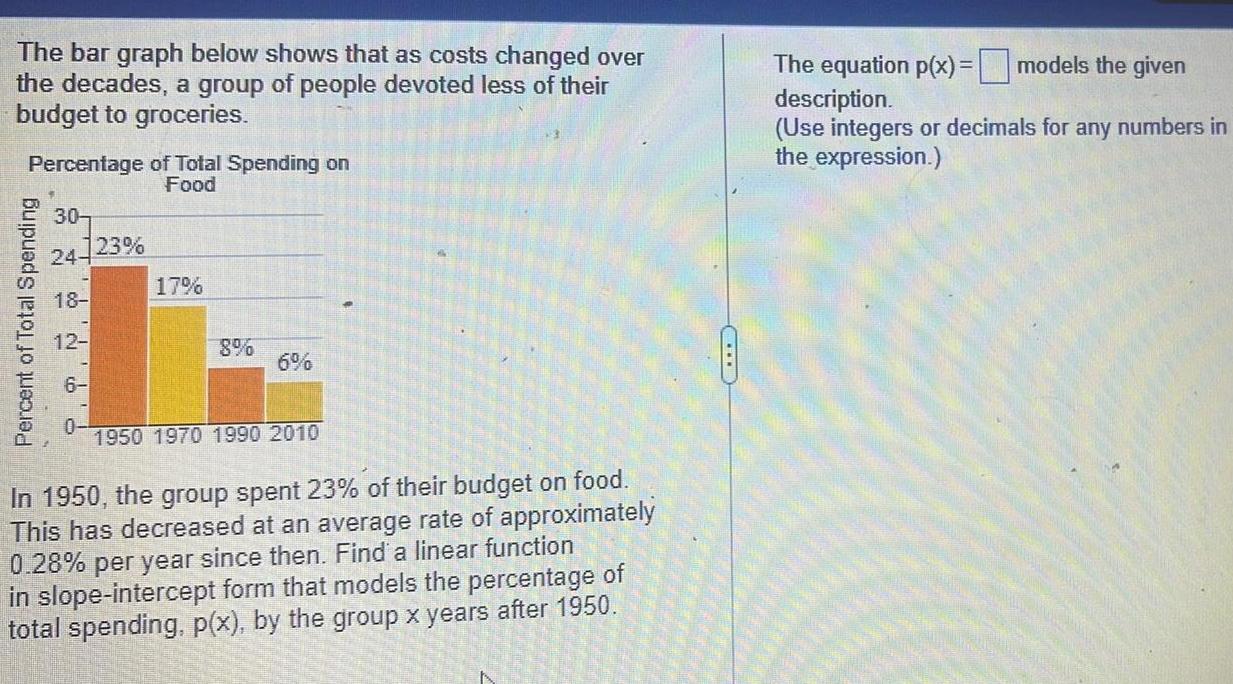
Application of derivativesThe bar graph below shows that as costs changed over the decades a group of people devoted less of their budget to groceries Percentage of Total Spending on Food Percent of Total Spending 30 24 18 12 6 23 17 8 6 1950 1970 1990 2010 In 1950 the group spent 23 of their budget on food This has decreased at an average rate of approximately 0 28 per year since then Find a linear function in slope intercept form that models the percentage of total spending p x by the group x years after 1950 The equation p x models the given description Use integers or decimals for any numbers in the expression
Calculus
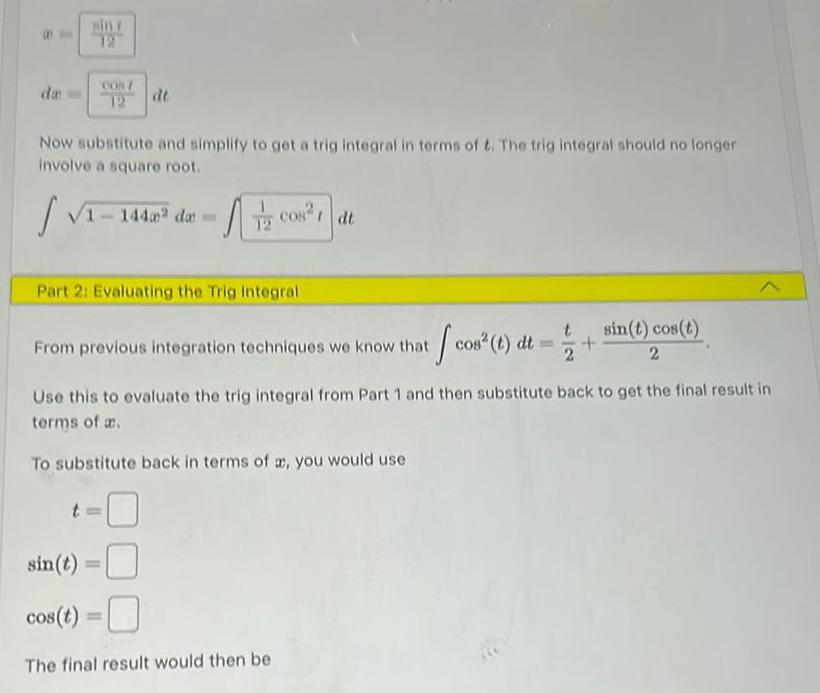
Application of derivativesda sin z 12 COS 12 Now substitute and simplify to get a trig integral in terms of t The trig integral should no longer involve a square root Tz cos 1 dt 1 14 dt 1 144m da Part 2 Evaluating the Trig Integral From previous integration techniques we know that cos t dt Use this to evaluate the trig integral from Part 1 and then substitute back to get the final result in terms of a To substitute back in terms of a you would use sin t cos t The final result would then be sin t cos t 2

Calculus
Application of derivatives2 Evaluate each limit Use algebraic methods if possible If not use graphs or tables x 7x 12 x 9 2K 4K a limx 31 X 8 b limx 8 2

Calculus
Application of derivativesa Are the events A and C independent Justify your answer b Are the events A and D independent Justify your answer c Compute 1 P AB and P AB Are they equal d Compute 1 P AB and P AB Are they equal 26 A large corporation has spent considerable time developing employee performance g scales to evaluate an employee s job performance on a regular basis so major adjustments e made when needed and employees who should be considered for a fast track can be isolat eys to this latter determination are ratings on the ability of an employee to perform to his or pabilities and on his or her formal training for the job


Calculus
Application of derivativesWhich inequality has a solution set of 5 00 0 1 4 0 1 4 0 1 4 02 124
Calculus
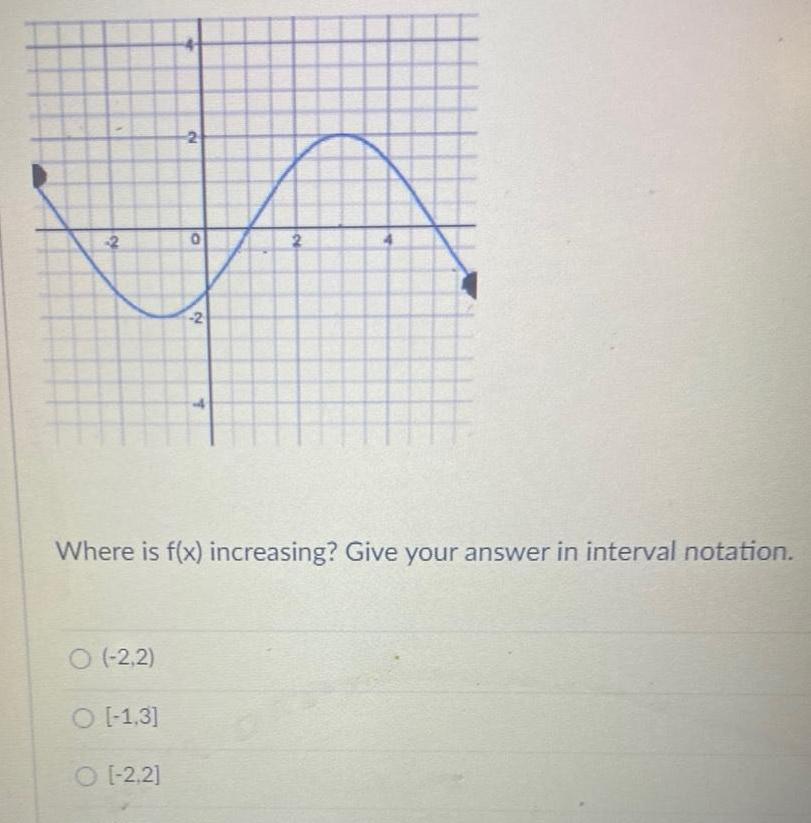
Application of derivatives2 O 2 2 O 1 3 O 2 2 0 2 T Where is f x increasing Give your answer in interval notation

Calculus
Application of derivativesWhich function has an x intercept of 12 and a y intercept of 3 Oy 4x 3 Oy 3x 12 O y 12x 3 Oy z 3


Calculus
Application of derivativesThe goal of this problem is to evaluate sin cos da using substitution 1 Because the cosine term has an odd power the first step is to rewrite cos5 x cos x cos x cos x cos x where n 0 2 Next replace the cos x term with 3 Now do a substitution with u and du dx 4 With this substitution the integral after multiplying out into a sum of powers of u becomes Odu Do not put a negative sign in front of the integral 5 Now antidifferentiate in terms of u and substitute back to get the final result siz C sin x cos5 x dx
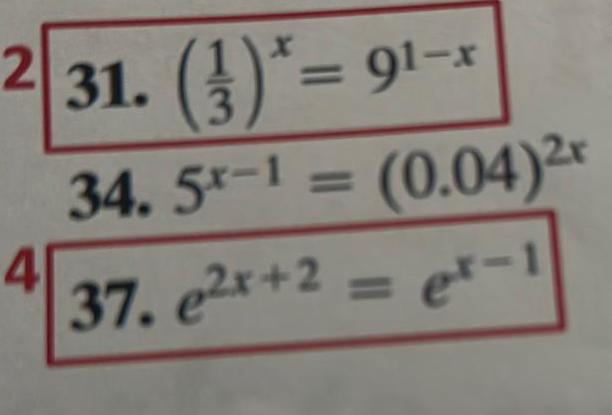

Calculus
Application of derivativesSolve for a in the given matrix equation 1 2 3 det 1 x 1 26 2 3 4 Choose the correct answer a x 2 Ob z O c C x 1 Od 2 13 e None of the options

Calculus
Application of derivatives1 Place the phases of the business cycle in order Recession Trough Peak Expansion How long do each business cycle last
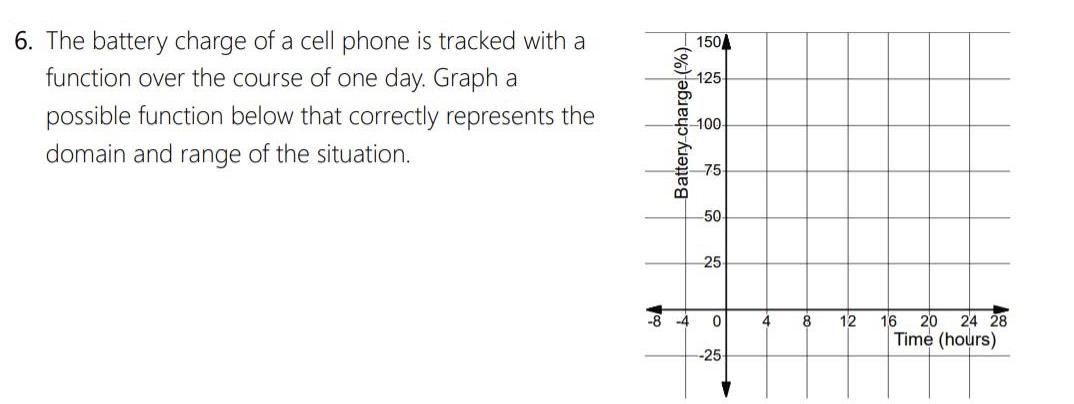
Calculus
Application of derivatives6 The battery charge of a cell phone is tracked with a function over the course of one day Graph a possible function below that correctly represents the domain and range of the situation Battery charge 150 125 100 75 50 25 8 4 0 25 4 8 12 16 20 24 28 Time hours

Calculus
Application of derivatives9 Which of the following functions has a domain given by x Rx 4 A f x x 4 B g x x 16 C h x 9 x D j x 2 3x 12
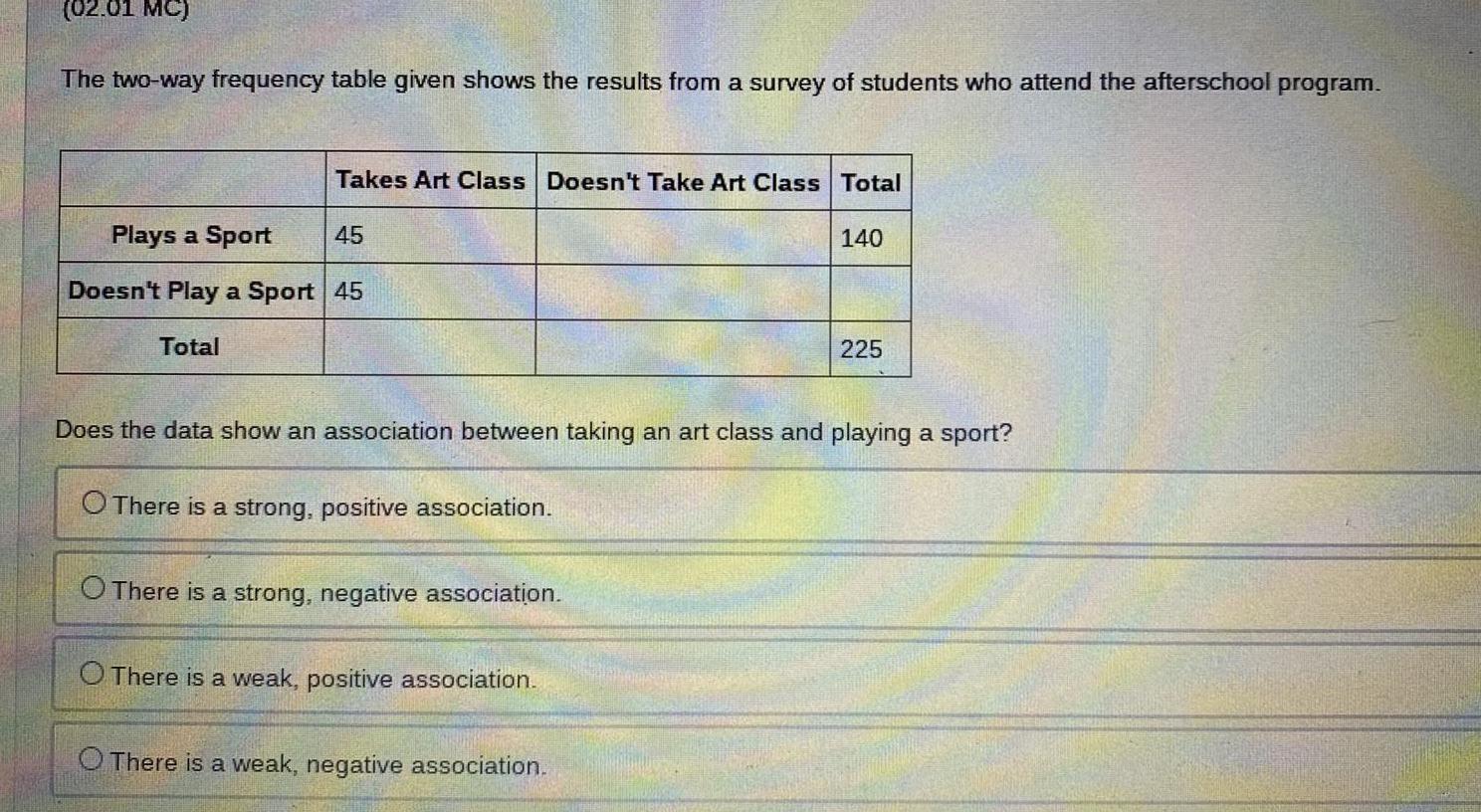
Calculus
Application of derivatives02 01 MC The two way frequency table given shows the results from a survey of students who attend the afterschool program Takes Art Class Doesn t Take Art Class Total 140 Plays a Sport Doesn t Play a Sport 45 Total 45 Does the data show an association between taking an art class and playing a sport O There is a strong positive association O There is a strong negative association O There is a weak positive association 225 O There is a weak negative association
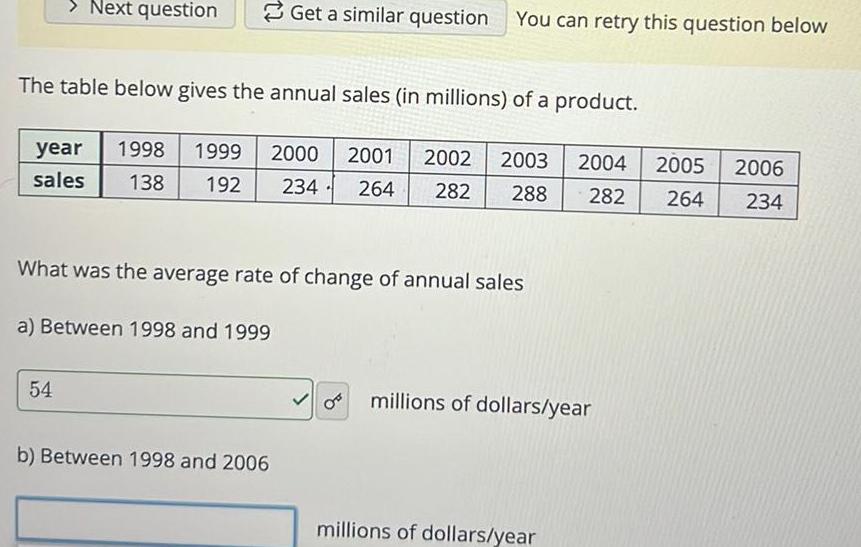
Calculus
Application of derivativesNext question The table below gives the annual sales in millions of a product year 1998 1999 2000 2001 2002 2003 2004 sales 138 192 234 264 282 288 282 What was the average rate of change of annual sales a Between 1998 and 1999 54 Get a similar question You can retry this question below b Between 1998 and 2006 millions of dollars year millions of dollars year 2005 2006 264 234
Calculus
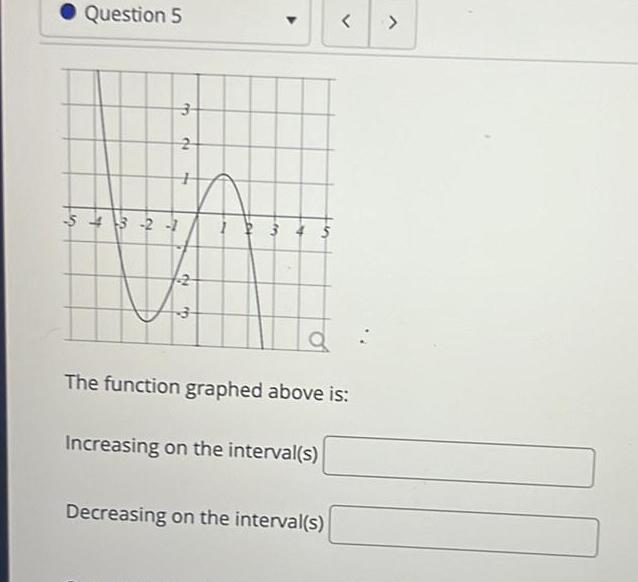
Application of derivativesir Question 5 3 2 1 3 2 My 2 3 2 3 4 S Increasing on the interval s a The function graphed above is Decreasing on the interval s

Calculus
Application of derivativesA db Fig 1 1 In this graph the points a and b are adjacent whereas b and c are non adjacent 2 Let V 1 2 3 4 and X 1 2 1 3 1 4 2 3 2 4 3 4 G V X is a 4 6 graph This graph is represented by the diagram as shown in Fig 1 2 Fig 1 2 In this graph the lines 1 3 and 2 4 intersect in the diagram and their intersection is not a point of the graph Fig 1 3 is another diagram for the graph given in Fig 1 2 Fig 1 3 3 The 10 15 graph given in Fig 1 4 is called a Petersen graph

Calculus
Application of derivativesWhich of the following functions has a domain given by x ER x 4 A f x x 4 B g x x 16 C h x 9 x 2 D j x 3x 12
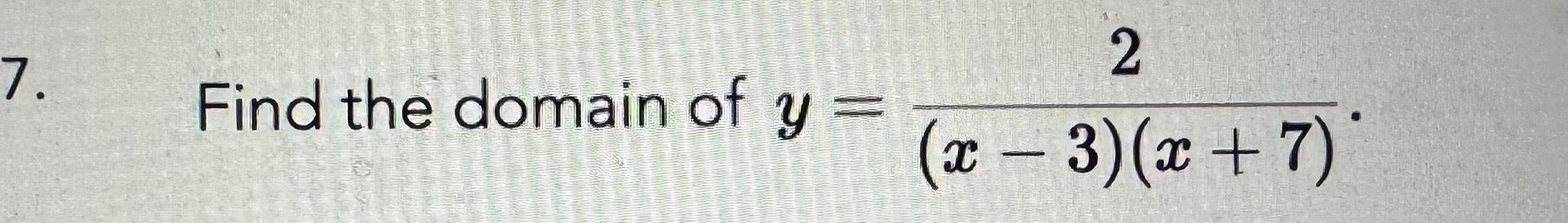

Calculus
Application of derivatives19 24 Explain using Theorems 4 5 6 and 8 why the fun tion is continuous at every number in its domain State the domain no 19 F x 4 THEOREM If f and g are continuous at a and c is a constant then the following functions are also continuous at a 1 f g 2 f g f 4 fg g 2x x 1 x 1 5 c h x x if g a 0 5 THEOREM a Any polynomial is continuous everywhere that is it is continuous on R 0 0 b Any rational function is continuous wherever it is defined that is it is continuous on its domain EXAMPLE 6 On what intervals is each function continuous a f x x100 2x 7 75 x 1 x 1 3 cf b g x TAM OF x 1 x 1 User p x 2x 17 x 1 8 THEOREM If g is continuous at a and f is continuous at g a then the composite function fo q given by fog x f g x is continuous at a
Calculus
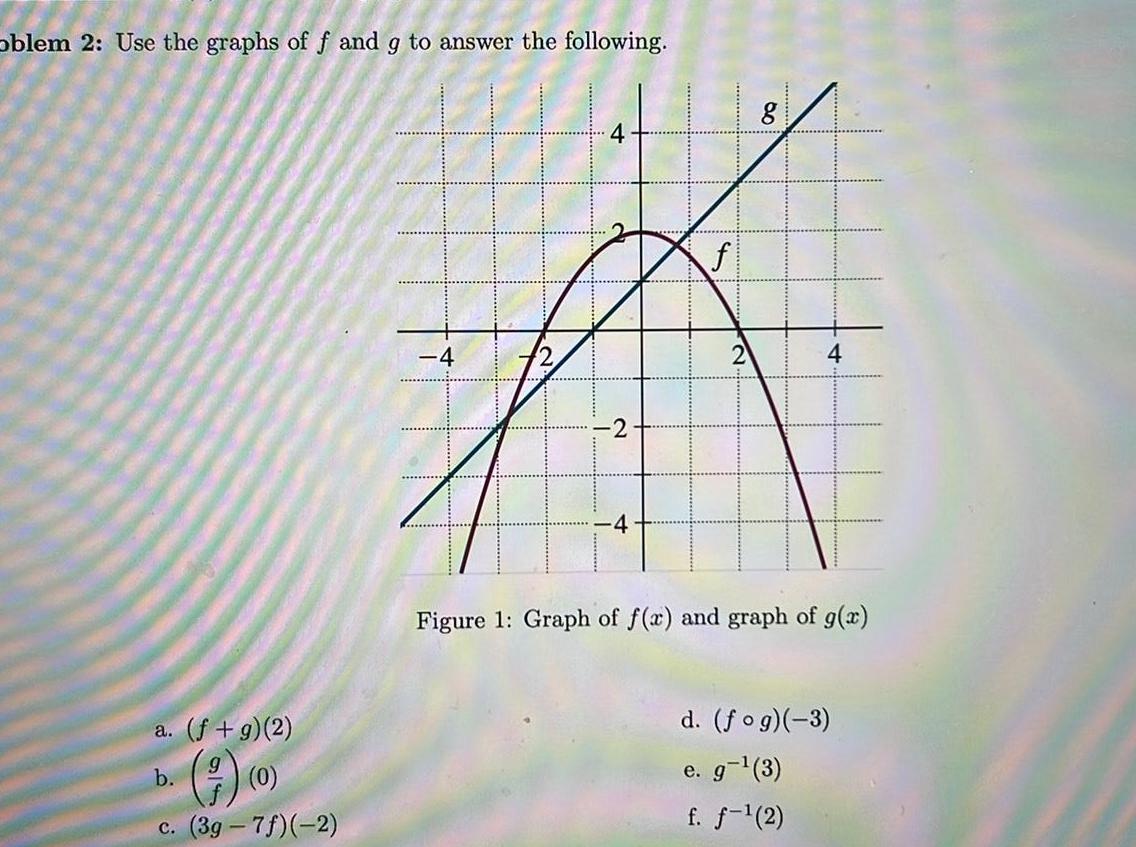
Application of derivativesoblem 2 Use the graphs of f and g to answer the following a f g 2 b c 3g 7f 2 4 4 2 4 f 8 4 Figure 1 Graph of f x and graph of g x d fog 3 e g 3 f f 2
Calculus
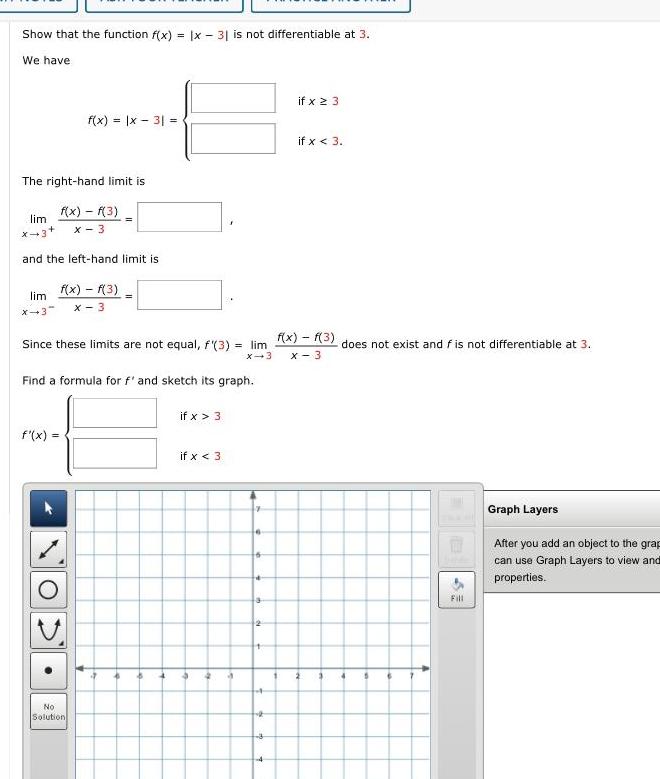
Application of derivativesShow that the function f x x 31 is not differentiable at 3 We have The right hand limit is f x f 3 x 3 lim X 3 f x x 3 and the left hand limit is lim f x f 3 X 3 X 3 Find a formula for f and sketch its graph f x Since these limits are not equal f 3 lim f x f 3 does not exist and f is not differentiable at 3 X 3 x 3 No Solution 2 if x 3 if x 3 4 4 a 6 2 a 3 if x 23 if x 3 2 3 4 Fill Graph Layers After you add an object to the grap can use Graph Layers to view and properties
Calculus
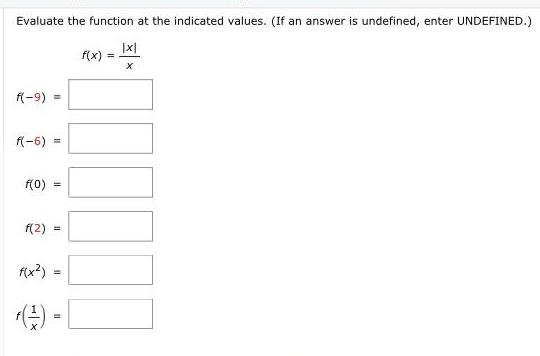
Application of derivativesEvaluate the function at the indicated values If an answer is undefined enter UNDEFINED x X f 9 f 5 f 0 f 2 f x f f x
Calculus
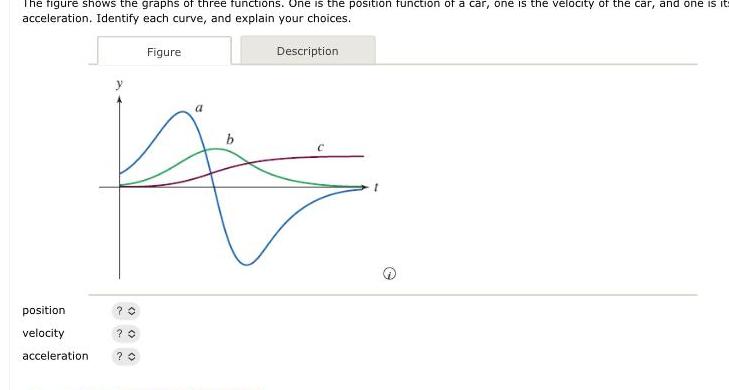
Application of derivativesThe figure shows the graphs of three functions One is the position function of a car one is the velocity of the car and one is it acceleration Identify each curve and explain your choices position velocity acceleration Figure 20 0 0 Description b A
Calculus
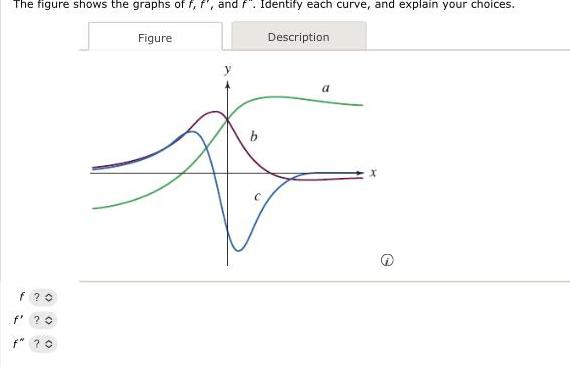
Application of derivativesThe figure shows the graphs of f f and f Identify each curve and explain your choices f 0 H f O f 70 Figure b Description a
Calculus
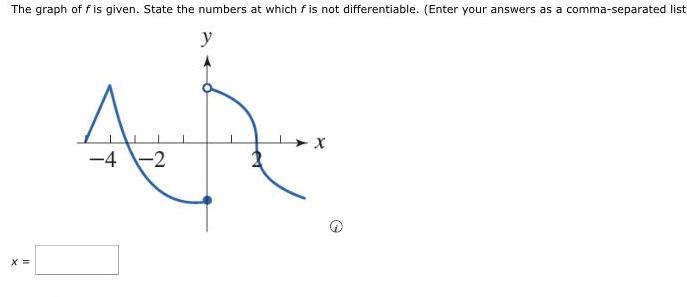
Application of derivativesThe graph of fis given State the numbers at which f is not differentiable Enter your answers as a comma separated list y X 4 2
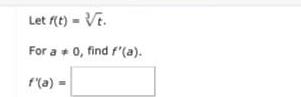

Calculus
Application of derivativesProblem 9 Consider the following matrices Problem 9 a Problem 9 b 4 033 13 15 10 B 1 4 2 4 2 3 a Let D BTC Find d21 i e find the entry in row 2 column 1 of the matrix D b Find tr 2BB c Let E B CA Find e32 i e find the entry in row 3 column 2 of the matrix E

Calculus
Application of derivativesK The velocity of a parachutist during free fall is f t 82 1 e 0 12t meters per second Answer the following questions using the graph Recall that acceleration is the derivative of velocity b What is the approximate acceleration when t 0 10 m sec2 c Approximately when is the parachutist s velocity 51 m sec 8 seconds d Approximately when is the acceleration 5 m sec CHE Ay 80 70 60 50 40 30 20 10 0 0 10 20 30 S
Calculus
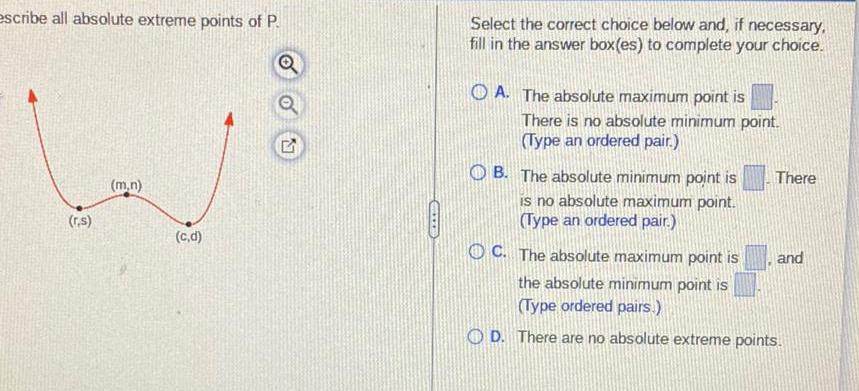
Application of derivativesescribe all absolute extreme points of P r s m n c d GALER Select the correct choice below and if necessary fill in the answer box es to complete your choice OA The absolute maximum point is There is no absolute minimum point Type an ordered pair B The absolute minimum point is is no absolute maximum point Type an ordered pair There OC The absolute maximum point is the absolute minimum point is Type ordered pairs OD There are no absolute extreme points and
Calculus
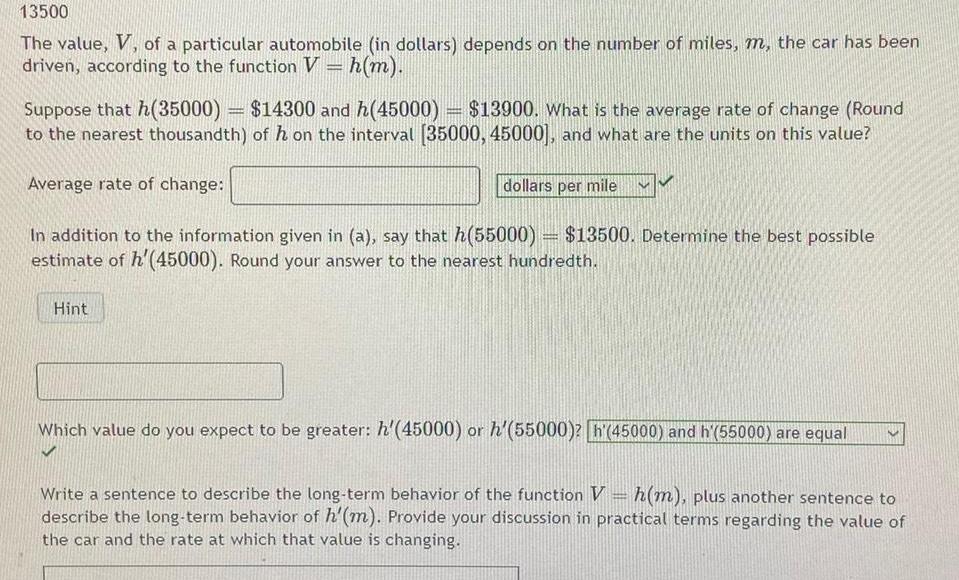
Application of derivatives13500 The value V of a particular automobile in dollars depends on the number of miles m the car has been driven according to the function V h m Suppose that h 35000 14300 and h 45000 13900 What is the average rate of change Round to the nearest thousandth of h on the interval 35000 45000 and what are the units on this value Average rate of change dollars per mile In addition to the information given in a say that h 55000 13500 Determine the best possible estimate of h 45000 Round your answer to the nearest hundredth Hint Which value do you expect to be greater h 45000 or h 55000 h 45000 and h 55000 are equal Write a sentence to describe the long term behavior of the function V h m plus another sentence to describe the long term behavior of h m Provide your discussion in practical terms regarding the value of the car and the rate at which that value is changing

Calculus
Application of derivativesK Find the poor of the rectangle Express the perimeter using the same unit of measure that appear on the green sis The part of the rectangle is